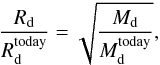| Issue |
A&A
Volume 532, August 2011
|
|
|---|---|---|
| Article Number | A118 | |
| Number of page(s) | 25 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201015021 | |
| Published online | 03 August 2011 | |
Online material
Appendix A: Scaling of the galaxy models
A.1. Assumptions
The model is based on several assumptions used to determine the main structural properties of the disc galaxy model by scaling current MW parameters to a smaller disc mass. A constant and time-independent proportionality between luminosity and mass is assumed, to allow to treat surface brightness and surface density similarly. This allows to apply the Tully-Fisher relation (Tully & Fisher 1977) to scale the circular velocities. Thus, also the validity of the Tully-Fisher relation independent of age or redshift and size of the disc galaxy is assumed, which seems to be acceptable, at least to a redshift z ≈ 1, following Vogt et al. (1997). Mao et al. (1998) have found no strong indications for a change in the relation, too. The gaseous galaxy-component is ignored, assuming a progenitor galaxy described by a pure exponential disc embedded in a spherical Hernquist dark-matter halo, which is used to model the empirically found flat rotation curves in disc galaxies and constitutes, in a non-Newtonian framework, the zeroth-order approximation to non-Newtonian dynamics.
A.2. Determination of parameters
To determine the parameters of the model, the stellar mass of the bulge component of the MW as seen today is taken as a starting point. Values range from 1.6 × 1010 M⊙ (Minniti & Zoccali 2008) to 1.8 × 1010 M⊙ (calculated using values from Binney & Tremaine 1987) or might be as low as 1.3 × 1010 M⊙ (Gerhard 2002). Based on the presupposition that a merger of two identical galaxies created the bulk of the bulge component, the mass of the model galaxy has to be about half of today’s bulge mass. Some mass loss might occur due to matter transported outwards along tidal arms. This leads to a stellar mass of Md = 8.0 × 109 M⊙ for the initial small disc galaxies in the case of the equal mass encounters. For the 4-to-1 mass ratio interactions, disc masses of 4.0 × 109 M⊙ and Md = 1.6 × 1010 M⊙ are adopted. After formation of the bulge the early Milky Way would still have accreted matter in a disc, forming today’s disc component within about 1010 years when accreting ~ 5 M⊙ yr-1. The dark matter halo component is chosen to be ten times more massive than the early disc.
Furthermore, the following common values are adopted as those of today’s MW and applied as starting points for the down-scaling: the disc scale length is chosen to be 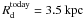 . Observations reveal similar values like 3.3 kpc from star counts from 2MASS performed by López-Corredoira et al. (2002), but lower values, like 2.1 kpc (Gerhard 2002), have been reported, too. The larger value is chosen here because the thick disc seems to have a larger scale length (3.7 kpc according to Ojha 2001) and, as it is composed of older stars, should trace the original mass distribution better. It is assumed that the mass of the MW disc is
. Observations reveal similar values like 3.3 kpc from star counts from 2MASS performed by López-Corredoira et al. (2002), but lower values, like 2.1 kpc (Gerhard 2002), have been reported, too. The larger value is chosen here because the thick disc seems to have a larger scale length (3.7 kpc according to Ojha 2001) and, as it is composed of older stars, should trace the original mass distribution better. It is assumed that the mass of the MW disc is 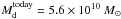 . Gerhard (2002) gives a value for the mass enclosed within 8 kpc of 5.5 × 1010 M⊙ including the bulge. Also, the International Astronomical Union (IAU) standard (Kerr & Lynden-Bell 1986) for the circular velocity near the Sun
. Gerhard (2002) gives a value for the mass enclosed within 8 kpc of 5.5 × 1010 M⊙ including the bulge. Also, the International Astronomical Union (IAU) standard (Kerr & Lynden-Bell 1986) for the circular velocity near the Sun 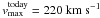 and the Galactocentric distance of the Sun
and the Galactocentric distance of the Sun 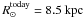 is adopted. The adopted parameters are compiled in Table A.1.
is adopted. The adopted parameters are compiled in Table A.1.
Assumed MW parameters.
A.3. Estimating the size of the young MW
The most important parameters to determine for an exponential disc are the scale length and the rotation curve. Furthermore the disc should be stable, even though small galaxies are often observed to be irregular (e.g. the LMC).
The circular velocity vrot(R) at a radius R around a mass distribution characterised by an enclosed mass of M( < R) is given by 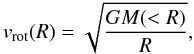 (A.1)where G is the gravitational constant. Using a two-component galaxy, the rotation curve is a result of the interplay between the disc- and the halo-mass-distribution, the respective circular velocities being added in quadrature (Hernquist 1993).
(A.1)where G is the gravitational constant. Using a two-component galaxy, the rotation curve is a result of the interplay between the disc- and the halo-mass-distribution, the respective circular velocities being added in quadrature (Hernquist 1993).
As a first estimate for the disc scale length, the central surface brightness is demanded to be constant for all galaxies and independent of the Hubble parameter (van der Kruit 1987, see also Binney & Tremaine 1987). With the previously mentioned assumption of a proportionality between luminosity and mass, this translates into a constant central surface density Σ0. Naab & Ostriker (2006) applied the same assumption of a constant central surface density when studying the evolution of the MW. For the central surface brightness the following equation holds in the case of a thin exponential disc with a total mass Md and a scale length Rd, 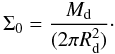 (A.2)This leads to the scaling relation
(A.2)This leads to the scaling relation
Another possibility to scale Rd avoids inclusion of the MW disc mass but starts from the disc surface density 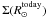 in the Solar neighbourhood. Assuming an exponential disc, the central MW surface density Σ0 is calculated via
in the Solar neighbourhood. Assuming an exponential disc, the central MW surface density Σ0 is calculated via
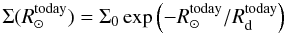 and then Eq. (A.2) is solved for the scale length, yielding Rd = 1.5 kpc when accepting a value of
and then Eq. (A.2) is solved for the scale length, yielding Rd = 1.5 kpc when accepting a value of 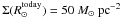 as indicated from observations (see Naab & Ostriker 2006, and references therein).
as indicated from observations (see Naab & Ostriker 2006, and references therein).
An estimate completely independent of today’s MW properties can be derived from typical properties of galaxies. Binney & Tremaine (1987) stated that the typical disc scale length for galaxies scales with Rd = 3/h kpc, where h is the dimensionless Hubble-parameter defined by H0 ≡ 100 h km s-1 Mpc-1. Assuming a closed universe with currently H0 = 71 km s-1 Mpc-1, mass-density parameter ΩM = 0.27 from Spergel et al. (2003) and vacuum density Ωvac = 0.73, the time about 10 Gyr ago corresponds to a redshift of z ≈ 2. The Hubble parameter at that redshift is given by
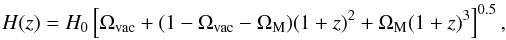 and was approximately H(z = 2) ≈ 200 km s-1 Mpc-1 at that time, so h(z = 2) ≈ 2.0. This again leads to Rd = 1.5 kpc which is in good agreement with the first two estimates. Finally, a slightly larger scale length of 1.6 kpc is choosen for the model, because a bigger value increases the stability of the disc. This is because more halo mass (in relation to disc mass), with particles of random motions, is inside the disc’s volume. The disc is truncated at 5 times this scale length, close to the frequently used value of 4.5 times (van der Kruit 1987). Note that the disc of a gas component today is understood to be more extended than the stellar disc.
and was approximately H(z = 2) ≈ 200 km s-1 Mpc-1 at that time, so h(z = 2) ≈ 2.0. This again leads to Rd = 1.5 kpc which is in good agreement with the first two estimates. Finally, a slightly larger scale length of 1.6 kpc is choosen for the model, because a bigger value increases the stability of the disc. This is because more halo mass (in relation to disc mass), with particles of random motions, is inside the disc’s volume. The disc is truncated at 5 times this scale length, close to the frequently used value of 4.5 times (van der Kruit 1987). Note that the disc of a gas component today is understood to be more extended than the stellar disc.
The rotation curve is demanded to be flat and the maximum velocity is estimated by applying the Tully-Fisher relation. The maximum rotational velocity to adjust the density profiles to is thus scaled using the mass ratio of today’s and the model galaxy’s disc mass. This leads to:
 depending on the slope of the Tully-Fisher relation. An intermediate value is adopted, aiming at a rotation velocity of
depending on the slope of the Tully-Fisher relation. An intermediate value is adopted, aiming at a rotation velocity of 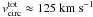 .
.
As the primary objective is to set up the disc component, whose mass-distribution is already fixed with the scale length, the rotation curve is adjusted with the dark matter halo. The halo properties are thus determined by demanding it to give that circular velocity.
For the disc, the rotational velocity 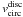 at the cut-off radius can be estimated using Eq. (A.1), inserting the total disc mass Md and the maximum disc radius
at the cut-off radius can be estimated using Eq. (A.1), inserting the total disc mass Md and the maximum disc radius 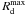 . Having
. Having 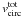 and
and 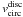 ,
, 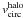 is easily calculated making use of the fact that circular velocities add in quadrature. This results in
is easily calculated making use of the fact that circular velocities add in quadrature. This results in 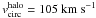 .
.
In a Hernquist dark-matter halo profile (Hernquist 1990), the density ρh at a radial distance R is given by
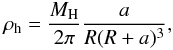 with the core radius a and the total halo mass MH. The mass inside a radius R is
with the core radius a and the total halo mass MH. The mass inside a radius R is 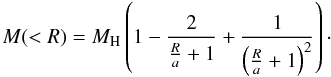 (A.3)Again making use of Eq. (A.1), the mass within
(A.3)Again making use of Eq. (A.1), the mass within 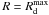 , the maximum disc particle radius, is determined. With the use of Eq. (A.3) the halo core radius can be estimated.
, the maximum disc particle radius, is determined. With the use of Eq. (A.3) the halo core radius can be estimated.
The model’s halo needs to have 1.9 × 1010 M⊙ within a radius of 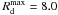 kpc. In the case of a finite Hernquist profile with maximum radius
kpc. In the case of a finite Hernquist profile with maximum radius 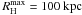 this results in a core radius of a = 10.0 kpc. After virialisation, the rotation curve of the disc component has a maximum at ≈ 122 km s-1.
this results in a core radius of a = 10.0 kpc. After virialisation, the rotation curve of the disc component has a maximum at ≈ 122 km s-1.
It should be emphasized that this “dark-matter” halo has not been constructed for consistency with the CDM hypothesis, but merely to model the actual gravitational behaviour of the empirical flat rotation curves of the young galaxy. What the true explanation for this gravitational behaviour might be is the topic of other studies (see e.g. Kroupa et al. 2010).
For a quicker reference, the model parameters are compiled in Table 1. Interestingly, the resulting values are quite similar to those found for M 33, which is a bulge-less galaxy, too (see for example Magrini et al. 2007), justifying the choice of parameters as physically reasonable.
Furthermore, several models with a mass ratio of 4:1 between the target and the infalling galaxy are calculated. Their parameters are determined in the same manner and can also be found in Table 1, while their results are discussed in Sect. 5.
A.4. Model setup
The model galaxy is created using the code MaGalie (Boily et al. 2001). It is based on a method by Hernquist (1993) to generate multi-component galaxies. The code is highly efficient for generating multi-component disc galaxies with many particles as the computational time scales only linearly with the particle number.
The disc components are set up with 5 × 105 particles, the halo components are made up of 106 particles. These numbers represent a compromise between resolution (demanding high particle numbers) and calculation time. They result in disc particle masses of 1.6 × 103 M⊙ for the equal-mass model or 0.8 × 103 M⊙ and 3.2 × 103 M⊙ for the infalling and target galaxy in the 4-to-1 mass ratio models.
As the integration code Superbox++ demands all particles in one galaxy to be of equal mass, the following standard work-around is used to allow the modelling of the stellar disc with a suitable number of particles without increasing the total particle number to an unfeasible value. The idea is to split up the galaxy into a disc and a halo component and to treat them as separate galaxies whose centres of mass have the same position. That way, the mass per halo particle can be higher, resulting in fewer halo particles and thus speeding up the computations. Furthermore, the splitting in two models allows to tailor the grid sizes to the respective components’ size and therefore gives a higher resolution to the important disc components. The total number of grids is doubled by this splitting, leading to an increase in computational time by about a factor two. But the reduced computation time through the smaller number of halo particles, scaling about linearly, outweights this.
The number of grid cells per dimension is 64. The gridsizes (radii) are 10, 30, and 400 kpc for the disc component galaxy model and 40, 120 and 400 kpc for the dark matter halo component. This gives grid cells with side lengths of 0.33, 1.0 and 13.33 kpc for the disc component and 1.33, 4.0 and 13.33 kpc for the halo component.
The newly set up model still suffers from minor numerical set-up mismatches because velocities and positions are stored as discrete values. Consequently the galaxy has to virialise to arrive at dynamical equilibrium. For this the model, consisting of disc and halo component, is calculated in isolation with Superbox++ for 3000 steps with a time-step size of 0.5 Myr, corresponding to about 7 orbiting times at a radius of 4 kpc. The galaxy is in dynamical equilibrium thereafter. The total energy error during virialisation is less than 0.2 per cent, the Lagrange-Radii expand slightly as the sharp edge at the maximum particle distance cut-off is smoothed out.
Appendix B: Tables of parameter scans
Equal-mass fly-by: particle numbers.
Equal-mass fly-by: properties of the two populations.
4-to-1-mass merger, retrograde infalling galaxy: properties of the two populations. Parameters defined as with Table B.2.
4-to-1-mass merger, prograde infalling galaxy: particle numbers. Parameters defined as with Table B.1.
4-to-1-mass merger, prograde infalling galaxy: properties of the two populations. Parameters defined as with Table B.2.
© ESO, 2011
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.