| Issue |
A&A
Volume 528, April 2011
|
|
|---|---|---|
| Article Number | A35 | |
| Number of page(s) | 18 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/200913941 | |
| Published online | 23 February 2011 | |
Online material
Appendix A: The rest-frame 8 μm, 15 μm, 25 μm and 35 μm LFs
We aim to derive the rest-frame 8 μm, 15 μm, 25 μm and 35 μm LF from our 24 μm sample. This is done here for several reasons. While the derivation of the rest-frame 8 μm LF has already been addressed in some previous studies (Caputi et al. 2007), our 24 μm sample reaches flux limits ~ 3 times fainter, providing improved constraints on the LF break. The rest-frame 15 μm LF provides continuity with what we have computed in Magnelli et al. (2009). The rest-frame 25 μm LF was not derived in Magnelli et al. (2009) but it does have several points of interest. First, it reduces the k-correction that one has to apply when observing infrared sources at zs2 using a 70 μm passband or at zs3 using a 100 μm passband. Hence, this rest-frame LF could be compared with future 70 μm and 100 μm observations made using the Photodetector Array Camera and Spectrometer (PACS) instrument onboard the Herschel satellite. Second, the rest-frame 25 μm LF offers a means to compare directly with IRAS 25 μm observations of galaxies in the local universe. Third, and perhaps most importantly, the rest-frame 25 μm luminosity has been shown to provide a reliable and fairly direct measurement of star formation in galaxies (e.g., Calzetti et al. 2007). Hence, one may want to use these measurements in the future to directly derive the SFR distribution function without using intermediate bolometric corrections. The rest frame 35 μm LF also provides continuity with quantities derived in Magnelli et al. (2009) and corresponds at zs2 to the observed 100 μm flux density. As a result, this rest-frame LF would be a standard comparison for the zs2 LF computed using PACS 100 μm observations.
The various rest-frame luminosities are derived using the same method as that used to compute 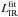 . For each 24 μm source we deduce its 70 μm flux density using the L24 μm/(1 + z) − L70 μm/(1 + z) correlation. Then we choose in the CE01 library the scaled template which best fits these 24 and 70 μm fluxes densities. Using this scaled template we then compute the rest-frame luminosities of this galaxy in our four passbands of interest (i.e., at 8 μm, 15 μm, 25 μm and 35 μm). The corresponding rest-frame LFs are computed using the 1/Vmax method. All the LF are then fitted using a double power law function with fixed slopes estimated using a bivariate method (see Table A.1).
. For each 24 μm source we deduce its 70 μm flux density using the L24 μm/(1 + z) − L70 μm/(1 + z) correlation. Then we choose in the CE01 library the scaled template which best fits these 24 and 70 μm fluxes densities. Using this scaled template we then compute the rest-frame luminosities of this galaxy in our four passbands of interest (i.e., at 8 μm, 15 μm, 25 μm and 35 μm). The corresponding rest-frame LFs are computed using the 1/Vmax method. All the LF are then fitted using a double power law function with fixed slopes estimated using a bivariate method (see Table A.1).
Figure A.1 presents the rest-frame 8 μm LF derived in our two redshift bins using the 1/Vmax method. These LF are compared with the local reference of Huang et al. (2007) and with the zs2 LF derived by Caputi et al. (2007). Our estimates agree well with those of Caputi et al. (2007), but extend to lower luminosities.
Figure A.2 presents the rest-frame 15 μm LF derived in our two redshift bins using the 1/Vmax method. Comparing to the local reference of Xu (2000) and with the zs0.55, zs0.85 and zs1.15 reference of Magnelli et al. (2009), we note the strong evolution of this LF with redshift.
Figure A.3 presents the rest-frame 25 μm LF derived in our two redshift bins using the 1/Vmax method as well as the local reference of Shupe et al. (1998).
Finally Fig. A.4 presents the rest-frame 35 μm LF derived in our two redshift bins using the 1/Vmax method as well as the local reference derived from Shupe et al. (1998), and the LFs derived in Magnelli et al. (2009) at zs0.55, zs0.85 and zs1.15.
 |
Fig. A.1
The rest-frame 8 μm LF estimated in two redshift bins with the 1/Vmax method. Red squares are obtained using scaled CE01 templates which best fit the L24 μm/(1 + z) − L70 μm/(1 + z) correlation. Empty triangles and blue dashed-dotted line present the rest-frame 8 μm LF obtained at zs2 by Caputi et al. (2007). Asterisks show the local reference taken from Huang et al. (2007) and the dotted line presents the best-fit to these data points with a double power law function with fixed slopes (see Table A.1). The dark shaded area span all the solutions obtained with the χ2 minimization method and compatible, within 1σ, with our data points. The dashed line represents the best fit of the rest-frame 8 μm LF. |
| Open with DEXTER | |
 |
Fig. A.2
The rest-frame 15 μm LF estimated in two redshift bins with the 1/Vmax method. Red squares are obtained using scaled CE01 templates which best fit the L24 μm/(1 + z) − L70 μm/(1 + z) correlation. Asterisks show the local reference taken from Xu (2000) and the dotted line presents the best-fit to these data points with a double power law function with fixed slopes (see Table A.1). The dark shaded area span all the solutions obtained with the χ2 minimization method and compatible, within 1σ, with our data points. The dashed line represents the best fit of the rest-frame 15 μm LF. In the first redshift panel, we reproduce in green, blue, yellow and red the best fit of the LF obtained at 0.4 < z < 0.7, 0.7 < z < 1.0, 1.0 < z < 1.3 (Magnelli et al. 2009), and 1.8 < z < 2.3 respectively. |
| Open with DEXTER | |
 |
Fig. A.3
The rest-frame 25 μm LF estimated in two redshift bins with the 1/Vmax method. Red squares are obtained using scaled CE01 templates which best fit the L24 μm/(1 + z) − L70 μm/(1 + z) correlation. Asterisks show the local reference taken from Shupe et al. (1998) and the dotted line presents the best-fit to these data points with a double power law function with fixed slopes (see Table A.1). The dark shaded area span all the solutions obtained with the χ2 minimization method and compatible, within 1σ, with our data points. The dashed line represents the best fit of the rest-frame 25 μm LF. |
| Open with DEXTER | |
 |
Fig. A.4
The rest-frame 35 μm LF estimated in two redshift bins with the 1/Vmax method. Red squares are obtained using scaled CE01 templates which best fit the L24 μm/(1 + z) − L70 μm/(1 + z) correlation. Asterisks show the local reference derived from Shupe et al. (1998) and the dotted line presents the best-fit to these data points with a double power law function with fixed slopes (see Table A.1). The dark shaded area span all the solutions obtained with the χ2 minimization method and compatible, within 1σ, with our data points. The dashed line represents the best fit of the rest-frame 35 μm LF. In the first redshift panel, we reproduce in green, blue, yellow and red the best fit of the LF obtained at 0.4 < z < 0.7, 0.7 < z < 1.0, 1.0 < z < 1.3 (Magnelli et al. 2009), and 1.8 < z < 2.3 respectively. |
| Open with DEXTER | |
Parameter values of the rest-frame 8 μm, 15 μm, 25 μm and 35 μm LF.
The rest-frame 8 μm LF derived from the 1/Vmax analysis.
The rest-frame 15 μm LF derived from the 1/Vmax analysis.
The rest-frame 25 μm LF derived from the 1/Vmax analysis.
The rest-frame 35 μm LF derived from the 1/Vmax analysis.
The infrared LF derived from the 1/Vmax analysis using 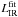 .
.
The infrared LF derived from the 1/Vmax analysis using 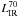 .
.
Appendix B: Source list
At the resolution of Spitzer most of the sources in our fields are point sources (i.e. FWHMs5.9″ and 18″ at 24 μm and 70 μm respectively). Therefore, to derive their photometry we decided to use a PSF fitting technique that take into account, as prior information, the expected position of the sources. Starting from IRAC positions (GOODS-N: GOODS legacy program, Dickinson et al., in prep.; GOODS-S: SIMPLE catalog, ?) we extract all 24 μm sources. Then, using our 24 μm catalogs, we extract all 70 μm sources. This method deals with a large part of the blending issues encountered in dense fields and allows straightforward multi-wavelength association between near-, mid- and far-infrared sources. The disadvantage of this method is that we have to assume that all sources present in our mid-infrared images have already been detected at IRAC wavelengths. In our case this assumption is true because our IRAC 3.6 μm data are 30 times deeper than our current 24 μm observations and that the typical S24 μm/S3.6 μm ratio spans the range [2–20].
In this online material we release our complete 24 μm and 70 μm source catalogs for both GOODS fields. These catalogs expend below the 80% completeness limit, and cover the full area (approximately 10′ × 16′) of the GOODS-S region (i.e., not only the smaller 10′ × 10′ region with the deepest 70 μm imaging that is used for the analysis in this paper). The noise level in the GOODS 24 μm data is homogeneous over most of the field, with some degradation near the edge where the exposure time is somewhat reduced. We restrict our release to regions with exposure time higher than 9500 s per pixel. This limit corresponds to a quarter of the exposure time of the deep inner region (s38 000 s). This degradation does not really affect the depth of our 24 μm catalogs in that region since uncertainties are still dominated by confusion (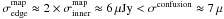 Jy). At 70 μm, the noise level is roughly uniform throughout GOODS-N (s12 000 s per pixel). However, in GOODS-S the deepest 70 μm data, with noise similar to those in GOODS-N, are limited to a region approximately 10′ × 10′ in extent. The outer region portions of the GOODS-S field have somewhat shallower 70 μm data (s6000 s per pixel).
Jy). At 70 μm, the noise level is roughly uniform throughout GOODS-N (s12 000 s per pixel). However, in GOODS-S the deepest 70 μm data, with noise similar to those in GOODS-N, are limited to a region approximately 10′ × 10′ in extent. The outer region portions of the GOODS-S field have somewhat shallower 70 μm data (s6000 s per pixel).
At 24 μm, sources are detected using an empirical 24 μm PSF constructed with isolated point like objects present in the mosaic. At 70 μm no reliable empirical PSF could be constructed because only a few isolated sources could be found in each map. We then decided to use the appropriate 70 μm Point Response Function (PRF) estimated on the extragalactic First Look Survey mosaic (xFLS; Frayer et al. 2006a) and available on the Spitzer web site. At both wavelengths an aperture correction is applied to all flux densities to account for the finite size of our PSFs. Those aperture corrections are taken from the Spitzer data handbook.
Calibration factors used to generate the final 24 and 70 μm mosaics are derived from stars, whose SED at these wavelengths are generally very different from those of distant galaxies. Hence, color-corrections have to be applied to all flux densities (at most s10%). In the catalogs released here, 70 μm flux densities have been color-corrected using a systematic and standard correction of 1.09 (see Spitzer data handbook). This 70 μm color-correction is computed for distant galaxies with dust temperature of s40 K. This color-correction differs from those applied in our study and which take into account the redshift of each source (see discussion in Sect. 2.1). No color–corrections are applied to our 24 μm flux densities since, for those data, color-corrections are more strongly dependent on the redshift of the source. Indeed, 24 μm data probes different part of galaxy SED as function of the redshift (black-body emission of dust or PAH emission).
Our 24 μm and 70 μm data are the deepest observations taken by Spitzer and have been designed to reach the confusion limit of this satellite. Flux uncertainties are therefore a complex combination of photon and confusion noise. In order to estimate these complex flux uncertainties and to characterize the quality of our 24 μm and 70 μm catalogs we use two different approaches. First, we compute the noise of each detection using our residual maps. Second, we estimate a statistical flux uncertainty based on extensive Monte-Carlo simulations.
Noises estimated on residual maps correspond to the pixel dispersion, around a given source, of the residual map convolved with the appropriate PSF. This method has the advantage of taking into account the rms of the map and the quality of our fitting procedure. These noise estimates are given in our released catalogs as σmap. These estimates are almost equal to the rms of our maps, i.e., σmaps3 μJy/beam at 24 μm in both GOODS-N and GOODS-S, 0.3 mJy/beam at 70 μm in GOODS-N and in the deepest region of GOODS-S, and 0.45 mJy/beam at 70 μm in the shallowest region of GOODS-S.
In order to estimate the effect of confusion noise we performed extensive Monte-Carlo simulations. We added artificial sources in the 24 μm and 70 μm images with a flux distribution matching approximately the measured number counts (see Frayer et al. 2006b; Papovich et al. 2004). To preserve the original statistics of the image (especially the crowding properties) the numbers of artificial objects added in the image was kept small (we only added 40 sources into the 24 μm images and 4 sources into 70 μm images). We then performed our source extraction method and compared the resulting photometry to the input values. To increase the statistic, we used repeatedly the same procedure with different positions in the same field. For each field we introduced a total of 20 000 artificial objects. Results of these Monte-Carlo simulations are shown in Fig. 1 of Magnelli et al. (2009) and are summarized hereafter.
MIPS sources in GOODS-N with 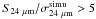 .
.
MIPS sources in GOODS-N with 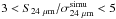 .
.
MIPS sources in GOODS-S with 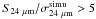 .
.
MIPS sources in GOODS-S with 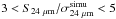 .
.
From these Monte-Carlo simulations we derive three important quantities: the photometric accuracy, the completeness and the contamination of our catalogs as function of flux density. Completeness is define as the fraction of simulated sources extracted with a flux accuracy better than 50%. The contamination is defined as the fraction of simulated sources introduced with S < 2σmap which are extracted with S > 3σmap.
Using these Monte-Carlo simulations, we find that in both GOODS fields our 24 μm catalogs are 80% complete at s30 μJy. At this flux density, the flux accuracy is better that 20% and the contamination is s10%. The flux accuracy of our source extraction reaches 33% around 20 μJy. This limit could be defined as the “real” 3σsimu limit of our data because this estimate take into account confusion noise. At 20 μJy, the completeness of our catalog is s40% and the contamination is s15%.
For our deep 70 μm data in GOODS-N and -S, Monte-Carlo simulations show that our catalogs are 80% complete at 2.5 mJy. The 33% flux accuracy is reached at 2 mJy with a completeness of s50% and a contamination of s15%. For the shallow 70 μm data of GOODS-S, the 80% completeness limit is reached at 3 mJy, and the 33% flux accuracy is reached at 2.5 mJy. At 2.5 mJy, the completeness is 45% and the contamination is 15%.
Flux uncertainties derived using our Monte-Carlo simulations are denoted by σsimu. These flux uncertainties present the advantage of accounting for nearly all sources of noise, which explains why they are almost always larger than noise estimates based on residual maps (i.e., σmap). However, this noise estimate is computed independently of the actual position of the individual sources, it is statistical. In some cases, local effects can dominate the noise as it is the case when two sources are blended. This local effect, together with the background fluctuation due to the photometric confusion noise (i.e. the noise due to sources fainter that the detection limit that were not subtracted from the image to produce the residual image), is better accounted for in the noise estimated from the residual maps, which is estimated locally. To be conservative, users should always use the highest uncertainties between σmap and σsimu, but not the quadratic combination of both since they are not independent.
Tables B.1–B.4 give excerpt of our complete GOODS-N/S 24 μm and 70 μm catalogs available at CDS. For each field we decide to split our 24 μm catalogs into two (i.e., sources with 3 < σsimu < 5 and sources with 5 > σsimu) in order to highlight
that in deep and confused fields the use of sources below 5-σ has to be done with caution. Positions of the 24 μm and 70 μm sources correspond to the IRAC positions used as priors to our source extraction. IRAC coordinates are calibrated to match the GOODS ACS version 2 coordinate system. For 24 μm sources that are not individually detected at 70 μm, we report an upper flux limit computed from our residual maps (i.e., 5-σmap at the position of the source).
© ESO, 2011
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


