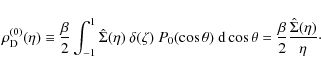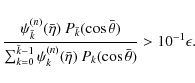| Issue |
A&A
Volume 519, September 2010
|
|
|---|---|---|
| Article Number | A47 | |
| Number of page(s) | 20 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201014387 | |
| Published online | 10 September 2010 | |
Online Material
Appendix A: Construction of the models by an iterative procedure
Equation (18), with the boundary conditions
(20), is solved by means of a modified version of the
iterative procedure presented earlier by Prendergast & Tomer (1970) in view of a completely different problem (the
study of nonspherical models for rotating elliptical galaxies).
It is based on the classical expansion in Legendre polynomials, a
natural approach in the case of axisymmetric systems. However, the
original method is viable only for gravitational potentials that
are regular at large radii. In contrast, in our model, the
potential of the isothermal halo diverges at large radii. This
difficulty has been overcome by separating the potential of the
dark matter halo into two different parts: a regular part, which
converges to finite values at large radii, and a divergent one,
which follows the asymptotic prescription of Eq. (20).
Below we provide the details of the technique developed in the
present paper.
Here it is convenient to work with standard spherical coordinates
![]() and their dimensionless analogue
and their dimensionless analogue
![]() .
We start by recalling briefly the method devised by
Prendergast & Tomer (1970). The solution of the two-dimensional Poisson
equation
.
We start by recalling briefly the method devised by
Prendergast & Tomer (1970). The solution of the two-dimensional Poisson
equation
is obtained by iteratively solving the equations
to which the same boundary conditions as in Eq. (A.1) are imposed. The potential at the iterative step (n+1),
and
For completeness, we display the general solution of the nth iterative step:
![\begin{displaymath}\begin{array}{ll}
\psi^{(n+1)}(\eta, \theta)=& \Psi +\left[\i...
...{k+2}\hat\rho^ {(n)}_{k}(\eta'){\rm d}\eta' \right]
\end{array}\end{displaymath}](/articles/aa/olm/2010/11/aa14387-10/img194.png)
|
(A.5) |
where we have used the notation
The dark matter gravitational potential is then separated into two parts:
The potential defined as
and has the same asymptotic behavior as in Eq. (20). In this way the potential
can be directly solved by the iterative multipole expansion outlined previously.
Obviously, there is an infinite number of pairs
![]() that meet the conditions of Eqs. (A.8) and (20). Therefore, the construction method proposed below just reflects one reasonable choice. We decided to take
that meet the conditions of Eqs. (A.8) and (20). Therefore, the construction method proposed below just reflects one reasonable choice. We decided to take
![]() and
and
![]() with spherical symmetry, because the relevant asymptotic condition for
with spherical symmetry, because the relevant asymptotic condition for
![]() is characterized by spherical symmetry and because the spherical Poisson equation admits a simple explicit solution:
is characterized by spherical symmetry and because the spherical Poisson equation admits a simple explicit solution:
The precise choice of the form of the density
We start by defining what we call an ``observed'' pseudo-potential, constructed from the observed rotation curve:
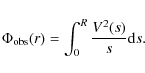
|
(A.11) |
At large radii it has the asymptotic expression
where the radius
![]() can be calculated from the precise form of the rotation curve. The behavior of Eq. (A.12) naturally relates the potential
can be calculated from the precise form of the rotation curve. The behavior of Eq. (A.12) naturally relates the potential
![]() (and its dimensionless counterpart
(and its dimensionless counterpart
![]() )
to a density distribution with isothermal functional shape:
)
to a density distribution with isothermal functional shape:
As shown in Eq. (10), the value of the constant
![]() is determined by the value of the radius
is determined by the value of the radius
![]() only, and is thus fixed. Having made this points clear, we can define
only, and is thus fixed. Having made this points clear, we can define
![]() to be
to be
where we have introduced a regularizing core structure with characteristic size ![]() and subtracted the monopole term of the stellar density
and subtracted the monopole term of the stellar density
With this density profile, from Eq. (A.10) we calculate the gravitational potential
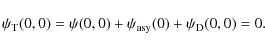
|
(A.16) |
A.1 The truncation of the angular expansion
A code has been written to solve Eq. (A.9)
through the technique described in the previous section. The code is
able to manage automatically the appropriate number of multipole terms
to meet a required accuracy (see Eq. (A.6)). At each iterative step, the relevant number of multipole orders is calculated from the following prescription:
In words, at the nth iteration step, the multipole term of order ![]() is retained in the expansion if its (relative) contribution to the gravitational potential
is retained in the expansion if its (relative) contribution to the gravitational potential
![]() (calculated with the previous
(calculated with the previous ![]() multipole orders only) is comparable to the accuracy level
multipole orders only) is comparable to the accuracy level ![]() we want to meet. This comparison is made at the coordinates
we want to meet. This comparison is made at the coordinates
![]() ,
chosen in the region where the deviation from spherical symmetry is strongest:
,
chosen in the region where the deviation from spherical symmetry is strongest:
![]() and
and
![]() .
.
The models described in the paper are calculated with an accuracy prescription of
![]() .
Obviously, the number of iterations required by such precision depends
on the gravitational importance of the stellar disk (which determines
the flattening of the halo). For values of the pair
.
Obviously, the number of iterations required by such precision depends
on the gravitational importance of the stellar disk (which determines
the flattening of the halo). For values of the pair
![]() that represent an astrophysically realistic configuration (see Sect. 4), the number of required iterations is
that represent an astrophysically realistic configuration (see Sect. 4), the number of required iterations is ![]() ,
with a number of multipole orders of
,
with a number of multipole orders of ![]() .
.
Appendix B: Anomalous rotation curves
![\begin{figure}
\par\includegraphics[width=8.7cm, angle=0]{14387fg22.eps} \end{figure}](/articles/aa/olm/2010/11/aa14387-10/Timg228.png)
|
Figure B.1:
Contours of the function |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.7cm, angle=0]{14387fg23.eps} \end{figure}](/articles/aa/olm/2010/11/aa14387-10/Timg229.png)
|
Figure B.2:
Contours of the function |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.7cm, angle=0]{14387fg24.eps} \end{figure}](/articles/aa/olm/2010/11/aa14387-10/Timg230.png)
|
Figure B.3:
Disk-halo decomposition associated with
the best self-consistent fit of the case
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.7cm, angle=0]{14387fg25.eps} \end{figure}](/articles/aa/olm/2010/11/aa14387-10/Timg231.png)
|
Figure B.4:
Contours of the function |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.7cm, angle=0]{14387fg26.eps} \vspace*{1.5mm}
\end{figure}](/articles/aa/olm/2010/11/aa14387-10/Timg232.png)
|
Figure B.5:
Contours of the function |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.7cm, angle=0]{14387fg27.eps} \end{figure}](/articles/aa/olm/2010/11/aa14387-10/Timg233.png)
|
Figure B.6:
Disk-halo decomposition associated with
the best self-consistent fit of the case
|
| Open with DEXTER | |
The results for the fast rising rotation curve are shown in Figs. B.1 and B.2. In the parametric decomposition method we find again the bimodality of the fit, as noted in the case of NGC 3198. The self-consistent method instead identifies a decomposition with an important stellar disk; the fit for the rotation curve is illustrated in Fig. B.3.
The results for the slowly rising rotation curve are shown in Figs. B.4 and B.5.
The degeneracy pattern is clearly present in the parametric
decomposition, but in this case it is less marked with respect to the
cases studied earlier in this paper. Here, the parametric fit is
``pushed'' in the direction of an insignificant disk, because the
observed
![]() is too small and can only be ascribed to a dominant dark matter halo.
On the other hand, the self-consistent decomposition appears to be able
to handle also this case (see Fig. B.6).
is too small and can only be ascribed to a dominant dark matter halo.
On the other hand, the self-consistent decomposition appears to be able
to handle also this case (see Fig. B.6).
From the point of view of the quality of the fits, it is apparent that
both decomposition methods work best when fitting the case of
![]() ,
that is for a rotation curve that follows the empirical correlation illustrated in Fig. 1. This is the aspect of conspiracy that was introduced and described in Sect. 2.1. In this case, the values of the function
,
that is for a rotation curve that follows the empirical correlation illustrated in Fig. 1. This is the aspect of conspiracy that was introduced and described in Sect. 2.1. In this case, the values of the function ![]() corresponding to the best-fitting
corresponding to the best-fitting
![]() pairs are the smallest. In particular, Fig. B.3
shows that the case of a fast rising rotation curve cannot be properly
described without including a central concentrated mass component, such
as a bulge; the value of the residuals
pairs are the smallest. In particular, Fig. B.3
shows that the case of a fast rising rotation curve cannot be properly
described without including a central concentrated mass component, such
as a bulge; the value of the residuals ![]() in correspondence of the best-fit (see Fig. B.2) is considerably higher if compared for example to the good fit of Fig. 12.
Similarly, for the opposite case of a slowly rising rotation curve, it
is the parametric model which is quite unable to account for such a
shape of the rotation velocity, with a similar high value for the
best-fit residuals (see Fig. B.4).
in correspondence of the best-fit (see Fig. B.2) is considerably higher if compared for example to the good fit of Fig. 12.
Similarly, for the opposite case of a slowly rising rotation curve, it
is the parametric model which is quite unable to account for such a
shape of the rotation velocity, with a similar high value for the
best-fit residuals (see Fig. B.4).
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![\begin{displaymath}\nabla^2\psi(\eta,\theta)=\hat\rho\left[\eta, \theta; \psi(\eta, \theta)\right]
\end{displaymath}](/articles/aa/olm/2010/11/aa14387-10/img188.png)
![\begin{displaymath}\nabla^2\psi^{(n+1)}(\eta,\theta)=\hat\rho\left[\eta, \theta; \psi^ {(n)}(\eta, \theta)\right]
\end{displaymath}](/articles/aa/olm/2010/11/aa14387-10/img189.png)
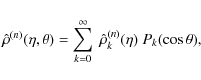
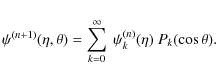
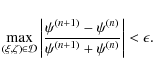
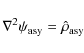
![\begin{displaymath}\left({1\over\xi}{\partial\over{\partial\xi}}\xi{\partial\ove...
...t[\psi_{\rm asy}+\psi_{\rm D}+\psi\right]}- \hat\rho_{\rm asy}
\end{displaymath}](/articles/aa/olm/2010/11/aa14387-10/img202.png)
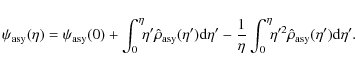
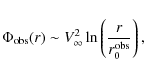
![\begin{displaymath}{1\over{\eta^2}}{{\rm d}\over{{\rm d}\eta}}\eta^2{{\rm d}\ove...
...a_{\rm obs}\exp\left[\psi_{\rm obs}(\eta)\right] ;\ \eta\gg1 .
\end{displaymath}](/articles/aa/olm/2010/11/aa14387-10/img212.png)
![\begin{displaymath}\hat\rho_{\rm asy}(\eta)\equiv-\alpha_{\rm obs}\exp\left[\psi...
...2+\eta_{\rm c}^2}\right)\right]+\hat\rho_{\rm D}^{(0)}(\eta) ,
\end{displaymath}](/articles/aa/olm/2010/11/aa14387-10/img213.png)