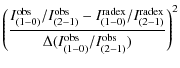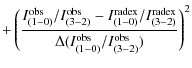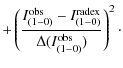EDP Sciences
Home All issues Volume 519 (September 2010) A&A, 519 (2010) A27 Online Material
Free Access
Issue
A&A
Volume 519, September 2010
Article Number A27
Number of page(s) 19
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/200913919
Published online 08 September 2010

Online Material

Appendix A: 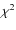$\chi ^{2}$ surfaces for RADEX fits

Figures A.1-A.8 show the $\chi ^{2}$ surfaces from the non-LTE analysis of the line integrated intensity ratios for each of the positions studied. The $\chi ^{2}$ has been calculated using Eq. (A.1), where $I_{(J_{\rm up}-J_{\rm low})}^{{\rm obs}}$ is the observed integrated intensity of the transition between $J_{\rm up}$ and $J_{\rm low}$, $\Delta$(x) is the uncertainty on the quantity x and, finally, $I_{(J_{\rm up}-J_{\rm low})}^{{\rm radex}}$ is the integrated intensity for each transition as modelled by RADEX, for each combination of temperature and gas column density

                         $\displaystyle \chi^{2}$ = $\displaystyle \left(\frac{I_{(1-0)}^{{\rm obs}}/I_{(2-1)}^{{\rm obs}} - I_{(1-0... ...^{{\rm radex}}}{\Delta(I_{(1-0)}^{{\rm obs}}/I_{(2-1)}^{{\rm obs}})}\right)^{2}$  
    $\displaystyle + \left(\frac{I_{(1-0)}^{{\rm obs}}/I_{(3-2)}^{{\rm obs}} - I_{(1... ...{{\rm radex}}} {\Delta(I_{(1-0)}^{{\rm obs}}/I_{(3-2)}^{{\rm obs}})}\right)^{2}$  
    $\displaystyle + \left(\frac{I_{(1-0)}^{{\rm obs}} - I_{(1-0)}^{{\rm radex}}}{\Delta(I_{(1-0)}^{{\rm obs}})}\right)^{2}\cdot$ (A.1)

For each case, the $\chi ^{2}$ is plotted as a function of the RADEX output temperature and gas column density. Given the use of 3 quantities in the fit, we consider $\chi^{2}<3$, i.e. the reduced- $\chi^{2}<1$ a good fit. All figures have contours at $\chi^{2}=1$, 2 and 3 with the exception of ND (Fig. A.4) and SD (Fig. A.8).

\begin{figure} \par\includegraphics[scale=.37,angle=-90]{13919fga1.eps} \end{figure} Figure A.1:

$\chi ^{2}$ surface for the integrated intensity ratios at position NA.

Open with DEXTER

\begin{figure} \par\includegraphics[scale=.37,angle=-90]{13919fga2.eps} \end{figure} Figure A.2:

$\chi ^{2}$ surface for the integrated intensity ratios at position NB.

Open with DEXTER

\begin{figure} \par\includegraphics[scale=.37,angle=-90]{13919fga3.eps} \end{figure} Figure A.3:

$\chi ^{2}$ surface for the integrated intensity ratios at position NC.

Open with DEXTER

\begin{figure} \par\includegraphics[scale=.37,angle=-90]{13919fga4.eps} \end{figure} Figure A.4:

$\chi ^{2}$ surface for the integrated intensity ratios at position ND. Contour at 25.

Open with DEXTER

\begin{figure} \mbox{\includegraphics[scale=.37,angle=-90]{13919fga5a.eps} \h... ...egraphics[scale=.37,angle=-90]{13919fga5b.eps} } \hfill \hfill \end{figure} Figure A.5:

$\chi ^{2}$ surfaces for the integrated intensity ratios at position SA: SA1 (LVC) on the left, and SA2 (HVC) on the right.

Open with DEXTER

\begin{figure} \mbox{\includegraphics[scale=.37,angle=-90]{13919fga6a.eps} \h... ...udegraphics[scale=.37,angle=-90]{13919fga6b.eps} } \hfill \hfill\end{figure} Figure A.6:

$\chi ^{2}$ surface for the integrated intensity ratios at position SB: SB1 (LVC) on the left, and SB2 (HVC) on the right.

Open with DEXTER

\begin{figure} \mbox{\includegraphics[scale=.37,angle=-90]{13919fga7a.eps} \h... ...degraphics[scale=.37,angle=-90]{13919fga7b.eps} } \hfill \hfill \end{figure} Figure A.7:

$\chi ^{2}$ surface for the integrated intensity ratios at position SC: SC1 (LVC) on the left and SC2 (HVC) on the right.

Open with DEXTER

\begin{figure} \mbox{\includegraphics[scale=.38,angle=-90]{13919fga8a.eps} \h... ...degraphics[scale=.38,angle=-90]{13919fga8b.eps} } \hfill \hfill\end{figure} Figure A.8:

$\chi ^{2}$ surface for the integrated intensity ratio at position SD: SD1 (LVC) on the left, and SD2 (HVC) on the right. Note the different colour scale for SC2. Contours are 6 for SD1 and 18 for SD2.

Open with DEXTER

Appendix B: C18O intensities and abundances

Table B.1 presents the best fit integrated intensities from the non-LTE (RADEX) modelling (Appendix A) , together with the observed values, and the implied C18O abundances.

Table B.1:   Modelled integrated intensities and resulting abundances.

For positions ND, SB, SC and SD, the H2 column densities derived from the dust and used to estimate the abundance of C18O were calculated using a dust temperature of 10 K. Assuming a temperature of 15 K for all 4 positions (ND, SB, SC and SD) would reduce the H2 column densities by a factor of 2.1, representing an equivalent rise of the fractal abundance of C18O by the same amount.

The derived C18O fractional abundance (which is averaged along the line of sight) implies a depletion of C18O of between a factor of 1.4 (for NC) and 4.3 (for SC), with an average of 2.5 compared to the abundance of $1.7\times10^{-7}$ in dark clouds (Frerking et al. 1982). Given that the ratio between C17O and C18O has shown these two species to be optically thin, with an intensity ratio of $\sim$3.5, a factor 2.5 depletion of C18O implies the same depletion factor for C17O.

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.