Online Material

Appendix A: NLTE modeling

Figure A.1: a), b): departure coefficients of the Ba  II atomic levels vs. height in a representative granular ( left) and intergranular ( right) models. Thick solid and thick dash lines: the -coefficients for the ground and upper levels of the Ba  II 4554 Å line, respectively. Dash-dotted lines: the -coefficients for the upper level of the Ba  II 4934 Å resonance line. Dotted lines: the -coefficients for the Ba  II levels with excitation potentials above 5 eV. c), d): the line source function SL of the Ba  II 4554 Å line (dash) and Planck function B (solid) in units of the temperature vs. height for the same models. e), f): the Ba  II 4554 Å line profiles for the representative granule and itergranule. Solid and dotted lines: NLTE and LTE, respectively. g), h): spatially averaged granular and intergranular profiles.

Open with DEXTER

Figure A.2: The NLTE (solid line) and LTE (open circles) heights of formation of the core of the Ba  II 4554 Å line along the slice of the snapshot yi=0.6 Mm. Dash-dotted line: continuum height of formation at 4554 Å. Dotted line: height of formation of the line wing for the wavelength position  mÅ. The background image is the snapshot vertical velocity Vz. Negative (upflow) velocities VZ correspond to granules (dark), while positive (downflow) velocities to intergranules (light).

Open with DEXTER

Figure A.1 (panels a to f) shows the population departure coefficients, the Ba  II 4554 Å line source functions and line profiles for two spatial grid points of the 3D snapshot representing the typical granular and intergranular models. We use these models to illustrate the difference in the NLTE results for granules and intergranules. The population departure coefficients are defined as where and are the NLTE and LTE atomic level populations, respectively. The Complex behaviour of the -coefficients shown in Fig. A.1a, b is a result of the interaction of several NLTE mechanisms described in detail by Bruls et al. (1992); Carlsson et al. (1992); Shchukina & Trujillo Bueno (2001). Here we just point out that for the barium atom the most important of them are ultraviolet line pumping, ultraviolet overionization, resonance line scattering and photon losses. The resonance line scattering and photon losses manifest themselves as a divergence of the lower and upper , levels of the Ba  II resonance lines. This divergence results from the surface losses near the layer where the optical depth is equal to unity. The losses propagate by scattering to far below that layer. Interestingly, for the integranule the divergence of the -coefficients arises in the innermost layers. This happens because the photon losses occur mainly through the line wings of the Ba  II 4554 Å line. As follows from Fig. A.2 the line wings in integranules are formed considerably deeper than in granules. Such a difference in the formation heights is a result of the Doppler shift of the line opacity coefficient caused by the velocity field. As a consequence, in the intergranular model (see Fig. A.1a, b) the divergence starts already in the lower photosphere while in the granular model it happens only in upper photosphere at heights around 400 km.

Another important conclusion that follows from Fig. A.2 concerns the height of formation of the Ba  II 4554 Å line. The lower departure coefficient is close to unity. So the scaling of the line opacity with this coefficient cannot lead to an appreciable difference between the NLTE and LTE heights of formation of this line.

The excess of Ba  II ions at the levels with excitation potentials above 5 eV visible in the granule model is produced by the pumping via the ultraviolet Ba  II lines starting at , , levels. For the intergranule model the overpopulation arises only in the uppermost layers. Such behaviour of the -coefficients corresponds to the temperature stratification of the models. The overpopulation of the high excitation levels of Ba  II in granules occurs because here the excitation temperature of the ultraviolet pumping radiation field appreciably exceeds the electron temperature. In integranules such superthermal radiation, and hence the level overpopulation, is present only above the temperature minimum region. In addition, in the intergranular photospheric layers the photon losses in the ultraviolet lines are more pronounced than in granules.

Figure A.3: The total source function measured in the Planck function units for three wavelength points  mÅ situated in the blue wing of the Ba  II 4554 Å line profile. Left: Maps of the at the mean intensity formation heights at these wavelengths. Horizontal line corresponds to the slice yi=0.6 Mm and the filled circles to the surface positions xi=1.8 Mm (granule), xi=2.4 Mm (intergranule). Right: scatter plots of and velocities Vz for the same wavelengths. The velocities are taken at heights of formation of continuum intensity.

Open with DEXTER

The ratio of the upper and lower level departure coefficients of the Ba  II 4554 Å line sets the departure of its line source function S_L from the Planck function B. Figure A.1 (c, d) shows that this departure (reflecting the corresponding departure coefficient divergence in the upper panels of this figure) is larger in the intergranular than in the granular model.

Figure A.3 demonstrates that such behaviour is typical also for the total source function at the wavelengths corresponding to the inner wings (  mÅ). On average, in intergranular regions it drops below the Planck function while in granules the effect is less pronounced. Moreover, in granular areas with strong upflows the total source function can exceed the Planck function. This excess can be understood if one takes into account that the resonance source line function is described by the two-level approximation, i.e. it approximately equals mean intensity J. In the regions with small photon losses (like granules) the J > B, hence, and have to be greater than B as well.

Figure A.1e, f show the NLTE and LTE disc-centre line profiles for the individual granular and integranular models. The profiles displayed in Fig. A.1g result from averaging of the emergent intensities corresponding only to the granular models. Averaged intergranular profiles are shown in Fig. A.1h. These two bottom panels quantify the statistical effect produced by the deviation from the LTE in two such types of the atmospheric models. The main conclusions that may be drawn from the results presented in Figs. A.1-A.3 are the following:

• the source function deficit, as compared to the LTE assumption, is the main mechanism that controls the formation of the Ba  II 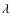4554 Å line. The line opacity deficit is small and, hence, unimportant;
• the divergence between 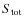and B changes the shape of the individual profiles, particularly the intergranular ones.
• On average, the deviations from the LTE lead to deepening (i.e. strengthening) of the spatially averaged Ba  II 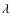4554 Å line profiles. The NLTE effects are most pronounced around the line core and are generally more important in the intergranular regions than in the granular ones. The mean difference between the NLTE and LTE line core residual intensities does not exceed 5% for granules and 10% for intergranules.
• Towards the wings, the LTE becomes a valid description for the Ba  II 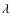4554 Å line profile;