| Issue |
A&A
Volume 506, Number 3, November II 2009
|
|
|---|---|---|
| Page(s) | 1393 - 1404 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/200912048 | |
| Published online | 11 August 2009 | |
A&A 506, 1393-1404 (2009)
The solar Ba 4554 Å line as a Doppler diagnostic:
NLTE analysis in 3D hydrodynamical model
4554 Å line as a Doppler diagnostic:
NLTE analysis in 3D hydrodynamical model![[*]](/icons/foot_motif.png)
N. G. Shchukina1 - V. L. Olshevsky1 - E. V. Khomenko2,1
1 - Main Astronomical Observatory, NAS, 03680 Kyiv,
Zabolotnogo str. 27, Ukraine
2 - Instituto de Astrofísica de
Canarias, 38205, C/ vía Láctea, s/n, Tenerife, Spain
Received 12 March 2009 / Accepted 25 June 2009
Abstract
Aims. The aim of this paper is to analyse the validity of the Dopplergram and ![]() -meter techniques for the Doppler diagnostics of solar photospheric velocities using the Ba II 4554 Å line.
-meter techniques for the Doppler diagnostics of solar photospheric velocities using the Ba II 4554 Å line.
Methods. Both techniques are evaluated by means of NLTE radiative transfer calculations of the Ba II
4554 Å line in a three-dimensional hydrodynamical model of solar
convection. We consider the cases of spatially unsmeared profiles and
the profiles smeared to the resolution of ground-based observations.
Results. We find that: (i) speckle-reconstructed
Dopplergram velocities reproduce the ``true'' velocities well at
heights around 300 km, except for intergranular lanes with strong
downflows where the velocity can be overestimated; (ii) the ![]() -meter
velocities give a good representation of the ``true'' velocities
through the whole photosphere, both under the original and reduced
spatial resolutions. The velocities derived from the inner wing of
smeared Ba II 4554 Å line profiles are more
reliable than those for the outer wing. Only under high spatial
resolution does the inner wing velocities calculated in intergranular
regions give an underestimate (or even a sign reversal) compared with
the model velocities; (iii) NLTE effects should be taken into account
in modelling the Ba II 4554 Å line profiles. Such effects are more pronounced in intergranular regions.
-meter
velocities give a good representation of the ``true'' velocities
through the whole photosphere, both under the original and reduced
spatial resolutions. The velocities derived from the inner wing of
smeared Ba II 4554 Å line profiles are more
reliable than those for the outer wing. Only under high spatial
resolution does the inner wing velocities calculated in intergranular
regions give an underestimate (or even a sign reversal) compared with
the model velocities; (iii) NLTE effects should be taken into account
in modelling the Ba II 4554 Å line profiles. Such effects are more pronounced in intergranular regions.
Conclusions. Our analysis supports the opinion that the Dopplergram technique applied to the Ba II 4554 Å line is a valuable tool for the Doppler diagnostics of the middle photosphere around 300 km. The ![]() -meter
technique applied to this line gives us a good opportunity to ``trace''
the non-thermal motions along the whole photosphere up to the
temperature minimum and lower chromosphere.
-meter
technique applied to this line gives us a good opportunity to ``trace''
the non-thermal motions along the whole photosphere up to the
temperature minimum and lower chromosphere.
Key words: Sun: photosphere - Sun: granulation - line: formation - techniques: spectroscopic - hydrodynamics - radiative transfer
1 Introduction
First studies of the barium lines in stellar spectra started in the 1930s. One of the examples of these earlier studies is by Bidelman & Keenan (1951), who pointed out that the anomalous strength of the Ba II 4554 Å line in some stars could be explained by a deviation from local thermodynamic equilibrium (NLTE). At the present time stellar studies are aimed at the abundance determination of barium isotopes using one-dimensional (1D) plane-parallel atmospheric models and the NLTE assumption (Mashonkina et al. 2008; Mashonkina & Gehren 2000; Mashonkina & Zhao 2006; Mashonkina et al. 2003; Short & Hauschildt 2006; Gigas 1988). Such studies play important role in estimating the yields of s- and r-processes in the nucleosynthesis of heavy elements in the Galaxy.
Barium lines in the solar spectrum have been studied since 1960s. Until the mid-seventies most the studies aimed at determining the solar barium abundance using a 1D+LTE approach (Holweger & Müller 1974; Goldberg et al. 1960; Lambert & Warner 1968). The only exception was the publication of Tandberg-Hanssen & Smythe (1970); Tandberg-Hanssen (1964), who had shown the importance of NLTE effects for the formation of the Ba II 4554 Å line. Later, Rutten & Milkey (1979); Rutten (1977,1978) tackled in detail the NLTE Ba II line formation problem. Empirical analyses of centre-to-limb observations by Rutten (1978) have shown that the source function of the Ba II 4554 Å line deviates significantly from the Planck function. The effects of partially coherent scattering have also to be taken into account in order to reproduce observations away from the disc centre. The hyperfine structure and isotopic shift play a very important role in the analysis of this line as well.
For several reasons, a new debate has arisen in the recent
literature on the solar Ba II 4554 line.
Firstly, a more realistic representation of the solar atmosphere
by three-dimensional (3D) hydrodynamical simulations has become
available. Relaxing the constraints of the plane-parallel (1D)
modelling a new LTE abundance analysis by Asplund et al. (2005)
resulted in a photospheric barium abundance of
![]() ,
close to the meteoritic value
,
close to the meteoritic value
![]() .
While the recent NLTE
analysis by Olshevsky et al. (2008) based on a 3D model lowers the value of
.
While the recent NLTE
analysis by Olshevsky et al. (2008) based on a 3D model lowers the value of
![]() strictly to the meteoritic one.
Note that the classical 1D-approach resulted in a rather wide spread of the solar barium abundance
strictly to the meteoritic one.
Note that the classical 1D-approach resulted in a rather wide spread of the solar barium abundance
![]() (Ross & Aller 1976),
(Ross & Aller 1976),
![]() (Grevesse 1984), and
(Grevesse 1984), and
![]() (Rutten 1978).
(Rutten 1978).
Secondly, according to the atlas of the ``Second Solar spectrum''
(Gandorfer 2002), the linear polarization Q/I of this line close to
the limb (![]() )
is very strong (0.6%). The recently
published theoretical investigation on the role of resonance
scattering and magnetic fields in the polarization signals of
both Ba II 4934 Å, and 4554 Å resonance lines by
Belluzzi et al. (2007) has demonstrated their importance for the
measurements of weak magnetic fields on Sun and stars.
)
is very strong (0.6%). The recently
published theoretical investigation on the role of resonance
scattering and magnetic fields in the polarization signals of
both Ba II 4934 Å, and 4554 Å resonance lines by
Belluzzi et al. (2007) has demonstrated their importance for the
measurements of weak magnetic fields on Sun and stars.
Finally, several properties of the Ba II 4554 Å line have drawn attention to it as a diagnostic tool for the velocity field of the solar atmosphere. Due to the large atomic weight of barium (137.4 a.u.), one might expect low sensitivity of the line opacity to temperature variations and line-width insensitivity to thermal broadening. In addition, the Ba II 4554 Å line has steep wings and a deep core. In a standard 1D model the core of this line is formed around 700 km in the chromosphere while the wings are photospheric (Olshevsky et al. 2008; Sütterlin et al. 2001). As a result, the Ba II 4554 Å line gives an excellent opportunity to ``trace'' non-thermal motions (granulation and supergranulation velocity field and waves) throughout photosphere and even in the lower chromosphere. Noyes (1967) was one of the first to draw attention to the Doppler diagnostic potential of this line. Later, Rutten (1978) confirmed the Ba II 4554 Å line to be a perfect tool for investigating the velocity structure of the solar photosphere and lower chromosphere. Recently, Sütterlin et al. (2001) have made the first serious attempt to use the Ba II 4554 Å line for mapping the line-of-sight (LOS) velocities (Dopplershift map) of different structures in the solar photosphere. They presented observations with the Dutch Open Telescope (DOT) testing the Dopplergram capability of narrow-band (80 mÅ) Lyot filter (Skomorovsky et al. 1976) imaging the solar surface in the wings of this line in combination with speckle reconstruction. The Ba II 4554 Å line is found to be an excellent tool for high-resolution Doppler mapping.
Summarizing all the above, the Ba II 4554 Å line provides a
valuable diagnostic tool for the solar and stellar atmospheres.
It is thus extremely important to investigate carefully the
validity of the different data-processing techniques and
interpretations applied to this line to obtain information on
physical conditions in the solar atmosphere.
Our paper presents an example of such an investigation. Below we
analyse two techniques used for recovering the solar velocity field
from observations in this line. The aim of our analysis is to
consider the advantages and disadvantages of these techniques and
to evaluate to what extent the LOS velocities provided by them
give a correct measure of the solar values.
We keep in mind that, besides the techniques themselves, there is
another important source of uncertainties that can affect
Doppler diagnostics. The ground-based observations are typically
affected by the Earth's atmospheric turbulence (seeing) and
instrumental effects due to light diffraction on the telescope
aperture (the finite spatial resolution of the telescope), the
finite instrumental width of the filters used, stray light, etc.
So we tackle the problem taking into account seeing and
instrumental effects.
The first technique analysed in this paper is a 5-point
Dopplergram method used by Sütterlin et al. (2001). The second technique is known as a ![]() -meter, first proposed by Stebbins & Goode (1987). In subsequent years it has been adopted by several researchers (see Kostik & Khomenko 2007; Khomenko et al. 2001; Kostyk & Shchukina 2004, and more references therein) for spectral observations of different
Fraunhofer lines.
-meter, first proposed by Stebbins & Goode (1987). In subsequent years it has been adopted by several researchers (see Kostik & Khomenko 2007; Khomenko et al. 2001; Kostyk & Shchukina 2004, and more references therein) for spectral observations of different
Fraunhofer lines.
The organization of this paper is as follows.
Sects. 2.1 and 2.2 describe the 3D hydrodynamical model, atomic
data and numerical methods needed for the NLTE radiative transfer
calculations with the barium atomic model. In Sects. 2.3 and 2.4
we discuss the procedure used to simulate spatial smearing of the
two-dimensional maps of the synthetic Ba II 4554 Å line
profiles. We focus on seeing and instrumental effects. We
establish theoretical calibration dependences between the
granulation contrast and the Fried parameter (which specifies the
characteristic size of atmospheric turbulence cells) based on a
3D-approach. Section 2.5 defines artificial datasets employed in
discuss the validity of the 5-point Dopplergram technique used to
obtain LOS velocities from the speckle-reconstructed observations
of the Ba II 4554 Å line. Section 5 presents the results for
the ![]() -meter method. We discuss the granulation velocity field
that one would expect from observations of this line under perfect
spatial resolution (Sect. 5.1) and under different seeing
conditions of the ground-based observations (Sect. 5.2). An
extra point of particular interest has been to establish heights
from which the information on the velocity and intensity variations
originate. We discuss this problem in Sect. 5.3. Finally,
Sect. 6 presents our conclusions, while the Appendix gives a
brief description of our NLTE modelling with emphasis on the NLTE
mechanisms of formation of the Ba II 4554 Å line. We show
population departure coefficients, NLTE source functions and
profiles of this line to illustrate the difference in NLTE results
for granules and intergranules.
-meter method. We discuss the granulation velocity field
that one would expect from observations of this line under perfect
spatial resolution (Sect. 5.1) and under different seeing
conditions of the ground-based observations (Sect. 5.2). An
extra point of particular interest has been to establish heights
from which the information on the velocity and intensity variations
originate. We discuss this problem in Sect. 5.3. Finally,
Sect. 6 presents our conclusions, while the Appendix gives a
brief description of our NLTE modelling with emphasis on the NLTE
mechanisms of formation of the Ba II 4554 Å line. We show
population departure coefficients, NLTE source functions and
profiles of this line to illustrate the difference in NLTE results
for granules and intergranules.
2 Method
2.1 3D atmospheric model
We use a 3D snapshot from realistic radiation hydrodynamical
simulations of solar convection (Stein & Nordlund 1998; Asplund et al. 2000b,a,1999). This simulation is
based on a realistic equation of state, opacities and detailed
radiative transfer. The size of the simulation box is
![]() Mm, with 1.1 Mm being located above the
continuum optical depth equal to one. To reduce the amount of
time-consuming NLTE radiative transfer calculations, the snapshot
was interpolated from the original resolution of 200 grid points
in the horizontal direction to a coarser resolution of 50 grid points.
At the same time, we increased the resolution in the vertical
direction, taking only the upper 1.1 Mm part of the snapshot
between -200 km and 900 km and interpolating from 82 to 121 grid
points. Thus, the final 3D model has
Mm, with 1.1 Mm being located above the
continuum optical depth equal to one. To reduce the amount of
time-consuming NLTE radiative transfer calculations, the snapshot
was interpolated from the original resolution of 200 grid points
in the horizontal direction to a coarser resolution of 50 grid points.
At the same time, we increased the resolution in the vertical
direction, taking only the upper 1.1 Mm part of the snapshot
between -200 km and 900 km and interpolating from 82 to 121 grid
points. Thus, the final 3D model has
![]() grid
points or
grid
points or
![]() 1D models.
1D models.
It was concluded from previous studies that the 3D model used here performs very satisfactory in terms of spectral line formation both for line shape and asymmetries (Asplund et al. 2000a,1999; Shchukina & Trujillo Bueno 2001; Shchukina et al. 2005; Shchukina & Trujillo Bueno 2009; Asplund et al. 2000b,2004; Trujillo Bueno et al. 2004). The model reproduces all the main features of solar convective velocities and intensities (Kostyk & Shchukina 2004). It reproduces as well the root-mean-square (rms) contrast of solar granulation at the 6301 Å continuum wavelength (as obtained by HINODE), centre-to-limb variation of continuum intensity, and the polarization of the solar continuum (Trujillo Bueno & Shchukina 2009).
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12048fig1.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12048-09/Timg37.png)
|
Figure 1:
Grotrian diagram of an atomic model for Ba I +Ba II. Solid lines indicate radiative bound-bound transitions.
The Ba II |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12048fig2.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12048-09/Timg38.png)
|
Figure 2: Hyperfine and isotopic structure of the Ba II 4554 Å line. Top: splitting profile patterns (thin solid lines) and resulting profile (thick solid line) in the 1D MACKKL model (Maltby et al. 1986). Two blends are shown by dotted (Cr I 4553.945 Å) and dashed (Zr II 4553.970 Å) lines. Middle: equivalent widths and isotopic shift of the patterns. Bottom: bisector due to isotopic shift (small open circles) calculated in the MACKKL model and bisector of the spatially averaged profile (3D model) caused by the granular velocity field (solid line). |
| Open with DEXTER | |
2.2 Spectral synthesis
According to Rutten (1978), Rutten & Milkey (1979), Olshevsky et al. (2008) NLTE is the crucial factor that should be taken into account when calculating the Ba II 4554 Å solar line profile. Here we considered the NLTE barium line formation problem neglecting the effects of horizontal radiative transfer (1.5D approximation). A self-consistent solution of the kinetic and radiative transfer equations has been obtained with an efficient multilevel transfer code ``NATAJA'' developed by Shchukina & Trujillo Bueno (2001) to facilitate NLTE radiative transfer simulations with very complex atomic models. Before the code was successfully used for NLTE interpretation of iron, oxygen, titanium, and strontium solar spectra (Kostyk et al. 2006; Shchukina et al. 2005; Shchukina & Trujillo Bueno 2009; Trujillo Bueno & Shchukina 2007; Trujillo Bueno et al. 2004; Shchukina & Trujillo Bueno 2001; Khomenko et al. 2001; Kostyk & Shchukina 2004). The code is based on iterative methods for radiative transfer calculations (see Trujillo Bueno & Fabiani Bendicho 1995; Socas-Navarro & Trujillo Bueno 1997, and more references therein) that allow a fast and accurate solution of NLTE transfer problems.
Our atomic model includes 40 energy levels of Ba I and
Ba II (see Fig. 1). Note that all levels with
hyperfine structure (HFS) were treated as a single level, i.e. for
the HFS sublevels the population departure coefficients ![]() were taken to be equal. The levels are interconnected by 99 bound-bound
and 39 bound-free radiative transitions. All levels are coupled
via collisions with electrons. The atomic model and atomic data,
including oscillator strengths, bound-free cross-sections,
electron collisional rates, etc., are described in detail by
Olshevsky et al. (2008).
were taken to be equal. The levels are interconnected by 99 bound-bound
and 39 bound-free radiative transitions. All levels are coupled
via collisions with electrons. The atomic model and atomic data,
including oscillator strengths, bound-free cross-sections,
electron collisional rates, etc., are described in detail by
Olshevsky et al. (2008).
The departure coefficients ![]() found from the
self-consistent solution of the kinetic and radiative transfer
equations were used as input to carry out the formal solution of
the radiative transfer equation for the Ba II 4554 Å line.
At this step of the solution we took
into account the hyperfine structure (HFS) and isotopic
shift of the Ba II 4554 Å line (see
Fig. 2). Note that because of non-zero nuclear spin
only two isotopes (
found from the
self-consistent solution of the kinetic and radiative transfer
equations were used as input to carry out the formal solution of
the radiative transfer equation for the Ba II 4554 Å line.
At this step of the solution we took
into account the hyperfine structure (HFS) and isotopic
shift of the Ba II 4554 Å line (see
Fig. 2). Note that because of non-zero nuclear spin
only two isotopes (
![]() and
and
![]() )
have
HFS-splitting. The energies of HFS-sublevels are calculated according
to a formula given by Radzig and Smirnov (1985). The hyperfine
structure constant A needed for these calculations was taken
from Rutten (1978). We neglected the interaction of electrons
with a nuclear electric quadrupole momentum of because this
effect is rather small. The isotopic shift was derived using mass
shift and field shift constants from Berengut et al. (2003) and
mean square nuclear radii from Sakakihara & Tanaka (2001). We
synthesized the Ba II 4554 Å line profiles employing
the isotopic abundance ratio (Radzig & Smirnov 1985) for 17
sub-components. We included 2 blends (Cr I 4553.945 Å and Zr II 4553.970 Å) and 6 spectral lines of other
elements observed in the far wings of this line. The upper panel of
Fig. 2 shows that these blends produce only minor
effects on the synthesized profile.
)
have
HFS-splitting. The energies of HFS-sublevels are calculated according
to a formula given by Radzig and Smirnov (1985). The hyperfine
structure constant A needed for these calculations was taken
from Rutten (1978). We neglected the interaction of electrons
with a nuclear electric quadrupole momentum of because this
effect is rather small. The isotopic shift was derived using mass
shift and field shift constants from Berengut et al. (2003) and
mean square nuclear radii from Sakakihara & Tanaka (2001). We
synthesized the Ba II 4554 Å line profiles employing
the isotopic abundance ratio (Radzig & Smirnov 1985) for 17
sub-components. We included 2 blends (Cr I 4553.945 Å and Zr II 4553.970 Å) and 6 spectral lines of other
elements observed in the far wings of this line. The upper panel of
Fig. 2 shows that these blends produce only minor
effects on the synthesized profile.
We calculated the emergent intensities
![]() along
the Ba II 4554 Å line profile for the set of
along
the Ba II 4554 Å line profile for the set of
![]() wavelength points and for every (xi,yi) vertical
column of the 3D snapshot corresponding to the solar disc centre
wavelength points and for every (xi,yi) vertical
column of the 3D snapshot corresponding to the solar disc centre
![]() (
(![]() being the heliocentric angle). The
profiles were normalized to the mean continuum intensity
being the heliocentric angle). The
profiles were normalized to the mean continuum intensity
![]() averaged over the snapshot. The continuum
intensity was also used as a criterion to separate granular and
intergranular regions. The (xi,yi)-grid points with continuum
intensity greater than
averaged over the snapshot. The continuum
intensity was also used as a criterion to separate granular and
intergranular regions. The (xi,yi)-grid points with continuum
intensity greater than
![]() were taken as granules
(and the opposite for intergranules).
were taken as granules
(and the opposite for intergranules).
Since we are doing calculations for the disc centre, we assume complete frequency redistribution (CRD) for the Ba II 4554 Å line. According to Rutten & Milkey (1979); Rutten (1978) the effects of partial frequency redistribution (PRD) increase towards the limb, where the frequency-dependent wing source structure becomes noticeable. At the disc centre the differences between the PRD and CRD profiles of this line are small (1% of the continuous intensity in the core) so we can safely neglect the effects of PRD.
We do not use any ad hoc parameters such as micro- or
macroturbulence for the synthesis since the profiles are broadened
in a natural way by the velocity field existing in the 3D model.
The damping constant for the barium lines was determined as
the sum
![]() of van der Waals
collisional broadening
of van der Waals
collisional broadening
![]() by neutral hydrogen and helium
atoms and radiative broadening
by neutral hydrogen and helium
atoms and radiative broadening
![]() .
The other
collisional broadening processes (Stark broadening, quadrupole
broadening) are negligible (Rutten 1978). We employ the
.
The other
collisional broadening processes (Stark broadening, quadrupole
broadening) are negligible (Rutten 1978). We employ the
![]() based on a theory in which the van der Waals
potential is replaced by a Smirnov-Roueff potential for the close
interactions (Deridder & van Rensbergen 1976).
In view of the uncertainty of collisional damping, we treat the
based on a theory in which the van der Waals
potential is replaced by a Smirnov-Roueff potential for the close
interactions (Deridder & van Rensbergen 1976).
In view of the uncertainty of collisional damping, we treat the
![]() -value as a free parameter by introducing the usual
enhancement factor E.
In this study we use
E=1.3 and
-value as a free parameter by introducing the usual
enhancement factor E.
In this study we use
E=1.3 and
![]() derived earlier by
Olshevsky et al. (2008) from the Ba II 4554 Å 1.5D NLTE line
modelling in the same 3D snapshot. For these values of E and
derived earlier by
Olshevsky et al. (2008) from the Ba II 4554 Å 1.5D NLTE line
modelling in the same 3D snapshot. For these values of E and
![]() the authors obtained excellent agreement between
the spatially averaged synthetic profile and the observed one taken
from Liége atlas (Delbouille et al. 1973). We understand the limitations of the Smirnov-Roueff potential
approximation for the close interactions. These limitations might
be overcome using the semi-classical theory of
Barklem & O'Mara (1998). The introduction of the broadening for
P-D states given by these authors can be important for a proper
modelling of the Ba II 4554 Å line, particularly, for any
accurate calculation of the polarization Stokes amplitudes (Q/I)produced by scattering processes in the solar atmosphere. The
elastic collisions with neutral hydrogen atoms are known to be
efficient in modifying the atomic level population of long-lived
levels, like Ba II
the authors obtained excellent agreement between
the spatially averaged synthetic profile and the observed one taken
from Liége atlas (Delbouille et al. 1973). We understand the limitations of the Smirnov-Roueff potential
approximation for the close interactions. These limitations might
be overcome using the semi-classical theory of
Barklem & O'Mara (1998). The introduction of the broadening for
P-D states given by these authors can be important for a proper
modelling of the Ba II 4554 Å line, particularly, for any
accurate calculation of the polarization Stokes amplitudes (Q/I)produced by scattering processes in the solar atmosphere. The
elastic collisions with neutral hydrogen atoms are known to be
efficient in modifying the atomic level population of long-lived
levels, like Ba II
![]() .
Recent investigation of the
role of collisional depolarization of the Ba II 4554 Å line in
the low chromosphere by Derouich (2008) shows that this line
is clearly affected by isotropic collisions with neutral hydrogen
atoms through the effect of collisions on the
.
Recent investigation of the
role of collisional depolarization of the Ba II 4554 Å line in
the low chromosphere by Derouich (2008) shows that this line
is clearly affected by isotropic collisions with neutral hydrogen
atoms through the effect of collisions on the
![]() level.
However, the impact of depolarizing elastic collisions on the
emergent intensity (I) profiles in a weekly anisotropic medium
like the solar photosphere is expected to be negligible
(e.g., see the book by Landi Degl'Innocenti & Landolfi 2004).
level.
However, the impact of depolarizing elastic collisions on the
emergent intensity (I) profiles in a weekly anisotropic medium
like the solar photosphere is expected to be negligible
(e.g., see the book by Landi Degl'Innocenti & Landolfi 2004).
In Appendix A we summarize the NLTE effects on the formation of the Ba II 4554 Å line in the 3D snapshot and the compare NLTE and LTE calculations.
Below, we use the concept of the Eddington-Barbier height
of line formation, i.e. we evaluate the height H where the line
optical depth at a given wavelength point
![]() is
unity:
is
unity:
![]() .
We then assume that the
information about vertical velocity Vz at wavelength point
.
We then assume that the
information about vertical velocity Vz at wavelength point
![]() originates from height H. The reader should
be aware of the practical limitations of such a concept
(see Sánchez Almeida et al. 1996). However, for the purposes of
statistical quantification of the errors in Doppler diagnostic
methods it is reasonable and convenient to use the concept of the
Eddington-Barbier height of formation. We assumed that
two-dimensional maps of the synthesized intensity profiles
represent observations in the case of perfect seeing conditions
and no instrumental effects. We then use such ``perfect
observations'' to compute Dopplergrams and
originates from height H. The reader should
be aware of the practical limitations of such a concept
(see Sánchez Almeida et al. 1996). However, for the purposes of
statistical quantification of the errors in Doppler diagnostic
methods it is reasonable and convenient to use the concept of the
Eddington-Barbier height of formation. We assumed that
two-dimensional maps of the synthesized intensity profiles
represent observations in the case of perfect seeing conditions
and no instrumental effects. We then use such ``perfect
observations'' to compute Dopplergrams and ![]() -meter
velocities and to compare them to the ``true'' snapshot velocities
at the corresponding heights H.
-meter
velocities and to compare them to the ``true'' snapshot velocities
at the corresponding heights H.
2.3 Spatial smearing
Since ``perfect observations'' are only of theoretical interest to an observer, we study here the case of several degrading effects applied to the profiles. Observed images are degraded because of the Earth's atmospheric turbulence (seeing) and light diffraction by the telescope aperture (the finite spatial resolution of the telescope). There are other factors, such as stray light, but we expect that the observations are corrected for them during the reduction process.
Mathematically, the Fourier transform of the image registered by
detector is related to the Fourier transform of the original image
via the modulation transfer function (MTF) as follows:
| (1) |
where
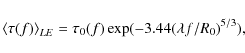
|
(2) |
where
![\begin{displaymath}\tau_0(f) = {2\over \pi} \left[{\rm cos}^{-1}\left({\lambda f...
...t(1 - \left({\lambda f
\over D}\right)^2\right)^{1/2} \right],
\end{displaymath}](/articles/aa/full_html/2009/42/aa12048-09/img61.png)
|
(3) |
if
At each wavelength, the original 2D intensity maps were Fourier-transformed and multiplied by the MTF calculated for a known telescope diameter and Fried's parameter R0. An inverse Fourier transform gives us the images registered by detector, i.e. the ``observed'' images, affected by the diffraction by the telescope aperture and the seeing effects.
2.4 Determination of Fried's parameter
In order to make a direct comparison between the synthetic and
observed spectra we have to know Fried's parameter R0. There is
no direct way to measure such a parameter in observations.
Ricort et al. (1981) proposed determining R0 from the
observed rms continuum contrast
![]() of solar granulation. Their computations are based
on using an analytical form for the power spectrum of the intensity
distribution at
of solar granulation. Their computations are based
on using an analytical form for the power spectrum of the intensity
distribution at
![]() Å obtained by
Ricort & Aime (1979) from speckle interferometric observations of
the solar granulation. To establish calibration dependence between
R0 and
Å obtained by
Ricort & Aime (1979) from speckle interferometric observations of
the solar granulation. To establish calibration dependence between
R0 and
![]() at other wavelengths
Ricort et al. (1981) used simplified assumptions that the solar
photosphere behaves as a blackbody, and that the differences in
formation heights of continuum radiation as a function of
wavelength can be ignored.
at other wavelengths
Ricort et al. (1981) used simplified assumptions that the solar
photosphere behaves as a blackbody, and that the differences in
formation heights of continuum radiation as a function of
wavelength can be ignored.
Here we propose another way to set up calibration curves for determination of R0 from granular contrast in observations. Our calculations use a 3D radiative transfer solution for the solar continuum intensity obtained by Trujillo Bueno & Shchukina (2009) in the same 3D snapshot as was employed above for the Ba II profile synthesis (see Sect. 2.1). Note that such a 3D approach gives a possibility of avoiding the simplification used by Ricort et al. (1981). The theoretical calibration curves for the wavelengths between 4000 Å and 8000 Å are plotted in Fig. 3.
In order to verify the 3D approach we compare the empirical
calibration curve at
![]() Å taken from Fig. 1 of
Ricort et al. (1981) with our theoretical curve. The analysis of
the results presented in Fig. 3 allows us to
conclude that at
Å taken from Fig. 1 of
Ricort et al. (1981) with our theoretical curve. The analysis of
the results presented in Fig. 3 allows us to
conclude that at
![]() Å both the empirical (open
circles) and the theoretical (dash line) curves in fact coincide.
Keeping in mind such a good agreement we use our theoretical
3D approach for determination of R0 in
Sect. 3.
Å both the empirical (open
circles) and the theoretical (dash line) curves in fact coincide.
Keeping in mind such a good agreement we use our theoretical
3D approach for determination of R0 in
Sect. 3.
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12048fig3.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12048-09/Timg63.png)
|
Figure 3:
Root-mean-square continuum contrast
|
| Open with DEXTER | |
2.5 Definition of artificial datasets
Here we define the nomenclature for the artificial datasets to be used in the rest of the paper.
D OT-LIKE DATA. Sütterlin et al. (2001) used an Irkutsk barium
filter (Skomorovsky et al. 1976) installed on the Dutch Open Telescope to
obtain Dopplergrams in the Ba II 4554 Å line. We have calculated
Dopplergrams from the synthetic profiles in order to model the
results of Sütterlin et al. (2001). To do that, we smeared the
original profiles using the DOT's diameter of D = 48 cm. In
addition, spectral smearing was performed by convolving the
profiles in wavelength with a Gaussian of
![]() (full width half
maximum) of 80 mÅ, corresponding to the barium filter spectral
profile. The Dopplergrams were constructed as a second-order
polynomial fit to the five points on the line profile situated at
(full width half
maximum) of 80 mÅ, corresponding to the barium filter spectral
profile. The Dopplergrams were constructed as a second-order
polynomial fit to the five points on the line profile situated at
![]() ,
-35, 0, 35 and 70 mÅ. The observations of
Sütterlin et al. (2001) were speckle-reconstructed, so we assumed
that the influence of the Earth's atmosphere was minimized, and that no
smearing with the Fried parameter was applied.
,
-35, 0, 35 and 70 mÅ. The observations of
Sütterlin et al. (2001) were speckle-reconstructed, so we assumed
that the influence of the Earth's atmosphere was minimized, and that no
smearing with the Fried parameter was applied.
V TT-LIKE DATA. The second type of artificial data represents
observations done with the German Vacuum Tower Telescope (VTT) and
Triple Etalon SOlar Spectrometer (TESOS; Tritschler et al. 2002).
The synthetic profiles were convolved using the telescope diameter
D = 70 cm, and a spectral bandwidth of TESOS of
FWHM = 15 mÅ. The Fried parameters in this case ranged
from R0=10 cm (medium seeing) to R0= 38 cm (excellent
seeing).
According to Fig. 3
(thick solid line and filled circles)
the corresponding root-mean-square continuum contrast
![]() of solar granulation
at the wavelength of the Ba II 4554 Å line
varies from 7.5% to 16.5%.
of solar granulation
at the wavelength of the Ba II 4554 Å line
varies from 7.5% to 16.5%.
3 Comparison to observations
In this paper we used observations of the Ba II 4554 Å line,
obtained in September 2006 by Khomenko, Collados and
Centeno at the 70-cm German Vacuum Tower Telescope (VTT) at the
Observatorio del Teide in Tenerife with the help of Triple Etalon
SOlar Spectrometer (TESOS; Tritschler et al. 2002). The quiet Sun
region close to the disc centre was observed, the presence of the
magnetic activity was controlled by the simultaneous observation
with the Tenerife Infrared Polarimeter II (TIP
II; Collados et al. 2007) in Fe I lines at 1.56 ![]() m. We took a single
TESOS wavelength scan in Ba II 4554 Å line made on September 2, which represents a series of 36 narrow-band filter images
(FWHM = 15 mÅ) obtained with 10 mÅ interval along the 4554 Å line profile. Each image was taken with a 500
m. We took a single
TESOS wavelength scan in Ba II 4554 Å line made on September 2, which represents a series of 36 narrow-band filter images
(FWHM = 15 mÅ) obtained with 10 mÅ interval along the 4554 Å line profile. Each image was taken with a 500 ![]() s exposure,
taking around 26 s to scan the complete line profile. The pixel
resolution of the TESOS camera was 0.089 arcsec. Due to the
instrument specifics, the TESOS field of view is circular. Taking
into account that the image quality towards its edge is worse we
have chosen a
s exposure,
taking around 26 s to scan the complete line profile. The pixel
resolution of the TESOS camera was 0.089 arcsec. Due to the
instrument specifics, the TESOS field of view is circular. Taking
into account that the image quality towards its edge is worse we
have chosen a
![]() pixel square cut from the central
part of each image. By spatially averaging each of the 36 filter
images we got the mean intensity profile of the Ba II 4554 Å line normalized to the mean continuum intensity of the Liège
Atlas (Delbouille et al. 1973).
pixel square cut from the central
part of each image. By spatially averaging each of the 36 filter
images we got the mean intensity profile of the Ba II 4554 Å line normalized to the mean continuum intensity of the Liège
Atlas (Delbouille et al. 1973).
Figure 4 shows observed and computed spatially averaged profiles of the Ba II 4554 Å line. The top panel of Fig. 4 demonstrates that the profile computed using the 3D snapshot is in a good agreement with the observed one taken from the Liége atlas (Delbouille et al. 1973). The central part of the line is reproduced very well while the fit for the outer red wing of the computed profile is a little worse. The averaged line profile obtained in 2006 with the TESOS instrument at the VTT is shown in the bottom panel of Fig. 4. Again, both computed and observed profiles agree well. The saw-tooth shape of far wings of the observed profile arises because of tuning effects of the TESOS etalons (Tritschler et al. 2002). We would like to stress that such a good match of the observations is not based on free parameter fitting but has been achieved self-consistently through the NLTE plane-parallel modeling combining a realistic atomic model and the 3D hydrodynamical snapshot.
Figure 5 shows the run of the rms contrast
with wavelength along the Ba II 4554 Å line for three sets of
single-wavelength images: observed, smeared, and non-smeared
synthetic data. The synthetic profiles were smeared employing the
method developed in Sect. 2.3. We applied
the theoretical calibration curve at
![]() Å shown in
Fig. 3 (thick solid line) to define the Fried
parameter from the VTT observations of the Ba II 4554 Å line. We found that during observations the rms continuum
contrast
Å shown in
Fig. 3 (thick solid line) to define the Fried
parameter from the VTT observations of the Ba II 4554 Å line. We found that during observations the rms continuum
contrast
![]() at the wavelength of this line
was around 7%. Thus, we estimate R0 to range
range between 9 and 10 cm. Synthetic data in
Fig. 5 are smeared using R0=9 cm.
at the wavelength of this line
was around 7%. Thus, we estimate R0 to range
range between 9 and 10 cm. Synthetic data in
Fig. 5 are smeared using R0=9 cm.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12048fig4.eps} %
\end{figure}](/articles/aa/full_html/2009/42/aa12048-09/Timg67.png)
|
Figure 4: Calculated and observed intensity disc-centre profiles of the Ba II 4554 Å line. Solid line: the spatially averaged NLTE profile for the 3D model. Small open circles: the profile from the Liège Atlas ( top); spatially averaged profile obtained from observations at the VTT with TESOS in 2006 ( bottom). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12048fig5.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12048-09/Timg68.png)
|
Figure 5:
Root-mean-square contrast at different wavelengths along
the Ba II 4554 line profile. Dashed line:
|
| Open with DEXTER | |
Seeing effects influence the rms contrast in the line wings,
while in the line core its influence is not so significant,
although the wing contrast is much higher than the contrast in the
line core. Two local maxima near
![]() mÅ are not so high and sharp in the observed data as in the smeared
computed profiles. While at other wavelengths the agreement is
fairly good. Such blurring of the maxima may be due to the wider
bandwidth of TESOS filter system than given by
Tritschler et al. (2002).
mÅ are not so high and sharp in the observed data as in the smeared
computed profiles. While at other wavelengths the agreement is
fairly good. Such blurring of the maxima may be due to the wider
bandwidth of TESOS filter system than given by
Tritschler et al. (2002).
Comparison of the synthetic and observed line profiles performed in this section suggests that 3D atmospheric model of Asplund et al. (2000a) together with our NLTE calculations and treating of atmospheric and instrumental influence, reproduce well the average characteristics of the observed granulation pattern in Ba II 4554 Å line.
4 Dopplergram technique
We discuss in this section the range of validity of the 5-point
Dopplergram technique used by Sütterlin et al. (2001) at the DOT
to obtain LOS velocities.
The comparison between the Dopplergram velocities from the
DOT-like data ![]() and the ``true'' snapshot velocities Vz is
given in Fig. 6. The velocities
and the ``true'' snapshot velocities Vz is
given in Fig. 6. The velocities ![]() were
corrected for the asymmetry caused by the hyperfine structure (the
bottom panel of Fig. 2).
were
corrected for the asymmetry caused by the hyperfine structure (the
bottom panel of Fig. 2).
When applying the Dopplergram technique, it is important to
identify the height in the atmosphere from where the velocities
originate. We assumed that the information about velocities
at different points around the snapshot comes from nearly the same
heights. Then we calculated the correlation coefficient between
the maps of ![]() and Vz, taking the latter at different
heights, as shown in Fig. 6a. This correlation
tells us at what height the Dopplergram velocities
of the DOT-like data measure the real solar velocities. As we can
see, the correlation coefficient strongly depends on the
atmospheric height, for both the smeared and non-smeared data. The
maximum correlation reaches the value
and Vz, taking the latter at different
heights, as shown in Fig. 6a. This correlation
tells us at what height the Dopplergram velocities
of the DOT-like data measure the real solar velocities. As we can
see, the correlation coefficient strongly depends on the
atmospheric height, for both the smeared and non-smeared data. The
maximum correlation reaches the value ![]() 0.9 at heights around
300 km. Thus, we can identify a rather narrow layer where the
Dopplergram velocities originate.
0.9 at heights around
300 km. Thus, we can identify a rather narrow layer where the
Dopplergram velocities originate.
Figure 6b gives the scatter plot of ![]() and
Vz, the latter taken at the height of maximum correlation (285 km). It demonstrates that in general the speckle-reconstructed
Dopplergram velocities correspond to the true snapshot velocities
rather well, with the standard deviation being less than 0.4 km s-1.
The surface maps of
and
Vz, the latter taken at the height of maximum correlation (285 km). It demonstrates that in general the speckle-reconstructed
Dopplergram velocities correspond to the true snapshot velocities
rather well, with the standard deviation being less than 0.4 km s-1.
The surface maps of ![]() and Vz also agree rather well (panels
c and d). Thus, the Dopplergram velocities reproduce in many
details the ``true'' granulation velocity structure existing at
heights around 300 km. Nevertheless, it can be seen from the maps
that at some locations in intergranular lanes the Dopplergram
velocities overestimate the snapshot velocities. These are the
locations with strong downflows. The difference between
and Vz also agree rather well (panels
c and d). Thus, the Dopplergram velocities reproduce in many
details the ``true'' granulation velocity structure existing at
heights around 300 km. Nevertheless, it can be seen from the maps
that at some locations in intergranular lanes the Dopplergram
velocities overestimate the snapshot velocities. These are the
locations with strong downflows. The difference between ![]() and
Vz can be as high as 1 km s-1 at these locations. Such an
excess manifests itself in Dopplergram velocity maps as patches of
enhanced brightness (Fig. 6c, location marked by
(1)), being absent in the snapshot velocity maps.
and
Vz can be as high as 1 km s-1 at these locations. Such an
excess manifests itself in Dopplergram velocity maps as patches of
enhanced brightness (Fig. 6c, location marked by
(1)), being absent in the snapshot velocity maps.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{12048fig6.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12048-09/Timg71.png)
|
Figure 6:
Comparison of the snapshot vertical velocities Vz with the Dopplergram velocities |
| Open with DEXTER | |
Interestingly, with the narrower bandwidth and larger
diameter of the telescope than in the case of the DOT observations
the overestimation of the Doppler velocities ![]() in
intergranular areas with strong downflows found from the
``speckle-reconstructed observations'' turns out to be appreciably
larger. We display such a case for VTT-like data in
Fig. 7. As follows from the figure, the
deviation reaches approximately 3 km s-1.
in
intergranular areas with strong downflows found from the
``speckle-reconstructed observations'' turns out to be appreciably
larger. We display such a case for VTT-like data in
Fig. 7. As follows from the figure, the
deviation reaches approximately 3 km s-1.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12048fig7.eps} %
\end{figure}](/articles/aa/full_html/2009/42/aa12048-09/Timg72.png)
|
Figure 7:
Comparison of the snapshot vertical velocities Vz with the Dopplergram velocities |
| Open with DEXTER | |
Figure 8 explains why such bright patches can arise in speckle-reconstructed observations and why it happens specifically in intergranular areas. It displays examples of the parabolic fit to the five fixed wavelength points of the original profiles (top) and DOT-like smeared profiles (bottom). The profiles are taken at the spatial locations marked (1) and (2) in Fig. 6b-d. The profile marked (1) originates from the area with a high intergranular downflow (left) and the profile marked (2) originates from the area with a high granular upflow (right). According to Fig. 8a, it seems impossible to measure correctly the velocity from the weak twisted intergranular profile provided that the strong redshift forces four of the five wavelength points used for fitting to be situated in the blue wing. As a consequence, the parabola turns out to be much more redshifted than the original profile. So the Dopplergram velocity derived from the wavelength position of the parabola bisector (thin vertical line) will be considerably greater compared to the velocity inferred from the bisector of the original profile (small open circles). Smearing caused by the telescope and filter to some degree smoothes the irregular shape of the intergranular profile and decreases the redshift of the parabola (Fig. 8b). Nevertheless, the velocity remains overestimated. Thus, we conclude that the Dopplergram velocities calculated from the speckle-reconstructed DOT-like data in intergranular lanes can be appreciably greater than the real ones.
Contrary to the intergranular profile the deep and more symmetric
granular profile allows us to estimate the velocity from the
parabolic fit rather well (Fig. 8c). The
effects of smearing are less pronounced in this case
(Fig. 8d). So in granular areas with strong
upflows one can expect a reasonable agreement between the ``true''
velocities Vz and velocities ![]() recovered from the DOT-like
data.
recovered from the DOT-like
data.
![\begin{figure}
\par\includegraphics[width=6.3cm,clip]{12048fig8a.eps}\includegraphics[width=6.3cm,clip]{12048fig8b.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12048-09/Timg73.png)
|
Figure 8:
Ba II 4554 Å line profiles at two selected locations corresponding to a high downflow ( left) and a high upflow ( right), marked by (1) and (2) in Fig. 6. a), c): profiles without smearing. Thin lines with dots: parabolic fit to the five wavelength positions
|
| Open with DEXTER | |
Summarizing the conclusion of this Section, the five-point Dopplergram technique applied to the Ba II 4554 Å line profiles in speckle-reconstructed DOT-like data is a valuable tool for the diagnostic of the solar velocity field at heights around 300 km. Only in intergranular lanes with strong downflows can the velocity be overestimated producing artificially bright points at the Dopplergram velocity maps like those obtained by Sütterlin et al. (2001). These authors interpreted the bright points as locations of the magnetic flux tubes. However, our calculations show that at least part of such bright points may be simply an artefact caused by the parabolic fit.
5
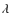 -meter technique
-meter technique
The ![]() -meter method of Stebbins & Goode (1987) can be
considered as a form of the ``bisector shift'' technique proposed
earlier by Kulander & Jefferies (1966) to evaluate the
atmospheric velocity field from the asymmetries in observed line
profiles. The
-meter method of Stebbins & Goode (1987) can be
considered as a form of the ``bisector shift'' technique proposed
earlier by Kulander & Jefferies (1966) to evaluate the
atmospheric velocity field from the asymmetries in observed line
profiles. The ![]() -meter method deals with two line profile
parameters such as the line bisector and the full spectral line
width
-meter method deals with two line profile
parameters such as the line bisector and the full spectral line
width
![]() .
.
The displacement of a midpoint of a section of the line profile of
a certain width
![]() is assumed to be a result of
the Doppler shift of the line opacity coefficient caused by the
non-thermal velocities in the layer where this section is formed.
According to Stebbins & Goode (1987) the velocities and intensities
from progressively deeper sections of the line profile correspond
to progressively higher layers in the atmosphere. Following the
is assumed to be a result of
the Doppler shift of the line opacity coefficient caused by the
non-thermal velocities in the layer where this section is formed.
According to Stebbins & Goode (1987) the velocities and intensities
from progressively deeper sections of the line profile correspond
to progressively higher layers in the atmosphere. Following the
![]() -meter procedure we introduced a set of line profile
widths
-meter procedure we introduced a set of line profile
widths
![]() ranging from 306 to 78 mÅ (see
Fig. 8). Due to the irregular shape of the
Ba II 4554 Å line core, a significant number of synthetic
profiles never have a spectral line width lower than 78 mÅ. At
the same time shallow far wings of many profiles do not allow us
to detect and analyse velocities at widths above
ranging from 306 to 78 mÅ (see
Fig. 8). Due to the irregular shape of the
Ba II 4554 Å line core, a significant number of synthetic
profiles never have a spectral line width lower than 78 mÅ. At
the same time shallow far wings of many profiles do not allow us
to detect and analyse velocities at widths above
![]() mÅ. The selected
mÅ. The selected
![]() range
corresponds to the intensities of spatially averaged profile
varying between 0.86 and 0.16. The corresponding range of the mean
formation heights lies between
range
corresponds to the intensities of spatially averaged profile
varying between 0.86 and 0.16. The corresponding range of the mean
formation heights lies between ![]() -50 and
-50 and ![]() 500 km.
500 km.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{12048fig9.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12048-09/Timg75.png)
|
Figure 9:
Correlation coefficients between |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{12048fig10.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12048-09/Timg76.png)
|
Figure 10:
Comparison between the |
| Open with DEXTER | |
We slightly modified the standard ![]() -meter procedure
keeping in mind that velocity field shifts the line opacity
coefficients of various atmospheric layers towards one wing of the
static line and away from the other. Such a shift expands the
optical line depth
-meter procedure
keeping in mind that velocity field shifts the line opacity
coefficients of various atmospheric layers towards one wing of the
static line and away from the other. Such a shift expands the
optical line depth
![]() on one side of
the line and compresses on the other side. As a consequence, the
height of formation of the equal intensity points in the blue
on one side of
the line and compresses on the other side. As a consequence, the
height of formation of the equal intensity points in the blue
![]() and red
and red
![]() wings belonging
the same spectral width
wings belonging
the same spectral width
![]() tends to be
different. Our modified
tends to be
different. Our modified ![]() -meter procedure is the
following. We applied the above set of spectral widths both to
the spatially averaged profile and to the individual profiles
over the snapshot. The spatially averaged profile corrected for
asymmetry due to granulation velocity field (see
Fig. 2, bottom) was considered as a reference
profile representing a stationary case. Since our study deals only
with the relative changes of the Ba II 4554 Å line parameters
no correction for the asymmetry caused by the hyperfine structure
and isotopic shift was made. We derived the
-meter procedure is the
following. We applied the above set of spectral widths both to
the spatially averaged profile and to the individual profiles
over the snapshot. The spatially averaged profile corrected for
asymmetry due to granulation velocity field (see
Fig. 2, bottom) was considered as a reference
profile representing a stationary case. Since our study deals only
with the relative changes of the Ba II 4554 Å line parameters
no correction for the asymmetry caused by the hyperfine structure
and isotopic shift was made. We derived the ![]() -meter
velocities
-meter
velocities
![]() in the blue wings by measuring the
Doppler shift of the blue intensity point belonging a certain
spectral width relatively the corresponding blue point of the
spatially averaged profile (same applies to the red wings).
in the blue wings by measuring the
Doppler shift of the blue intensity point belonging a certain
spectral width relatively the corresponding blue point of the
spatially averaged profile (same applies to the red wings).
The velocities
![]() obtained by this method were
compared to the corresponding snapshot velocities Vz. The Vzvalues were specified separately for the blue
obtained by this method were
compared to the corresponding snapshot velocities Vz. The Vzvalues were specified separately for the blue
![]() and red
and red
![]() wavelengths belonging the same line
width. These velocities were taken at heights where the optical
depth at the corresponding wavelength points was equal to unity (see
Sect. 2.2). The results of these calculation are displayed in
Figs. 9 to 14.
wavelengths belonging the same line
width. These velocities were taken at heights where the optical
depth at the corresponding wavelength points was equal to unity (see
Sect. 2.2). The results of these calculation are displayed in
Figs. 9 to 14.
5.1  -meter: original resolution
-meter: original resolution
Figure 9 shows the correlation coefficients
between the maps of ![]() -meter velocities
-meter velocities
![]() and
the snapshot velocities Vz taken at corresponding heights. It
gives several cases for different seeing conditions (value of the
parameter R0) for the VTT-like data and also the case of no
smearing.
When the smearing is absent, the correlation coefficient for both
blue and red wing velocities is rather high. It reaches a maximum
value of
and
the snapshot velocities Vz taken at corresponding heights. It
gives several cases for different seeing conditions (value of the
parameter R0) for the VTT-like data and also the case of no
smearing.
When the smearing is absent, the correlation coefficient for both
blue and red wing velocities is rather high. It reaches a maximum
value of ![]() 0.97 around
0.97 around
![]() mÅ,
being slightly smaller in the inner wing of the line.
mÅ,
being slightly smaller in the inner wing of the line.
The scatter plots and maps of the
![]() and Vzvelocities in the inner wing of the line at
and Vzvelocities in the inner wing of the line at
![]() mÅ are presented in Fig. 10 for the case of
no smearing. As follows from panel (a) of this figure, in the
inner blue wing
mÅ are presented in Fig. 10 for the case of
no smearing. As follows from panel (a) of this figure, in the
inner blue wing ![]() -meter
velocities agree essentially with
the true snapshot velocities at that height in most of the grid
points. The correlation coefficient between them is very high and
is close to 0.9. The comparison of the velocity maps in
panels (c) and (d) supports this conclusion. Nevertheless, there
is a set
of grid points belonging mainly to intergranular lanes where the
fit is fairly bad.
The map of the true velocities Vz in Fig. 10d
reveals the presence of a number of intergranular lanes (as
defined by the continuum intensity) where the upflowing velocities
are observed at heights of formation of the blue wing intensity at
-meter
velocities agree essentially with
the true snapshot velocities at that height in most of the grid
points. The correlation coefficient between them is very high and
is close to 0.9. The comparison of the velocity maps in
panels (c) and (d) supports this conclusion. Nevertheless, there
is a set
of grid points belonging mainly to intergranular lanes where the
fit is fairly bad.
The map of the true velocities Vz in Fig. 10d
reveals the presence of a number of intergranular lanes (as
defined by the continuum intensity) where the upflowing velocities
are observed at heights of formation of the blue wing intensity at
![]() mÅ. The
mÅ. The ![]() -meter velocities do
not recover such upflowing points well, suggesting significantly
smaller absolute value of the velocities or even their sign
reversal. An example of such a location is marked by an open
circle in Fig. 10.
-meter velocities do
not recover such upflowing points well, suggesting significantly
smaller absolute value of the velocities or even their sign
reversal. An example of such a location is marked by an open
circle in Fig. 10.
Figure 10b demonstrates that in the red inner wing
the match between Vz and
![]() is appreciably worse.
The
is appreciably worse.
The ![]() -meter velocities tend to be more redshifted.
According to Fig. 11, the blue and the red wing
-meter velocities tend to be more redshifted.
According to Fig. 11, the blue and the red wing
![]() are essentially the same (except for a few grid
points), whereas the corresponding Vz are not. The reason for
that lies in the different formation heights of the blue and red
wing intensities at the same
are essentially the same (except for a few grid
points), whereas the corresponding Vz are not. The reason for
that lies in the different formation heights of the blue and red
wing intensities at the same
![]() (we discuss this
point in more details in Sect. 5.3). The velocities measured by
the
(we discuss this
point in more details in Sect. 5.3). The velocities measured by
the ![]() -meter technique correspond better to the heights
where the blue-wing intensities are formed.
-meter technique correspond better to the heights
where the blue-wing intensities are formed.
Figure 12a, b gives two more examples of the
correlation between the ![]() -meter velocities and the
snapshot velocities in the outer wings of the line. The match is
typically rather good and the correlation is high, except that the
amplitudes of the
-meter velocities and the
snapshot velocities in the outer wings of the line. The match is
typically rather good and the correlation is high, except that the
amplitudes of the ![]() -meter velocities are systematically
lower. The latter is easy to understand bearing in mind that the
method gives the average information over a certain height range,
thus leading to a decrease in the amplitude.
-meter velocities are systematically
lower. The latter is easy to understand bearing in mind that the
method gives the average information over a certain height range,
thus leading to a decrease in the amplitude.
In summary, under perfect conditions, the ![]() -meter
technique allows us to obtain information about the LOS velocities
with a rather good precision over the whole photosphere, the
agreement being a little worse for the inner wings of the
line. The blue and the red wing
-meter
technique allows us to obtain information about the LOS velocities
with a rather good precision over the whole photosphere, the
agreement being a little worse for the inner wings of the
line. The blue and the red wing
![]() velocities are
very close to each other.
velocities are
very close to each other.
5.2  -meter: reduced resolution
-meter: reduced resolution
Apart from the case of the original resolution discussed above,
Fig. 9 contains the calculation of the correlation
coefficients between Vz and
![]() for the VTT-like
data smeared to have a different spatial resolution by varying the
Fried parameter from 38 to 10 cm. As expected, the correlation
coefficient gets lower compared to the case of perfect seeing
conditions. Nevertheless, even for the medium spatial resolution
(R0=10 cm) the correlation for the inner wings (
for the VTT-like
data smeared to have a different spatial resolution by varying the
Fried parameter from 38 to 10 cm. As expected, the correlation
coefficient gets lower compared to the case of perfect seeing
conditions. Nevertheless, even for the medium spatial resolution
(R0=10 cm) the correlation for the inner wings (
![]() mÅ) is rather high (
mÅ) is rather high (![]() 0.7). For the
higher values of R0 the correlation coefficient increases up to
0.8-0.9. Opposite the case for no smearing, the correlation
coefficient decreases from the inner to the outer wings. The
velocity measured in the outer wings (
0.7). For the
higher values of R0 the correlation coefficient increases up to
0.8-0.9. Opposite the case for no smearing, the correlation
coefficient decreases from the inner to the outer wings. The
velocity measured in the outer wings (
![]() mÅ) is less precise.
mÅ) is less precise.
The effects produced by the spatial smearing on the amplitudes of
the measured velocities
![]() are shown in
Fig. 12. The following points can be underlined from
this figure:
are shown in
Fig. 12. The following points can be underlined from
this figure:
- In the original data the maximum absolute values of the velocities are higher above intergranular lanes than above granules. Spatial smearing reduces both the absolute values of the velocities and the asymmetry in the scatter plots. Nevertheless, the velocity asymmetry is still present.
- Even under excellent seeing conditions (R0=29 cm) the outer
wing
 -meter velocities for
-meter velocities for
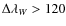 mÅ are less reliable that the inner wing velocities.
mÅ are less reliable that the inner wing velocities.
- The inner wing velocities (
 mÅ) still give a fairy good measure of the true velocities
for the Fried parameter (R0=10 cm).
mÅ) still give a fairy good measure of the true velocities
for the Fried parameter (R0=10 cm).
- As the inner wings of the line are less sensitive to spatial smearing, the Ba II 4554 Å line can be useful to measure velocities mainly in the upper photosphere.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12048fig11.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12048-09/Timg85.png)
|
Figure 11:
Scatter plot of the red and blue wing |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12048fig12.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12048-09/Timg86.png)
|
Figure 12:
Scatter plot of the |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=11.5cm,clip]{12048fig13.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12048-09/Timg87.png)
|
Figure 13: Formation heights of the intensity along the line profiles calculated for a set of spectral widths in the blue ( left) and red ( right) wings for all grid points from the 3D snapshot. Thick solid lines and open circles: mean formation heights and their standard deviation, respectively. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=11.5cm,clip]{12048fig14.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12048-09/Timg88.png)
|
Figure 14:
a), c): formation heights of the blue wing intensities vs. formation heights of the red wing intensities at
two spectral widths:
|
| Open with DEXTER | |
5.3 Intensity formation heights along the line profile
The ![]() -meter technique only yields qualitative results as
long as it is not accompanied by the knowledge of heights where
the information on the velocity and intensity variations comes
from. In this section we give the results of the calculation of such
heights. We calculated the Eddington-Barbier formation heights
(see Sect. 2.2) for the intensity at each section of the Ba II 4554 Å line profile having a certain spectral width
-meter technique only yields qualitative results as
long as it is not accompanied by the knowledge of heights where
the information on the velocity and intensity variations comes
from. In this section we give the results of the calculation of such
heights. We calculated the Eddington-Barbier formation heights
(see Sect. 2.2) for the intensity at each section of the Ba II 4554 Å line profile having a certain spectral width
![]() .
Below we use the notation
.
Below we use the notation ![]() for the blue wing
intensity formation heights calculated at
for the blue wing
intensity formation heights calculated at
![]() positions in the blue wing, and similarly for the red wing intensity
formation heights
positions in the blue wing, and similarly for the red wing intensity
formation heights ![]() ,
calculated at
,
calculated at
![]() positions in the red wing. Both
positions in the red wing. Both ![]() and
and ![]() correspond to the
same
correspond to the
same
![]() .
We repeated the calculation for the all
grid points of the 3D snapshot. The results of such calculations
are presented in Figs. 13 and 14.
These figures give an answer to several important questions.
.
We repeated the calculation for the all
grid points of the 3D snapshot. The results of such calculations
are presented in Figs. 13 and 14.
These figures give an answer to several important questions.
Firstly, how realistic is to assume that ![]() and
and ![]() belonging
to the same
belonging
to the same
![]() are constant over the 3D
snapshot? The results shown in Fig. 13 suggest
that this assumption is far from reality. At each fixed
are constant over the 3D
snapshot? The results shown in Fig. 13 suggest
that this assumption is far from reality. At each fixed
![]() ,
both
,
both ![]() and
and ![]() vary in a rather wide range. In
outermost sections of the profile (
vary in a rather wide range. In
outermost sections of the profile (
![]() mÅ) the heights vary between about -175 km and +75 km,
while in the inner section (
mÅ) the heights vary between about -175 km and +75 km,
while in the inner section (
![]() mÅ) the
range of the variations is larger and lies between +300 km and
+800 km. Despite the large scatter, the mean formation heights
of the each section of the profile
mÅ) the
range of the variations is larger and lies between +300 km and
+800 km. Despite the large scatter, the mean formation heights
of the each section of the profile
![]() have a
well pronounced dependence on
have a
well pronounced dependence on
![]() (thick solid
curves in Fig. 13). This makes it possible to assign
in, a certain way, a height dependence to the velocity
measurements by
(thick solid
curves in Fig. 13). This makes it possible to assign
in, a certain way, a height dependence to the velocity
measurements by ![]() -meter technique. This can be done by
ascribing the response of each
-meter technique. This can be done by
ascribing the response of each
![]() section of the
spectral line to the mean height
section of the
spectral line to the mean height
![]() .
.
Secondly, is it correct to assume that the ![]() and
and ![]() formation heights belonging to the same
formation heights belonging to the same
![]() are
equal? In order to answer this question, we show in
Fig. 14 two representative cases for
are
equal? In order to answer this question, we show in
Fig. 14 two representative cases for ![]() and
and
![]() calculated at two positions in the inner (
calculated at two positions in the inner (
![]() mÅ) and the outer (
mÅ) and the outer (
![]() mÅ) wings of the line. The
mÅ) wings of the line. The
![]() mÅ corresponds to the section of the Ba II 4554 Å where the line
opacity profile is shallow. So one can expect the difference in
heights of formation
mÅ corresponds to the section of the Ba II 4554 Å where the line
opacity profile is shallow. So one can expect the difference in
heights of formation ![]() and
and ![]() caused by the Doppler shift
of the opacity profile to be small. The
width
caused by the Doppler shift
of the opacity profile to be small. The
width
![]() mÅ belongs to the inner
section of the Ba II 4554 Å characterized by a steeper part of
the line opacity profile. It is expected that the same Doppler
shifts produce a more important difference in the optical depths
on opposite sides of the Ba II 4554 Å line and, hence, a
somewhat greater difference between the
mÅ belongs to the inner
section of the Ba II 4554 Å characterized by a steeper part of
the line opacity profile. It is expected that the same Doppler
shifts produce a more important difference in the optical depths
on opposite sides of the Ba II 4554 Å line and, hence, a
somewhat greater difference between the ![]() and
and ![]() heights.
What is the magnitude of this difference?
heights.
What is the magnitude of this difference?
As follows from Fig. 14a, in the outer wings of
the Ba II 4554 Å line the blue ![]() and red
and red ![]() heights are
indeed very close to each other, both varying over the 3D
snapshot. The histograms displayed in Fig. 14b
demonstrate that the distributions of
heights are
indeed very close to each other, both varying over the 3D
snapshot. The histograms displayed in Fig. 14b
demonstrate that the distributions of ![]() and
and ![]() are
similar and have a sharp cut off. It means that outer wings are
formed in a narrow atmospheric layer with mean heights
are
similar and have a sharp cut off. It means that outer wings are
formed in a narrow atmospheric layer with mean heights
![]() and
and
![]() of the blue and red wings being very close to each other.
of the blue and red wings being very close to each other.
Figure 14c shows a similar calculation for the
inner sections of the Ba II 4554 Å line. The Doppler shift of
the line opacity profile leads to a complex behaviour of the ![]() and
and ![]() heights. Two groups of points can be distinguished in
the scatter plot of
heights. Two groups of points can be distinguished in
the scatter plot of ![]() vs.
vs. ![]() calculated over the snapshot.
For the first group (symbols above diagonal), the
calculated over the snapshot.
For the first group (symbols above diagonal), the ![]() heights
are concentrated in a rather narrow band around +200 km while the
heights
are concentrated in a rather narrow band around +200 km while the
![]() heights extend for several hundreds of kilometres from nearly
+100 km to +800 km. This group of points belong largely to
the profiles coming from granular regions. For the second group of
points (symbols below the diagonal) the behaviour is the
opposite. This group originates mostly in intergranular lanes.
Only a relatively small number of the profiles have approximately
the same
heights extend for several hundreds of kilometres from nearly
+100 km to +800 km. This group of points belong largely to
the profiles coming from granular regions. For the second group of
points (symbols below the diagonal) the behaviour is the
opposite. This group originates mostly in intergranular lanes.
Only a relatively small number of the profiles have approximately
the same ![]() and
and ![]() heights (symbols along the diagonal).
heights (symbols along the diagonal).
The histograms of the ![]() and
and ![]() heights for the inner
sections of the Ba II 4554 Å line (Fig. 14d)
are not symmetric. The histograms have a maximum at heights around
+200 km and a sharp cut-off below this height. There is a long
tail toward 600-800 km. This tail is more pronounced for the red
wing heights
heights for the inner
sections of the Ba II 4554 Å line (Fig. 14d)
are not symmetric. The histograms have a maximum at heights around
+200 km and a sharp cut-off below this height. There is a long
tail toward 600-800 km. This tail is more pronounced for the red
wing heights ![]() .
Such an asymmetry suggests that the
information in the inner wing comes from two distinct layers. In
most of the grid points the intensity at
.
Such an asymmetry suggests that the
information in the inner wing comes from two distinct layers. In
most of the grid points the intensity at
![]() mÅ is formed around +300 km, whereas in a
smaller but still appreciable number of points the intensity comes
from higher layers between +400 and +800 km. On the whole, the
mean formation height of the inner red wing is larger than that
of the inner blue wing.
mÅ is formed around +300 km, whereas in a
smaller but still appreciable number of points the intensity comes
from higher layers between +400 and +800 km. On the whole, the
mean formation height of the inner red wing is larger than that
of the inner blue wing.
6 Conclusions
In this paper we have analysed the range of validity of the two
Doppler diagnostic techniques using the Ba II 4554 Å line,
i.e. the 5-point Dopplergram technique (Sütterlin et al. 2001) and
the ![]() -meter technique (Stebbins & Goode 1987). We have
performed NLTE radiative transfer calculations of the Ba II 4554
Å intensity profiles in the 3D snapshot of hydrodynamical
simulations of solar convection (Asplund et al. 2000a), neglecting
the effects of horizontal radiative transfer, but considering a
realistic barium atomic model and taking into account the
hyperfine structure and isotopic shift. The original resolution
profiles were smeared to reproduce the DOT-like and VTT-like data
and study the effects of the limited resolution into the
reliability of the results produced by the two Doppler diagnostic
techniques.
-meter technique (Stebbins & Goode 1987). We have
performed NLTE radiative transfer calculations of the Ba II 4554
Å intensity profiles in the 3D snapshot of hydrodynamical
simulations of solar convection (Asplund et al. 2000a), neglecting
the effects of horizontal radiative transfer, but considering a
realistic barium atomic model and taking into account the
hyperfine structure and isotopic shift. The original resolution
profiles were smeared to reproduce the DOT-like and VTT-like data
and study the effects of the limited resolution into the
reliability of the results produced by the two Doppler diagnostic
techniques.
Our results for the 5-point Dopplergram technique can be summarized as follows:
- The NLTE simulations using the 3D hydrodynamical model support the opinion that the speckle-reconstructed Dopplergram velocities obtained from the DOT-like data give appropriate representation of the solar photospheric velocity field.
- The information on the velocities obtained from such Dopplergrams comes from a thin atmospheric layer located at heights around 300 km. The speckle-reconstructed Dopplergram velocity maps reproduce in many details the ``true'' velocity structures existing in this layer.
- The Dopplergram technique can overestimate the velocities in intergranular areas with strong downflows. This excess appears in the speckle-reconstructed maps as localized points with enhanced brightness. The interpretation of such bright points in terms of magnetic fields has to be carried out with caution. At least some of them may be an artefact caused by the Dopplergram technique itself.
- Under perfect seeing conditions the
 -meter
technique allows us to obtain information about the LOS
velocities throughout the photosphere with rather good
precision. Only in the upper photosphere is the particular velocity
structure with upflowing points in intergranular lanes not
always well reproduced.
-meter
technique allows us to obtain information about the LOS
velocities throughout the photosphere with rather good
precision. Only in the upper photosphere is the particular velocity
structure with upflowing points in intergranular lanes not
always well reproduced.
- The velocities measured by the
 -meter technique
correspond better to the ``true'' snapshot velocities taken at
heights of formation of the blue line wing, rather that the red
wing.
-meter technique
correspond better to the ``true'' snapshot velocities taken at
heights of formation of the blue line wing, rather that the red
wing.
- Even for rather medium seeing conditions the inner wings of the Ba II 4554 Å line give reliable information about the velocity field in the upper photosphere. The results from the outer wings are less reliable.
- The mean formation heights of each section of
the Ba II 4554 Å line profile have a well-pronounced
dependence on the spectral width of the section. This gives the
possibility to assign height dependence to the velocity
measurements by the
 -meter technique. The non-thermal
motions can be reliably measured with the
-meter technique. The non-thermal
motions can be reliably measured with the  -meter
technique applied to the Ba II 4554 Å line throughout the
photosphere up to the temperature minimum.
-meter
technique applied to the Ba II 4554 Å line throughout the
photosphere up to the temperature minimum.
This work was partially supported by the Spanish Ministerio de Educación y Ciencia (projects AYA2007-63881 and AYA2007-66502), and by the National Academy of Sciences of Ukraine (project 1.4.6/7-233B).
References
- Asplund, M., Nordlund, Å., & Trampedach, R. 1999, in Theory and Tests of Convection in Stellar Structures, ed. A. Giménez, E. F. Guinan, & B. Montesinos, ASP Conf. Ser., 173, 221
- Asplund, M., Ludwig, H.-G., Nordlund, A., et al. 2000a, A&A, 359, 669 [NASA ADS]
- Asplund, M., Nordlund, Å., Trampedach, R., Allende Prieto, C., & Stein, R. F. 2000b, A&A, 359, 729 [NASA ADS]
- Asplund, M., Grevesse, N., Sauval, A. J., Allende Prieto, C., & Kiselman, D. 2004, A&A, 417, 751 [NASA ADS] [CrossRef] [EDP Sciences]
- Asplund, M., Grevesse, N., & Sauval, A. J. 2005, in Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis, ed. P. N. Bash, & T. G. Barners, ASP Conf. Ser., 336, 25
- Barklem, P. S., & O'Mara, B. J. 1998, MNRAS, 300, 863 [NASA ADS] [CrossRef]
- Belluzzi, L., Trujillo Bueno, J., & Degl'Innocenti, E. L. 2007, ApJ, 666, 588 [NASA ADS] [CrossRef]
- Berengut, J. C., Dzuba, V. A., & Flambaum, V. V. 2003, Phys. Rev. A, 68, id. 022502
- Bidelman, P. W., & Keenan, P. C. 1951, ApJ, 114, 473 [NASA ADS] [CrossRef]
- Bruls, J. H. M. J., Rutten, R. J., & Shchukina, N. G. 1992, A&A, 265, 237 [NASA ADS]
- Carlsson, M., Rutten, R. J., & Shchukina, N. G. 1992, A&A, 253, 567 [NASA ADS]
- Collados, M., Lagg, A., Díaz García, et al. 2007, in The Physics of Chromospheric Plasmas, ed. P. Heinzel, I. Dorotovic, & R. J. Rutten, ASP Conf. Ser., 368, 611
- Delbouille, L., Roland, G., Neven, L. 1973, Photometric atlas of the solar spectrum from 3000 a 10 000, Institut d'Astrophysique de Université de Liège, Liège, Belgium
- Deridder, G., & van Rensbergen, W. T. 1976, A&AS, 23, 147 [NASA ADS]
- Derouich, M. 2008, A&A, 481, 845 [NASA ADS] [CrossRef] [EDP Sciences]
- Fried, D. L. 1966, J. Opt. Soc. Am., 56, 1372 [NASA ADS] [CrossRef]
- Gandorfer, A. 2002, The Second Solar Spectrum, II: 3910 A to 4630 A (Zürich: VdF)
- Gigas, D. 1988, A&A, 192, 264 [NASA ADS]
- Goldberg, L., Müller, E. A., & Aller, L. H. 1960, ApJS, 5, 1 [NASA ADS] [CrossRef]
- Grevesse, N. 1984, Phys. Scr., 8, 49 [NASA ADS] [CrossRef]
- Holweger, H., & Müller, E. A. 1974, Sol. Phys., 39, 19 [NASA ADS] [CrossRef]
- Khomenko, E. V., Kostik, R. I., & Shchukina, N. G. 2001, A&A, 369, 660 [NASA ADS] [CrossRef] [EDP Sciences]
- Korff, D. 1973, J. Opt. Soc. Am. 63, 971
- Kostik, R. I., & Khomenko, E. V. 2007, A&A, 476, 341 [NASA ADS] [CrossRef] [EDP Sciences]
- Kostyk, R. I., & Shchukina, N. G. 2004, Astron. Rep. (Soviet Astron.), 48(9),769
- Kostyk, R. I., Shchukina, N. G., & Khomenko, E. V. 2006, Astron. Rep. (Soviet Astron.), 50(7), 588
- Kulander, J., & Jefferies, J. 1966, ApJ, 146, 194 [NASA ADS] [CrossRef]
- Lambert, D. L., & Warner, B. 1968, MNRAS, 140, 197 [NASA ADS]
- Landi Degl'Innocenti, E., & Landolfi, M. 2004, Polarization in Spectral Lines (Dordrecht: Kluwer)
- Maltby, P., Avrett, E. H., Carlsson, M., et al. 1986, ApJ, 306, 284 [NASA ADS] [CrossRef]
- Mashonkina, L., & Gehren, T. 2000, A&A, 364, 249 [NASA ADS]
- Mashonkina, L., & Zhao, G. 2006, A&A, 456, 313 [NASA ADS] [CrossRef] [EDP Sciences]
- Mashonkina, L., Gehren, T., Travaglio, C., et al. 2003, A&A, 397, 275 [NASA ADS] [CrossRef] [EDP Sciences]
- Mashonkina, L., Zhao, G., Gehren, T., et al. 2008, A&A, 478, 529 [NASA ADS] [CrossRef] [EDP Sciences]
- Noyes, R. W. 1967, in Aerodynamic Phenomena in Stellar Atmospheres, ed. R. N. Thomas (London: Acad. Press), 293
- Olshevsky, V. L., Shchukina, N. G., & Vasilyeva, I. E. 2008, Kinemat. Phys. Celest. Bodies, 24(3), 198 (Russian ed.)
- Radzig, A. A., & Smirnov, B. M. 1985, Reference Data on Atoms, Molecules and Ions, Springer Ser. Chem. Phys. 31 (Berlin: Springer)
- Ricort, G., & Aime, C. 1979, A&A, 76, 324 [NASA ADS]
- Ricort, G., Aime, C., Roddier, C., et al. 1981, Sol. Phys., 69, 223 [NASA ADS] [CrossRef]
- Ross, J. E., & Aller, L. H. 1976, Science, 191, 1223 [NASA ADS] [CrossRef]
- Rutten R. J. 1977, Sol. Phys., 51, 3 [NASA ADS]
- Rutten R. J. 1978, Sol. Phys., 56, 237 [NASA ADS]
- Rutten R. J., & Milkey R. W. 1979, ApJ, 231, 277 [NASA ADS] [CrossRef]
- Sakakihara, S., & Tanaka, Y. 2001, Nucl. Phys. A, 691, 649 [NASA ADS] [CrossRef]
- Sánchez Almeida, J., Ruiz Cobo, B., & del Toro Iniesta, J. C. 1996, A&A, 314, 295 [NASA ADS]
- Shchukina, N. G., & Trujillo Bueno, J. 2001, ApJ, 550, 970 [NASA ADS] [CrossRef]
- Shchukina, N. G., & Trujillo Bueno, J. 2009, in Solar Polarization 5, ed. S. Berdyugina, K. N. Nagenda, & R. Ramelli, ASP Conf. Ser., in press
- Shchukina, N. G., Trujillo Bueno, J., & Asplund, M. 2005, ApJ, 618, 939 [NASA ADS] [CrossRef]
- Short, C. I., & Hauschildt, P. H. 2006, ApJ, 641, 494 [NASA ADS] [CrossRef]
- Skomorovsky, V., Merkulenko, V., & Poliakov, V. 1976, Solnechnye dannye, 5, 73
- Socas-Navarro, H., & Trujillo Bueno, J. 1997, ApJ, 490, 383 [NASA ADS] [CrossRef]
- Stebbins, R., & Goode, P. 1987, Sol. Phys., 110, 237 [NASA ADS] [CrossRef]
- Stein, R. F., & Nordlund, Å. 1998, ApJ, 499, 914 [NASA ADS] [CrossRef]
- Sütterlin, P., Rutten, R. J., & Skomorovsky, V. I. 2001, A&A, 378, 251 [NASA ADS] [CrossRef] [EDP Sciences]
- Tandberg-Hanssen, E. 1964, ApJS, 9, 107 [NASA ADS] [CrossRef]
- Tandberg-Hanssen, E., & Smythe, C. 1970, ApJ, 161, 289 [NASA ADS] [CrossRef]
- Tritschler, A., Schmidt, W., Langhans, K., et al. 2002, Sol. Phys., 211, 17 [NASA ADS] [CrossRef]
- Trujillo Bueno, J., & Fabiani Bendicho, P. 1995, ApJ, 455, 646 [NASA ADS] [CrossRef]
- Trujillo Bueno, J., & Shchukina, N. G. 2007, ApJ, 664, L135 [NASA ADS] [CrossRef]
- Trujillo Bueno, J., & Shchukina, N. G. 2009, ApJ, in press
- Trujillo Bueno, J., Shchukina, N. G., et al. 2004, Nature, 430, 326 [NASA ADS] [CrossRef]
Online Material
Appendix A: NLTE modeling
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12048figA1.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12048-09/Timg96.png)
|
Figure A.1:
a), b): departure coefficients |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm]{12048figA2.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12048-09/Timg97.png)
|
Figure A.2:
The NLTE (solid line) and LTE (open circles) heights of formation of the core of the Ba II 4554 Å line along the slice of the snapshot yi=0.6 Mm. Dash-dotted line: continuum height
of formation at 4554 Å. Dotted line: height of formation of the
line wing for the wavelength position
|
| Open with DEXTER | |
Figure A.1 (panels a to f) shows the population
departure coefficients, the Ba II ![]() 4554 Å line source
functions and line profiles for two spatial grid points of the
3D snapshot representing the typical granular and intergranular
models. We use these models to illustrate the difference in the
NLTE results for granules and intergranules. The population
departure coefficients are defined as
4554 Å line source
functions and line profiles for two spatial grid points of the
3D snapshot representing the typical granular and intergranular
models. We use these models to illustrate the difference in the
NLTE results for granules and intergranules. The population
departure coefficients are defined as
![]() where
where
![]() and
and
![]() are the NLTE and
LTE atomic level populations, respectively. The Complex behaviour
of the
are the NLTE and
LTE atomic level populations, respectively. The Complex behaviour
of the ![]() -coefficients shown in Fig. A.1a, b is a
result of the interaction of several NLTE mechanisms described in
detail by Bruls et al. (1992); Carlsson et al. (1992); Shchukina & Trujillo Bueno (2001). Here we just point out that for the
barium atom the most important of them are ultraviolet line
pumping, ultraviolet overionization, resonance line scattering and
photon losses.
The resonance line scattering and photon losses manifest
themselves as a divergence of the lower
-coefficients shown in Fig. A.1a, b is a
result of the interaction of several NLTE mechanisms described in
detail by Bruls et al. (1992); Carlsson et al. (1992); Shchukina & Trujillo Bueno (2001). Here we just point out that for the
barium atom the most important of them are ultraviolet line
pumping, ultraviolet overionization, resonance line scattering and
photon losses.
The resonance line scattering and photon losses manifest
themselves as a divergence of the lower
![]() and upper
and upper
![]() ,
,
![]() levels
of the Ba II resonance lines. This divergence results from the
surface losses near the layer where the optical depth is equal to
unity. The losses propagate by scattering to far below that layer.
Interestingly, for the integranule the divergence of the
levels
of the Ba II resonance lines. This divergence results from the
surface losses near the layer where the optical depth is equal to
unity. The losses propagate by scattering to far below that layer.
Interestingly, for the integranule the divergence of the
![]() -coefficients arises in the innermost layers. This happens
because the photon losses occur mainly through the line wings of
the Ba II 4554 Å line. As follows from
Fig. A.2 the line wings in integranules are
formed considerably deeper than in granules. Such a difference in
the formation heights is a result of the Doppler shift of the line
opacity coefficient caused by the velocity field. As a
consequence, in the intergranular model (see
Fig. A.1a, b) the divergence starts already in the
lower photosphere while in the granular model it happens only in
upper photosphere at heights around 400 km.
-coefficients arises in the innermost layers. This happens
because the photon losses occur mainly through the line wings of
the Ba II 4554 Å line. As follows from
Fig. A.2 the line wings in integranules are
formed considerably deeper than in granules. Such a difference in
the formation heights is a result of the Doppler shift of the line
opacity coefficient caused by the velocity field. As a
consequence, in the intergranular model (see
Fig. A.1a, b) the divergence starts already in the
lower photosphere while in the granular model it happens only in
upper photosphere at heights around 400 km.
Another important conclusion that follows from
Fig. A.2 concerns the height of formation of the
Ba II 4554 Å line. The lower departure coefficient ![]() is close to unity. So the scaling of the line opacity with this
coefficient cannot lead to an appreciable difference between the
NLTE and LTE heights of formation of this line.
is close to unity. So the scaling of the line opacity with this
coefficient cannot lead to an appreciable difference between the
NLTE and LTE heights of formation of this line.
The excess of Ba II ions at the levels with excitation
potentials above 5 eV visible in the granule model is produced
by the pumping via the ultraviolet Ba II lines starting at
![]() ,
,
![]() ,
,
![]() levels.
For the intergranule model the overpopulation arises only in the
uppermost layers. Such behaviour of the
levels.
For the intergranule model the overpopulation arises only in the
uppermost layers. Such behaviour of the ![]() -coefficients
corresponds to the temperature stratification of the models. The
overpopulation of the high excitation levels of Ba II in granules
occurs because here the excitation temperature of the ultraviolet
pumping radiation field appreciably exceeds the electron
temperature. In integranules such superthermal radiation, and
hence the level overpopulation, is present only above the
temperature minimum region. In addition, in the intergranular
photospheric layers the photon losses in the ultraviolet lines are
more pronounced than in granules.
-coefficients
corresponds to the temperature stratification of the models. The
overpopulation of the high excitation levels of Ba II in granules
occurs because here the excitation temperature of the ultraviolet
pumping radiation field appreciably exceeds the electron
temperature. In integranules such superthermal radiation, and
hence the level overpopulation, is present only above the
temperature minimum region. In addition, in the intergranular
photospheric layers the photon losses in the ultraviolet lines are
more pronounced than in granules.
![\begin{figure}
\par\includegraphics[width=9cm]{12048figA3.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12048-09/Timg106.png)
|
Figure A.3:
The total source function
|
| Open with DEXTER | |
The
![]() ratio of the upper and lower level
departure coefficients of the Ba II 4554 Å line sets the
departure of its line source function SL from the Planck
function B. Figure A.1 (c, d) shows that this
departure (reflecting the corresponding departure coefficient
divergence in the upper panels of this figure) is larger in the
intergranular than in the granular model.
ratio of the upper and lower level
departure coefficients of the Ba II 4554 Å line sets the
departure of its line source function SL from the Planck
function B. Figure A.1 (c, d) shows that this
departure (reflecting the corresponding departure coefficient
divergence in the upper panels of this figure) is larger in the
intergranular than in the granular model.
Figure A.3 demonstrates that such behaviour is typical
also for the total source function
![]() at the
wavelengths corresponding to the inner wings (
at the
wavelengths corresponding to the inner wings (
![]() mÅ). On average, in intergranular regions it drops below
the Planck function while in granules the effect is less
pronounced. Moreover, in granular areas with strong upflows the
total source function can exceed the Planck function. This excess
can be understood if one takes into account that the resonance
source line function is described by the two-level approximation,
i.e. it approximately equals mean intensity J. In the regions
with small photon losses (like granules) the J > B, hence,
mÅ). On average, in intergranular regions it drops below
the Planck function while in granules the effect is less
pronounced. Moreover, in granular areas with strong upflows the
total source function can exceed the Planck function. This excess
can be understood if one takes into account that the resonance
source line function is described by the two-level approximation,
i.e. it approximately equals mean intensity J. In the regions
with small photon losses (like granules) the J > B, hence,
![]() and
and
![]() have to be greater than B as well.
have to be greater than B as well.
Figure A.1e, f show the NLTE and LTE disc-centre line profiles for the individual granular and integranular models. The profiles displayed in Fig. A.1g result from averaging of the emergent intensities corresponding only to the granular models. Averaged intergranular profiles are shown in Fig. A.1h. These two bottom panels quantify the statistical effect produced by the deviation from the LTE in two such types of the atmospheric models. The main conclusions that may be drawn from the results presented in Figs. A.1-A.3 are the following:
- the source function deficit, as compared to the LTE assumption,
is the main mechanism that controls the formation of the Ba
II
 4554 Å line. The line opacity deficit is small
and, hence, unimportant;
4554 Å line. The line opacity deficit is small
and, hence, unimportant;
-
the divergence between
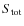 and B changes the shape of
the individual profiles, particularly the intergranular ones.
and B changes the shape of
the individual profiles, particularly the intergranular ones.
- On average, the deviations from the LTE lead to deepening (i.e.
strengthening) of the spatially averaged Ba II
 4554 Å
line profiles. The NLTE effects are most pronounced around the line
core and are generally more important in the intergranular regions than
in the granular ones. The mean difference between the NLTE and LTE line
core residual intensities does not exceed 5% for granules
and 10% for intergranules.
4554 Å
line profiles. The NLTE effects are most pronounced around the line
core and are generally more important in the intergranular regions than
in the granular ones. The mean difference between the NLTE and LTE line
core residual intensities does not exceed 5% for granules
and 10% for intergranules.
- Towards the wings, the LTE becomes a valid description for the
Ba II
 4554 Å line profile;
4554 Å line profile;
Footnotes
- ... model
![[*]](/icons/foot_motif.png)
- Appendix is only available in electronic form at http://www.aanda.org
All Figures
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12048fig1.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12048-09/Timg37.png)
|
Figure 1:
Grotrian diagram of an atomic model for Ba I +Ba II. Solid lines indicate radiative bound-bound transitions.
The Ba II |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12048fig2.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12048-09/Timg38.png)
|
Figure 2: Hyperfine and isotopic structure of the Ba II 4554 Å line. Top: splitting profile patterns (thin solid lines) and resulting profile (thick solid line) in the 1D MACKKL model (Maltby et al. 1986). Two blends are shown by dotted (Cr I 4553.945 Å) and dashed (Zr II 4553.970 Å) lines. Middle: equivalent widths and isotopic shift of the patterns. Bottom: bisector due to isotopic shift (small open circles) calculated in the MACKKL model and bisector of the spatially averaged profile (3D model) caused by the granular velocity field (solid line). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12048fig3.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12048-09/Timg63.png)
|
Figure 3:
Root-mean-square continuum contrast
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12048fig4.eps} %
\end{figure}](/articles/aa/full_html/2009/42/aa12048-09/Timg67.png)
|
Figure 4: Calculated and observed intensity disc-centre profiles of the Ba II 4554 Å line. Solid line: the spatially averaged NLTE profile for the 3D model. Small open circles: the profile from the Liège Atlas ( top); spatially averaged profile obtained from observations at the VTT with TESOS in 2006 ( bottom). |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{12048fig5.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12048-09/Timg68.png)
|
Figure 5:
Root-mean-square contrast at different wavelengths along
the Ba II 4554 line profile. Dashed line:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{12048fig6.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12048-09/Timg71.png)
|
Figure 6:
Comparison of the snapshot vertical velocities Vz with the Dopplergram velocities |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12048fig7.eps} %
\end{figure}](/articles/aa/full_html/2009/42/aa12048-09/Timg72.png)
|
Figure 7:
Comparison of the snapshot vertical velocities Vz with the Dopplergram velocities |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=6.3cm,clip]{12048fig8a.eps}\includegraphics[width=6.3cm,clip]{12048fig8b.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12048-09/Timg73.png)
|
Figure 8:
Ba II 4554 Å line profiles at two selected locations corresponding to a high downflow ( left) and a high upflow ( right), marked by (1) and (2) in Fig. 6. a), c): profiles without smearing. Thin lines with dots: parabolic fit to the five wavelength positions
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{12048fig9.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12048-09/Timg75.png)
|
Figure 9:
Correlation coefficients between |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{12048fig10.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12048-09/Timg76.png)
|
Figure 10:
Comparison between the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{12048fig11.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12048-09/Timg85.png)
|
Figure 11:
Scatter plot of the red and blue wing |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm,clip]{12048fig12.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12048-09/Timg86.png)
|
Figure 12:
Scatter plot of the |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=11.5cm,clip]{12048fig13.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12048-09/Timg87.png)
|
Figure 13: Formation heights of the intensity along the line profiles calculated for a set of spectral widths in the blue ( left) and red ( right) wings for all grid points from the 3D snapshot. Thick solid lines and open circles: mean formation heights and their standard deviation, respectively. |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=11.5cm,clip]{12048fig14.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12048-09/Timg88.png)
|
Figure 14:
a), c): formation heights of the blue wing intensities vs. formation heights of the red wing intensities at
two spectral widths:
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{12048figA1.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12048-09/Timg96.png)
|
Figure A.1:
a), b): departure coefficients |
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=8.5cm]{12048figA2.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12048-09/Timg97.png)
|
Figure A.2:
The NLTE (solid line) and LTE (open circles) heights of formation of the core of the Ba II 4554 Å line along the slice of the snapshot yi=0.6 Mm. Dash-dotted line: continuum height
of formation at 4554 Å. Dotted line: height of formation of the
line wing for the wavelength position
|
| Open with DEXTER | |
| In the text | |
![\begin{figure}
\par\includegraphics[width=9cm]{12048figA3.eps}
\end{figure}](/articles/aa/full_html/2009/42/aa12048-09/Timg106.png)
|
Figure A.3:
The total source function
|
| Open with DEXTER | |
| In the text | |
Copyright ESO 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


