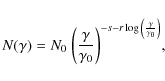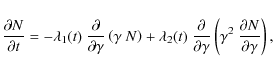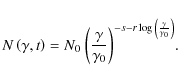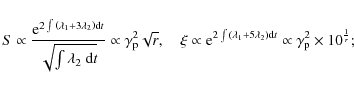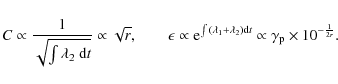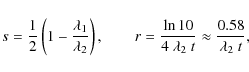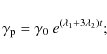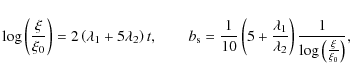EDP Sciences
Home All issues Volume 504 / No 3 (September IV 2009) A&A, 504 3 (2009) 821-828 Online Material
Free Access
Issue
A&A
Volume 504, Number 3, September IV 2009
Page(s) 821 - 828
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/200912237
Published online 16 July 2009

Online Material

Appendix A: Log-parabolic spectra

In this Appendix we show how electron populations with a log-parabolic energy distribution of the form expressed by Eq. (3), that is,

\begin{displaymath} N(\gamma)=N_0~{\left({\frac{\gamma}{\gamma_0}}\right)}^{-s-r\log{\left({\frac{\gamma}{\gamma_0}}\right)}}, \end{displaymath} (A.1)

emit log-parabolic spectra via the SSC process. The related particle synchrotron emissivity

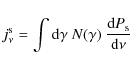\begin{displaymath}j_\nu^{\rm s} = \int{{\rm d}\gamma~N(\gamma)~\frac{{\rm d}P_{\rm s}}{{\rm d}\nu}} \end{displaymath} (A.2)

is easily computed on using the close approximation to the single particle emission in the shape of a delta-function (see Rybicki & Lightmann 1979), that is, $\frac{{\rm d}P_{\rm s}}{{\rm d}\nu}\approx P_{\rm s}~\delta~{\left( {\nu-\gamma^2~\nu_{\rm c}}\right) }$ with $P_{\rm s}={1}/{6\pi}~\sigma_{\rm T}~\gamma^2~c~{B^2}$ and $\nu_{\rm c}\approx 1.22\times {10}^6~ B\mbox{ Hz}$ (with B measured in Gauss) is the synchrotron critical frequency. This leads to (Massaro et al. 2004a) a log-parabolic differential flux

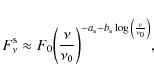\begin{displaymath}F_\nu^{\rm s} \approx F_0{\left( {\frac{\nu}{\nu_0}}\right)}^{-a_{\rm s}-b_{\rm s}\log{\left( {\frac{\nu}{\nu_0}}\right) }}, \end{displaymath} (A.3)

and to a SED again of log-parabolic shape

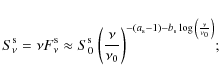\begin{displaymath}S_\nu^{\rm s} =\nu F_\nu^{\rm s}\approx S_0^{\rm s}~{\left( {... ...{\rm s}-1)-b_{\rm s}\log{\left( {\frac{\nu}{\nu_0}}\right) }}; \end{displaymath} (A.4)

its slope at the synchrotron reference frequency $\nu_0$ is given in terms of s, by

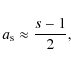\begin{displaymath}a_{\rm s}\approx\frac{s-1}{2}, \end{displaymath} (A.5)

the spectral curvature by

\begin{displaymath} b_{\rm s}\approx\frac{r}{4}, \end{displaymath} (A.6)

and the peak value $S'\propto R^3~B^2~n~\gamma_{\rm p}^2~\sqrt{r}$ occurs at a frequency $\xi'\propto B~\gamma_{\rm p}^2\times 10^{\frac{1}{r}}$ ( $\gamma _{\rm p}$, n, B and R are defined in Sect. 2.1 of the main text).

For IC radiation in the Thomson regime we may write to a fair approximation $\frac{{\rm d}P_{\rm c}}{{\rm d}\nu}\approx P_{\rm c}~\delta~{\left( {\nu-\frac{4}{3}~\gamma^2~\xi'}\right) }$ (see Rybicky & Lightmann 1979) where $P_{\rm c}=\frac{4}{3}~\sigma_{\rm T}~\gamma^2~c~\epsilon_\nu$ is the power radiated by a single-particle IC scattering in the Thomson regime, having denoted with $\epsilon_\nu\propto R~B^2~n~\gamma_{\rm p}^2$ the synchrotron radiation density[*] . We obtain once again a log-parabolic SED

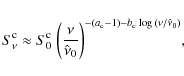\begin{displaymath}S_\nu^{\rm c} \approx S_0^{\rm c}~{\left( {\frac{\nu}{\hat{\n... ...rm c}-1)-b_{\rm c}\log{\left( {{\nu}/{\hat{\nu}_0}}\right) }}, \end{displaymath} (A.7)

where the slope at the IC reference frequency $\hat{\nu}_0$ is given by

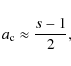\begin{displaymath}a_{\rm c}\approx\frac{s-1}{2}, \end{displaymath} (A.8)

and the spectral curvature reads

\begin{displaymath} b_{\rm c}\approx\frac{r}{4}\cdot \end{displaymath} (A.9)

The peak value $C'\propto R^4~B^2~n^2~\gamma_{\rm p}^4~\sqrt{r}$ is attained at a frequency $\epsilon'\propto B~\gamma_{\rm p}^4$.

For the Klein-Nishina (KN) regime instead it necessary to consider the convolution

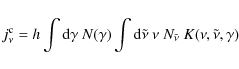\begin{displaymath}j_\nu^{\rm c} =h \int{{\rm d}\gamma~N(\gamma) \int{{\rm d}\tilde\nu~\nu~N_{\tilde\nu}~K(\nu,\tilde\nu,\gamma)}} \end{displaymath} (A.10)

where $\tilde\nu$ and $\nu$ are the electron frequencies before and after the scattering, respectively, $N_{\tilde\nu}$ is the number spectrum of seed photons, and $K(\nu,\tilde\nu,\gamma)$ is the full Compton kernel (Jones 1968). Only in the extreme KN regime one may again approximate

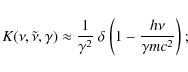\begin{displaymath}K(\nu,\tilde\nu,\gamma)\approx\frac{1}{\gamma^2}~\delta~{\left( {1-\frac{h\nu}{\gamma m c^2}}\right) }~; \end{displaymath} (A.11)

on approximating $N_{\tilde\nu}$ with its mean value for a homogeneous, spherical optically thin source

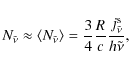\begin{displaymath}N_{\tilde\nu}\approx \left\langle {N_{\tilde\nu}}\right\rangl... ...frac{3}{4}\frac{R}{c}\frac{j_{\tilde\nu}^{\rm s}}{h\tilde\nu}, \end{displaymath} (A.12)

one obtains again a SED with a log-parabolic shape

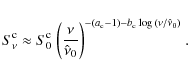\begin{displaymath}S_\nu^{\rm c} \approx S_0^{\rm c}~{\left( {\frac{\nu}{\hat{\n... ... c}-1) -b_{\rm c}\log{\left( {{\nu}/{\hat{\nu}_0}}\right) }}~. \end{displaymath} (A.13)

Now the slope at $\hat{\nu}_0$

\begin{displaymath}a_{\rm c}\approx s, \end{displaymath} (A.14)

is steeper, and the spectral curvature

\begin{displaymath} b_{\rm c}\approx r \end{displaymath} (A.15)

is larger than in the Thomson regime. The peak value $C'\propto R^4~B~n^2~\sqrt{r}$ occurs at a frequency $\epsilon'\propto \gamma_{\rm p}\times 10^{-\frac{1}{2r}}$.

The transition between the two regimes occurs when $2~\gamma_{\max}~ h~\xi'\approx m c^2$, where $\gamma_{\max}=\sqrt{\xi'/\nu_{\rm c}}$, that is, when

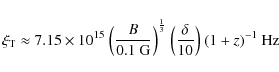\begin{displaymath}\xi_{\rm T}\approx 7.15\times 10^{15}~{\left({\frac{B}{0.1\mb... ...}{3}}~ {\left({\frac{\delta}{10}}\right)}~(1+z)^{-1}\mbox{ Hz} \end{displaymath} (A.16)

holds, or equivalently

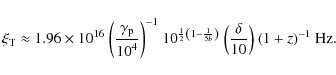\begin{displaymath} \xi_{\rm T}\approx 1.96\times 10^{16}~{\left({\frac{\gamma_{... ...t)}~ {\left({\frac{\delta}{10}}\right)}~(1+z)^{-1}\mbox{ Hz} . \end{displaymath} (A.17)

We close these calculations with two remarks. First, the (primed) quantities used here refer to the rest frame of the emitting region, while the observed (unprimed) quantities must be multiplied by powers of the beaming factor

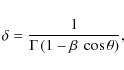\begin{displaymath}\delta=\frac{1}{\Gamma \left( {1-\beta~\cos{\theta}}\right)}, \end{displaymath} (A.18)

$\Gamma$ being the bulk Lorentz factor of the relativistic electron flow in the emitting region, $\theta$ the angle between its velocity $\varv$ and the line of sight, and $\beta=\varv/c$; so we obtain $S=S'~\delta^4$, $C=C'~\delta^4$, and $\xi=\xi'~\delta$, $\epsilon=\epsilon'~\delta$. Second, we note that the actual specific powers $\frac{{\rm d}P}{{\rm d}\nu}$ radiated by a single particle differ from delta-function shape, slightly for the synchrotron emission and considerably for the IC radiation in the Thomson regime (see discussion in Rybicky & Lightmann 1979). However, the above spectral shapes still approximatively apply, as confirmed by numerical simulations (Massaro 2007); in detail, the convolution with a broader single particle power yields a less curved spectrum, so that Eqs. (A.6) and (A.9) become $b_{\rm s} \approx r/5$ (Massaro et al. 2006) and $b_{\rm c}\approx r/10$, respectively.

Appendix B: Particle acceleration processes

 \begin{figure} \par\includegraphics[width=9cm,clip]{12237fg7.eps} \end{figure} Figure B.1:

Example of time evolution of the $\gamma^2~N(\gamma)$ distribution (with peak energy $\gamma _{\rm p}$) due to stochastic and systematic accelerations ( upper panel) with $\lambda_1 = 5\times {10}^{-3}\mbox{ days}^{-1}$, $\lambda_2 = 5\times {10}^{-4}\mbox{ days}^{-1}$ from the initial value $\gamma _{\rm p}={10}^3$, and of the related evolution for the SSC SEDs ( lower panel). In terms of the stochastic acceleration time $\tau _2$, the time interval between each pair of lines is $t_2-t_1={10}^{-2} \tau _2$, corresponding to an observed time interval of about two days.
Open with DEXTER

 \begin{figure} \par\includegraphics[width=9cm,clip]{12237fg8.eps} \end{figure} Figure B.2:

Example of time evolution of the $\gamma^2~N(\gamma)$ distribution (with peak energy $\gamma _{\rm p}$) due to stochastic and systematic accelerations ( upper panel) with $\lambda_1 = 5\times {10}^{-3}\mbox{ days}^{-1}$, $\lambda_2 = 5\times {10}^{-4}\mbox{ days}^{-1}$ from the initial value $\gamma _{\rm p}=5\times 10^4$, and of the related evolution for the SSC SEDs ( lower panel). In terms of the stochastic acceleration time $\tau _2$, the time interval between each pair of lines is $t_2-t_1={10}^{-2} \tau _2$, corresponding to an observed time interval of about two days.
Open with DEXTER

Here we derive a log-parabolic electron energy distribution $N\left({\gamma ,t}\right)$ from a kinetic continuity equation of the Fokker-Planck type; following Kardashev (1962), in the jet rest frame this reads

\begin{displaymath} \frac{\partial N}{\partial t}=- \lambda_1 (t)~ \frac{\parti... ...mma}\left({\gamma^2~\frac{\partial N}{\partial\gamma}}\right), \end{displaymath} (B.1)

where $\gamma~ m~c^2$ is the particle energy, t denotes time, and $\lambda_1$ and $\lambda_2$ describe systematic and stochastic acceleration rates, occurring on timescales $t_1=1/\lambda_1$ and $t_2=1/\lambda_2$, respectively. For example, in the picture of Fermi accelerations (e.g., Vietri 2006), the accelerations rates $\lambda_1$ and $\lambda_2$ can be expressed in terms of physical quantities related to processes occurring in shocks; in this framework a plane shock front of thickness $\ell_{\rm s}$ moves with speed $V_{\rm s}$ and gas clouds of average size $\ell$ move downstream of the shock with speed V; it is found that $\lambda_1=V_{\rm s}/\ell_{\rm s}$ and $\lambda_2=V^2/2c\ell$ hold (see Kaplan 1956; Paggi 2007), $\lambda_2\ll\lambda_1$. On the other hand, numerical values of $\lambda_1$ and $\lambda_2$ are directly derived from the emitted spectrum as shown later.

The Fokker-Planck Eq. (B.1) describes the evolution of the electron distribution function; with an initially mono-energetic distribution in the form of a delta-function $N(\gamma ,0) = n ~\delta(\gamma -\gamma_0)$ (n is the initial particle number density) the solution at subsequent times t takes the form of the log-parabolic energy distribution assumed in Eq. (3) of the main text (see also A.1), reading

\begin{displaymath} N\left({\gamma ,t}\right)= N_0~ {\left({\frac{\gamma}{\gamma_0}}\right)}^{-s-r\log{\left({\frac{\gamma}{\gamma_0}}\right)}}. \end{displaymath} (B.2)

Here the time depending slope at $\gamma=\gamma_0$ is given by

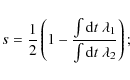\begin{displaymath}s=\frac{1}{2}\left( {1-\frac{\int{{\rm d}t~\lambda_1}}{\int{{\rm d}t~\lambda_2}}}\right); \end{displaymath} (B.3)

meanwhile, the curvature of $N(\gamma)$ driven by the diffusive (stochastic) term in Eq. (B.1), irreversibly decreases in time after

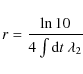\begin{displaymath}r=\frac{\ln{10}}{4\int{{\rm d}t~\lambda_2}} \end{displaymath} (B.4)

from the large initial values corresponding to the initially mono-energetic distribution. Correspondingly, the time-dependent height at $\gamma=\gamma_0$ follows

\begin{displaymath}N_0=\frac{1}{2\sqrt{\pi}}\frac{n}{\gamma_0}\frac{1} {\sqrt{\i... ...mbda_2}}\right)}^2} {4\int{{\rm d}t~\lambda_2}}}\right]}}\cdot \end{displaymath} (B.5)

To wit, Eq. (B.2) describes the evolution of the electron distribution, growing broader and broader under the effect of stochastic acceleration, while its peak moves from $\gamma_0$ to the current position

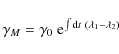\begin{displaymath}\gamma_{M}=\gamma_0~ {\rm e}^{\int{{\rm d}t~(\lambda_1-\lambda_2)}} \end{displaymath} (B.6)

under the contrasting actions of the systematic and stochastic accelerations. An important quantity to focus on for the emission properties is the rms energy
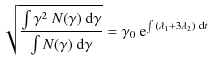                           $\displaystyle {\gamma_{\rm p}}$ $\textstyle \equiv$ $\displaystyle \sqrt{\frac{\int{\gamma^2~ N(\gamma)~ {\rm d}\gamma}}{\int{ N(\gamma)~ {\rm d}\gamma}}}=\gamma_0~ {\rm e}^{\int{(\lambda_1+3\lambda_2)~{\rm d}t}}$  
  = $\displaystyle \gamma_0~ {10}^{\frac{2-s}{2r}} =\gamma_{M}~{\rm e}^{{4\int{\lambda_2~{\rm d}t}}},$ (B.7)

which is also the position for the peak of the distribution $\gamma^2~N(\gamma)$.

We have already derived in Appendix A the shapes of the spectra (synchrotron, and IC in both the Thomson and KN regimes) emitted by the distribution given in Eq. (3); here we stress the time dependence of their main spectral features. We can write for the synchrotron emission[*]

\begin{displaymath} S\propto \frac{{\rm e}^{2\int{\left({\lambda_1+3\lambda_2}\r... ...ght){\rm d}t}}\propto\gamma_{\rm p}^2\times 10^{\frac{1}{r}} ; \end{displaymath} (B.8)

for IC emission we have in the Thomson regime

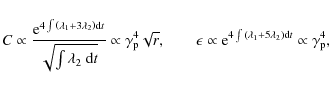\begin{displaymath}C\propto \frac{{\rm e}^{4\int{\left({\lambda_1+3\lambda_2}\ri... ...\lambda_1+5\lambda_2}\right){\rm d}t}}\propto\gamma_{\rm p}^4, \end{displaymath} (B.9)

and in the extreme KN regime

\begin{displaymath} C\propto \frac{1}{\sqrt{\int{\lambda_2~{\rm d}t}}}\propto \s... ...ight){\rm d}t}}\propto\gamma_{\rm p}\times 10^{-\frac{1}{2r}}. \end{displaymath} (B.10)

Note that during flares, since $\lambda_1\gg \lambda_2$, we expect the curvature to vary so little that we can therefore approximatively write $S\propto\xi$ (see main text).

Now we focus the above relations for the simple case of time independent $\lambda_1$ and $\lambda_2$, when $\int{\lambda_{1,2}~ {\rm d}t}\approx\lambda_{1,2}~ t$; then we have

\begin{displaymath} s=\frac{1}{2}\left( {1-\frac{\lambda_1}{\lambda_2}}\right),\... ...\frac{\ln{10}}{4~\lambda_2~t}\approx \frac{0.58}{\lambda_2~t}, \end{displaymath} (B.11)

while for the rms energy we have

\begin{displaymath} \gamma_{\rm p}=\gamma_0 ~{e}^{\left({\lambda_1+3\lambda_2}\right)t}; \end{displaymath} (B.12)

so for the peak frequency and the spectral curvature we have

\begin{displaymath} \log{\left({\frac{\xi}{\xi_0}}\right)}={2 \left({\lambda_1+5... ...a_2}}\right) \frac{1}{\log{\left({\frac{\xi}{\xi_0}}\right)}}, \end{displaymath} (B.13)

where $\xi_0$ is a normalization frequency. It is seen that soon after the injection the curvature $b_{\rm s}$ (proportional to r) drops rapidly, then progressively decreases more and more gently, while the peak frequency still increases.

The value of $\lambda_2$ can be evaluated from observing the synchrotron spectral curvatures b2 and b1 at two times t2 and t1, respectively (recall that $b_{\rm s} \approx r/5$); denoting with t2 - t1 this time interval, we have

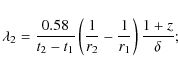\begin{displaymath}\lambda_2=\frac{0.58}{{t_2 - t_1}}\left( {\frac{1}{r_2}-\frac{1}{r_1}}\right) \frac{1+z}{\delta}; \end{displaymath} (B.14)

on the other hand, form observing the related synchrotron peaks $\xi_2$ and $\xi_1$, the value of $\lambda_1$ can be evaluated as

\begin{displaymath}\lambda_1=\left[{\frac{1}{2\left({t_2 - t_1}\right)}\ln{\left... ...{1}{r_2}-\frac{1}{r_1}}\right)}\right] \frac{1+z}{\delta}\cdot \end{displaymath} (B.15)

For example, in the case of Mrk 501 in the states of 7 and 16 April 1997, we obtain (on assuming $B\approx\mbox{const.}$) $\lambda_1 = (2.3\pm 1.1)\mbox{ yr}^{-1}$ and $\lambda_2 = (1.8\pm 1.7){10}^{-1}\mbox{ yr}^{-1}$, corresponding to acceleration times $\tau_1=1/\lambda_1=(4.3\pm 2.0){10}^{-1}\mbox{ yr}$ and $\tau_2=1/\lambda_2=(5.5\pm 5.0)\mbox{ yr}$. Note that with the current data the evaluations of $\lambda_1$ and $\lambda_2$ turn out to be affected by uncertainties considerably larger than the single curvatures $b_1=0.161\pm 0.007$ and $b_2=0.148\pm 0.005$.

If the total energy available to the jet is limited (e.g., by the BZ limit, see text) we expect that $\int{{\rm d}t~\lambda_1}$ and $\int{{\rm d}t~\lambda_2}$ cannot grow indefinitely, but are to attain a limiting value. At low energies where $\int{{\rm d}t~\lambda_1}\gg\int{{\rm d}t~\lambda_2}$ holds, we have $S\propto\xi$ and $C\propto \epsilon$ as before; at higher energies when $\int{{\rm d}t~\lambda_1}$ reaches its limit, $\int{{\rm d}t~\lambda_1}\ll\int{dt~\lambda_2}$ holds, leading to $S\propto \xi^{0.6}$ and $C\propto \epsilon^{0.6}$. Eventually also $\int{{\rm d}t~\lambda_2}$ reaches its limit, and both the fluxes and the peak frequencies cannot grow any more.

Appendix C: Prefactors for Eqs. (4)-(13)

The HSZ SSC model is, as stated before, characterized by five parameters: the rms particle energy $\gamma _{\rm p}$, the particle density n, the magnetic field B, the size of the emitting region R and the beaming factor $\delta$. So the model may be constrained by five observables that we denote with

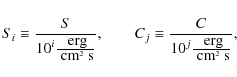\begin{displaymath}S_i\equiv\frac{S}{{10}^{i}\frac{\mbox{ erg}}{\mbox{ cm}^2\mbo... ...iv\frac{C}{{10}^{j}\frac{\mbox{ erg}}{\mbox{ cm}^2\mbox{ s}}}, \end{displaymath} (C.1)


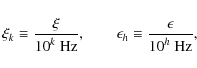\begin{displaymath}\xi_k\equiv\frac{\xi}{{10}^{k}\mbox{ Hz}} , \qquad \epsilon_h\equiv\frac{\epsilon}{{10}^{h}\mbox{ Hz}} , \end{displaymath} (C.2)

where the indexes i,j,k,h express the normalizations demonstrated below; in addition, we denote with $\Delta t_{\rm d}$ the time in days for the source variations, and with D the distance of the source in Gpc.

In the Thomson regime we find

                                         B = $\displaystyle 1.04\times 10^{-1}$  
    $\displaystyle \times\left[{{b}^{\frac{1}{8}}~{D}^{-\frac{1}{2}}~{\left({1+z}\ri... ...}{2}}~ {\epsilon_{22}}^{-\frac{3}{2}}~{S_{-11}}^{-\frac{1}{2}}}\right]\mbox{ G}$ (C.3)
$\displaystyle {\delta}$ = 13.5  
    $\displaystyle \times\left[{{D}^{\frac{1}{2}}~{b}^{-\frac{1}{8}}~{\left({1+z}\ri... ...xi_{14}}^{-1}~{C_{-11}}^{-\frac{1}{4}}{\Delta t_{\rm d}}^{-\frac{1}{2}}}\right]$ (C.4)
R = $\displaystyle 3.50\times 10^{16}$  
    $\displaystyle \times\left[{{D}^{\frac{1}{2}} {b}^{-\frac{1}{8}}{\left({1\!+\!z}... ...m d}}^{\frac{1}{2}}~ {\xi_{14}}^{-1}~{C_{-11}}^{-\frac{1}{4}}}\right]\mbox{ cm}$ (C.5)
n = $\displaystyle 5.74 \times \left[{b}^{\frac{1}{8}}~{D}^{\frac{1}{2}}~{\left({1+z... ...}^{\frac{1}{2}}\times 10^{\left({\frac{1}{5b}-1}\right)}~ {\xi_{14}}^{2}\right.$  
    $\displaystyle \times\left.{C_{-11}}^{\frac{5}{4}}~ {\epsilon_{22}}^{-\frac{3}{2... ...S_{-11}}^{-\frac{3}{2}}~{\Delta t_{\rm d}}^{-\frac{1}{2}}\right]\mbox{ cm}^{-3}$ (C.6)
$\displaystyle {\gamma_{\rm p}}$ = $\displaystyle 2.74\times 10^3~\left[{ {10}^{\frac{1}{2}\left({1-\frac{1}{5b}}\right)}~ {\epsilon_{22}}^{\frac{1}{2}}~{\xi_{14}}^{-\frac{1}{2}}}\right].$ (C.7)

For the extreme KN regime we obtain
                                         B = $\displaystyle 1.72\times 10^{-2}$  
    $\displaystyle \times\left[{{D}^{\frac{2}{5}}{b}^{\frac{1}{10}}{(1+z)}^{-\frac{2... ...}{5}}{C_{-11}}^{-\frac{1}{5}}{\Delta t_{\rm d}}^{-\frac{2}{5}}}\right]\mbox{ G}$ (C.8)
$\displaystyle {\delta}$ = $\displaystyle 4.21 \times\left[{D}^{\frac{2}{5}}~{b}^{-\frac{1}{10}}~ {10}^{\fr... ...{1}{5b}-1}\right)}~ {(1+z)}^{\frac{3}{5}}~ {\epsilon_{26}}^{\frac{2}{5}}\right.$  
    $\displaystyle \times \left. {S_{-10}}^{\frac{2}{5}}~ {\xi_{18}}^{-\frac{3}{5}}~{C_{-11}}^{-\frac{1}{5}}~{\Delta t_{\rm d}}^{-\frac{2}{5}}\right]$ (C.9)
R = $\displaystyle 1.09~ {10}^{16} \times\left[{D}^{\frac{2}{5}}~{b}^{-\frac{1}{10}}... ...1}{5b}-1}\right)}~{(1+z)}^{-\frac{2}{5}}~ {\epsilon_{26}}^{\frac{2}{5}} \right.$  
    $\displaystyle \times \left. {S_{-10}}^{\frac{2}{5}}~{\Delta t_{\rm d}}^{\frac{3}{5}}~ {\xi_{18}}^{-\frac{3}{5}}~{C_{-11}}^{-\frac{1}{5}}\right]\mbox{ cm}$ (C.10)
n = $\displaystyle 952 \times\left[{b}^{\frac{1}{5}}~{D}^{-\frac{4}{5}}\times 10^{\f... ...^{\frac{11}{5}}~{C_{-11}}^{\frac{7}{5}}~ {\epsilon_{26}}^{-\frac{4}{5}} \right.$  
    $\displaystyle \times \left. {S_{-10}}^{-\frac{9}{5}}~{\Delta t_{\rm d}}^{-\frac{1}{5}}\right]\mbox{ cm}^{-3}$ (C.11)
$\displaystyle {\gamma_{\rm p}}$ = $\displaystyle 6.07\times 10^{5}\times\left[{b}^{\frac{1}{10}}~{D}^{-\frac{2}{5}... ...}^{\frac{2}{5}}~ {\xi_{18}}^{\frac{3}{5}}~{\epsilon_{26}}^{\frac{3}{5}} \right.$  
    $\displaystyle \times \left. {C_{-11}}^{\frac{1}{5}}~{\Delta t_{\rm d}}^{\frac{2}{5}}~ {S_{-10}}^{-\frac{2}{5}}\right].$ (C.12)


Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.