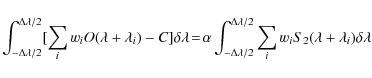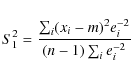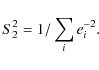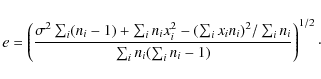The CN isotopic ratios in comets

J. Manfroid; E. Jehin; D. Hutsemékers; A. Cochran; J.-M. Zucconi; C. Arpigny; R. Schulz; J. A. Stüwe; I. Ilyin

doi:10.1051/0004-6361/200911859

Free Access

Issue		A&A Volume 503, Number 2, August IV 2009


Page(s)		613 - 624
Section		Planets and planetary systems
DOI		https://doi.org/10.1051/0004-6361/200911859
Published online		02 July 2009

Online Material

Table 8: Individual spectra. r is the heliocentric distance in astronomical units (AU), $\Delta$ the geocentric distance, Spectro the spectrograph used, $\rm MJD=JD-2~400~000.5$ the Modified Julian Day, Run the run number, Exp the exposure time in seconds, R the spectral resolution. Slit and Offset give the size of the entrance slit of the spectrograph and the offset from the nucleus. T and Q are the parameters used for the collisional effects in the synthetic spectra.

Appendix A: Estimating the isotopic ratios

Because of uncertainties in the models and systematic errors in the observations, the parameters $\alpha$ and $\beta$ (Eq. (5)) cannot be estimated directly. Additional parameters are required to deal with the exact central wavelength of the lines, and the exact level of a possible residual background $C_k(\lambda)$ .

The spectra are divided into small domains surrounding the central wavelength $\lambda_i$ of the most intense, unblended R lines of ¹³C¹⁴N and ¹²C¹⁵N, i.e., regions where $\alpha S_{k,2}(\lambda)$ or $\beta S_{k,3}(\lambda)\gg S_{k,1}(\lambda)$ . This is necessary because the accuracy of the ¹²C¹⁴N model is not perfect, especially in the wings of intense lines. Lines of other molecules must also be avoided, e.g., an unidentified feature at $\lambda\sim3867.92$ Å precludes the use of the R10 line of ¹²C¹⁵N close to the nucleus (see Sect. 7).

The line profile of the strongest lines can be fitted by a Gaussian, or their intensity can be estimated by direct integration, providing sets of $\alpha$ and $\beta$ which can then be averaged.

However, in order to reduce the number of free parameters, we used a different procedure. Instead of fitting separately $O(\lambda) - C_i$ over the intervals $[\lambda_i-\Delta\lambda/2,\lambda_i+\Delta\lambda/2]$ , we superimpose the profiles by shifting the line centers to $\lambda=0$ , optimally coadd them, and fit the resulting profile over the resulting domain $[-\Delta\lambda/2,\Delta\lambda/2]$ (see Fig. A.1). Hence, dropping the subscript k, we write, for the ¹³C¹⁴N lines,

$\begin{displaymath}% \sum_i w_i [O(\lambda+\lambda_i) \!-\! C_i] \!\equiv\!\sum_... ...mbda_i) \!-\! C \!=\!\alpha \sum_i w_i S_2(\lambda+\lambda_i)~ \end{displaymath}$

(A.1)

and the corresponding formula with S₃ and $\beta$ for the ¹²C¹⁵N lines. The C_is merge into a single free parameter $\sum_i w_i C_i\equiv C$ . The weight factor w_i is estimated from the expected intensity $f(\lambda_i) I_i$ of line i in the SN-normalized spectrum (Eqs. (2), (3)).

The width of the observed ``coadded'' profile $\sum_i w_i O(\lambda+\lambda_i)$ is found to be equal to that of the synthetic profile $\sum_i w_i S_2(\lambda+\lambda_i)$ (or $\sum_i w_i S_3(\lambda+\lambda_i)$ ) and it is symmetric about zero. This confirms that the identification of the ¹³C¹⁴N and ¹²C¹⁵N lines is correct, as well as the theoretical wavelengths adopted for them.

The analysis is done either by profile fitting around $\lambda=0$ or by direct integration. In the latter case we write

$\begin{displaymath}% \int_{-\Delta\lambda/2}^{\Delta\lambda/2} [\sum_i w_i O(\... ...ta\lambda/2} \sum_i w_i S_2(\lambda+\lambda_i)\delta\lambda~ \end{displaymath}$

(A.2)

for the ¹³C¹⁴N lines, and an equivalent formula for the ¹²C¹⁵N lines.

The choice of the lines i depends on the quality of the spectra and on particular circumstances, especially the heliocentric distance. Figures 3 and 4 shows that the width of the envelope of the CN band decreases at large r. The relative intensity of the lines of high quantum number drops rapidly. Many lines could be used efficiently for the coadded profiles of comets de Vico or X5 (Fig. A.1), up to 11 for ¹²C¹⁵N and 8 for ¹³C¹⁴N. On the contrary, at large r, a few lines dominate overwhelmingly. As shown in Sect. 7, some blends may become less troublesome far from the nucleus.

$\begin{figure} \par\includegraphics[angle=-90,width=8.2cm,clip]{11859_11.eps} \end{figure}$

Figure A.1:

Coadded observed (solid line) and synthetic (with and without the rare isotopologues) spectra of comet C/2002 X5 (Kudo-Fujikawa). The upper panel is centered on ¹³C¹⁴N lines (in this instance, R1-R6, R14 and R16), the lower one on ¹²C¹⁵N lines (R1-R5, R11-R13, R15-R17). The large number of useable isotopic lines is allowed by the good quality of the spectra used in the combination. Intensity is in arbitrary units.

Open with DEXTER

R lines of ¹³C¹⁴N and ¹²C¹⁵N with low quantum numbers are slightly blended and also - depending on the spectral resolution - with the corresponding R line of ¹²C¹⁴N. An additional difficulty is the presence of faint lines of the B-X (0-0) band of CH. This region of the spectrum needs special care (e.g., some iterative procedure) and may have to be ignored for the lowest quality spectra.

Appendix B: Averages

While weighted averages of measurements x_i with errors e_i ( $i=1,\ldots,n$ ) are easily defined as $m={\sum_i x_i e^{-2}_i}/{\sum_i e^{-2}_i}$ , estimating the resulting error on this value is less obvious. The global data set is far from homogeneous. Systematic errors affect the various data sets in different ways. The instrumentation and the circumstances are never identical. Two estimates of the standard error S are sometimes used:

$\begin{displaymath}% S^2_1=\frac{\sum_i (x_i-m)^2 e^{-2}_i}{(n-1)\sum_i e^{-2}_i} \end{displaymath}$

(B.1)

and

$\begin{displaymath}% S^2_2=1/\sum_i e^{-2}_i. \end{displaymath}$

(B.2)

They are not satisfying, particularly for a small data set. Equation (B.1) does not take properly into account the individual errors, except for the weighting factors, so that a few x_i with large e_i but grouped by chance around m would give an unrealistically small S₁. On the other hand Eq. (B.2) does not take into account the inter-group variations which can be large in the case of systematic effects. The larger of S₁ and S₂ may be taken, but we choose a different approach by simulating the x_i as the average of n_i individual observations y_i,j ( $j=1,\ldots,n_i$ ) with a standard deviation e_i. The weighting is obtained by taking n_i proportional to e^-2_i i.e., the standard deviation is the same for each data set, $\sigma_i=\sigma$ and $n_i=\sigma^2 e_i^{-2}$ . It is then possible to combine several x_i by merging their respective data sets. The mean value is the same as above and the standard deviation of the mean is given by

$\begin{displaymath}% e=\left(\frac{\sigma^2 \sum_i (n_i-1) +\sum_i n_i x_i^2 -(\... ..._i)^2/\sum_i n_i}{\sum_i n_i (\sum_i n_i-1)}\right)^{1/2}\cdot \end{displaymath}$

(B.3)

For large $\sigma$ , this is equivalent to Eq. (B.2), i.e., the result is dominated by the internal dispersion of each data set. Choosing a reasonable value of $\sigma$ is thus critical. We adopt the value of $\sigma$ yielding the smallest realistic samples, $\min(n_i)=2$ . This gives the largest, conservative estimates of the errors.

Appendix C: Spectra

$\begin{figure} \par\includegraphics[angle=270,width=14cm,clip]{11859_12.eps} \end{figure}$

Figure C.1:

Observed (2DCoudé) and synthetic (dotted) spectra of comet 122P/de Vico. In this and the following graphs, the upper (red) ticks indicate the position of the major R lines of ¹³C¹⁴N the lower (blue) ticks indicate the position of the major R lines of ¹²C¹⁵N. The corresponding quantum numbers are indicated in the upper panel midway between the strong ¹²C¹⁴N lines and the faint isotopic lines. The intensity scale is in relative units.

Open with DEXTER

$\begin{figure} \par\includegraphics[angle=270,width=14cm,clip]{11859_13.eps} \end{figure}$	Figure C.2: Observed (2DCoudé) and synthetic (dotted) spectra of comet C/1996 B2 (Hyakutake).
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=270,width=14cm,clip]{11859_14.eps} \end{figure}$	Figure C.3: Observed (2DCoudé) and synthetic (dotted) spectra of comet C/1996 B2 (Hyakutake).
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=270,width=14cm,clip]{11859_15.eps} \end{figure}$	Figure C.4: Observed (2DCoudé) and synthetic (dotted) spectra of comet C/1995 O1 (Hale-Bopp).
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=270,width=14cm,clip]{11859_16.eps} \end{figure}$	Figure C.5: Observed (2DCoudé) and synthetic (dotted) spectra of comet C/1995 O1 (Hale-Bopp).
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=270,width=14cm,clip]{11859_17.eps} \end{figure}$	Figure C.6: Observed (SOFIN) and synthetic (dotted) spectra of comet C/1995 O1 (Hale-Bopp).
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=270,width=14cm,clip]{11859_18.eps} \end{figure}$	Figure C.7: Observed (2DCoudé) and synthetic (dotted) spectra of comet 55P/Tempel-Tuttle.
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=270,width=14cm,clip]{11859_19.eps} \end{figure}$	Figure C.8: Observed (2DCoudé) and synthetic (dotted) spectra of comet C/1999 H1 (Lee).
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=270,width=14cm,clip]{11859_20.eps} \end{figure}$	Figure C.9: Observed (2DCoudé) and synthetic (dotted) spectra of comet C/1999 S4 (LINEAR).
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=270,width=14cm,clip]{11859_21.eps} \end{figure}$	Figure C.10: Observed (2DCoudé) and synthetic (dotted) spectra of comet C/1999 T1 (McNaught-Hartley).
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=270,width=14cm,clip]{11859_22.eps} \end{figure}$	Figure C.11: Observed (2DCoudé) and synthetic (dotted) spectra of comet C/2001 A2-A (LINEAR).
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=270,width=14cm,clip]{11859_23.eps} \end{figure}$	Figure C.12: Observed (UVES) and synthetic (dotted) spectra of comet C/2000 WM1 (LINEAR).
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=270,width=14cm,clip]{11859_24.eps} \end{figure}$	Figure C.13: Observed (2DCoudé) and synthetic (dotted) spectra of comet 153P/Ikeya-Zhang.
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=270,width=14cm,clip]{11859_25.eps} \end{figure}$	Figure C.14: Observed (UVES) and synthetic (dotted) spectra of comet C/2002 X5 (Kudo-Fujikawa).
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=270,width=14cm,clip]{11859_26.eps} \end{figure}$	Figure C.15: Observed (UVES) and synthetic (dotted) spectra of comet C/2002 V1 (NEAT).
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=270,width=14cm,clip]{11859_27.eps} \end{figure}$	Figure C.16: Observed (UVES) and synthetic (dotted) spectra of comet C/2002 Y1 (Juels-Holvorcem).
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=270,width=14cm,clip]{11859_28.eps} \end{figure}$	Figure C.17: Observed (UVES) and synthetic (dotted) spectra of comet 88P/Howell.
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=270,width=14cm,clip]{11859_29.eps} \end{figure}$	Figure C.18: Observed (UVES) and synthetic (dotted) spectra of comet C/2002 T7 (LINEAR).
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=270,width=14cm,clip]{11859_30.eps} \end{figure}$	Figure C.19: Observed (UVES) and synthetic (dotted) spectra of comet C/2001 Q4 (NEAT).
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=270,width=14cm,clip]{11859_31.eps} \end{figure}$	Figure C.20: Observed (UVES) and synthetic (dotted) spectra of comet C/2001 Q4 (NEAT).
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=270,width=14cm,clip]{11859_32.eps} \end{figure}$	Figure C.21: Observed (UVES) and synthetic (dotted) spectra of comet C/2003 K4 (LINEAR).
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=270,width=14cm,clip]{11859_33.eps} \end{figure}$	Figure C.22: Observed (UVES) and synthetic (dotted) spectra of comet C/2003 K4 (LINEAR).
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=270,width=14cm,clip]{11859_34.eps} \end{figure}$	Figure C.23: Observed (HIRES) and synthetic (dotted) spectra of comet 9P/Tempel 1.
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=270,width=14cm,clip]{11859_35.eps} \end{figure}$	Figure C.24: Observed (UVES) and synthetic (dotted) spectra of comet 9P/Tempel 1.
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=270,width=14cm,clip]{11859_36.eps} \end{figure}$	Figure C.25: Observed (UVES) and synthetic (dotted) spectra of comet 73P-B/Schwassmann-Wachmann 3.
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=270,width=14cm,clip]{11859_37.eps} \end{figure}$	Figure C.26: Observed (2DCoudé) and synthetic (dotted) spectra of comet 73P-B/Schwassmann-Wachmann 3.
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=270,width=14cm,clip]{11859_38.eps} \end{figure}$	Figure C.27: Observed (UVES) and synthetic (dotted) spectra of comet 73P-C/Schwassmann-Wachmann 3.
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=270,width=14cm,clip]{11859_39.eps} \end{figure}$	Figure C.28: Observed (2DCoudé) and synthetic (dotted) spectra of comet 73P-C/Schwassmann-Wachmann 3.
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=270,width=14cm,clip]{11859_40.eps} \end{figure}$	Figure C.29: Observed (2DCoudé) and synthetic (dotted) spectra of comet C/2006 M4 (SWAN).
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=270,width=14cm,clip]{11859_41.eps} \end{figure}$	Figure C.30: Observed (HIRES) and synthetic (dotted) spectra of comet 17P/Holmes.
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=270,width=14cm,clip]{11859_42.eps} \end{figure}$	Figure C.31: Observed (2DCoudé) and synthetic (dotted) spectra of comet 17P/Holmes.
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=270,width=14cm,clip]{11859_43.eps} \end{figure}$	Figure C.32: Observed (2DCoudé) and synthetic (dotted) spectra of comet 8P/Tuttle.
Open with DEXTER

$\begin{figure} \par\includegraphics[angle=270,width=14cm,clip]{11859_44.eps} \end{figure}$	Figure C.33: Observed (2DCoudé) and synthetic (dotted) spectra of comet C/2007 N3 (Lulin).
Open with DEXTER

D Synthetic spectra

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{11859_45.eps} \end{figure}$

Figure D.1:

Small region of the B-X 0-0 band of the three CN isotopologues. The synthetic spectra were computed using isotopic abundances of 1, 1/89 and 1/145 for ¹²C¹⁴N (black), ¹³C¹⁴N (red) and ¹²C¹⁵N (blue), respectively, in the absence of collisional effects, and with r=1 AU, $\dot{r}=0$ . The Gaussian profile has FWHM = 0.05 Å. The intensity scale is arbitrary, but coherent with the three following plots.

Open with DEXTER

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{11859_46.eps} \end{figure}$	Figure D.2: Same as Fig. D.1 for a region of the B-X 0-1 band.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{11859_47.eps} \end{figure}$	Figure D.3: Same as Fig. D.1 for a region of the A-X 2-0 band.
Open with DEXTER

$\begin{figure} \includegraphics[width=8.5cm,clip]{11859_48.eps} \end{figure}$	Figure D.4: Same as Fig. D.1 for a region of the A-X 1-0 band.
Open with DEXTER

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.