Table 4.
Fitting parameters of the period–activity relationship in terms of the CgIW scenario along with the effective temperature.
| Temperature range | βg | βi | Psat | Pg−to−I | Rosat | Rog−to−I | 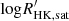 |
AgeC−to−g | Ageg−to−I | PI−to−W | AgeI−to−W |
|---|---|---|---|---|---|---|---|---|---|---|---|
| (K) | (day) | (day) | (Myr) | (Myr) | (day) | (Gyr) | |||||
| 3500−4000 | 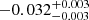 |
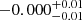 |
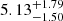 |
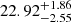 |
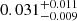 |
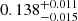 |
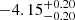 |
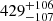 |
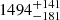 |
116 | 19.5 |
| 3750−4250 | 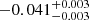 |
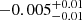 |
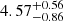 |
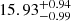 |
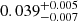 |
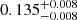 |
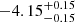 |
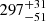 |
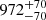 |
82 | 13.8 |
| 4000−4500 | 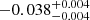 |
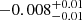 |
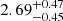 |
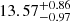 |
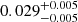 |
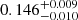 |
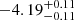 |
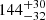 |
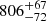 |
65 | 10.9 |
| 4250−4750 | 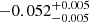 |
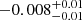 |
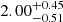 |
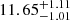 |
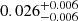 |
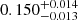 |
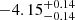 |
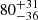 |
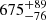 |
54 | 9.1 |
| 4500−5000 | 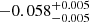 |
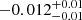 |
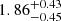 |
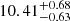 |
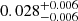 |
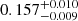 |
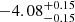 |
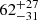 |
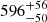 |
47 | 7.7 |
| 4750−5250 | 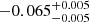 |
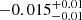 |
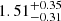 |
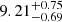 |
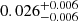 |
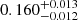 |
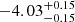 |
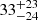 |
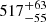 |
40 | 6.7 |
| 5000−5500 | 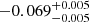 |
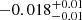 |
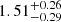 |
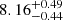 |
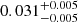 |
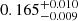 |
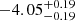 |
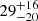 |
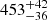 |
35 | 5.7 |
| 5250−5750 | 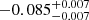 |
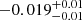 |
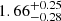 |
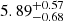 |
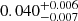 |
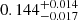 |
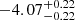 |
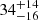 |
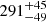 |
29 | 4.7 |
| 5500−6000 | 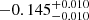 |
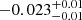 |
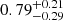 |
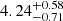 |
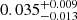 |
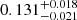 |
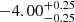 |
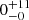 |
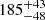 |
22 | 3.7 |
| 5750−6250 | 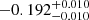 |
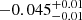 |
0 | 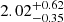 |
0 | 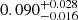 |
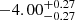 |
0 | 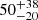 |
16 | 2.6 |
| 6000−6500 | – | 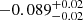 |
0 | 0 | 0 | 0 | – | 0 | 0 | 7 | 1.1 |
Notes. The period–activity relationship in terms of the CgIW scenario along with the effective temperature is shown in Fig. F.1, Fig. F.2, and Fig. F.3. This table present the fitting results. The parameters β represents the slope in each evolution phase. The parameters P and Ro represent the critical rotation periods and Rossby number that separate two neighboring phases, respectively. The parameter 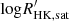 represents the saturated activity. The parameter Age represents the corresponding age of the critical rotation period, which is derived from Eq. (5). The critical Rossby number of the transition from the I phase to the W phase is 0.7 (van Saders et al. 2016), which is used to calculate PI−to−W and AgeI−to−W. The median of the temperature range is used to calculate Rossby number and the critical ages. The uncertainty of
represents the saturated activity. The parameter Age represents the corresponding age of the critical rotation period, which is derived from Eq. (5). The critical Rossby number of the transition from the I phase to the W phase is 0.7 (van Saders et al. 2016), which is used to calculate PI−to−W and AgeI−to−W. The median of the temperature range is used to calculate Rossby number and the critical ages. The uncertainty of 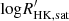 is calculated using the 1σ scatter of the fit.
is calculated using the 1σ scatter of the fit.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


