EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 699 (July 2025) A&A, 699 (2025) A264 Full HTML
Open Access
Issue
A&A
Volume 699, July 2025
Article Number A264
Number of page(s) 7
Section Atomic, molecular, and nuclear data
DOI https://doi.org/10.1051/0004-6361/202452981
Published online 16 July 2025

© The Authors 2025

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

Magnesium sulfide (MgS) molecules and microcrystals are of great interest to astrophysicists as a widespread dust component in carbon-rich (C-rich) evolved stars, especially asymptotic giant branch (AGB) stars. Forrest et al. (1981) detected a wide emission band around 30 μm (333 cm−1) in the infrared (IR) spectrum of circumstellar dust shells surrounding carbon stars and two planetary nebulae. This emission band displays a prominent broad emission excess in the IR spectrum, extending from 24 to 45 μm (42-222 cm−1). Subsequently, Goebel & Moseley (1985) proposed attributing this emission feature to MgS, and Begemann et al. (1994) compared the optical data of MgS to the thermal continuum emission of the CW Leo ploughing star (Nuth et al. 1985; Cox 1993), further supporting this perspective. It is notable that observations from the Infrared Space Observatory (ISO; Kessler 2002) have shown the presence of 30 μm features in a large number of carbon-rich stars (e.g., Justtanont et al. 1998; Jiang et al. 1999; Hony et al. 2003), noting that their intensity, shape, and width exhibit significant diversity. Zhang et al. (2009) studied the 30 μm emission feature in the protoplan-etary nebula HD 56126 by employing pure MgS grains in their modeling. Assuming a relatively high absorption rate for wavelengths shorter than 10 μm, analysis has predicted that up to ten times the available atomic sulfur content of MgS is required to observe the intensity of the 30 μm feature in the circumstellar dust envelope of the star HD 56126. This mass problem raises doubts about the rationality of MgS as the main carrier for this IR spectrum feature. Lombaert et al. (2012) observed composite grains in the outflow of the high mass-loss rate in AGB star LL Peg (also known as AFGL3068), indicating that MgS is a feasible candidate for explaining the 30 μm feature and independent of the absorbing efficiencies of these grains at λ <10 μm. Furthermore, assuming that the grains are in thermal contact with other substances in the outflow, the mass problem in HD 56126 reported by Zhang et al. (2009) does not occur in the star LL Peg. Hony & Bouwman (2004) investigated the influence of magnesium sulfide grains in the extended separated dust shell surrounding a carbon star on the IR spectra and the luminosity of these stars by constructing a radiative transfer model. They found that dust containing MgS coexisted with molecular gases in two specific carbon stars, R Scl and U Cam, suggesting that the dust in the shell reflects a carbon-rich chemical composition.

Due to the fact that metals are highly refractory, it is difficult to detect metal-bearing molecules in the gas phase. Most metal-bearing molecules have been detected in the circumstellar medium of the evolving star IRC+10216 (e.g., Cernicharo & Guelin 1987; Ziurys et al. 1995, 2002; Ziurys 1997; Pulliam et al. 2010; Agúndez et al. 2014; Cernicharo et al. 2019, 2023; Pardo et al. 2021; Changala et al. 2022; Cabezas et al. 2023; Gupta et al. 2024), the lensed quasar B0218+357 (Combes & Wiklind 1998), the Galactic center source Sgr B2 (Walmsley et al. 2002), and the oxygen-rich supergiant star VY Canis Majoris (Tenenbaum & Ziurys 2009, 2010). Recently, Rey-Montejo et al. (2024) discovered metal molecules, NaS and MgS, in the interstellar medium (ISM), as well as a preliminary detection of CaO in the molecular cloud G+0.693-0.027 (G+0.693) at the middle of the Galactic center molecular cloud. It is notable that G+0.693 is one of the best celestial bodies for discovering new interstellar molecules (including refractory molecular materials like MgS) in the gas phase, since spectroscopic investigations of G+0.693 have provided detections of over a dozen molecules from this celestial body (see, Jiménez-Serra et al. 2020, 2022; Rivilla et al. 2021a,b, 2020, 2022a,b; Rodríguez-Almeida et al. 2021a,b; Zeng et al. 2021, 2023; Sanz-Novo et al. 2023, 2024a,b; San Andrés et al. 2024).

The formation mechanism of MgS is not yet clear. In 1985, Nuth et al. (1985) and Goebel & Moseley (1985) first proposed that MgS may be formed through reactions on the surface of carbon grains. Kimura et al. (2005) conducted laboratory studies attempting to investigate the condensation of MgS on coal, but did not provide direct insights into its formation process. Zhukovska & Gail (2008) concluded through some thermochemical calculations and a detailed analysis of particle growth dynamics in stellar winds that magnesium sulfide can only be formed in stellar winds by depositing on preexisting dust particles, and that MgS is likely to be produced in the form of a shell on the surface of silicon carbide (SiC) grains formed in high-temperature regions near the star. Due to the presence of Si and Mg in both olivine and pyroxenes, which are the main components of refractory cores in interstellar dust, some authors (Fabian et al. 2001; Draine 2003; Min et al. 2007) proposed that the chemical properties of silicon serve as a proxy for the chemical behavior of magnesium in the gas phase, and thus postulated that the formation of MgS in G+0.693 may be due to “ion + neutral gas-phase reactions” and neutral molecule gas-phase interactions, such as HMgS++e−→H+MgS or Mg+S/S2/HS, which were proposed by Podio et al. (2017). However, considering that the volume density of the H2 gas in the G+0.693 star is too low (Zeng et al. 2020), the three-body exothermic reaction 2Mg+S2 → 2MgS (Takano et al. 1989) cannot occur.

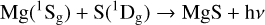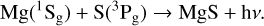In the present paper, we consider the possibility of MgS forming through radiative association in the collision of magnesium and sulfur atoms, Mg(1Sg)+S(1Dg)→MgS+hν\rm Mg(^1S_g)+S(^1D_g)\to MgS+h\nu(1) Mg(1Sg)+S(3Pg)→MgS+hν\rm Mg(^1S_g)+S(^3P_g)\to MgS+h\nu(2)

Although the environmental conditions in the G+0.693 molecular cloud reduce the efficiency of the radiative association process, the process in Equations (1) and (2) remains non-negligible, as radiative association represents the possible molecular formation processes, especially considering the applicability of two body kinetics and the abundance of magnesium and sulfur in this region.

The radiative association is a mechanism of molecular formation that plays an important role in the chemical evolution of small molecules detected in supernovae (Liu & Dalgarno 1994), novae (Rawlings 1988), molecular efflux regions (Glassgold et al. 1991), interstellar clouds (Herbst & Bates 1988), and stellar atmospheres (Langer & Glassgold 1990; Glassgold 1996). We refer to the work of Gunnar Nyman & Antipov (2015) for a review and systematic summary of the theoretical and computational methods of radiative association between diatomic molecules and ions. Furthermore, Bai et al. (2021) conducted a systematic theoretical investigation of the radiative association of the MgO molecule in the ISM conditions. Given the structural and chemical similarities between MgO and MgS, the present study adopts a similar computational framework and additionally includes radiative association processes involving both triplet and singlet states, in order to comprehensively explore the formation mechanism of MgS.

In this work, we investigate the radiative association process of Equations (1) and (2) following an ab initio procedure. Firstly, an advanced electron correlation method was used to calculate the potential energy curves (PECs) and the electric dipole transition moments (EDTMs) for the electronic states corresponding to the first singlet and first triplet dissociation limits. Based on this background, the radiative association cross sections (RACs) were calculated using the quantum mechanical scattering theory. It is notable that this method provides the nuclear wave function through the first-order perturbation theory, taking into account the resonance and tunneling effects. Finally, the rate coefficients were calculated based on the RACs and fitting the RACs to the three-parameter Arrhenius Kooij function.

2 Method of calculation

2.1 Molecular structure

Walker & Gerry (1997), Marcano & Barrow (1970), and Takano et al. (1989) conducted spectroscopic experiments on MgS molecules, measuring the equilibrium bond length, the ground state, and vibrational and rotational constants of one excited state. Partridge et al. (1988), Srnec & Zahradník (2005), and Chambaud et al. (2008) calculated theoretically the spectral constants of several low-lying excited states. Ribas et al. (2010) studied the first three dissociation limits of MgS molecules and calculated the corresponding PECs and EDTMs, and some spectral constants. As far as we know, there have been no new studies on the PEC and transition dipole moment of MgS molecules since then that provide the necessary and more comprehensive datasets. Therefore, we employed a new basis set, extended the range of nuclear distances considered, and computed PECs and EDTMs for the Mg(1Sg) state in relation to the S(1Dg) and S(3Pg) states using current state-of-the-art techniques.

Using the MOLPRO2012 package (Werner et al. 2012), the PECs and EDTMs of a group of low-lying singlet electronic states involved in radiative association processes were calculated. The entire calculation process was carried out at the MRCI+Q level: the Iartree Fock (IF) approach was used to generate a single configuration wave function. Then, the state-averaged complete active space self-consistent-field (CASSCF) method was used to optimize the wave function and generate multi-configuration wave functions. Finally, the multi-reference configuration interaction (MRCI) method, along with the Davidson correction (MRCI+Q), was applied for the final calculations. The basis sets used in the present work are aug-cc-pVQZ-DK type, a widely known accurate basis set, and the scalar relativistic effect was taken into account by the third-order Douglas Kroll Iamiltonian approximation (Reiher & Wolf 2004a,b). The PECs and EDTMs of the MgS molecule were calculated over a nuclear spacing range (r) from 1.0 to 10.5 A.

It is important to highlight that MOLPRO requires the use of Abelian subgroups when calculating molecular properties for molecules with degenerate symmetry. Therefore, with C2v, symmetry was used to calculate MgS molecular properties that the C2v point group has irreducible representations of (A1, B1, B2, A2), corresponding to Σ+=Α1, Π=Β1+Β2, Δ=Α1+Α2, Σ− = A2. In this study, the 1s22s22p6 shells of Mg and S atoms were placed in a closed shell layer. All electrons in 3S3P shells of the Magnesium atom and 3S AO of the sulfur atom were placed in the active space, so that the valence molecular orbitals were defined as (4,2,2,0) in the C2v representations.

Recombination reactions of the Mg(1Sg)+S(1Dg) and Mg(1 Sg)+S(3Pg) form five electronic states of MgS, namely Χ1Σ+, 11Π, 11Δ, a3Π, and 13Σ−, and there are eight transition modes between these electronic states. Due to the fact that the energy of electrons and the square of the EDTMs are factors determining the size of the RACs, we consider only the transition dipole moment here, and do not consider the permanent dipole moment.

We have neglected spin-orbit coupling effects on the spin-forbidden association processes in MgS, since the corresponding radiative rate constants in similar diatomic molecules are too small (on the order of 10-0.1 s−1), Xiao et al. (2024b), Ågren et al. (1996). The EDTMs of the spin-forbidden Π → Σ transitions are about 10−3 ea0 for such molecules of the second period, which could produce negligible radiative association rate coefficients in comparison with the ones obtained in the present study

To calculate the RACs and rate coefficients of the MgS molecules, it is necessary to extrapolate the PECs and EDTMs functions over the short and long range of interatomic distance (r). In this work, the PECs were divided into short, medium, and long ranges of internuclear distances, whereby the PEC of the medium-range part was obtained by solving the vibrational Schrödinger equation of molecular systems using the ab initio calculations.

At bond separations less than 1 Å, the PECs were smoothly fit to the potential functions of the form 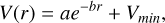V(r)=ae−br+VminV(r)=ae^{-br}+V_{min}(3)

where a and b are fitting parameters.

For r > 10.5 Å, the long-range interaction potentials were obtained by extrapolation according to the following function: 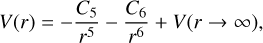V(r)=−C5r5−C6r6+V(r→∞)V(r)=-\frac{C_5}{r^5}-\frac{C_6}{r^6}+V(r\to\infty)(4)

where C5 is the quadrupole-quadrupole electrostatic interaction parameter (Chang 1967), estimated by fixing the value of C6, and using the ab initio point fit while keeping the dissociation limit constant, C6 is the dipole-dipole dispersion (van der Waals) coefficient and can be calculated by the London formula (London 1937). 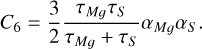C6=32τMgτSτMg+τSαMgαSC_6=\frac{3}{2}\frac{\tau_{Mg} \tau_S}{\tau_{Mg} + \tau_S}\alpha_{Mg}\alpha_S(5)

Here, τMg and τS are the ionization energies of the Mg and S atoms, and αMg and αS are the static dipolar polarizabilities of the Mg and S atoms. Their values are 150 and 23 a.u., respectively, and thus C6=557.767. Meanwhile, to ensure smooth and continuous curves, the cubic spline interpolation method was used to interpolate the points of the curve. The EDTMs of the MgS molecule were extrapolated using a 1/r4 function for r > ms Å.

2.2 Radiative association cross sections and rate coefficients

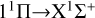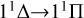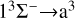Our task is to calculate the function of collision energy between Mg and S atoms using a quantum mechanical method, and to obtain the RACs through the 11Π→X1Σ+1$^1$$\Pi$$\to$X$^1$$\Sigma$$^+$, 11Δ→11Π1$^1$$\Delta$$\to$1$^1$$\Pi$, and 13Σ−→a3Π1$^3$$\Sigma$$^-$$\to$a$^3$$\Pi$ transitions. The cross sections for radiative association are based on the first-order perturbation theory.

The total cross section of radiative association transition from a continuous state (Λ) to bound state (Λ′) transition can be expressed as (Nyman et al. 2015) 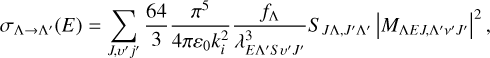σΛ→Λ′(E)=∑J,υ′j′643π54πε0ki2fΛλEΛ′Sυ′J′3SJΛ,J′Λ′|MΛEJ,Λ′ν′J′|2\sigma_{\Lambda\to\Lambda'}(E)=\sum_{J,\upsilon'j'}\frac{64}{3}\frac{\pi^5}{4\pi\varepsilon_0k_i^2}\frac{f_\Lambda}{\lambda^3_{E\Lambda'S\upsilon'J'}}S_{J\Lambda,J'\Lambda'} \left \lvert M_{\Lambda EJ,\Lambda'\nu'J'}\right\rvert^2(6)

where the sum is over the initial partial waves with angular momenta, J, final vibrational, v′, and final rotational, J′, quantum numbers. 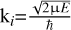ki=2μEℏk$_i$=$\frac{\sqrt{2\upmu E}}{\hbar}$ stands for the wave number of the scattering state, ε0 stands for the vacuum permittivity, and 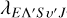λEΛ′Sυ′J′$\lambda_{E\Lambda'S\upsilon'J'}$ stands for the wavelength of the emitted photon.

The Mg(1Sg)+S(1Dg) collision forms three electronic states with five possible proximity channels. Therefore, the weight factor that appears in the RAC transition from Λ state to Λ′ state is 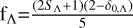fΛ=(2SΛ+1)(2−δ0,Λ)5f$_\Lambda$=$\frac{(2S_\Lambda+1)(2-\delta_{0,\Lambda})}{5}$. Here, SΛ is the spin of the Λ state, and δ0,Λ is the Kronecker coefficient. When Λ is Σ, δ0,Λ =0; otherwise, it is equal to 1. Therefore, fΛ=2/5 for 11Π and 11Δ states. Similarly, for Mg(1Sg)+S(3Pg) association, the weight factor is modified to 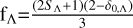fΛ=(2SΛ+1)(2−δ0,Λ)3f$_\Lambda$=$\frac{(2S_\Lambda+1)(2-\delta_{0,\Lambda})}{3}$. Thus, fΛ=1/3 for 13Σ−.

The 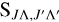SJΛ,J′Λ′S$_{J\Lambda, J'\Lambda'}$ value in Equation (6) is the Hönl-London factor, which is the factor that gives the dependence of spectroscopic line intensities on the rotational quantum numbers, J (Herzberg 1950). The value of 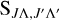SJΛ,J′Λ′S$_{J\Lambda, J'\Lambda'}$ is shown in Table 1. Here, the Hönl-London factors for the Π→Σ, Δ→Π, and Σ→Π transitions are four times smaller than the factors given by Hansson & Watson (2005), which will result in a fourfold reduction in the obtained cross section and rate coefficient. 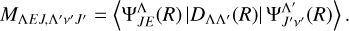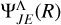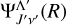The EDTM matrix element was factorized as MΛEJ,Λ′ν′J′=⟨ΨJEΛ(R)|DΛΛ′(R)|ΨJ′ν′Λ′(R)⟩M_{\Lambda EJ,\Lambda'\nu'J'}=\left\langle \Psi^{\Lambda}_{JE}(R)\left\lvert D_{\Lambda\Lambda'}(R)\right\rvert\Psi^{\Lambda'}_{J'\nu'}(R)\right\rangle(7)

Here, ΨJEΛ(R)$\Psi^{\Lambda}_{JE}(R)$ and ΨJ′ν′Λ′(R)$\Psi^{\Lambda'}_{J'\nu'}(R)$ are the radial parts of the total wavefunctions, between any two electronic states with the same spin quantum number, if Λ = Λ′, 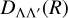DΛΛ′(R)$D_{\Lambda\Lambda'}(R)$ is the transition dipole moment (otherwise, it is the permanent dipole moment).

The rate coefficient of radiative association was calculated by integrating the cross sections on the Maxwell Boltzmann distribution with a temperature range of 10-10 000 K, as is given by the following equation: 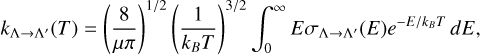kΛ→Λ′(T)=(8μπ)1/2(1kBT)3/2∫0∞EσΛ→Λ′(E)e−E/kBTdEk_{\Lambda\to\Lambda'}(T)=\left(\frac{8}{\mu\pi}\right)^{1/2}\left(\frac{1}{k_BT}\right) ^{3/2}\int_{0}^{\infty} E\sigma_{\Lambda\to\Lambda'}(E)e^{-E/k_BT}\,dE(8)

where μ is the reduced mass of MgS, kB is the Boltzmann constant, E is the collision energy, and 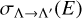σΛ→Λ′(E)$\sigma_{\Lambda\to\Lambda'}(E)$ are the selected RACs.

Table 1

Hönl-London factors, 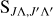SJΛ,J′Λ′S$_{J\Lambda, J'\Lambda'}$.

3 Results and discussion

3.1 PECs and EDTMs

The calculated molecular spectral constants are presented in Table 2, alongside previous experimental and theoretical values to verify the accuracy of our results. For the Χ1Σ+ state, ωe and Re values are 511.7714 cm−1 and 2.1717 Å, respectively, with ωe showing errors of 3.21% (Marcano & Barrow 1970) and 2.79% (Chase et al. 1982), and Re showing an error of 1.36% (Marcano & Barrow 1970; Chase et al. 1982). However, when compared to theoretical values, the errors in ωe are 0.04% (Ribas et al. 2010), 0.15% (Partridge et al. 1988), and 2.33% (Chambaud et al. 2008), while the errors in Re are 0.34% (Ribas et al. 2010), 0.10% (Partridge et al. 1988), and 0.98% (Chambaud et al. 2008), respectively. Our calculated values show a good agreement with the ones reported by Ribas et al. (2010) at the CASSCF/MRCI/cc-pVQZ level. Specifically, our calculated result for Be in the X1 Σ+ state is 0.2610 cm−1, while the two experimental values are 0.26797 cm−1 (Marcano & Barrow 1970) and 0.26570 cm−1 (Chase et al. 1982), respectively. The error is within 3%, which falls within an acceptable range. It is also important to emphasize that the rotational constant, Be , plays a critical role in ensuring the accuracy of quantum chemical methods for structure determination.

There are no experimental data for the 11Π and 11Δ emission rates; only theoretical results are available. Our data were compared with the latest theoretical results (Ribas et al. 2010), giving deviations in ωe and Re for the 11Π state within the range of 0.06 and 0.74%, respectively. For the 11Δ state, the ωe and Re deviations are 4.84 and 0.37%, respectively. Overall, the calculated spectral constants are consistent with experimental and theoretical values.

The adiabatic PECs of the calculated MgS electronic states are shown in Fig. 1. The X1 Σ+, 11Π, and a3Π states are bound, characterized by deep potential wells. In contrast, the 11Δ state exhibits a significant potential barrier at r = 2.725 A, while the 13Σ− state shows a barrier at r = 2.175 A. As r decreases, the PECs exhibit a repulsive behavior in the entrance channel. The results for the PECs calculated by Ribas et al. (2010) are consistent with our data.

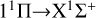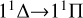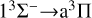For the singlet and the triplet electronic states, we considered the 11Π→X1Σ+1$^1$$\Pi$$\to$X$^1$$\Sigma$$^+$, 11Δ→11Π1$^1$$\Delta$$\to$1$^1$$\Pi$, and 13Σ−→a3Π1$^3$$\Sigma$$^-$$\to$a$^3$$\Pi$ transitions, and the calculated EDTMs are shown in Fig. 2. In order to more intuitively check our accuracy, we also included the theoretical results of the 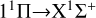11Π→X1Σ+1$^1$$\Pi$$\to$X$^1$$\Sigma$$^+$ transition (Ribas et al. 2010) in Fig. 2 and it was found that the two sets of calculated results are consistent.

Table 2

Spectroscopic constants of the bound states of MgS.

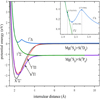thumbnail Fig. 1

PECs of MgS.
thumbnail Fig. 2

EDTMs of MgS.
thumbnail Fig. 3

Cross sections of MgS radiative association.

3.2 Cross sections

The results for the RACs using Equations (1) and (2) are shown in Fig. 3. For the RACs of the 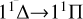11Δ→11Π1$^1$$\Delta$$\to$1$^1$$\Pi$ transition, many resonance features are visible at lower collision energies, which can be attributed to a shape resonance. This type of resonance is usually caused by quasi-bound states, as is shown in the PEC of the 11Δ state in Fig. 1. Due to the existence of a potential barrier, the initial potential energy of VΛ (R) combines with the centrifugal term of 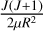J(J+1)2μR2$\frac{J(J+1)}{2\mu R^2}$ to form the effective potential of VΛ, 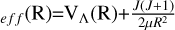_{eff}(R)=VΛ(R)+J(J+1)2μR2\textit{$_{eff}$}(R)=V$_\Lambda$(R)+$\frac{J(J+1)}{2\mu R^2}$. Therefore, the PEC can be divided into three parts with R = 2.7 À as the boundary to analyze the cross sections. When R > 2.7 À, the PEC exhibits a repulsive state, and the cross sections resonate due to tunneling at low collision energies. Due to the existence of a potential barrier of 0.3816 eV around 2.7 À, the cross section experiences a sudden increase in collision energy between 0.25-0.38 eV. This results in the 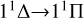11Δ→11Π1$^1$$\Delta$$\to$1$^1$$\Pi$ transition playing a major role in the radiative association process when the collision energy is greater than 0.3 eV. Additionally, the presence of the potential barrier slows down the tunneling velocity, leading to the disappearance of the resonance. When R < 2.7 À, there is a potential well above the dissociation limit of 0.1385 eV at R = 2.35 À, and the PEC shows a quasibound state. At this point, the resonance is related to short-range potential extrapolation and effective potential. Considering that our νΛ(R) is negative, νΛeff(R) will gradually decrease with the increase of the rotational quantum number, J, and the resonance peak will gradually decrease until J reaches a specific value, making νΛeff (R)=0. That is, when the collision energy is around 1.5 eV, the resonance peak disappears, and at the collision energy of 2.5 eV the cross section sharply decreases due to the Franck-Condon principle.

The trend of the RAC for the 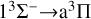13Σ−→a3Π1$^3$$\Sigma$$^-$$\to$a$^3$$\Pi$ transition is similar to that of the 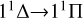11Δ→11Π1$^1$$\Delta$$\to$1$^1$$\Pi$ transition. Although the magnitude of the cross section for the 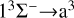13Σ−→a3Π1$^3$$\Sigma$$^-$$\to$a$^3$$\Pi$ transition is smaller, this does not necessarily imply that it is negligible in astrophysical environments. The relative importance of this transition depends on the ratio of S(1D) to S(3P) in the source.

The 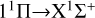11Π→X1Σ+1$^1$$\Pi$$\to$X$^1$$\Sigma$$^+$ transition dominates the radiative association process when the collision energy is less than 3 eV. The cross section exhibits resonance in the low-energy region and increases with the increase in collision energy. When the collision energy is greater than 0.015 eV, the resonance gradually decreases and disappears with the increase in collision energy. In the collision range of 1 × 10−4 eV, the cross sections gradually decrease with the increase in collision energy, and at a collision energy of 1.5 eV, the cross sections sharply decrease. Due to the fact that the potential well of 11 H is much deeper than that of 11Δ, there are more resonances in the cross sections of the 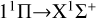11Π→X1Σ+1$^1$$\Pi$$\to$X$^1$$\Sigma$$^+$ transition.

thumbnail Fig. 4

Rate coefficients of MgS radiative association.

3.3 Rate coefficients

The calculated rate coefficients are shown in Fig. 4. At low temperatures, the rate coefficient of the 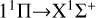11Π→X1Σ+1$^1$$\Pi$$\to$X$^1$$\Sigma$$^+$ transition slowly increases. It then slowly decreases with increasing temperature, from about 3.7535×10−18 cm3 s−1 at 10 K to 2.9902×10−18 cm3 s−1 at 10 000 K. Overall, the rate coefficient does not change significantly with temperature. For the 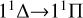11Δ→11Π1$^1$$\Delta$$\to$1$^1$$\Pi$ transition, at temperatures below approximately 400 K, the rate coefficient is significantly lower than that of the 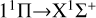11Π→X1Σ+1$^1$$\Pi$$\to$X$^1$$\Sigma$$^+$ transition, resulting in a low efficiency. At temperatures greater than 400 K, the rate coefficient sharply increases from 1.03×10−19 cm3 s−1 at 400 K to 4.50×10−17 cm3 s−1 at 10 000 K. 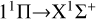It is noteworthy that at a temperature of about 1600 K, the rate coefficient reaches 5.13×10−18 cm3 s−1, approaching the rate coefficient of the 11Π→X1Σ+1$^1$$\Pi$$\to$X$^1$$\Sigma$$^+$ transition, and then surpassing the 11Π→X1Σ+1$^1$$\Pi$$\to$X$^1$$\Sigma$$^+$ transition with increasing temperature, occupying the dominant position in the radiative association process. This is because the potential barrier of the 11 Δ state rapidly increases the RACs of the 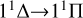11Δ→11Π1$^1$$\Delta$$\to$1$^1$$\Pi$ transition, leading to a rapid increase in the rate coefficient also. The radiative association rate coefficient for the 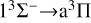13Σ−→a3Π1$^3$$\Sigma$$^-$$\to$a$^3$$\Pi$ transition is several orders of magnitude lower than that for the 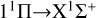11Π→X1Σ+1$^1$$\Pi$$\to$X$^1$$\Sigma$$^+$ transition at low temperatures, and also lower than that for the 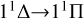11Δ→11Π1$^1$$\Delta$$\to$1$^1$$\Pi$ transition at high temperatures. Moreover, since the 13Σ− state is almost completely repulsive, the corresponding rate coefficient exhibits a monotonically increasing trend at temperatures above 100 K. In addition, the resonance also influences the rate coefficient of radiative association. In a radiative association study of the S2− ions, Xiao et al. (2024a) compare the rate coefficient with and without resonance and find that the error is less than 3%.

Finally, the total rate coefficients for singlet-singlet and triplet-triplet transitions were calculated; they are listed in column 2 of Table 3. The rate coefficients, ksinglet and ktriplet, were fit separately to the three-parameter Arrhenius-Kooij function: 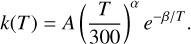k(T)=A(T300)αe−β/Tk(T)=A\left(\frac{T}{300} \right)^\alpha e^{-\beta/T}(9)

The rate coefficients, ksinglet and ktriplet, were separately fit into six temperature ranges. The fitting parameters are shown in Table 4.

Table 3

Radiative association rate coefficients for singlet-singlet (ksinglet) and triplet-triplet (ktriplet) transitions of MgS.

Table 4

Fitting parameters of MgS.

4 Conclusion

Motivated by the fact that magnesium sulfide molecules and microcrystals are of great interest to astrophysicists as a widespread dust component in carbon-rich stars, we have in this work focused on the formation and spectral characteristics of this compound. We predicted the rate coefficients of MgS formation through the radiative association process of the atomic Mg (1Sg) + S (1Dg) and Mg (1Sg) + S (3Pg) collision based on potential energy surfaces and transition density matrices calculated at a high level of quantum chemical methodology. We found that the 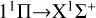11Π→X1Σ+1$^1$$\Pi$$\to$X$^1$$\Sigma$$^+$ transition has a major impact on the radiative association process at low temperatures, and that the rate coefficient decreases with increasing temperature. The transition 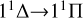11Δ→11Π1$^1$$\Delta$$\to$1$^1$$\Pi$ is crucial for the radiative association process at high temperatures, and the rate coefficient increases with temperature due to the existence of a potential barrier in the 11Δ state. In the range of 10-10000 K, the rate coefficient for the singlet-singlet transitions of MgS generation is as high as 3.78×10−18 cm3 s−1→4.79×10−17 cm3 s−1, while for the triplet-triplet transition it spans from 2.02×10−22 cm3 s−1→6.79×10−18 cm3 s−1. These values imply that the radiative association process is a prominent channel for the formation of MgS in carbon-rich stars. We thus believe that our study can improve the chemical model of MgS formation in the G+0.693 astrophysical region.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant No.12274178, No.11874177); the Ministry of Education and Science of Ukraine (Grant No. 0122U000760); The High Performance Computing Center (HPCC) of Jilin University and the high-performance computing cluster Tiger at IAMP. Finally, would also like to thank Professors Yong Wu and Jianguo Wang for their help.

References

  1. Agúndez, M., Cernicharo, J., & Guélin, M. 2014, A&A, 570, A45 [Google Scholar]
  2. Ågren, H., Vahtras, O., & Minaev, B. 1996, Adv. Quantum Chem., 27, 71 [Google Scholar]
  3. Bai, T., Qin, Z., & Liu, L. 2021, MNRAS, 500, 2496 [Google Scholar]
  4. Begemann, B., Dorschner, J., Henning, T., Mutschke, H., & Thamm, E. 1994, ApJ, 423, L71 [NASA ADS] [CrossRef] [Google Scholar]
  5. Cabezas, C., Pardo, J. R., Agúndez, M., et al. 2023, A&A, 672, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Cernicharo, J., & Guelin, M. 1987, A&A, 183, L10 [Google Scholar]
  7. Cernicharo, J., Cabezas, C., Pardo, J. R., et al. 2019, A&A, 630, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Cernicharo, J., Cabezas, C., Pardo, J. R., et al. 2023, A&A, 672, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Chambaud, G., Guitou, M., & Hayashi, S. 2008, Chem. Phys., 352, 147 [Google Scholar]
  10. Chang, T. Y. 1967, Rev. Mod. Phys., 39, 911 [Google Scholar]
  11. Changala, P. B., Gupta, H., Cernicharo, J., et al. 2022, ApJ, 940, L42 [NASA ADS] [CrossRef] [Google Scholar]
  12. Chase, M. W. J., Curnutt, J. L., Downey, J. R. J., et al. 1982, J. Phys. Chem. Ref. Data, 11, 695 [Google Scholar]
  13. Combes, F., & Wiklind, T. 1998, A&A, 334, L81 [NASA ADS] [Google Scholar]
  14. Cox, P. 1993, ASP Conf. Ser., 41, 163 [Google Scholar]
  15. Draine, B. T. 2003, ARA&A, 41, 241 [NASA ADS] [CrossRef] [Google Scholar]
  16. Fabian, D., Henning, T., Jäger, C., et al. 2001, A&A, 378, 228 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Forrest, W. J., Houck, J. R., & McCarthy, J. F. 1981, ApJ, 248, 195 [Google Scholar]
  18. Glassgold, A. E. 1996, ARA&A, 34, 241 [Google Scholar]
  19. Glassgold, A. E., Mamon, G. A., & Huggins, P. J. 1991, ApJ, 373, 254 [NASA ADS] [CrossRef] [Google Scholar]
  20. Goebel, J. H., & Moseley, S. H. 1985, ApJ, 290, L35 [NASA ADS] [CrossRef] [Google Scholar]
  21. Gunnar Nyman, M. G., & Antipov, S. V. 2015, Int. Rev. Phys. Chem., 34, 385 [Google Scholar]
  22. Gupta, H., Changala, P. B., Cernicharo, J., et al. 2024, ApJ, 966, L28 [Google Scholar]
  23. Hansson, A., & Watson, J. K. G. 2005, J. Mol. Spectr., 233, 169 [Google Scholar]
  24. Herbst, E., & Bates, D. R. 1988, ApJ, 329, 410 [Google Scholar]
  25. Herzberg, G. 1950, Molecular Spectra and Molecular Structure, Spectra of diatomic molecules (Berlin: Springer), 1 [Google Scholar]
  26. Hony, S., & Bouwman, J. 2004, A&A, 413, 981 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Hony, S., Tielens, A. G. G. M., Waters, L. B. F. M., & de Koter, A. 2003, A&A, 402, 211 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Jiang, B. W., Szczerba, R., & Deguchi, S. 1999, IRAS 03313+6058: an AGB star with 30 micron emission [Google Scholar]
  29. Jiménez-Serra, I., Martín-Pintado, J., Rivilla, V. M., et al. 2020, Astrobiology, 20, 1048 [Google Scholar]
  30. Jiménez-Serra, I., Rodríguez-Almeida, L. F., Martín-Pintado, J., et al. 2022, A&A, 663, A181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Justtanont, K., Cami, J., Yamamura, I., de Jong, T., & Waters, L. B. F. M. 1998, Ap&SS, 255, 351 [Google Scholar]
  32. Kessler, M. F. 2002, Adv. Space Res., 30, 1957 [Google Scholar]
  33. Kimura, Y., Kurumada, M., Tamura, K., et al. 2005, A&A, 442, 507 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Langer, W. D., & Glassgold, A. E. 1990, ApJ, 352, 123 [NASA ADS] [CrossRef] [Google Scholar]
  35. Liu, W., & Dalgarno, A. 1994, ApJ, 428, 769 [NASA ADS] [CrossRef] [Google Scholar]
  36. Lombaert, R., de Vries, B. L., de Koter, A., et al. 2012, A&A, 544, L18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. London, F. 1937, Trans. Faraday Soc., 33, 8b [Google Scholar]
  38. Marcano, M., & Barrow, R. F. 1970, Trans. Faraday Soc., 66, 2936 [Google Scholar]
  39. Min, M., Waters, L. B. F. M., de Koter, A., et al. 2007, A&A, 462, 667 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Nuth, J. A., Moseley, S. H., Silverberg, R. F., Goebel, J. H., & Moore, W. J. 1985, ApJ, 290, L41 [Google Scholar]
  41. Nyman, G., Gustafsson, M., & and, S. V. A. 2015, Int. Rev. Phys. Chem., 34, 385 [Google Scholar]
  42. Pardo, J. R., Cabezas, C., Fonfría, J. P., et al. 2021, A&A, 652, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Partridge, H., Langhoff, S. R., & Bauschlicher, Charles W. J. 1988, J. Chem. Phys., 88, 6431 [Google Scholar]
  44. Podio, L., Codella, C., Lefloch, B., et al. 2017, MNRAS, 470, L16 [Google Scholar]
  45. Pulliam, R. L., Savage, C., Agúndez, M., et al. 2010, ApJ, 725, L181 [NASA ADS] [CrossRef] [Google Scholar]
  46. Rawlings, J. M. C. 1988, MNRAS, 232, 507 [Google Scholar]
  47. Reiher, M., & Wolf, A. 2004a, J. Chem. Phys., 121, 2037 [Google Scholar]
  48. Reiher, M., & Wolf, A. 2004b, J. Chem. Phys., 121, 10945 [Google Scholar]
  49. Rey-Montejo, M., Jiménez-Serra, I., Martín-Pintado, J., et al. 2024, ApJ, 975, 174 [NASA ADS] [CrossRef] [Google Scholar]
  50. Ribas, V. W., Ferrão, L. F. A., Roberto-Neto, O., & Machado, F. B. C. 2010, Chem. Phys. Lett., 492, 19 [Google Scholar]
  51. Rivilla, V. M., Martín-Pintado, J., Jiménez-Serra, I., et al. 2020, ApJ, 899, L28 [Google Scholar]
  52. Rivilla, V. M., Jiménez-Serra, I., García de la Concepción, J., et al. 2021a, MNRAS, 506, L79 [NASA ADS] [CrossRef] [Google Scholar]
  53. Rivilla, V. M., Jiménez-Serra, I., Martín-Pintado, J., et al. 2021b, Proc. Natl. Acad. Sci., 118, e2101314118 [NASA ADS] [CrossRef] [Google Scholar]
  54. Rivilla, V. M., Colzi, L., Jiménez-Serra, I., et al. 2022a, ApJ, 929, L11 [NASA ADS] [CrossRef] [Google Scholar]
  55. Rivilla, V. M., García De La Concepción, J., Jiménez-Serra, I., et al. 2022b, Front. Astron. Space Sci., 9, 829288 [NASA ADS] [CrossRef] [Google Scholar]
  56. Rodríguez-Almeida, L. F., Jiménez-Serra, I., Rivilla, V. M., et al. 2021a, ApJ, 912, L11 [Google Scholar]
  57. Rodríguez-Almeida, L. F., Rivilla, V. M., Jiménez-Serra, I., et al. 2021b, A&A, 654, L1 [CrossRef] [EDP Sciences] [Google Scholar]
  58. San Andrés, D., Rivilla, V. M., Colzi, L., et al. 2024, ApJ, 967, 39 [CrossRef] [Google Scholar]
  59. Sanz-Novo, M., Rivilla, V. M., Jiménez-Serra, I., et al. 2023, ApJ, 954, 3 [NASA ADS] [CrossRef] [Google Scholar]
  60. Sanz-Novo, M., Rivilla, V. M., Jiménez-Serra, I., et al. 2024a, ApJ, 965, 149 [Google Scholar]
  61. Sanz-Novo, M., Rivilla, V. M., Müller, H. S. P., et al. 2024b, ApJ, 965, L26 [Google Scholar]
  62. Srnec, M., & Zahradník, R. 2005, Chem. Phys. Lett., 407, 283 [Google Scholar]
  63. Takano, S., Yamamoto, S., & Saito, S. 1989, Chem. Phys. Lett., 159, 563 [Google Scholar]
  64. Tenenbaum, E. D., & Ziurys, L. M. 2009, Int. Symp. Mol. Spectr., 64, WI03 [Google Scholar]
  65. Tenenbaum, E. D., & Ziurys, L. M. 2010, INT. Symp. Mol. Spectr., 65, WG02 [Google Scholar]
  66. Walker, K. A., & Gerry, M. C. L. 1997, J. Mol. Spectr., 182, 178 [Google Scholar]
  67. Walmsley, C. M., Bachiller, R., Pineau des Forêts, G., & Schilke, P. 2002, ApJ, 566, L109 [Google Scholar]
  68. Werner, H., Knowles, P., Knizia, G., Manby, F., & Schütz, M. 2012, Wiley Interdisciplinary Reviews: Computational Molecular Science (Hoboken: Wiley), 2, 242 [Google Scholar]
  69. Xiao, L., Chen, Y., Liu, D., Minaev, B. F., & Yan, B. 2024a, Astron. Comput., 49, 100877 [Google Scholar]
  70. Xiao, L., Wei, Q., An, S., Minaev, B. F., & Yan, B. 2024b, J. Quant. Spec. Radiat. Transf., 320, 108979 [Google Scholar]
  71. Zeng, S., Zhang, Q., Jiménez-Serra, I., et al. 2020, MNRAS, 497, 4896 [NASA ADS] [CrossRef] [Google Scholar]
  72. Zeng, S., Jiménez-Serra, I., Rivilla, V. M., et al. 2021, ApJ, 920, L27 [NASA ADS] [CrossRef] [Google Scholar]
  73. Zeng, S., Rivilla, V. M., Jiménez-Serra, I., et al. 2023, MNRAS, 523, 1448 [NASA ADS] [CrossRef] [Google Scholar]
  74. Zhang, K., Jiang, B. W., & Li, A. 2009, ApJ, 702, 680 [Google Scholar]
  75. Zhukovska, S., & Gail, H. P. 2008, A&A, 486, 229 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  76. Ziurys, L. M. 1997, IAU Symp., 170, 370 [Google Scholar]
  77. Ziurys, L. M., Apponi, A. J., Guelin, M., & Cernicharo, J. 1995, ApJ, 445, L47 [NASA ADS] [CrossRef] [Google Scholar]
  78. Ziurys, L. M., Savage, C., Highberger, J. L., et al. 2002, ApJ, 564, L45 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Hönl-London factors, SJΛ,J′Λ′S$_{J\Lambda, J'\Lambda'}$.

In the text
Table 2

Spectroscopic constants of the bound states of MgS.

In the text
Table 3

Radiative association rate coefficients for singlet-singlet (ksinglet) and triplet-triplet (ktriplet) transitions of MgS.

In the text
Table 4

Fitting parameters of MgS.

In the text

All Figures

thumbnail Fig. 1

PECs of MgS.
In the text
thumbnail Fig. 2

EDTMs of MgS.
In the text
thumbnail Fig. 3

Cross sections of MgS radiative association.
In the text
thumbnail Fig. 4

Rate coefficients of MgS radiative association.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.