EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 698 (May 2025) A&A, 698 (2025) L5 Full HTML
Open Access
Issue
A&A
Volume 698, May 2025
Article Number L5
Number of page(s) 5
Section Letters to the Editor
DOI https://doi.org/10.1051/0004-6361/202554549
Published online 27 May 2025

© The Authors 2025

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

It is currently accepted that millisecond pulsars (MSPs) are the product of low-mass X-ray binaries (LMXBs) or intermediate mass X-ray binaries (IMXBs) when the pulsar passes through a recycling process, in which accretes matter and angular momentum from its companion star, and is spun up to periods of the order of milliseconds (i.e., MSPs) (Alpar et al. 1982). An intriguing group of eclipsing MSPs was identified (Fruchter et al. 1988), which called for an explanation.

More recently, in the last decade or so, the Fermi γ-ray Space Telescope discoveries have significantly increased the number of these eclipsing radio MSP systems, with orbital periods of Porb < 24 hours, in the Galactic field. This enabled a classification in these systems based on the mass of their companion star Mc: some of them termed “Redbacks” (RBs, 0.1 ≲ Mc/M⊙ ≲ 0.4) and others (in which evidence of ablation of the companion was found Fruchter et al. 1988) named “Black Widows” (BWs, 0.1 ≲ Mc/M⊙) (Roberts 2013). Because of the BW name given after the original discovery, and the RB denomination was suggested by Australians for their similarity, the combination of both groups is now known as “spiders”.

Some ideas have been suggested to explain the spider systems and their possible conceptual unification. Chen et al. (2013) argued that irradiation by a strong and isotropic wind emitted by the pulsar would form RBs or BWs, based on how strong the wind really is. Therefore, they concluded that RBs do not evolve into BWs. Alternatively, Benvenuto et al. (2014) (BDVH14) concluded that for reproducing the spiders’ orbital parameters, X-ray irradiation feedback (IFB) due to the photons produced by the accretion near the NS is necessary. They also found that some RBs can be progenitors of BWs. A similar conclusion was recently reached by Misra et al. (2025a), who were also able to reproduce the two newly discovered spider systems: “Tidarrens” (Romani et al. 2016) and “Huntsman” (Strader et al. 2015). The Tidarrens are, in fact, a subclass of BWs, but with Porb < 2 h. Just three of those systems have been detected (see Pletsch et al. 2012; Romani et al. 2012, 2014), and the spectra suggest they are hydrogen-poor, a feature acknowledged by Kong et al. (2014) for 2FGL J1653.6-0159, and also studied by Romani et al. (2014).

At first glance, the Huntsman systems are quite similar to RBs, but their orbital periods are one order of magnitude larger, and harbor fully recycled pulsars. Just one system is confirmed as a Huntsman (PSR J1417-4402; Strader et al. 2015), with its spin determined through observations performed with the CSIRO Parkes telescope, as 2.66 ms (Camilo et al. 2016), and where the distance determination is still in some doubt, but confirmed to be ≥4 kpc with Gaia parallax (Strader et al. 2015). The other reported system is a strong candidate (PSR J1947-1120; Strader et al. 2019), and new searches should enlarge the class.

The Huntsman systems are thought to reach Roche-Lobe OverFlow (RLOF) when the companion star has exhausted the hydrogen core. Recently, Strader et al. (2025) suggested that those systems originate when the companion star has reached the RLOF condition in the “red Bump” region of the red giant branch, with initial orbital periods between 2.6 d and 7.0 d. Misra et al. (2025a) found that Huntsman pulsars are reproduced regardless of how strong the pulsar wind is, but the efficiency of the mass accretion during RLOF is important to reproduce the spin found in the only confirmed system PSR J1417-4402. This highlights the importance of considering a broad range of initial orbital periods Porb, i when studying spider systems.

These findings suggest that the unification of all spider systems would require the implementation of additional physics, such as IFB and pulsar wind evaporation, to reproduce the positions in the Porb versus M2 plane (where M2 is the mass of the companion, donor star) and their full evolutionary tracks. The consideration of a broad range of orbital parameters is also necessary for reproducing, among others, the Huntsman systems.

We shall show in this work how Huntsman systems arise by performing explicit binary evolution calculations. The minimum and maximum periods expected from theory are found assuming the standard magnetic braking, for both solar metallicity and a low metallicity Z = 10−3, which bracket future systems that have yet to be identified. The behavior of the radius is also given explicitly. In fact, the evolutionary stage suggested to be associated with Huntsman pulsars was already present in our first calculations (i.e., BDVH14), although that stage was not specifically analyzed in that paper.

The remainder of this Letter is organized as follows: In Section 2 we present our evolutionary calculations. Finally, in Section 3 we discuss the meaning of these results and give some concluding remarks.

2. The Huntsman state along the binary evolution

We have employed the code constructed and described in Benvenuto & De Vito (2003) to compute the evolution of a suite of systems formed by a donor star of initial mass M2, i = 1.25 M⊙, together with a NS companion of MNS, i = 1.3 M⊙ with Porb, i logarithmically evenly spaced with steps of 20%. We assumed a conservative mass transfer; considering, as usual, that the NS can accrete matter up to the Eddington rate: ṀEdd = 2 × 10−8 (M/M⊙) M⊙ yr−1. The orbital evolution was computed from the ZAMS. For this purpose, we have assumed the same physics as described in Echeveste et al. (2024). Here we considered the standard magnetic braking prescription (Verbunt & Zwaan 1981). For solar metallicity models we considered 0.69 d ≤ Porb, i ≤ 18.48 d whereas for Z = 10−3 we employed 0.40 d ≤ Porb, i ≤ 46.00 d. In these calculations we have not considered IFB (see below).

We show in Fig. 1 the evolution of these systems in the Porb versus M2 plane. As is well known, models without IFB undergo a long-standing mass transfer episode on a timescale of megayears or even gigayears depending on the initial orbital period. The first episode in which the star detaches from its lobe is due to the stage in which the H-shell burning reaches a step-like discontinuity in the H-profile left by the very deep outer convective zone. The H-shell burning detachment will be referred to as “HSBD” in the rest of this work. The star reacts by detaching from its lobe for a timescale of a few megayears. In the case of isolated stars, this behavior (found long ago by, e.g., Thomas 1967) is connected with the occurrence of a red bump (Christensen-Dalsgaard 2015) seen in the Hertzsprung – Russell diagram (HRD) of globular (Loriga et al. 2025) and open clusters (Anthony-Twarog et al. 2018). After detachment, the advancement of the H-shell burning forces the star to swell substantially to reestablish the RLOF. During detachment, Porb and M2 remain almost unchanged. Although there is gravitational radiation, and maybe some wind mass loss associated with this stage, both are minor effects. Therefore, there is a well-defined point-like region in the Porb versus M2 plane, at which detachment occurs. This is shown in Fig. 1, where the heavy blue (pink) dots on each track, corresponding to solar composition (Z = 10−3) mark the place where HSBD occurs. It is clear that the two candidates are located in the galactic plane, and feature a near-solar metallicity. However, since the red bump feature is expected for a wide range of metallicities, we have added results corresponding to them, because we do expect this kind of spider pulsar will soon be discovered among objects with these abundances. Thus, the low-metallicity results have been included as a kind of prediction of the conditions in which we expect them to be detected. For completeness, in Fig. 2 we present the HRD corresponding to the case of solar composition models.

thumbnail Fig. 1.

The orbital period as a function of the donor mass for a suite of systems formed by a donor star of 1.25 M⊙, a NS of 1.3 M⊙ with Porb, i logarithmically evenly spaced with steps of 20%. The orbital evolution was computed from the ZAMS. Black (magenta) lines denote results corresponding to solar metallicity (Z = 10−3). The detached stages, in which Huntsman pulsars are expected, are denoted in blue for solar metallicity and in pink for Z = 10−3. Horizontal bars correspond to the measurements of the system PSR J1947-1120 (green) and PSR J1417-4402 (black). MB0 denotes the standard magnetic braking prescription.

thumbnail Fig. 2.

HR diagram showing the trajectories and the intervals where the Huntsman states occur (blue). The first initial period that allows the mass transfer (the so-called case B) is clearly seen on the bottom, producing the ample and slanted “V” track is Porb, i = 1 d, while all shorter periods end in downward tracks. It is important to remind the reader that this is somewhat sensitive to the treatment of the physics and small variations may occur for different choices of the braking and other features (see, e.g., Istrate et al. 2014; Misra et al. 2025b).

In Tables 1–2 we present the main characteristics of the detached phase of these models. In those tables, R2 is the radius of the companion donor star, whereas RL is the radius of a sphere with a volume equal to the one of its Roche lobe. Notice that, compared to solar composition models, low-metallicity ones undergo HBSD at higher Porb (starting from higher Porb, i) and appreciably higher luminosities. This indicates that the H-shell burning is more intense, making the detachment stage appreciably shorter. Nevertheless, the masses of the components and filling factors are similar for both compositions considered here.

Table 1.

Main characteristics of the detached stage of systems with a solar composition donor star of M2, i = 1.25 M⊙ and a MNS, i = 1.3 M⊙.

Table 2.

Same as Table 1, but for the case of a low metallicity Z = 10−3.

We should stress that there is a well-defined range of Porb, i values for which HSBD is expected to occur. In this suite of calculations, for solar composition and Z = 10−3, it happens if 1 d ≤ Porb, i ≤ 12.83 d and 1.44 d ≤ Porb, i ≤ 26.62 d respectively. For somewhat lower Porb, i values, the H-core is not exhausted before RLOF. For higher Porb, i values, the H-shell burning reaches the H-step profile before RLOF. It should be remembered that these numbers change slightly with the exact physical ingredients entering the evolution code. The full emerging picture will be given in a forthcoming work, that will also explore the issue of different initial NS masses and other related effects.

In Fig. 3 we show the Roche lobe filling factor defined as R2/RL as a function of time for solar composition models. There, we have not included all those undergoing HBSD since for those with 3.58 d ≤ Porb, i ≤ 12.83 d, curves are very similar. Interestingly, the values of the calculated filling factors are high, in the range of 0.868 − 0.901 (see De Vito et al. 2020, especially their Table 2).

thumbnail Fig. 3.

R2/RL filling factor for some of the solar composition models presented in Fig. 1 as a function of age. Models with larger Porb, i that undergo HSBD are not included since they behave very similar to the case of Porb, i = 3.58 d. Labels on each curve correspond to Porb, i. The fractions marked with heavy blue lines correspond to conditions in which the system is detached, allowing for the detection of the pulsar companion.

An important issue is whether models with IFB-driven pulsed mass transfer also undergo HSBD. To address this issue, we have computed a set of models with IFB similar to those presented in BDVH14. To include IFB, we assumed the Hameury & Ritter (1997) treatment: the irradiation flux Firr is given by Firr = αirrLirr/(4πa2) where αirr ≤ 1 is the fraction of accretion luminosity Lirr that effectively participates in the donor irradiation, and a is the orbital semiaxis. Furthermore, 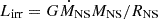L irr = G M ˙ NS M NS / R NS $ L_{\mathrm{irr}}= G \dot{M}_{\mathrm{NS}} M_{\mathrm{NS}}/R_{\mathrm{NS}} $ where G is the gravitational constant and ṀNS, MNS, and RNS are the accretion rate, the mass and the radius of the NS companion, respectively. Among the irradiated models, we have selected the case of a system formed by a donor star of M2, i = 1 M⊙, a NS of MNS, i = 1.4 M⊙ with Porb, i = 1 d and moderate IFB assuming αirr = 0.1. In Fig. 4 we present the filling factor as a function of time for the entire time interval in which the system undergoes mass transfer. It is seen that pulsed mass transfer occurs before and also after HSBD. This is an expected situation, since HSBD is nuclear burning-driven, acting on very deep layers, whereas IFB is essentially a surface phenomenon.

thumbnail Fig. 4.

R2/RL filling factor for a system formed by a solar composition donor star of 1 M⊙, a NS of 1.4 M⊙ with Pinic, i = 1 d. We considered moderate IFB assuming αirr = 0.10. Blue lines represent detached conditions whereas black lines depict stages with a mass transfer rate Ṁ ≥ 10−11 M⊙ yr−1. IFB-driven pulsed mass transfer and HSBD occur in the model.

3. Discussion and conclusions

To account for the very existence of BWs and RBs, it has been suggested in previous works (Benvenuto et al. 2014, BDVH14) that models have to include IFB and/or evaporation. Both phenomena act on the surface of the donor star. On the contrary, HSBD is associated with the deep interior of the star, and does not depend on the former, which acts quite independently in these systems.

An important feature is that the two detected Huntsman systems have relatively short periods (5.374 d and 10.265 d for PSR J1417-4402 and PSR J1947-1120, respectively). This automatically means that their companion stars belong to the less massive end of the donor mass range (M2 ≲ 0.5 M⊙) which allows a Huntsman state. The shorter period system is particularly restrictive (see Fig. 1), although a lower metallicity and a different initial donor mass would improve the agreement, as we shall show in detail elsewhere.

In the calculations presented in Benvenuto et al. (2015) we have considered IFB that leads to pulsed mass transfer. Depending on the strength of irradiation, when detached, models have values of 0.92 ≤ R2/RL ≤ 0.99 (see Fig. 7 of Benvenuto et al. 2015). IFB does not quench HSBD. Indeed, IFB-driven pulsed mass transfer and HSBD occur in the same model star as shown above, in Fig. 4.

Alternatively, Chen et al. (2013) have suggested that BWs and RBs are due to different evaporation regimes and follow separate evolutionary tracks. In that picture, BWs (RBs) undergo moderate (severe) evaporation. Since the Roche lobe filling factor values attained in these models are far lower than the filling factor during HSBD (De Vito et al. 2020), model detachment is led by evaporation and precludes the occurrence of HSBD.

Thus, we conclude that the identification of the Huntsman pulsars with HSBD suggested by Strader et al. (2025) seems very plausible. However, additional ingredients are still needed to account for all spider pulsars. Indeed, it seems natural that pulsars with high enough values of Porb, i (although not too high) will undergo HSBD and also pulsed mass transfer due to IFB action. Depending on the precise value of Porb, i, they will evolve through the RB stage, and some will finally reach the BW stage. If evaporation is not too weak, they will become “normal” BWs. If evaporation is weak, the orbit will remain close to that predicted by standard models that are driven solely by gravitational radiation and will become Tidarrens. Hunstman systems are, as discussed above, one relatively short stage expected from evolutionary considerations, emerging from the overall spider family. Thus, this picture (with ingredients anchored in observational evidence, IFB (Turchetta et al. 2025) and ablation (Fruchter et al. 1988) provides a natural and quite complete view of the evolution of these systems.

Acknowledgments

OGB is a member of the Carrera del Investigador Científico of the Comisión de Investigaciones Científicas Of the Province of Buenos Aires, Argentina (CIC-PBA). MADV is a member of the Carrera del Investigador Científico of the Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET). LN is a CONICET fellow. This work was supported by the FAPESP Agency (São Paulo State) under the grant 2024/16892-2 and the CNPq (Federal Government) for the award of a Research Fellowship to JEH. Co-funded by the European Union (ERC-2022-AdG, “StarDance: the non-canonical evolution of stars in clusters”, Grant Agreement 101093572, PI: E. Pancino). Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Research Council. Neither the European Union nor the granting authority can be held responsible for them.

References

  1. Alpar, M., Cheng, A., Ruderman, M., & Shaham, J. 1982, Nature, 300, 728 [NASA ADS] [CrossRef] [Google Scholar]
  2. Anthony-Twarog, B. J., Lee-Brown, D. B., Deliyannis, C. P., & Twarog, B. A. 2018, AJ, 155, 138 [NASA ADS] [CrossRef] [Google Scholar]
  3. Benvenuto, O., & De Vito, A. 2003, MNRAS, 342, 50 [NASA ADS] [CrossRef] [Google Scholar]
  4. Benvenuto, O. G., De Vito, M. A., & Horvath, J. E. 2014, ApJ, 786, L7 [NASA ADS] [CrossRef] [Google Scholar]
  5. Benvenuto, O. G., De Vito, M. A., & Horvath, J. E. 2015, ApJ, 798, 44 [Google Scholar]
  6. Camilo, F., Reynolds, J. E., Ransom, S. M., et al. 2016, ApJ, 820, 6 [NASA ADS] [CrossRef] [Google Scholar]
  7. Chen, H.-L., Chen, X., Tauris, T. M., & Han, Z. 2013, ApJ, 775, 27 [NASA ADS] [CrossRef] [Google Scholar]
  8. Christensen-Dalsgaard, J. 2015, MNRAS, 453, 666 [NASA ADS] [CrossRef] [Google Scholar]
  9. De Vito, M. A., Benvenuto, O. G., & Horvath, J. E. 2020, MNRAS, 493, 2171 [Google Scholar]
  10. Echeveste, M., Novarino, M. L., Benvenuto, O. G., & De Vito, M. A. 2024, MNRAS, 530, 4277 [NASA ADS] [CrossRef] [Google Scholar]
  11. Fruchter, A. S., Stinebring, D. R., & Taylor, J. H. 1988, Nature, 333, 237 [Google Scholar]
  12. Hameury, J. M., & Ritter, H. 1997, A&AS, 123, 273 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Istrate, A. G., Tauris, T. M., Langer, N., & Antoniadis, J. 2014, A&A, 571, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Kong, A. K. H., Jin, R., Yen, T. C., et al. 2014, ApJ, 794, L22 [NASA ADS] [CrossRef] [Google Scholar]
  15. Loriga, M., Pallanca, C., Ferraro, F. R., et al. 2025, A&A, 695, A156 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Misra, D., Linares, M., & Ye, C. S. 2025a, A&A, 693, A314 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Misra, D., Koljonen, K. I., & Linares, M. 2025b, MNRAS, submitted [arXiv:2504.05372] [Google Scholar]
  18. Pletsch, H. J., Guillemot, L., Fehrmann, H., et al. 2012, Science, 338, 1314 [CrossRef] [Google Scholar]
  19. Roberts, M. S. E. 2013, in Neutron Stars and Pulsars: Challenges and Opportunities After 80 years, ed. J. van Leeuwen, IAU Symp., 291, 127 [Google Scholar]
  20. Romani, R. W., Filippenko, A. V., Silverman, J. M., et al. 2012, ApJ, 760, L36 [NASA ADS] [CrossRef] [Google Scholar]
  21. Romani, R. W., Filippenko, A. V., & Cenko, S. B. 2014, ApJ, 793, L20 [NASA ADS] [CrossRef] [Google Scholar]
  22. Romani, R. W., Graham, M. L., Filippenko, A. V., & Zheng, W. 2016, ApJ, 833, 138 [NASA ADS] [CrossRef] [Google Scholar]
  23. Strader, J., Chomiuk, L., Cheung, C. C., et al. 2015, ApJ, 804, L12 [NASA ADS] [CrossRef] [Google Scholar]
  24. Strader, J., Swihart, S., Chomiuk, L., et al. 2019, ApJ, 872, 42 [Google Scholar]
  25. Strader, J., Ray, P. S., Urquhart, R., et al. 2025, ApJ, 980, 124 [Google Scholar]
  26. Thomas, H. C. 1967, Z. Astrophys., 67, 420 [Google Scholar]
  27. Turchetta, M., Sen, B., Simpson, J., et al. 2025, MNRAS, 538, 380 [Google Scholar]
  28. Verbunt, F., & Zwaan, C. 1981, A&A, 100, L7 [NASA ADS] [Google Scholar]

All Tables

Table 1.

Main characteristics of the detached stage of systems with a solar composition donor star of M2, i = 1.25 M⊙ and a MNS, i = 1.3 M⊙.

In the text
Table 2.

Same as Table 1, but for the case of a low metallicity Z = 10−3.

In the text

All Figures

thumbnail Fig. 1.

The orbital period as a function of the donor mass for a suite of systems formed by a donor star of 1.25 M⊙, a NS of 1.3 M⊙ with Porb, i logarithmically evenly spaced with steps of 20%. The orbital evolution was computed from the ZAMS. Black (magenta) lines denote results corresponding to solar metallicity (Z = 10−3). The detached stages, in which Huntsman pulsars are expected, are denoted in blue for solar metallicity and in pink for Z = 10−3. Horizontal bars correspond to the measurements of the system PSR J1947-1120 (green) and PSR J1417-4402 (black). MB0 denotes the standard magnetic braking prescription.
In the text
thumbnail Fig. 2.

HR diagram showing the trajectories and the intervals where the Huntsman states occur (blue). The first initial period that allows the mass transfer (the so-called case B) is clearly seen on the bottom, producing the ample and slanted “V” track is Porb, i = 1 d, while all shorter periods end in downward tracks. It is important to remind the reader that this is somewhat sensitive to the treatment of the physics and small variations may occur for different choices of the braking and other features (see, e.g., Istrate et al. 2014; Misra et al. 2025b).
In the text
thumbnail Fig. 3.

R2/RL filling factor for some of the solar composition models presented in Fig. 1 as a function of age. Models with larger Porb, i that undergo HSBD are not included since they behave very similar to the case of Porb, i = 3.58 d. Labels on each curve correspond to Porb, i. The fractions marked with heavy blue lines correspond to conditions in which the system is detached, allowing for the detection of the pulsar companion.
In the text
thumbnail Fig. 4.

R2/RL filling factor for a system formed by a solar composition donor star of 1 M⊙, a NS of 1.4 M⊙ with Pinic, i = 1 d. We considered moderate IFB assuming αirr = 0.10. Blue lines represent detached conditions whereas black lines depict stages with a mass transfer rate Ṁ ≥ 10−11 M⊙ yr−1. IFB-driven pulsed mass transfer and HSBD occur in the model.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.