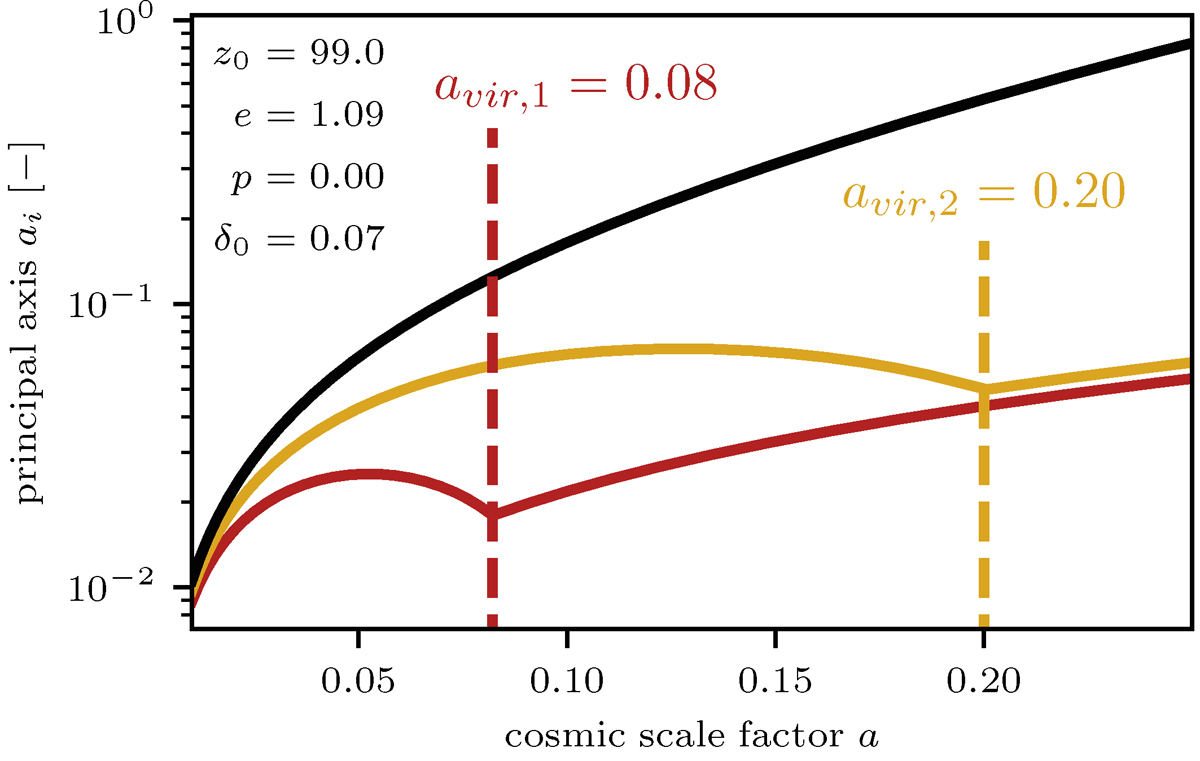
Example of ellipsoidal collapse in a ΛCDM background for a homogeneous ellipsoid with mass M = 5 × 10⁹ M_⊙ h⁻¹. The equation of motion, Eq. (C.1), preserves the homogeneity of the initial conditions and it is thus sufficient to observe the evolution of the axis scale factors a_i(a). After an initial expansion, each axis turns around, contracts and freezes out according to the steady-state tensor virial theorem, Eq. (C.6). The subsequent evolution is fixed to ensure a constant comoving axis size R_i = a_i(a)R_ini/a. We identify a filament as an object with two frozen axes – in the depicted scenario realized at z = 4. The residual triaxiality, i.e., the mismatch between the yellow and red lines at large a, is ignored for the construction of our filament population.