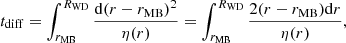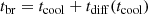EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 691 (November 2024) A&A, 691 (2024) L21 Full HTML
Highlight
Open Access
Issue
A&A
Volume 691, November 2024
Article Number L21
Number of page(s) 6
Section Letters to the Editor
DOI https://doi.org/10.1051/0004-6361/202452539
Published online 26 November 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

White dwarf (WD) stars are the most common end point of stellar evolution, as all main sequence stars with masses lower than 9 − 12 M⊙ will eventually become WDs. Therefore, the WD population is considered a powerful tool for investigating a wide variety of astrophysical problems, from the formation and evolution of our Galaxy to the ultimate fate of planetary systems (see Althaus et al. 2010, for a review). In particular, WDs contain valuable information about the evolution of their progenitor stars, and can be used to constrain nuclear reaction rates (De Gerónimo et al. 2019), the initial-to-final-mass relation (Catalán et al. 2008; Cummings et al. 2018), and the occurrence of third dredge-up episodes in the asymptotic giant branch (AGB) (Althaus et al. 2015), among others.

The presence of magnetic fields on the surface of WDs has been known for more than 50 years (Kemp et al. 1970; Angel & Landstreet 1970), and yet its origin is still not well understood (see Ferrario et al. 2015, for a review). Several explanations have been proposed, involving both single evolution and binary interactions. One possibility is that WDs inherit a magnetic field from their formation history, and this is indeed consistent with the magnetic fields observed on the surface of peculiar Ap and Bp stars. More recently, it has been proposed that the mixing instability induced by WD crystallization in fast-rotating WDs can generate a dynamo magnetic field (Isern et al. 2017). Other explanations involve close binary interactions: the magnetic field can be generated either during a merger episode (García-Berro et al. 2012) or in a dynamo acting during a post-common-envelope phase (Tout et al. 2008). Although there are more than 600 magnetic WDs reported in the literature (Ferrario et al. 2020), an important step forward in the interpretation of the origin of WD magnetism comes from the recent determination of a 20pc volume-limited sample of magnetic WDs (Bagnulo & Landstreet 2021; Kawka et al. 2007). These authors checked each of the WDs within 20 pc from the Sun individually for the presence of magnetic fields, thus eliminating the observational biases of the previous magnitude-limited samples of magnetic WDs. Based on their analysis, Bagnulo & Landstreet (2021) conclude that the occurrence of magnetism is significantly higher in WDs that have undergone the process of core crystallization than in WDs with fully liquid cores. Bagnulo & Landstreet (2022) expanded the volume-limited sample to 40 pc, although only including WDs younger than 0.6 Gyr, reconfirming their results. In summary, the incidence of magnetism in young (non-crystallized) WDs is ∼10%, whereas this number raises to ∼30% for old (crystallized) WDs. Bagnulo & Landstreet (2021, 2022) interpreted that this increase could be due to a crystallization-driven dynamo, but it could also be an internal field produced in an earlier evolutionary stage that gradually relaxes to the surface from the interior.

Authors have recently explored the possibility that the convective motions induced by crystallization in the overlying liquid mantle are efficient enough to explain the high intensity of the observed magnetic fields on the surface of WDs, which range from 103 to 109 Gauss (Camisassa et al. 2022a; Ginzburg et al. 2022; Montgomery & Dunlap 2024). Among these studies, Castro-Tapia et al. (2024a) and Fuentes et al. (2023, 2024) showed that efficient convection could only take place at the onset of crystallization, and that thermohaline convection takes place during most of the crystallization process, thus demonstrating that only the dynamos driven at the onset of crystallization could account for the high-intensity magnetic fields detected in WDs. Additionally, recent works by Blatman & Ginzburg (2024a,b) showed that, due to the large electrical conductivity in the WD interior (and consequently the small magnetic diffusivity), even if the crystallization-driven dynamos are able to account for the intensity of the observed magnetic field, this field cannot emerge to the surface immediately, taking from ∼1 to ∼7 Gyr to do so.

In the present paper, we study a different mechanism able to account for the origin of magnetism in WDs and compare it with the crystallization-driven dynamo hypothesis. Main sequence stars with masses ≳1.1 M⊙ burn hydrogen through the CNO cycle, thus developing convective cores, in which a magnetic dynamo is expected to take place. WDs more massive than ∼0.55 M⊙ are the descendants of these main sequence stars with convective cores. In the last decade, Fuller et al. (2015) proposed that the presence of strong magnetic fields in the core of red giant stars can alter the propagation of the gravity waves, decreasing the mode visibility in a phenomenon known as the “magnetic greenhouse effect”. Based on this effect, asteroseismology has proven the existence of very strong magnetic fields (B ≳ 105 G) trapped in the interior of many red giant branch stars that are not detectable at their surfaces (Li et al. 2023, 2022; Deheuvels et al. 2023). Indeed, Stello et al. (2016) studied the strength of dipolar oscillation modes in low- and intermediate-mass red giant stars, finding that strong core fields only occur in red giants more massive than 1.1 M⊙. Also, these authors found that the occurrence rate is at least 50% for stars with masses from 1.6 to 2.0 M⊙, indicating that powerful dynamos should take place in the H-burning convective cores of main sequence stars. Cantiello et al. (2016) and Bagnulo & Landstreet (2022) proposed that this magnetic field generated during the main sequence convective core dynamo can survive the entire evolutionary path into the WD phase. In this Letter, we examine this possibility by estimating the breakout time in which this field, initially trapped in the stellar interior, should reach the stellar surface during the WD phase. Then, we compare those estimations with predictions for the emergence timescale of crystallization-driven dynamos and with the volume-limited sample of magnetic WDs of Bagnulo & Landstreet (2022).

2. Methods

2.1. Main sequence dynamo hypothesis

Assuming an initial-to-final-mass relation (e.g., Catalán et al. 2008; Cummings et al. 2018), the progenitors of WDs more massive than ∼0.55 M⊙ are main sequence stars with masses ≳1.1 M⊙ that harbor convective cores during their main sequence phase that could sustain dynamo magnetic fields (see Käpylä et al. 2023). The strength of the generated magnetic fields is predicted to be in the range of 104 − 106 G by numerical magnetohydrodynamic (MHD) simulations (Brun et al. 2005; Featherstone et al. 2009; Hidalgo et al. 2024) and by estimations assuming equipartition between the magnetic energy density and the kinetic energy density (Cantiello et al. 2016). Furthermore, the MHD simulations of Augustson et al. (2016) show that the field strength can be larger than 106 G in the convective cores of 10 M⊙ B-type stars. Assuming magnetic flux conservation, these values are compatible with the lower limits obtained for magnetic field strengths in the cores of red giant branch stars and in the surface of WD stars (Cantiello et al. 2016; Stello et al. 2016).

In Fig. 1 we plot a Kippenhahn diagram from the main sequence to the planetary nebula phase of a 4.0 M⊙ star with Z = 0.02 taken from Miller Bertolami (2016), where the final WD mass is 0.83 M⊙. The green hatched area is the extension of the convective core, first during central H burning (left panel) and later during the central helium burning (right panel). The hatched blue area shows the location of the outer convective zone. The deepest penetrations of the outer convective zone correspond to the first and second dredge up, respectively. The pulse-driven (or intershell) convective zones, which are short lived and driven by the He shell flashes during the thermally pulsing AGB, are not visible in this plot due to their short timescales. The boundaries of convective regions were set by the Schwarzschild criterion allowing for turbulent mixing beyond these boundaries (see Miller Bertolami 2016, for details on the overshooting treatment).

thumbnail Fig. 1.

Kippenhahn diagram of a 4.0 M⊙ star with Z = 0.02 from the main sequence to the end of the thermally pulsing AGB from Miller Bertolami (2016). The hatched green and blue areas indicate the central and outer convective zones, respectively. The orange and purple lines indicate the outer limits of the H- and He-depleted regions, respectively. The pink shaded area is the region where the magnetic fields are expected to be buried. The intershell convective zones driven by the thermal pulses on the AGB are not visible in this plot. The final WD mass of this model is 0.83 M⊙.

In the present paper, we assume a magnetic field generated by dynamo action during the central H-burning phase. Because the Ohmic diffusion timescales during the main sequence and red giant phases are too long (Cantiello et al. 2016), magnetic fields present in the stellar core at the main sequence are frozen in their Lagrangian mass coordinate. This means that, during the main sequence (left panel), the magnetic field is confined to the pink shaded area, which denotes the maximum extension of the central convective zone. This assumption is probably not valid in areas of the star that become convective after the main sequence phase. Indeed, if the convective energy density, ϵcon, exceeds the magnetic energy density, ϵmag, convection can distort the preexisting field into an unstable configuration. Conversely, if ϵcon < ϵmag, the magnetic field can remain unchanged. We stress that whether convection can disrupt preexisting stable magnetic field configurations remains uncertain (see Cantiello et al. 2016, for a thorough analysis). In the present work, we simply assume that the magnetic field vanishes in the regions where the outer convective zone has penetrated. Therefore, the outer boundary of the magnetized region, which we refer to as the magnetic boundary (MB), is dictated by the maximum extent of the outer convective region, which can occur either during the first dredge-up or second dredge-up (in those stars in which a second dredge-up takes place). Nevertheless, in stars with masses lower than ∼2 M⊙, the outer convective zone does not reach the mass coordinates where the magnetic field was present and, for these stars, the MB is determined by the maximum extent of the main sequence convective core. Also, in these stars, vigorous convection is developed in the core during core He flashes, which will likely affect the magnetic field configuration. Furthermore, in such stars, the convective core is larger during central He burning than it is during central H burning, and the magnetic breakout times that we obtain for the WD descendants of these stars are larger than the Hubble timescale. Based on this information, we consider that in stars with initial masses lower than ∼2 M⊙, it is unlikely that the field can survive the entire evolution and emerge in the WD phase. Finally, we have ignored the fact that the pulse-driven convective zones can alter the field configuration. However, we do not expect this choice to alter our main results, as in those WDs where the magnetic field can emerge to the surface within the Hubble timescale, the pulse-driven convective regions are above the assumed magnetic field boundary.

In Fig. 2 we plot the boundary of the magnetized regions (i.e., the MB) that we obtained while considering different stellar evolutionary models, that is, the final outer boundary of the pink region in Fig. 1. The x-axis is the WD mass, and the y-axis corresponds to the logarithm of 1 minus the mass coordinate at the MB normalized to the WD mass, which, in other words, is the logarithm of the mass that the magnetic field has to diffuse through in order to reach the WD surface. It is important to stress that these values depend on the treatment of the convective boundaries and on the mass-loss rates considered by each model. However, all sets of models predict that the MB is closer to the surface for more massive WDs. As the different stellar evolutionary codes and the different physical inputs predict different values of the mass coordinate at the MB, we employed a cubic prescription to fit log(1 − MMB/MWD) in terms of the WD mass (black solid line). We allow a deviation of ±0.30 dex from the cubic fit (black dotted lines), which encompasses all the theoretical predictions from the different stellar evolutionary codes.

thumbnail Fig. 2.

Logarithm of the outer mass fraction from the boundary where the magnetic field is expected to be trapped, i.e., the MB, in terms of WD mass. We plot the theoretical predictions for CO WDs from Miller Bertolami (2016) and Dominguez et al. (1999), and the Full-Network Repository of Updated Isotopic Tables & Yields (FRUITY) database (Cristallo et al. 2015), and those for oxygen-neon (ONe) WDs from Siess (2010) and Limongi et al. (2024). These models consider different metallicities spreading around the solar value. A cubic polynomial fit to the data with MWD > 0.575 M⊙ is shown with a solid black line. A deviation of ±0.30 from the cubic fit is shown using dotted black lines, which comprises all models considered in this work.

2.2. Crystallization-driven dynamo hypothesis

For the WD crystallization-driven dynamos, we consider the MB to be the outer boundary of the Rayleigh-Taylor unstable region induced by crystallization, as is done in Blatman & Ginzburg (2024a). We employed the stellar evolutionary code LPCODE (see Althaus et al. 2005, for details) to calculate the WD evolutionary models, employing the phase diagram of Horowitz et al. (2010) to model CO crystallization. The outer boundary of the convective region is determined by imposing a positive carbon abundance gradient in the star, ∇X = dlnX/dlnP ≥ 0 (where, X is the C abundance and P is the pressure; see Camisassa et al. 2022a,b, 2019, for details). We note that the mass coordinate at the MB for the crystallization dynamo moves outward as evolution proceeds and the crystallized core grows in mass, unlike the MB for the main sequence dynamo, which stays in the same mass coordinate throughout the entire WD phase.

2.3. Magnetic diffusion and magnetic breakout times

In order to obtain the magnetic breakout time (tbr), we first estimate the diffusion time (tdiff) that the magnetic field takes to diffuse from the MB to the WD surface using (Cantiello et al. 2016):

t diff = ∫ r MB R WD d ( r − r MB ) 2 η ( r ) = ∫ r MB R WD 2 ( r − r MB ) d r η ( r ) , $$ \begin{aligned} t_{\rm diff}= \int _{r_{\rm MB}}^{R_{\rm WD}} \frac{\mathrm{d}(r-r_{\rm MB})^2}{\eta (r)}= \int _{r_{\rm MB}}^{R_{\rm WD}} \frac{2(r-r_{\rm MB})\mathrm{d} r}{\eta (r)}, \end{aligned} $$(1)

where rMB is the radius that corresponds to the MB, RWD is the WD radius, and η(r) is the magnetic diffusivity. Here, η(r) = c2/(4πσ(r)), where σ(r) is the electrical conductivity, which was obtained using Eq. (1) from Cumming (2002) for the fully degenerate regime, the Spitzer formula for the non-degenerate regime (Spitzer 1962, Eq. (19) in Cumming 2002), and an interpolation in between those regimes (i.e., when 0.1Tf < T < 10Tf, where Tf is the Fermi temperature). We note that tdiff is different at each time step, because σ(r) and rMB vary with time. We calculated WD evolutionary models using LPCODE, obtaining σ(r), rMB, and tdiff at each time step. Once tdiff is calculated for each WD cooling time, tcool, we find tbr by calculating the earliest tbr when the equation

t br = t cool + t diff ( t cool ) $$ \begin{aligned} t_{\rm br}= t_{\rm cool}+t_{\rm diff}(t_{\rm cool}) \end{aligned} $$(2)

is satisfied.

3. Results

In Fig. 3 we overlay the estimated magnetic field breakout times onto the distribution of WD masses versus cooling ages for the sample of magnetic WDs of Bagnulo & Landstreet (2021, 2022). Our theoretical prediction for the magnetic field emergence for crystallization-driven dynamos in CO-core WDs (blue line) is in agreement with the results of Blatman & Ginzburg (2024a). We find that most of the magnetic WDs in this volume-limited sample cannot be explained by the crystallization-driven dynamo hypothesis, because they lie on the left of the magnetic field emergence line (blue line). Even if the crystallization-driven dynamo can sustain a strong magnetic field, this field will be trapped in the WD interior for a very long period of time, ranging from ∼1 Gyr in our most massive model (1.29 M⊙) to ∼7.3 Gyr in our least massive model (0.53 M⊙). On the contrary, if the main sequence dynamo magnetic field can survive trapped in the stellar interior all the way to the white phase, it can emerge to the surface, and account for many of the magnetic WDs in this sample. Depending on the parametrization of the MB considered, the magnetic field emergence should occur on a timescale longer than the Hubble time for WDs with masses ≲0.6 M⊙. If we consider our fit for the MB, allowing a deviation of ±0.30 dex, the main sequence dynamo magnetic field emerges in the shaded area of Fig. 3, accounting for most of the magnetic WDs in the sample. Nevertheless, the main sequence dynamo hypothesis cannot explain magnetic fields in WDs with masses ≲0.55 M⊙, because the main sequence progenitors of theses stars should have a radiative core. However, this hypothesis can explain the fact that magnetic field emergence occurs earlier in more massive WDs, because the MB is closer to the WD surface in these stars, regardless of the set of stellar models considered (see Fig. 2). It is important to recall that the location of the MB for the main sequence dynamo hypothesis is subject to very large uncertainties in the modeling, as it depends on the treatment of convective boundaries, the mass-loss rates, and the initial-to-final-mass relation. Therefore, we cannot obtain a precise prediction of the time for the main-sequence-dynamo field emergence, but we can say that it would take place within the WD phase for masses ≳0.65 M⊙, and that it should occur earlier for more massive WDs. This hypothesis can explain the well-known fact that magnetic WDs are in general more massive than non-magnetic WDs (Ferrario et al. 2020; Kawka 2020).

thumbnail Fig. 3.

Magnetic field breakout times for CO WDs. The crystallization onset is depicted with a green line and the magnetic field breakout time considering a crystallization-driven dynamo is plotted as a blue line. The magnetic breakout times considering a main sequence dynamo are shown with a black line for our cubic fit prescription, and the shaded area shows a deviation of ±0.3 from it. The magnetic (non-magnetic) WDs from the spectropolarimetric surveys of Bagnulo & Landstreet (2021, 2022) are plotted using filled red circles (red crosses), and the radius of the surrounding circles is proportional to the magnetic field amplitude. These spectropolarimetric surveys are volume limited up to 20 pc for all WDs and up to 40 pc for those WDs younger than 0.6 Gyr.

The radius (normalized to the WD radius) at the MB and the magnetic diffusion times as a function of the WD cooling age are shown in the upper and lower panels of Fig. 4, respectively. The breakout time and the crystallization onset are marked using empty and filled circles, respectively. Although the normalized radius at the MB stays almost constant during the WD phase for the main sequence dynamo hypothesis, it increases drastically with cooling time for the crystallization-driven dynamo hypothesis. This is because the outer convective boundary of the Rayleigh-Taylor unstable region moves outward as the crystallized core grows. This boundary may also be subject to uncertainties in the chemical profile at the beginning of the WD phase (see Blatman & Ginzburg 2024a, for a through discussion). For the crystallization-driven dynamo hypothesis, we find diffusion times compatible with those of Blatman & Ginzburg (2024a); although the breakout times we obtain are larger because these authors consider that the field starts to diffuse at the crystallization onset and we consider a time-dependent calculation. In both our 0.66 and 0.83 M⊙ models, we obtain that the magnetic field breakout takes place earlier in the evolution when considering the main sequence dynamo hypothesis than if we consider the crystallization-driven dynamo hypothesis. We stress that the breakout timescale for crystallization-driven dynamos could be significantly longer than calculated here. As discussed by Fuentes et al. (2024), if crystallization is responsible for the strong magnetic fields observed in WDs, the dynamo must initiate at the onset of crystallization. However, due to the lack of detailed models for transport processes in 1D evolution codes, the extent of the convection zone is uncertain. The outer boundary of the convective region at the beginning of crystallization could lie anywhere between ∼0.1RWD and ∼0.5RWD, depending on how convective mixing is implemented in the code (the lower limit assumes that mixing occurs according to the Ledoux criterion, whereas the upper limit assumes mixing whenever the composition gradient is unstable). In the worst-case scenario (Ledoux), the diffusion time for the magnetic field to travel from the outer boundary of the convective region to the WD surface would be much larger than the age of the Universe; in the best-case scenario, it would be of the order of 12 Gyr. Nevertheless, strong magnetic fields can significantly enhance compositional mixing in thermohaline convection (see, e.g., Harrington & Garaud 2019; Fraser et al. 2024). This enhanced mixing could, in principle, push the outer boundary of the convective region closer to the WD surface, shortening the timescale for magnetic field emergence.

thumbnail Fig. 4.

Upper panel: Radius at the MB normalized to the WD radius for our 0.66 and 0.83 M⊙ CO WD models. For the crystallization-driven dynamo models (solid lines), this radius is the outer boundary of the Rayleigh-Taylor unstable region induced by crystallization. For the main sequence dynamo models (dashed lines), this radius corresponds to the mass coordinate reached when the deepest penetration of the outer convective zone occurs in the WD progenitor evolution, either during the first or second dredge up. The filled circle indicates the crystallization onset in our models, and the empty circle indicates the time when the magnetic field breaks out to the WD surface. Lower panel: Magnetic diffusion time (tdiff) calculated using Eq. (1) for our 0.66 and 0.83 M⊙ WD models.

4. Conclusions

White dwarfs with masses greater than ∼0.55 M⊙ should have had convective cores in their main sequence progenitor life that can drive dynamo magnetic fields. This idea is supported by MHD simulations of convection in main sequence stars and by the strong magnetic fields inferred by asteroseismology in red giant branch stars. Although subsequent convective regions can disrupt this magnetic field, we have estimated that this field may survive trapped in the stellar interior all the way to the WD phase for stars with initial masses MZAMS ≳ 2 M⊙. We have estimated the mass coordinate at which the magnetic field is supposed to be buried in WD stars, despite the large uncertainties in this boundary predicted by the different stellar evolutionary codes and different physical inputs. We have calculated the time needed for the magnetic field to diffuse from this boundary, MB, to the WD surface, finding the breakout times, tbr, in which this field should emerge for CO-core WDs with masses in the range of 0.58 − 1.29 M⊙. For comparison, we have calculated diffusion times and breakout times for the crystallization-driven magnetic fields of CO-core WDs in the mass range of 0.53 − 1.29 M⊙. It is important to note that WDs with masses ≳1.05 M⊙ should have ONe cores, as predicted by the stellar evolutionary models of super AGB stars that we employed to obtain the MB (Siess 2010; Limongi et al. 2024). However, a non-negligible fraction of WDs with masses ≳1.05 M⊙ formed in single stellar evolution could have CO cores (Althaus et al. 2021), thus supporting our assumption of a CO-core for all WDs considered in this exploratory work. We defer the calculations for ONe WDs to a future work.

In agreement with previous results (Castro-Tapia et al. 2024b), we find that, even if the crystallization-induced mixing can sustain a strong dynamo magnetic field, this hypothesis cannot explain the presence of magnetism in most of the magnetic WDs. This is because, for the current mixing prescriptions implemented in evolution models, this field would be trapped in the WD interior for a very long time. Conversely, our calculations show that magnetic fields generated on the main sequence can emerge to the WD surface within the age of the Universe for WDs more massive than ∼0.65 M⊙. The more massive the WD, the earlier the field should emerge at the surface (in agreement with the crystallization-driven dynamos). The reason for this relies on the fact that, for stars more massive than ∼0.65 M⊙, the main sequence convective core has a greater mass than the final WD mass. However, we expect the outer convective zones penetrating during the first and second dredge up to annihilate the magnetic field in the outer layers of the star, thus burying the magnetic field in inner mass coordinates. Therefore, the outer stellar mass that the field has to diffuse through in order to reach the WD phase is smaller in higher-mass WDs, and the magnetic breakout time is shorter.

We cannot predict the precise location of the boundary of the trapped magnetic field from stellar models. This translates into an uncertainty of up to several gigayears in the timing of the magnetic breakout. These uncertainties arise from factors such as the treatment of convective boundaries, mass-loss rates, and the initial-to-final mass relation. Consequently, we cannot provide a definitive prediction for the emergence time of the main sequence dynamo field. However, we can predict that, if a magnetic field is generated during the main sequence dynamo and it can survive trapped in the stellar interior all the evolution to the WD phase, it will emerge at the surface during the WD phase for masses ≳0.65 M⊙. Also, it will emerge at the surface earlier in more massive WDs. These results are consistent with the observations of the volume-limited sample of magnetic WDs from Bagnulo & Landstreet (2021, 2022), and with the longstanding finding that magnetic WDs tend to be more massive than their non-magnetic counterparts. It should be noted that magnetic fields generated as a result of stellar mergers can also explain the incidence of magnetism and the mass distribution of isolated magnetic WDs, as shown by population synthesis studies (Briggs et al. 2015; García-Berro et al. 2012; Tout et al. 2008).

As a significant number of strongly magnetic WDs are found in close binaries, the predictions of any scenario for the origin of WD magnetic fields should be confronted with observations of magnetic WDs in close binaries. Schreiber et al. (2021) recently suggested an evolutionary sequence based on the crystallization-driven dynamo that for the first time explains the existence and relative numbers of magnetic WDs in cataclysmic variables, detached WD binaries with strongly magnetic WDs (Parsons et al. 2021), and radio-pulsing WD binary stars (Marsh et al. 2016). Assuming the main sequence dynamo we propose here instead of the crystallization-driven dynamo, this evolutionary sequence remains plausible. As long as strong magnetic fields appear in WDs in cataclysmic variables, angular momentum transfer from the WD to the orbit, a subsequent detached phase, and synchronization are predicted.

In any case, it seems likely that the main sequence dynamo cannot explain the magnetic field in all WDs, and there is likely a variety of channels for the occurrence of WD magnetism. In particular, the main sequence dynamo cannot account for magnetism in WDs that descend from main sequence stars that hold radiative cores. Nevertheless, this scenario can account for the young massive magnetic WDs observed in globular clusters, which cannot be explained by the merger or crystallization hypotheses (Caiazzo et al. 2020). It is important to stress that there is no clear evidence that the magnetic field is trapped in the stellar interior of red giant stars nor clump stars more massive than ∼2 M⊙ (Crawford et al. 2024). In order to adequately test the capability of main sequence dynamos to explain WD magnetism, a through analysis of the field evolution through all stages of stellar evolution should be carried out. Furthermore, a better estimation of the time of emergence and the predicted surface magnetic field strength can be obtained by solving the induction equation as in Castro-Tapia et al. (2024b). Finally, we want to emphasize the potential of magnetic WDs as tools with which to understand the efficiency of main sequence dynamos, in addition to asteroseismological studies of red giant stars. Indeed, the study of magnetic WDs can help to improve our understanding of stellar dynamos and stellar evolution.

Acknowledgments

MC acknowledges grant RYC2021-032721-I, funded by MCIN/AEI/10.13039/501100011033 and by the European Union NextGenerationEU/PRTR. JRF is supported by NASA Solar System Workings grant 80NSSC24K0927. MRS thanks for support from FONDECYT (grant number 1221059) and eRO-STEP (grant SA 2131/15-2, project number 414059771). This work was partially supported by the AGAUR/Generalitat de Catalunya grant SGR-386/2021, by the Spanish MINECO grant PID2020-117252GB-I00 and by PID2021-123110NB-I00 financed by MCIN/AEI/10.13039/501100011033/FEDER, UE. This research was supported by the Munich Institute for Astro-, Particle and BioPhysics (MIAPbP), which is funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy – EXC-2094 – 390783311. MC acknowledges Jim Fuller, Lilia Ferrario, Stefano Bagnulo and Ilaria Caiazzo for useful discussions. The authors acknowledge the anonymous referee, whose comments have helped to improve the manuscript.

References

  1. Althaus, L. G., Serenelli, A. M., Panei, J. A., et al. 2005, A&A, 435, 631 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Althaus, L. G., Córsico, A. H., Isern, J., & García-Berro, E. 2010, A&ARv, 18, 471 [NASA ADS] [CrossRef] [Google Scholar]
  3. Althaus, L. G., Camisassa, M. E., Miller Bertolami, M. M., Córsico, A. H., & García-Berro, E. 2015, A&A, 576, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Althaus, L. G., Gil-Pons, P., Córsico, A. H., et al. 2021, A&A, 646, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Angel, J. R. P., & Landstreet, J. D. 1970, ApJ, 160, L147 [NASA ADS] [CrossRef] [Google Scholar]
  6. Augustson, K. C., Brun, A. S., & Toomre, J. 2016, ApJ, 829, 92 [Google Scholar]
  7. Bagnulo, S., & Landstreet, J. D. 2021, MNRAS, 507, 5902 [NASA ADS] [CrossRef] [Google Scholar]
  8. Bagnulo, S., & Landstreet, J. D. 2022, ApJ, 935, L12 [NASA ADS] [CrossRef] [Google Scholar]
  9. Blatman, D., & Ginzburg, S. 2024a, MNRAS, 528, 3153 [NASA ADS] [CrossRef] [Google Scholar]
  10. Blatman, D., & Ginzburg, S. 2024b, MNRAS, 533, L13 [NASA ADS] [CrossRef] [Google Scholar]
  11. Briggs, G. P., Ferrario, L., Tout, C. A., Wickramasinghe, D. T., & Hurley, J. R. 2015, MNRAS, 447, 1713 [CrossRef] [Google Scholar]
  12. Brun, A. S., Browning, M. K., & Toomre, J. 2005, ApJ, 629, 461 [Google Scholar]
  13. Caiazzo, I., Heyl, J., Richer, H., et al. 2020, ApJ, 901, L14 [NASA ADS] [CrossRef] [Google Scholar]
  14. Camisassa, M. E., Althaus, L. G., Córsico, A. H., et al. 2019, A&A, 625, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Camisassa, M. E., Raddi, R., Althaus, L. G., et al. 2022a, MNRAS, 516, L1 [NASA ADS] [CrossRef] [Google Scholar]
  16. Camisassa, M. E., Althaus, L. G., Koester, D., et al. 2022b, MNRAS, 511, 5198 [NASA ADS] [CrossRef] [Google Scholar]
  17. Cantiello, M., Fuller, J., & Bildsten, L. 2016, ApJ, 824, 14 [NASA ADS] [CrossRef] [Google Scholar]
  18. Castro-Tapia, M., Cumming, A., & Fuentes, J. R. 2024a, ApJ, 969, 10 [NASA ADS] [CrossRef] [Google Scholar]
  19. Castro-Tapia, M., Zhang, S., & Cumming, A. 2024b, ApJ, 975, 63 [NASA ADS] [CrossRef] [Google Scholar]
  20. Catalán, S., Isern, J., García-Berro, E., & Ribas, I. 2008, MNRAS, 387, 1693 [Google Scholar]
  21. Crawford, C. L., Bedding, T. R., Li, Y., et al. 2024, MNRAS, 528, 7397 [NASA ADS] [CrossRef] [Google Scholar]
  22. Cristallo, S., Straniero, O., Piersanti, L., & Gobrecht, D. 2015, ApJS, 219, 40 [Google Scholar]
  23. Cumming, A. 2002, MNRAS, 333, 589 [NASA ADS] [CrossRef] [Google Scholar]
  24. Cummings, J. D., Kalirai, J. S., Tremblay, P. E., Ramirez-Ruiz, E., & Choi, J. 2018, ApJ, 866, 21 [NASA ADS] [CrossRef] [Google Scholar]
  25. De Gerónimo, F. C., Battich, T., Miller Bertolami, M. M., Althaus, L. G., & Córsico, A. H. 2019, A&A, 630, A100 [EDP Sciences] [Google Scholar]
  26. Deheuvels, S., Li, G., Ballot, J., & Lignières, F. 2023, A&A, 670, L16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Dominguez, I., Chieffi, A., Limongi, M., & Straniero, O. 1999, ApJ, 524, 226 [NASA ADS] [CrossRef] [Google Scholar]
  28. Featherstone, N. A., Browning, M. K., Brun, A. S., & Toomre, J. 2009, ApJ, 705, 1000 [Google Scholar]
  29. Ferrario, L., de Martino, D., & Gänsicke, B. T. 2015, Space Sci. Rev., 191, 111 [Google Scholar]
  30. Ferrario, L., Wickramasinghe, D., & Kawka, A. 2020, Adv. Space Res., 66, 1025 [NASA ADS] [CrossRef] [Google Scholar]
  31. Fraser, A. E., Reifenstein, S. A., & Garaud, P. 2024, ApJ, 964, 184 [NASA ADS] [CrossRef] [Google Scholar]
  32. Fuentes, J. R., Cumming, A., Castro-Tapia, M., & Anders, E. H. 2023, ApJ, 950, 73 [NASA ADS] [CrossRef] [Google Scholar]
  33. Fuentes, J. R., Castro-Tapia, M., & Cumming, A. 2024, ApJ, 964, L15 [NASA ADS] [CrossRef] [Google Scholar]
  34. Fuller, J., Cantiello, M., Stello, D., Garcia, R. A., & Bildsten, L. 2015, Science, 350, 423 [Google Scholar]
  35. García-Berro, E., Lorén-Aguilar, P., Aznar-Siguán, G., et al. 2012, ApJ, 749, 25 [CrossRef] [Google Scholar]
  36. Ginzburg, S., Fuller, J., Kawka, A., & Caiazzo, I. 2022, MNRAS, 514, 4111 [NASA ADS] [CrossRef] [Google Scholar]
  37. Harrington, P. Z., & Garaud, P. 2019, ApJ, 870, L5 [CrossRef] [Google Scholar]
  38. Hidalgo, J. P., Käpylä, P. J., Schleicher, D. R. G., Ortiz-Rodríguez, C. A., & Navarrete, F. H. 2024, A&A, 691, A326 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Horowitz, C. J., Schneider, A. S., & Berry, D. K. 2010, Phys. Rev. Lett., 104, 231101 [NASA ADS] [CrossRef] [Google Scholar]
  40. Isern, J., García-Berro, E., Külebi, B., & Lorén-Aguilar, P. 2017, ApJ, 836, L28 [NASA ADS] [CrossRef] [Google Scholar]
  41. Käpylä, P. J., Browning, M. K., Brun, A. S., Guerrero, G., & Warnecke, J. 2023, Space Sci. Rev., 219, 58 [CrossRef] [Google Scholar]
  42. Kawka, A. 2020, IAU Symp., 357, 60 [NASA ADS] [Google Scholar]
  43. Kawka, A., Vennes, S., Schmidt, G. D., Wickramasinghe, D. T., & Koch, R. 2007, ApJ, 654, 499 [NASA ADS] [CrossRef] [Google Scholar]
  44. Kemp, J. C., Swedlund, J. B., Landstreet, J. D., & Angel, J. R. P. 1970, ApJ, 161, L77 [NASA ADS] [CrossRef] [Google Scholar]
  45. Li, G., Deheuvels, S., Ballot, J., & Lignières, F. 2022, Nature, 610, 43 [NASA ADS] [CrossRef] [Google Scholar]
  46. Li, G., Deheuvels, S., Li, T., Ballot, J., & Lignières, F. 2023, A&A, 680, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Limongi, M., Roberti, L., Chieffi, A., & Nomoto, K. 2024, ApJS, 270, 29 [NASA ADS] [CrossRef] [Google Scholar]
  48. Marsh, T. R., Gänsicke, B. T., Hümmerich, S., et al. 2016, Nature, 537, 374 [NASA ADS] [CrossRef] [Google Scholar]
  49. Miller Bertolami, M. M. 2016, A&A, 588, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Montgomery, M. H., & Dunlap, B. H. 2024, ApJ, 961, 197 [NASA ADS] [CrossRef] [Google Scholar]
  51. Parsons, S. G., Gänsicke, B. T., Schreiber, M. R., et al. 2021, MNRAS, 502, 4305 [CrossRef] [Google Scholar]
  52. Schreiber, M. R., Belloni, D., Gänsicke, B. T., Parsons, S. G., & Zorotovic, M. 2021, Nat. Astron., 5, 648 [NASA ADS] [CrossRef] [Google Scholar]
  53. Siess, L. 2010, A&A, 512, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Spitzer, L. 1962, Physics of Fully Ionized Gases, 2nd edn. (New York: Interscience) [Google Scholar]
  55. Stello, D., Cantiello, M., Fuller, J., et al. 2016, Nature, 529, 364 [Google Scholar]
  56. Tout, C. A., Wickramasinghe, D. T., Liebert, J., Ferrario, L., & Pringle, J. E. 2008, MNRAS, 387, 897 [NASA ADS] [CrossRef] [Google Scholar]

All Figures

thumbnail Fig. 1.

Kippenhahn diagram of a 4.0 M⊙ star with Z = 0.02 from the main sequence to the end of the thermally pulsing AGB from Miller Bertolami (2016). The hatched green and blue areas indicate the central and outer convective zones, respectively. The orange and purple lines indicate the outer limits of the H- and He-depleted regions, respectively. The pink shaded area is the region where the magnetic fields are expected to be buried. The intershell convective zones driven by the thermal pulses on the AGB are not visible in this plot. The final WD mass of this model is 0.83 M⊙.
In the text
thumbnail Fig. 2.

Logarithm of the outer mass fraction from the boundary where the magnetic field is expected to be trapped, i.e., the MB, in terms of WD mass. We plot the theoretical predictions for CO WDs from Miller Bertolami (2016) and Dominguez et al. (1999), and the Full-Network Repository of Updated Isotopic Tables & Yields (FRUITY) database (Cristallo et al. 2015), and those for oxygen-neon (ONe) WDs from Siess (2010) and Limongi et al. (2024). These models consider different metallicities spreading around the solar value. A cubic polynomial fit to the data with MWD > 0.575 M⊙ is shown with a solid black line. A deviation of ±0.30 from the cubic fit is shown using dotted black lines, which comprises all models considered in this work.
In the text
thumbnail Fig. 3.

Magnetic field breakout times for CO WDs. The crystallization onset is depicted with a green line and the magnetic field breakout time considering a crystallization-driven dynamo is plotted as a blue line. The magnetic breakout times considering a main sequence dynamo are shown with a black line for our cubic fit prescription, and the shaded area shows a deviation of ±0.3 from it. The magnetic (non-magnetic) WDs from the spectropolarimetric surveys of Bagnulo & Landstreet (2021, 2022) are plotted using filled red circles (red crosses), and the radius of the surrounding circles is proportional to the magnetic field amplitude. These spectropolarimetric surveys are volume limited up to 20 pc for all WDs and up to 40 pc for those WDs younger than 0.6 Gyr.
In the text
thumbnail Fig. 4.

Upper panel: Radius at the MB normalized to the WD radius for our 0.66 and 0.83 M⊙ CO WD models. For the crystallization-driven dynamo models (solid lines), this radius is the outer boundary of the Rayleigh-Taylor unstable region induced by crystallization. For the main sequence dynamo models (dashed lines), this radius corresponds to the mass coordinate reached when the deepest penetration of the outer convective zone occurs in the WD progenitor evolution, either during the first or second dredge up. The filled circle indicates the crystallization onset in our models, and the empty circle indicates the time when the magnetic field breaks out to the WD surface. Lower panel: Magnetic diffusion time (tdiff) calculated using Eq. (1) for our 0.66 and 0.83 M⊙ WD models.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.