| Issue |
A&A
Volume 691, November 2024
|
|
|---|---|---|
| Article Number | A130 | |
| Number of page(s) | 7 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202347278 | |
| Published online | 05 November 2024 | |
Main-belt comets as contributors to the near-Earth objects population
1
Centrum Badań Kosmicznych Polskiej Akademii Nauk,
ul. Bartycka 18A,
00–716
Warszawa,
Poland
2
Polish Astronomical Society,
ul. Bartycka 18,
00–716
Warszawa,
Poland
3
Chorzów Astronomical Observatory, IAU MPC 553,
Chorzów, al. Planetarium 4,
41–500
Chorzów,
Poland
★ Corresponding author; r.gabryszewski@cbk.waw.pl
Received:
24
June
2023
Accepted:
6
September
2024
Aims. Most studies of the dynamics of main-belt objects describing the evolution of the bodies in inner Solar System have been carried with models that include weak nongravitational forces, such as the Yarkovsky and YORP effects. Only about 19 objects exhibit cometary-type activity, with sublimation being the principal mechanism. This paper presents a study of the influence of cometary- type nongravitational forces on the dynamics of main-belt comets, and the possible paths and timescales of evolution into other Solar System regions.
Methods. We used the standard Marsden model for cometary-type activity. This model was designed for elongated orbits and the continuous ejection of mass, while the main-belt comets exhibit a different mode of activity. For this reason, we propose a simple model of nongravitational force activation that is consistent with observations. The dynamical evolution of objects was studied using a fifteenth-order RADAU integrator implemented in the REBOUND package.
Results. The paper presents the dynamical routes of main-belt comets in the inner Solar System when cometary-type nongravitational forces are included in calculations. The forces significantly shorten the time of transition to other regions compared to the Yarkovsky effect, shortening this time to as little as a few thousand years depending on the frequency of the activity and the A1, A2, and A3 Marsden constants. There is a large probability of a transition to near-Earth object(NEO)-type orbits for bodies with A2 < 0, which means that cometary-type nongravitational forces can be a non-negligible mechanism increasing the number of bodies in that population. The forces can also deliver active main-belt objects into mean motion resonances but can equally eject bodies into outer planetary regions on far shorter timescales than the Yarkovsky and YORP effects. Cometary-type nongravitational effects should be included in dynamical studies of individual sublimating active asteroids.
Key words: minor planets, asteroids: general
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Asteroid-like bodies on orbits intersecting those of inner planets have been discovered since the end of the 19th century. The first mechanisms explaining the formation of these bodies were proposed in the 1960s and 1970s. Possible sources of Apollo and Amor objects were presented by Wetherill (1976). This author indicated a few possible mechanisms, such as close encounters with Mars, and mean motion and secular resonances able to produce near-Earth objects (NEOs) from bodies residing in the main belt. Investigations of these mechanisms revealed ν6 secular resonance, and 3/1, 5/2, and 2/1 mean motion resonances (MMRs) with Jupiter as the main sources of the NEO population (Moons & Morbidelli 1995; Gladman et al. 1997; Morbidelli & Gladman 1998; Moons et al. 1998). The main belt is also crossed by a large number of weak MMRs with Jupiter and Saturn (Murray & Holman 1997; Nesvorný et al. 2002), and the chaotic diffusion outside the asteroid belt region is also indicated as a mechanism that enriches the NEO population. However, both resonance and chaotic diffusion mechanisms have been unable to explain the observed number of objects in the NEO population assuming its steady-state dynamical distribution.
Another mechanism appeared in the early 2000s as the main nongravitational force influencing the dynamics of asteroids, namely the Yarkovsky effect (Bottke et al. 2002; Morbidelli & Vokrouhlicky 2003; Bottke et al. 2006). Together with the YORP (Yarkovsky–O’Keefe–Radzievskii–Paddack) effect, the Yarkovsky effect allows solutions to be found to the problem of long diffusion times from the near resonance regions among giant planets. The effects were indicated as the main mechanisms delivering objects to NEO orbits and maintaining the NEO population in a quasi-stable state (Tsiganis et al. 2003).
The first attempts to include cometary-type nongravitational (NG) forces to understand the existence of decoupled orbits in the inner parts of the Solar System were made by Sitarski (1988) and Harris & Bailey (1998). Although asteroids dominate the NEO population, sublimating bodies play a minor role. Levison et al. (2001) suggested that the contribution of comets from the Oort Cloud is minimal, providing less than 1% of the total NEO population. The contribution from the Kuiper Belt has been more challenging to quantify due to limited data prior to the year 2000. Simulations by Harris & Bailey (1996) indicated that only about 2% of the cometary bodies transition to stable orbits within the inner Solar System. More recent studies by Michel (2008) suggest that around (8 ± 5)% of the total NEO population may have originated from comet-like bodies from the outer Solar System. This aligns with findings by DeMeo & Binzel (2008), who concluded that (8 ± 3)% of asteroid-like NEOs could have cometary origins. While some NEOs exhibit characteristics that suggest a cometary origin, such as 4015 Wilson-Harrington and 3200
Phaethon, most NEOs with identified cometary traits remain as the minority within the broader NEO population. Direct imaging and follow-up studies have not revealed many NEOs with active cometary features, such as tails or comae; DeMeo & Binzel (2008) found that only about 3% of objects in near-Earth space are active comets. However, the same study indicated that a larger fraction of NEOs, around (8 ± 5)%, could have a cometary origin based on their physical and dynamical characteristics.
Dynamical models and observational evidence suggest that while comets contribute to the NEO population, their role is secondary to that of asteroids. The transition time for comets to become NEOs is relatively short, at around 105 years, but the overall number of such transitions is low. Thus, while cometary bodies do add to the diversity of the NEO population, they do not constitute a major component.
Improvements to observation techniques allowed the discovery of active objects in the main belt and NEA populations (Jewitt 2012; Jewitt et al. 2015). As of March 2023, 43 active asteroids had been observed, and the sublimation process was indicated as the principal cause of activity for 19 of them. These sublimating bodies are frequently called main-belt comets due to their comet-like activity, such as dust comae or tails close to their perihelion passages (Kelley et al. 2023).
Models of the nongravitational effects caused by the sublimation of volatiles from objects – known as cometary-type nongravitational effects – are based on an empirical model (Marsden et al. 1973). In the context of heliocentric motion, non- gravitational accelerations of a small body due to sublimation can be defined as follows:
![${\mathop {\bf{r}}\limits^{..} _{NG}} = g(r)\left[ {{A_1}{{\bf{r}} \over {\bf{r}}} + {A_2}{{r\mathop {\bf{r}}\limits^. - \mathop {\bf{r}}\limits^. {\bf{r}}} \over h} + {A_3}{{\bf{h}} \over h}} \right],$](/articles/aa/full_html/2024/11/aa47278-23/aa47278-23-eq1.png) (1)
(1)
In equations (1), (2), and (3), r is the object’s heliocentric distance vector, g(r) is the function scaling nongravitational accelerations, and A1, A2, and A3 are numerical constants determined separately for each body from observations. The other constants in the standard Marsden model are defined as follows: r0 = 2.808 AU, m = 2.15, n = 5.093, k = 4.6142, and α = 0.111262.
An interesting development of the model was proposed by Sitarski (1990), who introduced rotationally averaged components of the NG acceleration into the equations of motion. However, a number of extensions have been proposed to achieve better agreement between the model and observations. One such model assumes that the sublimation of ice from the surface of a comet reaches a maximum not when the comet is at perihelion but rather later (Yeomans & Chodas 1989). This can be modeled as follows:
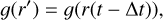 (4)
(4)
where g(r) is a standard function proposed by Marsden and Δt denotes the time shift of the maximum ejection of volatiles from the body. Another model assumes a change in the sublimation rate as a function of time. This can be modeled in a simple way by modifying the function g(r) by multiplying it by a linear factor of 1 + βt, where β is an empirically determined constant. Finally, one can also take into account both the change over time of the sublimation rate and the shift of the maximum of this rate (Aksnes & Mysen 2011). All of the models assume isotropic sublimation of volatiles from the body. Nongravitational force models that remove this constraint have also been proposed, such as that of Maquet et al. (2012).
The most important difference between Yarkovsky/YORP (Y/Y) and cometary-type NG interactions concerns the timescale over which the dynamics of the object are influenced by these completely different physical mechanisms. While the influence of Y/Y interactions is visible on long timescales: several hundred thousand years or more for bodies of up to tens of kilometres in size (see Fig. 2 in Bottke et al. (2006)), NG forces can change an object’s dynamics on much shorter timescales, of up to 104 revolutions (roughly 30 000–40 000 years for bodies in the main belt). Table 1 presents a comparison of a semi-major drift due the Yarkovsky effect (daY /dt) and one attributable to cometary-type NG forces (daNG/dt). The semi-major drift due to cometary-type NG forces is larger even for bodies with low values of the Marsden coefficient (see 133P and 288P in Table 2) and even three to six orders of magnitude larger for bodies with A2 of higher than −10−8 (AU/day2).
As Table 1 shows, the influence of NG forces can be several orders of magnitude greater than that of the Yarkovsky effect, and the NG forces are able to significantly affect the dynamics of small bodies. Up to now, many main-belt objects have been found to exhibit cometary-type activity driven by sublimation processes (Snodgrass et al. 2017). Moreover, there are Marsden model coefficients determined for selected active asteroids (Hui & Jewitt 2017). Moreover, earlier papers (e.g., Hsieh & Jewitt 2006) concluded that a much larger undiscovered population (perhaps on the order of 100 such objects) could exist in the asteroid belt, leading to the recognition of active asteroids as a new dynamical class of comets, making the asteroid belt the third known source of cometary (i.e., ice-bearing) objects in the Solar System after the Kuiper Belt and the Oort Cloud.
The aim of this study is to investigate how NG forces affect the dynamical evolution of the main-belt comets and enrich other classes of objects. We used the standard Marsden model of NG forces in our calculations.
Influence of the Yarkovsky effect and cometary-type NG forces on changes in semi-major axis: daY /dt and daNG/dt.
Orbital elements, loss mass mechanisms and A1 , A2 and A3 coefficients of objects selected for the studies.
2 Numerical model and initial conditions
The paper by Hui & Jewitt (2017) includes the list of 18 main- belt comets for which the NG parameters A1 , A2 , and A3 have been determined from observations available until the first half of July 2016. These parameters were applied to the isothermal water-ice sublimation model devised by Marsden.
We selected a sample of objects for which sublimation activity processes were indicated as the most probable mass-loss mechanisms: 133P, 176P, 238P, 259P, 288P, 313P, 324P, and 358P (Jewitt & Hsieh 2022). The objects 107P and 2201 Oljato were excluded due to their large orbital eccentricities – the bodies cross orbits of at least one planet, which means they are unstable on short timescales. As all of the selected bodies in the sample are located in the outer asteroid belt, close to the 2/1 MMR with Jupiter, we also added four other bodies: 259P, 311P, 331P, and 354P, which are located closer to or in the inner asteroid belt. The activity of the last three of these bodies may be caused by disintegration or impact mechanisms, but they should also result in sublimation processes from newly exposed volatilerich surfaces (we assume that all bodies in the main belt have a fraction of volatiles under the crust).
Table 2 gathers orbital elements, mass-loss mechanisms, and Marsden model constants for the selected sample of bodies. The left panel of Fig. 1 shows the positions of the objects in (a–e) and (a–i) phase space, while the right panel presents objects in the same phase space over the range of 3.15–3.17 AU.
Observations of active bodies show that sublimation is visible mainly at perihelia and post-perihelia distances (Hsieh 2015) but transient activity is also frequently observed over the entire orbit. Water ice is thermodynamically unstable when exposed to sunlight at main-belt distances, but can be preserved on billion-year timescales beneath layers of porous refractory debris (Fanale & Salvail 1989; Schorghofer 2008). Sublimation can also be induced by small impacts or some other disturbance of the surface, such as disruption events. In this scenario, sublimation would proceed from an exposed region until a new refractory covering (Jewitt et al. 2015). The observations also show that the activity is not detected at every orbital revolution. For these reasons, we decided to include the simple model of the NG activity for bodies located in the main belt.
In the model, we assume that, during each revolution around the barycentre, the object can be in one of two states: low activity (L) or high activity (H). The probability that the active asteroid is in the low activity state is P1 while that for the high activity state is P2. As we assume that the object cannot be in any state other than the two mentioned above, we have P1 + P2 = 1. Let p1 be the probability that the object is active when in a low- activity state. Similarly, let p2 be the probability that the object is active while in a high-activity state. Obviously, p2 > p1 and in general p1 + p2 ≠ 1. The schematic diagram of the activity selection is presented in Fig. 2. The object is active if one of the following sequences of events occurs: START → L → 1 or START → H → 1. The probability that the first sequence of events occurs is P1p1, while that for the second is P2p2. Thus, the probability P that the asteroid is active in a given revolution is P = P1p1 + P2p2. Our calculations were done for two activity states: low with P = 0.1 and medium with P = 0.4. In both of these states p1 was set to 0.1 and p2 was set to 0.9.
Both the Marsden standard model of NG forces and the models by Sekanina (1984) and Bielicki & Sitarski (1991) lead to satisfactory orbital fits only up to a few apparitions (Aksnes & Mysen 2011). This means that a selected sample of objects can only be treated as fictitious test particles when integrating their equations of motion over timescales of longer than tens of perihelion passages. This means we can study the objects’ dynamics only in a statistical way. That is why we generated 40 clones for every selected object: 10 clones with identical positions and velocities, and activity probabilities P set to 0.1 and 0.4, and a number of orbital revolutions in which NG forces are active: 1000 and 10 000. The equations of motion were also integrated in a purely gravitational model. This gave us 451 initial conditions in total. Upon every revolution of an object, NG forces were included (or not) with the assumed probability P.
Dynamical evolution was investigated by integrating a nine- body problem in a barycentric reference frame, with the Sun as the central mass, and seven planets from Venus to Neptune, with Mercury’s mass added to the mass of the Sun, and a massless particle corresponding to a clone of the selected body. Initial conditions consisted of the positions and velocities of the planets and of the massless particle, and the same A1 , A2 , and A3 values for NG forces – the same values for all clones of a selected body. In different integrations, the NG activity was introduced at a different moments in time. The orbital elements for the planets and objects were taken from the database (JPL HORIZONS)1. The values of A1 , A2 , and A3 for the test particles were taken from Hui & Jewitt (2017).
The integrations were performed using IAS15, the fifteenthorder RADAU integrator (Everhart 1985) implemented in the REBOUND package (Rein & Liu 2012; Rein & Spiegel 2015). This integrator adjusts the step size to maintain the same accuracy for all objects taking part in the integration. The maximum time of integration was set to 1 Myr, but the integrations were also stopped when a particle’s perihelion distance was less than 1 AU or its eccentricity was greater than 0.9.
 |
Fig. 1 Distributions of objects selected for studies in the (a–e) and (a–i) planes. The color of the dots denotes the mass-loss mechanism: dark blue for sublimation and light green for rubble-pile disintegration or impact. The right panel presents the range 3.15–3.17 AU of the semi-major axis. |
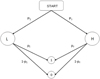 |
Fig. 2 Schematic diagram showing how asteroid activity was modeled. An object, in a single revolution around the Sun, is active when the sequence of events leads to a “1” state, otherwise it is inactive (0” state). The detailed description was presented in the text. |
3 Results
Pure gravitational integrations of all the test particles indicated that their orbits are stable over the maximum time span of the integration. This result is consistent with earlier findings (Dermott et al. 2021). Even 259P with a qMIN of close to 1.75 AU, which is only 0.05 AU greater than the Mars aphelion, did not experience any trend in periodic changes caused by planetary perturbations. The particle with the largest and most irregular changes in purely gravitational integration is 311P. This body is located close to the inner edge of the main belt and the ν6 secular resonance. However, the changes in semi-major axis and other orbital elements seem to have the effect of crossing the Mars orbit – the body can have close approaches to this planet.
In the integration, we found that NG forces do not influence the dynamical evolution of particles on 1 Myr timescale if their Marsden constants are lower than 10−10 AU/day2. The changes in semi-major axis, eccentricity, and inclination are within the same ranges as for gravitational integrations, and the character of the changes is identical. The same type of evolution is observed for all test particles for objects 133P, 176P, and 288P.
NG forces start to have an important influence on the dynamics of the bodies when at least one of the three components has a value of 10−9 AU/day2 or more. This type of behaviour can be observed in Fig. 3. NG forces are able to change the semi-major axis of the test particles over a short timescale, which is less than 105 years for P = 0.4 and about 3 × 105 years for P = 0.1. The changes made by NG forces are also visible in the eccentricity plot but the variations due to NG are much smaller compared to gravitational changes.
Eccentricity variations due to NG forces are clearly seen in Fig. 4. As expected (Hui & Jewitt 2017), the values of the particles’ semi-major axis decrease for A2 < 0. The rate of change strongly depends on the P parameter: the smaller P is, the smaller the changes in the semi-major axis. Similar changes also concern the eccentricity variation but not inclination. A possible influence on orbits with large values of NG force and A2 > 0 can be found in Fig. 5. Strong NG forces mean that orbits are able to cross MMRs and the body is able to evolve into different orbital types. A fraction of the bodies are able to transit to NEO-type orbits. This is only possible for objects that are within a narrow area of initial semi-major axes and are due to increase in eccentricity. These orbits are very unstable, and the bodies can stay on this orbital type only for 20–30 revolutions in our calculations. This increase in eccentricity also causes objects to cross Jupiter’s orbit and raises the possibility of close approaches to the planet and a change in the orbital type to Jupiter Family. Some objects can then enter the long-period comets orbital type. We observed no evolution into Themis Family or Centaur-type orbits during this study.
 |
Fig. 3 Variations of semi-major axis, eccentricity and inclination for a clone of 311P. Purple lines denote purely gravitational integrations, while pale-blue and green lines denote integrations which include NG interactions with P = 0.4 and 0.1 respectively. With A2 > 0, the particle evolves outwards Solar System until it is locked in the 9/1 MMR with Saturn and 4/7 MMR with Mars. NG forces affect both semi-major axis and eccentricity. |
4 Conclusions and discussion
Our results show that cometary-type NG forces are one of the mechanisms responsible for transporting main belt objects to NEO and other regions of the Solar System. Even weak NG forces are able to change the dynamics of bodies over much shorter timescales than Y/Y effects, as presented in Table 1.
The evolution to NEO-type orbits was observed for both A2 > 0 and A2 < 0. In the former case, both the semi-major axis and eccentricity of a particle in our sample increase. When the eccentricity falls within the range of 0.52 to 0.53 and the semi-major axis is approximately 2.8 AU, the perihelion distance decreases below 1.3 AU, with TJ exceeding 3.05. Consequently, the particle can be classified as a NEO-type body. Next such particles can evolve towards JFC- and LPC-type orbits; see Fig. 5.
When A2 < 0, the nature of the evolution to NEO-type orbits is different. NG forces tend to decrease both semi-major axis and eccentricity, and a body evolving in this way moves to the Solar System interior. The orbit of the particle becomes circularized as the value of its semi-major axis decreases until the end of the integration. We find that 100% of test particles with 0 > A2 > −10−8 (AU/day2) evolve to NEO orbits within 104 revolutions. Table 3 presents the number of revolutions needed for the 20%, 40%, 60%, 80%, and 100% clones to reach the NEOtype orbit. The results show that non-negligible NG forces can efficiently change the orbital type of active main-belt bodies, and objects are able to transit to NEO-type orbits within hundreds or thousands of revolutions.
A Marsden model of NG forces was constructed for cometary-type (elongated) orbits for which activity is observed in the inner Solar System, mainly in the vicinity of perihelion passage. The orbits of the main-belt bodies are far more circular and sublimation processes can occur on any fragment of the orbit. For these reasons, we introduced a simple model of asteroid activity, which leads to improved agreement between the model and observations. Despite the model assumption of only low or medium activity of the particles, the results show that NG forces can significantly affect small body dynamics: all bodies tend to enter quasi-circular NEO orbits in an inner Solar System for A2 < 0, but even a small fraction of bodies with A2 > 0 can experience a short NEO-type orbital episode.
We also tested the original Marsden model in the inner Solar System. As this model was first created for elongated orbits, we wanted to verify that it did not introduce errors on circular orbits in the inner Solar System. At every perihelion distance, we checked the values of test particle accelerations, both total (gravitational and nongravitational) and NG only. In all integration processes, NG-only accelerations were a few orders of magnitude smaller than the total ones.
The original Marsden model assumes A1, A2, and A3 parameters are constant over the whole time span of integrations. It works very well linking a few object’s apparitions to determine its orbit. However, the Marsden model is not optimized for longer integrations, as NG jets can fade in time, and so our conclusions regarding the timescales on which orbit-type changes can take place should be perceived as only one of many possibilities. For the same reason, this model should not be used for longterm dynamical evolution studies, as our results show that the evolution strongly depends on A1 , A2, and A3.
Similarly, we cannot deduce a great deal of information about the history of the bodies. The change in orbital elements due to their activity suggests that these objects likely resided outside the main-belt region. However, their exact past location is difficult to determine because the history of their activity remains unknown.
The results presented in this paper show that the sublimation activity of the bodies located in the main-belt region should not be omitted in studies of their dynamical evolution.
 |
Fig. 4 Variations of semi-major axis, eccentricity and inclination for a clone of 238P. Purple lines denote purely gravitational integrations, while pale-blue and green lines denote integrations which include NG interactions with P = 0.4 and 0.1 respectively. With A2 < 0, the particle evolves inwards, NG forces also circularize the orbit. The integration is finished at perihelion distance q = 1.0 AU. The figure shows that NG forces are able to affect also eccentricity comparing to purely gravitational changes but they do not influence inclination. |
The number of revolutions to become a NEO.
 |
Fig. 5 Dynamical evolution of a clone of 354P. Top panel denotes distinct orbital types the particle occupies during the evolution. MBC – main- belt object, TF – Themis family type object, JFC – Jupiter family comet type object, CL – Centaur type object, LPC – long period comet type object, NEO – near-Earth type object. The lower panels shows variations of semi-major axis, eccentricity and inclination in time. Purple lines denote purely gravitational integrations, while pale-blue and green lines denote integrations which include NG interactions with P = 0.4 and 0.1 respectively. With A2 > 0, the particle evolves outwards Solar System, NG forces affect both semi-major axis and eccentricity. For specific starting values for a and e, there is a possibility that the test particle fulfills the definition for NEOs (q < 1.3 AU and TJ > 3.05) for several revolutions. Then the further increase in semi-major axis and eccentricity evolves the particle towards JFCs and then LPCs type orbits. The integration is stopped at e = 0.9. |
Acknowledgements
We thank the anonymous referee for the comments and helpful suggestions. They allowed to significantly improve the paper.
References
- Aksnes, K., & Mysen, E., 2011, AJ, 142, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Bielicki, M., & Sitarski, G. 1991, Acta Astron., 41, 309 [NASA ADS] [Google Scholar]
- Bottke, W. F., Morbidelli, A., Jedicke, R., et al. 2002, Icarus, 156, 399 [NASA ADS] [CrossRef] [Google Scholar]
- Bottke, W. F., Vokrouhlicky, D., Rubincam, D. P., & Nevorny, D. 2006, Annu. Rev. Earth. Planet. Sci., 2006, 157 [CrossRef] [Google Scholar]
- DeMeo, F., & Binzel, R. P. 2008, Icarus, 194, 436 [NASA ADS] [CrossRef] [Google Scholar]
- Dermott, F. S., Dan Li, D., Christou A. A., et al. 2021, MNRAS, 505, 1917 [NASA ADS] [CrossRef] [Google Scholar]
- Everhart, E. 1985, Dynamics of Comets: Their Origin and Evolution, eds. A. Carusi, & G. B. Valsecchi, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Fanale, F. P., & Salvail, J. R., 1989 Icarus, 82, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Gladman, B., Migliorini, F., Morbidelli, A., et al. 1997, Science, 277, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Greenberg A. H., Margot J.-L., Verma A. K., Taylor P. A., & Hodge S. E. 2020, AJ, 159, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, N. W., & Bailey, M. E. 1996, Irish Astron. J., 23, 151 [NASA ADS] [Google Scholar]
- Harris, N. W., & Bailey, M. E. 1998, MNRAS, 297, 1227 [NASA ADS] [CrossRef] [Google Scholar]
- Hsieh, H. H. 2015, Proceedings IAU Symposium, 10, 99 [CrossRef] [Google Scholar]
- Hsieh, H. H., & Jewitt, D. 2006, Science, 312, 561 [NASA ADS] [CrossRef] [Google Scholar]
- Hui, M.-T., & Jewitt, D. 2017, AJ, 153, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Jewitt, D. 2012, AJ, 143, 66 [CrossRef] [Google Scholar]
- Jewitt, D., & Hsieh, H. H. 2022, arXiv e-prints [arXiv:2203.01397] [Google Scholar]
- Jewitt, D., Hsieh, H. H., & Agarval, J. 2015, ASTEROIDS IV, eds. by P. Michel, F. DeMeo, & W. Bottke (University of Arizona), 221 [Google Scholar]
- Kelley, M. S. P., Hsieh, H. H., Bodewits, D., et al. 2023, Nature, 619, 720 [NASA ADS] [CrossRef] [Google Scholar]
- Levison, H. F, Dones, L., & Duncan, M. J. 2001, AJ, 121, 2253 [NASA ADS] [CrossRef] [Google Scholar]
- Maquet, L., Colas, F., Jorda, L., & Crovisier, J. 2012, A&A, 548, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marsden, B. G., Sekanina, Z., & Yeomans, D. K. 1973, AJ, 78, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Michel, P. 2008, EPSC Abstr., 3, EPSC2008-A-00 092 [Google Scholar]
- Moons, M., & Morbidelli, A. 1995, Icarus, 114, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Moons, M., Morbidelli, A., & Migliorini, F. 1998, Icarus, 135, 458 [NASA ADS] [CrossRef] [Google Scholar]
- Morbidelli, A., & Gladman, B. 1998, Meteor. Planet. Sci., 33, 999 [NASA ADS] [CrossRef] [Google Scholar]
- Morbidelli, A., & Vokrouhlicky, D. 2003, Icarus, 163, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Murray, N., & Holman, M. 1997, AJ, 114, 1246 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvorný, D., Ferraz-Mello, S., Holman, M., & Morbidelli, A. 2002, Asteroids III, eds. W. F. Bottke Jr., et al. (Tucson: University of Arizona) [Google Scholar]
- Rein, H., & Liu, S. F. 2012, A&A, 537, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rein, H., & Spiegel, D. S. 2015, MNRAS, 446, 1424 [Google Scholar]
- Schorghofer, N. 2008, AJ, 682, 697 [NASA ADS] [Google Scholar]
- Sekanina, Z. 1984, AJ, 89, 1573 [NASA ADS] [CrossRef] [Google Scholar]
- Sitarski, G. 1988, Acta Astron., 38, 269 [NASA ADS] [Google Scholar]
- Sitarski, G. 1990, Acta Astron., 40, 405 [NASA ADS] [Google Scholar]
- Snodgrass, C., Agarwal, J., Combi, M., et al. 2017, A&AR, 25, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Tsiganis, K., Varvoglis, H., & Morbidelli, A. 2003, Icarus, 166, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Wetherill, G. W. 1976, Geochim. Cosmochim. Acta, 40, 1297 [CrossRef] [Google Scholar]
- Yeomans, D. K., & Chodas, P. W. 1989, AJ, 98, 1083 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Influence of the Yarkovsky effect and cometary-type NG forces on changes in semi-major axis: daY /dt and daNG/dt.
Orbital elements, loss mass mechanisms and A1 , A2 and A3 coefficients of objects selected for the studies.
All Figures
 |
Fig. 1 Distributions of objects selected for studies in the (a–e) and (a–i) planes. The color of the dots denotes the mass-loss mechanism: dark blue for sublimation and light green for rubble-pile disintegration or impact. The right panel presents the range 3.15–3.17 AU of the semi-major axis. |
| In the text | |
 |
Fig. 2 Schematic diagram showing how asteroid activity was modeled. An object, in a single revolution around the Sun, is active when the sequence of events leads to a “1” state, otherwise it is inactive (0” state). The detailed description was presented in the text. |
| In the text | |
 |
Fig. 3 Variations of semi-major axis, eccentricity and inclination for a clone of 311P. Purple lines denote purely gravitational integrations, while pale-blue and green lines denote integrations which include NG interactions with P = 0.4 and 0.1 respectively. With A2 > 0, the particle evolves outwards Solar System until it is locked in the 9/1 MMR with Saturn and 4/7 MMR with Mars. NG forces affect both semi-major axis and eccentricity. |
| In the text | |
 |
Fig. 4 Variations of semi-major axis, eccentricity and inclination for a clone of 238P. Purple lines denote purely gravitational integrations, while pale-blue and green lines denote integrations which include NG interactions with P = 0.4 and 0.1 respectively. With A2 < 0, the particle evolves inwards, NG forces also circularize the orbit. The integration is finished at perihelion distance q = 1.0 AU. The figure shows that NG forces are able to affect also eccentricity comparing to purely gravitational changes but they do not influence inclination. |
| In the text | |
 |
Fig. 5 Dynamical evolution of a clone of 354P. Top panel denotes distinct orbital types the particle occupies during the evolution. MBC – main- belt object, TF – Themis family type object, JFC – Jupiter family comet type object, CL – Centaur type object, LPC – long period comet type object, NEO – near-Earth type object. The lower panels shows variations of semi-major axis, eccentricity and inclination in time. Purple lines denote purely gravitational integrations, while pale-blue and green lines denote integrations which include NG interactions with P = 0.4 and 0.1 respectively. With A2 > 0, the particle evolves outwards Solar System, NG forces affect both semi-major axis and eccentricity. For specific starting values for a and e, there is a possibility that the test particle fulfills the definition for NEOs (q < 1.3 AU and TJ > 3.05) for several revolutions. Then the further increase in semi-major axis and eccentricity evolves the particle towards JFCs and then LPCs type orbits. The integration is stopped at e = 0.9. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



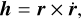
![$g(r) = \alpha {\left( {{r \over {{r_0}}}} \right)^{ - m}}{\left[ {1 + {{\left( {{r \over {{r_0}}}} \right)}^n}} \right]^{ - k}}.$](/articles/aa/full_html/2024/11/aa47278-23/aa47278-23-eq3.png)