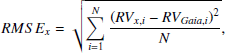| Issue |
A&A
Volume 690, October 2024
|
|
|---|---|---|
| Article Number | L17 | |
| Number of page(s) | 11 | |
| Section | Letters to the Editor | |
| DOI | https://doi.org/10.1051/0004-6361/202451596 | |
| Published online | 21 October 2024 | |
Letter to the Editor
An ‘alien’ called the Oosterhoff dichotomy?
1
INAF - Osservatorio Astronomico di Capodimonte, Via Moiariello 16, I-80131 Naples, Italy
2
European Southern Observatory, Karl-Schwarzschild-Strasse 2, 85748 Garching bei München, Germany
3
INAF, Osservatorio di Astrofisica e Scienza dello Spazio di Bologna, via Piero Gobetti 93/3, 40129 Bologna, Italy
4
Department of Physics, University Federico II, via Cinthia 6, 80126 Napoli, Italy
Received:
22
July
2024
Accepted:
5
September
2024
Aims. In this Letter we investigate the origin of the Oosterhoff dichotomy in light of recent discoveries related to several ancient merging events of external galaxies with the Milky Way (MW). In particular, we aim to clarify if the subdivision in terms of the Oosterhoff type between Galactic globular clusters (GGCs) and field RR Lyrae (RRLs) can be traced back to one or more ancient galaxies that merged with the MW in its past.
Methods. We first explored the association of GGCs with the past merging events according to different literature studies. Subsequently, we compiled the positions, proper motions, and radial velocities of 10 138 field RRL variables from Gaia Data Release 3. To infer the distances, we adopted the MG–[Fe/H] relation, with [Fe/H] values estimated via empirical relationships involving individual periods and Fourier parameters. We then calculated the orbits and the integrals of motion using the Python library Galpy for the whole sample. By comparing the location of the field RRLs in the energy–angular momentum diagram with that of the GGCs, we determined their likely origin. Finally, using GaiaG-band light curves, we determined the Oosterhoff types of our RRL stars based on their location in the Bailey diagram.
Results. The analysis of the Bailey diagrams for Galactic RRL stars and GGCs associated with an ‘in situ’ versus ‘accreted’ halo origin shows remarkable differences. The in situ sample shows a wide range of metallicities with a continuous distribution and no sign of the Oosterhoff dichotomy. Conversely, the accreted RRLs clearly show the Oosterhoff dichotomy and a significantly smaller dispersion in metallicity.
Conclusions. Our results suggest that the Oosterhoff dichotomy was imported into the MW by the merging events that shaped the Galaxy.
Key words: stars: variables: RR Lyrae / globular clusters: general / Galaxy: halo / Galaxy: kinematics and dynamics / Galaxy: structure
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
RR Lyrae (RRLs) are important standard candles and excellent tracers of old populations (age > 10 Gyr) in the Milky Way (MW) and the Local Group (Smith 1995; Catelan & Smith 2015). One of the open problems concerning RRLs is the Oosterhoff dichotomy, namely the subdivision of Galactic globular clusters (GGCs) into two distinct groups according to the average period, ⟨Pab⟩, of their fundamental mode RRL variables (RRabs; Oosterhoff 1939). In particular, in some GGCs containing RRLs, the ⟨Pab⟩ is about 0.55 days, while in others it is close to 0.65 days, with a period gap between these two groups, which are named Oosterhoff I (OoI) and Oosterhoff II (OoII), respectively.
Among the various explanations suggested in the past for this dichotomy (e.g. Fabrizio et al. 2021; Zhang et al. 2023, for recent reviews), Sandage (1981) proposed that the dichotomy originated from an intrinsically higher luminosity of OoII RRabs at a fixed temperature (assuming similar masses), resulting in longer periods. However, this implies an anti-correlation between metallicity and helium, since OoII GGCs are generally more metal-poor than the OoI ones and only a significant He enrichment can justify the assumed OoII RRLs’ over-luminosity (e.g. Bencivenni et al. 1991). Alternatively, van Albada & Baker (1973) hypothesized that in the ‘OR’ region of the instability strip1 the RRLs found within OoI and OoII GGCs pulsate in the fundamental and first-overtone modes, respectively. This was later supported by theoretical work by Bono et al. (1997). In this case, OoI RRabs would extend to higher temperatures and thus in turn have a shorter ⟨Pab⟩2 than OoII ones. Fabrizio et al. (2019) find that their spectroscopic sample of field RRLs plotted in the Bailey diagram shows a continuous variation when moving from the metal-poor ([Fe/H] ∼ −3.0 dex) to the metal-rich ([Fe/H] ∼ 0 dex) regime. They conclude that the smooth transition in the peak of the period distribution as a function of the metallicity proves that the Oosterhoff dichotomy is not present in the field and its occurrence in GGCs is due to the lack of metal-intermediate clusters hosting RRLs. However, Gaia Data Release 3 (DR3; Gaia Collaboration 2016, 2023; Clementini et al. 2023) shows a clear separation between field OoI and OoII RRL locations in the Bailey diagram, thus suggesting that the Oosterhoff dichotomy is still an open problem.
Moreover, Catelan (2009) noted that the gap between the two Oosterhoff types, when plotting the average RRab period as a function of their metallicity, is filled by globular clusters in MW’s satellite galaxies, identifying them as intermediate Oosterhoff types. This suggests that the Oosterhoff dichotomy might be useful for understanding the mechanisms underlying the formation of the Galactic halo.
Gaia data releases DR2 and DR3 (Gaia Collaboration 2018; Helmi et al. 2018; Helmi 2020) recently led to discovery of several ancient merging events in the MW’s past, most notably Gaia-Enceladus, Sequoia, and Kraken, with new insights into the formation and evolution of our Galaxy (e.g. Gaia Collaboration 2018; Helmi et al. 2018; Helmi 2020, and references therein). These discoveries were possible because the remnants of the progenitor galaxies occupy the same region in the integrals of motion space (IoM; see the following sections) as predicted by the numerical simulations of Helmi & de Zeeuw (2000). In particular, Massari et al. (2019), by studying the IoM of the GGCs, were able to associate a significant number of them with different progenitor galaxies. This discovery led us to hypothesize a possible connection between the ancient merging episodes that shaped the Galactic halo and the Oosterhoff dichotomy. Is it possible that the Oosterhoff dichotomy was ‘imported’ into the MW? In the following, we try to answer this question using a sample of GGCs and field RRLs for which it was possible to calculate the IoM and determine their origin.
2. Observed sample of GGCs
We adopted the GGCs inventory and relative fundamental parameters listed by Baumgardt and collaborators3 (B&Co hereafter; see also Baumgardt & Vasiliev 2021; Vasiliev & Baumgardt 2021). This database reports accurate astrometric, kinematic, and structural data for GGCs, largely based on results of the Gaia satellite. Concerning the possible association of each GGC with a past merging event, we relied on the classification originally proposed by Massari et al. (2019) and further refined by Callingham et al. (2022). In the latter work, almost all GGCs are associated with a progenitor according to the the IoM and actions and by adopting a complex machine learning technique. The eight identified progenitors are listed in Table B.5. To further explore the association with ancient merging episodes, we also considered the separation into ‘in situ’ and ‘accreted’ clusters determined by Belokurov & Kravtsov (2024) for 158 of the GGCs listed by B&Co using the [Al/Fe] ratio4.
Belokurov & Kravtsov (2024) report the result of this aluminium-based classification on the (E, Lz) plane. They were able to identify the GGC populations due to their distinct spatial, kinematic, and chemical abundance distributions.
The last piece of information we gathered from the literature concerns the Oosterhoff type, which is found for only 47 GGCs by Stobie (1971) and van den Bergh (2011).
Finally, we computed the IoM for each GGC. Assuming an axisymmetric potential for the MW, the commonly considered IoM are the energy, E, the angular momentum component along the z-axis perpendicular to the Galactic plane, Lz, and the modulus of the angular momentum vector lying in the Galactic plane, 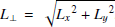 . However, the action quantities (Jr, Jϕ, and Jz), being adiabatic invariants, are better conserved for the Gaia DR3 sample, which extends considerably farther than the previous release (Helmi 2020). In the following, we use the quantities E and Lz to represent the considered GGCs in the same plane as used in the classification method papers (Belokurov & Kravtsov 2024; Callingham et al. 2022).
. However, the action quantities (Jr, Jϕ, and Jz), being adiabatic invariants, are better conserved for the Gaia DR3 sample, which extends considerably farther than the previous release (Helmi 2020). In the following, we use the quantities E and Lz to represent the considered GGCs in the same plane as used in the classification method papers (Belokurov & Kravtsov 2024; Callingham et al. 2022).
In addition, the action quantities (Jr, Jϕ, and Jz) are used to classify the field RRL sample with the RandomForestClassifier (as shown in Sect. 3.2).
To calculate the IoM and the actions, we employed the Python library Galpy (Bovy 2015) and integrated the orbits of the targets for a period of 3 Gyr. The input six-dimensional parameters – right ascension (RA), declination (Dec), distance (d), proper motion right ascension (μRA) and declination (μDec), and radial velocity (RV) – for the GGCs were taken from the B&Co database. These quantities allowed us to compute the IoM with Galpy and determine a potential for the MW, which, in our case, is the axisymmetric McMillan2017 potential (for details see McMillan 2017). The sample of GGCs used in this work together with all the information needed to calculate the IoM and the actions, as well as the classification in terms of in situ or accreted, are reported in Table B.6.
3. Field RRL sample
In addition to the GGC sample, we also examined field RRLs. Collecting the six parameters needed to study the dynamics of these objects is not as straightforward as for the GGCs because there is no single database that lists all the necessary information. Gaia DR3 provides the positions and proper motions of all the RRLs in our study, but only a fraction of the RVs (Table B.1). Furthermore, given the large distances at which many of our targets are located, we find that the Gaia parallaxes are often not informative, leading to unreliable individual distance measurements. Therefore, we decided to use the fact that RRLs are excellent standard candles and calculated their distances using their luminosity–metallicity relation. As shown in the next section, to infer distances from this relation we needed individual metal abundances, which can be obtained from the ϕ31 and R21 parameters of the light curve Fourier decomposition. Therefore, for the selection of field RRLs, we first considered the Gaia DR3 sample of RRLs from the Specific Object Study (SOS) pipeline (vari_rrlyrae table in the Gaia DR3 archive; Clementini et al. 2023), which consists of about 270 000 objects. We did not use data from other photometric surveys in order to keep the homogeneity of our photometric sample. Of the Gaia RRLs, we selected fundamental-mode pulsators (i.e. RRabs) because they ‘neatly’ show the Oosterhoff dichotomy in the Bailey diagram (e.g. Fig. 35 in Clementini et al. 2023) and retained only DR3 RRLs with P > 0.4 days to avoid possibly misclassified first-overtone pulsators. In addition, we retained only those RRabs for which Fourier parameters are available in the DR3 vari_rrlyrae table. The third selection criterion was based on the availability of the average RVs in the Gaia DR3 archive, which are only available for a few thousand fundamental-mode RRLs. To enlarge the sample, we therefore scanned the literature and gathered additional RRLs that have measured RVs (see Appendix A for details). Our final sample of field RRLs includes 10 138 variable stars. Their identifications, positions, metallicities, Fourier amplitudes, and other parameters are listed in Table B.7.
3.1. Determination of distances to the RRLs
To determine the distances to the field RRLs, we adopted the luminosity–metallicity relation in the G band (MG–[Fe/H]) from Li et al. (2023). This relation can provide distances to the investigated RRLs from their de-reddened apparent magnitudes and metallicity. G-band absorption values for the RRLs were taken from the vari_rrlyrae table in the Gaia DR3 archive (Clementini et al. 2023). The same Gaia catalogue also provides individual metallicity estimates for the RRLs. However, the Fourier parameter–metallicity calibration used in Gaia (based on the work by Nemec et al. 2013) overestimates the metallicity for [Fe/H] values larger than ∼ − 1.3 dex (see Sect. 5.1 of Clementini et al. 2023). We calculated the metallicities using the equation from Li et al. (2023) valid for RRab stars, connecting the [Fe/H] value to the period, P, and the Fourier parameters R21 and ϕ31. The individual RRL distances were then determined from the inferred metal abundances and the Gaia de-reddened G magnitudes. The errors associated with distance determinations were determined by propagating uncertainties in the evaluated MG and the de-reddened apparent magnitude (G0) using the distance modulus relation. The first term is the RMS of the adopted MG-[Fe/H] relation, taken from Li et al. (2023), while the second was calculated by propagating the errors on the two quantities measured by Gaia (G and A(G)). All the inferred individual distances are reported in Table B.7.
3.2. Random forest to classify field RRLs
The last piece of information we needed was the classification of field RRLs in terms of in situ or accreted populations, similar to what is available in the literature for GGCs. To this aim, we adopted the same two classifications used for GGCs, according to Belokurov & Kravtsov (2024) and Callingham et al. (2022), respectively, on the assumption that the satellite galaxies that were involved in merging episodes with the MW carried with them both GGCs and field RRLs, which thus would occupy the same region in the IoM space. We adopted the classifications used for GGCs as training sets to identify the different regions in IoM space where the field RRLs would be located using the scikit-learn library of the RandomForestClassifier (Breiman 2001), with the hyper-parameters reported in Table B.2. In particular, we trained the model using GGC data and the attributes calculated with Galpy based on the B&Co database (E, Jr, Jϕ, and Jz). According to the Belokurov & Kravtsov (2024) scheme, we classified them as in situ or accreted. Then, following Callingham et al. (2022), we classified the RRLs according to their eight proposed progenitor types (see Table B.5). The test results are reported in Tables B.3 and B.4 based on the in situ versus accreted and progenitor classifications, respectively. The top-left panel of Fig. 1 shows the distribution of GGCs in the (E, Lz) plane used as a training set to classify the field RRLs. The objects formed in the pristine Galaxy and those carried into the MW by merging satellites are labelled as in situ and accreted, respectively. The figure also shows, for the sake of completeness, the van den Bergh (2011)–Stobie (1971) Oosterhoff classification. Similarly, in the bottom-left panel of Fig. 1 we show the GGCs in the same plane as above but classified according to the eight progenitor types proposed by Callingham et al. (2022, see our Table B.5). The classification of the field RRLs based on the GGCs is shown in the right-hand panels of Fig. 1 for the two classification methods. The field RRLs are colour-coded according to the classification obtained with the RandomForestClassifier. The percentage of field RRLs and GGCs classified as in situ and accreted is shown in Fig. B.1.
 |
Fig. 1. (E, Lz) diagrams Top left: GGCs considered in this work. OoI, OoII, and non-Oosterhoff-type GGCs are shown as filled circles, diamonds, and crosses, respectively. The GGCs are classified as either in situ or accreted according to Belokurov & Kravtsov (2024) and plotted in different colours (see labels). Bottom left: Same but according to the classification into eight progenitor types (Callingham et al. 2022). Each progenitor type is identified with a different colour in the figure (see the labels). Top right: Same as in the top-left panel but for the field RRLs. Bottom right: Same as in the bottom-left panel but for the field RRLs. |
4. Is the Oosterhoff dichotomy linked to the past merging history of the MW?
After classifying the field RRLs into in situ and accreted populations, we looked for a possible connection with the Oosterhoff dichotomy. To assign the Oosterhoff type, we used the Bailey diagram (see Fig. 2) and find that the two populations have remarkably different distributions. The in situ population shows a wide and continuous range of metallicities, from low [Fe/H] (at longer periods) to high [Fe/H] (at shorter periods); there is no sign of the Oosterhoff dichotomy as the distribution of pulsators is almost uniform at all periods. The distributions of the accreted population seem to tell a different story. They show different Oosterhoff types together with a sharp separation in metallicity; the OoI and OoII types have intermediate ([Fe/H] ∼ − 1.5 dex) and metal-poor ([Fe/H] > − 2.0 dex) metallicities, respectively. Also, the total metallicity range spanned by the accreted RRLs is much smaller compared with the in situ population. A further confirmation of this occurrence is apparent in Fig. B.2, where we show the Bailey diagram as a histogram. Again, we find two sharper peaks for the accreted population and a smoother distribution for the in situ population. These results suggest that the Oosterhoff dichotomy was imported into the MW via the merging events that shaped the Galaxy.
 |
Fig. 2. Bailey diagrams of RRLs in GGCs associated with the in situ population (top left), RRLs in GGCs associated with the accreted population (bottom left), field RRLs associated with the in situ population (top right), and field RRLs associated with the accreted population (bottom right). Sources are colour-coded according to their metallicity. The red curve separating the two types of Oosterhoff dichotomies is described by the following polynomial: y = −8.70 ⋅ 105 x7 − 1.63 ⋅ 106 x6 − 1.28 ⋅ 106 x5 − 5.44 ⋅ 105 x4 − 1.35 ⋅ 105 x3 − 1.95 ⋅ 104 x2 − 1.54 ⋅ 103 x − 52.14. |
We then checked to see if the same trend was present among the GGC RRLs. We cross-matched the RRLs in the Gaia DR3 catalogue with the database of RRLs in GGCs from Clement et al. (2001), finding 1157 matches for the fundamental mode RRLs, and gathered the GGC metallicities from the latest version (December 2010) of the Harris (1996) database. The adopted data for the RRLs in GGCs are shown in Table B.8. The classification of the GGCs into in situ and accreted populations is the same as in the previous sections (see Table B.6), and the results are shown in the left panels of Fig. 2. While the statistics are not large, it appears that, like for GGCs, the Oosterhoff dichotomy was imported into the MW by ancient merging events.
We repeated this exercise for each of the eight progenitors from Callingham et al. (2022) for our RRL sample. The Bailey diagrams for the three progenitors of Galactic origin (equivalent to the in situ population) are shown in Fig. B.3, while those associated with the five progenitors of extragalactic origin (equivalent to the accreted population) are shown in Fig. B.4. Again, we can see that the ‘Galactic’ progenitors do not show the Oosterhoff dichotomy but that each of the five ‘extragalactic’ progenitors does.
This is further evidence of a strong link between the past merging history of the MW and the Oosterhoff dichotomy. We note that our result is not in contradiction with findings by Fabrizio et al. (2019, 2021). Indeed, we confirm their results if we consider the in situ RRL populations only.
However, our results now raise new questions. Firstly, why do the progenitors that merged in the MW long ago show the Oosterhoff dichotomy and the dwarf spheroidal galaxies that orbit the Galaxy today do not? How would OoIII GGCs such as NGC6388 and NGC6441 fit into such a scenario?
The answer to these questions is beyond the scope of this Letter. However, we note that among the many ultra-faint dwarf galaxies identified within the halo of the MW (and M31) in the last 20 years, those that are more dispersed and poorly populated seem to host RRLs that conform to an Oosterhoff dichotomy, hence somewhat supporting our interpretation of the dichotomy as an ‘alien’ imported from the outside. Luckily, the improved data that will be released in Gaia DR4, along with future large and deep photometric surveys such as the Legacy Survey of Space and Time (LSST), data collected by the Vera Rubin Telescope, and big spectroscopic surveys such as those to be conducted with WEAVE (WHT Enhanced Area Velocity Explorer)5 and 4MOST (4-metre Multi-Object Spectroscopic Telescope)6 in a couple of years, will allow us to calculate the IoM for tens of thousands of RRLs, thus providing new crucial insights into the formation and evolution of the Galactic halo.
Data availability
Full Tables B.6–B.8 are available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/690/L17
Aluminium is produced by type II supernovae and only partially by asymptotic giant branch stars. Therefore, its abundance is sensitive to different chemical enrichment histories (Hawkins et al. 2015).
Acknowledgments
We warmly thank our anonymous Referee for their suggestions. This research has made use of the SIMBAD database operated at CDS, Strasbourg, France. We acknowledge support from Project PRIN MUR 2022 (code 2022ARWP9C) “Early Formation and Evolution of Bulge and HalO (EFEBHO)”, PI: Marconi, M., funded by European Union – Next Generation EU; INAF Large grant 2023 MOVIE (PI: M. Marconi); INAF GO-GTO grant 2023 “C-MetaLL - Cepheid metallicity in the Leavitt law” (P.I. V. Ripepi). This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular, the institutions participating in the Gaia Multilateral Agreement. This research was supported by the Munich Institute for Astro-, Particle and BioPhysics (MIAPbP), which is funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy – EXC-2094 – 390783311. This work is supported through an internship programme at the European Southern Observatory (ESO) in Garching, Germany.
References
- Baumgardt, H., & Vasiliev, E. 2021, MNRAS, 505, 5957 [NASA ADS] [CrossRef] [Google Scholar]
- Belokurov, V., & Kravtsov, A. 2024, MNRAS, 528, 3198 [CrossRef] [Google Scholar]
- Bencivenni, D., Caputo, F., Manteiga, M., & Quarta, M. L. 1991, ApJ, 380, 484 [NASA ADS] [CrossRef] [Google Scholar]
- Bono, G., Caputo, F., Castellani, V., & Marconi, M. 1997, A&AS, 121, 327 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bovy, J. 2015, ApJS, 216, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Breiman, L. 2001, Mach. Learn., 45, 5 [Google Scholar]
- Callingham, T. M., Cautun, M., Deason, A. J., et al. 2022, MNRAS, 513, 4107 [NASA ADS] [CrossRef] [Google Scholar]
- Catelan, M. 2009, Ap&SS, 320, 261 [Google Scholar]
- Catelan, M., & Smith, H. A. 2015, Pulsating Stars (Wiley-VCH) [Google Scholar]
- Clement, C. M., Muzzin, A., Dufton, Q., et al. 2001, AJ, 122, 2587 [NASA ADS] [CrossRef] [Google Scholar]
- Clementini, G., Ripepi, V., Garofalo, A., et al. 2023, A&A, 674, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fabrizio, M., Bono, G., Braga, V. F., et al. 2019, ApJ, 882, 169 [Google Scholar]
- Fabrizio, M., Braga, V. F., Crestani, J., et al. 2021, ApJ, 919, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Babusiaux, C., et al.) 2018, A&A, 616, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Vallenari, A., et al.) 2023, A&A, 674, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harris, W. E. 1996, AJ, 112, 1487 [Google Scholar]
- Hawkins, K., Jofré, P., Masseron, T., & Gilmore, G. 2015, MNRAS, 453, 758 [NASA ADS] [CrossRef] [Google Scholar]
- Helmi, A. 2020, ARA&A, 58, 205 [Google Scholar]
- Helmi, A., & de Zeeuw, P. T. 2000, MNRAS, 319, 657 [Google Scholar]
- Helmi, A., Babusiaux, C., Koppelman, H. H., et al. 2018, Nature, 563, 85 [Google Scholar]
- Li, X.-Y., Huang, Y., Liu, G.-C., Beers, T. C., & Zhang, H.-W. 2023, ApJ, 944, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Massari, D., Koppelman, H. H., & Helmi, A. 2019, A&A, 630, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McMillan, P. J. 2017, MNRAS, 465, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Nemec, J. M., Cohen, J. G., Ripepi, V., et al. 2013, ApJ, 773, 181 [CrossRef] [Google Scholar]
- Oosterhoff, P. T. 1939, Observatory, 62, 104 [NASA ADS] [Google Scholar]
- Sandage, A. 1981, ApJ, 244, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, H. A. 1995, Camb. Astrophys. Ser., 27 [Google Scholar]
- Stobie, R. S. 1971, ApJ, 168, 381 [NASA ADS] [CrossRef] [Google Scholar]
- van Albada, T. S., & Baker, N. 1973, ApJ, 185, 477 [NASA ADS] [CrossRef] [Google Scholar]
- van den Bergh, S. 2011, PASP, 123, 1044 [NASA ADS] [CrossRef] [Google Scholar]
- Vasiliev, E., & Baumgardt, H. 2021, MNRAS, 505, 5978 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, S., Liu, G., Huang, Y., et al. 2023, MNRAS, 525, 5915 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Radial velocities
Average RV measurements from the Gaia catalogue are available for only 3442 RRabs (Table B.1). Therefore, to complement our sample, we considered several large spectroscopic surveys, namely the Apache Point Observatory Galactic Evolution Experiment (APOGEE), Sloan Digital Sky Survey (SDSS), Large Sky Area Multi-Object Fiber Spectroscopic Telescope Low Resolution Spectrograph (LAMOST LRS), and Galactic Archaeology with HERMES (GALAH; see Table B.1 for details). We performed the following steps: (i) we cross-matched the catalogue of RRLs selected as explained above with each of these surveys; and (ii) in cases of multiple matches for the same star, we retained only one measurement, using preferentially the data as listed from top to bottom in Table B.1. The same table lists the number of RRLs with RV data from each survey.
We estimated the root-mean-square error (RMSE) value for the RV data of each survey using Gaia data as the model:
where x refers to a generic survey (not Gaia) and N is the number of stars that have RV data from both survey x and Gaia. The ratio between the RMSE and the error of each star is higher than 1, which led us to consider the RMSE calculated for the survey as the error related to the RV of each star in that survey. All the adopted RV measurements and relative errors are listed in Table B.7.
Appendix B: Additional tables and figures
Number of stars from each survey.
Hyper-parameters used in RandomForestClassifier.
Classification report of field RRLs for the Belokurov & Kravtsov (2024) method.
Classification report of field RRLs for the Callingham et al. (2022) method.
Eight progenitor classes identified by Callingham et al. (2022) with the respective acronyms.
Considered GGCs.
Data of the field RRLs used in this Letter.
Data for the RRLs in GGCs.
 |
Fig. B.1. Bar chart of the field RRL sample (left) and the GGC sample (right). Dark violet and dark orange indicate the in situ and accreted populations, respectively. |
 |
Fig. B.2. ‘Rectification’ of the Bailey diagram. The histogram shows the distribution of Δ log (P) = log (P)−log (Pfunc), where ‘func’ is the line (polynomial function) separating the Oosterhoff types shown in Fig. 2. The in situ and accreted populations are shown in blue and red, respectively. |
 |
Fig. B.3. Bailey diagram of field RRLs associated with the in situ population, separated according to the Callingham et al. (2022) progenitor classification (see the labels). Sources are colour-coded according to their metallicity. |
 |
Fig. B.4. Bailey diagram of field RRLs associated with the accreted population, separated according to the Callingham et al. (2022) progenitor classification (see labels). Sources are colour-coded according to their metallicity. |
All Tables
Classification report of field RRLs for the Belokurov & Kravtsov (2024) method.
Eight progenitor classes identified by Callingham et al. (2022) with the respective acronyms.
All Figures
 |
Fig. 1. (E, Lz) diagrams Top left: GGCs considered in this work. OoI, OoII, and non-Oosterhoff-type GGCs are shown as filled circles, diamonds, and crosses, respectively. The GGCs are classified as either in situ or accreted according to Belokurov & Kravtsov (2024) and plotted in different colours (see labels). Bottom left: Same but according to the classification into eight progenitor types (Callingham et al. 2022). Each progenitor type is identified with a different colour in the figure (see the labels). Top right: Same as in the top-left panel but for the field RRLs. Bottom right: Same as in the bottom-left panel but for the field RRLs. |
| In the text | |
 |
Fig. 2. Bailey diagrams of RRLs in GGCs associated with the in situ population (top left), RRLs in GGCs associated with the accreted population (bottom left), field RRLs associated with the in situ population (top right), and field RRLs associated with the accreted population (bottom right). Sources are colour-coded according to their metallicity. The red curve separating the two types of Oosterhoff dichotomies is described by the following polynomial: y = −8.70 ⋅ 105 x7 − 1.63 ⋅ 106 x6 − 1.28 ⋅ 106 x5 − 5.44 ⋅ 105 x4 − 1.35 ⋅ 105 x3 − 1.95 ⋅ 104 x2 − 1.54 ⋅ 103 x − 52.14. |
| In the text | |
 |
Fig. B.1. Bar chart of the field RRL sample (left) and the GGC sample (right). Dark violet and dark orange indicate the in situ and accreted populations, respectively. |
| In the text | |
 |
Fig. B.2. ‘Rectification’ of the Bailey diagram. The histogram shows the distribution of Δ log (P) = log (P)−log (Pfunc), where ‘func’ is the line (polynomial function) separating the Oosterhoff types shown in Fig. 2. The in situ and accreted populations are shown in blue and red, respectively. |
| In the text | |
 |
Fig. B.3. Bailey diagram of field RRLs associated with the in situ population, separated according to the Callingham et al. (2022) progenitor classification (see the labels). Sources are colour-coded according to their metallicity. |
| In the text | |
 |
Fig. B.4. Bailey diagram of field RRLs associated with the accreted population, separated according to the Callingham et al. (2022) progenitor classification (see labels). Sources are colour-coded according to their metallicity. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.