| Issue |
A&A
Volume 690, October 2024
|
|
|---|---|---|
| Article Number | A351 | |
| Number of page(s) | 9 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/202348607 | |
| Published online | 22 October 2024 | |
Origin of the break in the cosmic-ray electron plus positron spectrum at ∼1 TeV
Department of Physics, Khalifa University, PO Box 127788 Abu Dhabi, United Arab Emirates
Received:
14
November
2023
Accepted:
7
September
2024
Recent measurements of the cosmic-ray electron plus positron spectrum in several experiments have confirmed the presence of a break at ∼1 TeV. The origin of the break is still not clearly understood. In this work, we explored different possibilities for the origin, which include an electron source spectrum with a broken power law, a power law with an exponential or super-exponential cutoff, and the absence of potential nearby cosmic-ray sources. Based on the observed electron plus positron data from the DAMPE and the H.E.S.S experiments, and considering supernova remnants as the main sources of cosmic rays in the Galaxy, we find statistical evidence in favor of the scenario with a broken power-law source spectrum, with the best-fit source parameters obtained as Γ = 2.39 for the source spectral index, E0 ≈ 1.6 TeV for the break energy, and f = 1.59 × 1048 ergs for the amount of supernova kinetic energy injected into cosmic-ray electrons. This power-law break in the spectrum has been predicted for electrons confined inside supernova remnants after acceleration via diffusive shock acceleration process, and also indicated by the multi-wavelength study of supernova remnants. All of this evidence shows that the observed spectral break provides a strong indication of a direct link between cosmic-ray electrons and their sources. Our findings further show that electrons must undergo spectral changes while escaping the source region in order to reconcile the difference between the spectral index of electrons observed inside supernova remnants and that obtained from Galactic cosmic-ray propagation studies.
Key words: acceleration of particles / diffusion / cosmic rays / ISM: supernova remnants
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
High-energy cosmic-ray (CR) electrons and positrons with energies above ∼10 GeV suffer radiative losses mainly through synchrotron and inverse Compton processes during their propagation through the Galaxy. For a power-law source spectrum of E−Γ as predicted by the diffusive shock acceleration (DSA) theory (e.g., Drury 1983), radiative losses coupled with an energy-dependent diffusive propagation of CRs are expected to produce an equilibrium electron spectrum in the Galaxy that follows a power law E−(Γ + 1 − ξ) for stationary sources uniformly distributed throughout the Galactic disk (Ginzburg & Ptuskin 1976; Atoyan et al. 1995), where ξ ∼ (0.2 − 0.35), depending on the index of the CR diffusion coefficient D(E)∝Ea, which is typically in the range of a ∼ (0.3 − 0.6) in common models of CR propagation in the Galaxy (Jones et al. 2001; Strong et al. 2010).
In recent years, unprecedented high-precision measurements of CR electrons plus positrons in several experiments, such as those with the Alpha Magnetic Spectrometer (AMS-02; Aguilar et al. 2019a), Calorimetric Electron Telescope (CALET; Adriani et al. 2017), Dark Matter Particle Explorer (DAMPE; Ambrosi et al. 2017), Fermi Large Area Telescope (Fermi-LAT; Abdollahi et al. 2017), and the High Energy Stereoscopic System (H.E.S.S.; Aharonian et al. 2008, 2009), have revealed spectral structures that deviate from theoretical expectations. Two prominent features are a gradual hardening above ∼(30 − 50) GeV and a sharp break or steepening at ∼1 TeV (=103 GeV). Evidence for the break was first reported by the H.E.S.S. experiment and later confirmed by the DAMPE experiment with its high-resolution measurement covering an energy range of 25 GeV − 4.6 TeV. The observed spectrum closely follows E−3 and E−4 below and above the break, respectively.
The origin of the spectral break is still not clearly understood. However, it can be understood that the break cannot be due to the observed suppression in the positron flux at high energies, as positrons represent only a small fraction of the combined electron and positron flux. The positron fraction increases steadily from about 5% at ∼8 GeV to a maximum of about 15% at ∼(300 − 400) GeV, above which it shows a continuous decrease (Aguilar et al. 2019b). At ∼1 TeV, positrons make up only about 10% of the combined electron plus positron flux. This indicates that the spectral break has to do with the electron component, which is therefore our main focus in this work.
The break is difficult to explain as an effect of the propagation of CR electrons in the Galaxy. In the standard model of CR propagation in the Galaxy, where we sought a steady-state solution, CR electrons are expected to have a spectrum that steepens continuously with energy without any break as discussed above, unless certain special conditions are imposed (Lipari 2019). Features may arise that are related to the sudden drop in the energy loss rate of high-energy electrons as the inverse Compton scattering cross-section changes from the Thomson limit to the Klein-Nishina regime (Schlickeiser & Ruppel 2010). However, this drop is expected to produce an upturn in the spectrum (Evoli et al. 2020), not a steepening, which is what is shown by the measurements.
The observed break is most likely caused by an effect related to the source properties of CRs, such as the absence of nearby sources and a cutoff or break in the source spectrum itself. At energies where radiative losses are significant, electrons cannot travel far distances in the Galaxy, and the space-time volume that contains the sources contributing to the observed CR electrons becomes smaller (see e.g., Lipari 2019). This can lead to only a small number of sources contributing at high energies, and can thus produce a spectrum at the Earth that is exponentially suppressed (Kobayashi et al. 2004). For a typical interstellar medium (ISM) environment and standard CR propagation parameters, electrons of 1 TeV have an average diffusion length of ∼1 kpc in the Galaxy (see Sect. 2 for details). Therefore, if potential CR sources are missing or if they are significantly less numerous in the local ISM within ∼1 kpc of Earth, the observed CR electron flux can be significantly suppressed at TeV energies. Hereafter, we refer to this as the “missing sources” scenario.
Based on theoretical grounds and observational evidence, supernova remnants (SNRs) are considered to be the most plausible sources of CRs in the Galaxy (e.g., Ginzburg & Syrovatsky 1961; Drury 1983; Reynolds & Keohane 1999). Theoretically, the DSA process at the supernova shocks can accelerate supra-thermal particles of the ISM to very high energies. For electrons, the maximum energy can be limited by different factors, which can lead to different shapes of the spectral cutoff at the highest energies. For instance, for the widely adopted case of Bohm-type diffusion of particles, the electron spectrum follows the most commonly adopted form, the “exponential cutoff” exp(−E/E0), if the maximum energy is limited by the presence of a free-escape boundary ahead of the shock in the upstream region (see Yamazaki et al. 2014 and references therein). This type of spectral cutoff is widely used in CR propagation studies, for both the leptonic and hadronic species (Kobayashi et al. 2004; Thoudam et al. 2016), as well as in the study of radio and X-ray observations from SNRs (Reynolds & Keohane 1999). If the maximum energy is limited by radiative losses or by the finite age of the SNR, a “super-exponential cutoff” exp(−E2/E02) is expected (Kang et al. 2009; Kang 2011). This shape of the spectral cutoff is primarily expected for cases where the CR diffusion coefficient around the shock has a strong energy dependence, such as in the case of a Bohm-like diffusion (Zirakashvili & Aharonian 2007; Blasi 2010). The super-exponential cutoff is also found to explain better the observed synchrotron spectrum from shell-type SNRs when a more correct calculation of synchrotron emission is implemented, instead of the widely adopted δ-function approximation (Zirakashvili & Aharonian 2007). Recently, this form for the spectral cutoff was used to study spectral features in the CR electron spectrum (Fang et al. 2018; Evoli et al. 2020).
Another spectral feature that is naturally expected to be found for electrons present inside SNRs is a break in the power-law spectrum (hereafter, the “broken power-law” scenario). In the DSA process applied to supernova shocks, the majority of the particles escape downstream of the shock after acceleration and remain confined, during which time high-energy electrons suffer radiative losses. At a given age of the remnant, tage, electrons below a certain energy Eb, whose energy loss time tloss > tage will maintain the spectrum generated at the shock E−Γ, while those above Eb with tloss < tage will follow a steeper spectrum E−(Γ + 1) (Thoudam & Hörandel 2011; Ohira & Yamazaki 2017). Detailed simulations of time-dependent DSA have confirmed the presence of such a break in the power-law electron spectrum inside SNRs (Kang 2011). They found the break at around 1 TeV when the SNR age is about 1000 yr, while the exponential cutoff remained at ∼(40 − 50) TeV for a reasonable set of ISM parameters and a downstream magnetic field of ∼100 μG for the remnant. Recently, Morlino & Celli (2021) have shown that generation of this sharp break in the electron spectrum requires a large amplification of the magnetic field in the downstream region of the shock, possibly generated by the combined effect of both CR-related and turbulent instabilities. Also discussed in recent works (Diesing & Caprioli 2019; Cristofari et al. 2021) is the importance of this efficient magnetic field amplification operating until the late stages of the remnant’s evolution, in order to produce a steeper source index of electrons compared to that of protons, as revealed by Galactic CR propagation studies.
In this work, we compared the different scenarios described above – missing sources, exponential cutoff, super-exponential cutoff, and broken power-law – in terms of the quality of fit to the observed CR electron spectrum, and show that the broken power-law scenario best explains the observed break as well as the overall spectrum.
This paper is organized as follows. In Sect. 2, we present the CR propagation model used in our study, and in Sect. 3, the different scenarios for the spectral break are described in detail. Section 4 presents the electron plus positron data that we used to test the different scenarios, and Sect. 5 describes the spectrum calculation for the different scenarios and the fitting procedure that we adopted for this work. Section 6 presents the fit results, and Sect. 7 discusses the results in detail.
2. Propagation of cosmic-ray electrons in the Galaxy
For a stationary and uniform distribution of CR sources in the Galactic disk, the diffusive propagation of CR electrons in the Galaxy subject to synchrotron and inverse Compton radiative losses is described as
where E is the kinetic energy, N(r, E) is the differential number density at a position r ≡ (r, ϕ, z) in cylindrical coordinates (with r representing the radial position, ϕ the azimuthal, and z the perpendicular position to the Galactic plane), and q(r, E) is the source term denoting the electron injection rate per unit volume into the ISM. The diffusion coefficient is taken as D(E) = D0β(E/E0)a, where D0 = 1.55 × 1028 cm2 s−1 is the diffusion constant, β = v/c is the ratio of the particle velocity v to the velocity of light c, E0 = 3 GeV, and a = 0.54 is the diffusion index (Thoudam & Hörandel 2013). This form of D(E) neglects the break at ∼300 GeV reported in some recent studies based on the secondary-to-primary ratios measured by the AMS-02 experiment (Ferronato Bueno et al. 2024). b(E) is the radiative energy loss rate, which is the sum of synchrotron and inverse Compton losses. Following Schlickeiser & Ruppel (2010), we took
where σT is the Thomson cross-section, mec2 is the electron rest-mass energy, and UB = B2/8π is the energy density of the magnetic field of strength B. We took B = 3 μG. This value of the magnetic field is the average over the z = ±5 kpc region below and above the Galactic plane, calculated at the galactocentric radius of 8.5 kpc using the relation B(z) = B0 e−|z|/3kpc μG adopted in the GALPROP CR propagation code (Strong et al. 2010). We took B0 = 6 μG, the local magnetic field value (Beck 2001). A recent detailed study reports a slightly lower value of the Galactic magnetic field (Unger & Farrar 2024). The summation in Eq. (2) represents the sum of the inverse Compton losses in the Klein-Nishina limit over four different diffuse photon fields present in the ISM – (1) photons from spectral type B stars, (2) photons from spectral type G-K stars, (3) infrared radiation, and (4) cosmic microwave background, where Wi denotes the respective photon energy density, and Ei is the critical Klein-Nishina energy above which the Thomson cross-section starts to break down. (Wi, Ei) for the four photon fields are taken as (0.09 eV/cm3, 40 GeV), (0.3 eV/cm3, 161 GeV), (0.4 eV/ cm3, 4.0 × 104 GeV), and (0.25 eV/cm3, 3.0 × 105 GeV), respectively (Schlickeiser & Ruppel 2010). More details on the relativistic treatment of inverse Compton losses of high-energy electrons can be found in Delahaye et al. (2010).
As high-energy electrons cannot travel far distances in the Galaxy because of radiative losses, the effect of diffusion boundary of the Galaxy on the solution of Eq. (1) can be neglected for energies within our scope of interest, that is, above ∼10 GeV. The Green’s function of Eq. (1) can be obtained as
The CR density at a position r is obtained by convolving the Green’s function with the source term q(r, E) as
For a uniform source distribution in the Galactic disk, and assuming azimuthal symmetry, the source term can be written independent of r and ϕ as q(r, E) = νQ(E)δ(z), where ν denotes the frequency of supernova explosions per unit surface area in the Galactic disk, and Q(E) is the source spectrum. We took ν = 25 Myr−1 kpc−2, which corresponds to ∼3 supernova explosions per century in the Galaxy (Grenier 2000). Then, the CR density at the position of the Earth, taken to be r = 0, due to all the sources being located beyond a radial distance r0 in the Galactic disk, is obtained as
Defining 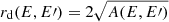 , Eq. (6) can be written as
, Eq. (6) can be written as
rd(E, E′) corresponds to the average diffusion length of electron of energy E′ before it cools down to energy E. For the diffusion coefficient D(E)∝Ea and energy loss coefficient b(E)∝E2, as expected in the case of synchrotron losses and inverse Compton losses in the Thomson regime, we can write an exact analytical expression of Eq. (3) as
where tloss(E)∝1/E is the energy loss time for electrons of energy E. For the values of the diffusion parameters and the Galactic magnetic field strength of B = 3 μG used in the present study, the diffusion length for an electron of 1 TeV before losing half its energy was calculated to be rd ∼ 1.16 kpc. In general, for a < 1 and E′≫E, that is, when the electron has lost a significant fraction of its energy (E = ηE′, where η ≪ 1), from Eq. (8), we have  . For a = 0.54, which is the value adopted in this work, rd was found to scale with energy as rd ∝ E−0.23, which shows that high-energy electrons traverse a smaller region of the Galaxy compared to the low-energy ones. This can lead to a significant suppression of the observed electron flux at high energies if potential CR sources are absent in the nearby region, due to the dominant effect of the exponential term in Eq. (7).
. For a = 0.54, which is the value adopted in this work, rd was found to scale with energy as rd ∝ E−0.23, which shows that high-energy electrons traverse a smaller region of the Galaxy compared to the low-energy ones. This can lead to a significant suppression of the observed electron flux at high energies if potential CR sources are absent in the nearby region, due to the dominant effect of the exponential term in Eq. (7).
By setting r0 = 0 in Eq. (7), the CR electron flux at Earth from a continuous distribution of sources throughout the Galactic disk can be obtained as
For a single power-law source spectrum in the form Q(E)∝E−Γ, Eq. (9) gives a spectrum at Earth that follows N(E)∝E−Γ − 1 + ξ for the case of D(E)∝Ea and b(E)∝E2. The spectrum steepens mainly due to radiative losses, but with a correction factor ξ = (1 − a)/2 arising from the diffusive nature of the propagation. For a = 0.54, the correction factor is ξ = 0.23.
3. Different scenarios for the spectral break
As mentioned briefly in Sect. 1, the observed spectral break at ∼1 TeV is most likely due to an effect related to the sources, such as missing nearby CR sources or an intrinsic cutoff (or break) in the CR source spectrum. In this section, we discuss the different possibilities in detail.
3.1. Missing sources
The absence of potential CR sources in the local ISM can lead to a suppression in the CR electron flux at high energies, which may appear as a break or exponential cutoff in the observed spectrum (Kobayashi et al. 2004; Lipari 2019). The energy above which the suppression occurs depends on the distance of the closest source. To produce a suppression above ∼1 TeV, the nearest source must be located around 1 kpc from Earth, as discussed in Sect. 2 based on Eq. (7).
The shape of the spectral break in this case is determined by the exp(−r02/rd2) term in Eq. (7). Defining r0 as the diffusion length of electrons corresponding to the break energy E0, we can write 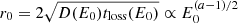 . For a = 0.54, this gave r0 ∝ E0−0.23, and together with the rd ∝ E−0.23 obtained in Sect. 2, the exponential cutoff in Eq. (7) could be written in terms of energy as exp[−(E/E0)0.46], which is close to
. For a = 0.54, this gave r0 ∝ E0−0.23, and together with the rd ∝ E−0.23 obtained in Sect. 2, the exponential cutoff in Eq. (7) could be written in terms of energy as exp[−(E/E0)0.46], which is close to 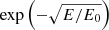 . Therefore, the missing sources scenario is expected to exhibit a spectral cutoff that is harder than the commonly adopted exponential and super-exponential cutoffs, which are discussed below.
. Therefore, the missing sources scenario is expected to exhibit a spectral cutoff that is harder than the commonly adopted exponential and super-exponential cutoffs, which are discussed below.
3.2. Exponential cutoff
In the DSA process, if the maximum energy of the particles is limited by free escape from the acceleration region, the spectral cutoff can follow an exponential cutoff of the form exp(−E/E0) (see e.g., Caprioli et al. 2009; Ohira et al. 2010 and references therein). This type of cutoff is also most commonly used in CR propagation studies (e.g., Kobayashi et al. 2004; Thoudam et al. 2016), as well as in the study of non-thermal radio and X-ray emission from SNRs (Reynolds & Keohane 1999; Bamba et al. 2003).
In the test particle approximation, assuming the presence of an escape boundary at a distance L ahead of the shock in the upstream region, the maximum energy Em of the particles that remain confined is given as the condition Ds(Em)/u = L, where Ds ∝ Eβ is the diffusion coefficient of the particles in the accelerator region, and u is the velocity of the shock expanding into a stationary medium. The spectrum at the shock in this case follows (Caprioli et al. 2009; Ohira et al. 2010; Yamazaki et al. 2014), as
where q = 3r/(r − 1), with the shock compression ratio r = 4 for strong shocks. At energies E ≫ Em, the spectrum reduces to f0(E)∝exp[−q(E/Em)β]. For particles diffusing in the Bohm regime, β = 1, which gives a cutoff shape of the form exp(−E/E0), where we took E0 = Em/q.
3.3. Super-exponential cutoff
If the maximum energy of the electrons in the DSA process is limited by radiative losses or by the finite age of the accelerator, the high-energy cutoff is expected to follow a super-exponential cutoff exp[−(E/E0)2] for the widely adopted Bohm-type diffusion (Zirakashvili & Aharonian 2007; Kang et al. 2009; Blasi 2010).
The asymptotic form of the electron spectrum at the shock front in the very high energy regime where the radiative energy losses dominate over acceleration is given as (Zirakashvili & Aharonian 2007)
where, for the same energy dependence of the radiative losses and the diffusion coefficient in the downstream and upstream regions of the shock, 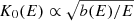 , and S0(E) can be approximated as (see also Yamazaki et al. 2014)
, and S0(E) can be approximated as (see also Yamazaki et al. 2014)
Using the condition that the maximum energy is determined by equating the acceleration time tacc(Em)≈4Ds(Em)/u2 (Bell 2013), with the radiative energy loss time tloss(Em)∝1/Em, Eq. (12) becomes S0(E)≈q(E/Em)β + 1. For Bohm-like diffusion, the shape of the spectral cutoff then follows exp[−(E/E0)2], where 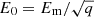 .
.
3.4. Broken power-law
In the standard DSA theory as applied to supernova shock waves, a major fraction of the particles escape downstream of the shock and remain confined within the remnant without crossing the shock again. During the confinement, if high-energy electrons suffer severe radiative losses, this can lead to a power-law break in the cumulative electron spectrum (Thoudam & Hörandel 2011; Kang 2011; Ohira & Yamazaki 2017). However, the presence of such a break requires a large magnetic field amplification in the downstream that continues until the late stages of the SNR evolution (Morlino & Celli 2021). This strong field is also required to produce the difference in the source spectral index between protons and electrons above ∼10 GeV that is required in CR propagation studies (Diesing & Caprioli 2019; Cristofari et al. 2021).
The temporal evolution of the electron spectrum during the confinement downstream, subject to severe radiative losses and continuous injection into the downstream after acceleration at the shock fronts, can be written as (Kardashev 1962; Thoudam & Hörandel 2011)
where Γ is the spectral index of electrons accelerated at the supernova shocks. Equation (13) shows that the electron spectrum exhibits a break at an energy, E0 ∝ 1/t, whose value depends on the age of the remnant, t. It can be easily checked using Eq. (13) that the spectrum below the break follows E−Γ, while above, the spectrum becomes steeper as E−(Γ + 1). Interestingly, the electron spectrum measured by the H.E.S.S and the DAMPE experiments also exhibit a similar spectral difference below and above the break energy of 1 TeV.
4. Measured electron plus positron spectrum
Recently, various experiments, such as the AMS-02 (Aguilar et al. 2019a), CALET (Adriani et al. 2017), DAMPE (Ambrosi et al. 2017), Fermi-LAT (Abdollahi et al. 2017) and H.E.S.S. (Aharonian et al. 2008, 2009) instruments, have provided high-quality data on the total electron plus positron spectrum up to energies of a few teraelectronvolts. Their combined spectrum indicates a hardening above ∼(30 − 50) GeV with a power-law index of ∼3.0 and a steepening above ∼1 TeV to an index close to ∼4.0. While the results from the different experiments show a similar behavior over a wide energy range, there are systematic differences between the measured fluxes. For this reason, and also because DAMPE covers an energy range (25 GeV − 4.6 TeV) wide enough to detect the presence of the spectral break at ∼1 TeV in a single measurement, we use the DAMPE data to test the different scenarios for the spectral break described in Sect. 3 together with the H.E.S.S data to increase the statistic at TeV energies.
5. Calculation of CR electron spectrum and fitting the electron plus positron data
CR electron spectrum for the different scenarios can be calculated from Eq. (7) or Eq. (9) by taking their appropriate source spectrum Q(E). For the missing sources scenario, Eq. (7) was used by keeping r0 a model parameter, while for the rest, Eq. (9) was used where r0 was set to 0. Below are the different forms of Q(E) adopted in our calculation based on the description of the different scenarios given in Sect. 3:
where k is a normalization constant that is proportional to the fraction f of the supernova kinetic energy of 1051 ergs injected into CR electrons, Γ is the source index, and E0 is the exponential or super-exponential cutoff. For the broken power-law scenario, the function reproduces the spectral shapes E−Γ below the break energy E0 and E−(Γ + 1) above the break as described by Eq. (13). The smoothness parameter δ was fixed at 0.05 so as to produce a similar level of sharpness at E0 as the spectrum given as Eq. (13).
For each scenario, the fit to the observed data was performed using three parameters related to the source properties: (f, Γ, r0) for the missing sources and (f, Γ, E0) for the all other cases. We used the fraction f instead of k for the fit as it directly represents the amount of supernova kinetic energy that is converted into CR electrons. In this study, we calculated f on the basis of energy injected into electrons above 1 GeV. The fit was performed in two steps. First, as f only scales the normalization and does not affect the shape of the final spectrum, we treated it as a nuisance parameter and marginalized it to determine the set of values for (Γ, r0) or (Γ, E0) that gives the maximum likelihood, ℒ = ∑fℒf, fit to the observed data. The summation over f was carried out in steps of Δf = 0.02 (in units of 1049 ergs), and ℒf = exp(−χ2/2) with
where the summations are over the measured energy points Ei. (ID, σD), and (IH, σH) are the measured electron plus positron flux and the associated errors from the DAMPE and the H.E.S.S. experiments, respectively, at their respective Ei’s. IM(Ei) = Ie−(Ei)+Ie+(Ei). As such, Ie−(Ei) = (v/4π)N(Ei) is the electron flux predicted by the model (Eqs. (7) or (9)), and Ie+(Ei) is the observed positron flux from the AMS-02 experiment, which can be described as (Aguilar et al. 2019b)
where the first term represents contribution of the diffuse positron flux produced from the collision of CR nuclei with interstellar matter, and the second term represents an additional contribution of positrons, which could be originated from dark matter annihilation or astrophysical sources such as pulsars in the Galaxy. 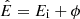 , with ϕ = 1.1 GeV, is the solar modulation parameter, K1 = 6.51 × 10−2 (m2 sr s GeV)−1, K2 = 6.80 × 10−5 (m2 sr s GeV)−1, E1 = 7.0 GeV, E2 = 60 GeV, γ1 = −4.07, γ2 = −2.58, and Ec ≈ 813 GeV. In writing Eq. (15), we assumed that the data points are uncorrelated.
, with ϕ = 1.1 GeV, is the solar modulation parameter, K1 = 6.51 × 10−2 (m2 sr s GeV)−1, K2 = 6.80 × 10−5 (m2 sr s GeV)−1, E1 = 7.0 GeV, E2 = 60 GeV, γ1 = −4.07, γ2 = −2.58, and Ec ≈ 813 GeV. In writing Eq. (15), we assumed that the data points are uncorrelated.
In the next step, (Γ, r0) or (Γ, E0) were fixed to the values that maximize ℒ, and we scanned over f in finer steps of Δf = 0.001 to determine its best-fit value that gives the minimum value of χ2. Table 1 lists the model parameters and their ranges used in the fit. The fit was performed for the energy range (20 − 3500) GeV. This range excludes the three highest energy data points of the measured spectrum shown in Fig. 1. Although measurement uncertainties are large at these energies, the rising trend in the flux might indicate the presence of one or several strong nearby sources, which we did not include in this study (Kobayashi et al. 2004). Considering SNRs located within 1 kpc of Earth and using a reasonable form of energy-dependent CR escape from the SNRs, Thoudam & Hörandel (2012) showed that nearby sources, in particular the Vela remnant, can be responsible for the steep rise in the observed spectrum at the highest energies. We note that for the energy range considered in this work, the effects of processes such as solar modulation, re-acceleration by interstellar magnetic turbulence or by encounters with old SNRs, convection by the Galactic wind, and energy losses due to ionization and bremsstrahlung on the electron spectrum at Earth are expected to be negligible. These processes are important mostly at energies below ∼20 GeV.
Model parameters (f, Γ, E0, r0) and their ranges considered in the fitting procedure.
 |
Fig. 1. Fit to the CR electron plus positron data from the DAMPE (Ambrosi et al. 2017) and the H.E.S.S. (Aharonian et al. 2008) experiments for the (20 − 3500) GeV fit range for different scenarios of the spectral beak: missing sources (top left), exponential cutoff (top right), super-exponential cutoff (bottom left), and broken power-law (bottom right). Line representation: best-fit electron plus positron spectrum (thick solid line), electron spectrum (dashed line) and positron spectrum (thin solid line). The positron spectrum and its data are from AMS-02 measurements (Aguilar et al. 2019b). The fits exclude the three highest energy data points. The best-fit values of the model parameters are listed in Table 2. |
In order to check the effect of the selected energy range on the fit results, we also performed a fit for another energy range of (100 − 3500) GeV. The ranges of the model parameters for this fit range are also listed in Table 1.
6. Results
The fit results for the (20 − 3500) GeV range are shown in Fig. 1 for the different scenarios of the spectral break where the best-fit electron plus positron spectrum (thick solid line), the electron component (dashed line) and the positron spectrum (thin solid line) are shown along with the measurements from the DAMPE and the H.E.S.S experiments. The positron spectrum in Fig. 1, given as Eq. (16), is a basic fit to the observed data from AMS-02 (Aguilar et al. 2019b), which is also shown in the figure.
All of the scenarios produce a reasonably good fit to the data up to energies close to ∼1 TeV, whereas above this energy, the broken power-law and the super-exponential cutoff scenarios show significantly better fits. The missing source and exponential cutoff scenarios did not produce spectra which are steep enough to explain the observed steepening above 1 TeV. Figure 1 also demonstrates that the positron fluxes do not account for the observed spectral break. The break is determined by the electron component.
To compare the quality of the fits between the different scenarios for the (20 − 3500) GeV fit range, we plotted the best-fit electron plus positron spectra of the different scenarios from Fig. 1 together into a single plot in Fig. 2 (top-left panel). It can be seen that all the scenarios predict an almost similar spectrum at lower energies, but above ∼1.5 TeV, their predictions start to deviate from each other, with the broken power-law (thick red line) and the super-exponential cutoff (blue line) scenarios explaining the data better than the missing sources (green line) and the exponential cutoff (black line) scenarios. The positron spectrum and its data shown in Fig. 2 are the same as in Fig. 1. The residuals of the spectral fits are shown in the bottom-left panel, calculated only with respect to the DAMPE data, although both DAMPE and H.E.S.S data were used in the fits. The filled circles in the residual plots show the data points that were not included in the fit, and the dashed lines show the ±20% residual levels to guide the eye. The right panels of Fig. 2 show similar plots for the (100 − 3500) GeV fit range. Above 100 GeV, the individual spectra and the relative differences between them are similar to those observed in the (20 − 3500) GeV fit range.
 |
Fig. 2. Comparison of the best-fit electron plus positron spectra of the different scenarios for the two different fit ranges: (20 − 3500) GeV (left) and (100 − 3500) GeV (right). Line representation: missing sources (green line), exponential cutoff (black line), broken power-law (thick red line), and super-exponential cutoff (blue line). For the (20 − 3500) GeV fit, the best-fit electron plus positron spectra are the same as shown in Fig. 1. The top plots show the spectral fits, and the bottom plots show the fit residuals. Residuals are shown only with respect to the DAMPE data, but the χ2 calculation includes both the DAMPE and the H.E.S.S. data. Filled circles in the residual plots represent data points not included in the fit. The dashed lines represent ±20% residual levels, shown only for reference. The best-fit values of the model parameters and the χ2 values are listed in Table 2. All of the data shown and the positron spectrum (thin red line) are the same as in Fig. 1. |
Table 2 gives the best-fit values of the different parameters, that is, (f, Γ, r0) for the missing sources scenario and (f, Γ, E0) for the other cases, along with the χ2 values of the fits. Based on the χ2 values, the broken power-law is found to give the best fit of all the scenarios for both the fit ranges. For the (20 − 3500) GeV fit, it gives the smallest χ2 value of 69 for a number of degrees of freedom of ndf = 43. The next best case, which is the super-exponential cutoff, gives χ2 = 87 for the same ndf. The exponential cutoff and the missing sources give χ2 = 114 and 125, respectively. For the 100 − 3500 GeV fit, we find similar results, where χ2 = 57 for the broken power-law compared to χ2 = 67 for the super-exponential cutoff, χ2 = 89 for the exponential cutoff, and χ2 = 111 for the missing sources scenario for ndf = 33. For both of the fit ranges, we find that the overall fit quality decreases in the following order of the scenarios: broken power-law, super-exponential cutoff, exponential cutoff, and missing sources. This demonstrates the robustness of the fit with respect to the chosen energy range.
Best-fit values of the model parameters (f, Γ, E0, r0) and the χ2 values of the fits.
For the (20 − 3500) GeV fit, which is the main result of this work, we find that the broken power-law scenario gives Γ = 2.39, E0 = 1576 GeV, and f = 0.159 × 1049 ergs, whereas the (100 − 3500) GeV fit gives a flatter source index of Γ = 2.36 together with smaller E0 and f values of E0 = 1482 GeV and f = 0.142 × 1049 ergs. This is because the (20 − 3500) GeV fit has to accommodate for the observed steeper spectrum below ∼100 GeV, which then requires larger values of E0 and f to explain both the observed spectral break and the flux level at the same time. For the exponential and the super-exponential cutoffs, we find the best-fit values for the (20 − 3500) GeV fit to be (Γ = 2.37, E0 = 6762 GeV, f = 0.154 × 1049 ergs) and (Γ = 2.39, E0 = 4588 GeV, f = 0.159 × 1049 ergs). These values are also larger than the corresponding values obtained for the (100 − 3500) GeV fit. The missing sources scenario gives Γ = 2.23, r0 = 0.85 kpc, and f = 0.272 × 1049 ergs for the (20 − 3500) GeV fit, compared to the values of Γ = 2.08, r0 = 1.3 kpc, and f = 0.378 × 1049 ergs for the (100 − 3500) GeV range. This can be explained as: a flatter Γ will require a larger r0 value (which corresponds to a lower cutoff energy) to compensate for the increase in the flux at higher energies, due to the flatter spectrum.
We note that our best-fit value for the source index value (for instance, Γ = 2.39 for the broken power-law scenario) is larger than the typical value of 2.0 predicted by the standard theory of DSA for strong shocks. However, this larger value of Γ is typical for CR propagation studies (see e.g., Ackermann et al. 2012). A similar value of Γ = 2.39 for CR electrons was also found in a recent study presented in Evoli et al. (2020). It is possible that this type of steep index is produced by CR modified shocks inside SNRs, as discussed recently in Caprioli et al. (2020), or by the presence of an efficient magnetic field amplification operating until the late stages of SNR evolution, when the shock already becomes weak (Diesing & Caprioli 2019; Cristofari et al. 2021).
7. Discussions and conclusions
We have explored different scenarios related to CR source properties for the origin of the observed break in the CR electron spectrum at ∼1 TeV, and find that the scenario with the broken power-law source spectrum best describes the data with the best-fit values of Γ = 2.39, E0 = 1576 GeV, and f = 0.159 × 1049 ergs. While the widely adopted exponential cutoff scenario as well as the scenario of the missing nearby sources are statistically disfavored, we find that the super-exponential cutoff also explains the data reasonably well, although it is statistically less favorable than the broken power-law case. Moreover, multi-wavelength observations of SNRs provide a strong indication favoring the broken power-law scenario for the TeV break, as discussed below.
DSA applied to supernova shocks in a regular ISM predicts an exponential or super-exponential cutoffs in the electron spectrum depending on the limiting condition for the maximum energy, as discussed in Sect. 3, but the cutoffs are expected to be at ∼(30 − 100) TeV (Reynolds 2008), which is much higher than the position of the observed break in the CR electron spectrum. Moreover, combined spectral fitting of radio and X-ray data of several young SNRs have also found a similar range of very high energy cutoffs for electrons (Reynolds & Keohane 1999), thereby disfavoring the exponential or super-exponential cutoffs in the source spectrum as a plausible explanation for the observed TeV break.
On the other hand, DSA simulations using standard SNR parameters have predicted a break in the power-law spectrum of electrons at GeV−TeV range (where the position of the break depends on the age of the remnant) arising from the radiative losses of electrons during their confinement in the downstream region (Kang 2011). The break energy which is given as the condition, tloss = tage, follows Eb ≈ 1/(αtage) for a continuous injection of electrons into the downstream (see e.g., Thoudam & Hörandel 2011). For synchrotron losses, α = 2.5 × 10−18(B/μG)2 GeV−1 s−1, indicating that our best-fit break energy of E0 = 1576 GeV ≈1.6 TeV corresponds to an SNR age of tage ≈ 3.3 × 104 yr for a conservative magnetic field strength of B = 15 μG in the downstream. This age is close to the onset of the radiative phase of an SNR, tr = 2.7 × 104(ESN/1051ergs)0.24(nH/cm3)−0.52 yr ≈2.7 × 104 yr, estimated for a standard supernova explosion energy of ESN = 1051 ergs and ISM density of nH = 1 H cm−3 (Sturner et al. 1997). It is generally considered that as an SNR enters the radiative phase, the shock slows down significantly and all of the particles confined downstream are released into the ISM. It is worth keeping in mind that our estimate of tr does not take into account the variety of interstellar environments in which supernova explosions can occur in the Galaxy. While thermonuclear or Type Ia supernova explosions generally occur in the regular ISM, core-collapse or Type II supernova explosions can occur in a more complex environment, which can be a low-density cavity formed by powerful winds originated from their massive progenitor stars (O-type stars) or a high-density environment of molecular clouds if the progenitors are of lower mass, such as B-type stars (Weaver et al. 1977; Chevalier 1999). In addition, most supernovae are expected to be found within star clusters where the environment can be even more complex due to the interacting stellar winds (Longmore et al. 2014). For a typical range of nH = (0.1 − 10) H cm−3, we estimate the start of the radiative phase to be in the range of tr ≈ (8 × 103 − 9 × 104) yr. The SNR age of tage ≈ 3.3 × 104 yr that we obtained corresponding to our best-fit break energy of E0 ∼ 1.6 TeV falls well within this range.
Strong observational evidence in favor of the broken power-law case comes from the extensive H.E.S.S. measurement of SNR RX J1713.7 − 3946, which is one of the most well-studied SNRs across different wavelengths (Abdalla et al. 2018). Simultaneous fitting of high-quality X-ray and GeV−TeV gamma-ray data shows a clear preference for a broken power-law particle spectrum which, for the leptonic origin, requires a power-law break at Eb = 2.5 TeV with an index Γ = 1.78 (2.93) below (above) the break and an exponential cutoff of Ec ∼ 88 TeV for a magnetic field strength of B ∼ 14 μG. The Γ value below the break obtained by the H.E.S.S measurement is smaller than our best-fit value of Γ = 2.39, but the spectral difference of ΔΓ ∼ 1.15 found with H.E.S.S. below and above the break is quite close to the ΔΓ ∼ 1.0 predicted by the power-law scenario in the present study, which is also the observed difference in the CR electron spectrum. In another study, a fit to the multi-wavelength data using a broken power-law electron spectrum with a super-exponential cutoff gives a slightly different result: Γ = 2.0 below the break, Eb = 3.5 TeV, Ec = 80 TeV, and B = 16 μG (Zang & Liu 2019). Although the exact origin (leptonic or hadronic) of the non-thermal emission from RX J1713.7 − 3946 is still under debate, we note that the hadronic scenario requires certain environmental conditions for the SNR to generate a broken power-law source spectrum, for instance, a supernova explosion in a molecular cloud that has already been swept away by a strong wind from the progenitor star (Gabici & Aharonian 2014). Such an environment may not be readily available for the majority of the SNRs in the Galaxy. On the other hand, in the leptonic case, a power-law spectral break is naturally expected, as discussed above in Sect. 3.4.
Additional evidence for the broken power-law case can be found in the multi-wavelength studies of several other SNRs. Zang & Liu (2019) studied a sample of seven middle-aged (several thousand years old) shell-type SNRs and finds that the majority of the SNRs in their sample show an electron spectrum with a power-law break at Eb ∼ (1.0 − 3.5) TeV and Γ ∼ 1.9 − 2.2 below the break, along with a high-energy super-exponential cutoff in the range of ∼(30 − 80) TeV and a magnetic field in the range of B ∼ (9 − 26) μG.
Zeng et al. (2019) considered a larger sample of 35 middle-aged and moderately old SNRs, and also finds a particle distribution that follows a broken power-law spectrum. They find the break energy to decrease with the SNR age in the range of ∼100 TeV − 1 GeV over ∼(103 − 6 × 104) yr age range with a spectral index Γ ∼ 1.2 − 2.3 below the break energy. However, they considered a combined population of electrons and protons to fit the multi-wavelength data, and assumed the two population to have the same spectral index and break energy, which may not necessarily be true in all cases (Diesing & Caprioli 2019; Morlino & Celli 2021). These reservations make it difficult infer information from their results that can be directly compared with our findings in this study, where our focus was purely on the electron spectrum.
Overall, the observation of a spectral break with ΔΓ ∼ 1.0 in the electron spectra of several SNRs, such as RX J1713.7 − 3946 and others as presented in Zang & Liu (2019), and our independent finding of a similar break and similar ΔΓ in the electron source spectrum from the study of CR propagation in the Galaxy, provide a strong indication of a direct link between the observed CR electrons and their sources. However, the Γ values of ∼(1.9 − 2.2) inferred from the SNRs are found to be relatively smaller than our best-fit value of 2.39 obtained from the CR electron data. The fact that the Γ values from the SNRs are quite close to the index predicted by the DSA process indicates that the electrons confined inside the remnants mostly preserve the shape of the spectrum produced at the shocks, except at energies above the break where the spectrum steepens by ΔΓ ∼ 1.0 due to radiative cooling. However, what is necessary for the study of CR propagation is the electron spectrum released by SNRs into the ISM. This spectrum is poorly known, and it may be different from the spectrum produced at the shocks. Our findings strongly indicate that a modification (steepening) of the electron spectrum must be happening while the electrons escape through the source region. Recent studies have shown that CR protons escaping from their sources can generate magnetic fluctuations around the source region due to both resonant and non-resonant streaming instabilities (Schroer et al. 2021, 2022). These fluctuations lead to the formation of low-diffusivity CR inflated bubbles surrounding the sources where CRs spend a considerable amount of time before finally being released into the ISM. For electrons, while they diffuse through these bubbles, their spectrum can be changed due to radiative losses. This may explain the observed difference in the spectral index of electrons obtained from SNRs and that required by the Galactic propagation study. A similar argument has also been raised to explain the difference in the source index of protons and electrons, as revealed by CR propagation studies considering that protons and electrons can suffer different spectral changes during their propagation through these bubbles (Schroer et al. 2021; Cristofari et al. 2021). The presence of such bubbles or cocoons around potential CR sources has also been proposed to predict the additional contribution of secondary CRs from the sources leading to a hardening in the secondary-to-primary ratios at TeV energies (Cowsik & Burch 2010).
Based on the best-fit results obtained in this work using the observed CR electron spectrum and the evidence reported from the multi-wavelength studies of SNRs, we conclude that if SNRs are the main sources of CRs in the Galaxy, the power-law break in the measured CR electron plus positron spectrum at ∼1 TeV is most likely an imprint of the radiative cooling break present in the electron source spectrum. Our findings further show that in order to reconcile the difference between the spectral index of electrons obtained from the study of SNRs and CR propagation, CR electrons must undergo spectral modifications while escaping the source region. A detailed investigation of this topic can help further strengthen the link between SNRs and CRs in the Galaxy.
Acknowledgments
Fundings from the ADEK grant (AARE19-224), and the Khalifa University ESIG-2023-008 and RIG-S-2023-070 grants are acknowledged.
References
- Abdalla, H., Abramowski, A., Aharonian, F., et al. 2018, A&A, 612, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Abdollahi, S., Ackermann, M., Ajello, M., et al. 2017, Phys. Rev. D, 95, 082007 [CrossRef] [Google Scholar]
- Ackermann, M., Ajello, M., Atwood, W. B., et al. 2012, ApJ, 750, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Adriani, O., Akaike, Y., Asano, K., et al. 2017, Phys. Rev. Lett., 119, 181101 [CrossRef] [PubMed] [Google Scholar]
- Aguilar, M., Ali Cavasonza, L., Alpat, B., et al. 2019a, Phys. Rev. Lett., 122, 101101 [NASA ADS] [CrossRef] [Google Scholar]
- Aguilar, M., Ali Cavasonza, L., Ambrosi, G., et al. 2019b, Phys. Rev. Lett., 122, 041102 [NASA ADS] [CrossRef] [Google Scholar]
- Aharonian, F. A., Akhperjanian, A. G., Barres de Almeida, U., et al. 2008, Phys. Rev. Lett., 101, 261104 [NASA ADS] [CrossRef] [Google Scholar]
- Aharonian, F. A., Akhperjanian, A. G., Anton, G., et al. 2009, A&A, 508, 561 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ambrosi, G., An, Q., Asfandiyarov, R., et al. 2017, Nature, 552, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Atoyan, A. M., Aharonian, F. A., & Völk, H. J. 1995, Phys. Rev. D., 52, 3265 [NASA ADS] [CrossRef] [Google Scholar]
- Bamba, A., Yamazaki, R., Ueno, M., & Koyama, K. 2003, ApJ, 589, 827 [Google Scholar]
- Beck, R. 2001, Space Sci. Rev., 99, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, A. R. 2013, Astropart. Phys., 43, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Blasi, P. 2010, MNRAS, 402, 2807 [Google Scholar]
- Caprioli, D., Blasi, P., & Amato, E. 2009, MNRAS, 396, 2065 [Google Scholar]
- Caprioli, D., Haggerty, C. C., & Blasi, P. 2020, ApJ, 905, 2 [Google Scholar]
- Chevalier, R. A. 1999, ApJ, 511, 798 [Google Scholar]
- Cowsik, R., & Burch, B. 2010, Phys. Rev. D, 82, 023009 [NASA ADS] [CrossRef] [Google Scholar]
- Cristofari, P., Blasi, P., & Caprioli, D. 2021, A&A, 650, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delahaye, T., Lavalle, J., Lineros, R., Donato, F., & Fornengo, N. 2010, A&A, 524, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Diesing, R., & Caprioli, D. 2019, Phys. Rev. Lett., 123, 071101 [Google Scholar]
- Drury, L. O. 1983, Rep. Prog. Phys., 46, 973 [Google Scholar]
- Evoli, C., Blasi, P., Amato, E., & Aloisio, R. 2020, Phys. Rev. Lett., 125, 051101 [Google Scholar]
- Fang, K., Bi, X.-J., & Yin, P.-F. 2018, ApJ, 854, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Ferronato Bueno, E., Derome, L., Genolini, Y., et al. 2024, A&A, 688, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gabici, S., & Aharonian, F. A. 2014, MNRAS, 445, L70 [NASA ADS] [CrossRef] [Google Scholar]
- Ginzburg, V. L., & Ptuskin, V. S. 1976, Rev. Mod. Phys., 48, 2 [Google Scholar]
- Ginzburg, V. L., & Syrovatsky, S. I. 1961, Prog. Theor. Phys. Suppl., 20, 1 [CrossRef] [Google Scholar]
- Grenier, I. A. 2000, A&A, 364, L93 [NASA ADS] [Google Scholar]
- Jones, F. C., Lukasiak, A., Ptuskin, V., & Webber, W. 2001, ApJ, 547, 264 [Google Scholar]
- Kang, H. 2011, JKAS, 44, 49 [NASA ADS] [Google Scholar]
- Kang, H., Ryu, D., & Jones, T. W. 2009, ApJ, 695, 1273 [NASA ADS] [CrossRef] [Google Scholar]
- Kardashev, N. S. 1962, Sov. Astron., 6, 317 [NASA ADS] [Google Scholar]
- Kobayashi, T., Komori, Y., Yoshida, K., & Nishimura, J. 2004, ApJ, 601, 340 [NASA ADS] [CrossRef] [Google Scholar]
- Lipari, P. 2019, Phys. Rev. D, 99, 043005 [NASA ADS] [CrossRef] [Google Scholar]
- Longmore, S. N., Kruijssen, J. M. D., Bastian, N., et al. 2014, eds. H. Beuther, et al. Protostars and Planets VI (Tucson, AZ: Univ. of Arizona Press), 291 [Google Scholar]
- Morlino, G., & Celli, S. 2021, MNRAS, 508, 6142 [NASA ADS] [CrossRef] [Google Scholar]
- Ohira, Y., & Yamazaki, R. 2017, JHEAp, 13, 17 [Google Scholar]
- Ohira, Y., Murase, K., & Yamazaki, R. 2010, A&A, 513, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reynolds, S. P. 2008, ARA&A, 46, 89 [Google Scholar]
- Reynolds, S. P., & Keohane, J. W. 1999, ApJ, 525, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Schlickeiser, R., & Ruppel, J. 2010, New J. Phys., 12, 033044 [Google Scholar]
- Schroer, B., Pezzi, O., Caprioli, D., Haggerty, C., & Blasi, P. 2021, ApJ, 914, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Schroer, B., Pezzi, O., Caprioli, D., Haggerty, C., & Blasi, P. 2022, MNRAS, 512, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Strong, A. W., Porter, T. A., Digel, S. W., et al. 2010, ApJ, 722, L58 [NASA ADS] [CrossRef] [Google Scholar]
- Sturner, S. J., Skibo, J. G., Dermer, C. D., & Mattox, J. R. 1997, ApJ, 490, 619 [NASA ADS] [CrossRef] [Google Scholar]
- Thoudam, S., & Hörandel, J. R. 2011, MNRAS, 414, 1432 [NASA ADS] [CrossRef] [Google Scholar]
- Thoudam, S., & Hörandel, J. R. 2012, MNRAS, 419, 624 [CrossRef] [Google Scholar]
- Thoudam, S., & Hörandel, J. R. 2013, MNRAS, 435, 2532 [NASA ADS] [CrossRef] [Google Scholar]
- Thoudam, S., Rachen, J. P., van Vliet, A., et al. 2016, A&A, 595, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Unger, M., & Farrar, G. R. 2024, ApJ, 970, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Weaver, R., McCray, R., Castor, J., Shapiro, P., & Moore, R. 1977, ApJ, 218, 377 [Google Scholar]
- Yamazaki, R., Ohira, Y., Sawada, M., & Bamba, K. A. 2014, RAA, 14, 165 [NASA ADS] [Google Scholar]
- Zang, X., & Liu, S. 2019, ApJ, 876, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Zeng, H., Xin, Y., & Liu, S. 2019, ApJ, 874, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Zirakashvili, V. N., & Aharonian, F. A. 2007, A&A, 465, 695 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Model parameters (f, Γ, E0, r0) and their ranges considered in the fitting procedure.
Best-fit values of the model parameters (f, Γ, E0, r0) and the χ2 values of the fits.
All Figures
 |
Fig. 1. Fit to the CR electron plus positron data from the DAMPE (Ambrosi et al. 2017) and the H.E.S.S. (Aharonian et al. 2008) experiments for the (20 − 3500) GeV fit range for different scenarios of the spectral beak: missing sources (top left), exponential cutoff (top right), super-exponential cutoff (bottom left), and broken power-law (bottom right). Line representation: best-fit electron plus positron spectrum (thick solid line), electron spectrum (dashed line) and positron spectrum (thin solid line). The positron spectrum and its data are from AMS-02 measurements (Aguilar et al. 2019b). The fits exclude the three highest energy data points. The best-fit values of the model parameters are listed in Table 2. |
| In the text | |
 |
Fig. 2. Comparison of the best-fit electron plus positron spectra of the different scenarios for the two different fit ranges: (20 − 3500) GeV (left) and (100 − 3500) GeV (right). Line representation: missing sources (green line), exponential cutoff (black line), broken power-law (thick red line), and super-exponential cutoff (blue line). For the (20 − 3500) GeV fit, the best-fit electron plus positron spectra are the same as shown in Fig. 1. The top plots show the spectral fits, and the bottom plots show the fit residuals. Residuals are shown only with respect to the DAMPE data, but the χ2 calculation includes both the DAMPE and the H.E.S.S. data. Filled circles in the residual plots represent data points not included in the fit. The dashed lines represent ±20% residual levels, shown only for reference. The best-fit values of the model parameters and the χ2 values are listed in Table 2. All of the data shown and the positron spectrum (thin red line) are the same as in Fig. 1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



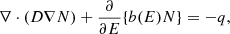
![$$ \begin{aligned} b(E)=\frac{4}{3}\sigma _{\rm T}c\left(\frac{E}{m_{\rm e}c^2}\right)^2\left[U_{\rm B}+\sum _{i=1}^4\frac{W_{\rm i}E_{\rm i}^2}{E^2+E_{\rm i}^2}\right], \end{aligned} $$](/articles/aa/full_html/2024/10/aa48607-23/aa48607-23-eq2.gif)
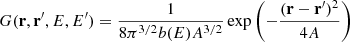
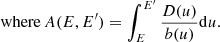
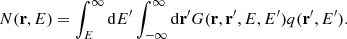
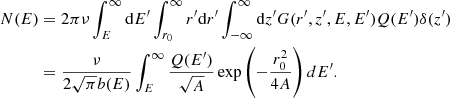
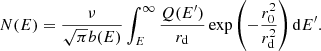
![$$ \begin{aligned} A(E,E^\prime )= \frac{1}{1-a}\left[D(E)t_{\rm loss}(E)-D(E^\prime )t_{\rm loss}(E^\prime )\right], \end{aligned} $$](/articles/aa/full_html/2024/10/aa48607-23/aa48607-23-eq9.gif)
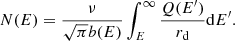
![$$ \begin{aligned} f_0(E)\propto \exp \left\{ -q\int ^E \frac{1}{1-\exp \left[-\frac{uL}{D_{\rm s}(E^\prime )}\right]}d\log E^\prime \right\} , \end{aligned} $$](/articles/aa/full_html/2024/10/aa48607-23/aa48607-23-eq14.gif)
![$$ \begin{aligned} f_0(E)\propto K_0(E) \exp \left[-S_0(E)\right], \end{aligned} $$](/articles/aa/full_html/2024/10/aa48607-23/aa48607-23-eq15.gif)
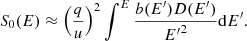
![$$ \begin{aligned} f(E,t)&\propto E^{-(\Gamma +1)}\left[1-\left(1-E/E_0\right)^{\Gamma -1}\right], \; \mathrm{for} \;E < E_0\nonumber \\&\propto E^{-(\Gamma +1)}, \;\mathrm{for} \; E\ge E_0, \end{aligned} $$](/articles/aa/full_html/2024/10/aa48607-23/aa48607-23-eq19.gif)
![$$ \begin{aligned} Q(E)&=kE^{-\Gamma },\,\mathrm {Missing\,sources} \nonumber \\&=kE^{-\Gamma }\exp \left(-\frac{E}{E_0}\right),\,\mathrm {Exponential\,cutoff} \nonumber \\&=kE^{-\Gamma }\exp \left(-\frac{E^2}{E_0^2}\right),\,\mathrm {Super\,exponential\,cutoff} \nonumber \\&=kE^{-\Gamma }\left[1+\left(\frac{E}{E_0}\right)^{1/\delta }\right]^{-\delta },\,\mathrm {Broken\,power\,law} , \end{aligned} $$](/articles/aa/full_html/2024/10/aa48607-23/aa48607-23-eq20.gif)
![$$ \begin{aligned} \chi ^2=\sum _{i}\frac{\left[I_{\rm D}(E_{\rm i})-I_{\rm M}(E_{\rm i})\right]^2}{\sigma _{\rm D}^2(E_{\rm i})} + \sum _{i}\frac{\left[I_{\rm H}(E_{\rm i})-I_{\rm M}(E_{\rm i})\right]^2}{\sigma _{\rm H}^2(E_{\rm i})}, \end{aligned} $$](/articles/aa/full_html/2024/10/aa48607-23/aa48607-23-eq21.gif)
![$$ \begin{aligned} I_{e^+}(E_{\rm i})=\frac{E_{\rm i}^2}{\hat{E}^2}\left[K_1\left(\frac{\hat{E}}{E_1}\right)^{\gamma _1}+K_2\left(\frac{\hat{E}}{E_2}\right)^{\gamma _2} \exp \left(-\frac{\hat{E}}{E_{\rm c}}\right)\right], \end{aligned} $$](/articles/aa/full_html/2024/10/aa48607-23/aa48607-23-eq22.gif)