EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 689 (September 2024) A&A, 689 (2024) A286 Full HTML
Open Access
Issue
A&A
Volume 689, September 2024
Article Number A286
Number of page(s) 7
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/202450444
Published online 20 September 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

Fast radio bursts (FRBs) are radio bursts with a duration of milliseconds discovered more than a decade ago (Lorimer et al. 2007). To date, hundreds of FRBs have been detected at frequencies ranging between 400 MHz–8 GHz by several ground-based radio telescopes (see e.g. CHIME/FRB Collaboration 2021). Some of them have been shown to repeat (Spitler et al. 2016; Kumar et al. 2019; CHIME/FRB Collaboration 2019, 2023). All the observed FRBs have large dispersion measures (DMs), suggesting an extragalactic origin (Lorimer et al. 2007; Thornton et al. 2013; Cordes & Chatterjee 2019). This has been proven by the identification of the host galaxy of FRB 121102, which is characterised by a redshift of z = 0.1932 (Chatterjee et al. 2017; Tendulkar et al. 2017).

The physical origin of FRBs is not established, especially because an observed counterpart at other wavelengths is still lacking (see however DeLaunay et al. 2016). The only exception is the detection of a bright radio burst reported by the CHIME/FRB Collaboration (2020) and by the Survey for Transient Astronomical Radio Emission 2 (STARE2) radio array (Bochenek et al. 2020) that is spatially and temporally coincident with an X-ray burst from the Galactic magnetar SGR 1935+2154 (Mereghetti et al. 2020). This established the first direct link between magnetars and FRBs. Other evidence supporting the magnetar origin for FRBs comes from the properties of the host galaxy of the first repeating FRB 121102 (Tendulkar et al. 2017; Bassa et al. 2017) and the discovery of a persistent radio synchrotron source that is spatially coincident with it (Marcote et al. 2017) and points to a young magnetar born from a catastrophic event, such as superluminous supernovae (SLSNe) and long gamma-ray bursts (GRBs; Metzger et al. 2017; Nicholl et al. 2017). This has been confirmed by FRB 20180916B (Marcote et al. 2020; Tendulkar et al. 2021) and FRB 20201124A (Nimmo et al. 2022), although FRB 20200120E was localised in a globular cluster (Kirsten et al. 2022; Nimmo et al. 2023).

Long and short GRBs have both been suggested to be powered by magnetars (Dai & Lu 1998; Zhang & Mészáros 2001; Corsi & Mészáros 2009; Metzger et al. 2011). This proposition was shown to be very successful in reproducing different observed properties of the X-ray emission of GRBs, at least from a phenomenological point of view (Metzger et al. 2008; Dall’Osso et al. 2011; Bucciantini et al. 2012; Rowlinson et al. 2013; Bernardini et al. 2013; Gompertz et al. 2014; Bernardini 2015; Stratta et al. 2018; Dall’Osso et al. 2023). The merger of binary systems of compact objects that contained at least one neutron star were proven to be the progenitors of short GRBs (Abbott et al. 2017) and the progenitors of at least a fraction of long GRBs (Rastinejad et al. 2022).

Many FRB progenitor models1 recently proposed scenarios that indicate a possible association with GRBs. These models can be grouped into two main categories: non-catastrophic models (mainly related to repeating FRBs) and catastrophic models (mainly related to non-repeating FRBs). Non-catastrophic models include magnetar flares (e.g. Kulkarni et al. 2014; Margalit & Metzger 2018; Dall’Osso et al. 2024) and giant pulses from neutron stars (Cordes & Wasserman 2016), and catastrophic models include the collapse of supramassive neutron stars (Zhang 2014; Falcke & Rezzolla 2014; Punsly & Bini 2016) and the merger of compact stars (Liu et al. 2016). Depending on the scenario considered, the FRB could occur from milliseconds before to up to years after the GRBs.

Several searches for a systematic association of FRBs with GRBs have been performed in the last years (e.g. Martone et al. 2019; Guidorzi et al. 2020; Curtin et al. 2023; Ashkar et al. 2023), and only two possible associations were found so far: FRB 20171209 with the long GRB 110715A, whose afterglow is consistent with being powered by a magnetar (Wang et al. 2020), and FRB 20190309A with the short GRB 060502B (Lu et al. 2024). The lack of other coincident detections might be due to the sensitivity of high-energy instruments (e.g. Guidorzi et al. 2020; Mereghetti et al. 2021) or to different beaming angles for the radio and high-energy emission (e.g. Sridhar et al. 2021).

In this work, we perform a new systematic search for a GRB-FRB association using the most recent catalogue of FRBs, which collects data obtained with the Canadian Hydrogen Intensity Mapping Experiment (CHIME) instrument, and the sample of all GRBs detected by Swift so far. We used the precise localisation of GRB afterglows in our search, and we allowed a few years of time delay between a GRB and an FRB. The paper is organised as follows: in Sect. 2 we describe our search method and the results we found; in Sect. 3 we assess the significance of the results of our search to confirm or exclude the association between GRBs and FRBs; and finally, we discuss in Sect. 4 our results and summarize our conclusions.

2. Search for an association between gamma-ray bursts and fast radio bursts using archival data

We searched for possible associations between GRBs and FRBs using currently available catalogues.

2.1. Cross-match between GRB and FRB catalogues

We selected2 all the GRBs (both short and long) that were detected by the Neil Gehrels Swift Observatory (Swift) until March 2023 for which there is an X-Ray Telescope (XRT) detection and for which based on this, the position is available with an accuracy σGRB ≲ 5″ (1276 GRBs). We also drew from this sample a subsample of GRBs for which a reliable redshift measurement was available (400 GRBs). In order to extend the time window of the research, we also considered a sample of pre-Swift GRBs from BeppoSAX, the High Energy Transient Explorer II (HETE-II), and the INTErnational Gamma-Ray Astrophysics Laboratory (INTEGRAL), which have a localisation with an accuracy of σGRB < 10″ and a redshift (32 GRBs; the first is GRB 970228).

We considered all the FRBs from the FRBSTATS Catalogue3 (Spanakis-Misirlis 2021) available until March 2023 (828 FRBs; the last is FRB 20221128A), both repeating and not-repeating. From these, we selected the FRBs with an accuracy in the localisation4σFRB ≤ 30′ (633 FRBs).

We then searched for any Swift GRB that is spatially coincident with an FRB from the two samples described above, without any further restriction. In order to have a coincidence, we required that the distance between the two is smaller than 3σ, with 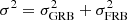σ 2 = σ GRB 2 + σ FRB 2 $ \sigma^2=\sigma_{\rm GRB}^2+\sigma_{\rm FRB}^2 $, and in any case, not larger than 30′. We find 28 matches. However, the most likely scenarios are that the FRB is either coincident or follows the GRB event.

When we concentrate on the cases in which the FRB follows the GRB event, we find 21 the positive matches. These are shown in Fig. 1 and listed in Table A.1. All the positive matches involve non-repeating FRBs. In two cases, the same GRB matches two different close-by FRBs (GRB 110223A with FRB 20190519H and FRB 20190609A, and GRB 090813 with FRB 20190425B and FRB 20190609B).

thumbnail Fig. 1.

FRBs and GRBs with a positive match. The GRB names are also shown.

For GRBs with a redshift (6 out of 21 spatially coincident GRBs with an FRB), we can also use the information on the distance and compare it to the inferred redshift of the corresponding FRB, available in the FRBSTATS Catalogue. Specifically, since the FRB redshift is estimated from the DM, we required that the redshift of the GRB is at least lower than the redshift inferred for the FRB. Only two matches satisfy this criterion:

  • (a)

    GRB 110715A, a long GRB at zGRB = 0.82, and FRB 20171209A5, a non-repeating FRB discovered by Parkes with an inferred distance of zFRB = 1.17;

  • (b)

    GRB 060502B, a short GRB at an estimated redshift zGRB = 0.287, and FRB 20190309A6, a non-repeating FRB discovered by CHIME with an inferred distance of zFRB = 0.32.

Candidate a was reported by Wang et al. (2020) with a low significance (2.28−2.55σ). This is interesting because based on its characteristics, GRB 110715A was associated with a magnetar central engine (Wang et al. 2020).

Candidate b was also reported before by Lu et al. (2024) with a chance probability of 0.05. The distance between the two events is 13′, which is smaller than 1σ (σ = 21′). In addition, the two events have a very similar redshift. However, the redshift of the GRB is that of a massive red galaxy that was suggested to be its host galaxy using associative and probabilistic arguments (Bloom et al. 2007). This association is debated, especially due to the extremely large offset (Church et al. 2011).

Therefore, we re-analysed the coincidence of the GRB 060502B with the putative host galaxy. We downloaded the candidate field from the Panoramic Survey Telescope and Rapid Response System 1 (Pan-STARRS1) public archive7 in the r band. We computed the probability of a chance coincidence (Pcc) for the putative host galaxy with respect to the best afterglow position for GRB 06052B. Following the prescriptions from O’Connor et al. (2022), given the r-band host magnitude of ∼19.2 mag (AB, hereafter) and the angular separation from the XRT localisation of ∼17.8″, we found that Pcc ≃ 0.10, which is higher than the previous estimate (Bloom et al. 2007). Since the limiting magnitude in the field is ∼23 mag, we cannot exclude other potential fainter hosts, consistent with the best localisation of the GRB. However, Bloom et al. (2007) found no better potential associations in the region even with a deeper image. They reported several sources that are marginally consistent with the XRT position, with magnitudes ranging from 24 to 26 mag, and excluded other possible coincident hosts down to magnitude ∼26.5 mag. The presence of an extremely faint host (> 26.5 mag) beneath the position of the GRB, due to a higher redshift or because it is a red dwarf galaxy, as was recently discussed for a sample of short GRBs by Nugent et al. (2024), cannot be ruled out.

In addition to the low probability of an association between GRB 060502B and the putative host galaxy at z = 0.287, Church et al. (2011) showed that a ≳70 kpc offset would be extremely difficult to attribute to the birth-kick velocity. They proposed a globular cluster nature for the birth site of the compact object binary system, which would guarantee the possibility of observing significantly larger offsets between the birth and merger sites. We also note that according to the short GRB offset sample by Fong et al. (2022), GRB 060502B would be one of the outliers in the offset distribution, with < 1% of the events found at > 70 kpc.

We performed a further search for an association between GRBs and FRBs with the pre-Swift GRBs with redshift, and we found two matches when we only considered the spatial and temporal information:

  • GRB 030226, a long GRB discovered by HETE-II at zGRB = 1.98, and FRB 20190303C, a non-repeating FRB discovered by CHIME with an inferred distance of zFRB = 1.09;

  • GRB 051022, a long GRB discovered by HETE-II at zGRB = 0.81, and FRB 20190608A, a non-repeating FRB discovered by CHIME with an inferred distance of zFRB = 0.68;

However, neither of these matches is confirmed when accounting for the information on the distance, since in both cases, the FRB is closer than the GRB.

2.2. Chance probability of the association between fast radio bursts and gamma-ray bursts

Given the size of the samples of GRBs and FRBs considered in Sect. 2.1, we estimated the probability that a specific number of GRBs and FRBs are associated just by chance. To do this, we proceeded as follows.

We focused on the FRBs that were discovered by CHIME (516 out of the 633 FRBs that we considered in Sect. 2.1) in order to better control the simulations with a homogeneous sample that represents more than 80% of the FRBs of our original sample. We generated a synthetic population of 1276 GRBs and another population of 516 FRBs in the sky. We assumed GRBs and FRBs to have an isotropic and homogeneous distribution in space, and for the FRBs, we restricted our simulations to the northern hemisphere (declination between −11 deg and 90 deg) to take the CHIME observable sky into account (see e.g. CHIME/FRB Collaboration 2021). We assumed that the uncertainty in the localisation for the GRBs is negligible since the mean value of the accuracy in the localisation for the GRBs detected and localised by Swift/XRT is 1.86″. We extracted the uncertainty in the localisation for the FRBs from a Gaussian distribution whose mean (14.9′) and standard deviation (6.2′) were taken from the distribution for the CHIME FRBs with σFRB ≤ 30′. We then assigned to each source a redshift, randomly extracted from the observed redshift distribution of Swift GRBs8 and CHIME FRBs (CHIME/FRB Collaboration 2021). We also assigned to each GRB a random occurrence time between November 20, 2004 (the starting time of Swift operations), and March 21, 2023. For FRBs, we considered a time interval between July 25, 2018, which is the starting date of the CHIME FRB catalogue, and November 28, 2022, which corresponds to the most recently detected FRB reported in the catalogue. To have enough statistics, we performed 105 realisations of these two populations.

For the entire population of GRBs, regardless of the information on the distance, we find that the distribution of the number of matches with FRBs has a mean value of 11.4 (median 11) and a standard deviation of 3.4. When we impose that the FRB follows the GRB, the mean value is 9.8 (median 10) with a standard deviation of 3.1. When we further require that the GRB is closer than the FRB, the mean value of the number of matches is 1.6 (median 1), with a standard deviation of 0.9.

In Sect. 2.1 we found only one match between CHIME FRBs and Swift GRBs when we applied the spatial, temporal, and distance constraints. This is consistent with the expected number of chance coincidences. When we only considered spatial and temporal constraints, the number of matches we found (19 CHIME FRBs) is higher than the expected number of chance coincidences (see Fig. 2), although it is still consistent at the 3σ level with expectations.

thumbnail Fig. 2.

Normalised distribution of the number of chance coincidences between GRBs and FRBs obtained by cross-matching the 105 realisations of GRB and FRB samples when only spatial and temporal constraints (cyan) were applied and when the distance constraint (blue) was also taken into account. The vertical solid lines mark the 3σ confidence interval, and the vertical arrow marks the number of matches using real samples when only spatial and temporal constraints were considered.

3. Can we rule out the association between gamma-ray bursts and fast radio bursts?

Although there is no clear association between GRBs and FRBs, it may be questioned whether this is sufficient to exclude any connection between them. In other words, we need to determine how likely it is to detect an FRB from a GRB under the hypothesis that all GRBs are associated with FRBs.

To answer this question, we started from the assumption that every GRB event is associated with an FRB without choosing an a priori time delay because we did not rely on a specific model, and we estimated the detection rate of this population of FRBs. We only considered non-repeating FRBs because they are more likely related to cataclysmic events of the same type as those that stem from GRBs. The inclusion of repeating FRBs requires a detailed modelling of the energy distribution and time-domain behaviour of bursts from a single source, and a dedicated analysis of the rates expected in this scenario will be investigated in a separate work.

To do this, we generated a synthetic population of 106 FRBs and assigned to each of them (i) a redshift and (ii) a rest-frame isotropic energy.

(i) The redshift was drawn from the redshift distribution of Swift GRBs, and we considered the short and long populations together. This choice was motivated by the fact that we focused on the FRBs that might be associated with GRBs, and these might only represent a subsample of the whole FRB population.

(ii) The rest-frame isotropic energy was drawn from the FRB energy distribution Φ(E). The FRB luminosity and energy distributions were investigated in the past by several authors, and they were typically assumed to follow a Schechter function (Schechter 1976). For instance, Luo et al. (2020) used a heterogeneous sample of 46 FRBs (both repeating and non-repeating) that were observed with different instruments: the Parkes, Arecibo, and Green Bank Telescopes, UTMOST, and the Australian Square Kilometre Array Pathfinder (ASKAP). They measured the FRB luminosity function with a Bayesian approach and took selection effects such as the survey sensitivity into account. Assuming a Schechter function and neglecting the cosmic evolution of FRBs, they found a slope of the luminosity function Φ(L) of 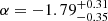α = − 1 . 79 − 0.35 + 0.31 $ \alpha=-1.79^{+0.31}_{-0.35} $ and a lower cut-off luminosity L0 < 9.1 × 1041 erg s−1. Shin et al. (2023) used the full sample of 536 FRBs from the first CHIME catalogue (CHIME/FRB Collaboration 2021). They modelled the FRB energy distribution with a Schechter function and assumed that Φ(E) does not evolve with redshift. They found a differential power-law index of 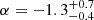α = − 1 . 3 − 0.4 + 0.7 $ \alpha=-1.3^{+0.7}_{-0.4} $ and a characteristic exponential cut-off energy of 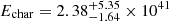E char = 2 . 38 − 1.64 + 5.35 × 10 41 $ E_{\mathrm{char}}=2.38^{+5.35}_{-1.64} \times 10^{41} $ erg. Hashimoto et al. (2022, hereafter H22) used a homogeneous subsample of FRBs from the first CHIME catalogue. They divided the selected FRBs into repeaters and non-repeaters and then into several subsamples, filling different redshift bins that covered the range between 0.05 and 3.6. Because the results may depend on how the redshift bins are selected, they performed their analysis considering two different sets of redshift bins (called redshift A and redshift B) to take this uncertainty into account. They fitted Schechter functions to the derived energy functions and took the redshift evolution into account. They found 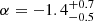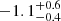α = − 1 . 4 − 0.5 + 0.7 $ \alpha=-1.4^{+0.7}_{-0.5} $ ( − 1 . 1 − 0.4 + 0.6 $ -1.1^{+0.6}_{-0.4} $) for redshift bin A (redshift bin B). Similar results were also presented in other papers (see e.g. Lu & Piro 2019). Despite the different methods and different FRB samples used, the reported results broadly agree within the errors. It is important to note that the observed energy and luminosity distributions were allowed to include the contribution from different FRB populations (e.g. with different progenitors), which might have made individual distributions different from each other.

In this work, we used the energy distribution derived by H22, and, as already mentioned, we considered non-repeating FRBs. Since the redshift range of GRBs is wider than the range considered in H22, we assumed that the energy distribution of FRBs with z < 0.05 (> 3.6) was the same as obtained for the lowest (highest) redshift bin, and we considered redshift A and redshift B cases, with the parameters reported in Table 1 of H22. We focused on the CHIME survey because it currently has the best combination in terms of sensitivity and field of view (fov). We then associated a rest-frame isotropic energy integrated over the bandwidth Δν = 400 MHz (the CHIME frequency width), Erest, 400, with each FRB. We assumed a fiducial value for the minimum FRB rest-frame energy of 1037 ergs, which is the minimum energy of the FRBs in the CHIME catalogue, and a maximum value of 1050 ergs.

From these values, we computed the observed fluence Fν in the CHIME frequency band (400 MHz–800 MHz) as

F ν = ( 1 + z ) 2 − γ E rest , 400 4 π d L 2 ( z ) Δ ν , $$ \begin{aligned} {F_\nu =\frac{(1+z)^{2-\gamma } E_{\mathrm{rest,400}}}{4 \pi d_{\rm L}^{2}(z) \Delta \nu },} \end{aligned} $$(1)

where dL(z) is the luminosity distance at redshift z, estimated with the cosmological parameters from Planck Collaboration XIII (2016), Δν is the frequency bandwidth (taken as 400 MHz), and γ is the FRB spectral index (F ∝ ν−γ), which we assumed to be equal to 1.4 (see e.g. Shin et al. 2023).

Then, to evaluate how many FRBs caused by GRBs can be detected with CHIME, we compared the values of Fν with the completeness threshold (95% c.l.) of Flim = 5 Jy ms to account for the different sources of the sensitivity variation (CHIME/FRB Collaboration 2021). The percentage of simulated FRBs with a fluence greater than Flim = 5 Jy ms is 1% for redshift bin A and 2% for redshift bin B (see Fig. 3, left panel).

thumbnail Fig. 3.

Percentage of simulated FRBs with a fluence greater than or equal to Fν vs. Fν for redshift bin A (in blue) and redshift bin B (in red). Fν has been computed in the CHIME frequency band (left) and at 1.4 GHz (right). The vertical coloured lines mark the position of the assumed fluence threshold for CHIME, Parkes, ASKAP, and SKA1-MID.

We then estimated the detection rate of FRBs associated with GRBs detected by Swift (RFRB) by multiplying these percentages by the Swift average detection rate (85 GRBs yr−1 discovered by BAT and 70 GRBs yr−1 detected also by XRT)9 and an instantaneous fov of 120° ×2° (CHIME/FRB Collaboration 2021), obtaining RFRB = [5 − 11]×10−3 yr−1, where the lower and upper boundaries correspond to redshift bin A and B, respectively (see Table 1). These detection rates were obtained by assuming that each GRB is associated with one FRB, and this implicitly takes into account that there is a model-dependent time delay between the two events. Despite many uncertainties in the modelling of the FRB population and the simplified description of the detection process used, this result shows that the absence of a clear association between FRBs in the current (4 years) CHIME catalogue and Swift GRBs cannot exclude that the two phenomena can have a common progenitor.

Table 1.

Parameters used to estimate the FRB detection rates.

We then performed the same analysis considering Parkes and ASKAP. In this case, we evaluated the detection rates by calculating the observed fluence Fν at 1.4 GHz and comparing it to the completeness threshold (95% c.l.) of Flim = 2 and 26 Jy ms, respectively (Bhandari et al. 2018; Shannon et al. 2018). The percentage of simulated FRBs with a fluence greater than Flim is 0.8% and 0.1% for redshift bin A, and it is 1.7% and 0.3% for redshift bin B (see Fig. 3, right panel).

For Parkes, we considered a duty cycle of 100% and a fov of 0.6 deg2 (Luo et al. 2020) and obtained RFRB = [1 − 2]×10−5 yr−1, where the lower and upper boundaries correspond to redshift bin A and B, respectively. For ASKAP, we considered a duty cycle of 100% and a fov of 150 deg2 (Luo et al. 2020) and obtained RFRB = [4 − 8]×10−4 yr−1, where the lower and upper boundaries correspond to redshift bin A and B, respectively (see Table 1).

It is important to highlight that the rates obtained in this work might underestimate the actual rates because we did not consider the population of repeating FRBs in our analysis. The inclusion of repeating FRBs could increase the detection rates because we would have multiple FRBs for each GRB.

4. Discussion and conclusions

We performed a comprehensive search for a possible association between GRBs and FRBs by cross-matching Swift/GRBs with all the FRBs reported in the FRBSTATS catalogue. We initially applied only spatial and temporal constraints association, and then we also considered the distance information of the subsample of Swift/GRBs with a known redshift. In this last case, we identified two matches: (a) GRB 110715A/FRB 20171209A, and (b) GRB 060502B/FRB 20190309A. In previous searches (Wang et al. 2020), candidate a was reported as a low-significance match. Candidate b was also reported by Lu et al. (2024) with a statistical significance < 3σ. In addition the redshift estimate for the GRB is debated, which further weakens the association. In any case, the number of matches found in our searches is consistent at the 3σ level with the expectations from chance coincidences.

The lacking unambiguous cross-match between the GRB and FRB catalogues does not mean that the two populations are not connected. Even under the hypothesis that all GRBs are associated with non-repeating FRBs and that their collimation is such that it does not prevent a coincident detection (e.g. Sridhar et al. 2021), a survey with the same characteristics as CHIME would take hundreds of years to detect at least one FRB associated with a GRB that was discovered by Swift, as shown in Sect. 3. The expectations are even less promising for other current facilities such as Parkes and ASKAP.

Our results are valid for any delay time between GRBs and FRBs. However, our analysis can only provide constraints on models that predict a time delay between the two events from zero to a few dozen years, assuming a typical expected lifetime of the instruments considered in this work. Much longer time delays cannot be probed with direct observations of the two phenomena.

The Square Kilometre Array (SKA) is a planned large radio interferometer that is designed to operate over a wide range of frequencies, and its sensitivity and survey speed are an order of magnitude greater than those of any current radio telescope. The SKA will comprise two separate arrays, one in Western Australia and the other in South Africa, and it is designed to be built in phases. The first (SKA1) is expected to become fully operational by the late 2020s and consists of three elements: the first element operating at low frequency (SKA1-LOW, [50−350] MHz), the second element at intermediate/high frequency (SKA1-MID, [1.2−1.7] GHz), and the third element will be optimized for surveys (SKA1-survey). For SKA1-MID, considering a completeness threshold of Flim = 0.014 Jy ms (Fender et al. 2015), we obtain RFRB = [1 − 3]×10−3 yr−1, where the lower and upper boundaries correspond to redshift bin A and B, respectively (see Table 1). Therefore, despite its much higher sensitivity, the expectations for a joint detection are comparable to CHIME performances because the fov is smaller. However, we here considered the population of CHIME FRBs as representative of the whole population(s) of FRBs, which is not necessarily the case. With its higher sensitivity, SKA will probe the faint end of the FRB energy distribution and might discover new features that are not accounted for in our model.

The rates were also derived assuming that GRBs are associated with non-repeating FRBs. If instead they were connected with the population of repeaters, we would have multiple FRBs for one GRB, which would accordingly increase the detection probability. As already mentioned in Sect. 3, a dedicated analysis of the rates expected in this scenario will be investigated in a separate work.

Another way to increase the probability of having a joint FRB-GRB detection is a more efficient GRB discovery machine, such as the Transient High Energy Sky and Early Universe Surveyor (THESEUS; Amati et al. 2018). The space mission concept THESEUS was selected by ESA as a candidate mission (launch in 2037) with the aim of exploiting GRBs to study the early Universe and of providing a fundamental contribution to time-domain and multi-messenger astrophysics. THESEUS will detect a factor ∼10 more GRBs than Swift in the redshift range up to ∼2.5 with an accurate localisation in the sky (Ghirlanda et al. 2021), which opens the possibility of observing a GRB associated with a detectable FRB by a facility with the same characteristics as CHIME within a lifetime of ∼10 yr.

4

Although the error regions of FRBs are elliptical, for the well-localised case, the distribution of δ = (σRA − σDec)/σDec has a mean value μδ = 0.15 and standard deviation σδ = 1.1. Thus, in what follows, we approximate the error regions as circular.

Acknowledgments

We acknowledge use of the CHIME/FRB Public Database, provided at https://www.chime-frb.ca/ by the CHIME/FRB Collaboration. We thank Paolo D’Avanzo, Sara Elisa Motta and Sergio Campana for useful discussions.

References

  1. Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2017, ApJ, 848, L13 [CrossRef] [Google Scholar]
  2. Amati, L., O’Brien, P., Götz, D., et al. 2018, Adv. Space Res., 62, 191 [Google Scholar]
  3. Ashkar, H., El Bouhaddouti, M., Fegan, S., & Schüssler, F. 2023, PoS, ICRC2023, 555 [Google Scholar]
  4. Bassa, C. G., Tendulkar, S. P., Adams, E. A. K., et al. 2017, ApJ, 843, L8 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bernardini, M. G. 2015, J. High Energy Astrophys., 7, 64 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bernardini, M. G., Campana, S., Ghisellini, G., et al. 2013, ApJ, 775, 67 [NASA ADS] [CrossRef] [Google Scholar]
  7. Bhandari, S., Keane, E. F., Barr, E. D., et al. 2018, MNRAS, 475, 1427 [Google Scholar]
  8. Bloom, J. S., Perley, D. A., Chen, H. W., et al. 2007, ApJ, 654, 878 [NASA ADS] [CrossRef] [Google Scholar]
  9. Bochenek, C. D., Ravi, V., Belov, K. V., et al. 2020, Nature, 587, 59 [NASA ADS] [CrossRef] [Google Scholar]
  10. Bucciantini, N., Metzger, B. D., Thompson, T. A., & Quataert, E. 2012, MNRAS, 419, 1537 [NASA ADS] [CrossRef] [Google Scholar]
  11. Chatterjee, S., Law, C. J., Wharton, R. S., et al. 2017, Nature, 541, 58 [NASA ADS] [CrossRef] [Google Scholar]
  12. CHIME/FRB Collaboration (Amiri, M., et al.) 2019, Nature, 566, 235 [NASA ADS] [CrossRef] [Google Scholar]
  13. CHIME/FRB Collaboration (Andersen, B. C., et al.) 2020, Nature, 587, 54 [Google Scholar]
  14. CHIME/FRB Collaboration (Amiri, M., et al.) 2021, ApJS, 257, 59 [NASA ADS] [CrossRef] [Google Scholar]
  15. CHIME/FRB Collaboration (Andersen, B. C., et al.) 2023, ApJ, 947, 83 [NASA ADS] [CrossRef] [Google Scholar]
  16. Church, R. P., Levan, A. J., Davies, M. B., & Tanvir, N. 2011, MNRAS, 413, 2004 [NASA ADS] [CrossRef] [Google Scholar]
  17. Cordes, J. M., & Chatterjee, S. 2019, ARA&A, 57, 417 [NASA ADS] [CrossRef] [Google Scholar]
  18. Cordes, J. M., & Wasserman, I. 2016, MNRAS, 457, 232 [NASA ADS] [CrossRef] [Google Scholar]
  19. Corsi, A., & Mészáros, P. 2009, ApJ, 702, 1171 [NASA ADS] [CrossRef] [Google Scholar]
  20. Curtin, A. P., Tendulkar, S. P., Josephy, A., et al. 2023, ApJ, 954, 154 [NASA ADS] [CrossRef] [Google Scholar]
  21. Dai, Z. G., & Lu, T. 1998, A&A, 333, L87 [NASA ADS] [Google Scholar]
  22. Dall’Osso, S., Stratta, G., Guetta, D., et al. 2011, A&A, 526, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Dall’Osso, S., Stratta, G., Perna, R., De Cesare, G., & Stella, L. 2023, ApJ, 949, L32 [CrossRef] [Google Scholar]
  24. Dall’Osso, S., La Placa, R., Stella, L., Bakala, P., & Possenti, A. 2024, ArXiv e-prints [arXiv:2407.04095] [Google Scholar]
  25. DeLaunay, J. J., Fox, D. B., Murase, K., et al. 2016, ApJ, 832, L1 [NASA ADS] [CrossRef] [Google Scholar]
  26. Falcke, H., & Rezzolla, L. 2014, A&A, 562, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Fender, R., Stewart, A., Macquart, J. P., et al. 2015, Advancing Astrophysics with the Square Kilometre Array (AASKA14), 51 [Google Scholar]
  28. Fong, W.-F., Nugent, A. E., Dong, Y., et al. 2022, ApJ, 940, 56 [NASA ADS] [CrossRef] [Google Scholar]
  29. Ghirlanda, G., Salvaterra, R., Toffano, M., et al. 2021, Exp. Astron., 52, 277 [NASA ADS] [CrossRef] [Google Scholar]
  30. Gompertz, B. P., O’Brien, P. T., & Wynn, G. A. 2014, MNRAS, 438, 240 [NASA ADS] [CrossRef] [Google Scholar]
  31. Guidorzi, C., Marongiu, M., Martone, R., et al. 2020, A&A, 637, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Hashimoto, T., Goto, T., Chen, B. H., et al. 2022, MNRAS, 511, 1961 [NASA ADS] [CrossRef] [Google Scholar]
  33. Kirsten, F., Marcote, B., Nimmo, K., et al. 2022, Nature, 602, 585 [NASA ADS] [CrossRef] [Google Scholar]
  34. Kulkarni, S. R., Ofek, E. O., Neill, J. D., Zheng, Z., & Juric, M. 2014, ApJ, 797, 70 [NASA ADS] [CrossRef] [Google Scholar]
  35. Kumar, P., Shannon, R. M., Osłowski, S., et al. 2019, ApJ, 887, L30 [NASA ADS] [CrossRef] [Google Scholar]
  36. Liu, T., Romero, G. E., Liu, M.-L., & Li, A. 2016, ApJ, 826, 82 [NASA ADS] [CrossRef] [Google Scholar]
  37. Lorimer, D. R., Bailes, M., McLaughlin, M. A., Narkevic, D. J., & Crawford, F. 2007, Science, 318, 777 [Google Scholar]
  38. Lu, W., & Piro, A. L. 2019, ApJ, 883, 40 [Google Scholar]
  39. Lu, M.-X., Li, L., Wang, X.-G., et al. 2024, ApJ, 961, 45 [NASA ADS] [CrossRef] [Google Scholar]
  40. Luo, R., Men, Y., Lee, K., et al. 2020, MNRAS, 494, 665 [NASA ADS] [CrossRef] [Google Scholar]
  41. Marcote, B., Paragi, Z., Hessels, J. W. T., et al. 2017, ApJ, 834, L8 [CrossRef] [Google Scholar]
  42. Marcote, B., Nimmo, K., Hessels, J. W. T., et al. 2020, Nature, 577, 190 [NASA ADS] [CrossRef] [Google Scholar]
  43. Margalit, B., & Metzger, B. D. 2018, ApJ, 868, L4 [NASA ADS] [CrossRef] [Google Scholar]
  44. Martone, R., Guidorzi, C., Margutti, R., et al. 2019, A&A, 631, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Mereghetti, S., Savchenko, V., Ferrigno, C., et al. 2020, ApJ, 898, L29 [Google Scholar]
  46. Mereghetti, S., Topinka, M., Rigoselli, M., & Götz, D. 2021, ApJ, 921, L3 [NASA ADS] [CrossRef] [Google Scholar]
  47. Metzger, B. D., Quataert, E., & Thompson, T. A. 2008, MNRAS, 385, 1455 [CrossRef] [Google Scholar]
  48. Metzger, B. D., Giannios, D., Thompson, T. A., Bucciantini, N., & Quataert, E. 2011, MNRAS, 413, 2031 [Google Scholar]
  49. Metzger, B. D., Berger, E., & Margalit, B. 2017, ApJ, 841, 14 [NASA ADS] [CrossRef] [Google Scholar]
  50. Nicholl, M., Williams, P. K. G., Berger, E., et al. 2017, ApJ, 843, 84 [NASA ADS] [CrossRef] [Google Scholar]
  51. Nimmo, K., Hewitt, D. M., Hessels, J. W. T., et al. 2022, ApJ, 927, L3 [NASA ADS] [CrossRef] [Google Scholar]
  52. Nimmo, K., Hessels, J. W. T., Snelders, M. P., et al. 2023, MNRAS, 520, 2281 [NASA ADS] [CrossRef] [Google Scholar]
  53. Nugent, A. E., Fong, W.-F., Castrejon, C., et al. 2024, ApJ, 962, 5 [NASA ADS] [CrossRef] [Google Scholar]
  54. O’Connor, B., Troja, E., Dichiara, S., et al. 2022, MNRAS, 515, 4890 [CrossRef] [Google Scholar]
  55. Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Platts, E., Weltman, A., Walters, A., et al. 2019, Phys. Rep., 821, 1 [NASA ADS] [CrossRef] [Google Scholar]
  57. Punsly, B., & Bini, D. 2016, MNRAS, 459, L41 [NASA ADS] [CrossRef] [Google Scholar]
  58. Rastinejad, J. C., Gompertz, B. P., Levan, A. J., et al. 2022, Nature, 612, 223 [NASA ADS] [CrossRef] [Google Scholar]
  59. Rowlinson, A., O’Brien, P. T., Metzger, B. D., Tanvir, N. R., & Levan, A. J. 2013, MNRAS, 430, 1061 [NASA ADS] [CrossRef] [Google Scholar]
  60. Schechter, P. 1976, ApJ, 203, 297 [Google Scholar]
  61. Shannon, R. M., Macquart, J. P., Bannister, K. W., et al. 2018, Nature, 562, 386 [NASA ADS] [CrossRef] [Google Scholar]
  62. Shin, K., Masui, K. W., Bhardwaj, M., et al. 2023, ApJ, 944, 105 [NASA ADS] [CrossRef] [Google Scholar]
  63. Spanakis-Misirlis, A. 2021, Astrophysics Source Code Library [record ascl:2106.028] [Google Scholar]
  64. Spitler, L. G., Scholz, P., Hessels, J. W. T., et al. 2016, Nature, 531, 202 [NASA ADS] [CrossRef] [Google Scholar]
  65. Sridhar, N., Zrake, J., Metzger, B. D., Sironi, L., & Giannios, D. 2021, MNRAS, 501, 3184 [NASA ADS] [CrossRef] [Google Scholar]
  66. Stratta, G., Dainotti, M. G., Dall’Osso, S., Hernandez, X., & De Cesare, G. 2018, ApJ, 869, 155 [NASA ADS] [CrossRef] [Google Scholar]
  67. Tendulkar, S. P., Bassa, C. G., Cordes, J. M., et al. 2017, ApJ, 834, L7 [NASA ADS] [CrossRef] [Google Scholar]
  68. Tendulkar, S. P., Gil de Paz, A., Kirichenko, A. Y., et al. 2021, ApJ, 908, L12 [CrossRef] [Google Scholar]
  69. Thornton, D., Stappers, B., Bailes, M., et al. 2013, Science, 341, 53 [NASA ADS] [CrossRef] [Google Scholar]
  70. Wang, X.-G., Li, L., Yang, Y.-P., et al. 2020, ApJ, 894, L22 [NASA ADS] [CrossRef] [Google Scholar]
  71. Zhang, B. 2014, ApJ, 780, L21 [Google Scholar]
  72. Zhang, B., & Mészáros, P. 2001, ApJ, 552, L35 [CrossRef] [Google Scholar]

Appendix A: GRBs and FRBs matches

Table A.1.

List of GRBs and FRBs for which a match has been found.

All Tables

Table 1.

Parameters used to estimate the FRB detection rates.

In the text
Table A.1.

List of GRBs and FRBs for which a match has been found.

In the text

All Figures

thumbnail Fig. 1.

FRBs and GRBs with a positive match. The GRB names are also shown.
In the text
thumbnail Fig. 2.

Normalised distribution of the number of chance coincidences between GRBs and FRBs obtained by cross-matching the 105 realisations of GRB and FRB samples when only spatial and temporal constraints (cyan) were applied and when the distance constraint (blue) was also taken into account. The vertical solid lines mark the 3σ confidence interval, and the vertical arrow marks the number of matches using real samples when only spatial and temporal constraints were considered.
In the text
thumbnail Fig. 3.

Percentage of simulated FRBs with a fluence greater than or equal to Fν vs. Fν for redshift bin A (in blue) and redshift bin B (in red). Fν has been computed in the CHIME frequency band (left) and at 1.4 GHz (right). The vertical coloured lines mark the position of the assumed fluence threshold for CHIME, Parkes, ASKAP, and SKA1-MID.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.