EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 686 (June 2024) A&A, 686 (2024) A189 Full HTML
Open Access
Issue
A&A
Volume 686, June 2024
Article Number A189
Number of page(s) 5
Section Numerical methods and codes
DOI https://doi.org/10.1051/0004-6361/202449459
Published online 12 June 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

A fraction of early-type, main sequence stars, with spectral types ranging from B to F, exhibit stable and globally organised magnetic fields on their surfaces (Donati & Landstreet 2009; Wade et al. 2016; Sikora et al. 2019). These fields, ranging in strength from a few hundred G to tens of kG, give rise to inhomogeneous surface chemical distributions (e.g. Kochukhov 2017, and references therein), vertical chemical stratification (e.g. LeBlanc et al. 2009), and radio-emitting magnetospheres (Das et al. 2022). As magnetic stars rotate, their non-uniform surfaces are seen from varying aspect angles by a remote observer, resulting in periodic changes of brightness, broad-band photometric colours, spectral energy distributions, and line profiles.

Two types of direct magnetic field measurements are most commonly applied to detect and characterise magnetic fields of early-type stars. We can analyse Zeeman-induced circular polarisation in spectral lines using photopolarimetric methods (Landstreet 1980; Bohlender et al. 1993), low- (Bagnulo et al. 2002b, 2015), medium- (Monin et al. 2012; Semenko et al. 2022), and high-resolution (Mathys & Hubrig 1997; Wade et al. 2000) spectropolarimetry, deriving the so-called mean longitudinal magnetic field, 〈Bz〉, (Mathys 1991). This magnetic observable corresponds to the weighted average of the line-of-sight component of the stellar magnetic field over the stellar disk. On the other hand, it is also possible to obtain the disk-average absolute value of magnetic field, the mean field modulus, 〈B〉, by measuring separation of the Zeeman-split line components in the optical (Mathys et al. 1997; Mathys 2017) and near-infrared (Chojnowski et al. 2019) high-resolution spectra. In some studies, 〈B〉 was deduced with the help of detailed theoretical line profile modelling, even when no resolved Zeeman components were detectable in stellar spectra (e.g. Kochukhov et al. 2004, 2006, 2013).

Both the mean longitudinal magnetic field, 〈Bz〉, and the mean field modulus, 〈B〉, vary periodically with stellar rotation. The rotational phase curves of 〈Bz〉 and 〈B〉 typically exhibit a smooth single- or double-wave behaviour. This suggests that the global magnetic topologies of early-type stars are dominated by dipolar components. With a few exceptions notwithstanding (Donati et al. 2006; Kochukhov et al. 2011), this conclusion has been reinforced by Zeeman Doppler imaging (ZDI, Kochukhov 2016) studies, where dipolar-like magnetic configurations were retrieved as a result of Stokes profile inversions carried out without any prior assumptions on the global field geometries (e.g. Kochukhov et al. 2014, 2017, 2019, 2023). These observational results, along with theoretical modelling of equilibrium fossil magnetic fields in radiative stellar interiors (Braithwaite & Nordlund 2006; Duez & Mathis 2010), validate the usefulness of dipolar field as a first-order approximation of the surface magnetic field topology of early-type stars.

The most common method for deriving the parameters of dipolar magnetic field, such as the polar strength Bd, involves collecting a large number of 〈Bz〉 and, for a smaller number of targets, 〈B〉 measurements; then the resulting phase curves are fitted with dipolar models (e.g. Landstreet & Mathys 2000; Aurière et al. 2007; Bagnulo et al. 2002a; Sikora et al. 2019; Shultz et al. 2019). This is a time-consuming methodology that requires significant investments of observing time and a prior knowledge of the stellar rotational period. In the present paper, I explore an alternative possibility of constraining Bd using a small number of magnetic measurements. I show that cumulative magnetic observables calculated from a few 〈Bz〉 or 〈B〉 observations can be statistically related to Bd, opening up prospects for estimating dipolar field strength for large stellar samples.

Whenever high-resolution spectropolarimetric data are available, a multitude of diagnostic methods can be applied to extract parameters of global stellar magnetic fields. This includes analyses of higher order moments of Stokes profiles (Mathys 1995), utilising cumulative integral of Stokes V spectra (Kochukhov 2015; Gayley 2017), applying a principal component analysis (Martínez González et al. 2008; Lehmann & Donati 2022), Bayesian inference (Petit & Wade 2012), forward Stokes profile modelling (Bagnulo et al. 2001), and ZDI. These techniques are particularly powerful when applied to Doppler-broadened Stokes profiles of rapidly rotating stars. However, restrictions in terms of stellar parameters and the type of required observational data make these approaches less suitable for large-scale statistical studies compared to traditional 〈Bz〉 diagnostic.

2 Methods and analysis

2.1 Magnetic observables

In situations when the 〈Bz〉 phase curves are incomplete or when considering statistical properties of large stellar samples, a small number of individual longitudinal field measurements cannot be directly used to assess the intrinsic stellar field strength due to a strong rotational phase dependence of 〈Bz〉. To alleviate this problem, it is customary to convert a set of longitudinal field measurements to a cumulative observable known as the root mean square (rms) longitudinal field (Borra et al. 1983; Thompson et al. 1987; Bohlender et al. 1993). This quantity, defined as: 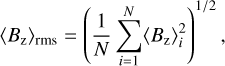(1)

has been catalogued for over a thousand early-type stars (Bychkov et al. 2003, 2009; Hubrig et al. 2006; Romanyuk & Kudryavtsev 2008), including several samples of stars in young open clusters (Semenko et al. 2022; Romanyuk et al. 2023). The field strength statistics based on 〈Bz〉rms has been extensively used to study the origin and evolution of the magnetic fields in the upper main sequence stars (Kochukhov & Bagnulo 2006; Hubrig et al. 2007; Landstreet et al. 2007, 2008) and to assess the overall distribution function of field strengths (Kholtygin et al. 2010; Medvedev et al. 2017; Makarenko et al. 2021).

The equivalent cumulative mean magnetic field modulus observable is the average 〈B〉, 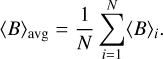(2)

Its usage is somewhat less common in the literature, reflecting a considerably smaller number of stars with 〈B〉 time series compared to repeated 〈Bz〉 observations. Nevertheless, 〈B〉avg has been compiled by several studies (Mathys et al. 1997; Mathys 2017; Chojnowski et al. 2019; Giarrusso et al. 2022), resulting in a data base of over 200 stars.

2.2 Dipolar magnetic field

Assuming a centred dipolar magnetic field geometry with a polar strength, Bd and a linear limb-darkening law specifying variation of the continuum intensity, I, as a function of the cosine, µ, of the limb angle, 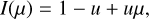(3)

we can derive the following analytical relations for the rotational phase curves of 〈Bz〉 and 〈B〉 (Hensberge et al. 1977; Leroy et al. 1994): 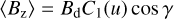(4)

and (5)

Here, the parameters C1–C3 are functions of the linear limb-darkening coefficient, u, 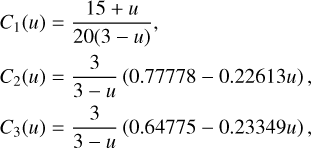(6)

and γ corresponds to the angle between the dipolar field axis and the line of sight. This angle can be calculated, for a spherical stellar surface, from the stellar inclination angle, i, the magnetic obliquity angle, β, and the phase angle, φ as follows: 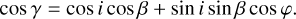(7)

In this equation, the angles i and β can take values in the interval [0, π] and are fixed for a given star, whereas φ varies between 0 and 2π in the course of stellar rotation.

2.3 Numerical simulations

In the present paper, I use numerical simulations to establish statistical relations between 〈Bz〉rms and 〈B〉avg on the one hand and the dipolar field strength, Bd, on the other hand. In these calculations, I employed Eqs. (4) and (5) and postulated an isotropic distribution of the stellar rotational and magnetic axes. This was numerically implemented by sampling i and β according to: (8)

where r1 and r2 are independent random numbers drawn from a uniform distribution between −1 and +1. Another set of uniformly distributed random numbers r3 between 0 and 1 was used to assign N rotational phases, φ = 2πr3. I considered two possibilities for phase sampling. In the first case, all N phases were chosen randomly. In the second case, the first phase was selected randomly and the remaining N – 1 phases were calculated assuming an equidistant phase sampling with a step of 1/N. These two scenarios correspond to the situation when the stellar rotational period is unknown prior to magnetic observations (the first case) and when this period is known and the timing of observations can be planned accordingly (the second case).

I considered N from 1 to 30, performing calculations for 106 random combinations of i, β and one of the two options of defining random sets of ψ angles for each N. Calculations were carried out for a single value of the linear limb-darkening coefficient, u = 0.5. This choice, yielding C1 = 0.310, C2 = 0.798, and C3 = 0.637, roughly corresponds to the V-band continuum limb darkening of a main sequence star with solar metallicity and the A0 spectral type (Claret 2000; Pecaut & Mamajek 2013). The function C1(u) varies by about ±6% around the assumed value for the entire 7000–20 000 K Teff range, where global magnetic fields are typically found in the upper main sequence stars. Considering the linear dependence of 〈Bz〉rms on C1, we can rescale the results presented below for any desired value of u. On the other hand, the functions C2(u) and C3(u) change by less than 1% in the same Teff interval; so their variation with the stellar temperature can be safely neglected.

The resulting probability density functions of the 〈Bz〉rms/Bd and 〈B〉avg/Bd ratios are shown in Fig. 1 for a random sampling and in Fig. 2 for an equidistant rotational phase sampling. The median values of these distributions are plotted as a function of N in Fig. 3 and are reported in Table 1. The numerical results are presented in this table only up to N = 3 for the equidistant phase sampling case since there is no change in the shape of distributions for larger N values. Figures 1–3 and Table 1 also provide confidence intervals containing 68.3%, 95.5%, and 99.7% of the simulation results (i.e. 1-, 2-, and 3-σ intervals of a normal distribution). I note that the N = 1 calculation for both phase sampling cases corresponds to different realisations of essentially the same numerical test. Accordingly, there is no discernible difference between the top panels of Figs. 1 and 2. A small discrepancy in the corresponding numbers in Table 1 reflects numerical uncertainty associated with establishing percentiles for a distribution lacking a well-defined central peak.

thumbnail Fig. 1

Probability distributions of the 〈Bz〉rms/Bd (left column) and 〈B〉avg/Bd (right column) ratios for different number of randomly distributed measurements. The vertical dashed line corresponds to the median of each distribution. The grey rectangles in the background indicate the 1-, 2-, and 3-σ confidence intervals.

3 Discussion

The results presented in the upper panels of Fig. 1 or Fig. 2 demonstrate that a single measurement of either 〈Bz〉 or 〈B〉 is difficult to relate to Bd. The distribution of 〈Bz〉rms/Bd is flat between 0 and 0.31, indicating that a more appropriate interpretation of a single 〈Bz〉 data point is calculating a lower limit Bd ≥ |〈Bz〉|/C1 or Bd ≥ 3.226|〈Bz〉| for the present choice of the limb-darkening coefficient u = 0.5. Similarly, a single 〈B〉 measurement can be interpreted in terms of the upper and lower limits of the dipolar field strength, 1.254 〈B〉 ≤ Bd ≤ 1.569 〈B〉.

By the time the three measurements at random rotational phases become available, the 〈Bz〉rms/Bd and 〈B〉avg/Bd PDFs start resembling a unimodal, normal-like distribution. In fact, 〈Bz〉rms/Bd changes by merely 3% and 〈B〉avg/Bd by less than 1% when going from N = 3 to N = 30. At the same time, the 1-σ confidence intervals shrink by about 40% for both observables, illustrating the benefit of N > 3 measurements. In the limit of a large number of randomly distributed data points, 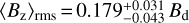and 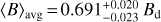, where the quoted uncertainties correspond to the 1-σ confidence intervals. Inverting these numbers yields conversion factors 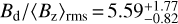and 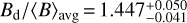, which can be used in the context of large surveys and statistical stellar magnetism studies. In all cases, 〈B〉 observations provide a tighter constraint on Bd than the same number of 〈Bz〉 measurements.

It is interesting to note that in the case of equidistantly spaced observations, the asymptotic 〈Bz〉rms/Bd and 〈B〉avg/Bd ratios determined above are already recovered at N = 3 and do not change with increasing number of measurements. The corresponding confidence intervals do not improve either (see Fig. 3). In this case, the PDFs settle on unimodal, but distinctly asymmetric and non-Gaussian probability distributions. Another way to arrive at these distributions is to replace the sums in Eqs. (1) and (2) with an integral over φ, yielding: 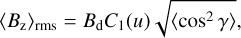(9) (10)

with the phase-averaged cos2 γ and sin2 γ functions given by (11) (12)

and the angles i, β sampled with isotropic distributions as before.

For completeness, I also calculated the ratio of the rms longitudinal field to the average field modulus, 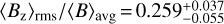, valid for N = 30 in the first phase sampling case and N ≥ 3 in the second one. This corresponds to the conversion 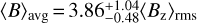, which could be used to obtain from 〈Bz〉rms a representative average field strength parameter rather than its extreme value at the magnetic poles.

The importance of spreading out a few magnetic measurements over stellar rotational cycle is a noteworthy conclusion of the present study. The perfectly equidistant sampling considered for the calculations in Sect. 2.3 is evidently an idealisation. Nevertheless, it is not too distant from reality since the information on rotational periods of early-type stars is readily available at present from decades of ground-based photometric observations (e.g. Hümmerich et al. 2016; Netopil et al. 2017; Bernhard et al. 2020) and from the high-precision spaceborne light curves (Wraight et al. 2012; Cunha et al. 2019; Holdsworth et al. 2021, 2024). It is therefore feasible to carefully plan magnetic observations of stars with known rotational properties, thereby minimising the number of required data points.

thumbnail Fig. 2

Same as Fig. 1, but for measurements equidistant in rotational phase.
Table 1

Median values and confidence intervals for the 〈Bz〉rms/Bd and 〈B〉avg/Bd ratio distributions for different number of magnetic measurements distributed randomly and equidistantly in rotational phase.

thumbnail Fig. 3

Median values (solid red line) and the 1-, 2-, and 3-σ confidence intervals (grey outlines) of the 〈Bz〉rms/Bd (top row) and 〈B〉avg/Bd (bottom row) ratios as a function of the number of magnetic measurements distributed randomly (left column) and equidistantly (right column) in the rotational phase.

Acknowledgements

I acknowledge support by the Swedish Research Council (grant agreement nos. 2019-03548 and 2023-03667), the Swedish National Space Agency, and the Royal Swedish Academy of Sciences. This research was also partly supported by the Munich Institute for Astro-, Particle and Bio–Physics (MIAPbP) which is funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy – EXC–2094 – 390783311.

References

  1. Aurière, M., Wade, G. A., Silvester, J., et al. 2007, A&A, 475, 1053 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Bagnulo, S., Wade, G. A., Donati, J.-F., et al. 2001, A&A, 369, 889 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Bagnulo, S., Landi Degl’Innocenti, M., Landolfi, M., & Mathys, G. 2002a, A&A, 394, 1023 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Bagnulo, S., Szeifert, T., Wade, G. A., Landstreet, J. D., & Mathys, G. 2002b, A&A, 389, 191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Bagnulo, S., Fossati, L., Landstreet, J. D., & Izzo, C. 2015, A&A, 583, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Bernhard, K., Hümmerich, S., & Paunzen, E. 2020, MNRAS, 493, 3293 [NASA ADS] [CrossRef] [Google Scholar]
  7. Bohlender, D. A., Landstreet, J. D., & Thompson, I. B. 1993, A&A, 269, 355 [Google Scholar]
  8. Borra, E. F., Landstreet, J. D., & Thompson, I. 1983, ApJS, 53, 151 [NASA ADS] [CrossRef] [Google Scholar]
  9. Braithwaite, J., & Nordlund, Å. 2006, A&A, 450, 1077 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Bychkov, V. D., Bychkova, L. V., & Madej, J. 2003, A&A, 407, 631 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Bychkov, V. D., Bychkova, L. V., & Madej, J. 2009, MNRAS, 394, 1338 [NASA ADS] [CrossRef] [Google Scholar]
  12. Chojnowski, S. D., Hubrig, S., Hasselquist, S., et al. 2019, ApJ, 873, L5 [NASA ADS] [CrossRef] [Google Scholar]
  13. Claret, A. 2000, A&A, 363, 1081 [NASA ADS] [Google Scholar]
  14. Cunha, M. S., Antoci, V., Holdsworth, D. L., et al. 2019, MNRAS, 487, 3523 [NASA ADS] [CrossRef] [Google Scholar]
  15. Das, B., Chandra, P., Shultz, M. E., et al. 2022, ApJ, 925, 125 [NASA ADS] [CrossRef] [Google Scholar]
  16. Donati, J.-F., & Landstreet, J. D. 2009, ARA&A, 47, 333 [NASA ADS] [CrossRef] [Google Scholar]
  17. Donati, J. F., Howarth, I. D., Jardine, M. M., et al. 2006, MNRAS, 370, 629 [NASA ADS] [CrossRef] [Google Scholar]
  18. Duez, V., & Mathis, S. 2010, A&A, 517, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Gayley, K. G. 2017, ApJ, 851, 113 [NASA ADS] [CrossRef] [Google Scholar]
  20. Giarrusso, M., Cecconi, M., Cosentino, R., et al. 2022, MNRAS, 514, 3485 [NASA ADS] [CrossRef] [Google Scholar]
  21. Hensberge, H., van Rensbergen, W., Deridder, G., & Goossens, M. 1977, A&A, 61, 235 [NASA ADS] [Google Scholar]
  22. Holdsworth, D. L., Cunha, M. S., Kurtz, D. W., et al. 2021, MNRAS, 506, 1073 [NASA ADS] [CrossRef] [Google Scholar]
  23. Holdsworth, D. L., Cunha, M. S., Lares-Martiz, M., et al. 2024, MNRAS, 527, 9548 [Google Scholar]
  24. Hubrig, S., North, P., Schöller, M., & Mathys, G. 2006, Astron. Nachr., 327, 289 [NASA ADS] [CrossRef] [Google Scholar]
  25. Hubrig, S., North, P., & Schöller, M. 2007, Astron. Nachr., 328, 475 [NASA ADS] [CrossRef] [Google Scholar]
  26. Hümmerich, S., Paunzen, E., & Bernhard, K. 2016, AJ, 152, 104 [CrossRef] [Google Scholar]
  27. Kholtygin, A. F., Fabrika, S. N., Drake, N. A., et al. 2010, Astron. Lett., 36, 370 [NASA ADS] [CrossRef] [Google Scholar]
  28. Kochukhov, O. 2015, A&A, 580, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Kochukhov, O. 2016, in Lecture Notes in Physics, 914, Lecture Notes in Physics, eds. J.-P. Rozelot, & C. Neiner, 177 [NASA ADS] [CrossRef] [Google Scholar]
  30. Kochukhov, O. 2017, A&A, 597, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Kochukhov, O., & Bagnulo, S. 2006, A&A, 450, 763 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Kochukhov, O., Drake, N. A., Piskunov, N., & de la Reza, R. 2004, A&A, 424, 935 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Kochukhov, O., Tsymbal, V., Ryabchikova, T., Makaganyk, V., & Bagnulo, S. 2006, A&A, 460, 831 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Kochukhov, O., Lundin, A., Romanyuk, I., & Kudryavtsev, D. 2011, ApJ, 726, 24 [NASA ADS] [CrossRef] [Google Scholar]
  35. Kochukhov, O., Alentiev, D., Ryabchikova, T., et al. 2013, MNRAS, 431, 2808 [NASA ADS] [CrossRef] [Google Scholar]
  36. Kochukhov, O., Lüftinger, T., Neiner, C., Alecian, E., & MiMeS Collaboration. 2014, A&A, 565, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Kochukhov, O., Silvester, J., Bailey, J. D., Landstreet, J. D., & Wade, G. A. 2017, A&A, 605, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Kochukhov, O., Shultz, M., & Neiner, C. 2019, A&A, 621, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Kochukhov, O., Gürsoytrak Mutlay, H., Amarsi, A. M., et al. 2023, MNRAS, 521, 3480 [NASA ADS] [CrossRef] [Google Scholar]
  40. Landstreet, J. D. 1980, AJ, 85, 611 [NASA ADS] [CrossRef] [Google Scholar]
  41. Landstreet, J. D., & Mathys, G. 2000, A&A, 359, 213 [NASA ADS] [Google Scholar]
  42. Landstreet, J. D., Bagnulo, S., Andretta, V., et al. 2007, A&A, 470, 685 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Landstreet, J. D., Silaj, J., Andretta, V., et al. 2008, A&A, 481, 465 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. LeBlanc, F., Monin, D., Hui-Bon-Hoa, A., & Hauschildt, P. H. 2009, A&A, 495, 937 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Lehmann, L. T., & Donati, J. F. 2022, MNRAS, 514, 2333 [CrossRef] [Google Scholar]
  46. Leroy, J. L., Bagnulo, S., Landolfi, M., & Degl’Innocenti, E. L. 1994, A&A, 284, 174 [Google Scholar]
  47. Makarenko, E. I., Igoshev, A. P., & Kholtygin, A. F. 2021, MNRAS, 504, 5813 [NASA ADS] [CrossRef] [Google Scholar]
  48. Martínez González, M. J., Asensio Ramos, A., Carroll, T. A., et al. 2008, A&A, 486, 637 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Mathys, G. 1991, A&AS, 89, 121 [NASA ADS] [Google Scholar]
  50. Mathys, G. 1995, A&A, 293, 733 [NASA ADS] [Google Scholar]
  51. Mathys, G. 2017, A&A, 601, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Mathys, G., & Hubrig, S. 1997, A&AS, 124, 475 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Mathys, G., Hubrig, S., Landstreet, J. D., Lanz, T., & Manfroid, J. 1997, A&AS, 123, 353 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  54. Medvedev, A. S., Kholtygin, A. F., Hubrig, S., et al. 2017, Astron. Nachr., 338, 910 [NASA ADS] [CrossRef] [Google Scholar]
  55. Monin, D., Bohlender, D., Hardy, T., Saddlemyer, L., & Fletcher, M. 2012, PASP, 124, 329 [NASA ADS] [CrossRef] [Google Scholar]
  56. Netopil, M., Paunzen, E., Hümmerich, S., & Bernhard, K. 2017, MNRAS, 468, 2745 [NASA ADS] [CrossRef] [Google Scholar]
  57. Pecaut, M. J., & Mamajek, E. E. 2013, ApJS, 208, 9 [Google Scholar]
  58. Petit, V., & Wade, G. A. 2012, MNRAS, 420, 773 [NASA ADS] [CrossRef] [Google Scholar]
  59. Romanyuk, I. I., & Kudryavtsev, D. O. 2008, Astrophys. Bull., 63, 139 [NASA ADS] [CrossRef] [Google Scholar]
  60. Romanyuk, I. I., Moiseeva, A. V., Yakunin, I. A., Aitov, V. N., & Semenko, E. A. 2023, Astrophys. Bull., 78, 36 [NASA ADS] [CrossRef] [Google Scholar]
  61. Semenko, E., Romanyuk, I., Yakunin, I., Kudryavtsev, D., & Moiseeva, A. 2022, MNRAS, 515, 998 [CrossRef] [Google Scholar]
  62. Shultz, M. E., Wade, G. A., Rivinius, T., et al. 2019, MNRAS, 490, 274 [NASA ADS] [CrossRef] [Google Scholar]
  63. Sikora, J., Wade, G. A., Power, J., & Neiner, C. 2019, MNRAS, 483, 3127 [NASA ADS] [CrossRef] [Google Scholar]
  64. Thompson, I. B., Brown, D. N., & Landstreet, J. D. 1987, ApJS, 64, 219 [NASA ADS] [CrossRef] [Google Scholar]
  65. Wade, G. A., Donati, J.-F., Landstreet, J. D., & Shorlin, S. L. S. 2000, MNRAS, 313, 851 [CrossRef] [Google Scholar]
  66. Wade, G. A., Neiner, C., Alecian, E., et al. 2016, MNRAS, 456, 2 [Google Scholar]
  67. Wraight, K. T., Fossati, L., Netopil, M., et al. 2012, MNRAS, 420, 757 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Median values and confidence intervals for the 〈Bz〉rms/Bd and 〈B〉avg/Bd ratio distributions for different number of magnetic measurements distributed randomly and equidistantly in rotational phase.

In the text

All Figures

thumbnail Fig. 1

Probability distributions of the 〈Bz〉rms/Bd (left column) and 〈B〉avg/Bd (right column) ratios for different number of randomly distributed measurements. The vertical dashed line corresponds to the median of each distribution. The grey rectangles in the background indicate the 1-, 2-, and 3-σ confidence intervals.
In the text
thumbnail Fig. 2

Same as Fig. 1, but for measurements equidistant in rotational phase.
In the text
thumbnail Fig. 3

Median values (solid red line) and the 1-, 2-, and 3-σ confidence intervals (grey outlines) of the 〈Bz〉rms/Bd (top row) and 〈B〉avg/Bd (bottom row) ratios as a function of the number of magnetic measurements distributed randomly (left column) and equidistantly (right column) in the rotational phase.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.