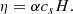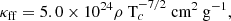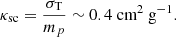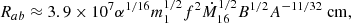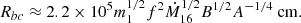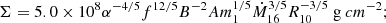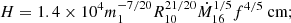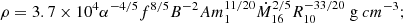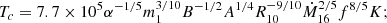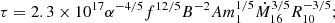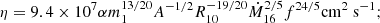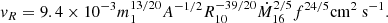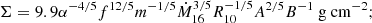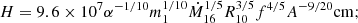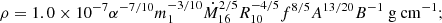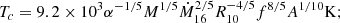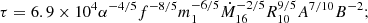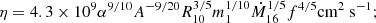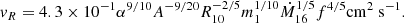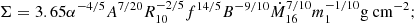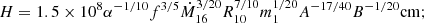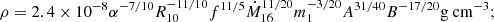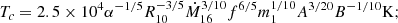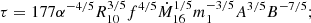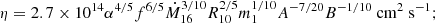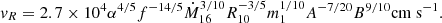| Issue |
A&A
Volume 685, May 2024
|
|
|---|---|---|
| Article Number | A24 | |
| Number of page(s) | 11 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/202348461 | |
| Published online | 30 April 2024 | |
Accretion discs onto supermassive compact objects: A portal to dark matter physics in active galaxies
1
Departamento de Física, Facultad de Ciencias Exactas y Naturales, Universidad de Buenos Aires, Pabellón I, Ciudad Universitaria, 1428 Buenos Aires, Argentina
2
ICRANet, Piazza della Repubbli ca 10, 65122 Pescara, Italy
3
Instituto de Astrofísica de La Plata, UNLP & CONICET, Paseo del Bosque, B1900FWA La Plata, Argentina
e-mail: carguelles@fcaglp.unlp.edu.ar
4
Instituto Argentino de Radioastronomía (IAR, CONICET/CIC/UNLP), C.C.5, (1894) Villa Elisa, Buenos Aires, Argentina
5
Fac. de Ciencias Astron. y Geofísicas, Universidad Nacional de La Plata, Paseo del Bosque, B1900FWA La Plata, Argentina
Received:
1
November
2023
Accepted:
15
February
2024
Context. The study of the physics of the accretion discs that develop around supermassive black hole (BH) candidates provides essential theoretical tools to test their nature.
Aims. Here, we study the accretion flow and associated emission using generalised α-discs accreting onto horizonless dark compact objects in order to make comparisons with the traditional BH scenario. The BH alternative proposed here consists in a dense and highly degenerate core made of fermionic dark matter (DM) and surrounded by a more diluted DM halo. This dense core–diluted halo DM configuration is a solution of Einstein’s equation of general relativity (GR) in spherical symmetry, which naturally arises once the quantum nature of the DM fermions is duly accounted for.
Methods. The methodology followed in this work consists in first generalising the theory of α-discs to work in the presence of regular and horizonless compact objects, and then applying it to the case of core–halo DM profiles typical of active-like galaxies.
Results. The fact that the compactness of the dense and transparent DM core scales with particle mass allows the following key findings of this work: (i) There is always a given core compacity – corresponding particle mass – that produces a luminosity spectrum that is almost indistinguishable from that of a Schwarzschild BH of the same mass as the DM core. (ii) The disc can enter deep inside the non-rotating DM core, allowing accretion-powered efficiencies of as high as 28%, which is comparable to that of a highly rotating Kerr BH.
Conclusions. These results, together with the existence of a critical DM core mass of collapse into a supermassive BH, open new avenues of research for two seemingly unrelated topics: AGN phenomenology and dark matter physics.
Key words: accretion / accretion disks / cosmology: miscellaneous / dark matter
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
One of the central results of the Lambda cold dark matter (ΛCDM) standard cosmological model is the necessity to invoke a dark matter component in the composition of the Universe (Bahcall et al. 1999). However, how this component is distributed on inner galactic scales, and the precise nature and mass of the dark matter particles, are long-standing open questions (Bullock & Boylan-Kolchin 2017). A main available tool to tackle these questions is based on cosmological N-body (classical) simulations with adequate initial conditions; for example the ones provided by the ΛCDM paradigm (see e.g. Ivanov & Simonović 2020 and references therein). Although this paradigm provides a sound explanation as to the distribution of dark matter on large scales (> Mpc), it faces various challenges on short galactic scales (Diemand et al. 2005; Battaglia et al. 2008; Joung et al. 2009; Bullock & Boylan-Kolchin 2017).
Within the framework of cosmological simulations, different state-of-the-art alternatives are being provided in an attempt to solve these problems, including the possibility that cold DM is self-interacting (Kaplinghat & Ren 2020), considering warm instead of cold DM (Bozek et al. 2019), or even abandoning the hypothesis of classical particles by incorporating quantum effects into the simulations (Schive et al. 2014). In an attempt to include the quantum nature of the DM particles explicitly in the physics of the DM halos, an alternative (semi-analytical) approach was recently proposed whereby fermionic DM is considered in a cosmological framework (Argüelles et al. 2021). This addresses the problems of DM halo formation, overall morphology, and stability from first principle physics. In particular, it includes (quantum) statistical mechanics and thermodynamics in the presence of self-gravity, offering solutions to some of the problems that the ΛCDM paradigm faces at short scales (see e.g. Krut et al. 2023; Argüelles & Becerra-Vergara 2023a for a recent work and a review, respectively).
Fermionic mass distributions of this sort are obtained by solving the equations of a self-gravitating system of neutral fermionic (spin 1/2) particles in hydrostatic and thermodynamic equilibrium in general relativity (GR). Some generic solutions to this model have been obtained by various authors aiming to address the problem of DM halos (Chau et al. 1984; Ingrosso & Ruffini 1988; Gao et al. 1990; Chavanis & Sommeria 1998; Bilic et al. 2002; Chavanis 2006; Destri et al. 2013; Argüelles & Ruffini 2014; Ruffini et al. 2015; Chavanis et al. 2015), and just recently a more realistic version of this theory – including particle evaporation and central (fermion) degeneracy – was developed in GR by Argüelles et al. (2018, 2019, 2021) and is referred to here as the (extended) Ruffini-Argüelles-Rueda (RAR) model1. This model implies novel DM density profiles, which self-consistently account for the Pauli exclusion principle, yielding a source of quantum pressure towards the centre of the configurations with key implications for galactic nuclei. The more general DM profiles develop a ‘dense core–diluted halo’ morphology, which, unlike other phenomenological profiles in the literature, depends on the mass of the particle. Remarkably, these fermionic DM halos can explain the galaxy rotation curves in different galaxy types (Argüelles et al. 2018, 2019; Krut et al. 2023), while the degenerate fermion core can mimic their central BHs (Argüelles et al. 2018, 2019, 2022b,a, 2021; Becerra-Vergara et al. 2020; Becerra-Vergara & Argüelles 2021). Moreover, as demonstrated in Argüelles et al. (2021, 2023b,c) based on dynamical and thermodynamical stability criteria in GR, the central DM core can reach a critical mass for collapse and therefore provides a novel channel for supermassive BH formation in the early Universe (see also Chavanis & Alberti 2020; Alberti & Chavanis 2020 for a first dynamical and thermodynamical instability study in GR of the self-gravitating Fermi gas at finite temperature leading to BH formation).
In the present work, we centre our attention on fermionic core–halo profiles applied to typical active-like galaxies, together with their central accretion processes. Our study of the free parameters of the theory (including particle mass) focuses on solutions whose central core has not yet reached the critical mass for collapse, and therefore represents an alternative to the traditional BH scenario. This choice is motivated by our ambition to try to understand the very nature of the massive compact objects at the centres of galaxies, their formation channel, surrounding emission, and finally their relation with the host galaxy and AGN phenomenology.
Motivated by distinct branches of theoretical physics and astrophysics, different alternative models to that of the classical BHs have been proposed (see e.g. Cardoso & Pani 2019 for a review). When dealing with galaxy centres, a typical example studied in the recent past is the boson star (Schunck & Mielke 1999; Torres et al. 2000; Guzmán 2006; Vincent et al. 2016; Olivares et al. 2020), which is a horizonless and massive compact object made of self-gravitating scalar fields. In particular, the different observational signatures of boson stars have been studied, such as the luminosity spectra of α-discs (Guzmán 2006); strong-field images and luminosity patterns in boson stars surrounded by a disc torus (Vincent et al. 2016); and accretion flow via general relativistic magnetohydrodynamic simulations in the space-time of a boson star (Olivares et al. 2020).
In analogy to the above study cases, it is our objective to start a research program for AGN phenomenology dedicated to the RAR model for a self-gravitating system of fermions representing the DM in galaxies. In order to cover the main observational signatures associated with the emission of galaxy centres, we start in this work by studying the accretion of barionic matter onto supermassive compact cores made of fermionic DM, and the corresponding luminosity. To this end, we first extend the standard disc model of Shakura and Sunyaev (Shakura & Sunyaev 1973) in the presence of a fermionic DM distribution using a Keplerian disc and a classical treatment. We are motivated to use fermionic particles because of the numerous efforts made in the last decade to shed light on the nature of such supermassive dark compact objects and the surrounding DM halo in a unified description (Argüelles & Becerra-Vergara 2023a).
The data coming from observational campaigns dedicated to the stellar motions around Sgr A* (Ghez et al. 2005, 2008; Genzel et al. 2010; GRAVITY Collaboration 2018) – confirming the presence of a supermassive compact object – have been used to show that the core–halo RAR solutions accurately reproduce the orbital motion of the S stars, including its relativistic effects (Becerra-Vergara et al. 2020; Becerra-Vergara & Argüelles 2021; Argüelles et al. 2022b). Additionally, observations of the relativistic images using Very Long Base Interferometry (VLBI) in both M87 and the Milky Way (The Event Horizon Telescope Collaboration 2019; Akiyama et al. 2022) can be used to further test the RAR solution, for which it is essential to study the accretion physics in this new paradigm.
The present article is organised as follows: We briefly describe our extended RAR model in Sect. 2. In Sect. 3, we study the efficiency, spectra, and solutions of steady-state thin discs that accrete in the background metric of the RAR model. Finally, in Sect. 4 we present the conclusions we derive from this work.
2. Model
2.1. Extended RAR solution
The RAR model consists in a spherical system of self-gravitating tempered fermions distributed in phase-space according to the following Fermi–Dirac-like distribution function:
where 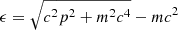 is the particle kinetic energy, μ is the chemical potential with the particle rest-energy subtracted from it, T is the effective temperature, k is the Boltzmann constant, h is the Planck constant, c is the speed of light, and m is the fermion mass. Anti-fermions are not included as temperatures T ≪ mc2/k are considered. The full set of (functional) dimensionless parameters of the model is made up of temperature, degeneracy, and cutoff parameters, β = kT/(mc2), θ = μ/kT, and W = ϵc/(kT), respectively.
is the particle kinetic energy, μ is the chemical potential with the particle rest-energy subtracted from it, T is the effective temperature, k is the Boltzmann constant, h is the Planck constant, c is the speed of light, and m is the fermion mass. Anti-fermions are not included as temperatures T ≪ mc2/k are considered. The full set of (functional) dimensionless parameters of the model is made up of temperature, degeneracy, and cutoff parameters, β = kT/(mc2), θ = μ/kT, and W = ϵc/(kT), respectively.
Interestingly, a coarse-grained phase-space distribution of this kind can be linked with halo formation processes, because it can be obtained from a generalised kinetic theory in the presence of gravity as demonstrated in Chavanis (2004). Indeed, it was shown there that Eq. (1) is a (quasi-) stationary solution of a generalised Fokker-Planck equation for fermions (Chavanis 2004, 2006). Such a kinetic theory includes the physics of violent relaxation appropriate for non-linear structure formation – as originally presented in Lynden-Bell (1967) for classical particles –, though further extended to include particle evaporation and applied to realistic DM halos (Chavanis et al. 2015; Argüelles et al. 2021). This kind of phase-space distributions has been shown to fulfil a maximisation entropy principle during the collisionless relaxation process, until the halo reaches the steady state that is currently observed. More recently, this formation mechanism of fermionic halos was applied in Krut et al. (2023) to a sample of 120 galaxies, and compared with phenomenological profiles as obtained from cosmological N-body simulations.
The corresponding four parametric fermionic equations of state at a given radius r, that is, ρ(β, θ, W, m), P(β, θ, W, m), are directly obtained as the corresponding integrals (bounded from above by ϵ ≤ ϵc) of fc(p). These components are the diagonal part of the stress–energy tensor in the Einstein equations, which are solved under the perfect fluid approximation within a background metric with spherical symmetry, which reads
where (r, Θ, ϕ) are the spherical coordinates, and ν and λ only depend on the radial coordinate r. The system of Einstein equations (i.e. the mass and the Tolman–Oppenheimer–Volkoff equations below) is solved together with the Tolman and Klein thermodynamic equilibrium conditions (involved in Eqs. (5)–(6) below), and (particle) energy conservation along a geodesic (Eq. (7) below). The dimensionless system of highly non-linear ordinary differential equations reads:
where the dimensionless quantities are:  ,
, 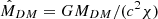 ,
, 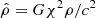 ,
, 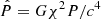 , with χ = 2π3/2(ℏ/(mc))(mp/m) and
, with χ = 2π3/2(ℏ/(mc))(mp/m) and 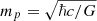 the Planck mass. The system of Eqs. (3)–(7) constitutes a boundary condition problem, which, for fixed DM particle mass m, has to be solved for a given set of free parameters (β0,θ0,W0) defined at the centre of the configuration.
the Planck mass. The system of Eqs. (3)–(7) constitutes a boundary condition problem, which, for fixed DM particle mass m, has to be solved for a given set of free parameters (β0,θ0,W0) defined at the centre of the configuration.
The most general solution results in a degenerate compact core (governed by Pauli degeneracy pressure) surrounded by an extended and more diluted halo (governed by thermal pressure) as detailed in the following section and in Argüelles et al. (2018). The core mass Mc = MDM(rc) is given at the core radius, which is defined as the first maximum of the rotation curve. This latter corresponds to the radius where the central density has decreased by about one-tenth of the central value, which is where fermion degeneracy starts to vanish. In the following section, we show different solutions for well-motivated values of m, with DM core masses and total halo masses typical of active-like galaxies, following Argüelles et al. (2019).
2.2. Application to active-like galaxies
The application of the extended RAR model to large galaxies with dark and regular compact cores reaching mass values of ∼107–108 M⊙ typical of AGN was first shown in Argüelles et al. (2019). This was done for a DM particle mass of m ≈ 50 keV, which was motivated by the excellent results obtained for the Milky Way (Argüelles et al. 2018, 2022b; Becerra-Vergara et al. 2020; Becerra-Vergara & Argüelles 2021), where the corresponding DM core explains the motion of the S-cluster stars around SgrA*. For a similar value of fermion mass, the highly degenerate core reaches the critical mass of collapse 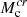 into a supermassive black hole (SMBH) of ≈2 × 108 M⊙ (Argüelles et al. 2021). Particle masses of the order of ∼100 − 350 keV have also been analysed within this DM model with excellent results (see e.g., Argüelles et al. 2018, 2023b). As demonstrated in Argüelles & Ruffini (2014) and Argüelles et al. (2021), the larger the m, the lower the critical core masses
into a supermassive black hole (SMBH) of ≈2 × 108 M⊙ (Argüelles et al. 2021). Particle masses of the order of ∼100 − 350 keV have also been analysed within this DM model with excellent results (see e.g., Argüelles et al. 2018, 2023b). As demonstrated in Argüelles & Ruffini (2014) and Argüelles et al. (2021), the larger the m, the lower the critical core masses 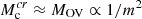 (roughly following the Oppenheimer-Volkoff limit; Oppenheimer & Volkoff 1939), with m ≈ 350 keV leading to a critical mass of a DM core collapsing to a SMBH of ≈4 × 106 M⊙ as for SgrA* (Argüelles et al. 2018; Becerra-Vergara et al. 2020).
(roughly following the Oppenheimer-Volkoff limit; Oppenheimer & Volkoff 1939), with m ≈ 350 keV leading to a critical mass of a DM core collapsing to a SMBH of ≈4 × 106 M⊙ as for SgrA* (Argüelles et al. 2018; Becerra-Vergara et al. 2020).
An important result of the core–halo family of RAR DM profiles for given m, is that it follows different universal scaling relations, such as: the Ferrarese relation (Ferrarese 2002; Bogdán & Goulding 2015), which connects the halo and its supermassive central object masses; the DM surface density relation (Donato et al. 2009), and the radial acceleration relation (McGaugh & Lelli 2016), as shown in Argüelles et al. (2019), Krut et al. (2023). Indeed, in Fig. 1 we show an example of RAR profiles with m = 48 keV (solutions A1 − A3), corresponding to a halo mass window of Mtot ∼ 1011 − 1012 M⊙ and supermassive DM compact objects of masses of Mc ∼ 106 − 108 M⊙, in excellent agreement with the Ferrarese relation (RAR models with m = 200 keV are also in agreement with the correlation, though reach up to Mc ∼ 107 M⊙).
 |
Fig. 1. Core–halo RAR solutions for DM particle mass of mc2 = 48 keV, in agreement with the Ferrarese relation connecting the halo mass with the supermassive central object mass (Ferrarese 2002). |
One of the central objectives of this work is to analyse the accretion power efficiencies and consequent luminosity spectrum caused by supermassive compact objects alternative to BHs. Due to the fact that larger fermion masses imply more compact and denser DM cores at a given core mass (see e.g. Argüelles et al. 2018), we study two different families of profiles here: those with mc2 = 48 keV (which we call RAR model A), and those with mc2 = 200 keV (RAR model B). Table 1 shows the main parameters of the two models: for a typical DM compact-core mass of 107 M⊙, model B2 gives a more compact core than the A2 solution (see Fig. 2 for a comparison of the two profiles). The DM core mass in solution B2 is close to the critical mass of gravitational collapse to a Schwarzschild BH of that mass and therefore implies very similar metric functions (see Fig. 3).
 |
Fig. 2. Density profiles corresponding to a core mass of Mc = 1.0 × 107 M⊙, and particle masses of mc2 = 48 keV (A2, blue) and mc2 = 200 keV (B2, red). These DM halos correspond to typical Elliptical galaxies. |
 |
Fig. 3. Metric components corresponding to the same RAR solutions as in Fig. 2 but with a core mass of Mc = 107 M⊙, and particle masses of mc2 = 48 keV (A2, blue) and mc2 = 200 keV (B2, red). A comparison with the metric of a Schwarzschild BH of mass MBH = 107 M⊙ is also shown (BH, green). |
Main parameters of the different RAR models.
Figure 2 shows the density profiles for models A2 and B2. These clearly demonstrate the existence of compact and massive cores corresponding to the highest density trends, and the diluted halo at larger radii. This is because the system goes from being governed by fermionic degeneracy pressure at small radii to be governed by thermal pressure at larger radii. The density profile therefore transitions from a degenerate core of almost constant density to a Boltzmann-like regime in the outer halo, where the density falls off as a power law followed by an exponential decrease determining the galaxy border.
3. Accretion discs
3.1. Efficiency
There is an essential difference between the Schwarzschild BH solution and the RAR DM model regarding the motion of massive particles in their surroundings. Because the former is a singular solution of the Einstein equations and the latter is not, the existence of the innermost stable circular orbit (ISCO) becomes discernable. Due to the regularity of the central object in the RAR case, there is no critical angular momentum of the particle for which a potential barrier is no longer present, and therefore no ISCO can be reached (Crespi 2022). This behaviour directly implies that the disc has no clear inner boundary2. To set an inner constraint in this regard, we study the binding energy of a test particle in the disc, and analyse when it saturates towards a maximum.
In the case of BHs, the efficiency of the accretion process is related to the binding energy per unit rest mass at the innermost stable circular orbit (ISCO), that is:
where Ec corresponds to the particle’s energy at the last stable circular orbit. This accretion efficiency represents the maximum fraction of the rest mass energy of the accreted particle that can be converted into radiated energy. In standard astrophysical scenarios such as a neutron star of radius ∼10 km, the efficiency is of the order of 10%, while in the case of BH accretion the efficiency varies between 5.7% and 42% for Schwarzschild and Kerr (maximal rotation with a prograde disc) solutions, respectively3 (Novikov et al. 1973). In analogy to the BH case, and in order to define the corresponding accretion efficiency in the RAR model, we seek a maximum in the radial behaviour of the (normalised) binding energy of a test particle. Therefore, in the RAR solution, the binding energy normalised to the rest mass reads
where g00(r) = eν(r) is the temporal component of the metric, and the prime symbol indicates derivation with respect to r. We show this binding energy behaviour in Fig. 4 for the case of a Schwarzschild BH obtained by replacing g00(r) in Eq. (9) by 1 − 2GM/r-, and for two different RAR solutions with the same DM core mass of Mc = MBH = 107 M⊙ but different core compacities. For the RAR solutions, the binding energy asymptotically reaches the maximum as r → 0, and saturates (see definition below) at a given radius rin. The definition for rin implies that it is always smaller than the core radius, with the binding energy remaining approximately constant as the particle’s orbit gets smaller and smaller (i.e. until rmin ∼ 10−7rg ≈ 10−13 pc, the smallest representable radius admitted by computer precision for such core–halo solutions). As the inner radius of the disc, rin, we adopt the value at which the relative error for the change in the maximum efficiency of the binding energy is equal to or lower than 1%, that is
 |
Fig. 4. Accretion efficiencies (labelled with coloured dots) for two different DM core compacities (i.e. different m) with the same core mass of Mc = 107 M⊙ (RAR solutions A2 and B2). For comparison, the case of a Schwarzschild BH with a mass equal to Mc is also shown. Interestingly, solution B2 reaches an accretion efficiency of 14%, which is considerably larger than that of the Schwarzschild BH. |
Adopting this definition, the inner radius typically corresponds to one-tenth of the core radius rin ∼ 0.1rc (for 1% of relative error). In Table 2, we list the values of the inner radius and efficiency for the different RAR models. We compare the efficiencies of the RAR models A2 and B2 (labelled εA2 and εB2 in Fig. 4) with the Schwarzschild efficiency labelled εBH. Remarkably, as the disc can enter deep inside the DM core (i.e. the Keplerian orbits in the disc can have r < rc), the binding energy of RAR solutions with sufficiently compact cores can surpass the maximum Schwarzschild value. Figure 4 shows an example of a subcritical DM core (solution B2) with an efficiency of 14%, to be compared with the 5.7% of the BH case. Moreover, when the degenerate core achieves its critical mass of collapse, the accretion efficiency can be as large as ≈28%, which is similar to that of a highly rotating Kerr BH. This interesting result is not new, and analogous conclusions were obtained for relativistic clusters with constant density and different compacities by Cocco et al. (1995).
rin considered for the different models.
These results, exemplified in Fig. 4, have potential implications for the astrophysics of AGNs. In the context of the Soltan argument (Soltan 1982), and based on observational results regarding the mean accretion efficiency of SMBHs (both from the local and the AGN-relic Universe; Yu & Tremaine 2002; Ueda et al. 2003; Marconi et al. 2004), a mean value of ϵ ≈ 0.1 arises, which falls between that predicted by the Schwarzschild and Kerr BH cases. Additionally, a data analysis of different populations of AGNs showed that the required efficiencies are ϵ > 0.1 (Raimundo & Fabian 2009), with the majority of cases exhibiting ϵ ∼ 0.2-0.3 and the minority reaching down to as low as 0.04 (such low values are compatible with the findings of Marconi et al. 2004). Given these values, the relevance of the results presented here for the accretion efficiencies onto the compact DM cores becomes clear: depending on the compacity of the fermion core, the efficiency can go from below the typical Schwarzschild case up to values of larger than 0.1, which is typical of Kerr BHs. Further discussions about the challenges faced in observationally confirming the Kerr BH space-time at galaxy centres – which are mainly related to degeneracy in models regarding the mass of the compact object, and in particular the spin parameter and possible deviations from the Kerr metric – can be found in Bambi (2017).
3.2. The steady standard disc model embedded in DM
In this section, we consider the model of steady thin discs developed by (Shakura & Sunyaev 1973), and extend it to be applied in the context of RAR solutions. To this end, and following the treatment presented in Frank et al. (2002), we use cylindrical polar coordinates (r, ϕ, z), and assume that matter is very close to the plane z = 0, and is rotating with an angular velocity Ω(r) that remains very close to the Keplerian value:
Here, M(r) is the mass distribution of the DM core–halo solution contained up to r. The circular velocity is given by vϕ = rΩK(r).
In addition, the gas is assumed to possess a small radial ‘drift’ velocity vR(r), which is negative near the central object so that matter is accreted. The disc is characterised by its surface density Σ(r), which is the mass per unit surface area of the disc, given by integrating the gas density ρ in the z-direction. For a steady disc, the conservation of mass and angular momentum can be written as:
respectively. Here, Ṁ is the accretion rate (in units of g s−1), η is the cinematic viscosity, rin is the internal radius of the disc (see Sect. 3.1), and Min = M(rin).
In analogy to the BH case, we engineer the viscous torques to vanish at the maximum of the binding energy, which in the case of the RAR model corresponds to the inner radius rin. This allows us to explicitly obtain the viscous dissipation per unit disc face area, as
It can be seen that, as in the standard solution, the viscous dissipation is independent of the physical nature of the viscosity η. Finally, the total disc luminosity is obtained by integrating D(r) along the disc area.
We also consider an optically thick disc in the z-direction, and therefore each element of the disc radiates as a black body with temperature T(r), given by the equation of the viscous dissipation per unit disc face area D(r) = σT4(r), where σ is the Stefan-Boltzmann constant. Figure 5 shows a comparison between the A and B RAR models and a BH of M ∼ 107 M⊙.
 |
Fig. 5. Comparison of disc temperatures for the A and B RAR models with that of a BH with a mass of MBH ∼ 107 M⊙. The dots indicate the location of the Rc for each RAR model. |
For an observer at a distance d from the centre of the disc, whose line of sight makes an angle i with respect to the normal of the disc plane, the flux at frequency ν is
The outer radius rout can be estimated using the condition that the disc becomes locally self-gravitating (Bogdán & Goulding 2015). This is determined by analysing the stability criterion for a differential rotation disc:
where Ω is the angular velocity given in Eq. (11). The condition QT = 1 defines the self-gravitating disc:
Knowing the density of the accretion disc, the outer radius can be determined. Further details are discussed in Appendix A, where we obtain rout ≈ 103rg − 104rg, depending on the model studied. Nevertheless, the disc beyond 103rg does not contribute significantly to the total luminosity, and therefore we adopt this value as the outer limit for all models.
Figure 6 shows the luminosities obtained for models A and B. In all cases, we consider Ṁ = 0.1 ṀEdd, where ṀEdd is the Eddington accretion rate, defined as the accretion rate at which the compact source radiates at an efficiency of ϵ ∼ 0.1 of the Eddington luminosity, that is ṀEdd = LEdd/ϵc2 ∼ 1.4 × 1016(Mc/M⊙) erg s−1. Moreover, we show the comparison with a black hole of M ∼ 107 M⊙. See also points (ii) and (iii) in Sect. 4 for a relevant discussion regarding the RAR model predictions for disc luminosities.
 |
Fig. 6. Comparison of the luminosity for the A and B models with a BH of M ∼ 107 M⊙. |
Figure 7 only shows the luminosity for RAR models with Mc = 107 M⊙, using two values for the fermion mass: mc2 = 48 keV (model A2) and mc2 = 200 keV (model B2); we also compare this result with a disc around a Schwarzschild BH of MBH = Mc. This important result shows that a core compacity (i.e. solution B2) exists at which the luminosity spectrum is almost indistinguishable from that of a Schwarzschild BH of the same mass as the DM core.
 |
Fig. 7. Comparison of the luminosity in the A2 and B2 models and that of a BH of ∼107 M⊙. |
In the standard thin disc model, different hypotheses are considered: the azimuthal velocity vϕ remains close to the Keplerian value; the disc remains thin at all radii (i.e. the height scale H is much smaller than the extent of the disc H ≪ r); and the disc is optically thick in the z-direction. In order to verify that the solutions here obtained for the RAR model are consistent with the above thin disc ansatz, we consider a disc in hydrostatic equilibrium in the z-direction, meaning that there is no flow in the vertical direction. Then, for H ≪ r and 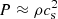 (with cs the sound speed), the solution satisfies:
(with cs the sound speed), the solution satisfies:
The local standard Kepler velocity should be highly supersonic.
If the thin disc condition in Eq. (18) holds, the circular matter velocity vϕ satisfies
It can be seen that vϕ is very close to the Keplerian value, as assumed above. Figure 8 shows both hypotheses for model A2 as an example; though it is satisfied by all solutions, as we have verified.
 |
Fig. 8. Hypothesis validation for model A2: Keplerian velocity must be highly supersonic, while radial velocity must be highly subsonic. Vertical dashed (and doted) lines specify Rab (and Rbc), i.e. the radii at which the behaviour of the disc changes between the inner and intermediate region (and between the intermediate and outer region), respectively (see Appendix A). |
At this point, it is worth emphasising that the complete structure of the disc is not needed in order to compute the spectra for the RAR solutions. However, in order to be able to verify the hypothesis mentioned above, in Appendix A we write out the generalisation of the Shakura & Sunyaev set of equations within the fermionic DM model, and solve for the complete disc structure within the α prescription of the viscosity (see Frank et al. 2002 in order to make the analogous demonstration in the case of the standard α disc theory).
4. Discussion and final remarks
We extended the standard, steady thin disc model in order to study the accretion onto horizonless dark compact objects at the centres of galaxies. The BH alternative investigated here consists in a dense and highly degenerate core made of neutral fermions, surrounded by a more diluted mass distribution that is able to explain the DM halo in galaxies. This dense core–diluted halo DM configuration is known as the RAR model, and is a non-analytic solution of the Einstein equations of GR, which naturally arises once the quantum nature (i.e. Pauli principle) of the fermions is duly accounted for. The attention in this work is focused on active-like galaxies together with their central accretion processes, luminosity spectra, and efficiencies.
We used core–halo RAR solutions for two different fermion masses, 48 keV and 200 keV, the latter corresponding to a very dense DM core with a mass of 107 M⊙, close to its critical value of gravitational collapse to a BH. The fact that, as m increases, the DM-core of given mass becomes more compact (see Fig. 2) makes the above choice particularly relevant to the analysis of how similar the luminosity spectra of α-discs can be to those of a BHs. Moreover, a particle mass falling within this range is totally compatible with both linear structure formation in cosmology and non-linear structure formation, including galaxy rotation curves and scaling relations (see Argüelles & Becerra-Vergara 2023a for a review and references therein).
The main results of our work can be summarised as follows:
-
The fact that the dense DM core is transparent implies that the accretion disc can enter inside reaching down to event-horizon scales. As a consequence, it can achieve accretion efficiencies of as large as ϵ = 28.5%, which is comparable to that of a highly rotating Kerr BH. Figure 4 shows a relevant example comparing a 107 M⊙ Schwarzschild BH with two different RAR solutions of increasing particle mass (A2 and B2) with the same core mass. We show that for m = 48 keV (solution A2) the efficiency is below 1% while for m = 200 keV (solution B2), the stable (i.e. below critical) DM core is compact enough to reach an accretion efficiency at rin < rc that is more than two times that of the BH. The maximum efficiency of ϵ = 28.5% is achieved for the critical core mass. The relevance of achieving Kerr-like efficiencies in active galaxies is supported by observational results (Raimundo & Fabian 2009) based on the Soltan argument.
-
At a given DM core mass Mc, the larger the particle mass, the more compact the degenerate core, and consequently the more luminous and energetic the discs. This result, when considered in light of the efficiency trend explained above, implies that there always exists a given core compacity at which the luminosity spectrum is almost indistinguishable from that of a Schwarzschild BH of the same mass as the DM core. This important RAR model prediction is explicitly shown in Fig. 7 for a BH mass of 107 M⊙, which is typical of an active galaxy.
-
At fixed DM particle mass, it is possible to have different DM core masses Mc (see Table 1) with surrounding DM halos fulfilling the observationally inferred Ferrarese scaling relation (Ferrarese 2002; see Fig. 1 and Argüelles et al. 2019). A novel RAR model prediction found in this work is that when Mc increases, the peak frequency of the luminosity spectra also increases (see e.g. the trend in the red curves B1 and B2 of Fig. 6). This is due to the degeneracy of the core, which implies more compact solutions for more massive cores (at given m). This result is at odds with what is expected from accretion onto a BH, and could be a fundamental tool for testing the RAR model (see discussion below).
Further detailed work is needed in order to differentiate the two above paradigms of supermassive compact objects; for example making use of real spectral energy distributions (SED) of AGNs, or calculating the relativistic images produced by the emitted photons via ray-tracing techniques. The latter is an important project that has already been started by our team, and will allow us to compare observations of the shadow-like features predicted by the RAR model with those predicted by the BH.
Regarding the observational access to SEDs of AGNs relative to this work, the most important is the narrow window of low central-object masses of ∼106 − 107 M⊙ (for the m = 200 keV case), or ∼107 − 108 M⊙ (for m = 48 keV), before the corresponding DM core becomes critical and collapses to a BH4. An eventual observational detection of the luminosity peaks that shift towards higher ν in such a small DM core-mass window is challenging. This is mainly because of the lack of data in the UV band (at about the UV bump) due to the absorption of the IGM; the large error bars at the blue bump; or the fact that most of the observed SEDs are obtained for relatively large central object masses, that is, of > 108 M⊙ (Collinson et al. 2017).
In summary, the original results presented in this work and summarised above may imply an important landmark – and may open new avenues of research – in the field of AGN theory and phenomenology in connection to DM physics and SMBHs.
The term ‘relativistic fermionic King model’ is also used in the literature (Chavanis 2022).
General relativistic simulations of fluid dynamics should be performed to tackle this problem in analogy to boson stars either for unmagnetised (Meliani et al. 2016) or magnetised scenarios (Olivares et al. 2020), though both are out of the scope of this paper.
When considering the effects of the radiation of the disc on the rotation of the black hole, the maximum spin reduces, and the efficiency results in 32.4% (Thorne 1974; Laor & Netzer 1989).
Once the SMBH is formed from DM core collapse, it will grow further via baryonic accretion (Argüelles et al. 2023b) and show the standard spectral energy features.
Acknowledgments
C.R.A. acknowledges supported from CONICET of Argentina, the ANPCyT (grant PICT-2018-03743), and ICRANet. F.L.V. acknowledges support from the Argentine agency CONICET (PIP 2021-0554). V.C. thanks financial support from CONICET, Argentina. M.F.M. acknowledges support from CONICET (PIP2169) and from the Universidad Nacional de La Plata (G168).
References
- Akiyama, K., Alberdi, A., Alef, W., et al. 2022, ApJ, 930, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Alberti, G., & Chavanis, P.-H. 2020, Eur. Phys. J. B, 93, 208 [NASA ADS] [CrossRef] [Google Scholar]
- Argüelles, C. R., & Ruffini, R. 2014, Int. J. Mod. Phys. D, 23, 1442020 [CrossRef] [Google Scholar]
- Argüelles, C. R., Krut, A., Rueda, J. A., & Ruffini, R. 2018, Phys. Dark Univ., 21, 82 [CrossRef] [Google Scholar]
- Argüelles, C. R., Krut, A., Rueda, J. A., & Ruffini, R. 2019, Phys. Dark Univ., 24, 100278 [CrossRef] [Google Scholar]
- Argüelles, C. R., Díaz, M. I., Krut, A., & Yunis, R. 2021, MNRAS, 502, 4227 [CrossRef] [Google Scholar]
- Argüelles, C. R., Becerra-Vergara, E. A., Krut, A., et al. 2022a, Int. J. Mod. Phys. D, 31, 2230002 [CrossRef] [Google Scholar]
- Argüelles, C. R., Mestre, M. F., Becerra-Vergara, E. A., et al. 2022b, MNRAS, 511, L35 [CrossRef] [Google Scholar]
- Argüelles, C. R., Becerra-Vergara, E. A., et al. 2023a, Universe, 9, 197 [CrossRef] [Google Scholar]
- Argüelles, C. R., Boshkayev, K., Krut, A., et al. 2023b, MNRAS, 523, 2209 [CrossRef] [Google Scholar]
- Argüelles, C. R., Rueda, J. A., & Ruffini, R., 2023c ApJ, submitted [arXiv:2312.07461] [Google Scholar]
- Bahcall, N. A., Ostriker, J. P., Perlmutter, S., & Steinhardt, P. J., 1999, Science, 284, 1481 [NASA ADS] [CrossRef] [Google Scholar]
- Bambi, C. 2017, Rev. Mod. Phys., 89, 025001 [NASA ADS] [CrossRef] [Google Scholar]
- Battaglia, G., Helmi, A., Tolstoy, E., et al. 2008, ApJ, 681, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Becerra-Vergara, E. A., Argüelles, C. R., Krut, A., et al. 2020, A&A, 641, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Becerra-Vergara, E. A., Argüelles, C. R., et al. 2021, MNRAS, 505, L64 [NASA ADS] [CrossRef] [Google Scholar]
- Bilic, N., Munyaneza, F., Tupper, G. B., & Viollier, R. D. 2002, Prog. Part. Nucl. Phys., 48, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Bogdán, A., & Goulding, A. D. 2015, ApJ, 800, 124 [CrossRef] [Google Scholar]
- Bozek, B., Fitts, A., Boylan-Kolchin, M., et al. 2019, MNRAS, 483, 4086 [NASA ADS] [CrossRef] [Google Scholar]
- Bullock, J. S., & Boylan-Kolchin, M. 2017, ARA&A, 55, 343 [Google Scholar]
- Cardoso, V., & Pani, P. 2019, Liv. Rev. Relativ., 22, 4 [CrossRef] [Google Scholar]
- Chau, W. Y., Lake, K., & Stone, J. 1984, ApJ, 281, 560 [NASA ADS] [CrossRef] [Google Scholar]
- Chavanis, P.-H. 2004, Phys. A Stat. Mech. Appl., 332, 89 [Google Scholar]
- Chavanis, P. H. 2006, Int. J. Mod. Phys. B, 20, 3113 [NASA ADS] [CrossRef] [Google Scholar]
- Chavanis, P.-H. 2022, Phys. Rev. D, 106, 043538 [NASA ADS] [CrossRef] [Google Scholar]
- Chavanis, P.-H., & Alberti, G. 2020, Phys. Lett. B, 801, 135155 [NASA ADS] [CrossRef] [Google Scholar]
- Chavanis, P. H., & Sommeria, J. 1998, MNRAS, 296, 569 [CrossRef] [Google Scholar]
- Chavanis, P.-H., Lemou, M., & Méhats, F. 2015, Phys. Rev. D, 92, 123527 [NASA ADS] [CrossRef] [Google Scholar]
- Cocco, V., Pascale, E., & Ruffini, R. 1995, Nuovo Cimento B Serie, 110B, 95 [Google Scholar]
- Collinson, J. S., Ward, M. J., Landt, H., et al. 2017, MNRAS, 465, 358 [NASA ADS] [CrossRef] [Google Scholar]
- Crespi, V. 2022, M.sc. Thesis, UNLP. Universidad Nacional de La Plata, Argentina [Google Scholar]
- Destri, C., de Vega, H. J., & Sanchez, N. G. 2013, New Astron., 22, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Diemand, J., Zemp, M., Moore, B., Stadel, J., et al. 2005, MNRAS, 364, 665 [NASA ADS] [CrossRef] [Google Scholar]
- Donato, F., Gentile, G., Salucci, P., et al. 2009, MNRAS, 397, 1169 [Google Scholar]
- Ferrarese, L. 2002, ApJ, 578, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Frank, J., King, A., & Raine, D. J. 2002, Accretion Power in Astrophysics: Third Edition (Cambridge, UK: Cambridge University Press) [Google Scholar]
- Gao, J. G., Merafina, M., & Ruffini, R. 1990, A&A, 235, 1 [NASA ADS] [Google Scholar]
- Genzel, R., Eisenhauer, F., & Gillessen, S. 2010, Rev. Mod. Phys., 82, 3121 [Google Scholar]
- Ghez, A. M., Salim, S., Hornstein, S. D., et al. 2005, ApJ, 620, 744 [NASA ADS] [CrossRef] [Google Scholar]
- Ghez, A. M., Salim, S., Weinberg, N. N., et al. 2008, ApJ, 689, 1044 [Google Scholar]
- GRAVITY Collaboration (Abuter, R., et al.) 2018, A&A, 618, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guzmán, F. S. 2006, Phys. Rev. D, 73, 021501 [CrossRef] [Google Scholar]
- Ingrosso, G., & Ruffini, R. 1988, Nuovo Cimento B Serie, 101, 369 [Google Scholar]
- Ivanov, M. M., Simonović, M., et al. 2020, Phys. Rev. D, 101, 083504 [NASA ADS] [CrossRef] [Google Scholar]
- Joung, M. R., Cen, R., & Bryan, G. L. 2009, ApJ, 692, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Kaplinghat, M., Ren, T., et al. 2020, J. Cosmol. Astropart. Phys., 2020, 027 [CrossRef] [Google Scholar]
- Krut, A., Argüelles, C. R., Chavanis, P. H., et al. 2023, ApJ, 945, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Laor, A., & Netzer, H. 1989, MNRAS, 238, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Lynden-Bell, D. 1967, MNRAS, 136, 101 [Google Scholar]
- Marconi, A., Risaliti, G., Gilli, R., et al. 2004, MNRAS, 351, 169 [Google Scholar]
- McGaugh, S. S., Lelli, F., et al. 2016, Phys. Rev. Lett., 117, 201101 [NASA ADS] [CrossRef] [Google Scholar]
- Meliani, Z., Grandclément, P., Casse, F., et al. 2016, Class. Quant. Grav., 33, 155010 [NASA ADS] [CrossRef] [Google Scholar]
- Novikov, I. D., & Thorne, K. S. 1973, in Black Holes (Les Astres Occlus), eds. C. Dewitt, & B. S. Dewitt, 343 [Google Scholar]
- Olivares, H., Younsi, Z., Fromm, C. M., et al. 2020, MNRAS, 497, 521 [Google Scholar]
- Oppenheimer, J. R., & Volkoff, G. M. 1939, Phys. Rev., 55, 374 [NASA ADS] [CrossRef] [Google Scholar]
- Raimundo, S. I., & Fabian, A. C. 2009, MNRAS, 396, 1217 [CrossRef] [Google Scholar]
- Ruffini, R., Argüelles, C. R., & Rueda, J. A. 2015, MNRAS, 451, 622 [CrossRef] [Google Scholar]
- Schive, H.-Y., Chiueh, T., & Broadhurst, T. 2014, Nat. Phys., 10, 496 [NASA ADS] [CrossRef] [Google Scholar]
- Schunck, F. E., & Mielke, E. W. 1999, GR and Gravitation, 31, 787 [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Soltan, A. 1982, MNRAS, 200, 115 [Google Scholar]
- Thorne, K. S. 1974, ApJ, 191, 507 [Google Scholar]
- The Event Horizon Telescope Collaboration (Akiyama, K., et al.) 2019, ApJ, 875, L1 [Google Scholar]
- Torres, D. F., Capozziello, S., & Lambiase, G. 2000, Phys. Rev. D, 62, 104012 [NASA ADS] [CrossRef] [Google Scholar]
- Ueda, Y., Akiyama, M., Ohta, K., & Miyaji, T. 2003, ApJ, 598, 886 [NASA ADS] [CrossRef] [Google Scholar]
- Vincent, F. H., Meliani, Z., Grandclément, P., Gourgoulhon, E., & Straub, O. 2016, Class. Quant. Grav., 33, 105015 [NASA ADS] [CrossRef] [Google Scholar]
- Yu, Q., & Tremaine, S. 2002, MNRAS, 335, 965 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Local structure of the disc
Here, we present the solution of the complete disc structure. To this end, we consider, as in the standard disc solution, the α− prescription for the viscosity, given by:
The following theoretical content of this Appendix is provided both for completeness and in order to be able to verify the three main hypotheses of the (extended) Shakura & Sunyaev theory: the geometrically thin disc (H(r) < < r) and the Keplerian velocity approximation, together with the optically thick (τ > 1) assumption, for which the solution of the full disc structure is needed. An example of such a verification is shown in Fig. 8 of the main text.
In the thin disc approximation, the determination of the disc structure is simplified. Following Shakura & Sunyaev (1973) and Frank et al. (2002), and using the results obtained in Section 3.2 for the generalised thin disc embedded within the RAR DM distribution, the set of disc equations results in:
-
ρ = Σ/H
-
H =
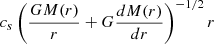 ,
, -
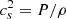 ,
, -
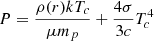 ,
, -
![$ \frac{4\sigma T_c^4}{3\tau} = \frac{3\dot{M}}{8\pi}\frac{GM(r)}{r^3}\left[1-\left(\frac{M_{\rm in}r_{\rm in}}{M(r)r}\right)^{1/2}\right]\left(1-\frac{r}{3M(r)}\frac{dM(r)}{dr}\right) $](/articles/aa/full_html/2024/05/aa48461-23/aa48461-23-eq33.gif) ,
, -
τ = ΣκR(ρ,Tc) = τ(Σ,ρ,Tc),
-
![$ \eta\Sigma = \frac{\dot{M}}{3\pi}\left[1-\left(\frac{M_{\rm in}r_{\rm in}}{M(r)r}\right)^{1/2}\right]\frac{1}{1-\frac{r}{3M(r)}\frac{dM(r)}{dr}} $](/articles/aa/full_html/2024/05/aa48461-23/aa48461-23-eq34.gif) ,
, -
η = η(ρ,Tc,Σ,α,…).
It is worth mentioning that in the limits M(r)→M and 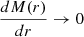 , the standard disc solutions are recovered.
, the standard disc solutions are recovered.
There are three distinct regions in the disc, determined by the relevant absorption mechanism, and the importance of Prad versus Pgas. Regarding the absorption mechanisms, we consider two main processes: free-free absorption, where the opacity is given by (see e.g. Shakura & Sunyaev (1973))
and scattering, where we adopt
The parameterisation of the complete solutions, together with the regions where Pgas dominates over Prad (and vice versa), can be found in Appendix A.
As in the standard solution, there are three distinct regions in the disc: (a) an inner region, where Prad ≫ Pgas and κes ≫ κff, (b) an intermediate region, where Pgas ≫ Prad and κes ≫ κff, and (c) an outer region, where Pgas ≫ Prad and κes ≪ κff. The complete solution of the set of Eqs. 1-8 for the inner, intermediate, and outer regions are presented in Eqs. A.7-A.9, A.14-A.19, and A.20-A.26, respectively. We define R10 = r/(1010cm), m1 = M(r)/M⊙, Ṁ16 = Ṁ/(1016 gs−1), 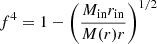 ,
, 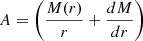 , and
, and 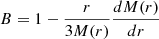 and we consider μ = 0.615 for a fully ionised gas.
and we consider μ = 0.615 for a fully ionised gas.
It is worth noting that the limits 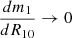 and M(r)→Min recover the standard disc solution around a compact object of a given mass M. Secondly, the α power is of the same order of magnitude as the standard solution. Hence, as α powers are low, the magnitudes calculated for the disc are not sensitive to the value of α.
and M(r)→Min recover the standard disc solution around a compact object of a given mass M. Secondly, the α power is of the same order of magnitude as the standard solution. Hence, as α powers are low, the magnitudes calculated for the disc are not sensitive to the value of α.
The transition radii between the regions result in
Inner region of the disc: Prad ≫ Pgas and κes ≫ κff:
Intermediate region: Pgas ≫ Prad and κes ≫ κff:
Outer region: Pgas ≫ Prad and κes ≪ κff:
We now consider the case of models A2 and B2 described in Table 1. We assume Ṁ = 0.1MEdd ≈ 1.4 × 1023 g s−1, and α = 0.1. We also compare to the standard disc around a Schwarzschild black hole of mass MBH = 107 M⊙.
Fig. A.1 shows the variation of both contributions to the total pressure in the different regions; in an analogous way, in Fig. A.2 we show the absorption coefficients due to scattering and free-free absorption. In both cases, we compare our models (centre and right) to the standard disc around a black hole (left).
 |
Fig. A.1. Variation of the radiation and gas pressures for a disc around a black hole (left), the RAR solution B2 (centre), and the RAR solution A2 (right). Dashed black and grey lines represent the limits of the different regions. |
 |
Fig. A.2. Variation of the absorption coefficients for a disc around a black hole (left), the RAR solution B2 (centre). and the RAR solution A2 (right). Dashed black and grey lines represent the limits of the different regions. |
 |
Fig. A.3. Variation of the opacity for a disc around a black hole (left), the RAR solution B2 (centre). and the RAR solution A2 (right). Dashed black and grey lines represent the limits of the different regions. |
 |
Fig. A.4. Thin disc approximation for a disc around a black hole (left), the RAR solution B2 (centre). and the RAR solution A2 (right). Dashed black and grey lines represent the limits of the different regions. |
An interesting result is obtained when varying the fermion mass from 200 keV to 48 keV (for the same mass of the core, model A2); in this case, only the outer region exists. This is due to the fact that the compacity of the core diminishes for lower masses of the fermion, which allows the disc to reach lower temperatures, as can be seen in Fig. 5.
Using the criterion given by Eq. 17, we can determined the outer radius of the disc. For both, model B2 and the black hole, rout = 1.9 × 1015cm and rout = 1.0 × 1014cm, respectively, which implies rout ≈ 103rg in both cases. It is interesting to analyse model A2, where only the outer region of the disc is present. In this case, we find that the disc becomes self-gravitating at rout = 1.3 × 1016cm ≈ 104rg.
All Tables
All Figures
 |
Fig. 1. Core–halo RAR solutions for DM particle mass of mc2 = 48 keV, in agreement with the Ferrarese relation connecting the halo mass with the supermassive central object mass (Ferrarese 2002). |
| In the text | |
 |
Fig. 2. Density profiles corresponding to a core mass of Mc = 1.0 × 107 M⊙, and particle masses of mc2 = 48 keV (A2, blue) and mc2 = 200 keV (B2, red). These DM halos correspond to typical Elliptical galaxies. |
| In the text | |
 |
Fig. 3. Metric components corresponding to the same RAR solutions as in Fig. 2 but with a core mass of Mc = 107 M⊙, and particle masses of mc2 = 48 keV (A2, blue) and mc2 = 200 keV (B2, red). A comparison with the metric of a Schwarzschild BH of mass MBH = 107 M⊙ is also shown (BH, green). |
| In the text | |
 |
Fig. 4. Accretion efficiencies (labelled with coloured dots) for two different DM core compacities (i.e. different m) with the same core mass of Mc = 107 M⊙ (RAR solutions A2 and B2). For comparison, the case of a Schwarzschild BH with a mass equal to Mc is also shown. Interestingly, solution B2 reaches an accretion efficiency of 14%, which is considerably larger than that of the Schwarzschild BH. |
| In the text | |
 |
Fig. 5. Comparison of disc temperatures for the A and B RAR models with that of a BH with a mass of MBH ∼ 107 M⊙. The dots indicate the location of the Rc for each RAR model. |
| In the text | |
 |
Fig. 6. Comparison of the luminosity for the A and B models with a BH of M ∼ 107 M⊙. |
| In the text | |
 |
Fig. 7. Comparison of the luminosity in the A2 and B2 models and that of a BH of ∼107 M⊙. |
| In the text | |
 |
Fig. 8. Hypothesis validation for model A2: Keplerian velocity must be highly supersonic, while radial velocity must be highly subsonic. Vertical dashed (and doted) lines specify Rab (and Rbc), i.e. the radii at which the behaviour of the disc changes between the inner and intermediate region (and between the intermediate and outer region), respectively (see Appendix A). |
| In the text | |
 |
Fig. A.1. Variation of the radiation and gas pressures for a disc around a black hole (left), the RAR solution B2 (centre), and the RAR solution A2 (right). Dashed black and grey lines represent the limits of the different regions. |
| In the text | |
 |
Fig. A.2. Variation of the absorption coefficients for a disc around a black hole (left), the RAR solution B2 (centre). and the RAR solution A2 (right). Dashed black and grey lines represent the limits of the different regions. |
| In the text | |
 |
Fig. A.3. Variation of the opacity for a disc around a black hole (left), the RAR solution B2 (centre). and the RAR solution A2 (right). Dashed black and grey lines represent the limits of the different regions. |
| In the text | |
 |
Fig. A.4. Thin disc approximation for a disc around a black hole (left), the RAR solution B2 (centre). and the RAR solution A2 (right). Dashed black and grey lines represent the limits of the different regions. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



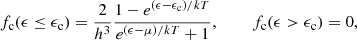
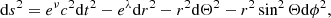
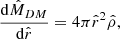
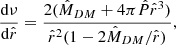
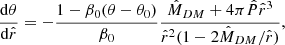
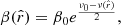
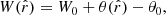
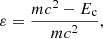
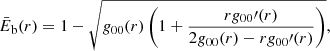
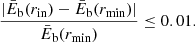
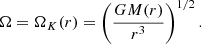
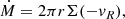
![$$ \begin{aligned} \eta \Sigma = \frac{\dot{M}}{3\pi }\left[1-\left(\frac{M_{\rm in}r_{\rm in}}{M(r)r}\right)^{1/2}\right] \left[1-\frac{r}{3M(r)}\frac{\mathrm{d}M(r)}{\mathrm{d}r}\right]^{-1}, \end{aligned} $$](/articles/aa/full_html/2024/05/aa48461-23/aa48461-23-eq21.gif)
![$$ \begin{aligned} D(r)&=\frac{1}{2}\eta \Sigma \Big (r \frac{\mathrm{d}\Omega }{\mathrm{d}r} \Big )^2\nonumber \\&=\frac{3\dot{M}}{8\pi }\frac{GM(r)}{r^3} \left[1-\left(\frac{M_{\rm in}r_{\rm in}}{M(r)r}\right)^{1/2}\right] \left[1-\frac{r}{3M(r)}\frac{\mathrm{d}M(r)}{\mathrm{d}r}\right]. \end{aligned} $$](/articles/aa/full_html/2024/05/aa48461-23/aa48461-23-eq22.gif)
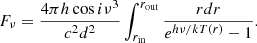
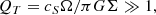
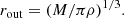
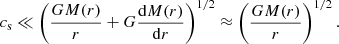
![$$ \begin{aligned} {v}_\phi = \sqrt{\frac{GM(r)}{r}+G\frac{\mathrm{d}M(r)}{\mathrm{d}r}}[1+O(M^{-2})]. \end{aligned} $$](/articles/aa/full_html/2024/05/aa48461-23/aa48461-23-eq28.gif)