EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 682 (February 2024) A&A, 682 (2024) A178 Full HTML
Highlight
Open Access
Issue
A&A
Volume 682, February 2024
Article Number A178
Number of page(s) 9
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/202348578
Published online 21 February 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

Within the population of about 3300 radio pulsars presently known (Manchester et al. 2005), there is a distinct sub-population of six binary systems where a normal (non-recycled) pulsar orbits a massive stellar companion. These binary systems have eccentric orbits with orbital periods on the order of months or years (Kaspi et al. 1996; Lorimer et al. 2006; Shannon et al. 2014) or even decades (Lyne et al. 2015). The secondary stars are O or B stars with masses exceeding 8 M⊙ (Bell et al. 1995; Lyne et al. 2015). For such systems located in our Galaxy, they are characterized by low Galactic latitudes. Table 1 summarises the main properties of the six pulsar and massive star binaries known to date.

Table 1.

The properties of the six currently known pulsar/massive star binaries.

Most of the systems exhibit significant interaction between the pulsar and the stellar wind or disc of the massive stellar companion (Andersen et al. 2023), leading to variations in scattering and dispersion (Madsen et al. 2012), eclipses of the pulsar emission (Wang et al. 2004), and/or X-ray or gamma-ray emission (Aharonian et al. 2005). As a result, these systems serve as exceptional laboratories for investigating binary interactions in stellar disks and winds. They are thought to be possible progenitors of double neutron star systems (Johnston et al. 1994).

The progenitors of these pulsar and massive star binaries are systems composed of two massive main sequence stars. In such systems, no stellar interaction is necessarily required, although it is possible that mass transfer has occurred in systems with small orbital periods. When the primary star undergoes supernova to form the neutron star, it sheds a large portion of its envelope (Matzner & McKee 1999). If a binary system loses more than half of its mass, the system is usually disrupted, because the orbital energy surpasses the binding energy (Hills 1983). Furthermore, asymmetries in the supernova explosion can impart a natal kick to the newborn neutron star and, depending on the velocity (speed and direction) of the kick with respect to the orbital velocity, the binary binding energy can be further altered, possibly counteracting the disruption of the binary or vice versa. In those cases where the binary remains bound, the neutron star will orbit the unaltered massive main sequence star in a wide orbit with high eccentricity (e.g., Brandt & Podsiadlowski 1995).

In 2017, PSR J0210+5845 was discovered as part of the LOFAR Tied-Array All-Sky Survey (LOTAAS), the LOFAR pulsar survey of the northern hemisphere (Sanidas et al. 2019). Tan et al. (2020) showed that initial timing observations revealed significant timing residuals that they argue could be caused by timing noise intrinsic to the pulsar. In this study, we show that the timing residuals are the result of binary motion with an Mc = 3.5–3.8 M⊙ companion in a moderately eccentric, long-period orbit. The PSR J0210+5845 system has the lowest-mass binary companion among known pulsar and massive star binaries, posing a challenge for its survival of the supernova explosion that formed the neutron star.

We present continued timing observations in Sect. 2 that show that the spindown of PSR J0210+5845 can be modelled by several higher order spin frequency derivatives. We find that a V ∼ 13.5 star is coincident with the pulsar timing position, we discuss its properties as the optical counterpart to PSR J0210+5854, and identify it as the binary companion of the pulsar in Sect. 3. In Sect. 4, we use the spin frequency derivatives to obtain orbital constraints and investigate formation scenarios in Sect. 5. We present our discussion and conclusions in Sect. 6.

2. Radio timing

The timing ephemeris of PSR J0210+5845 obtained by Tan et al. (2020), modelling the position, the spin period and its derivative, and the dispersion measure (DM), uses LOFAR observations obtained between December 2017 and December 2018. We extended that timing ephemeris with observations from 2019 to June 2022. All observations of PSR J0210+5845 were obtained with the same observational setup. We used the high-band antennas (HBAs) of the LOFAR core stations, recording dual-polarisation Nyquist sampled complex voltages for 400 subbands of 0.195 MHz bandwidth between 110 and 188 MHz. We followed the analysis procedure outlined in van der Wateren et al. (2023), where we used the LOFAR pulsar pipeline (Kondratiev et al. 2016) to coherently dedisperse and fold the observations with DSPSR (van Straten & Bailes 2011) to create pulse profiles in the PSRFITS1 format with 0.195 MHz channels and 5 second (s) subintegrations. The majority of radio frequency interference (RFI) was automatically removed using CLFD2 (Morello et al. 2019), followed by a manual inspection and RFI removal with the PSRZAP tool from the PSRCHIVE software suite (Hotan et al. 2004) where needed.

We used the timing model from Tan et al. (2020) to fold and dedisperse all observations, which were then fully averaged over time. To obtain a better constraint on the DM, the observations were split into two subbands with centre frequencies 129 and 167 MHz and both subbands were fully averaged in frequency. We combined the observations to one high signal-to-noise (S/N) profile of the full bandwidth, to which we modelled an analytical template profile as the sum of three von Mises functions using PAAS. The averaged observations were cross-correlated with the template to obtain times-of-arrival (TOAs) with PAT.

With PINTK, the interactive module of the pulsar timing package PINT3 (Luo et al. 2021) (v0.9.3), a new timing ephemeris was constructed modelling the celestial position (αJ2000, δJ2000), spin frequency, f, spin frequency derivative, ḟ, and the DM. As indicative in Fig. 1, higher order spin frequency derivatives were required to properly model the spindown behaviour of PSR J0210+5854. 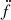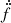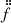We sequentially added spin frequency derivatives beyond ḟ to improve the timing ephemeris and obtained significant measurements for the second, third, and fourth spin frequency derivatives f ¨ $ \ddot{f} $, f ¨ ˙ $ \dot{\ddot{f}} $, and f ¨ ¨ $ \ddot{\ddot{f}} $. Fitting a timing ephemeris that also included a fifth spin frequency derivative in the fit resulted in a value that was not significant (less than 3σ significance). To assess the timing noise using the method from Arzoumanian et al. (1994), we fitted f, ḟ, and 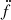f ¨ $ \ddot{f} $, keeping higher order frequency derivatives at zero, over a 108-s segment of the data to calculate 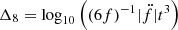Δ 8 = log 10 ( ( 6 f ) − 1 | f ¨ | t 3 ) $ \Delta_8 = \log_{10} \Big((6f)^{-1}|\ddot{f}|t^3\Big) $, with t = 108 s. The obtained value of Δ8 = 1.54 significantly exceeds the expected value for intrinsic timing noise of Δ8 = −1.3 based on the relation from Hobbs et al. (2010), which suggests that the higher order frequency derivatives are not primarily produced by intrinsic timing noise.

thumbnail Fig. 1.

Residuals from timing with one (a), two (b) three (c), and four (d) spin frequency derivatives. The residuals from fitting the model in Table 2 fitting up to and including five spin frequency derivatives are very similar to the residuals shown here.

The higher order spin frequency derivatives up to and including the fifth spin frequency derivative were included in the timing ephemeris. Even though the fifth spin frequency derivative was not significant, it was included due to the informative nature of its uncertainty, particularly in terms of the scale for this parameter, which was used in Sect. 4. The timing model was subsequently refitted for all parameters, resulting in the timing ephemeris shown in Table 2 and the timing residuals in Fig. 1.

Table 2.

Timing parameters for PSR J0210+5845.

To check that there were no unexpected covariances between the parameters in the timing ephemeris, we performed a Bayesian analysis using the Markov chain Monte Carlo (MCMC) fitter from PINT. The standard PINT approach was used by taking normally distributed priors based on the standard PINT fitting results and refitting all parameters in the timing ephemeris using the MCMC fitter. The parameters and their uncertainties are consistent between fitting methods and covariances are generally low except for pairs of odd and even spin frequency derivatives, as expected for a Taylor series.

To investigate any variations in terms of dispersion, we divided the TOAs into segments, each spanning 200 days, which were independently refitted for DM. This analysis revealed a maximum variation of 0.38(49) pc cm−3, with the uncertainty denoting the average error associated with the separately fitted DMs. Refitting the full data set for a time derivative of the DM resulted in 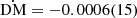DM ˙ = − 0.0006 ( 15 ) $ \dot{\mathrm{DM}}=-0.0006(15) $ pc cm−3 yr−1. Hence, we conclude that PSR J0210+5845 exhibits no significant DM variations among our dataset.

Coincident with the timing position of PSR J0210+5845 is an optical star for which the position and proper motions are documented in the Gaia DR3 catalogue (Gaia Collaboration 2023). In Sect. 3, we identify it as the binary companion of the pulsar. We refit the spin frequency, higher order derivatives of the spin frequency and the DM, incorporating the position and proper motions from the optical counterpart of PSR J0210+5845 as documented in the Gaia DR3 catalogue (Gaia Collaboration 2023). The resulting timing model remained consistent with the model in which the position was fitted and no proper motion was assumed. See Sect. 3 for more information on the optical counterpart.

3. Optical counterpart

A star (V = 13.5, B − V = 0.47; Henden et al. 2015) is located near the radio timing position of PSR J0210+5845. This star is present in many catalogues – for the remainder of the paper, we will refer to it as 2MASS J02105640+5845176 (Skrutskie et al. 2006). The Gaia DR3 (Gaia Collaboration 2023) astrometric solution provides a proper motion of μα cos δ = −1.116(12) mas yr−1 and μδ = −0.495(15) mas yr−1. At the epoch of the pulsar timing ephemeris, the position of this star is 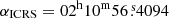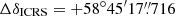α ICRS = 02 h 10 m 56 . s 4094 $ \alpha_{\mathrm{ICRS}}=02^{\mathrm{h}}10^{\mathrm{m}}56{{{\overset{\text{ s}}{.}}}}4094 $, Δ δ ICRS = + 58 ° 45 ′ 17 . ″ 716 $ \Delta \delta_{\mathrm{ICRS}} = +58^\circ45^{\prime}17{{\overset{\prime\prime}{.}}}716 $. This position is offset from the pulsar timing position by 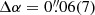Δ α = 0 . ″ 06 ( 7 ) $ \Delta \alpha=0{{\overset{\prime\prime}{.}}}06(7) $ in right ascension and 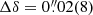Δ δ = 0 . ″ 02 ( 8 ) $ \Delta\delta= 0{{\overset{\prime\prime}{.}}}02(8) $ in declination; hence, it is coincident with the pulsar position as measured through timing.

The parallax of this star has been measured at ϖ = 0.354(15) mas in Gaia DR3. The Gaia GSP-Phot and FLAME modelling combine this parallax with Gaia photometry and stellar models to estimate a distance of d = 2.21 kpc, a nominal effective temperature of Teff = 10 930 K, and a mass of Mc = 3.10 M⊙ (Gaia Collaboration 2023). Similar stellar properties were obtained with the StarHorse Bayesian isochrone-fitting software (Queiroz et al. 2018) by combining the Gaia astrometric and photometric measurements with photometry from Pan-STARRS1, 2MASS, and AllWISE. Results based on Gaia DR2 are presented in Anders et al. (2019) and updated using Gaia EDR3 in Anders et al. (2022). These results are shown in Table 3.

Table 3.

The properties of 2MASS J02105640+584517.

The low-resolution spectroscopy of 2MASS J02105640+5845176 has been obtained as part of the LAMOST survey, which initially classified the star as an A1 V star and estimated a radial velocity of −7.6(5) km s−1 (Xiang et al. 2022). The stellar parameters derived from this spectrum vary between analysis methods, with Teff = 7840(253) K obtained by Xiang et al. (2019) from LAMOST DR5 and Teff = 14 279(603) K by Xiang et al. (2022) from LAMOST DR6. Queiroz et al. (2020) used the LAMOST DR5 stellar parameters for the lower effective temperature solution from Xiang et al. (2019) with the StarHorse software to obtain lower mass and distance estimates of 2MASS J02105640+5845176 (d = 1.95 kpc, Mc = 1.69 M⊙) compared to the photometric results (see Table 3). The higher effective temperature obtained in Xiang et al. (2022) is consistent with the mass and temperature estimates derived from astrometry and photometry.

To resolve this discrepancy in the effective temperature of 2MASS J02105640+5845176, we obtained four spectroscopic observations of 2MASS J02105640+5845176 during morning twilight on August 16 and 17, 2022 with the Intermediate Dispersion Spectrograph (IDS) at the 2.5 m Isaac Newton Telescope on La Palma (see Fig 2.). The R900V grating was used with 600-s exposures on the RED+2 detector. The seeing varied between 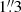1 . ″ 3 $ 1{{\overset{\prime\prime}{.}}}3 $ and 2 . 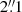″ 1 $ 2{{\overset{\prime\prime}{.}}}1 $. We used the 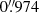0 . ″ 974 $ 0{{\overset{\prime\prime}{.}}}974 $ slit, covering the wavelength range of 3800–5400 Å at 0.70 Å pix−1, providing a resolution of R ∼ 3000. The observations were bias subtracted and spectra were extracted using the method described by Hynes (2002). Arc-lamp exposures taken prior to each observation of 2MASS J02105640+5845176 were used for the wavelength calibration. Radial velocities and spectral properties were determined by fitting the observed spectra against normalised model spectra from Munari et al. (2005). The model spectra were convolved with a truncated Gaussian to decrease their resolution of R = 20 000 to that of the observations.

thumbnail Fig. 2.

Normalised optical spectrum of 2MASS J02105640+5845176 (black), as observed with the Intermediate Dispersion Spectrograph at the Isaac Newton Telescope. The best-fitting model spectrum from Munari et al. (2005) is plotted in blue (shifted by +0.4 units vertically) and is characterised by Teff = 14 000 K, log g = 4.5 cgs, [M/H = 0, and vrot sin i = 75 km s−1]. The model spectrum has been convolved with the response of the slit to match the resolution of the observed spectrum. The LAMOST DR7 spectrum from Xiang et al. (2022) is shown in orange (shifted by +0.8 units vertically). Prominent absorption lines are indicated.

We found that the barycentred radial velocities are consistent with a mean velocity of v = −9(3) km s−1 (3.2 km s−1 rms around the mean). The observed spectrum is best represented by the models with Solar metallicity ([M/H] = 0), with an effective temperature Teff = 14 275(133) K, surface gravity log(g cgs−1) > 4.13 (2σ), and rotationally broadened by vrot sin i = 73(12) km s−1. At this effective temperature and surface gravity, 2MASS J02105640+5845176 can be classified as a B6 V star (Pecaut & Mamajek 2013).

The PARSEC stellar evolution models by Bressan et al. (2012), Tang et al. (2014), and Chen et al. (2014, 2015) predict a mass of Mc = 3.59(5) M⊙ and absolute V-band magnitude of MV = 0.28(4) for an [M/H] = 0 main sequence star with Teff = 14 275(133) K at an age of 10 Myr. At 40 Myr, the mass and absolute V-band magnitude are Mc = 3.72(6) M⊙ and MV = 0.06(4). The Green et al. (2019) Galactic extinction map predicts Eg − r = 0.38(2) to 0.40(2) mag for distances from 1.9 to 3.0 kpc. For these reddening values, the RV = 3.1 extinction coefficients from Schlafly & Finkbeiner (2011) yield AV = 1.15 to 1.21 mag. Combined with the observed magnitude of V = 13.507 (Henden et al. 2015) this yields distances of d = 2.54 kpc–2.80 kpc. From these observations, we conclude that the A1 V stellar classification and the Teff = 7840 K estimate by Xiang et al. (2019) is in error and that 2MASS J02105640+5845176 is a Mc = 3.5 to 3.8 M⊙, Teff ∼ 14 000 K B6 V star at a distance of d = 2.5–2.8 kpc.

At the location and DM of PSR J0210+5845, the NE2001 (Cordes & Lazio 2002) and YMW16 (Yao et al. 2017) Galactic electron density models predict distances of 2.52 and 1.95 kpc, respectively. Given the typically 20% uncertainties on DM-derived distances, these distances are consistent with the distances derived from the Gaia parallax measurement and the photometric and spectroscopic constraints.

The uncertainty in the tie between the pulsar position and the Gaia astrometry is dominated by the uncertainty in the former. The 99% confidence error ellipse on the pulsar timing position has an area of 0.053 sq. arcsec, while the Gaia DR3 object density towards PSR J0210+5854 is only 18.4 stars per sq. arcmin. Hence, the probability of finding an unrelated star from the Gaia DR3 catalogue in the error ellipse of PSR J0210+5854 is low p = 2.6 × 10−4. Given this low chance coincidence and the consistent distance estimates, we considered the optical counterpart 2MASS J02105640+5845176 as the binary companion to PSR J0210+5854 for the remainder of the paper.

Finally, we note that based on the light curves from ZTF Bellm et al. (2019), 2MASS J02105640+5845176 was identified as a periodic variable by Chen et al. (2020), with 0.042 mag variations in the r band on a 1.1248 d period, and classified as a variable of the RS CVn type. This classification is inconsistent with the spectral type obtained from spectroscopy and the mass and temperature estimates from astrometry and photometry. Additionally, our optical spectroscopy rules out radial velocity variations larger than 3 km s−1 over a 24 h period, ruling out the RS CVn classification. We consider it more likely that 2MASS J02105640+5845176 is a slowly pulsating B-star, a variable type that produces photometric variability of similar periodicity and amplitude in stars of spectral types ranging from B2 to B9 (Waelkens 1991; Fedurco et al. 2020).

4. Orbital constraints

To investigate whether binary motion between PSR J0210+5845 and 2MASS J02105640+5845176 can explain the observed higher order spin frequency derivatives in the timing of PSR J0210+5845, we used the method from Bassa et al. (2016). This method is based on the derivations of Joshi & Rasio (1997) and uses a Keplerian orbit to compute time derivatives of the line-of-sight position of the pulsar to predict spin frequency derivatives. We consider it unlikely that PSR J0210+5845 and 2MASS J02105640+5845176 are in an unbound, hyperbolic, orbit, as the time scale for gravitational interaction will be extremely short compared to the lifetime of the pulsar. Hence, we modelled the observed spin frequency derivatives with a bound Keplerian orbit described by the orbital period, Pb, projected semi-major axis, x, eccentricity, e, argument of perigee, ω, and true anomaly, ν.

For comparison of the observed spin frequency derivatives with predicted values from the Keplerian model, we used the first to fifth spin frequency derivatives. We implicitly assumed that the second-order and higher order spin frequency derivatives are entirely dominated by orbital motion, but need to correct the observed first-order spin frequency derivative, ḟobs, for the unknown intrinsic spin frequency derivative, ḟint, due to spin down. The contributions to ḟobs from the Shklovskii (Shklovskii 1970) effect and the differential and Galactic acceleration (e.g., Nice & Taylor 1995) are at least six orders of magnitude smaller than ḟobs and are therefore neglected. From the ATNF Pulsar Catalogue4 (version 1.67; Manchester et al. 2005), we found that the intrinsic spin frequency derivative distribution of normal, non-recycled pulsars (those with a spin period of P > 0.02 s) can be described by a log-normal distribution of the form log10 − ḟint = −14.3(1.3), for ḟint in units of s−2.

We performed a Monte Carlo simulation to predict spin frequency derivatives for 100 000 randomly sampled Keplerian orbits. Samples of e, ω, and ν were drawn from uniform distributions between 0 ≤ e < 1, 0° ≤ω < 360°, and 0° ≤ν < 360°, respectively. Using the drawn samples, we used the equations from Bassa et al. (2016) and solved for Pb and x. Random values for the intrinsic spin frequency derivative ḟint were drawn from the log-normal distribution to correct the observed spin frequency derivative and obtain the contribution due to orbital motion on ḟ. For each set of parameters, we calculated the spin frequency derivatives, which we compared to the observed values from the timing analysis in Sect. 2. We only retained parameter sets for which the predicted spin frequency derivatives were within 3σ of the observed values and for which the orbital inclination, i, was consistent with sin i < 1 for a 1.4 M⊙ pulsar and a Mc = 3.6 M⊙ binary companion.

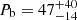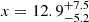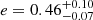The results of the Monte Carlo simulation are presented in Fig. 3 and they indicate that the observed spin frequency derivatives can be explained by a wide and moderately eccentric orbit with P b = 47 − 14 + 40 $ P_{\mathrm{b}}=47^{+40}_{-14} $ yr, x = 12 . 9 − 5.2 + 7.5 $ x=12.9^{+7.5}_{-5.2} $ AU and e = 0 . 46 − 0.07 + 0.10 $ e=0.46^{+0.10}_{-0.07} $ (68% confidence intervals). The orbital inclination is constrained to i = 52(18)° and with a true anomaly of ν ∼ 221°, the binary system had its previous apastron passage between 1988 and 2016 ( 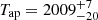T ap = 2009 − 20 + 7 $ T_{\mathrm{ap}}=2009^{+7}_{-20} $) while the next periastron passage is predicted to occur between 2030 and 2034 ( 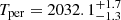T per = 2032 . 1 − 1.3 + 1.7 $ T_{\mathrm{per}}=2032.1^{+1.7}_{-1.3} $). At periastron, the distance between the binary components will be 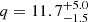q = 11 . 7 − 1.5 + 5.0 $ q=11.7^{+5.0}_{-1.5} $ AU. By correcting for the orbital motion of PSR J0210+5845, we obtained an intrinsic spin-down 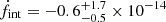f ˙ int = − 0 . 6 − 0.5 + 1.7 × 10 − 14 $ \dot{f}_{\mathrm{int}} = -0.6^{+1.7}_{-0.5}\times10^{-14}\, $s−2, constraining the characteristic age to 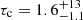τ c = 1 . 6 − 1.1 + 13 $ \tau_{\mathrm{c}}=1.6^{+13}_{-1.1} $ Myr.

thumbnail Fig. 3.

Parameter distributions of the orbital period (Pb), the projected semi-major axis (x), the eccentricity (e), the argument of perigee (ω), the true anomaly (ν), and the intrinsic spin frequency derivative (ḟint) resulting from the Monte Carlo simulation assuming Mc = 3.6 M⊙. The median values and the 68% confidence intervals for each parameter are displayed on top of the columns.

If we assume a lower companion mass of 1.7 M⊙, we obtain a very similar estimate for ν and slightly lower estimates for Pb, x, e, ω, and ḟint, but the values are consistent with those from Mc = 3.6 M⊙.

5. Formation scenarios

The formation of high-mass binary pulsars follows that of high-mass X-ray binaries and the first-born neutron star in double neutron star systems, where the more massive primary of a binary consisting of O and/or B stars undergoes a supernova explosion to form the neutron star (e.g., Brandt & Podsiadlowski 1995; Tauris et al. 2017 and references therein). Alternatively, an episode of mass transfer from the primary to the secondary can lead the primary to expel most of its envelope, leaving a helium star that can explode as a Type Ib/c supernova (Eldridge et al. 2008).

PSR J0210+5845 poses a challenge for these formation scenarios as, compared to other high-mass binary pulsars, it has a relatively low companion mass of ∼3.6 M⊙. Since, in the absence of mass transfer, the progenitor of the pulsar in PSR J0210+5845 must have had a mass larger than ≳8 M⊙ to form a ∼1.4 M⊙ neutron star (Woosley et al. 2002), at least 56% of the mass in the binary system would have been lost in a direct supernova explosion. As this exceeds the 50% limit above which the binary is disrupted (Hills 1983), a natal kick imparted on the neutron star during the supernova explosion would be required to keep the binary system bound.

To investigate the kick velocities required for the system to survive the mass loss in the supernova explosion, we used the formalism by Brandt & Podsiadlowski (1995) to calculate post-supernova orbits. As input for the direct supernova channel, we assumed as initial conditions a Mp = 8–12 M⊙ neutron star progenitor and a Mc = 3.6 M⊙ secondary in a wide orbit (initial orbital periods larger than Pb, ini > 1500 d) to ensure it does not fill its Roche lobe before the star explodes (Klencki et al. 2022). We assumed that the initial orbit is circularised due to tides from the neutron star progenitor. For these parameters, the Brandt & Podsiadlowski (1995) equations predict a maximum kick velocity of vkick < 96 km s−1, above which the system will not remain bound. Hence, random kick velocities were chosen with magnitudes up to this limit and we used the standard assumption that the distribution in kick directions is isotropic.

We found that the orbit only remains bound for kicks with magnitudes below vkick < 96 km s−1 and only if the kick direction is retrograde, namely, opposite to the orbital velocity at the time of the supernova explosion. The kick velocity limit for which the system remains bound decreases as the initial orbit is wider, and has vkick < 37 km s−1 for Pb, ini = 16 000 d (see Fig. 4). The fraction of cases that remain bound (assuming isotropic kicks) is relatively low and decreases for higher progenitor masses. Similarly, the probability for the system to remain bound improves for the alternative scenario, where mass is lost from the system to form a helium star. Repeating the calculations with a Mp = 2.4 to 4 M⊙ helium-star progenitor for the neutron star in a Pb, ini > 1000 d pre-explosion orbit, the calculations show that the binary system remains bound for retrograde kicks with velocities below vkick < 90 km s−1, but the probability increases to 100% for velocities below vkick < 11 km s−1, where prograde orbits are also possible.

thumbnail Fig. 4.

Results from supernova kick simulations. The left-hand panel shows the probability that the post-supernova binary remains bound as a function of kick velocity. These probabilities were computed with isotropic kicks for a range of pre-supernova primary masses for a helium-star progenitor of 2.4 and 4 M⊙ and direct supernova explosions of 8, 10, and 12 M⊙ progenitors as well as pre-supernova orbital periods of 1000, 4000, and 16 000 d. The right-hand panel shows the resulting post-supernova orbital period Pb, fin and eccentricity for a range of pre-supernova masses and orbital periods. The dash-dotted vertical lines indicate the pre-supernova orbital periods with the wedges the resulting post-supernova parameters. The orbital constraints for PSR J0210+5845 are shown in black with error bars.

If we consider a scenario with a less massive companion, the likelihood of the binary system surviving the supernova is diminished even further. Lower initial natal kicks to the neutron star are necessary to prevent disruption of the binary system.

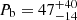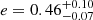The post-supernova orbits have a large range in possible orbital periods and eccentricities. Orbits that are initially wide are able to reproduce the observed orbital parameters determined with the spin frequency derivatives ( P b = 47 − 14 + 40 $ P_{\mathrm{b}}=47^{+40}_{-14} $ yr, e = 0 . 46 − 0.07 + 0.10 $ e=0.46^{+0.10}_{-0.07} $). The post-supernova orbital period does not strongly depend on the progenitor mass or the eccentricity, as shown in Fig. 4. We found that for the 8–12 M⊙ progenitor, the pre-supernova orbit would require orbital periods in the range of Pb, ini = 2000–40 000 d, while the helium star scenario with Mp = 2.4–4.0 M⊙ has compatible post-supernova orbits for Pb, ini = 3000–56 000 d.

As a result of the low natal kick velocities, the velocity imparted on the post-supernova binary centre-of-mass is also low. The formalism by Brandt & Podsiadlowski (1995) predicts system velocities of vsys = 25–45 km s−1 for a 10 M⊙ neutron star progenitor in a 1500 d pre-supernova orbit for the range of kick velocities in which the binary remains bound. These velocities decrease for lower mass neutron star progenitors and wider pre-supernova orbits.

6. Discussion and conclusions

The LOFAR timing observations of PSR J0210+5845 reveal large deviations from typical spin-down behaviour of isolated pulsars that can be modelled by a spin frequency and a spin frequency derivative. We argue that these deviations are caused by binary motion of the pulsar in a wide (as-yet-unresolved) orbit around the B6 V star 2MASS J02105640+5845176. This identification of 2MASS J02105640+5845176 as the binary companion of PSR J0210+5845 is based on the coincidence in celestial position, as well as the distance between the star and the pulsar, and the low probability for this coincidence to be due to random chance.

The properties of PSR J0210+5845, its B6 V binary companion, the orbital properties of this system and its location near the Galactic plane (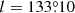 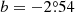l = 133 . ° 10 $ l=133{{\overset{\circ}{.}}}10 $, b = − 2 . ° 54 $ b=-2{{\overset{\circ}{.}}}54 $) are consistent with to those of high-mass binary pulsars. With this identification, PSR J0210+5845 becomes the seventh system with this classification, namely, non-recycled pulsars (P > 0.01 s) with main sequence star binary companions that have masses in excess of Mc > 1 M⊙ (Manchester et al. 2005). Compared to the other systems, PSR J0210+5845 stands out primarily due to the low mass of its binary companion. For those systems where companion masses have been reliably measured, the lowest mass is around ∼8 M⊙ (Table 1), while for the companion of PSR J0210+5845, we determined a mass of 3.5–3.8 M⊙. Similarly, among the high-mass X-ray binaries with measured masses, the lowest masses are around ∼8 M⊙ (from the HMXB catalogue by Fortin et al. 2023). The spin frequency derivatives determined from the timing of PSR J0210+5845 constrain the orbit as wide (Pb = 34–88 yr), with a moderate eccentricity of e = 0.39–0.56. Of the high-mass binary pulsars, only PSR J2032+4127 is in a wide orbit of 46 yr, though with a higher eccentricity of e = 0.96 (Lyne et al. 2015). All other systems have orbital periods below 2000 days.

Due to the low mass of the companion, we found that for the binary to remain bound after the supernova explosion that formed PSR J0210+5845, a low velocity, retrograde natal kick is required (vkick < 96 km s−1). This is true for both the direct collapse of a > 8 M⊙ neutron star progenitor and the collapse of a helium star.

Low-velocity natal kicks of a few tens of km s−1 are commonly attributed to electron-capture supernovae, where the rapid explosion does not allow for asymmetries to develop (e.g., Podsiadlowski et al. 2004; Gessner & Janka 2018). The progenitor mass range in which electron-capture supernovae occur is uncertain but estimated between 8 and 10 M⊙. Recently, Stevenson et al. (2022) have postulated that electron-capture supernovae would create non-recycled pulsars in wide (Pb ≳ 104 d) and moderately eccentric (e ∼ 0.7) orbits. Their population synthesis predicts a distribution of post-supernova orbital periods and eccentricities matching the observed properties of PSR J0210+5845. Therefore, PSR J0210+5845 is a possible candidate for this formation scenario.

Although large natal kicks of hundreds of km s−1 are predicted to be more common for traditional Fe core-collapse supernovae (Janka 2017, and references therein), observations show that lower natal kicks below 60 km s−1 are still possible (Verbunt et al. 2017). Due to the broader range of progenitor masses leading to a core-collapse supernova that produces a neutron star (Smartt 2009), this scenario is not to be disregarded.

The wide post-supernova orbit places constraints on the pre-supernova orbit, which we found also require for it to be wide, with orbital periods ranging from 2000 to 56 000 d. This would argue against the formation scenario in which an episode of mass transfer between the neutron star progenitor and the binary companion removes the envelope of the progenitor, allowing it to explode as a helium star. First, the current low mass of the companion does not allow the neutron star progenitor to have accreted much matter and, second, the wide pre-supernova orbit is not expected in this scenario where mass-transfer is required. However, through calculations of angular momentum pre- and post-interaction and assuming no accretion by the companion, we found that under the ideal assumption of isotropic mass loss (e.g., see Pols & Marinus 1994), orbital periods exceeding 4000 days are achievable for a helium star.

The orbital parameters indicate that the upcoming periastron passage is between 2030 and 2034. Continued timing observations around that time will significantly improve the orbital constraints. During periastron passage, the distance between the binary components is predicted to be 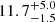11 . 7 − 1.5 + 5.0 $ 11.7^{+5.0}_{-1.5} $ AU, which, using the approximation from Eggleton (1983) and assuming a mass ratio of 1.4/3.6, gives a Roche lobe radius of 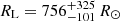R L = 756 − 101 + 325 R ⊙ $ R_{\mathrm{L}} = 756_{-101}^{+325}\,R_\odot $ (Eggleton 1983). Comparatively, a 3.6 M⊙ star has an approximate radius of 2.6 R⊙ (Demircan & Kahraman 1991), which indicates that there will be no Roche-lobe overflow.

At the nominal distance of 2.5 kpc, the observed proper motion of 2MASS J02105640+5845176 corresponds to a transverse velocity of 14.5 km s−1. This velocity is the sum of the projected orbital velocity of the star around the binary centre-of-mass, the projected post-supernova system velocity of the binary centre-of-mass imparted on the system due to the supernova kick, and the projected component of any pre-supernova system velocity of the binary system. From the orbital constraints, we obtained a projected orbital velocity of the pulsar companion around the binary centre-of-mass of 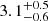3 . 1 − 0.6 + 0.5 $ 3.1^{+0.5}_{-0.6} $ km s−1. Assuming a random direction of the post-supernova system velocity, the projected component will be less than 22 km s−1, indicating that the majority of the observed proper motion is due to the system velocity of the binary.

It remains to be seen if the orbital motion of the B6 V star around the centre-of-mass of the binary system can be detected by Gaia. The orbital constraints based on the observed spin frequency derivatives of PSR J0210+5845 indicate that the projected acceleration due to orbital motion is small, of the order of 0.02 mas yr−2 at a distance of 2.5 kpc, and the Gaia DR3 astrometric solution for position, proper motion, and parallax reports no astrometric excess noise (Gaia Collaboration 2023).

It has been proposed that numerous radio pulsars that are considered to be isolated might, in fact, belong to exceptionally wide binary systems. Jones et al. (2023) estimate that approximately 30% of seemingly isolated pulsars with a measured 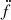f ¨ $ \ddot{f} $ value could hide a binary with orbital period < 1000 yr. In this paper, we demonstrate that even in these highly separated systems, the orbital motion of the pulsar can be measured through higher order frequency derivatives.

Acknowledgments

This paper is based (in part) on data obtained with the International LOFAR Telescope (ILT) under project codes LC9_023, LC9_041, LT10_015 and LT14_005. LOFAR (van Haarlem et al. 2013) is the Low Frequency Array designed and constructed by ASTRON. It has observing, data processing, and data storage facilities in several countries, that are owned by various parties (each with their own funding sources), and that are collectively operated by the ILT foundation under a joint scientific policy. The ILT resources have benefitted from the following recent major funding sources: CNRS-INSU, Observatoire de Paris and Université d’Orléans, France; BMBF, MIWF-NRW, MPG, Germany; Science Foundation Ireland (SFI), Department of Business, Enterprise and Innovation (DBEI), Ireland; NWO, The Netherlands; The Science and Technology Facilities Council, UK; Ministry of Science and Higher Education, Poland. This research was made possible by support from the Dutch National Science Agenda, NWA Startimpuls – 400.17.608. I.V.Y. and J.C. acknowledge support by the Spanish Ministry of Science under grant PID2020-120323GB-I00. The INT is operated on the island of La Palma by the Isaac Newton Group of Telescopes in the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias.

References

  1. Aharonian, F., Akhperjanian, A. G., Aye, K. M., et al. 2005, A&A, 442, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Anders, F., Khalatyan, A., Chiappini, C., et al. 2019, A&A, 628, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Anders, F., Khalatyan, A., Queiroz, A. B. A., et al. 2022, A&A, 658, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Andersen, B. C., Fonseca, E., McKee, J. W., et al. 2023, ApJ, 943, 57 [NASA ADS] [CrossRef] [Google Scholar]
  5. Arzoumanian, Z., Nice, D. J., Taylor, J. H., & Thorsett, S. E. 1994, ApJ, 422, 671 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bailer-Jones, C. A. L., Rybizki, J., Fouesneau, M., Demleitner, M., & Andrae, R. 2021, AJ, 161, 147 [Google Scholar]
  7. Bassa, C. G., Brisken, W. F., Nelemans, G., et al. 2011, MNRAS, 412, L63 [NASA ADS] [CrossRef] [Google Scholar]
  8. Bassa, C. G., Janssen, G. H., Karuppusamy, R., et al. 2016, MNRAS, 456, 2196 [NASA ADS] [CrossRef] [Google Scholar]
  9. Bell, J. F., Bessell, M. S., Stappers, B. W., Bailes, M., & Kaspi, V. M. 1995, ApJ, 447, L117 [NASA ADS] [CrossRef] [Google Scholar]
  10. Bellm, E. C., Kulkarni, S. R., Graham, M. J., et al. 2019, PASP, 131, 018002 [Google Scholar]
  11. Brandt, N., & Podsiadlowski, P. 1995, MNRAS, 274, 461 [NASA ADS] [CrossRef] [Google Scholar]
  12. Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [NASA ADS] [CrossRef] [Google Scholar]
  13. Chen, Y., Girardi, L., Bressan, A., et al. 2014, MNRAS, 444, 2525 [Google Scholar]
  14. Chen, Y., Bressan, A., Girardi, L., et al. 2015, MNRAS, 452, 1068 [Google Scholar]
  15. Chen, X., Wang, S., Deng, L., et al. 2020, ApJS, 249, 18 [NASA ADS] [CrossRef] [Google Scholar]
  16. Cordes, J. M., & Lazio, T. J. W. 2002, arXiv e-prints [arXiv:astro-ph/0207156] [Google Scholar]
  17. Demircan, O., & Kahraman, G. 1991, A&AS, 181, 313 [Google Scholar]
  18. Eggleton, P. P. 1983, ApJ, 268, 368 [Google Scholar]
  19. Eldridge, J. J., Izzard, R. G., & Tout, C. A. 2008, MNRAS, 384, 1109 [Google Scholar]
  20. Fedurco, M., Paunzen, E., Hümmerich, S., Bernhard, K., & Parimucha, Š. 2020, A&A, 633, A122 [EDP Sciences] [Google Scholar]
  21. Fortin, F., García, F., Simaz Bunzel, A., & Chaty, S. 2023, A&A, 671, A149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Gaia Collaboration (Vallenari, A., et al.) 2023, A&A, 674, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Gessner, A., & Janka, H.-T. 2018, ApJ, 865, 61 [Google Scholar]
  24. Green, G. M., Schlafly, E., Zucker, C., Speagle, J. S., & Finkbeiner, D. 2019, ApJ, 887, 93 [NASA ADS] [CrossRef] [Google Scholar]
  25. Henden, A. A., Levine, S., Terrell, D., & Welch, D. L. 2015, Am. Astron. Soc. Meet. Abstr., 225, 336.16 [Google Scholar]
  26. Hills, J. G. 1983, ApJ, 267, 322 [NASA ADS] [CrossRef] [Google Scholar]
  27. Hobbs, G., Lyne, A. G., & Kramer, M. 2010, MNRAS, 402, 1027 [NASA ADS] [CrossRef] [Google Scholar]
  28. Hotan, A. W., van Straten, W., & Manchester, R. N. 2004, PASA, 21, 302 [Google Scholar]
  29. Hynes, R. I. 2002, A&A, 382, 752 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Janka, H.-T. 2017, ApJ, 837, 84 [Google Scholar]
  31. Johnston, S., Manchester, R. N., Lyne, A. G., Nicastro, L., & Spyromilio, J. 1994, MNRAS, 268, 430 [NASA ADS] [Google Scholar]
  32. Jones, M. L., Kaplan, D. L., McLaughlin, M. A., & Lorimer, D. R. 2023, ApJ, 951, 20 [NASA ADS] [CrossRef] [Google Scholar]
  33. Joshi, K. J., & Rasio, F. A. 1997, ApJ, 479, 948 [NASA ADS] [CrossRef] [Google Scholar]
  34. Kaspi, V. M., Bailes, M., Manchester, R. N., Stappers, B. W., & Bell, J. F. 1996, Nature, 381, 584 [NASA ADS] [CrossRef] [Google Scholar]
  35. Klencki, J., Istrate, A., Nelemans, G., & Pols, O. 2022, A&A, 662, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Kondratiev, V. I., Verbiest, J. P. W., Hessels, J. W. T., et al. 2016, A&A, 585, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Lorimer, D. R., Faulkner, A. J., Lyne, A. G., et al. 2006, MNRAS, 372, 777 [NASA ADS] [CrossRef] [Google Scholar]
  38. Luo, J., Ransom, S., Demorest, P., et al. 2021, ApJ, 911, 45 [NASA ADS] [CrossRef] [Google Scholar]
  39. Lyne, A. G., Stappers, B. W., Keith, M. J., et al. 2015, MNRAS, 451, 581 [Google Scholar]
  40. Madsen, E. C., Stairs, I. H., Kramer, M., et al. 2012, MNRAS, 425, 2378 [NASA ADS] [CrossRef] [Google Scholar]
  41. Manchester, R. N., Hobbs, G. B., Teoh, A., & Hobbs, M. 2005, AJ, 129, 1993 [Google Scholar]
  42. Matzner, C. D., & McKee, C. F. 1999, ApJ, 510, 379 [Google Scholar]
  43. Morello, V., Barr, E. D., Cooper, S., et al. 2019, MNRAS, 483, 3673 [NASA ADS] [CrossRef] [Google Scholar]
  44. Munari, U., Sordo, R., Castelli, F., & Zwitter, T. 2005, A&A, 442, 1127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  45. Nice, D. J., & Taylor, J. H. 1995, ApJ, 441, 429 [NASA ADS] [CrossRef] [Google Scholar]
  46. Pecaut, M. J., & Mamajek, E. E. 2013, ApJS, 208, 9 [Google Scholar]
  47. Podsiadlowski, P., Langer, N., Poelarends, A. J. T., et al. 2004, ApJ, 612, 1044 [NASA ADS] [CrossRef] [Google Scholar]
  48. Pols, O. R., & Marinus, M. 1994, A&A, 288, 475 [NASA ADS] [Google Scholar]
  49. Queiroz, A. B. A., Anders, F., Santiago, B. X., et al. 2018, MNRAS, 476, 2556 [Google Scholar]
  50. Queiroz, A. B. A., Anders, F., Chiappini, C., et al. 2020, A&A, 638, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Sanidas, S., Cooper, S., Bassa, C. G., et al. 2019, A&A, 626, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [Google Scholar]
  53. Shannon, R. M., Johnston, S., & Manchester, R. N. 2014, MNRAS, 437, 3255 [Google Scholar]
  54. Shklovskii, I. S. 1970, Sov. Astron., 13, 562 [NASA ADS] [Google Scholar]
  55. Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
  56. Smartt, S. J. 2009, ARA&A, 47, 63 [NASA ADS] [CrossRef] [Google Scholar]
  57. Stevenson, S., Willcox, R., Vigna-Gómez, A., & Broekgaarden, F. 2022, MNRAS, 513, 6105 [NASA ADS] [CrossRef] [Google Scholar]
  58. Tan, C. M., Bassa, C. G., Cooper, S., et al. 2020, MNRAS, 492, 5878 [NASA ADS] [CrossRef] [Google Scholar]
  59. Tang, J., Bressan, A., Rosenfield, P., et al. 2014, MNRAS, 445, 4287 [NASA ADS] [CrossRef] [Google Scholar]
  60. Tauris, T. M., Kramer, M., Freire, P. C. C., et al. 2017, ApJ, 846, 170 [Google Scholar]
  61. van der Wateren, E., Bassa, C. G., Cooper, S., et al. 2023, A&A, 669, A160 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  62. van Haarlem, M. P., Wise, M. W., Gunst, A. W., et al. 2013, A&A, 556, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  63. van Straten, W., & Bailes, M. 2011, PASA, 28, 1 [Google Scholar]
  64. Verbunt, F., Igoshev, A., & Cator, E. 2017, A&A, 608, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  65. Waelkens, C. 1991, A&A, 246, 453 [NASA ADS] [Google Scholar]
  66. Wang, N., Johnston, S., & Manchester, R. N. 2004, MNRAS, 351, 599 [Google Scholar]
  67. Woosley, S. E., Heger, A., & Weaver, T. A. 2002, Rev. Mod. Phys., 74, 1015 [NASA ADS] [CrossRef] [Google Scholar]
  68. Xiang, M., Ting, Y.-S., Rix, H.-W., et al. 2019, ApJS, 245, 34 [Google Scholar]
  69. Xiang, M., Rix, H.-W., Ting, Y.-S., et al. 2022, A&A, 662, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Yao, J. M., Manchester, R. N., & Wang, N. 2017, ApJ, 835, 29 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1.

The properties of the six currently known pulsar/massive star binaries.

In the text
Table 2.

Timing parameters for PSR J0210+5845.

In the text
Table 3.

The properties of 2MASS J02105640+584517.

In the text

All Figures

thumbnail Fig. 1.

Residuals from timing with one (a), two (b) three (c), and four (d) spin frequency derivatives. The residuals from fitting the model in Table 2 fitting up to and including five spin frequency derivatives are very similar to the residuals shown here.
In the text
thumbnail Fig. 2.

Normalised optical spectrum of 2MASS J02105640+5845176 (black), as observed with the Intermediate Dispersion Spectrograph at the Isaac Newton Telescope. The best-fitting model spectrum from Munari et al. (2005) is plotted in blue (shifted by +0.4 units vertically) and is characterised by Teff = 14 000 K, log g = 4.5 cgs, [M/H = 0, and vrot sin i = 75 km s−1]. The model spectrum has been convolved with the response of the slit to match the resolution of the observed spectrum. The LAMOST DR7 spectrum from Xiang et al. (2022) is shown in orange (shifted by +0.8 units vertically). Prominent absorption lines are indicated.
In the text
thumbnail Fig. 3.

Parameter distributions of the orbital period (Pb), the projected semi-major axis (x), the eccentricity (e), the argument of perigee (ω), the true anomaly (ν), and the intrinsic spin frequency derivative (ḟint) resulting from the Monte Carlo simulation assuming Mc = 3.6 M⊙. The median values and the 68% confidence intervals for each parameter are displayed on top of the columns.
In the text
thumbnail Fig. 4.

Results from supernova kick simulations. The left-hand panel shows the probability that the post-supernova binary remains bound as a function of kick velocity. These probabilities were computed with isotropic kicks for a range of pre-supernova primary masses for a helium-star progenitor of 2.4 and 4 M⊙ and direct supernova explosions of 8, 10, and 12 M⊙ progenitors as well as pre-supernova orbital periods of 1000, 4000, and 16 000 d. The right-hand panel shows the resulting post-supernova orbital period Pb, fin and eccentricity for a range of pre-supernova masses and orbital periods. The dash-dotted vertical lines indicate the pre-supernova orbital periods with the wedges the resulting post-supernova parameters. The orbital constraints for PSR J0210+5845 are shown in black with error bars.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.