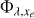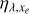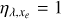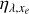| Issue |
A&A
Volume 680, December 2023
|
|
|---|---|---|
| Article Number | A33 | |
| Number of page(s) | 16 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202347066 | |
| Published online | 05 December 2023 | |
Self-consistent simulation of photoelectrons in exoplanet winds: Faster ionisation and weaker mass-loss rates
Université Paris Cité, Université Paris-Saclay, CEA, CNRS, AIM,
91191
Gif-sur-Yvette, France
e-mail: alexandre.gillet@cea.fr
Received:
1
June
2023
Accepted:
13
September
2023
Context. Close-in exoplanets undergo extreme irradiation levels leading to hydrodynamic atmospheric escape and the formation of planetary winds. The planetary mass-loss is governed by several physical mechanisms, including photoionisation that may impact the evolution of the atmosphere. The stellar radiation energy deposited as heat strongly depends on the energy of the primary electrons following photoionisation and on the local fractional ionisation. All these factors affect the model-estimated atmospheric mass-loss rates and other characteristics of the outflow in ways that have not been clearly elucidated. Moreover, the shape of the XUV stellar spectra strongly influences the photoionisation and heating deposition in the atmosphere. Substantial changes are to be expected in the planetary mass-loss rate.
Aims. We study the effect of secondary ionisation by photoelectrons on the ionisation and heating of the gas for different planet-star systems. We focus on the local and planet-wise effects, to clearly demonstrate the significance of these interactions.
Methods. Using the PLUTO code, we performed 1D hydrodynamics simulations for a variety of planets and stellar types. We included planets in the size range from Neptune to Jupiter, and stars from M dwarfs to Sun-like.
Results. Our results indicate a significant decrease in the planetary mass-loss rate for all planetary systems when secondary ionisation is taken into account. The mass-loss rate is found to decrease by 43% for the more massive exoplanets to 54% for the less massive exoplanets orbiting Sun-like stars, and up to 52% for a Jovian-like planet orbiting an M-type star. Our results also indicate much faster ionisation of the atmosphere due to photoelectrons.
Conclusions. We built a self-consistent model including secondary ionisation by photoelectrons to evaluate its impact on mass-loss rates. We find that photoelectrons affect the mass-loss rates by factors that are potentially important for planetary evolution theories. We also find that enhanced ionisation occurs at altitudes that are often probed with specific atomic lines in transmission spectroscopy. Future modelling of these processes should include the role of photoelectrons. For this purpose, we make a simple but accurate parameterisation for atomic hydrogen atmospheres available.
Key words: hydrodynamics / planets and satellites: atmospheres / planet-star interactions / stars: winds, outflows
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
It has long been proposed that the atmospheres of exoplanets that orbit close to their host stars must be escaping rapidly (Lammer et al. 2003; Baraffe et al. 2004). It remains a difficult task to accurately predict the mass-loss rates, however, because the starplanet interactions that participate in the mass-loss process are complex.
Planets can lose their atmospheres through multiple mechanisms that are broadly separated into thermal and non-thermal (see Gronoff et al. 2020, for a complete review of escape processes). Non-thermal processes such as ion sputtering, polar outflow or charge exchange with the stellar wind dominate for planets orbiting at large distances from their star. Thermal processes, which include Jeans and hydrodynamic escape, generally dominate in planets on short-period orbits. We focus here on hydrodynamic escape, which occurs when intense stellar radiation deposits its energy in the planetary atmosphere (at various altitudes, depending on the radiation wavelength), leading to the escape of the atmosphere into space.
The planetary wind interacts with the stellar wind and forms a number of hydrodynamic features, such as a bow shock, a comet-like tail, and Kelvin–Helmholtz instabilities (Tremblin & Chiang 2013). Insight into these processes can be gained by measuring the excess absorption that occurs at a number of atomic lines such as H I Lyα and Hα, or the He I triplet at 10 830 Å with in-transit spectroscopy. These features have been measured for hot Jupiters (e.g. Vidal-Madjar et al. 2003; Lecavelier Des Etangs et al. 2010; Jensen et al. 2012) and hot Neptunes (e.g. Kulow et al. 2014; Ehrenreich et al. 2015; Ben-Jaffel et al. 2022). A number of studies have been conducted to understand the global problem of planetary escape with hydro-dynamical 1D models (e.g. Yelle 2004; García Muñoz 2007; Murray-Clay et al. 2009; Koskinen et al. 2013). These models predict velocities for the planetary wind of a few km s−1 in the proximity of the planet. These velocities are consistent with the line broadening of Hα and the He I triplet measured with high-resolution spectroscopy (e.g. Salz et al. 2018; García Muñoz & Schneider 2019). However, the models fail to predict the velocities of ~100 km s−1 that are found with Lyα spectroscopy (e.g. Vidal-Madjar et al. 2003; Ben-Jaffel 2007). It remains an open question whether the velocities measured with Lyα spectroscopy are representative of the planetary wind or are instead indicative of stellar wind protons that become neutralised by chargeexchange with the planetary wind (Tremblin & Chiang 2013).
Many authors have studied this problem with 2D and 3D models that include self-consistent radiative transfer, with the goal of constraining the mass-loss rates from the planets (e.g. Tripathi et al. 2015; Debrecht et al. 2019). Recently, Shaikhislamov et al. (2021) developed a global 3D multi-fluid model to investigate the He 10 830 Å line, Daley-Yates & Stevens (2019) explored the star-planet interaction of the wind in the presence of a magnetic field, and Carolan et al. (2021) explored the effects of the stellar wind strength on a magnetised planetary wind, showing that the increased polar loss compensates for the decreased mass-loss in the dead zones of the planet.
It is essential to accurately predict the atmospheric mass-loss rate to answer fundamental questions about the evolution of planets. Some atmospheres, in particular, those of low-mass planets, may be escaping so efficiently that they can be completely lost to space on timescales shorter than the lifetime of the planet. The case of hydrodynamic escape of strongly irradiated exoplanets is the aim of this work. The mass-loss rate can only be calculated after determining how much of the stellar radiation energy is converted into heat, and how much otherwise goes to ionisation and excitation of the atmospheric gas.
We focus on atmospheric gas made of hydrogen atoms, H, because although H2 should be prevalent in primary atmospheres, the molecule will typically dissociate rapidly in the upper atmosphere of the planet. The physics of photoelectron interactions with H2 is also more complex than for H atoms because, being a molecule, H2 offers additional channels for excitation, dissociation, and ionisation that must be tracked individually (Hallett et al. 2005). We postpone such a study to future work and focus here on the essentials for an atomic atmosphere. Upon absorption by the atmospheric atomic gas, the stellar X-ray and extreme-UV photons (jointly referred to as XUV, and covering wavelengths from a few Å to the Lyman-continuum threshold at 912 Å) release high-velocity electrons. These so-called photo-electrons have energies E0 = hc/λ−13.6 eV, where h and c are Planck’s constant and the speed of light, respectively, and λ is the photon wavelength. The photoelectrons can excite the gas and produce secondary electrons while slowing down. The gas heating corresponds to the fraction of the initial energy E0 of the photoelectron that is not expended in excitation or ionisation, but instead goes into kinetic energy.
We emphasize the importance of two parameters that dictate the fraction of the initial photoelectron energy that is deposited as heat, namely the local fractional ionisation xe and the energy E0 of the primary photoelectrons. In particular, if the local fractional ionisation is high, elastic collisions between the fast and thermal electrons ensure that most of E0 is transferred to the thermal electrons, thereby heating the gas. Moreover, if E0 is lower than 10.2 eV, that is, below the lowermost threshold for inelastic collisions in the H atom, all of E0 is transferred as heat to the background gas in elastic collisions. Within these two limits, predicting the gas heating is relatively straightforward. Importantly, when the fractional ionisation is low or moderate and E0 is sufficiently high, additional electrons and ions are created during the secondary ionisation process, when the primary photoelectron interacts with other hydrogen atoms. For the most energetic primary electrons that are created after photoionisation, it follows a cascade of multiple ionisation events.
The fundamental information for the treatment of photo-electrons and for the assessment of how much of their energy goes into excitation, ionisation and heating of the gas has been available for decades. For example, Habing & Goldsmith (1971) and Shull (1979) studied the production of secondary electrons induced by soft X-rays and their interaction with a primordial gas using a Monte Carlo method. The outcome of these modelling efforts can readily be parameterised as a function of xe and E0 to take the effect of photoelectrons on the net ionisation rate and heating rate induced by XUV photons into account that impact the upper atmosphere of exoplanets on short-period orbits.
In this work, we revisit the problem by self-consistently exploring the simultaneous heating and ionisation that occurs as the photoelectrons slow down. To do this, we take advantage of recent advances in the characterisation of the XUV spectra of stars. This effect is often neglected in studies that model the hydrodynamic escape of planetary atmospheres (e.g. Lammer et al. 2003; Wu & Lithwick 2013; García Muñoz et al. 2020, 2021). With the ultimate goal of better predicting the loss rate and the main features of planetary winds, an arbitrary pre-fixed fraction (typically, 2–30%) of the photoelectron energy E0 is assumed to be transferred into heating in some cases (Linssen et al. 2022). Our work shows how these simplified treatments can partly be overcome, and we study the importance of photoelectrons in the strongly irradiated atmospheres of some exoplanets.
Guo & Ben-Jaffel (2016) covered related ideas, with an emphasis on the effects of the spectral energy distribution on the mass-loss rate and ionisation of strongly irradiated atmospheres. Following their initial study, we highlight the local and global effect of the photoelectrons on the atmosphere and we provide simple but accurate descriptions of the self-consistent implementation of these processes in the continuity and energy conservation equations of the gas. These prescriptions are useful for other modelling efforts. In addition, we use recent developments in the reconstruction of the XUV spectra for cool stars by observations at X-ray and far-UV wavelengths (France et al. 2016).
To examine the quantitative effect of photoelectrons and assess whether the planetary gravity plays a role, we performed 1D spherical hydrodynamic simulations with the PLUTO code (Mignone et al. 2007). We focused on the escaping atmospheres of four simulated planetary systems with masses ranging from 0.02 MJ to 0.69 MJ (similar to HD 209458b) and assessed the effect of different XUV spectra taken from the Measurements of the Ultraviolet Spectral Characteristics of Low-mass Exo-planetary Systems (MUSCLES) survey (France et al. 2016). We defined the planet size Rp so that the planet density remained constant in all cases. This is a somewhat arbitrary choice, but useful because of its simplicity. In the energy-limited limit, the mass-loss rate (Erkaev et al. 2007) is proportional to the inverse of the planetary density, in which case the assumption of a constant bulk density serves as a valid basis for a comparison against that limit. Our simulations incorporate the relevant physics of photoelectrons in the continuity and energy equations.
The plan of the paper is as follows: the model, including the PLUTO setup and our treatment of radiative transfer with photoelectrons, is described in Sect. 2. In Sect. 3, we describe the relevant physics of photoelectrons and its implementation in PLUTO. Section 4 is dedicated to the description of the results of the atmospheric escape of a Neptune-like planet. Section 5 describes the dependence of our results on the planet mass, and in Sect. 6, we finally study the impact of the shape of the stellar spectra of M- and K-type stars on secondary ionisation.
2 Model description
2.1 Physical model
The model was constructed with the hydrodynamics code PLUTO (Mignone et al. 2007), which solves the Euler equations in a rotating reference frame. The 1D equations for the conservation of mass, momentum, and energy solved in PLUTO are
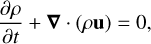 (1)
(1)
![${{\partial \left( {\rho {\bf{u}}} \right)} \over {\partial t}} + \nabla \cdot \left[ {\rho {\bf{uu}} + {P_T}{\bf{I}}} \right] = - \rho \nabla \phi + \rho {{\bf{F}}_{{\rm{cent}}}},$](/articles/aa/full_html/2023/12/aa47066-23/aa47066-23-eq2.png) (2)
(2)
![${{\partial \left( {E + \rho \phi } \right)} \over {\partial t}} + \nabla \cdot \left[ {\left( {E + {P_T} + \rho \phi } \right){\bf{u}}} \right] = \rho {{\bf{F}}_{{\rm{cent}}}}{\bf{u}} + H - C,$](/articles/aa/full_html/2023/12/aa47066-23/aa47066-23-eq3.png) (3)
(3)
where r is the distance as measured from the planet centre, and t is the time, and where u is the fluid velocity, ρ is the density, PT is the thermal pressure, E = PT/(γ − 1) + ρu2/2 is the total energy with γ = 5/3, the adiabatic index for a mono-atomic gas, and C and H are the cooling and heating terms to be defined in Sect. 2.3. The joint gravitational potential of the planet plus the star is defined as
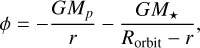 (4)
(4)
where G is the gravitational constant, and M⋆ and Mp are the mass of the star and the planet, respectively. Finally, the centrifugal force is written as:
 (5)
(5)
where Rorbit is the distance from the planet centre to the stellar centre. er is the unit vector in the outward radial direction.
We considered an atmosphere composed of atomic hydrogen in neutral H I and ionised H+ forms, plus thermal electrons. The density in the equations above corresponds to the total mass density 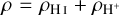 , which neglects the contribution of thermal electrons. We defined the neutral fraction xH I = ρH I/ρ and the fractional ionisation as xe = 1 − xH I, both taking values between 0 and 1. On the basis of charge neutrality, the number density of ions and electrons is the same. To determine the partitioning between H I, H+ and electrons, we considered the processes for collisional ionisation: H + e− → H+ + 2e−,
, which neglects the contribution of thermal electrons. We defined the neutral fraction xH I = ρH I/ρ and the fractional ionisation as xe = 1 − xH I, both taking values between 0 and 1. On the basis of charge neutrality, the number density of ions and electrons is the same. To determine the partitioning between H I, H+ and electrons, we considered the processes for collisional ionisation: H + e− → H+ + 2e−,
radiative recombination: H+ + e− → H + hν,
photoionisation: H + hv → H+ + e−.
In our hydrodynamic simulations, we adapted the Simplified Non-Equilibrium Cooling (SNeq) module from PLUTO (Teşileanu et al. 2008) in the optically thin limit to track the fraction of neutrals and ions of atomic hydrogen in the chemical reaction network equation. In this module, PLUTO solves the equation for the neutral fraction evolution,
![${{\partial {x_{{\rm{H}}{\,_{\rm{I}}}}}} \over {\partial t}} = {n_e}\,\left[ { - \left( {{c_r} + {c_i}} \right){x_{{\rm{H}}{\,_{\rm{I}}}}} + {c_r}} \right] - J{x_{{{\rm{H}}_{\rm{I}}}}},$](/articles/aa/full_html/2023/12/aa47066-23/aa47066-23-eq7.png) (6)
(6)
where cr = 2.6 · 10−11 × T−0.5 and ci = 5.83 · 10−11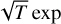 (−157 890/T) are the recombination and ionisation rate coefficients in cm3 s−1, both dependent on the temperature T [K] of the gas, and on the electron number density ne = (ρ/mp)xe, where mp is the proton mass [g/particle]. In this work, we added the additional term in Eq. (6) to account for the photoionisation of the gas by the stellar XUV photons impacting the planetary atmosphere. The formulation of the photoionisation rate coefficient J [s−1] is given in Sect. 2.3.
(−157 890/T) are the recombination and ionisation rate coefficients in cm3 s−1, both dependent on the temperature T [K] of the gas, and on the electron number density ne = (ρ/mp)xe, where mp is the proton mass [g/particle]. In this work, we added the additional term in Eq. (6) to account for the photoionisation of the gas by the stellar XUV photons impacting the planetary atmosphere. The formulation of the photoionisation rate coefficient J [s−1] is given in Sect. 2.3.
Our model considers a single thermal temperature to describe the kinetic energy of the neutral, ion and electron components of the gas. This tacitly assumes that the transfer of kinetic energy between them occurs very rapidly, which is a valid approximation for the relevant fractional ionisations.
 |
Fig. 1 Illustration of the photoionisation model and the heating of an atmosphere. The atmosphere is irradiated by XUV stellar photons with an incident flux Fxuv. The gas particles are under the influence of stellar gravity Fstar, planetary gravity Fplanet and centrifugal forces Fcent. |
2.2 Radiative transfer
The only heating source of the hydrogen gas included in our model is photoionisation. It is caused by XUV photons coming from the star (see Fig. 1). In principle, the XUV stellar spectrum should consider all possible wavelengths below 912 Å, which is the threshold at which ground-state H atoms can absorb. In practice, the atmosphere of a planet becomes thin at sufficiently short wavelengths, and these wavelengths can safely be neglected in the radiative transfer. We considered a solar spectrum that starts at 15 Å (see below), and we took this limit also as the shortest wavelength in our implementation of other stellar fluxes and the H atom cross sections.
In our simulations, we computed the local stellar flux F⋆ (r,λ) from a reference stellar flux spectrum at 1 AU, which was scaled by (1AU/Rorbit)2 to produce the top-of-the-atmosphere spectrum F⋆(r = TOA, λ), and was attenuated with an optical depth τλ using Beer-Lambert’s law. Namely
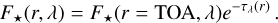 (7)
(7)
The wavelength-dependent optical depth τλ(r) in the direction towards the star is calculated through
 (8)
(8)
where the integral is performed along the planet-star line of sight. Here, nH I = (ρ/mp)xH I is the neutral number density [cm−3] and σλ [cm2] is the wavelength-dependent photoionisation cross section of hydrogen, given by
 (9)
(9)
where σ0 = 6.3 × 10−18 cm2 is the cross section at the threshold wavelength λ0 = 912 Å.
For the stellar irradiation, we adopted a solar spectrum that we downloaded from the SOLID1 project, as observed on December 13, 2021. We degraded the spectrum in 20 bins of equal size in the range from λmin = 15 Å to λ0 = 912 Å. We verified that the choice of 20 bins did not impact the results we present below in what follows by performing a few simulations with 40 equal-size bins. These simulations did not show any significant difference. Figure 2 displays the original solar spectrum in black along with the degraded spectrum, which represented by the blue bars. The XUV-integrated flux at 0.045 AU is 2174 erg cm−2 s−1.
 |
Fig. 2 Solar XUV spectrum. The original solar spectrum downloaded from SOLID at 1 AU is shown in black. The binned spectrum used in our calculations is shown as blue bars. |
2.3 Cooling, heating and ionisation rates
The cooling term C [erg s−1 cm−3] in Eq. (3) represents the sum of the thermal energy of the electrons that are lost by collisional ionisation and radiative recombination:
![$C = {n_e}{n_H}\,\left[ {{c_i}2.17 \times {{10}^{ - 11}}\,{x_{{{\rm{H}}_{\rm{I}}}}} + {c_r}1.07 \times {{10}^{ - 12}}\left( {1 - {x_{{{\rm{H}}_{\,{\rm{I}}}}}}} \right){T \over {11590}}} \right],$](/articles/aa/full_html/2023/12/aa47066-23/aa47066-23-eq12.png) (10)
(10)
Here,  is the total number of hydrogen nuclei, and cr and ci are the rate coefficients from Eq. (6). Our model does not include molecular chemistry, and therefore it neglects cooling by
is the total number of hydrogen nuclei, and cr and ci are the rate coefficients from Eq. (6). Our model does not include molecular chemistry, and therefore it neglects cooling by 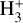 emission in the infrared, for example. In this expression, 2.17 × 10−11 erg is equivalent to the energy of 13.6 eV that is required to ionise the neutral atom. Correspondingly, 1.07 × 10−12(T/11 590) erg represents the ∼0.67 kT that are extracted from the kinetic energy of the thermal electrons and are lost to radiation if the environment is optically thin. In future work, we intend to proceed from the optically thin approximation and treat the recombination into the different bound levels separately. We also aim to track the radiated energy.
emission in the infrared, for example. In this expression, 2.17 × 10−11 erg is equivalent to the energy of 13.6 eV that is required to ionise the neutral atom. Correspondingly, 1.07 × 10−12(T/11 590) erg represents the ∼0.67 kT that are extracted from the kinetic energy of the thermal electrons and are lost to radiation if the environment is optically thin. In future work, we intend to proceed from the optically thin approximation and treat the recombination into the different bound levels separately. We also aim to track the radiated energy.
When the stellar radiation hits the planetary atmosphere, it ionises the gas and contributes to its heating. The photoionisation rate coefficient J [s−1] is given by
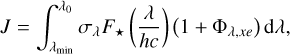 (11)
(11)
where F⋆ [erg cm−2 s−1Å−1] is the attenuated stellar flux described in Eq. (7). Φλ‚xe is the number of secondary ions created per photoionisation, to be described in Sect. 3.
The heating deposition rate H [erg s−1 cm−3] in the energy equation can be expressed as
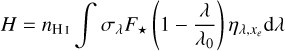 (12)
(12)
with 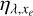 being the heating efficiency to be described in Sect. 3. Omitting the negative term in the parentheses of the above equation and assuming
being the heating efficiency to be described in Sect. 3. Omitting the negative term in the parentheses of the above equation and assuming  would provide the incident energy that is deposited in the gas. The negative term in parentheses subtracts from this the energy that is expended to produce the primary photoelectrons during photoionisation.
would provide the incident energy that is deposited in the gas. The negative term in parentheses subtracts from this the energy that is expended to produce the primary photoelectrons during photoionisation.
Models that adopt a number of secondary ions 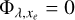 and a heating efficiency ηλ‚xe = 1 assume that the surplus energy of the photoelectrons after photoionisation is entirely expended in heating the gas. However, this is not generally true because the photoelectrons also cause excitation and ionisation of the surrounding neutral atoms. Ideally, the heating efficiency has to be precisely determined by estimating which fraction of the energy goes into heating and which fraction is used for the other processes.
and a heating efficiency ηλ‚xe = 1 assume that the surplus energy of the photoelectrons after photoionisation is entirely expended in heating the gas. However, this is not generally true because the photoelectrons also cause excitation and ionisation of the surrounding neutral atoms. Ideally, the heating efficiency has to be precisely determined by estimating which fraction of the energy goes into heating and which fraction is used for the other processes.
We aim to calculate the effect of photoelectrons on the chemistry and heating of the atmospheric gas properly. To do this, we take the dependence of these effects on the photoelectron energy and fractional ionisation into account. In Sect. 3 we detail the physical processes and determine and parameterise ηλ‚xe and Φλ,xe.
2.4 Numerical method and initial set-up
To solve Eqs. (1)–(3), we used the Harten-Lax-Van Leer approximate Riemann solver, which exactly solves stationary contact discontinuities between the cells (HLLC; see Toro 2009). We used a linear reconstruction for the spatial order of integration, and a third-order Runge-Kutta scheme (RK3) for the time evolution. According to the stiffness of Eqs. (3) (including cooling Eq. (10) and heating Eqs. (12)) and (6), a dynamically adaptive integration strategy was adopted (see Teşileanu et al. 2008, for more details).
PLUTO uses dimensionless units rather than cgs units so that flow quantities can be properly scaled to reasonable numbers (Mignone et al. 2007). We worked with three fundamental units : ρ0, L0, and V0. The reference density at the base of the atmosphere was fixed for all planetary systems at ρ0 = 1.326 × 10−10 g cm−3 corresponding to a pressure of 12 µbar (this value is taken from most models to define their boundary condition for a temperature of 1100 K). The reference length L0 was equal to the planetary radius Rp and the reference velocity V0 was calculated as V0 = (GMp/L0)0.5. Their values are given in Table 1 for the models we considered. The computational domain was composed of a stretched grid of 500 cells between 1 and 30 Rp with a stretch factor of 1.017. The grid was extended below 1 Rp by adding 10 cells of uniform size between 0.999 and 1 Rp. This extension was used by PLUTO to establish the boundary conditions at the bottom of our model.
In our simulations, the atmosphere was initialised with the density profile:
![$\rho \left( r \right) = {\rho _0}{\rm{exp}}\,\left[ {{\alpha _\rho }\,\left( {{{{R_p}} \over r} - 1} \right)} \right],$](/articles/aa/full_html/2023/12/aa47066-23/aa47066-23-eq20.png) (13)
(13)
where αp sets the initial density scale height in the atmosphere. For our simulations, αp was set to 20. The atmosphere was initialised everywhere at the equilibrium temperature Teq, which was equal to 1100 K in all our models in which the planet orbits a Sun-like star. The ideal gas law was used to initialise the pressure, the neutral hydrogen fraction profile was initially set to:
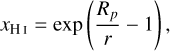 (14)
(14)
and the velocity was set to zero.
In Sects. 4 and 5, all planetary systems are considered to orbit a solar-type star with a separation of Rorbit = 0.045 AU. Table 1 lists the physical parameters we used for all simulations of each planetary system. We chose four different planetary masses : 0.02 0.05, 0.1, and 0.69 MJ They range from a sub-Neptune planet to a Jovian-like planet similar to HD 209458b. In Sect. 6, we consider different orbital distances for the planets around different stars to ensure that they have the same integrated flux.
At the inner boundary, we set the density and the pressure (12 µbar) to their initial value and the velocity to zero, and we assumed that the gas was entirely neutral. At the outer boundary, we used a free outflow boundary condition, with the gradients of all variables (P, ρ, υr and xHI) equal to 0.
 |
Fig. 3 Schematic of the energy channelling from an impacting photon into a photoelectron that can lead to the heating of the gas, its excitation, and secondary ionisation. |
Planet parameters and PLUTO parameters for each planetary system M0.69-M0.02.
3 Secondary ionisation by photoelectrons
3.1 Theoretical baseline
Before thermalising and depositing their kinetic energy into heat, photoelectrons interact with the neutral hydrogen atoms in the gas. At each collision, they loose a part of their energy. This interaction was investigated by a number of authors for a variety of astrophysical applications (Habing & Goldsmith 1971; Shull 1979; Furlanetto & Stoever 2010). In the investigation of exoplanetary atmospheres, Cecchi-Pestellini et al. (2006) and Shematovich et al. (2014) studied the effect of stellar X-ray irradiation on the heating by including the effect of photoelectrons. They found that the heating efficiency is notably lower than 1 if the atmosphere is mostly neutral when photoelectrons are included. Their simulations are not self-consistent, however, because their studies do not allow the modified hydrodynamic solution to alter the conditions that the photoelectrons experience. Guo & Ben-Jaffel (2016) investigated the production of secondary ions in H2/H atmospheres. They found an increase in the total ionisation rate by a factor of 10 in the region r < 1.05 Rp that is reached only by the shortest-wavelength photons. They also reported a drop in the mass-loss rate by less than a factor of 2 when photoelectrons were included, although the connection with the local heating efficiency is not established. García Muñoz (2023) studied the photoelectron-driven processes that affect the population of the first excited level of hydrogen that is sensed in transmission spectroscopy of the Hα line.
Based on the physics of the H I atom excitation and ionisation, several ranges of energies may be considered. For E0 < 10.2 eV, the threshold for the first excitation level, the entire energy of the photoelectrons is deposited as heat (Dalgarno & McCray 1972; Cravens et al. 1975). For energies 10.2 eV < E0 < 13.6 eV, the surplus of energy goes either into heating or into excitation. Finally, for energies E0 > 13.6eV, which defines the ionisation threshold, it can additionally be used to further ionise the gas (see Fig. 3). The energies 10.2 eV and 13.6 eV are the thresholds for E0 that enable excitation and ionisation of the atom after photoionisation, corresponding to the wavelengths 520 and 455 Å respectively. For even shorter-wavelength photons, the ejected photoelectron is able to excite or ionise the hydrogen atoms multiple times. It is reasonable to assume that the excited H I atom (resulting from either collisions of ground-state H with photoelectrons or with thermal electrons, or from the recombination of protons) will radiate its excitation energy. Although the Lyman-α line (and other lines in the Lyman series) is not optically thin, its effective radiative timescale is shorter than the collisional de-excitation timescale at the relevant atmospheric pressures even after opacity is accounting for (see García Muñoz 2023).
We calculated the heating efficiency and ionisation yield with the model described in García Muñoz (2023). The calculations were conducted over a grid in energy E0 that resolves the details in the heating efficiency and the ionisation yield at five values of the fractional ionisation well, namely, xe = 10−4, 10−3, 10−2, 10−1 and 1. Figure 4 shows the heating Eh as a function of the primary electron energy E0 and xe (different colours). The solid black line for xe = 1 coincides with Eh = E0. We define the heating efficiency, ηλ,xe = Eh/E0 which corresponds to the ratio of the energy that goes into heating Eh and the initial energy of the photoelectron E0. As noted earlier, for any prescribed xe. the heating efficiency depends on E0, or equivalently, on the energy of the incident photon hc/λ. It takes values from 0 to 1.
When ηλ,xe = 1, the entire energy is deposited as heat, while when ηλ,xe < 1, a fraction of the energy is diverted to excite or ionise other atoms. To facilitate its use in our hydrodynamical model and in other similar models, we fitted the Monte Carlo calculations of ηλ,xe to fourth-order polynomials,
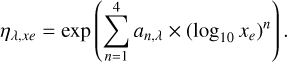 (15)
(15)
The polynomial coefficients an,λ can be found in Appendix A. When the fractional ionisation falls below 10−4, 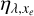 becomes essentially independent of xe. In these conditions, we fixed xe to 10−4 to estimate
becomes essentially independent of xe. In these conditions, we fixed xe to 10−4 to estimate  .
.
During the secondary ionisation process, a number Φλ,xe of secondary ions and electrons are produced from the primary electrons of energy E0. Figure 5 reports Monte Carlo model calculations of the number of secondary ions created for a primary electron of energy E0. and for a range of conditions of fractional ionisation xe. For high photoelectron energies, numerous secondary ions can be created. For instance, for E0 = 300 eV (λ = 39.5 Å), up to 5 secondary ions can be created if xe = 10−1 (green curve) and up to 10 if xe = 10−2 (orange curve). Simon Wedlund et al. (2011) have shown that about 8.5 secondary ions are expected to be created at E0 = 300 eV in a non-ionised atmosphere. We considered equally-spaced bins to sample the wavelength of the impacting photons, which translates into a first wavelength bin covering 15 Å (826.5 eV) to 59.85 Å (207.15 eV) (see Fig. 2). In this bin, we predict the average production of about 14 secondary ions, which is significantly higher because the considered bin encompasses a range of E0 that is wider than 300 eV on average. When we considered smaller wavelength bins, we recovered the production of 8.5 secondary ions at E0 = 300 eV predicted by Simon Wedlund et al. (2011). We reiterate nonetheless that our results are not significantly affected in smaller wavelength bins. Conversely, for low photoelectron energies, no additional ions are created (as expected, see Fig. 3).
Similarly, we performed a fourth-order polynomial fit:
 (16)
(16)
with bn,λ the polynomial coefficients derived in Appendix A. Because for sufficiently high energies E0, nλ,xe is small and Φλ,xe, is large when xe is small, significant effects on the heating and ionisation of the atmosphere are expected in the high-pressure region. The gas remains neutral in this region, and only very energetic photons can reach it. Conversely, we expect that farther out where the local fractional ionisation is high and the newly created photoelectrons have low energies, the effect of photoelectrons will be weak.
A note is due on the terminology used throughout this paper. We say that a calculation incorporates secondary ionisation when it is done with the parametrised forms of ηλ,xe and Φλ,xe described above. This clearly includes the effect of both excitation and ionisation by the primary and secondary electrons. Otherwise, we say that the calculation does not incorporate secondary ionisation when it is assumed that  and
and
 |
Fig. 4 Energy Eh deposited as heat by primary electrons of energy E0. The solid curves represent different fractional ionisations. The heating efficiency is given by ηλ,xe = Eh/E0. The figure is based on calculations from García Muñoz (2023). |
 |
Fig. 5 Secondary ions |
3.2 Photoionisation and heating rates
A main goal of this paper is to investigate the feedback between photoelectron-driven processes and the hydrodynamic outflow, which we detail in Sect. 4. Before this, and to demonstrate the effects of photoelectrons, we illustrate their on the energy deposition and ionisation for a prescribed atmospheric profile. For this demonstration, we assumed the atmospheric profile to be fixed, meaning that we did not consider the feedback driven by the photoelectron deposition in the gas. Through this exercise, we assessed the intricate link between the shape of the solar spectrum (Fig. 1) and the deposition of the associated energy into the atmosphere. The shape of the stellar XUV spectrum partly dictates where in the atmosphere and at which wavelengths the photoionisation and heat deposition are more prominent.
For this exercise, we considered a reference profile taken from one of our numerical simulations: the steady-state atmosphere of a Jovian-like planet with a mass of 0.69 Mj (M0.69 in Table 1). The top panel of Fig. 6 shows the fractional ionisation xe as a function of the neutral density nH I. In addition, we show in the bottom panels the wavelength contributions of photoionisation (left) and heating (right) at the five representative altitudes depicted in the top panel.
Each left panel of Fig. 6 shows two curves. The solid curve corresponds to 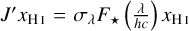 and shows the contribution to ionisation of each wavelength bin, excluding the effect of secondary ionisation by(the photo)electrons. In turn, the dotted curve corresponds to J′ (1 + Φλ‚xe) xH I and shows the total ionisation, including the production of secondary ions. The integral of the latter over wavelengths corresponds to the net ionisation rate J xH I of Eq. (6).
and shows the contribution to ionisation of each wavelength bin, excluding the effect of secondary ionisation by(the photo)electrons. In turn, the dotted curve corresponds to J′ (1 + Φλ‚xe) xH I and shows the total ionisation, including the production of secondary ions. The integral of the latter over wavelengths corresponds to the net ionisation rate J xH I of Eq. (6).
When the unattenuated stellar flux hits the upper atmosphere of the planet (see panel for 3.71 Rp, in magenta), only the longest wavelengths contribute to photoionisation. This produces the large peak observed at the threshold of 912 Å. This is largely because of the strong modulating effect of the photoionisation cross section, which prioritises the longer wavelengths. Deeper in the atmosphere (1.58 Rp, green), the number density increases by two orders of magnitude, the atmosphere becomes optically thicker, especially at the longer wavelengths, and a broader range of wavelengths contributes to photoionisation with multiple peaks (at 300 Å, 600 Å and 912 Å). At 1.29 Rp (in red), photoionisation is dominated by a peak around 300 Å. The atmosphere is optically thick at the longest wavelengths, and only those lower than 400 Å will reach this altitude because the photoionisation cross sections are smaller at short wavelengths. For the same reason, only the most energetic photons penetrate below 1.05 Rp (in blue). Photoionisation occurs at a slower rate at this altitude than in the upper atmosphere, but the number of electrons produced per volume unit is much larger, because it partly follows the hydrogen density.
Interestingly, much faster ionisation occurs when photoelectrons are taken into account (dotted lines). The enhancement of the ionisation rate by photoelectrons strengthens at the lowest altitudes. This is clearly seen at 1.05 Rp (in blue) and 1.02 Rp (in cyan) due to the multiplicative term ( ) in the integral of J xH I. In these deep layers, the photoelectrons enhance the double-peak structure between 15 and 200 Å, and ionisation is increased by a factor of two. The multiple peaks are caused by the shape of the stellar spectrum at short wavelengths and the additional modulating effect of
) in the integral of J xH I. In these deep layers, the photoelectrons enhance the double-peak structure between 15 and 200 Å, and ionisation is increased by a factor of two. The multiple peaks are caused by the shape of the stellar spectrum at short wavelengths and the additional modulating effect of  , at very short wavelengths.
, at very short wavelengths.
Similarly, the right panels of Fig. 6 show the energy term of Eq. (12), and we can define three contributions. H′ = nH IσλF⋆ depicts the energy available before photonionisation (solid lines); 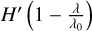 represents how much energy might be effectively deposited as heat after photoionisation (dashed lines); and lastly
represents how much energy might be effectively deposited as heat after photoionisation (dashed lines); and lastly 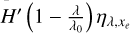 shows the total heating rate per wavelength bin, taking the effect of photoelectrons into account (dotted lines).
shows the total heating rate per wavelength bin, taking the effect of photoelectrons into account (dotted lines).
The energy deposition at different altitudes in the atmosphere is depicted in the right panels of Fig. 6. In the upper atmosphere, for the highest altitudes 3.71 and 1.58 Rp, the energy available before (solid line) and after (dashed line) photoionisation originates from a wide range of wavelengths. However, the heat deposition rate is 100 times higher at 1.58 Rp than at 3.70 Rp as a result of the higher density. For low-energy photons, the term (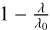 ) is close to 0. These photons spend most of their energy in the primary ionisation event, and very limited energy remains for heating (or for further ionisation or excitation). As the altitude decreases, the peak of the energy deposition shifts towards shorter wavelengths, and most of the net extracted (dashed line) from the available energy (solid lines) originates from λ < 400 Å. The peak observed at the photoionisation threshold of 912 Å at the two highest altitudes disappears because most of the available energy at these wavelengths has been used for primary ionisation at higher altitudes. In the region closest to the surface (in cyan), the energy available before H′ and after
) is close to 0. These photons spend most of their energy in the primary ionisation event, and very limited energy remains for heating (or for further ionisation or excitation). As the altitude decreases, the peak of the energy deposition shifts towards shorter wavelengths, and most of the net extracted (dashed line) from the available energy (solid lines) originates from λ < 400 Å. The peak observed at the photoionisation threshold of 912 Å at the two highest altitudes disappears because most of the available energy at these wavelengths has been used for primary ionisation at higher altitudes. In the region closest to the surface (in cyan), the energy available before H′ and after 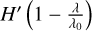 photoionisation overlaps. For wavelengths lower than 200 Å, the term (
photoionisation overlaps. For wavelengths lower than 200 Å, the term (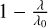 ) is close to one, and E0 is marginally impacted after removing 13.6 eV.
) is close to one, and E0 is marginally impacted after removing 13.6 eV.
An additional modulation occurs when secondary ionisation is considered (described by the dotted lines in the right panels). The attenuation of the peaks for altitudes lower than 1.29 Rp at wavelengths lower than 400 Å is considerable. For very short wavelengths, 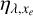 is rather small (∼0.12) and acts as a significant modulation factor that substantially reduces the heating rate arising from those wavelengths. In other words, the contribution of X-rays to heating is very weak at all altitudes in our investigation when secondary ionisation is taken into account.
is rather small (∼0.12) and acts as a significant modulation factor that substantially reduces the heating rate arising from those wavelengths. In other words, the contribution of X-rays to heating is very weak at all altitudes in our investigation when secondary ionisation is taken into account.
In summary, when photoelectrons are taken into account the ionisation rate deep in the atmosphere at short wavelengths increases significantly. Concomitantly, this increase implies that less energy is deposited into heat at these low altitudes, which clearly changes the steady state of the planetary atmosphere. We now investigate possible feedback in the atmosphere through numerical simulations.
4 Secondary ionisation of an escaping atmosphere of a Neptune-size planet
4.1 Characteristics of the escaping atmosphere
We now focus on the self-consistent simulations based on the PLUTO code, which include the hydrodynamics and photochemistry of the gas, and optionally, a parametrised description of secondary ionisation. The implementation of this new model was validated by comparing our results in the limit 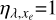 and
and 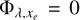 of no secondary ionisation with the version of the model described in García Muñoz (2007) adapted to the physical conditions of the current simulations. The comparison of the two simulation sets proved to be excellent. The errors in the main properties (mass-loss rates, temperature, densities and velocities) are smaller than a few percent. As a novel feature, we added the self-consistent effect of photoelectrons to our current model, as described in Sects. 2–3. We focus in this section on a Neptune-mass planet (case M0.05 in Table 1). Figure 7 shows the temperature, density, velocity, Mach number, pressure, neutral fraction profiles, and the ionisation and heating deposition rates as a function of the distance to the planet.
of no secondary ionisation with the version of the model described in García Muñoz (2007) adapted to the physical conditions of the current simulations. The comparison of the two simulation sets proved to be excellent. The errors in the main properties (mass-loss rates, temperature, densities and velocities) are smaller than a few percent. As a novel feature, we added the self-consistent effect of photoelectrons to our current model, as described in Sects. 2–3. We focus in this section on a Neptune-mass planet (case M0.05 in Table 1). Figure 7 shows the temperature, density, velocity, Mach number, pressure, neutral fraction profiles, and the ionisation and heating deposition rates as a function of the distance to the planet.
We first describe the case without secondary ionisation (black curves, Φλ‚xe = 0, ηλ‚xe = 1). The profiles show the usual features that have been reported by other models of close-in exoplanets. In particular, the density (a) and pressure (c) rapidly drop from the bottom to the top of the atmosphere, while the fractional ionisation increases monotonically (b). At 5 Rp, the gas remains mostly neutral with xe = 0.2. As the flow expands, it accelerates (d), slowly at low altitudes and faster at high altitudes, and reaches the sonic point at about 2.2 Rp, which is marked by a black dot on the Mach profile (f). Above this altitude, the planetary wind becomes supersonic, reaching velocities of about 13 km s−1 at 5 Rp. The temperature profile (g) shows a more complex behaviour. Very close to the bottom of the model, the temperature decreases with altitude because little XUV radiation reaches these layers. The availability of unattenuated XUV radiation causes the rapid increase in temperature (g), ionisation (e) and heating rate (h) that occurs immediately above. At higher altitudes, the temperature rises to about 7500 K at 8.5 Rp. Even higher than this, the temperature drops because the atmosphere expands and the energy deposition stalls as the gas becomes fully ionised and optically thin.
When secondary ionisation is taken into account (shown by the red lines in Fig. 7), the density (a) and pressure (c) drop faster with altitude, whereas the fractional ionisation (b) increases significantly at all altitudes. The flow velocity (d) also increases faster than in the case without secondary ionisation, but it reaches the sonic point at about the same distance of 2.1 Rp (marked by a red dot on the Mach profile). The temperature structure of the atmosphere is also affected when secondary ionisation is considered. The temperature (g) peaks closer to the planet at 5 Rp, and at a lower temperature it peaks around 5800 K. This cooler temperature is directly associated with the fact that photoelectrons extract some of the available energy to further excite and ionise the gas instead of heating it. Higher ionisation rates (e) cause higher fractional ionisations (b). The drop in the heating rates is particularly significant deep in the atmosphere, where the gas remains mostly neutral, and the heating efficiency is very low (see below).
We calculated the mass-loss rate as if the atmosphere were escaping symmetrically in all directions:
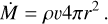 (17)
(17)
This is just a convenient assumption adopted by some ID models that can easily be modified when the gas is instead assumed to escapes only at the dayside, for instance, in which case the quoted mass-loss rates should be divided by 4. The calculated mass-loss rate for our planet M0.05 is Ṁ = 2.89 × 1011 g s−1 without secondary ionisation and Ṁ = 1.43 × 1011 g s−1 with secondary ionisation. This decreases the mass-loss rate by about 50%. This comparison shows that the drop in density when secondary ionisation is included dominates the increased velocities that are achieved. This 50% drop in the mass-loss rates can be connected to the heating efficiency of the gas (ηλ,xe in Sect. 3) at the altitudes where most of the stellar energy is deposited. This point is discussed at length in what follows. A drop in the mass-loss rate of this magnitude might have significant implications on atmospheric evolution studies and also on the detectability of diagnostic lines such as ΗI Lyα and Hα in transmission spectroscopy. These ideas will be explored in future work.
 |
Fig. 6 Expected effect of photoelectrons on ionisation and heating rates. Top panel: fractional ionisation xe as a function of neutral number density nH I when a Jovian-like planet is irradiated by a solar spectrum. Five particular altitudes are labelled by coloured squares and correspond to the series of panels below. Bottom left panels: contribution to the photoionisation rate at different altitudes, without secondary ionisation J xH I [s−1] (solid lines) and with photoelectrons (dotted lines), as a function of wavelength. Bottom right panels: contribution to the heating rate at different altitudes, H′ [erg s−1 cm−3] representing the energy available before photoionisation (solid lines). The dashed line represents the heating rate due to photoionisation without the effect of photoelectrons, and the dotted lines show the net heating rate with secondary ionisation. The dashed and dotted lines overlap at higher altitudes. The curves provide valuable insight into the wavelengths that contribute to heating at each altitude and how this energy is affected by photoelectrons. |
 |
Fig. 7 Evaporating atmosphere of the case M0.05 without (red lines) and with (black lines) the effect of secondary ionisation. Left panels from top to bottom: density, pressure, ionisation rate and temperature. Right panels from top to bottom: fractional ionisation, velocity, Mach number and heating rate. |
4.2 Heating efficiency
The amount of energy that is available to further excite and ionise the gas depends on the primary energy E0 and on the fractional ionisation xe (see Sect. 3). To better understand how the stellar energy is finally deposited into the atmosphere, and to determine the wavelengths and altitudes over which this occurs, the top panel of Fig. 8 shows the heating efficiency ηλ,xe for our M0.05 planet as a function of altitude and wavelength.
Following Fig. 4,  (grey regions) for λ > 520 Å at every altitude due to the low energies of the primary photoelectrons, see Sect. 3.1. The effect of photoelectrons is the strongest close to the surface (blue and green regions in Fig. 8) where the gas is largely neutral, with xe < 10−3. ηλ,xe steadily decreases from 0.45 at λ = 520 Å to 0.13 for the most energetic photons (λ < 82 Å). These photoelectrons spend 55 % to 87% of their energies to further excite and ionise the gas. We note that the heating efficiency for primary photoelectrons produced by radiation λ < 82 Å is particularly low and remains lower than 0.7 up to 3.5 Rp. Higher altitudes are mildly affected by the photoelectrons, and above 5 Rp the fractional ionisation xe is very close to one, rendering the effect of photoelectrons completely negligible (grey area). Above 5 Rp the fractional ionisation xe steadily increases and the photons ionising the atmosphere are low-energy, high-wavelength photons that do not lead to significant secondary ionisation (see Sect. 3).
(grey regions) for λ > 520 Å at every altitude due to the low energies of the primary photoelectrons, see Sect. 3.1. The effect of photoelectrons is the strongest close to the surface (blue and green regions in Fig. 8) where the gas is largely neutral, with xe < 10−3. ηλ,xe steadily decreases from 0.45 at λ = 520 Å to 0.13 for the most energetic photons (λ < 82 Å). These photoelectrons spend 55 % to 87% of their energies to further excite and ionise the gas. We note that the heating efficiency for primary photoelectrons produced by radiation λ < 82 Å is particularly low and remains lower than 0.7 up to 3.5 Rp. Higher altitudes are mildly affected by the photoelectrons, and above 5 Rp the fractional ionisation xe is very close to one, rendering the effect of photoelectrons completely negligible (grey area). Above 5 Rp the fractional ionisation xe steadily increases and the photons ionising the atmosphere are low-energy, high-wavelength photons that do not lead to significant secondary ionisation (see Sect. 3).
The efficiency  provides insight into the specifics of wavelength-by-wavelength energy deposition in the atmosphere. To gain insight into the local heating at each altitude, even if some information encoded in the dependence of
provides insight into the specifics of wavelength-by-wavelength energy deposition in the atmosphere. To gain insight into the local heating at each altitude, even if some information encoded in the dependence of 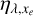 on wavelength is lost, we additionally defined an effective heating efficiency
on wavelength is lost, we additionally defined an effective heating efficiency  . At each altitude, it was calculated from the ratio of the actual heating deposition rate of Eq. (3) over the net energy endowed on the photoelectrons after photoionisation,
. At each altitude, it was calculated from the ratio of the actual heating deposition rate of Eq. (3) over the net energy endowed on the photoelectrons after photoionisation,
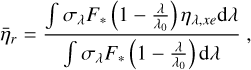 (18)
(18)
The bottom panel of Fig. 8 shows the variation of 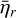 with altitude in the atmosphere for the M0.05 case. As altitude increases, the effective heating efficiency
with altitude in the atmosphere for the M0.05 case. As altitude increases, the effective heating efficiency 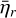 increases significantly because of the increase in the fractional ionisation and because most of the nascent photoelectrons have low energies. Above 3 Rp,
increases significantly because of the increase in the fractional ionisation and because most of the nascent photoelectrons have low energies. Above 3 Rp,  is close to one and most of the energy is directly converted into heat without any significant effect of secondary ionisation. Below 3 Rp,
is close to one and most of the energy is directly converted into heat without any significant effect of secondary ionisation. Below 3 Rp, 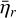 steadily decreases towards the bottom of the atmosphere, and it sharply decreases to reach 0.5 at 1.2 Rp and 0.13 at the bottom. This later latter region is particularly important for establishing the mass-loss rate because the XUV photons are deposited at these altitudes.
steadily decreases towards the bottom of the atmosphere, and it sharply decreases to reach 0.5 at 1.2 Rp and 0.13 at the bottom. This later latter region is particularly important for establishing the mass-loss rate because the XUV photons are deposited at these altitudes.
 |
Fig. 8 Heating efficiencies for the case M0.05. Top panel: heating efficiency |
 |
Fig. 9 Ionisation yields for the case M0.05. Top panel: number of total (primary plus secondary) ions created per primary photoelectron as a function of wavelength and altitude for the M0.05 planet. The grey regions indicate where |
4.3 Secondary ions per primary photoelectron
Similarly to the heating efficiency, we calculated the number of total (primary plus secondary) ions created per primary photoionisation event. The top panel of Fig. 9 shows 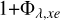 for the M0.05 planet as a function of altitude and wavelength.
for the M0.05 planet as a function of altitude and wavelength.
As anticipated, for wavelengths longer than 455 Å, the primary photoelectrons do not produce any secondary ions (grey area in the top panel; see Sect. 3.1). Each primary photoelectron is able to create one secondary ion on average for wavelengths between 455 and 306 Å close to the planet when the gas is mostly neutral. For higher energies of the primary photoelectrons, the region where secondary ions are created extends toward higher altitude. Correspondingly, below 2 Rp, only short-wavelength photons reach altitudes in which the fractional ionisation is low, and photoelectrons are be able to create numerous secondary ions after primary ionisation. For the shortest wavelengths below 82 Å, up to 14 ions can be created per primary ionisation. This substantially reducines the heating efficiency and boosts the photoionisation rate.
In order to evaluate the average number of ions created per primary energy E0, an effective 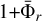 was defined at each altitude. It was calculated as
was defined at each altitude. It was calculated as
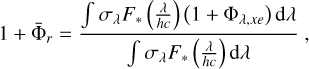 (19)
(19)
The bottom panel of Fig. 9 shows 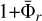 for the M0.05 case. The number of ions created by the primary photoelectron is close to one (i.e. no secondary photoelectrons are created) above 1.2 Rp, as expected because at these altitudes only low-energy photons interact with the gas and the fractional ionisation can be relatively high. The most striking feature of this panel is that close to the surface, up to 14 ions are created per primary ionisation. The significantly enhanced ionisation rate in this region is the ultimate cause of the faster overall ionisation of the atmosphere when secondary ionisation is considered.
for the M0.05 case. The number of ions created by the primary photoelectron is close to one (i.e. no secondary photoelectrons are created) above 1.2 Rp, as expected because at these altitudes only low-energy photons interact with the gas and the fractional ionisation can be relatively high. The most striking feature of this panel is that close to the surface, up to 14 ions are created per primary ionisation. The significantly enhanced ionisation rate in this region is the ultimate cause of the faster overall ionisation of the atmosphere when secondary ionisation is considered.
In summary, in the lower layers of the atmosphere, where only photoelectrons of high E0 are created, the heating efficiency is lowest and the number of secondary ions created is highest. The gas ionises faster when the effect of photoelectrons is included, which entails that the amount of deposited heat decreases and the cross section of the planet to XUV photons decreases as well. The diminution of heat deposition naturally translates into a more compact planetary atmosphere and a reduced net mass-loss. Moreover, the decrease in the heating rate we observe is not sufficient to cause non-thermal processes to dominate for planets on close-in orbits like this.
5 Dependence on planetary mass
The survival of a planetary atmosphere depends on the incoming stellar XUV flux and on how this energy is used to overcome the gravitational potential of the planet. The low gravitational potential of low-mass planets causes their atmospheres to extend more than those of higher-mass planets, with a larger pressure scale height. Depending on how the neutral density and fractional ionisation profiles change with planetary mass, the relative effect of photoelectrons can be more or less pronounced. We report in Table 2 the mass-loss rate for all cases presented in this study. A reduction of 43% of the mass-loss rate is observed for the case M0.69 and up to 54% for M0.02. A dependence on the planetary is shown: Secondary ionisation is slightly more efficient for low-mass planets.
To investigate this aspect, we now analyse the two extreme cases in our sample: A planet with Mp = 0.69MJ (model M0.69) and a planet with Mp = 0.02MJ (model M0.02) that is at the mass limit for Roche-lobe overflow.
Both models are represented in Fig. 10. For a given neutral density, the fractional ionisation xe is always lower for the least massive planet (M0.02) when secondary ionisation is not included (dotted lines). As a result, secondary ionisation is expected to be more effective for the low-mass planet because its lower ionisation fraction (at a given neutral density) implies that more energy is used to further excite and ionise the atmosphere instead of heating it. When secondary ionisation is included, this trend is indeed confirmed, and a slightly larger shift of the хе-nH I profile is observed for the low-mass planet (M0.05, blue lines) than for the higher-mass planet (M0.69, green lines).
In addition, in the two cases studied here, the peak of the ionisation rate (panel b) shifts to a higher altitude when secondary ionisation is included and the overall ionisation rate increases slightly. We note that these shifts and increases are more pronounced for the low-mass planet (M0.05, in blue). In parallel, the energy deposition rate in panel c is also significantly affected in both cases, similarly to case M0.05 (Sect. 4). Close to the surface, when photoelectrons are taken into account (dashed lines), the heating rate is reduced by one order of magnitude for M0.02 and is divided by 2 for M0.69. As a result, the effect of secondary ionisation is found to be important for all the planets, and it is most pronounced for the least massive planets we considered.
1D spherical mass-loss rates calculated for all planetary systems with and without the secondary ionisation by photoelectrons.
 |
Fig. 10 Comparison of two different planetary masses: a sub-Neptunelike planet of 0.02 MJ (M0.02, green) and a Jovian-like planet of 0.69 MJ (M0.69, blue). The dashed lines and dotted lines represent the cases with and without secondary ionisation, respectively. From top to bottom: fractional ionisation xe as a function of neutral density (a), photoionisation rate JxH I (b), and heating deposition rate H (c). |
6 Atmospheric escape with different stellar spectra
An accurate description of stellar spectra is fundamental for modelling atmospheric escape. However, the stellar output at XUV wavelengths is quite difficult to constrain and uncertainties remain in the stellar spectra that are adopted by models. One of the difficulties arises from the fact that the high-energy radiative output of stars is variable. The main difficulty, however, is that while the X-ray spectrum is usually measurable, the EUV part is strongly attenuated by the interstellar medium (ISM). Much work has been conducted in recent years to overcome some of these difficulties, either by exploring larger sets of stars at X-ray and FUV wavelengths or by complementing the available data with elaborate modelling of stellar coronas. We focus here on a planet similar to case M0.69 that orbits cool, low-mass stars, and we explore the impact of the XUV spectra of planets like this on the photoionisation and deposition rate into the atmospheres of close-in exoplanets.
6.1 Stellar spectral energy of K-and M-type stars
As described above, the conversion from stellar photon energy to energy powering the atmospheric escape depends, amongst other factors on the actual energy distribution of the primary photo-electrons. It is therefore expected that the stellar spectral energy distribution (SED) may have an impact on the macroscopic properties of planetary atmospheres.
For this purpose, we chose a sample of three stars taken from the MUSCLES data survey, GJ1214, GJ832 and HD 97658 (France et al. 2016)2. The aim of this survey was to obtain the SEDs of M and K dwarfs from 5 Å to 5.5 µm, with special emphasis on the XUV, which is difficult to constrain. Typically, the X-ray part of the spectrum are measurements from Chandra and XMM-Newton (Loyd et al. 2016), and the EUV part was reconstructed following the techniques described by Youngblood et al. (2016), who in turn used an empirical scaling relation based on Lyα flux (Linsky et al. 2013). However, the X-ray spectrum for HD 97658 does not come from XMM/Chandra observations, but was scaled from X-ray data of HD 85512 according to the ratio of the bolometric flux between the two stars because their levels of Fe XII emission are similar to the bolometric flux. The synthetic EUV spectrum of the M dwarf GJ 832 was taken from Fontenla et al. (2016). We selected the panchromatic spectrum with an adaptive resolution for our sample (panchromatic SED binned to a constant 1 Å resolution, downsampled in regions with a low signal-to-noise ratio to avoid negative fluxes). Choosing the spectrum without adaptive resolution does not affect our wavelength range of interest. A summary of the information about the stars in our sample and their implementation in our model is presented in Table 3.
Similarly to the Sun, we scaled the stellar fluxes taken at 1 AU by (1AU/Rorbit)2(see Sect. 2.2) and degraded their spectra into 20 bins of equal sizes. In order to focus on the shape of the SED, we changed the orbital distance of the planet around each star to ensure that all planets received the same integrated XUV flux (2174 erg cm−2 s−1) as in the preceding sections. We display the original MUSCLES spectra in the upper panel of Fig. 11 and the spectrum used in our model in the lower panel. The corresponding Rorbit are given in Table 1.
The bottom of the panel of in Fig. 11 shows that the scaled flux of both M dwarfs is higher than the flux of the Sun and of HD 97658 between 15 and 400 Å, and is lower above 400 Å. Because the effect of photoelectrons is stronger at high energies (i.e. short wavelengths), we expect the photoelectrons for the M dwarfs in our sample to be more strongly affected.
Stellar parameters for HD 97658, GJ832, GJ1214 and the Sun.
6.2 Heating efficiency and ionisation yield
Based on our hydrodynamic calculations as described in Sect. 3, the heating efficiency 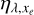 for each star-planet model is shown in the top panels of Fig. 12 organised by increasing effect of secondary ionisation from left to right. Similarly to the solar case (third column), the effect of photoelectrons is strongest close to the surface (blue and green regions in Fig. 12) where the gas is largely neutral, with xe < 10−3. However, the effect of secondary ionisation is more prominent for the M dwarfs (GJ1214 and GJ832, first and second columns). A larger region of the atmosphere is affected with
for each star-planet model is shown in the top panels of Fig. 12 organised by increasing effect of secondary ionisation from left to right. Similarly to the solar case (third column), the effect of photoelectrons is strongest close to the surface (blue and green regions in Fig. 12) where the gas is largely neutral, with xe < 10−3. However, the effect of secondary ionisation is more prominent for the M dwarfs (GJ1214 and GJ832, first and second columns). A larger region of the atmosphere is affected with  . Interestingly, the results for HD 97658 (last column) show similar heating efficiencies as the solar case, even though the differences in their binned spectra above 400 Å are significant. Figure 13 represents the heating efficiency
. Interestingly, the results for HD 97658 (last column) show similar heating efficiencies as the solar case, even though the differences in their binned spectra above 400 Å are significant. Figure 13 represents the heating efficiency 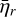 as a function of altitude for all stars. We observe that GJ1214 and GJ832 have lower
as a function of altitude for all stars. We observe that GJ1214 and GJ832 have lower 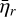 for a given altitude (in units of Rp). HD 976458 displays a similar
for a given altitude (in units of Rp). HD 976458 displays a similar 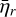 as our Sun.
as our Sun.
Along with the heating efficiencies, the bottom panels of Fig. 12 show the ionisation yield 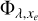 . For the M dwarfs, photoelectrons create at least one secondary ion on average in a larger region of the atmosphere (blue areas) than the Sun and HD 97658. The effect of secondary ionisation is the strongest for GJ1214 at the shortest wavelengths: up to 14 secondary ions are created below 3 Rp.
. For the M dwarfs, photoelectrons create at least one secondary ion on average in a larger region of the atmosphere (blue areas) than the Sun and HD 97658. The effect of secondary ionisation is the strongest for GJ1214 at the shortest wavelengths: up to 14 secondary ions are created below 3 Rp.
We report in Table 3 the mass-loss rate for all cases. A reduction of 52% of the mass-loss rate is found for GJ1214 when secondary ionisation is taken into account. We therefore confirm that the effect of secondary ionisation by photoelectrons is stronger for the M dwarfs of our sample.
 |
Fig. 11 XUV stellar spectra. Top panel: panchromatic SED downloaded from the MUSCLES Treasury Survey for GJ1214, GJ832 and HD 97658 and scaled at a distance of 1 AU. The solar spectrum at 1 AU used in the preceding section is shown by the black line. Bottom panel: scaled and binned spectra of our sample of stars. After scaling (see text), the integral over wavelength is the same for all four stars. |
 |
Fig. 12 Heating efficiencies and ionisation yields for different stars and the Sun. Top panel: heating efficiencies |
 |
Fig. 13 Heating efficiency |
7 Conclusion
We investigated the role of the XUV flux of a host star on planetary atmospheres, with a focus on the physics of photoelectrons. In order to understand how photoionisation and deposition of energy determine the structure of the planetary atmosphere, we parametrised the excitation, secondary ionisation, and heating due to photoelectrons in a planetary atmosphere. We implemented this parametrisation in the PLUTO code to perform 1D modelling of escaping atmosphere of exoplanets orbiting a Sunlike star with a mass range between 0.02 and 0.69 MJ assuming a constant planetary density. We studied the impact of secondary ionisation by photoelectrons on these processes and on the net mass-loss rate of the atmosphere. We characterised the importance of the fractional ionisation xe and the energy E0 of the primary photoelectrons on the gas in the planetary atmosphere. We emphasised the importance of the shape of the XUV flux by considering different stellar spectra of K- and M-type stars from the MUSCLES data survey (France et al. 2016).
We showed that the shape of the solar spectra in the XUV range significantly affects the photoionisation and the way in which the energy is deposited in the atmosphere. Photoelectrons lead to higher ionisation rates deep in the atmosphere, where the fractional ionisation of the gas is low. Consequently, the amount of energy that goes into heating is reduced when secondary ionisation is taken into account, and so is the mass-loss rate of the atmosphere. Furthermore, we find that the stellar X-ray flux contributes significantly less to the heating of the atmosphere, and therefore contributes significantly less to setting the strength of the atmospheric escape.
We found that the mass-loss rate prominently decreases from 43 to 54% when secondary ionisation is taken into account for planets with masses of 0.69 MJ and 0.02 MJ. We find that the net mass-loss rate is strongly reduced for planets with a lower gravitational potential than for the more massive ones.
The shape of the stellar spectrum is a key parameter for understanding the escape of planetary atmospheres. In particular, the SED of the XUV part of a solar-type star can vary greatly due to differences in mass, age, metallicity or magnetic activity. We implemented a sample of stellar spectra of K- and M-type stars in our model and studied the effect of the XUV shape on secondary ionisation and on the mass-loss rate. We found that, for a Jovian-like planet, the effect of secondary ionisation is stronger for the M dwarfs with lower heating efficiencies and higher ionisation yields than for the Sun. The contribution of this effect is largely due to wavelengths smaller than 400 Å, which are comparatively stronger than the solar spectrum for the two M dwarfs studied in this work. The EUV flux between 100 and 400 Å, which contributes most to the heating, is higher for GJ1214 and GJ832, meaning that these stars would heat up the atmosphere of their planets efficiently. On the other hand, active stars in the X-ray (λ < 100 Å) range will not necessarily affect the heating because most of the energy of the photoelectrons will be used to re-ionise the gas.
To conclude, we stress that secondary ionisation is an important physical process and must be taken into account when modelling an escaping planetary atmosphere in 1D. In a future work, we will assess how photoelectrons impact the detection of outflow when considering more realistic 2D and 3D geometries. In addition, it remains unclear how secondary ionisation affects the atmospheric outflow when Joule heating is considered. Because more ions are created, this may in some cases lead to an increased Joule heating (Cohen et al. 2014) and may impact the mass-loss rate. The presence of a magnetic field or the consideration of a more complex chemical network may therefore also modify the mass-loss rate, which we also aim to characterise in a subsequent work.
Acknowledgements
We acknowledge funding from the Programme National de Planétologie (INSU/PNP). A.S. acknowledges funding from the European Union’s Horizon-2020 research and innovation programme (grant agreement no. 776403 ExoplANETS-A) and the PLATO/CNES grant at CEA/IRFU/DAp.
Appendix A Polynomial coefficients
Polynomial coefficients for the parametrisation of the heating efficiency  (top table) and ionisation yield
(top table) and ionisation yield 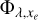 (bottom table) implemented in our hydrodynamical model. All polynomial coefficients go to zero at wavelengths longer than 520 Å for
(bottom table) implemented in our hydrodynamical model. All polynomial coefficients go to zero at wavelengths longer than 520 Å for 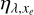 and 455 Å for
and 455 Å for 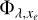 , corresponding to the wavelength thresholds for excitation and ionisation by the photoelectrons (see section 3.1).
, corresponding to the wavelength thresholds for excitation and ionisation by the photoelectrons (see section 3.1).
Calculated polynomial coefficient for the heating efficiency 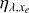
Calculated polynomial coefficient for the ionisation yield  .
.
References
- Baraffe, I., Selsis, F., Chabrier, G., et al. 2004, A & A, 419, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ben-Jaffel, L. 2007, ApJ, 671, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Ben-Jaffel, L., Ballester, G. E., García Muñoz, A., et al. 2022, Nat. Astron., 6, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Carolan, S., Vidotto, A., Villarreal D’Angelo, C., & Hazra, G. 2021, MNRAS, 500, 3382 [Google Scholar]
- Cecchi-Pestellini, C., Ciaravella, A., & Micela, G. 2006, A & A, 458, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cohen, O., Drake, J., Glocer, A., et al. 2014, ApJ, 790, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Cravens, T., Victor, G., & Dalgarno, A. 1975, Planet. Space Sci., 23, 1059 [NASA ADS] [CrossRef] [Google Scholar]
- Daley-Yates, S., & Stevens, I. R. 2019, MNRAS, 483, 2600 [NASA ADS] [CrossRef] [Google Scholar]
- Dalgarno, A., & McCray, R. 1972, ARA & A, 10, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Debrecht, A., Carroll-Nellenback, J., Frank, A., et al. 2019, MNRAS, 483, 1481 [NASA ADS] [CrossRef] [Google Scholar]
- Ehrenreich, D., Bourrier, V., Wheatley, P. J., et al. 2015, Nature, 522, 459 [Google Scholar]
- Erkaev, N., Kulikov, Y. N., Lammer, H., et al. 2007, A & A, 472, 329 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fontenla, J., Linsky, J. L., Garrison, J., et al. 2016, ApJ, 830, 154 [NASA ADS] [CrossRef] [Google Scholar]
- France, K., Loyd, R. P., Youngblood, A., et al. 2016, ApJ, 820, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Furlanetto, S. R., & Stoever, S. J. 2010, MNRAS, 404, 1869 [NASA ADS] [Google Scholar]
- García Muñoz, A. 2007, Planet. Space Sci., 55, 1426 [Google Scholar]
- García Muñoz, A. 2023, Icarus, 392, 115373 [CrossRef] [Google Scholar]
- García Muñoz, A., & Schneider, P. 2019, ApJ, 884, L43 [CrossRef] [Google Scholar]
- García Muñoz, A., Youngblood, A., Fossati, L., et al. 2020, ApJ, 888, L21 [Google Scholar]
- García Muñoz, A., Fossati, L., Youngblood, A., et al. 2021, ApJ, 907, L36 [Google Scholar]
- Gronoff, G., Arras, P., Baraka, S., et al. 2020, J. Geophys. Res. Space Phys., 125, e2019JA027639 [CrossRef] [Google Scholar]
- Guo, J., & Ben-Jaffel, L. 2016, ApJ, 818, 107 [Google Scholar]
- Habing, H., & Goldsmith, D. 1971, ApJ, 166, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Hallett, J. T., Shemansky, D. E., & Liu, X. 2005, ApJ, 624, 448 [NASA ADS] [CrossRef] [Google Scholar]
- Jensen, A. G., Redfield, S., Endl, M., et al. 2012, ApJ, 751, 86 [Google Scholar]
- Koskinen, T., Harris, M., Yelle, R., & Lavvas, P. 2013, Icarus, 226, 1678 [Google Scholar]
- Kulow, J. R., France, K., Linsky, J., & Loyd, R. P. 2014, ApJ, 786, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Lammer, H., Selsis, F., Ribas, I., et al. 2003, ApJ, 598, L121 [Google Scholar]
- Lecavelier Des Etangs, A., Ehrenreich, D., Vidal-Madjar, A., et al. 2010, A & A, 514, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Linsky, J. L., Fontenla, J., & France, K. 2013, ApJ, 780, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Linssen, D., Oklopčić, A., & MacLeod, M. 2022, A & A 667, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Loyd, R. P., France, K., Youngblood, A., et al. 2016, ApJ, 824, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Mignone, A., Bodo, G., Massaglia, S., et al. 2007, ApJS, 170, 228 [Google Scholar]
- Murray-Clay, R. A., Chiang, E. I., & Murray, N. 2009, ApJ, 693, 23 [Google Scholar]
- Salz, M., Czesla, S., Schneider, P. C., et al. 2018, A & A, 620, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shaikhislamov, I., Khodachenko, M., Lammer, H., et al. 2021, MNRAS, 500, 1404 [Google Scholar]
- Shematovich, V. I., Ionov, D. E., & Lammer, H. 2014, A & A, 571, A94 Shull, J. 1979, ApJ, 234, 761 [Google Scholar]
- Simon Wedlund, C., Gronoff, G., Lilensten, J., et al. 2011, Ann. Geophys., 29, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Teşileanu, O., Mignone, A., & Massaglia, S. 2008, A & A, 488, 429 [CrossRef] [EDP Sciences] [Google Scholar]
- Toro, E. F. 2009, in Riemann Solvers and Numerical Methods for Fluid Dynamics (Berlin: Springer), 315 [CrossRef] [Google Scholar]
- Tremblin, P., & Chiang, E. 2013, MNRAS, 428, 2565 [NASA ADS] [CrossRef] [Google Scholar]
- Tripathi, A., Kratter, K. M., Murray-Clay, R. A., & Krumholz, M. R. 2015, ApJ, 808, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Vidal-Madjar, A., Lecavelier Des Etangs, A., Désert, J.-M., et al. 2003, Nature, 422, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, Y., & Lithwick, Y. 2013, ApJ, 772, 74 [Google Scholar]
- Yelle, R. V. 2004, Icarus, 170, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Youngblood, A., France, K., Loyd, R. P., et al. 2016, ApJ, 824, 101 [NASA ADS] [CrossRef] [Google Scholar]
European comprehensive solar irradiance data exploitation; https://projects.pmodwrc.ch/solid
All Tables
1D spherical mass-loss rates calculated for all planetary systems with and without the secondary ionisation by photoelectrons.
All Figures
 |
Fig. 1 Illustration of the photoionisation model and the heating of an atmosphere. The atmosphere is irradiated by XUV stellar photons with an incident flux Fxuv. The gas particles are under the influence of stellar gravity Fstar, planetary gravity Fplanet and centrifugal forces Fcent. |
| In the text | |
 |
Fig. 2 Solar XUV spectrum. The original solar spectrum downloaded from SOLID at 1 AU is shown in black. The binned spectrum used in our calculations is shown as blue bars. |
| In the text | |
 |
Fig. 3 Schematic of the energy channelling from an impacting photon into a photoelectron that can lead to the heating of the gas, its excitation, and secondary ionisation. |
| In the text | |
 |
Fig. 4 Energy Eh deposited as heat by primary electrons of energy E0. The solid curves represent different fractional ionisations. The heating efficiency is given by ηλ,xe = Eh/E0. The figure is based on calculations from García Muñoz (2023). |
| In the text | |
 |
Fig. 5 Secondary ions |
| In the text | |
 |
Fig. 6 Expected effect of photoelectrons on ionisation and heating rates. Top panel: fractional ionisation xe as a function of neutral number density nH I when a Jovian-like planet is irradiated by a solar spectrum. Five particular altitudes are labelled by coloured squares and correspond to the series of panels below. Bottom left panels: contribution to the photoionisation rate at different altitudes, without secondary ionisation J xH I [s−1] (solid lines) and with photoelectrons (dotted lines), as a function of wavelength. Bottom right panels: contribution to the heating rate at different altitudes, H′ [erg s−1 cm−3] representing the energy available before photoionisation (solid lines). The dashed line represents the heating rate due to photoionisation without the effect of photoelectrons, and the dotted lines show the net heating rate with secondary ionisation. The dashed and dotted lines overlap at higher altitudes. The curves provide valuable insight into the wavelengths that contribute to heating at each altitude and how this energy is affected by photoelectrons. |
| In the text | |
 |
Fig. 7 Evaporating atmosphere of the case M0.05 without (red lines) and with (black lines) the effect of secondary ionisation. Left panels from top to bottom: density, pressure, ionisation rate and temperature. Right panels from top to bottom: fractional ionisation, velocity, Mach number and heating rate. |
| In the text | |
 |
Fig. 8 Heating efficiencies for the case M0.05. Top panel: heating efficiency |
| In the text | |
 |
Fig. 9 Ionisation yields for the case M0.05. Top panel: number of total (primary plus secondary) ions created per primary photoelectron as a function of wavelength and altitude for the M0.05 planet. The grey regions indicate where |
| In the text | |
 |
Fig. 10 Comparison of two different planetary masses: a sub-Neptunelike planet of 0.02 MJ (M0.02, green) and a Jovian-like planet of 0.69 MJ (M0.69, blue). The dashed lines and dotted lines represent the cases with and without secondary ionisation, respectively. From top to bottom: fractional ionisation xe as a function of neutral density (a), photoionisation rate JxH I (b), and heating deposition rate H (c). |
| In the text | |
 |
Fig. 11 XUV stellar spectra. Top panel: panchromatic SED downloaded from the MUSCLES Treasury Survey for GJ1214, GJ832 and HD 97658 and scaled at a distance of 1 AU. The solar spectrum at 1 AU used in the preceding section is shown by the black line. Bottom panel: scaled and binned spectra of our sample of stars. After scaling (see text), the integral over wavelength is the same for all four stars. |
| In the text | |
 |
Fig. 12 Heating efficiencies and ionisation yields for different stars and the Sun. Top panel: heating efficiencies |
| In the text | |
 |
Fig. 13 Heating efficiency |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.