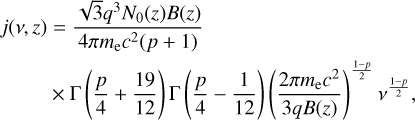EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 679 (November 2023) A&A, 679 (2023) A81 Full HTML
Open Access
Issue
A&A
Volume 679, November 2023
Article Number A81
Number of page(s) 6
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/202346379
Published online 16 November 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

Black-hole X-ray binaries (BHXRBs) exhibit many observational correlations, the most prominent of which is the correlation seen in the hard state between the radio flux FR, for example, at 8.6 GHz, and the X-ray flux FX, between 2 and 10 keV, for example (Hannikainen et al. 1998; Corbel et al. 2000, 2003; Gallo et al. 2003, Bright et al. 2020; Shaw et al. 2021). In the so-called standard track, the correlation is of the form 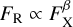FR∝FXβ${F_{\rm{R}}} \propto F_{\rm{X}}^\beta $, where β ≈ 0.7 (Gallo et al. 2003; Corbel et al. 2003) or β ≈ 0.6 (Corbel et al. 2013). Radio and X-ray emission also occurs in the hard-intermediate state, but the relation between the two has not yet been studied.

Extensive theoretical work has been undertaken on both the radio and the X-ray emissions from BHXRBs. It is well accepted that the hard X-rays originate by inverse Compton scattering in the corona around the black hole (see, e.g., Done et al. 2007; Kylafis & Belloni 2015) and the radio in the relativistic jet (e.g., Fender et al. 2004). Unlike wind-like outflows, the jet is considered to be a narrow structure, on the order of 10 gravitational radii at its base (e.g., Zdziarski et al. 2022), with a Lorentz factor γ ≫ 1. The jet and the corona are disjoint, but the jet is fed from the accretion flow – corona system, and this led Heinz & Sunyaev (2003) to examine scale invariant jet models, where they showed analytically that FR ∝ (Mṁ)17/12, where M is the mass of the black hole and ṁ is the accretion rate in units of the Eddington rate. For radiatively inefficient accretion flows, such as the advection dominated accretion flows (ADAFs; Narayan & Yi 1994, 1995; Abramowicz et al. 1995), for which FX ∝ Mṁq with q = 2.3, one has 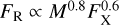FR∝M0.8FX0.6${F_{\rm{R}}} \propto {M^{0.8}}F_{\rm{X}}^{0.6}$, which adeptly explains the observations (Merloni et al. 2003). If q is somewhat different than 2.3, such as q = 2, the observed FR–FX correlation cannot be explained.

A common picture of the accretion flow in BHXRBs in their hard and hard-intermediate states consists of a geometrically thin, optically thick, outer disk (Shakura & Sunyaev 1973) and a hot inner flow, ADAF, which is geometrically thick and optically thin (Narayan & Yi 1994, 1995; Abramowicz et al. 1995). This hot inner flow is taken as the corona in many models, including Heinz & Sunyaev (2003) and Merloni et al. (2003). It is not widely recognized that, due to the positive Bernoulli integral of the hot inner flow, a mildly relativistic outflow must emanate from it (Blandford & Begelman 1999; Kazanas et al. 2015). In other words, the Comptonizing corona is not static, but is outflowing. This has tremendous implications.

We have been putting forward the idea that Comptoniza-tion in BHXRBs takes place mainly in the outflow (outflowing corona). As we discuss in Sect. 4, our picture explains a number of correlations, some of which have not been explained by any other model. Due to the magnetic field that is needed for the ejection of the outflow (e.g., Blandford & Payne 1982), the outflow also emits radio waves. Since it is the same electrons that perform the Compton up-scattering of the soft photons and the radio emission by synchrotron, it is likely that the radio and the X-rays are correlated. This is what we demonstrate below, restricting our study to GX 339-4, because it is well studied and we have previously modeled various correlations exhibited by this source (Reig & Kylafis 2015; Kylafis & Reig 2018; Kylafis et al. 2020).

Other studies have proposed an outflowing corona. The first such proposal was made by Beloborodov et al. (1999). Other works (e.g., Malzac et al. 2001; Markoff et al. 2005; Poutanen et al. 2023) have shown that the base of the outflow plays the role of the corona. We remark that the well-known jet emitting disk – standard accretion disk (JED-SAD) model (Marcel et al. 2019; Barnier et al. 2022; see also previous work by this group), which is able to reproduce the spectral behavior (X-ray and radio) of BHXRBs during their outbursts, relies on self-consistent accretion-ejection solutions, unlike our simple model, which assumes the structure of the outflowing corona.

The structure of our paper is as follows. We describe our model in Sect. 2, present our results in Sect. 3, and discuss our findings in Sect. 4.

2 The model

We performed Monte Carlo simulations of Comptonization in an extended outflowing region. In our previous works, we referred to this outflowing corona as the jet, because in the past, anything outflowing was called a “jet”. However, this name now appears inappropriate. The outflow may or may not include a relativistic jet close to the black-hole axis. Our model consists of a parabolic outflowing corona with two symmetric lobes, where both Comptonization and radio emission occur. We subsequently describe the lobe along the positive z axis.

2.1 The outflowing corona

Guided by previous observations (Asada & Nakamura 2012; Kovalev et al. 2020), we consider a parabolic outflowing corona whose radius at height z > 0 above the black hole is given by 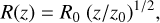R(z)=R0  (z/z0)1/2,$R\left( z \right) = {R_0}\,\,{\left( {{z \mathord{\left/ {\vphantom {z {{z_0}}}} \right. \kern-\nulldelimiterspace} {{z_0}}}} \right)^{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}}},$(1)

where R0 is the radius of the outflow at its base, which is taken to be at a height z0 above the black hole. Here, R0 and z0 are parameters of the model.

At the bottom of the outflow, there is an acceleration region, beyond which the flow speed is constant and equal to v0. Thus, the speed of the outflowing matter along the z axis is taken to be 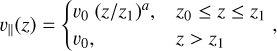υ‖(z)={ υ0 (z/z1)a,z0≤z≤z1υ0,z>z1 ,${\upsilon _}\left( z \right) = \left\{ {\matrix{ {{\upsilon _0}\,{{\left( {{z \mathord{\left/ {\vphantom {z {{z_1}}}} \right. \kern-\nulldelimiterspace} {{z_1}}}} \right)}^a},} \hfill & {{z_0} \le z \le {z_1}} \hfill \cr {{\upsilon _0},} \hfill & {z > {z_1}} \hfill \cr } } \right.,$(2)

where v0, z1, and a are three of the parameters of our model.

If ne(z) is the number density of electrons along the outflow, mass conservation requires that 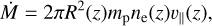M˙=2πR2(z)mpne (z)υ‖(z),$\dot M = 2\pi {R^2}\left( z \right){m_{\rm{p}}}{n_{\rm{e}}}\,\left( z \right){\upsilon _}\left( z \right),$(3)

where Ṁ is the mass-outflow rate and mp is the proton mass. The outflowing matter is considered to consist only of protons and electrons. Equation (3) implies that the number density of the electrons along the outflow is given by 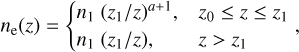ne(z)={ n1 (z1/z)a+1,z0≤z≤z1n1 (z1/z),z>z1 ,${n_{\rm{e}}}\left( z \right) = \left\{ {\matrix{ {{n_1}\,{{\left( {{z \mathord{\left/ {\vphantom {z {{z_1}}}} \right. \kern-\nulldelimiterspace} {{z_1}}}} \right)}^{a + 1}},} \hfill & {{z_0} \le z \le {z_1}} \hfill \cr {{n_1}\,\left( {{z \mathord{\left/ {\vphantom {z {{z_1}}}} \right. \kern-\nulldelimiterspace} {{z_1}}}} \right),} \hfill & {z > {z_1}} \hfill \cr } } \right.,$(4)

where n1 is the number density of electrons at z1, while the density at the base of the outflow is n0 = n1(z1/z0)a+1. The Thomson optical depth of the outflow along z is given by 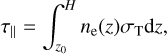τ‖=∫z0Hne (z)σTdz,${\tau _} = \int_{{z_0}}^H {{n_{\rm{e}}}\,\left( z \right){\sigma _{\rm{T}}}{\rm{d}}z} ,$(5)

where σT is the Thomson cross section and H is the height of the outflow. Instead of n0, we took τ‖ as a model parameter.

In the rest frame of the flow, the electrons are generally taken to have a power-law distribution of Lorentz γ, namely 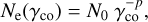Ne(γco)=N0 γco−p,${N_{\rm{e}}}\left( {{\gamma _{{\rm{co}}}}} \right) = {N_0}\,\gamma _{{\rm{co}}}^{ - p},$(6)

from γmin to γmax, where p, γmin, and γmax are parameters of the model. Readers can look below for details about N0. Here, γco is the Lorentz factor of the electrons in the co-moving frame.

In order to calculate the distribution of the electrons for an observer at rest, one would need to perform the transformation of the Lorentz factor from γco to γ. If one assumes that the velocity of the outflow is constant throughout, then it can be shown that γ is approximately proportional to γco, and thus Eq. (6) also holds for an observer at rest. Since the acceleration region is small, the contribution of the acceleration region to the radio emission of the outflow is small. Thus, we neglect the transformation from γco to γ and take the distribution of electrons for the observer at rest to be 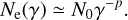Ne (γ)≃N0γ−p.${N_{\rm{e}}}\,\left( \gamma \right) \simeq {N_0}{\gamma ^{ - p}}.$(6a)

The normalization N0(z) can be calculated by integrating Eq. (6a) from γmin to γmax, and equating the expression with the co-moving electron density. This yields 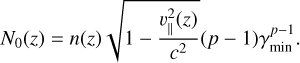N0(z)=n(z) 1−υ‖2(z)c2(p−1)γminp−1.${N_0}\left( z \right) = n\left( z \right)\,\sqrt {1 - {{\upsilon _^2\left( z \right)} \over {{c^2}}}} \left( {p - 1} \right)\gamma _{{\rm{min}}}^{p - 1}.$(7)

Parameter values. As in our previous work, we fixed all of the parameters, except for R0 and τ‖, which we varied. The rest of the parameters have the values z0 = 5Rg, where Rg = GM/c2 with M the black-hole mass, v0 = 0.8c, z1 = 50Rg, a = 1/2, p = 3, γmin = 1.0, and γmax = 500.

Our results and conclusions are insensitive to reasonable values of the above parameters. In particular, v0 can be significantly less than 0.8 and all of our previous work (see Sect. 4) is unaffected (Reig & Kylafis, in prep.). The crucial ingredient of our model is the parabolic shape of the outflow. Non-parabolic outflows might be necessary to explain the so-called outlier sources, but this will be the subject of a subsequent paper.

2.2 Radio emission

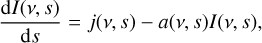Ignoring synchrotron self-Compton (for a justification, see Giannios 2005), the equation for the transfer of radio photons in the outflow, in direction n^${\hat n}$, along which length is measured by s, is given by dI(v,s)ds=j(v,s)−a(v,s)I(v,s),${{{\rm{d}}I\left( {v,s} \right)} \over {{\rm{d}}s}} = j\left( {v,s} \right) - a\left( {v,s} \right)I\left( {v,s} \right),$(8)

where j(ν, s) and a(ν, s) are the emission and absorption coefficients, respectively, and I(ν, s) is the intensity at frequency ν at position s. The formal solution of this equation is 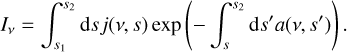Iv=∫s1s2ds j(v,s) exp (− ∫ss2ds′a(v,s′)).${I_v} = \int_{{s_1}}^{{s_2}} {{\rm{d}}s\,j\left( {v,s} \right)\,{\rm{exp}}\,\left( { - \,\int_s^{{s_2}} {{\rm{d}}s} \prime a\left( {v,s\prime } \right)} \right)} .$(9)

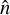For n^${\hat n}$ perpendicular to the outflow axis, this is simplified to Iv(z)=j(v,z)a(v,z)[ 1−exp{ −a(v,z)R(z) } ],${I_v}\left( z \right) = {{j\left( {v,z} \right)} \over {a\left( {v,z} \right)}}\left[ {1 - {\rm{exp}}\left\{ { - a\left( {v,z} \right)R\left( z \right)} \right\}} \right],$(10)

where R(z) is given by Eq. (1), since the emission and absorption coefficients only depend on z. The total power radiated per unit frequency, per unit solid angle is thus given by 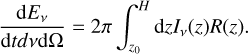dEvdtdvdΩ=2π ∫z0HdzIv(z)R(z).${{{\rm{d}}{E_v}} \over {{\rm{d}}tdv{\rm{d\Omega }}}} = 2\pi \,\int_{{z_0}}^H {{\rm{d}}z{I_v}\left( z \right)R\left( z \right)} .$(11)

We next needed to specify the absorption and emission coefficients. Since the radio emission of the outflow is due to synchrotron-emitting electrons, whose Lorentz factors follow a power law as in Eq. (6a), the absorption and emission coefficients can be calculated analytically (Rybicki & Lightman 1979). 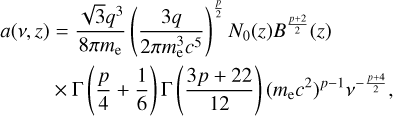The expressions are a(v,z)=3q38πme(3q2πme3c5)p2 N0(z)Bp+22(z)                × Γ (p4+16)Γ (3p+2212) (mec2)p−1v−p+42,$\matrix{ {a\left( {v,z} \right) = {{\sqrt 3 {q^3}} \over {8\pi {m_{\rm{e}}}}}{{\left( {{{3q} \over {2\pi m_{\rm{e}}^3{c^5}}}} \right)}^{{p \over 2}}}\,{N_0}\left( z \right){B^{{{p + 2} \over 2}}}\left( z \right)} \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \,{\rm{\Gamma }}\,\left( {{p \over 4} + {1 \over 6}} \right){\rm{\Gamma }}\,\left( {{{3p + 22} \over {12}}} \right)\,{{\left( {{m_{\rm{e}}}{c^2}} \right)}^{p - 1}}{v^{ - {{p + 4} \over 2}}},} \hfill \cr } $(12)

and j(v,z)=3q3N0(z)B(z)4πmec2(p+1)                × Γ (p4+1912)Γ (p4−112) (2πmec23qB(z))1−p2v1−p2,$\matrix{ {j\left( {v,z} \right) = {{\sqrt 3 {q^3}{N_0}\left( z \right)B\left( z \right)} \over {4\pi {m_{\rm{e}}}{c^2}\left( {p + 1} \right)}}} \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \,{\rm{\Gamma }}\,\left( {{p \over 4} + {{19} \over {12}}} \right){\rm{\Gamma }}\,\left( {{p \over 4} - {1 \over {12}}} \right)\,{{\left( {{{2\pi {m_{\rm{e}}}{c^2}} \over {3qB\left( z \right)}}} \right)}^{{{1 - p} \over 2}}}{v^{{{1 - p} \over 2}}},} \hfill \cr } $(13)

where q and me are the absolute value of the charge and the mass, respectively, of the electron, B(z) = B0(z0/z) is the strength of the magnetic field at height z assuming flux freezing B0 = B(z0), and Γ is the Gamma function.

Integrating Eq. (11) over solid angles gives the power per unit frequency radiated, 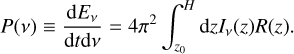P(v)≡dEvdtdv=4π2 ∫z0HdzIv(z)R(z).$P\left( v \right) \equiv {{{\rm{d}}{E_v}} \over {{\rm{d}}t{\rm{d}}v}} = 4{\pi ^2}\,\int_{{z_0}}^H {{\rm{d}}z{I_v}\left( z \right)R\left( z \right)} .$(14)

Since there are two outflows with opposite directions to each other, an observer at a distance d, whose line of sight makes a 90-degree angle with the outflow axis, measures a flux of 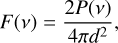F(v)=2P(v)4πd2,$F\left( v \right) = {{2P\left( v \right)} \over {4\pi {d^2}}},$(15)

where d is the distance to the source. Since the observer’s line of sight is taken to be perpendicular to the outflow axis, there is no need to account for a Doppler shift.

In Fig. 1, we show the flux of the radio emission of the outflow for p = 3, B0 = 2 × 105 G, and two values of the two main parameters, namely τ‖ = 8.6 and R0 = 110 Rg (the blue line, corresponding to the hard state), and τ‖ = 4.3 and R0 = 600 Rg (the red line, corresponding to the hard-intermediate state). The slope of the partially optically thick spectrum is α ≈ 0.2.

thumbnail Fig. 1

Flux per unit frequency produced by a power-law distribution of electrons with p = 3 and B0 = 2 × 105 G for R0 = 110Rg and τ‖ = 8.6 (blue curve), and R0 = 600Rg and τ‖ = 4.3 (red curve). The power-law spectral index is α ≈ 0.2 in both curves.

2.3 X-ray observations

The X-ray data analyzed in this work correspond to the 2007–2008 outburst of GX 339-4 and were obtained with the Rossi X-ray Timing Explorer (RXTE). The data cover the interval MJD 53769–54678. The details of the data analysis can be found in Reig et al. (2018) and Kylafis & Reig (2018). We remark that the data and the models used in this paper are the same as those used in Kylafis & Reig (2018). In this work, we restrict the analysis to the hard and hard-intermediate states during the rise of the outburst. We obtained the energy spectra using the standard-2 mode of the RXTE/PCA instrument in the energy range 3–9 keV to match the range used in Corbel et al. (2013). We fitted the spectra with a broken power-law model and a Gaussian component that represents the iron emission line at approximately 6.4 keV. We allowed for absorption at low energies. The hydrogen column density was fixed to NH = 4 × 1021cm−2 (Dunn et al. 2010).

In Fig. 2, we show the observed correlation between the 3–9 keV X-ray flux and the photon-number spectral index Γ. The blue dots correspond to the hard state and the red dots to the hard-intermediate state.

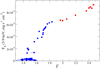thumbnail Fig. 2

Relationship between the observed X-ray flux in the 3–9 keV range and the photon index Γ. The blue dots correspond to the hard state and the red dots to the hard-intermediate one.

2.4 Comptonization

In our model, Compton up-scattering of the soft input photons takes place in the outflow. It is assumed that the soft photons come from the inner part of the accretion disk and have a black-body spectrum with kTBB = 0.2 keV. This value of kTBB is not crucial. The radiative transfer is undertaken by our Monte Carlo code, which has been in use for the past 20 yr. The soft photons are emitted isotropically upward at the base of the outflow. Typically, 107 photons are sufficient to obtain robust statistics. The emergent hard X-ray spectrum is a power law with photon number index Г.

In Kylafis & Reig (2018), we used this Comptonization model and reproduced the observed values of Г in the hard and hard-intermediate states, along with the observed time lags of the 9–15 keV with respect to the 2–6 keV photons. The same models that reproduce the correlation between the time lag and Г (Kylafis & Reig 2018) were used for this study to compute the radio spectra (see Fig. 1) and the radio flux at 8.6 GHz (used in Fig. 3).

For each model (i.e., τ‖ and R0) that produces, with Comptonization in the outflow, an index Г, we computed the radio flux that comes out of the outflow. In Fig. 3, we show the pairs (Г, FR) from our model. We remark that Fig. 3 is entirely theoretical. In other words, it is a quantitative, theoretical prediction of our model for a future outburst of GX 339-4 (and also for previous outbursts, if simultaneous radio and X-ray data exist), similar to the one examined here. Figure 3 applies to the specific outburst studied here, yet we assert that the same curve (scaled up or down) should be observed in any outburst of GX 339-4. It is difficult to imagine how such a correlation can be produced by the typically considered model (a hot inner flow and a relativistic jet), since Г is fixed by the hot inner flow (corona) and the radio flux from the jet, and the two do not seem to communicate with each other. While Fig. 3 depicts the rise of the outburst of GX 339-4, we predict that in the declining part of the outburst, the curve is traversed backwards, that is, from high Г to low Г, although the maximum radio flux is lower than in the rising part.

The radio-flux – Г prediction above is related, and qualitatively similar, to the prediction made by Kylafis & Reig (2018, see their Fig. 4) regarding the radio-break-frequency - Г correlation in GX 339-4. It is probably easier to confirm or reject the present prediction than the earlier one. As in Fig. 2, the blue dots in Fig. 3 correspond to the hard state and the red dots to the hard-intermediate state.

It is interesting to look at Figs. 2–4 from a different point of view. Figure 2 is an observational correlation between FX and Г. Figure 4 is an observational correlation between FX and FR, where we assume, for this discussion, that the sudden increase in FR and its subsequent sudden decrease in the hard-intermediate state (the red dots in Fig. 4) will be confirmed observationally. Therefore, it is an observational requirement that FR must be correlated with Г. In other words, Fig. 3 is an observational requirement that should be obeyed by all the models. As we demonstrated above, Fig. 3 is obeyed by the outflow model. It will be interesting to see if it is obeyed by the other models also.

thumbnail Fig. 3

Relationship between the theoretical radio flux at 8.6 GHz and the photon index Г. This relationship is a theoretical prediction. The blue dots correspond to the hard state and the red dots to the hard-intermediate one.

3 Results

Figures 2 and 3 show that we can find the correlation between FR and FX, We proceeded as follows: we binned the X-ray data using the photon index Г in bins of 0.02 in size for the hard state, and of 0.1 for the hard-intermediate state. We computed the average value for each bin. We then found the Monte Carlo model that produces a similar Г and took the radio flux computed by it. In this way, we have pairs (FR, FX) that correspond to the same Г.

In Fig. 4, we plotted the pairs (FR, FX). As in Figs. 2 and 3, the blue dots correspond to the hard state and the red dots to the hard-intermediate state. The straight black line is not a fit to the blue dots, but represents the observational correlation found by Corbel et al. (2013). It is a power-law function 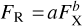FR=aFXb${F_{\rm{R}}} = aF_{\rm{X}}^b$, where а = 1.85 and b = 0.62. This power law breaks down when the source enters the hard-intermediate state. There, the radio flux initially increases sharply and then sharply decreases within a narrow range of FX values (see also Fig. 3) and this is a prediction of our model.

The radio flux depends on the value of B0 as FR ~ B(p+1)/2, where p is the exponent in the electron energy distribution (Eq. (6a)). Thus, we selected the appropriate B0 by only shifting the data points vertically, until they matched the observational correlation (the solid line in Fig. 4). In other words, the slope of the data points is correct. The shifting of the points vertically was done by the parameter B0.

The careful reader may have noticed that we have used Eq. (10) for the calculation of the radio flux because of its simplicity. For an inclination angle between 40 and 60o, which is thought to be appropriate for GX339-4 (Shidatsu et al. 2011; Fürst et al. 2015), the calculation is much more complicated and the radio flux is lower than what we have calculated. The only effect from this is that the blue dots in Fig. 4 are not shifted vertically as much and the red dots do not reach such high values of FR. In other words, the inferred value of B0 is slightly less than 2 × 105 G.

thumbnail Fig. 4

Relationship between the observed X-ray flux in the 3–9 keV range and the computed radio flux at 8.6 GHz. The black line is not a fit to the blue dots, but is the observational correlation of Corbel et al. (2013). The blue dots correspond to the hard state and the red dots to the hard-intermediate one.

4 Discussion

We find it interesting that the observed slope of the FR–FX correlation is so adeptly reproduced with our outflow model. As mentioned in the Introduction, a correlation between the two quantities is expected, because the same electrons perform the Comptonization and the synchrotron emission in the outflow model. Of course, this could be any correlation and not necessarily the one observed.

In the hard-intermediate state, the sharp drop of the radio flux has been observed in a few sources (Gallo et al. 2003; Homan et al. 2005; Fender et al. 2009; Coriat et al. 2009; van der Horst et al. 2013; Russell et al. 2020). Here, and for GX 339-4, we make the prediction that as the source moves from the hard to the hard-intermediate state, the radio flux first increases sharply and then sharply decreases. Since the hard-intermediate state during the outburst rise lasts only for approximately five days, high-cadence radio observations are needed to confirm this.

In this work, we have assumed that the observed radio emission comes from the outflowing corona. It is not clear whether there is a narrow relativistic jet in the central part of the outflow. If there is, our model makes the tacit assumption that it is not dominant. We remark that, in sources seen at high or moderate inclination (such as GX 339-4), the emission from a relativistic jet (Lorentz γ ≫ 1) is expected to be weaker from the side rather than in the jet direction, because of Lorentz boosting. In such cases, the radio is expected to be dominated by the outflowing corona.

A question then naturally arises as to why sources whose radio emission comes mainly from the relativistic jet and sources whose radio emission is dominated by the outflow exhibit more or less the same FR–FX correlation. The answer seems to be that both the jet and the outflow are fed by the hot inner flow (ADAF). Whether the Comptonization takes place in the corona, which is rotating around the black hole (hot inner flow, ADAF), or in an outflowing corona (outflow), the hard X-ray flux is more or less the same. Similarly, the scaling relations of Heinz & Sunyaev (2003) and Merloni et al. (2003) are valid whether the Blandford & Payne (1982) mechanism is active and an outflow is produced, whether the Blandford & Znajek (1977) mechanism operates and a relativistic jet is produced, or both.

Another question arises as to whether the outflow model is preferable to the typically considered model. In our opinion, the answer is unequivocally yes, and for the following reasons: (1) A model that in addition to explaining the observations also makes predictions, increases its credibility. The outflow model makes two predictions: that the radio flux should be correlated with Γ (Fig. 3) and that the radio flux in the hard-intermediate state must initially suddenly increase and then suddenly decrease (see the red dots in Fig. 3) as the source goes to the soft state. A related prediction was made in Kylafis & Reig (2018) involving the radio break frequency and the photon-number spectral index. (2) The outflow model is extremely simple, with only Comptonization in and radio emission from a parabolic outflowing corona. Nothing else is needed. (3) Despite its simplicity, the outflow model quantitatively explains many correlations and observations, some of which have not been explained by any other model. These are:

  • 1)

    the energy spectrum from radio to hard X-rays for the source XTE J1118+480 (Giannios 2005),

  • 2)

    the time-lag – Fourier frequency correlation in Cyg X-1 (Reig et al. 2003),

  • 3)

    the correlation between the time-lag and the photon-number spectral index Γ in GX 339-4 (Kylafis & Reig 2018) and other sources (Reig et al. 2018),

  • 4)

    the fact that this correlation depends on the inclination of the source (Reig & Kylafis 2019),

  • 5)

    the phase-lag — cutoff-energy correlation observed in GX 339-4 (Reig & Kylafis 2015),

  • 6)

    the narrowing of the auto-correlation function with increasing photon energy seen in Cyg X-1 (Giannios et al. 2004),

  • 7)

    the correlation between the Lorentzian frequencies in the power spectrum and the photon-number spectral index Γ in Cyg X-1 and GX 339-4 (Kylafis et al. 2008),

  • 8)

    the photon-number spectral index as a function of the phase of the type-B quasi periodic oscillation (QPO) in GX 339-4 (Kylafis et al. 2020),

  • 9)

    the outflow provides a natural lamppost for the hard X-ray photons that return to the disk, where reflection and reverberation occurs (Reig & Kylafis 2021),

  • 10)

    the FR – FX correlation in GX 339-4 (this work),

  • 11)

    and, finally, the outflow model may naturally explain the observed X-ray polarization in BHXRBs (see the final remark below).

All of the above correlations are explained with only two parameters of the outflow: the radius R0 at its base and the Thomson optical depth τ‖ along its axis. For all of the observations and correlations above, these two quantities vary in our model in the same narrow ranges of 10 ≲ R0/Rg ≲ 1000 and 1 ≲ τ‖ ≲ 10.

Due to the large density at the bottom of the parabolic outflow and its large size (10–103 Rg), the soft input photons from the accretion disk, coming from below, see something resembling a “slab” at the bottom of the outflow, parallel to the accretion disk. This is because for τ‖ ~ 10 (appropriate for the hard state of GX 339-4), the height h, at which τ‖ from the bottom of the outflow is 3, for example, is much less than the radius R(z0 + h) of the outflow there. Therefore, τ⊥ ≫ 3 and the bottom of the outflow appears to the soft photons as a slab. Compton scattering of X-rays in a slab parallel to the accretion disk produces polarization perpendicular to it, that is, along the outflow (Beloborodov 1998). This has been observed with IXPE (Krawczynski et al. 2022). If our picture is correct, then we predict that the X-ray polarization direction in GX 339-4 will change from parallel to perpendicular to the flow, as the source moves from the hard state (τ‖ ~ 10) to the hard-intermediate state (τ‖ ~ 1).

Acknowledgements

We would like to thank Pierre-Olivier Petrucci for very useful comments on an earlier version of this paper and Iossif Papadakis, Andrei Beloborodov, Tom Russell, and Greg Marcel for useful discussions. Also, N.D.K. acknowledges useful e-mail exchanges with Rob Fender and David Russell regarding radio observations in the hard-intermediate state.

References

  1. Abramowicz, M. A., Chen, X., Kato, S., & Regev, O. 1995, ApJ, 438, L37 [NASA ADS] [CrossRef] [Google Scholar]
  2. Asada, K., & Nakamura, M. 2012, ApJ, 745, 28 [Google Scholar]
  3. Barnier, S., Petrucci, P.-O., Ferreira, J., et al. 2022, A&A, 657, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Beloborodov, A. M. 1998, ApJ, 496, L105 [Google Scholar]
  5. Beloborodov, A. M. 1999, ApJ, 510, L123 [CrossRef] [Google Scholar]
  6. Blandford, R. D., & Begelman, M. C. 1999, MNRAS, 303, L1 [NASA ADS] [CrossRef] [Google Scholar]
  7. Blandford, R. D., & Payne, D. G. 1982, MNRAS, 199, 883 [CrossRef] [Google Scholar]
  8. Blandford, R. D., & Znajek, R. L. 1977, AREPS, 5, 111 [NASA ADS] [Google Scholar]
  9. Bright, J. S., Fender, R. P., Motta, S. E., et al. 2020, Nat. Astron., 4, 697 [NASA ADS] [CrossRef] [Google Scholar]
  10. Corbel, S., Fender, R. P., Tzioumis, A. K., et al. 2000, A&A, 359, 251 [NASA ADS] [Google Scholar]
  11. Corbel, S., Nowak, M. A., Fender, R. P., Tzioumis, A. K., & Markoff, S. 2003, A&A, 400, 1007 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Corbel, S., Coriat, M., Brocksopp, C., et al. 2013, MNRAS, 428, 2500 [Google Scholar]
  13. Coriat, M., Corbel, S., Buxton, M. M., et al. 2009, MNRAS, 400, 123 [Google Scholar]
  14. Done, C., Gierlinski, M., & Kubota, A. 2007, A&ARv, 15, 1 [Google Scholar]
  15. Dunn, R. J. H., Fender, R. P., Körding, E. G., Belloni, T., & Cabanac, C. 2010, MNRAS, 403, 61 [Google Scholar]
  16. Fender, R. P., Belloni, T. M., & Gallo, E. 2004, MNRAS, 355, 1105 [NASA ADS] [CrossRef] [Google Scholar]
  17. Fender, R. P., Homan, J., & Belloni, T. M. 2009, MNRAS, 396, 1370 [NASA ADS] [CrossRef] [Google Scholar]
  18. Fürst, F., Nowak, M. A., Tomsick, J. A., et al. 2015, ApJ, 808, 122 [Google Scholar]
  19. Gallo, E., Fender, R. P., & Pooley, G. G. 2003, MNRAS, 344, 60 [Google Scholar]
  20. Giannios, D. 2005, A&A, 437, 1007 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Giannios, D., Kylafis, N. D., & Psaltis, D. 2004, A&A, 425, 163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Hannikainen, D. C., Hunstead, R. W., Campbell-Wilson, D., & Sood, R. K. 1998, A&A, 337, 460 [NASA ADS] [Google Scholar]
  23. Heinz, S., & Sunyaev, R.A. 2003, MNRAS, 343, L59 [NASA ADS] [CrossRef] [Google Scholar]
  24. Homan, J., Buxton, M., Markoff, S., et al. 2005, ApJ, 624, 295 [NASA ADS] [CrossRef] [Google Scholar]
  25. Kazanas, D. 2015, ASSL, 414, 207 [NASA ADS] [Google Scholar]
  26. Kovalev, Y. Y., Pushkarev, A. B., Nokhrina, E. E., et al. 2020, MNRAS, 495, 3576 [NASA ADS] [CrossRef] [Google Scholar]
  27. Krawczynski, H., Muleri, F., Dovciak, M., et al. 2022, Science, 378, 650 [NASA ADS] [CrossRef] [Google Scholar]
  28. Kylafis, N. D., & Belloni, T. M. 2015, A&A, 574, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Kylafis, N. D., & Reig, P. 2018, A&A, 614, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Kylafis, N. D., Papadakis, I. E., Reig, P., Giannios, D., & Pooley, G. G. 2008, A&A, 489, 481 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Kylafis, N. D., Reig, P., & Papadakis, I. 2020, A&A, 640, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Malzac, J., Beloborodov, A. M., & Poutanen, J. 2001, MNRAS, 326, 417 [NASA ADS] [CrossRef] [Google Scholar]
  33. Marcel, G., Ferreira, J., Clavel, M., et al. 2019, A&A, 626, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Markoff, S., Nowak, M. A., & Wilms, J. 2005, ApJ, 635, 1203 [NASA ADS] [CrossRef] [Google Scholar]
  35. Merloni, A., Heinz, S., & di Matteo, T. 2003, MNRAS, 345, 1057 [Google Scholar]
  36. Narayan, R., & Yi, I. 1994, ApJ, 428, L13 [Google Scholar]
  37. Narayan, R., & Yi, I. 1995, ApJ, 452, 710 [NASA ADS] [CrossRef] [Google Scholar]
  38. Poutanen, J., Veledina, A., & Beloborodov, A. M. 2023, ApJ, 949, L10 [NASA ADS] [CrossRef] [Google Scholar]
  39. Reig, P., & Kylafis, N. D. 2015, A&A, 584, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Reig, P., & Kylafis, N. D. 2019, A&A, 625, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Reig, P., & Kylafis, N. D. 2021, A&A, 646, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Reig, P., Kylafis, N. D., & Giannios, D. 2003, A&A, 403, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Reig, P., Kylafis, N. D., Papadakis, I. E., & Costado, M. 2018, MNRAS, 473, 4644 [NASA ADS] [CrossRef] [Google Scholar]
  44. Russell, T. D., Luchini, M., Tetarenko, A. J., et al. 2020, MNRAS, 498, 5772 [NASA ADS] [CrossRef] [Google Scholar]
  45. Rybicki, G. B., & Lightman, A. P. 1979, Radiative Processes in Astrophysics (New York: Wiley) [Google Scholar]
  46. Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
  47. Shaw, A. W., Plotkin, R. M., Miller-Jones, J. C. A., et al. 2021, ApJ, 907, 34 [NASA ADS] [CrossRef] [Google Scholar]
  48. Shidatsu, M., Ueda, Y., Nakahira, S., et al. 2011, PASJ, 63, S803 [NASA ADS] [CrossRef] [Google Scholar]
  49. van der Horst, A. J., Curran, P. A., Miller-Jones, J. C. A., et al. 2013, MNRAS, 436, 2625 [NASA ADS] [CrossRef] [Google Scholar]
  50. Zdziarski, A. A., Tetarenko, A. J., & Sikora, M. 2022, ApJ, 925, 189 [NASA ADS] [CrossRef] [Google Scholar]

All Figures

thumbnail Fig. 1

Flux per unit frequency produced by a power-law distribution of electrons with p = 3 and B0 = 2 × 105 G for R0 = 110Rg and τ‖ = 8.6 (blue curve), and R0 = 600Rg and τ‖ = 4.3 (red curve). The power-law spectral index is α ≈ 0.2 in both curves.
In the text
thumbnail Fig. 2

Relationship between the observed X-ray flux in the 3–9 keV range and the photon index Γ. The blue dots correspond to the hard state and the red dots to the hard-intermediate one.
In the text
thumbnail Fig. 3

Relationship between the theoretical radio flux at 8.6 GHz and the photon index Г. This relationship is a theoretical prediction. The blue dots correspond to the hard state and the red dots to the hard-intermediate one.
In the text
thumbnail Fig. 4

Relationship between the observed X-ray flux in the 3–9 keV range and the computed radio flux at 8.6 GHz. The black line is not a fit to the blue dots, but is the observational correlation of Corbel et al. (2013). The blue dots correspond to the hard state and the red dots to the hard-intermediate one.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.