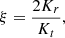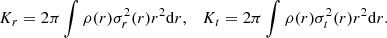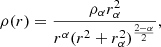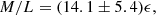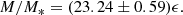| Issue |
A&A
Volume 678, October 2023
|
|
|---|---|---|
| Article Number | A110 | |
| Number of page(s) | 10 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202347487 | |
| Published online | 12 October 2023 | |
Structure of the equivalent Newtonian systems in MOND N-body simulations
Density profiles and the core-cusp problem
1
Dipartimento di Fisica “Giuseppe Occhialini”, Universitá di Milano Bicocca, Piazza della Scienza 3, 20126 Milano, Italy
e-mail: federico.re@unimib.it
2
INFN-Sezione di Milano Via Celoria 15, 20133 Milano, Italy
3
CNR-ISC, via Madonna del Piano 17, 50022 Sesto Fiorentino, Italy
e-mail: pierfrancesco.dicintio@cnr.it
4
INAF-Osservatorio Astronomico di Arcetri, Largo Enrico Fermi 5, 50125 Firenze, Italy
5
INFN-Sezione di Firenze, via Sansone 1, 50022 Sesto Fiorentino, Italy
Received:
17
July
2023
Accepted:
25
August
2023
Aims. We investigate the core-cusp problem of the Λ cold dark matter (ΛCDM) scenario in the context of the modified Newtonian dynamics (MOND) paradigm while exploiting the concept of an equivalent Newtonian system (ENS).
Methods. By means of particle-mesh N-body simulations in MOND, we explored the processes of galaxy formation via cold dissipationless collapse and the merging of smaller substructures. From the end states of our simulations, we recovered the associated ENS and studied the properties of their dark matter halos. We compared the simulation results with simple analytical estimates with a family of γ-models.
Results. We find that the dark matter density of ENSs of most spherical cold collapses have a markedly cored structure, particularly for the lowest values of the initial virial ratios. End states of some simulations with initially clumpy conditions have more complex profiles, and some of their ENSs exhibit a moderate cusp, with the logarithmic density slope always shallower than one.
Conclusions. In contrast to what one would expect from theoretical and numerical arguments in ΛCDM, these results seem to point towards the fact that the absence of a central DM cusp in most observed galaxies would be totally consistent in a MONDian description.
Key words: galaxies: kinematics and dynamics / galaxies: formation / gravitation / methods: analytical / methods: numerical
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
In the Λ cold dark matter scenario (hereafter ΛCDM), theoretical arguments and collisionless N-body simulations (Navarro et al. 1997) predict that galaxies are embedded in dark matter (DM) halos characterised by a ρ(r)∝r−1 central cusp. From the analysis of the central velocity dispersion profiles of dwarf galaxies, observational results seem to suggest that the DM distribution has a cored density distribution1 (see Moore 1994; Di Cintio et al. 2014).
Several solutions to this apparent contradiction – often referred to as ‘the core-cusp problem’ – including as self-interacting DM (e.g. see Lovell et al. 2012; Nguyen et al. 2021; Eckert et al. 2022), DM annihilation (e.g. see Vasiliev 2007), baryon feedback (e.g. see Governato et al. 2010; Cole et al. 2011; Pontzen & Governato 2012; Del Popolo & Pace 2016), or simply a misinterpretation of the observational data (McGaugh et al. 2003), have been proposed so far. However, notwithstanding the great amount of theoretical and observational work, a clear answer is still far from being obtained. Moreover, given the large interest in alternative theories of gravity, such as f(R) gravities (Buchdahl 1970; Sotiriou & Faraoni 2010), modified gravity (MoG; Moffat 2006; Moffat & Rahvar 2013), retarded gravity (Raju 2012; Yahalom 2022), emergent gravity (Verlinde 2011, 2017), refracted gravity (Cesare et al. 2020; Sanna et al. 2023), and fractional gravity (Giusti 2020; Benetti et al. 2023), among others, which have been proposed to avoid introducing the DM as a collisionless fluid of exotic particles, it is natural to ask what becomes of the core-cusp problem in those theories.
In this work, we investigate this matter in the modified Newtonian dynamics paradigm (hereafter MOND; Milgrom 1983). We recall that in the Bekenstein & Milgrom (1984) Lagrangian formulation of MOND (sometimes referred to as AQUAL), the classical Poisson equation for a density-potential pair (ρ; Φ),
is substituted by the non-linear field equation
In the equation above, a0 ≈ 10−8 cm s−2 is a scale acceleration and μ(x) is the MOND interpolating (monotonic) function known only by its asymptotic limits
so that for ||∇Φ|| ≫ a0 Eq. (2), one recovers the Newtonian regime, while for ||∇Φ|| ≪ a0, one obtains the so-called deep-MOND (hereafter dMOND) regime, and Eq. (2) simplifies to
We note that the non-linear operator in Eq. (4) is the special case of the p-Laplace operator (e.g. see Stein 1970) for p = 3, while Eq. (1) corresponds to the p = 2 case. In this respect, Eq. (2) somewhat ‘interpolates’ between the two regimes via the μ function. We also note that in both cases, any given baryonic mass density ρ can be taken out from Eq. (1) to obtain the relation
between the MOND and Newtonian force fields gM and gN and where S ≡ ∇ × h(ρ) is a density-dependent solenoidal field. It can be proven that the latter is identically null for systems in spherical, cylindrical, or planar symmetry, while it is generally non-zero for arbitrary configurations of mass. The extent to which the stellar system at hand with mass M is dominated by MOND effects is usually quantified by the dimensionless parameter
where rc is the scale of the baryon distribution. That is, for κ ≫ 1, the system is mainly in the Newtonian regime, and vice versa for κ ≤ 1 MOND effects, as they become strong at all scales.
For any given stationary model in MOND, one can always build the equivalent Newtonian system (hereafter ENS), defined as a system with the same baryonic mass density ρ* plus a DM halo with density ρDM such that their total potential Φ satisfying Eq. (1) is the same as the MOND potential entering Eq. (2) for the sole density ρ*. We note that, in principle, the positivity of the DM density of the ENS is not always assured (see Milgrom 1986), particularly for flattened systems (see Ciotti et al. 2006, 2012; Ko 2016). We recall that Milgrom (2010) introduced a Quasi-linear formulation of MOND (hereafter QuMOND) where the modified field equation has the same form as Eq. (2), with ν(||gN/a0||) in lieu of ν(||gM/a0||). The QuMOND interpolating function ν(y) can be recovered from μ(x), appearing in Eq. (2) as
It is easy to show that from a given baryonic density distribution, one obtains the MONDian potential Φ = ΦN + ΦpDM by first solving a classical Poisson equation for the Newtonian potential ΦN and that through an algebraic passage involving ν, such potential becomes the source for the potential ΦpDM of the so-called phantom Dark Matter via a second application of the Poisson equation. Notably, in this alternative bi-potential MOND formulation, the DM is de facto interpreted as the effect of the second potential. As in AQUAL, in QuMOND one can retrieve a dMOND regime that for spherical systems easily reads as 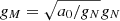 (see Milgrom 2021).
(see Milgrom 2021).
Though several works have investigated the differences between static equilibrium models in Newtonian and MOND gravities, or the interpretation of observations in both theories, much less is known about the formation and evolution of stellar systems. For obvious reasons, in observed systems, one has access only to de-projected properties for both stellar and dark components in the Newtonian framework. Numerical experiments, though with their intrinsic limitations, yield information on the full phase-space of the simulated models, in particular the 3D density profiles. In this paper, we explore the structure of the ENS of MOND N-body simulations of galaxy formation in order to shed some light on the possibility that the core-cusp problem is a MOND artefact in this paradigm of gravity. We stress the fact that the MOND core-cusp problem discussed here is different from that introduced recently by Eriksen et al. (2021), which deals with the modified gravity versus the modified inertia hypothesis (see Milgrom 2022).
The rest of this paper is structured as follows. In Sect. 2, we revise the definition of ENS and discuss their properties. In Sect. 3, we introduce the numerical models and the analysis of the simulations. In Sect. 4, we discuss the properties of the simulations’ end states. Finally, in Sect. 5, we summarise and discusses the implications and the relations to previous work.
2. Equivalent Newtonian systems
As anticipated above, the ENS of a MOND model is the Newtonian system with the same stellar (baryonic) mass distribution ρ* with an additional dark component ρDM such that the total potential (and thus the force field) is the same of the parent MOND system (see Sanders & Begeman 1994; Angus et al. 2006). For the case of an isolated spherical system, one has
since the solenoidal term S vanishes. We stress the fact that, Eq. (5) in QuMOND can be rewritten exactly as
If Eq. (9) is applied to a spherically symmetric system, one has ν(y) = x/y, and the total density of its ENS (i.e. baryonic plus phantom DM; see e.g. Hodson et al. 2020; Oria et al. 2021) becomes
We consider the family of spherical γ-models (Dehnen 1993; Tremaine et al. 1994) with the density profile given by
where M is the total baryonic mass, 0 ≤ γ < 3 is the logarithmic density slope, and rc is the scale radius.
If the density profile, Eq. (11), is substituted in Eq. (10), one obtains
where
with κ defined in Eq. (6). We note that for small radii r, Eq. (13) tends to zero if γ < 1, while it diverges for γ > 1. In practice, at least for the γ < 1 case, the model falls in the MOND regime, even in central regions. Strong MOND corrections in the centre are therefore associated with a dominant DM component ρDM in the ENS.
2.1. Massive galaxies
In this section, we consider a typical 1012 M⊙ massive elliptical galaxy with a scale radius of 3 kpc modelled with a γ-model. In this case, κ ≈ 102. Due to discreteness effects of the underlying stellar system, Eq. (11) can be considered reliable until the radius that contains a fraction of roughly 10−3 of the total mass M (in this case 109 M⊙; i.e. the typical mass of its central supermassive black hole). The Lagrangian radius enclosing such a mass fraction is
The region in the MOND regime has a far smaller radius such that γ ≤ 1 is obtained by 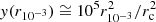 , varying between ≅2 × 102 and ≅2 × 103. And thus, even in the framework of (Qu)MOND, the phantom DM halo does not really dominate in the central region of a cored stellar density profile. In Fig. 1, we plot the ratio of the stellar to phantom DM for γ = 0, 0.5, 1, 1.5, 2, and 2.5, as well as their respective radial density profiles for κ = 102. We note that, remarkably, the models with a strong cusp (i.e. γ > 1) have phantom DM halos in their ENS characterised by a decreasing density inside the scale radius. Vice versa, cored models are associated with ENSs that have halos with a weak cusp and several slope changes.
, varying between ≅2 × 102 and ≅2 × 103. And thus, even in the framework of (Qu)MOND, the phantom DM halo does not really dominate in the central region of a cored stellar density profile. In Fig. 1, we plot the ratio of the stellar to phantom DM for γ = 0, 0.5, 1, 1.5, 2, and 2.5, as well as their respective radial density profiles for κ = 102. We note that, remarkably, the models with a strong cusp (i.e. γ > 1) have phantom DM halos in their ENS characterised by a decreasing density inside the scale radius. Vice versa, cored models are associated with ENSs that have halos with a weak cusp and several slope changes.
 |
Fig. 1. Ratio of the stellar to dark density in the ENS (top) and DM and stellar density profiles (bottom left and bottom right) in units of |
2.2. Diffuse galaxies
In this section, we consider a diffuse galaxy where κ ∼ 1, which allows its central region to fall within the MOND regime, even for radii bigger than r10−3. Typically, this occurs again if γ < 1. We found that limr → 0y(r) = 0 in the central region; hence, ν(y)∼y−1/2. If substituted in Eq. (12), this yields
In other words, the phantom DM component also dominates at small radii. In particular, the latter has a central profile given by
The equation above is characterised by a weak cusp with a logarithmic density slope of 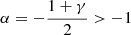 . For example, for γ = 0, the DM component in the ENS would have a cusp of ∝r−1/2. We note that this trend is valid for any spherically symmetric stellar distribution with a central core and not only for the γ = 0 Dehnen model. We also note it always implies a weak central cusp with a logarithmic density slope of α = −1/2 for the phantom dark matter. This has the interesting astrophysical implication that a galaxy with a cored stellar density profile could indeed be interpreted in the DM scenario as having a cored halo due to the fact that weak cusps can often be mistaken for cores.
. For example, for γ = 0, the DM component in the ENS would have a cusp of ∝r−1/2. We note that this trend is valid for any spherically symmetric stellar distribution with a central core and not only for the γ = 0 Dehnen model. We also note it always implies a weak central cusp with a logarithmic density slope of α = −1/2 for the phantom dark matter. This has the interesting astrophysical implication that a galaxy with a cored stellar density profile could indeed be interpreted in the DM scenario as having a cored halo due to the fact that weak cusps can often be mistaken for cores.
For the cases with γ > 1 and κ = 1 in which the gravitational field diverges in the centre, even though the stellar density is diffuse, the ENS is DM dominated only in the external region. This can be easily checked by substituting the asymptotic behaviour 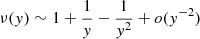 and finding from Eq. (12) that
and finding from Eq. (12) that
implying a vanishingly small central DM density. This is summarised in Fig. 2, where we plot the same quantities as in the previous figure but with κ = 1. As expected, in the upper plot showing ρ*/ρDM, for the values of γ 0 and 0.5 (corresponding to the red and orange lines) the density ratio falls everywhere below one, meaning the system is dominated by the phantom DM distribution at all radii. For the γ ≥ 1 cases, the phantom DM of the ENS dominates only in the external regions. We recall that Sánchez Almeida (2022) showed that galaxies with central regions in the MOND regime imply an ENS characterised by a decreasing baryon density and a cored DM.
3. Numerical code and models
3.1. Numerical code and initial conditions
The N-body simulations discussed here were performed with a modified version of the publicly available NMODY particle-mesh MOND code (Nipoti et al. 2007a; see also Londrillo & Nipoti 2011 for additional technical details). This code uses a non-linear Poisson solver to compute Φ from Eq. (2) on a Nr × Nϑ × Nφ spherical grid in polar coordinates through an iterative relaxation procedure starting from a guess solution given in this work by neglecting S in Eq. (5) (as for the linear Poisson methods, see Londrillo & Messina 1990; Londrillo et al. 1991). As a rule, in the simulations discussed we used a 128 × 32 × 64 grid. We also adopted the following form for the interpolation function
Alternative choices can also be implemented, but they always lead to qualitatively similar end states. The equation of motion was integrated using a standard fourth order leapfrog scheme (see e.g. Dehnen & Read 2011) with an adaptive timestep Δt conditioned by the stability threshold 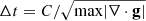 , where the Courant-Friedrichs-Lewy condition C was taken in the range 0.01 ≤ C ≤ 0.1.
, where the Courant-Friedrichs-Lewy condition C was taken in the range 0.01 ≤ C ≤ 0.1.
We performed two sets of numerical simulations with initial conditions defined as follows. In the first, the particle positions were sampled from Eq. (11). In the second, following Hansen et al. (2006), we first distributed the particles according to a Poissonian distribution inside a larger γ model where the centres of NC clumps2 are also described by Eq. (11) but with different choices of rc and γ, and we later populated said clumps with particles.
In both cases, the initial particle velocities were extracted from a position-independent isotropic Maxwell-Boltzmann distribution and normalised to obtain the desired value of the initial virial ratio 2K/|W|, where K is the total kinetic energy and W is the virial function defined for a (finite mass) continuum system of density ρ and potential Φ as
We recall that in isolated dMOND systems of finite mass, 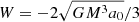 is constant (see Nipoti et al. 2007a). Curiously, even in systems of particles interacting with additive 1/r forces with logarithmic potential, the virial function is constant (see Di Cintio et al. 2013, 2017).
is constant (see Nipoti et al. 2007a). Curiously, even in systems of particles interacting with additive 1/r forces with logarithmic potential, the virial function is constant (see Di Cintio et al. 2013, 2017).
The simulations of this work span a range of N between 104 and 106. All simulations were extended up to t = 300tDyn, where 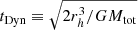 and rh is the radius containing half of the total mass of the system Mtot so that virial oscillations and phase-mixing are likely to be complete.
and rh is the radius containing half of the total mass of the system Mtot so that virial oscillations and phase-mixing are likely to be complete.
Following Ciotti et al. (2007), in some cases we enforced the spherical symmetry during the collapse by propagating particles, only using the radial part of the evaluated force field so that the system effectively behaves as a spherical shell model introduced in Newtonian gravity by Hénon (1964) and used in MOND by Sanders (2008), Malekjani et al. (2009) and by Di Cintio & Ciotti (2011), among others, for systems interacting with 1/rα forces.
3.2. Analysis of the end products
For all simulations presented here, we first extracted the intrinsic properties of the end products from their phase-space positions. We evaluated the triaxiality of the final particle distribution (see e.g. Nipoti et al. 2006a; Di Cintio et al. 2013 and references therein) by defining the tensor as
for the particles with positions ri within the Lagrangian radius r70 containing 70% of the stellar mass of the system and evaluating its three eigenvalues I1 ≥ I2 ≥ I3 with a standard iterative procedure. By applying a rotation ℛ to all particles of the system so that the three associated eigenvectors became oriented along the coordinate axes, we then obtained the three semiaxes a ≥ b ≥ c from I1 = Aa2, I2 = Ab2, and I3 = Ac2, where A is a numerical constant depending on the density profile. Finally, we defined the axial ratios 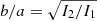 and
and 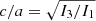 , and the ellipticities in the principal planes
, and the ellipticities in the principal planes 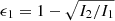 and
and 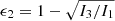 .
.
Following Nipoti et al. (2007a) and Di Cintio et al. (2013), we compared the surface density profiles of the end products with the Sersic (1968) law
where Σe is the projected mass density at the effective radius Re, which is the radius of the circle containing half of the projected mass, and the dimensionless parameters b, m are related by b ≃ 2m − 1/3 + 4/405m, as found by Ciotti & Bertin (1999).
Once the projected density in the three principal planes was circularised over elliptical shells, we determined the corresponding pair (Re, Σe) by particle counts (i.e. we assumed a constant mass-to-light ratio for each particle) and fit Eq. (21) for the three projections. We found that, in general, all three sets of (Σe, Re, m) are rather similar, differing only by less than 5%, we therefore, report only one (randomly selected) value of m per simulation.
In addition, for all simulations, we also evaluated the so-called anisotropy index (see Binney & Tremaine 2008) defined by
where Kr and Kt = Kθ + Kϕ are the radial and tangential components of the kinetic energy tensor, respectively, and read as
In the expressions above,  and
and  are the radial and tangential phase-space averaged square velocity components and are obtained for the end products of the simulations by particle counts over radial shells.
are the radial and tangential phase-space averaged square velocity components and are obtained for the end products of the simulations by particle counts over radial shells.
For each simulation, we recovered the (spherical) DM density of the ENS from Eq. (8), where the Newtonian force field gN was evaluated and averaged on the radial coordinate. In practice, we assumed a ‘sphericised’ system.
Finally, for the density distribution ρDM so obtained, we evaluated the logarithmic density slope α. We found that the profiles of ρDM are generally well fitted by the empirical law
where rα is a scale radius and ρα is the associated scale density. Equation (24) recovers the 1/r2 trend of the density of the ENS as predicted by the logarithmic behaviour of the far field MOND potential. The properties of the simulations and their initial conditions are summarised in Table 1.
Summary of the simulation properties.
4. N-body simulations
4.1. Spherical collapses
One of the main motivations of the present work is to establish whether the end products of MOND dissipationless collapses could, in principle, reproduce the structural properties of elliptical galaxies together with their inferred dark halos. Single component Newtonian collapses with spherical initial conditions are known to produce flatter end states for increasing values of their initial virial ratio (see Nipoti et al. 2006a,b; Di Cintio et al. 2013 and references therein) at a fixed initial density profile.
We found that this (partially) holds true for MOND spherical collapses, as shown in Fig. 3 (top-left and top-middle panels), where we plot the baryon density distribution at 300tDyn for γ = 0 and 1 and the increasing values of the virial ratio with increasingly lighter tones of blue and green in the range 10−3 ≤ 2K0/|W0|≤0.5. Using Eq. (8) for the angle-averaged final density profile on a spherical grid, we evaluated the density distribution of the DM component of the parent Newtonian model (Fig. 3, bottom panels). We found that in qualitative agreement with the structural properties of the ENS (see Figs. 1 and 2 in Sect. 2), cuspy end systems can be associated with cored or weakly cuspy phantom halos. In general, the end products of spherical collapses always have inner regions that are baryon dominated when building their ENS, even if the initial conditions are such that κ = 1 (in particular for the γ = 0 cases).
 |
Fig. 3. Final (t = 300tDyn) density profiles from MOND simulations (top panels) and the DM halo of the ENS (bottom panels) for cored γ0 = 0 (left), moderately cuspy γ = 1 (centre), and clumpy (right) initial conditions. The increasing initial values of the virial ratio in the models with spherical initial conditions with γ = 0 and 1 are mapped with increasingly lighter tones of blue and green, respectively. All clumpy initial conditions start with 2K0/|W|0 = 0.1. |
Consistent with Nipoti et al. (2007a), we observed that independent of the specific value of the initial virial ratio, initial conditions characterised by a moderate density cusp (i.e. 0.5 ≤ γ ≤ 2) tend to yield end products that are generally oblate (i.e. 0.5 ≲ c/a ≲ b/a) for Newtonian single component collapses. We typically observed major ellipticities up to ∼0.63 (corresponding to the gamma1v0b case, see Table 1). Remarkably, MOND collapses with cored initial conditions (i.e. γ = 0) evolve into rather prolate end states for 2K0/|W0|≳0.1 and markedly triaxial end states for lower values of the initial virial ratio. For both cored and moderately cuspy initial conditions, the inner slope α of the DM halo of the ENS, obtained by fitting with Eq. (24), increases for increasing values of the baryon initial virial ratio in the MOND simulation, as shown in Fig. 4 (top panel). The best-fit Sérsic index m, which measures the concentration of the projected stellar density profile, is always in the range of 2 ≤ m ≤ 4.5 for both choices of the initial density profile (Fig. 4, middle panel), while the major ellipticity ϵ = 1 − c/a is typically larger when the initial condition has a lower virial ratio, being smaller for larger values of the initial γ at fixed 2K0/|W0| (Fig. 4, bottom panel). Remarkably, no system was found to be more flattened than an E7 galaxy. However, as also found by Nipoti et al. (2007a), dMOND collapses may produce even flatter end states, as in the case of the gamma1v0dmd run, for which c/a ∼ 0.24 so that ϵ = 0.76. For a fixed initial virial ratio, the end states attain larger values of the central virial velocity dispersion σvir for increasing values of the initial density slope, while the anisotropy index ξ decreases (cf. Table 1). At a fixed initial density profile, the final values of σvir have little variation with 2K0/|W0|, while ξ is usually lower for the relaxed states of hotter initial conditions.
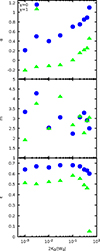 |
Fig. 4. Inner density slope of the ENS halo (top panel), best-fit Sérsic index (middle panel), and minor ellipticity ϵ = 1 − c/a as a function of the initial virial ratio for initial conditions with Dehnen profiles with γ = 0 (circles) and 1 (triangles). |
In order to clarify whether or not the properties of the halo in the ENS are an artefact of the angle-averaging procedure, we also performed a set of simulations in enforced spherical symmetry by propagating particles only using the radial component of the force field. By doing so, the system remains spherically symmetric (as no radial orbit instability is possible), and S = 0 de facto holds true at all times so that Eq. (8) could be applied exactly. In Fig. 5, we show the same quantities as in Fig. 4 as a function of the initial values of γ for systems starting with a virial ratio of 10−4 with (empty symbols) and without (filled symbols) enforced spherical symmetry. The trend as well as the values of α 3D and effective 1D simulations are comparable, and the same could also be noted for the Sérsic index m that attains considerably lower values (associated with a more concentrated density profile) for larger values of the initial logarithmic density slope. In all cases (cf. Table 1), as expected, 1D collapses relax to final states with rather large values of the orbital anisotropy ξ.
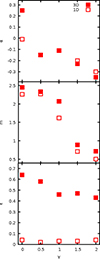 |
Fig. 5. Inner density slope of the ENS halo (top panel), best-fit Sérsic index (middle panel), and minor ellipticity ϵ = 1 − c/a as function of the logarithmic density slope γ of the initial condition for full 3D (filled symbols) and 1D simulations (empty symbols). |
Figure 6 shows the final angle-averaged density profiles for γ0 = 0, 1, and 1.5 in 3D and 1D simulations (solid lines) as well as the density profiles of the ENS halos (dashed lines). Notably, if the large r behaviour of the baryon density profiles ρ* (where the systems are mostly dominated by radial orbits) does not change significantly, the inner slope of ρ* is always higher for the end products of the 1D simulations and typically settles around 2.5. With the sole exception of the cored initial conditions (γ0 = 0), the DM halo of the ENS of the end products is denser (in units of the baryon component density ρ*, 50 evaluated at the half mass radius r50) for the 1D simulations, as it is considerably shallower than the parent baryon density in both cases.
 |
Fig. 6. Final baryon density profiles (coloured solid lines) and ENS halos (coloured dashed lines) for γ = 0, 1, and 1.5. The black lines refer to the 1D the cases with the same initial conditions. |
4.2. Clumpy collapses
The numerical studies carried out so far in MOND have typically explored spherical initial conditions (see Nipoti et al. 2007a, 2011; Ciotti et al. 2007; Sanders 2008; Malekjani et al. 2009); discs (Brada & Milgrom 1999; Tiret & Combes 2007, 2008a; Nipoti et al. 2007c; Ghafourian & Roshan 2017; Wittenburg et al. 2020); or galaxy merging (Nipoti et al. 2007b; Tiret & Combes 2008b and references therein). In this work, in addition to the usual spherical collapses, we also explored clumpy initial conditions. When starting with such initial states, MOND simulations tend (as expected) to yield markedly triaxial end states with broader ranges of both c/a and b/a. In general, for fixed values of the initial virial ratio, the systems tend to relax at later times with respect to their initially spherical counterparts for analogous choices of the virial ratio, as the oscillations of 2K/W damp out at about 50tDyn in spherical collapses (see Nipoti et al. 2007a), while in clumpy systems, this happens on average at around 140tDyn. We report here only the runs corresponding to 2K0/|W0| = 0.1 (see Table 1).
The final 3D (angle averaged) density profiles (Fig. 3, top-right panel) are strikingly more complex than those obtained from spherical initial conditions and individually bare more slope changes. The projected 2D density profiles were fitted with the Sérsic law with roughly the same (percentage) asymptotic standard error of about 3% on average regarding the spherical collapses, while the scatter in the m Sérsic parameter is slightly smaller for MOND clumpy systems (see top panel in Fig. 7). For comparison, we also ran the same clumpy initial conditions in dMOND, finding a larger scatter in m.
 |
Fig. 7. Matrix plot of the Sérsic index, slope of the DM profile in the ENS, major ellipticity, and anisotropy index for simulations with clumpy (diamonds) and spherical (circles) initial conditions. Empty symbols denote the dMOND runs. |
As a general trend, the DM halo of the circularised ENS of clumpy collapses is significantly more cored3 than what is typically obtained in spherical collapses. In several cases, the inner density slopes are negative, down to ∼ − 0.99, corresponding to a DM density profile that decreases in the central regions (middle panels in Fig. 7). Interestingly, no initially clumpy system was found to evolve into a state flatter than an E7 galaxy (thin dashed line in bottom panels of Fig. 7) in MOND simulations. However, some dMOND collapses resulted in considerably flatter end states (and often prolate) with major ellipticity reaching 0.87 for the clumpy1dmd.
We observed that final states with larger values of the anisotropy index ξ (i.e. more and more dominated by low-angular momentum orbits) are always associated with larger ellipticities ϵ and Sérsic indexes. A similar, though somewhat weaker, correlation was also found between α and ϵ, which could be read in the DM scenario as steeper inner DM profiles producing flatter stellar distributions.
4.3. The MOND mass-to-light ratio – ellipticity relation
Using a broad sample of elliptical galaxies from independent surveys and different methods to evaluate the mass-to-light ratio M/L (i.e. Jeans anisotropic modelling, gravitational lensing, X-ray spectra, and the dynamics of satellite star clusters) and the ellipticity ϵ, Deur (2014, 2020) and more recently Winters et al. (2023) recovered the linear relation
where the M/L is normalised such that M/L(ϵapp = 0.3)≡8 M⊙/L⊙ ≡ 4M/M*(ϵapp = 0.3) and the intrinsic ellipticity ϵ is extrapolated from its observed 2D projected value ϵapp, assuming that all systems are oblate, with a Gaussian distribution of projection angles θ so that
The equation above in the context of ΛCDM implies that a larger contribution of the DM mass MDM to the total mass M corresponds to a larger departure from the spherical symmetry (quantified here by a larger major ellipticity) for the stellar component. Winters et al. (2023) argue that, if true, such a correlation would contrast with the standard ΛCDM scenario of galaxy formation, where more massive (and rather spherical) DM halos embed less flattened stellar systems. We note that some peculiar elliptical galaxies (though excluded by the original sample of Winters et al. 2023), such as the ultrafaint dwarfs (Simon 2019), appear to go against the trend given by Eq. (25), having usually ϵ ≲ 0.1 with M/L in some cases up to 103.
Using the simulations discussed in the previous sections, we investigated relation (25) in the context of MOND, evaluating the effective DM mass MDM in the ENSs of both clumpy and spherical collapses. To do so, after recovering the ρDM from the angle-averaged ENS, we integrated it radially up to the radius containing all simulation particles.
In Fig. 8, we show the total-to-stellar mass (we assumed units such that M*/L = 1) ratio M/M* versus major ellipticity ϵ for collapses with both spherical and clumpy initial states, indicated by circles and diamonds, respectively, as well as the observational relation given in Eq. (25). We found that the end products of initially clumpy systems in (almost) all cases fall within the relation and error range (Fig. 8, shaded area) of Winters et al. (2023), while the spherical collapses fall on a rather steeper relation. We performed a linear fit (Fig. 8, orange dotted line), obtaining
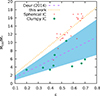 |
Fig. 8. Mass ratio against ellipticity relation for the final states of spherical (red circles) and clumpy (green diamonds) initial conditions. The purple dashed line marks the Deur (2014) relation with its uncertainty (blue shaded area), while the orange dotted line marks the linear fit for the models with spherical initial conditions. |
We stress the fact that none of the simulations discussed above produced final states that could be interpreted as ultrafaint dwarfs (except possibly some dMOND collapses), which in the standard cosmological scenario are supposed to be DM dominated at all radii (i.e. even in the central region where our simulations, when interpreted in the context of DM, have baryon dominated cores).
5. Discussion and conclusions
In this work, we investigated the structure of dark matter density profiles of (angular averaged) ENSs of the end states of MOND dissipationless collapse simulations. Moreover, we studied a broader range of initial conditions than those discussed by Nipoti et al. (2007a), including non-spherical ones.
The main results of this work can be summarised as follows: Simple analytical estimates in spherical symmetry suggest the presence of a core or even centrally decreasing DM distribution in ENSs of MOND models with cuspy stellar profiles. Conversely, cored stellar profiles are associated with ENS DM central density profiles ρDM ∝ 1/rα with α ≲ 1. Our MOND N-body simulations and the angle-averaged ENS of their end states nicely confirm this. This established, we can conclude that the flat-cored halos invoked by some observational studies can be reasonably considered to be in agreement with our numerical findings, as the dynamical effect of a weak cusp, independent of the specific value of the central logarithmic density slope of the baryons, can easily be mistaken for that of a cored dark mass distribution in the DM paradigm.
In general, we observed that for the simulations in Newtonian gravity in MOND, the stronger the collapse (i.e. lower initial virial ratio and/or larger initial density slope), the steeper the final density profile, and thus the dark halo of the ENS has a markedly cored, or sometimes even depleted, inner density. Obviously, the end product of simplified MOND N-body simulations with enforced spherical symmetry have an ENS with markedly flat cores, even for a broad spectrum of initial values of density slope and virial ratio, and baryon density is always dominated by a rather strong cusp at inner radii. Moreover, we also find that, if interpreted in the context of DM, the relaxed end states with smaller values of the ellipticity (i.e. less flattened) should have cuspier DM halos. In general, independent of the specific form of the initial density profile, colder initial conditions are always associated with flatter end states. As a by-product of this simulation study on ENSs, we also recovered a numerical confirmation of the claimed Deur (2014) observational linear correlation between M/L (or M/M*) and ϵ, though with a seemingly different slope when evaluating the dark matter content of ENSs in units of the baryon mass (the latter being a pre-defined simulation parameter).
Our findings led us to speculate that in the context of MOND, the core-cusp problem could be a ‘MOND artefact’ in the same sense as rings and DM shells discussed by Milgrom & Sanders (2008). Moreover, we stress the fact that in the DM halos reconstructed from observational data using the line-of-sight velocity dispersion of a given tracer stellar population, the effect of the velocity anisotropy profiles 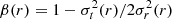 (and the intrinsic departure from the spherical symmetry) is neglected, as noted by Evans et al. (2009) for the case of dwarf spheroids. In fact, since the central stellar β profile imposes a constraint on the slope of the DM component in the form of the inequality β ≤ α/2 (see An & Evans 2006; Ciotti & Morganti 2009, 2010), the entity of the central density cusp or core inferred for observed galaxies is likely to bare a rather large uncertainty. In the context of (single component) MOND models, the relation between anisotropy and central density cusps has not been explored in detail, neither analytically nor in simulations. Simple numerical experiments (Di Cintio et al. 2013) with inverse power-law radial forces seem to suggest that the density slope anisotropy inequality is a rather general property of the relaxed states of collapses with long-range interactions. A natural follow-up of this work would be a systematic study of the interplay of the β profiles in MOND systems and the DM density profiles of the parent ENSs.
(and the intrinsic departure from the spherical symmetry) is neglected, as noted by Evans et al. (2009) for the case of dwarf spheroids. In fact, since the central stellar β profile imposes a constraint on the slope of the DM component in the form of the inequality β ≤ α/2 (see An & Evans 2006; Ciotti & Morganti 2009, 2010), the entity of the central density cusp or core inferred for observed galaxies is likely to bare a rather large uncertainty. In the context of (single component) MOND models, the relation between anisotropy and central density cusps has not been explored in detail, neither analytically nor in simulations. Simple numerical experiments (Di Cintio et al. 2013) with inverse power-law radial forces seem to suggest that the density slope anisotropy inequality is a rather general property of the relaxed states of collapses with long-range interactions. A natural follow-up of this work would be a systematic study of the interplay of the β profiles in MOND systems and the DM density profiles of the parent ENSs.
Technically speaking, in multi-component equilibrium self-gravitating systems, there exist analytical constraints on the magnitude of a component’s (e.g. stars) density given the logarithmic slope of the other one (e.g. Dark Matter; e.g. see Dubinski & Carlberg 1991; Ciotti & Pellegrini 1992; Ciotti 1996, 1999). Moreover, for a broad range of spherical density profiles, the central density slope constrains the value of the central anisotropy profile (An & Evans 2006).
Clumpy initial conditions were also explored in the context of Newtonian simulations by Nipoti (2015) and Ludlow & Angulo (2017) when investigating the relation of the initial density fluctuation power spectrum with the Sérsic index m (see below) conjectured by Cen (2014).
Notably, in Newtonian simulations of clumps in fall in DM halo, Cole et al. (2011) found that the central DM cusp is considerably weakened by the collapsing clumpy satellites.
Acknowledgments
We would like to express gratitude to Carlo Nipoti for the assistance with the simulation in NMODY and Michal Bílek for the discussions at an early stage of this work. One of us (PFDC) wishes to acknowledge funding by “Fondazione Cassa di Risparmio di Firenze” under the project HIPERCRHEL for the use of high performance computing resources at the university of Firenze.
References
- An, J. H., & Evans, N. W. 2006, ApJ, 642, 752 [NASA ADS] [CrossRef] [Google Scholar]
- Angus, G. W., Famaey, B., & Zhao, H. S. 2006, MNRAS, 371, 138 [Google Scholar]
- Bekenstein, J., & Milgrom, M. 1984, ApJ, 286, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Benetti, F., Lapi, A., Gandolfi, G., Salucci, P., & Danese, L. 2023, ApJ, 949, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Binney, J., & Tremaine, S. 2008, Galactic Dynamics: Second Edition (Princeton University Press) [Google Scholar]
- Brada, R., & Milgrom, M. 1999, ApJ, 519, 590 [NASA ADS] [CrossRef] [Google Scholar]
- Buchdahl, H. A. 1970, MNRAS, 150, 1 [NASA ADS] [Google Scholar]
- Cen, R. 2014, ApJ, 790, L24 [CrossRef] [Google Scholar]
- Cesare, V., Diaferio, A., Matsakos, T., & Angus, G. 2020, A&A, 637, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ciotti, L. 1996, ApJ, 471, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Ciotti, L. 1999, ApJ, 520, 574 [NASA ADS] [CrossRef] [Google Scholar]
- Ciotti, L., & Bertin, G. 1999, A&A, 352, 447 [NASA ADS] [Google Scholar]
- Ciotti, L., & Morganti, L. 2009, MNRAS, 393, 179 [Google Scholar]
- Ciotti, L., & Morganti, L. 2010, MNRAS, 408, 1070 [Google Scholar]
- Ciotti, L., & Pellegrini, S. 1992, MNRAS, 255, 561 [NASA ADS] [CrossRef] [Google Scholar]
- Ciotti, L., Londrillo, P., & Nipoti, C. 2006, ApJ, 640, 741 [NASA ADS] [CrossRef] [Google Scholar]
- Ciotti, L., Nipoti, C., & Londrillo, P. 2007, Collective Phenomena in Macroscopic Systems, 177 [CrossRef] [Google Scholar]
- Ciotti, L., Zhao, H., & de Zeeuw, P. T. 2012, MNRAS, 422, 2058 [Google Scholar]
- Cole, D. R., Dehnen, W., & Wilkinson, M. I. 2011, MNRAS, 416, 1118 [NASA ADS] [CrossRef] [Google Scholar]
- Dehnen, W. 1993, MNRAS, 265, 250 [NASA ADS] [CrossRef] [Google Scholar]
- Dehnen, W., & Read, J. I. 2011, Eur. Phys. J. Plus, 126, 55 [Google Scholar]
- Del Popolo, A., & Pace, F. 2016, Astrophys. Space Sci., 361, 162; Erratum: 361, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Deur, A. 2014, MNRAS, 438, 1535 [NASA ADS] [CrossRef] [Google Scholar]
- Deur, A. 2020, ArXiv e-prints [arXiv:2010.06692] [Google Scholar]
- Di Cintio, P., & Ciotti, L. 2011, Int. J. Bifurcation Chaos, 21, 2279 [NASA ADS] [CrossRef] [Google Scholar]
- Di Cintio, P., Ciotti, L., & Nipoti, C. 2013, MNRAS, 431, 3177 [NASA ADS] [CrossRef] [Google Scholar]
- Di Cintio, A., Brook, C. B., Macciò, A. V., et al. 2014, MNRAS, 437, 415 [Google Scholar]
- Di Cintio, P., Ciotti, L., & Nipoti, C. 2017, MNRAS, 468, 2222 [NASA ADS] [CrossRef] [Google Scholar]
- Dubinski, J., & Carlberg, R. G. 1991, ApJ, 378, 496 [Google Scholar]
- Eckert, D., Ettori, S., Robertson, A., et al. 2022, A&A, 666, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eriksen, M. H., Frandsen, M. T., & From, M. H. 2021, A&A, 656, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Evans, N. W., An, J., & Walker, M. G. 2009, MNRAS, 393, L50 [NASA ADS] [Google Scholar]
- Ghafourian, N., & Roshan, M. 2017, MNRAS, 468, 4450 [NASA ADS] [CrossRef] [Google Scholar]
- Giusti, A. 2020, Phys. Rev. D, 101, 124029 [NASA ADS] [CrossRef] [Google Scholar]
- Governato, F., Brook, C., Mayer, L., et al. 2010, Nature, 463, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, S., Moore, B., Zemp, M., & Stadel, J. 2006, JCAP, 0601, 014 [NASA ADS] [Google Scholar]
- Hénon, M. 1964, Annales d’Astrophysique, 27, 83 [Google Scholar]
- Hodson, A. O., Diaferio, A., & Ostorero, L. 2020, A&A, 640, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ko, C.-M. 2016, ApJ, 821, 111 [CrossRef] [Google Scholar]
- Londrillo, P., & Messina, A. 1990, MNRAS, 242, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Londrillo, P., Messina, A., & Stiavelli, M. 1991, MNRAS, 250, 54 [NASA ADS] [Google Scholar]
- Londrillo, P., & Nipoti, C. 2011, Astrophysics Source Code Library [record ascl:1102.001] [Google Scholar]
- Lovell, M. R., Eke, V., Frenk, C. S., et al. 2012, MNRAS, 420, 2318 [NASA ADS] [CrossRef] [Google Scholar]
- Ludlow, A. D., & Angulo, R. E. 2017, MNRAS, 465, L84 [Google Scholar]
- Malekjani, M., Rahvar, S., & Haghi, H. 2009, ApJ, 694, 1220 [CrossRef] [Google Scholar]
- McGaugh, S. S., Barker, M. K., & de Blok, W. J. G. 2003, ApJ, 584, 566 [CrossRef] [Google Scholar]
- Milgrom, M. 1983, ApJ, 270, 365 [Google Scholar]
- Milgrom, M. 1986, ApJ, 306, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Milgrom, M. 2010, MNRAS, 403, 886 [NASA ADS] [CrossRef] [Google Scholar]
- Milgrom, M. 2021, Phys. Rev. D, 103, 044043 [NASA ADS] [CrossRef] [Google Scholar]
- Milgrom, M. 2022, Phys. Rev. D, 106, 064060 [NASA ADS] [CrossRef] [Google Scholar]
- Milgrom, M., & Sanders, R. H. 2008, ApJ, 678, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Moffat, J. W. 2006, JCAP, 2006, 004 [Google Scholar]
- Moffat, J. W., & Rahvar, S. 2013, MNRAS, 436, 1439 [Google Scholar]
- Moore, B. 1994, Nature, 370, 629 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [Google Scholar]
- Nguyen, Q. L., Mathews, G. J., Phillips, L. A., et al. 2021, Mod. Phys. Lett. A, 36, 2130001 [NASA ADS] [CrossRef] [Google Scholar]
- Nipoti, C. 2015, ApJ, 805, L16 [CrossRef] [Google Scholar]
- Nipoti, C., Londrillo, P., & Ciotti, L. 2006a, MNRAS, 370, 681 [NASA ADS] [CrossRef] [Google Scholar]
- Nipoti, C., Londrillo, P., & Ciotti, L. 2006b, N-body Simulations of Dissipationless Galaxy Formation (Science and Supercomputing at CINECA), 2005, 122 [Google Scholar]
- Nipoti, C., Londrillo, P., & Ciotti, L. 2007a, ApJ, 660, 256 [NASA ADS] [CrossRef] [Google Scholar]
- Nipoti, C., Londrillo, P., & Ciotti, L. 2007b, MNRAS, 381, L104 [Google Scholar]
- Nipoti, C., Londrillo, P., Zhao, H., & Ciotti, L. 2007c, MNRAS, 379, 597 [NASA ADS] [CrossRef] [Google Scholar]
- Nipoti, C., Ciotti, L., & Londrillo, P. 2011, MNRAS, 414, 3298 [Google Scholar]
- Oria, P. A., Famaey, B., Thomas, G. F., et al. 2021, ApJ, 923, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Pontzen, A., & Governato, F. 2012, MNRAS, 421, 3464 [NASA ADS] [CrossRef] [Google Scholar]
- Raju, C. K. 2012, in The Sixth International School on Field Theory and Gravitation-2012, eds. W. Alves Rodrigues, Jr., R. Kerner, G. O. Pires, & C. Pinheiro, Am. Inst. Phys. Conf. Ser., 1483, 260 [NASA ADS] [Google Scholar]
- Sánchez Almeida, J. 2022, ApJ, 940, 46 [CrossRef] [Google Scholar]
- Sanders, R. H. 2008, MNRAS, 386, 1588 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, R. H., & Begeman, K. G. 1994, MNRAS, 266, 360 [Google Scholar]
- Sanna, A. P., Matsakos, T., & Diaferio, A. 2023, A&A, 674, A209 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sersic, J. L. 1968, Atlas de Galaxias Australes (Cordoba, Argentina: Observatorio Astronomico) [Google Scholar]
- Simon, J. D. 2019, ARA&A, 57, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Sotiriou, T. P., & Faraoni, V. 2010, Rev. Mod. Phys., 82, 451 [NASA ADS] [CrossRef] [Google Scholar]
- Stein, E. M. 1970, Singular Integrals and Differentiability Properties of Functions (PMS-30) (Princeton University Press) [Google Scholar]
- Tiret, O., & Combes, F. 2007, A&A, 464, 517 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tiret, O., & Combes, F. 2008a, A&A, 483, 719 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tiret, O., & Combes, F. 2008b, in Formation and Evolution of Galaxy Disks, eds. J. G. Funes, & E. M. Corsini, ASP Conf. Ser., 396, 259 [NASA ADS] [Google Scholar]
- Tremaine, S., Richstone, D. O., Byun, Y.-I., et al. 1994, AJ, 107, 634 [CrossRef] [Google Scholar]
- Vasiliev, E. 2007, Phys. Rev. D, 76, 103532 [CrossRef] [Google Scholar]
- Verlinde, E. 2011, J. High Energy Phys., 2011, 29 [CrossRef] [Google Scholar]
- Verlinde, E. P. 2017, SciPost Phys., 2, 016 [NASA ADS] [CrossRef] [Google Scholar]
- Winters, D. M., Deur, A., & Zheng, X. 2023, MNRAS, 518, 2845 [Google Scholar]
- Wittenburg, N., Kroupa, P., & Famaey, B. 2020, ApJ, 890, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Yahalom, A. 2022, Int. J. Mod. Phys. D, 31, 2242018 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Ratio of the stellar to dark density in the ENS (top) and DM and stellar density profiles (bottom left and bottom right) in units of |
| In the text | |
 |
Fig. 2. Same as in Fig. 1 but for κ = 1. |
| In the text | |
 |
Fig. 3. Final (t = 300tDyn) density profiles from MOND simulations (top panels) and the DM halo of the ENS (bottom panels) for cored γ0 = 0 (left), moderately cuspy γ = 1 (centre), and clumpy (right) initial conditions. The increasing initial values of the virial ratio in the models with spherical initial conditions with γ = 0 and 1 are mapped with increasingly lighter tones of blue and green, respectively. All clumpy initial conditions start with 2K0/|W|0 = 0.1. |
| In the text | |
 |
Fig. 4. Inner density slope of the ENS halo (top panel), best-fit Sérsic index (middle panel), and minor ellipticity ϵ = 1 − c/a as a function of the initial virial ratio for initial conditions with Dehnen profiles with γ = 0 (circles) and 1 (triangles). |
| In the text | |
 |
Fig. 5. Inner density slope of the ENS halo (top panel), best-fit Sérsic index (middle panel), and minor ellipticity ϵ = 1 − c/a as function of the logarithmic density slope γ of the initial condition for full 3D (filled symbols) and 1D simulations (empty symbols). |
| In the text | |
 |
Fig. 6. Final baryon density profiles (coloured solid lines) and ENS halos (coloured dashed lines) for γ = 0, 1, and 1.5. The black lines refer to the 1D the cases with the same initial conditions. |
| In the text | |
 |
Fig. 7. Matrix plot of the Sérsic index, slope of the DM profile in the ENS, major ellipticity, and anisotropy index for simulations with clumpy (diamonds) and spherical (circles) initial conditions. Empty symbols denote the dMOND runs. |
| In the text | |
 |
Fig. 8. Mass ratio against ellipticity relation for the final states of spherical (red circles) and clumpy (green diamonds) initial conditions. The purple dashed line marks the Deur (2014) relation with its uncertainty (blue shaded area), while the orange dotted line marks the linear fit for the models with spherical initial conditions. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



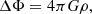
![$$ \begin{aligned} \nabla \cdot \left[\mu \left(\frac{||\nabla \Phi ||}{a_0}\right)\nabla \Phi \right]=4\pi G\rho . \end{aligned} $$](/articles/aa/full_html/2023/10/aa47487-23/aa47487-23-eq2.gif)
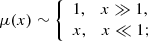
![$$ \begin{aligned} \nabla \cdot \left[||\nabla \Phi ||\nabla \Phi \right]=4\pi G\rho a_0. \end{aligned} $$](/articles/aa/full_html/2023/10/aa47487-23/aa47487-23-eq4.gif)
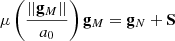
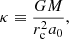
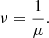
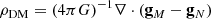
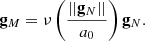
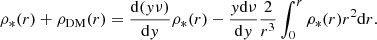
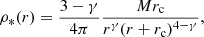
![$$ \begin{aligned} \rho _*+\rho _{\rm DM}=\rho _*\left[\frac{r_{\rm c}}{r+r_{\rm c}}\frac{\mathrm{d}(y\nu )}{\mathrm{d}y}-\frac{2}{3-\gamma }\frac{y \mathrm{d}\nu }{\mathrm{d}y}\right], \end{aligned} $$](/articles/aa/full_html/2023/10/aa47487-23/aa47487-23-eq13.gif)
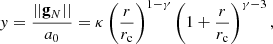
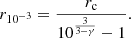
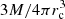
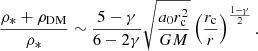
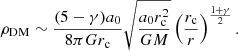
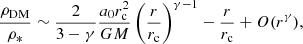
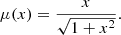
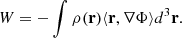
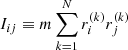
![$$ \begin{aligned} \Sigma (R)=\Sigma _{\rm e} e^{-b\left[\left(\frac{R}{R_{\rm e}}\right)^{1/m}-1\right]}, \end{aligned} $$](/articles/aa/full_html/2023/10/aa47487-23/aa47487-23-eq33.gif)