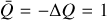| Issue |
A&A
Volume 678, October 2023
|
|
|---|---|---|
| Article Number | A17 | |
| Number of page(s) | 21 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202345840 | |
| Published online | 29 September 2023 | |
Three-dimensional magnetic field imaging of protoplanetary disks using Zeeman broadening and linear polarization observations
1
Department of Space, Earth and Environment, Chalmers University of Technology, Onsala Space Observatory,
439 92
Onsala, Sweden
e-mail: boy.lankhaar@chalmers.se
2
Leiden Observatory, Leiden University,
Post Office Box 9513,
2300 RA
Leiden, Netherlands
3
Department of Earth, Atmospheric, and Planetary Sciences, Massachusetts Institute of Technology,
Cambridge, MA
02139, USA
Received:
3
January
2023
Accepted:
14
April
2023
Context. Magnetic fields are predicted to have a crucial impact on the structure, evolution, and chemistry of protoplanetary disks. However, a direct detection of the magnetic field toward these objects has yet to be achieved.
Aims. In order to characterize the magnetic fields of protoplanetary disks, we investigate the impact of the Zeeman effect on the (polarized) radiative transfer of emission from paramagnetic molecules excited in protoplanetary disks.
Methods. While the effects of the Zeeman effect are commonly studied in the circular polarization of spectral lines, we also performed a comprehensive modeling of the Zeeman-induced broadening of spectral lines and their linear polarization. We developed simplified radiative transfer models adapted to protoplanetary disks, which we compare to full three-dimensional polarized radiative transfer simulations.
Results. We find that the radiative transfer of circular polarization is heavily affected by the expected polarity change of the magnetic field between opposite sides of the disk. In contrast, Zeeman broadening and linear polarization are relatively unaffected by this sign change due to their quadratic dependence on the magnetic field. We can match our simplified radiative transfer models to full polarization modeling with high fidelity, which in turn allows us to prescribe straightforward methods to extract magnetic field information from Zeeman broadening and linear polarization observations.
Conclusions. We find that Zeeman broadening and linear polarization observations are highly advantageous methods to characterize protoplanetary disk magnetic fields as they are both sensitive probes of the magnetic field and are marginally affected by any sign change of the disk magnetic field. Applying our results to existing circular polarization observations of protoplanetary disk specral lines suggests that the current upper limits on the toroidal magnetic field strengths have to be raised.
Key words: magnetic fields / radiative transfer / polarization / stars: formation / accretion / accretion disks / planets and satellites: formation
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
The formation of stars is associated with a protoplanetary disk in the late evolutionary stages. The protoplanetary disk is composed of gas and dust, and orbits a young star that is actively accreting mass through it. Planets are believed to be formed in the protoplanetary disk in a process that crucially depends on the disk structure, chemistry, and evolution (Armitage 2011).
The disk structure and evolution sensitively depends on the dominant accretion mechanism. Accretion requires the transport of angular momentum through the disk, which is facilitated by turbulence-enhanced viscosity, or through magnetic fields, that may either transport angular momentum radially through magnetic stresses or vertically through the launching of a disk wind (Balbus & Hawley 1991; Nelson et al. 2013; Lesur & Papaloizou 2010; Marcus et al. 2015; Wardle & Koenigl 1993; Shakura & Sunyaev 1976; Armitage & Kley 2019; Bai & Stone 2013). The lack of observational signatures of turbulence in protoplanetary disks catalyzed substantial progress in numerical modeling, which put forth disk winds as the dominant accretion mechanism (Flaherty et al. 2015, 2018; Teague et al. 2016; Bai 2016; Lesur 2021). The details of the disk wind crucially depend on the strength and morphology of the disk magnetic field (see, e.g., Bai 2016). Additionally, magnetic fields advected through the disk wind affect disk chemistry through the shielding of cosmic rays (Cleeves et al. 2013).
Despite its importance, the direct detection of the large-scale magnetic field that permeates a protoplanetary disk has not yet been achieved, even though several attempts have been made (Vlemmings et al. 2019; Harrison et al. 2021). Magnetic fields in molecular gas are commonly observed through the detection of linear polarization in dust continuum emission (Andersson et al. 2015; Pattle et al. 2023) or spectral lines, either in thermal emission (Goldreich & Kylafis 1981; Lankhaar & Vlemmings 2020b), in maser emission (Crutcher & Kemball 2019), or through the detection of the Zeeman effect in the circularly polarized spectral line emission of paramagnetic molecules (Crutcher & Kemball 2019). Applied to the protoplanetary disk, these methods of magnetic field detection have had limited success. While dust continuum polarization is readily detected with ALMA, radiation scattering affects the polarization signature, making interpretation of these observations for their magnetic field information difficult (Kataoka et al. 2015; Stephens et al. 2017). The linear polarization of spectral lines has been tentatively detected in 12CO and 13CO emission, but at low degrees of polarization due to the high density of these regions (Stephens et al. 2020; Teague et al. 2021; Lankhaar & Vlemmings 2020a; Lankhaar et al. 2022). Circular polarization observations have allowed stringent constraints to be put on the magnetic field strengths of TW Hya (Vlemmings et al. 2019) and AS 209 (Harrison et al. 2021), but failed to detect magnetic fields directly due to the high sensitivity requirements of circular polarization observations.
Zeeman observations in protoplanetary disks through circular polarization have high sensitivity requirements for two reasons. First, observation of circularly polarized emission of spectral lines is inherently affected by instrumental effects that require strong signals, as well as excellent atmospheric conditions, for proper calibration. Second, circular polarization observations are sensitive to the line-of-sight component of the magnetic field. This is problematic as protoplanetary disks are believed to be permeated by a magnetic field that is dominated by its toroidal component that is ≳10 times stronger than the vertical and radial components. Additionally, the projection of the toroidal and radial components of the magnetic field are expected to change sign between the front and back side of the disk (for details, see discussion after Eq. (23)). Therefore, for weakly inclined disks it is mainly the weak vertical component of the magnetic field that gives rise to circular polarization. On the other hand, (moderately) inclined disks are affected by complicated radiative transfer effects that cause lower degrees of polarization due to line broadening and the cancellation of the circular polarization due to the sign change of the toroidal magnetic field component (Mazzei et al. 2020).
In this paper, we propose using the broadening and linear polarization of paramagnetic spectral lines due to the Zeeman effect as tracers of the protoplanetary disk magnetic field. We argue that because Zeeman broadening and linear polarization are dependent on the square of the magnetic field strength (Crutcher et al. 1993), they are less sensitive to the sign change of the magnetic field that characterizes protoplanetary disks. Moreover, while circular polarization observations are sensitive to the line-of-sight component of the magnetic field, Zeeman-induced linear polarization is sensitive to the plane-of-the-sky component of the magnetic field and Zeeman broadening is dependent on the total magnetic field strength. Therefore, Zeeman broadening and Zeeman-induced linear polarization have a high magnetic field sensitivity also for weakly inclined disks. Finally, we argue that from the simultaneous observation of Zeeman-induced linear polarization with either Zeeman broadening or circular polarization, the three-dimensional (3D) direction and strength of the magnetic field can be derived.
This paper is structured as follows. In Sect. 2, we review the Zeeman effect and its manifestation in spectral lines. We discuss simple radiative transfer models that assist in the interpretation of intricate 3D radiative transfer modeling. Importantly, we show how to generalize the expressions for Zeeman broadening and linear polarization, derived in the seminal work of Crutcher et al. (1993), to arbitrary transitions. In Sect. 3, we present 3D simulations of the polarized radiative transfer of CN emission lines that are excited in a protoplanetary disk that is permeated by a magnetic field. We discuss the emergence of circular and linear polarization, as well as the Zeeman broadening, and show how to extract magnetic field information from synthetic observations. In Sect. 4, we discuss our results before concluding in Sect. 5.
2 Theory
In this work, we focus on the detection of magnetic fields in protoplanetary disks through the Zeeman effect. In the following we discuss the Zeeman splitting of spectral lines and their manifestation in circular polarization, linear polarization, and in the broadening of spectral lines. In particular, linear polarization and line broadening are often overlooked features of Zeeman-split spectral lines excited in interstellar matter, but are established tools of stellar magnetic field detection (Robinson 1980; Gray 1984; Rosén et al. 2015; Kochukhov et al. 2019). Here we derive simple relations for the polarization and broadening of spectral lines as a function of the magnetic field strength and orientation. After the review of Zeeman effects, we consider the manifestation of Zeeman effects in the spectral line emission from protoplanetary disks. We describe the radiative transfer in protoplanetary disks in terms of simplified radiative transfer models and discuss the impact of disk inclination and an optically thick dust layer. We conclude this section with a discussion of stacking procedures that can be applied to extract magnetic field information from (polarized) spectral line emission emerging from protoplanetary disks.
2.1 Zeeman-splitting of spectral lines
Spectral lines split into a manifold of transitions between their magnetic sublevels, due to the Zeeman effect. If we consider a transition between two states, with angular momentum F1 for the upper state and F2 for the lower state, transitions between magnetic sublevels are shifted in frequency by
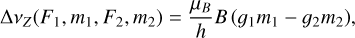 (1)
(1)
which is linearly dependent on the magnetic field B. In Eq. (1) µB is the Bohr magneton, h is Planck’s constant, g1 and g2 are the g-factors of the two states, and m1 and m2 are the magnetic quantum numbers that can assume values from −F1(−F2) to F1(F2) in increments of 1. The transition |F1m1〉 → |F2m2〉 is associated with a relative line strength 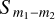 (F1, F2, m1) (see Eq. 3.16 in Degl’Innocenti & Landolfi 2006, for a definition of the relative line strength). Due to selection rules, only Δm = 0 (π0-transitions) and Δm = ±1 (σ±-transitions) transitions are allowed. The groups of π0- and σ± -transitions have different opacities for the different polarization modes of the radiation field which are a function of the projection angle θ between the line-of-sight direction and the magnetic field direction. For a magnetic field along the line of sight (cos θ = 1), σ± -transitions give rise to right- and left-handed circularly polarized radiation, while for a magnetic field perpendicular to the line of sight (cos θ = 0), σ±-transitions give rise to linear polarization perpendicular to the magnetic field direction in the plane of the sky. The π0-transitions are suppressed when the magnetic field is oriented along the line of sight, while for a magnetic field perpendicular to the line of sight, π0-transitions give rise to linear polarization parallel to the magnetic field direction in the plane of the sky.
(F1, F2, m1) (see Eq. 3.16 in Degl’Innocenti & Landolfi 2006, for a definition of the relative line strength). Due to selection rules, only Δm = 0 (π0-transitions) and Δm = ±1 (σ±-transitions) transitions are allowed. The groups of π0- and σ± -transitions have different opacities for the different polarization modes of the radiation field which are a function of the projection angle θ between the line-of-sight direction and the magnetic field direction. For a magnetic field along the line of sight (cos θ = 1), σ± -transitions give rise to right- and left-handed circularly polarized radiation, while for a magnetic field perpendicular to the line of sight (cos θ = 0), σ±-transitions give rise to linear polarization perpendicular to the magnetic field direction in the plane of the sky. The π0-transitions are suppressed when the magnetic field is oriented along the line of sight, while for a magnetic field perpendicular to the line of sight, π0-transitions give rise to linear polarization parallel to the magnetic field direction in the plane of the sky.
When there is no magnetic field present, the individual transitions between the magnetic sublevels are degenerate and the different propagation properties of the σ± – and π0 -transitions for different polarization modes are note expressed. Through interaction with the magnetic field, the degeneracy is lifted and the σ±- and π0-transitions are shifted with respect to each other, resulting in the partial polarization (circular and linear) and the broadening of the associated spectral line (Degl’Innocenti & Landolfi 2006). Most commonly, the signature of the Zeeman effect is sought in the circular polarization, but in this paper we also focus on the Zeeman signature in the linear polarization and line broadening.
To relate our discussion to the published literature on Zee-man effects, we first discuss the signature of the Zeeman effect in the spectral line circular polarization. The σ±-transitions are oppositely circularly polarized, and therefore a net polarization is produced when these transition groups are shifted with respect to one another. The groups of σ±-transitions are shifted from the line center (on average, weighted by intensity), in frequency by
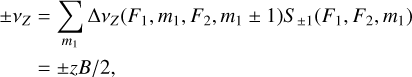 (2)
(2)
where z is the line-specific Zeeman coefficient and B is the magnetic field strength (Degl’Innocenti & Landolfi 2006; Larsson et al. 2019; Vlemmings et al. 2019). Since the expression of the Zeeman effect in the circular polarization is through a shift of the σ± line profiles, its relative strength is inversely proportional to the line width. It is therefore helpful to define the Zeeman shift in Doppler units,
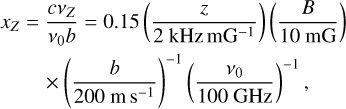 (3)
(3)
where v0 is the line frequency, and b is the Doppler b parameter that describes the line broadening and usually has a contribution both from the thermal broadening, 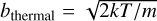 , where m is the particle mass and T the temperature, and from the turbulent broadening bturb. In addition to a shift between the transition groups, there is also a spread in frequency within the π0- and the σ±-transition groups that causes line broadening and impacts the production of linear polarization. For Zeeman shifts that are weaker than the Doppler broadening, the effects of intra-group broadening may be incorporated in the polarized radiative transfer perturbatively. Taking this into account, we derive in Appendix A, the polarized radiative transfer equation, which we report here only in the optically thin limit,
, where m is the particle mass and T the temperature, and from the turbulent broadening bturb. In addition to a shift between the transition groups, there is also a spread in frequency within the π0- and the σ±-transition groups that causes line broadening and impacts the production of linear polarization. For Zeeman shifts that are weaker than the Doppler broadening, the effects of intra-group broadening may be incorporated in the polarized radiative transfer perturbatively. Taking this into account, we derive in Appendix A, the polarized radiative transfer equation, which we report here only in the optically thin limit,
![${I_v} = {S_{{v_0}}}\,{\tau _{{v_0}}}\,\left[ {\bar \phi \left( x \right) + x_Z^2\,\left( {{{\bar Q} \over 4} - {{{\rm{\Delta }}Q} \over 4}\,{{\cos }^2}\,\theta } \right)\bar \phi \left( x \right)} \right],$](/articles/aa/full_html/2023/10/aa45840-23/aa45840-23-eq6.png) (4a)
(4a)
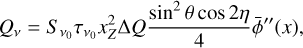 (4b)
(4b)
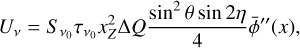 (4c)
(4c)
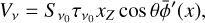 (4d)
(4d)
where  is the source function of a spectral line at frequency v0;
is the source function of a spectral line at frequency v0; 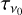 is its line optical depth at the line center; η is the angle between the magnetic field projected on the plane of the sky and the plane of the sky the northern direction; and
is its line optical depth at the line center; η is the angle between the magnetic field projected on the plane of the sky and the plane of the sky the northern direction; and 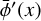 and
and 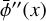 indicate the first- and second-derivative of the normalized line profile,
indicate the first- and second-derivative of the normalized line profile, 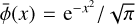 , with respect to the Doppler unit,
, with respect to the Doppler unit, 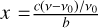 . We refer to the angle η as the magnetic field position angle in the remainder of this paper. The dimensionless coefficients
. We refer to the angle η as the magnetic field position angle in the remainder of this paper. The dimensionless coefficients 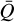 and ΔQ account for the contribution of the intragroup broadening to the total Zeeman broadening and the emergence of linear polarization. They are defined as
and ΔQ account for the contribution of the intragroup broadening to the total Zeeman broadening and the emergence of linear polarization. They are defined as 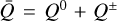 and ΔQ = Q0 – Q±, where
and ΔQ = Q0 – Q±, where
![$v_Z^2{Q^0} = \sum\limits_{{m_1}} {{{\left[ {{\rm{\Delta }}{v_Z}\,\left( {{F_1},{m_1},{F_2},{m_1}} \right)} \right]}^2}\,{S_0}\left( {{F_1},{F_2},{m_1}} \right),} $](/articles/aa/full_html/2023/10/aa45840-23/aa45840-23-eq18.png) (5a)
(5a)
![$v_Z^2{Q^ \pm } = \sum\limits_{{m_1}} {{{\left[ {{\rm{\Delta }}{v_Z}\,\left( {{F_1},{m_1},{F_2},{m_1} \pm 1} \right)} \right]}^2}\,{S_{ \pm 1}}\left( {{F_1},{F_2},{m_1}} \right),} $](/articles/aa/full_html/2023/10/aa45840-23/aa45840-23-eq19.png) (5b)
(5b)
are readily computed from the level-specific g-factors within a transition. We have tabulated them for CN (sub)millimeter transitions in Table 1.
In Fig. 1, we plot the normalized line profile and its derivatives. Comparing the Zeeman term in the total intensity in Eq. (4) to the second-derivative line profile, it is readily recognized that the Zeeman effect causes a broadening of the total intensity profile. While the term 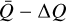 cos2 θ is always positive, ϕ″(x) is negative toward the line center and positive in its wings, and thus the Zeeman term effectively broadens the line profile. The ΔQ factor can be positive or negative, depending on the transition, and must be known to relate the linear polarization direction to the magnetic field direction. We also note that as the linear polarization adheres to a spectrum that changes sign toward the line wings (at
cos2 θ is always positive, ϕ″(x) is negative toward the line center and positive in its wings, and thus the Zeeman term effectively broadens the line profile. The ΔQ factor can be positive or negative, depending on the transition, and must be known to relate the linear polarization direction to the magnetic field direction. We also note that as the linear polarization adheres to a spectrum that changes sign toward the line wings (at 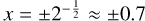 ), a spectral resolution that allows for the line profile to be resolved, in addition to a strong Zeeman effect, is required to observe the linear polarization.
), a spectral resolution that allows for the line profile to be resolved, in addition to a strong Zeeman effect, is required to observe the linear polarization.
We now discuss the radiative transfer solutions of Eq. (4), and quantify the impact of the Zeeman effect on the circular polarization, line broadening, and linear polarization. The Zee-man effect is most commonly sought in the Stokes V spectrum (i.e., the circular polarization. To quantify the circular polarization produced through the Zeeman effect, we use the circular polarization fraction
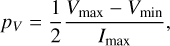 (6)
(6)
where the subscripts “max” and “min” indicate the maximum and minimum value of Vv, respectively. A single optically thin propagation, over a constant magnetic field, yields a polarization fraction
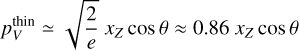 (7)
(7)
that is proportional to the line-of-sight component of the magnetic field: Blos ∝ xZ cos θ. To derive Eq. (7), we neglected the second-order contribution of the Zeeman effect to the total intensity profile, while we used max 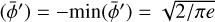 for the extremes of the circular polarization profile.
for the extremes of the circular polarization profile.
From Eq. (4a), we can see that the Zeeman effect also broadens spectral lines. We characterize the Zeeman broadening using the parameter
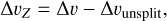 (8)
(8)
which is the difference between the full width at half maximum (FWHM) of the Zeeman-split line Δυ and the unsplit line Δυunsplit. We find that the Zeeman broadening of the total intensity profile is well described by
![${{{\rm{\Delta }}{\upsilon _Z}} \over b} \approx 0.84x_Z^2\,\left[ {\bar Q - {\rm{\Delta }}Q\,{{\cos }^2}\,\theta } \right],$](/articles/aa/full_html/2023/10/aa45840-23/aa45840-23-eq26.png) (9)
(9)
which, as can be seen from Fig. 2, is an excellent approximation for xZ ≲ 0.2. We note here that unlike the circular polarization, which is only dependent on the line-of-sight component of the magnetic field, the Zeeman broadening is the sum of two components: one proportional to the total magnetic field strength and one proportional to the line-of-sight component of the magnetic field. These are the terms 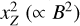 and
and 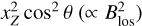 , respectively.
, respectively.
The production of linear polarization through the Zeeman effect is a function of the plane-of-the-sky component of the magnetic field. From Eqs. (4b,c) we see that the linear polarization fraction as a function of the magnetic field position angle 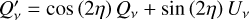 is given by
is given by
![${p_l} = {{{{\left[ {Q{\prime _v}} \right]}_{\max }}} \over {{I_{\max }}}} \simeq - {1 \over 2}\,x_Z^2{\rm{\Delta }}Q\,{\sin ^2}\,\theta ,$](/articles/aa/full_html/2023/10/aa45840-23/aa45840-23-eq31.png) (10)
(10)
where we note that the linear polarization fraction exhibits a quadratic dependence on the plane-of-the-sky magnetic field strength: 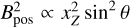 . The linear polarization has a spectral profile proportional to the second derivative of the total intensity, which is negative toward the line center and positive in the line wings. Therefore, for positive (negative) ΔQ, the linear polarization is oriented perpendicular (parallel) to the projected magnetic field direction toward the line center, and parallel (perpendicular) to the projected magnetic field direction in the line wings.
. The linear polarization has a spectral profile proportional to the second derivative of the total intensity, which is negative toward the line center and positive in the line wings. Therefore, for positive (negative) ΔQ, the linear polarization is oriented perpendicular (parallel) to the projected magnetic field direction toward the line center, and parallel (perpendicular) to the projected magnetic field direction in the line wings.
Zeeman parameters, frequencies, and Einstein coefficients of CN transitions relevant to ALMA polarization measurements.
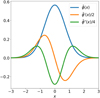 |
Fig. 1 Normalized Gaussian line profile and its first two derivatives plotted against the Doppler unit. |
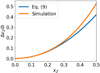 |
Fig. 2 Zeeman broadening of a Zeeman-split line as a function of the Doppler normalized Zeeman shift xZ. The predicted Zeeman broadening between proper polarized radiative transfer simulations and the fitted Eq. (9) are compared. The radiative transfer equations are performed using |
2.1.1 Simultaneous observation of Zeeman signatures
In Table 2, we report the sensitivity of the different spectral line Zeeman signatures to the magnetic field components of the traced region. While circular polarization is only dependent on the line-of-sight magnetic field strength, the Zeeman broadening also has a dependence on the total magnetic field strength. When either of these methods are combined with linear polarization observations that are sensitive to the square of the two magnetic field components projected onto the plane of the sky, then the full 3D vector of the magnetic field of the traced region can be readily derived. The circular polarization is linearly dependent on the line-of-sight magnetic field strength, while both Zeeman broadening and linear polarization observations are quadratically dependent on the magnetic field strength, and are therefore insensitive to the polarity of the magnetic field vector.
Comparing the Zeeman signatures to methods such as observation of spectral line polarization through the GK effect or through dust polarization observations, we note the advantageous property of Zeeman signatures: their effect is a function of the magnetic field strength and not just its direction. Therefore, while methods using dust polarization or the GK effect may only trace the magnetic field direction, Zeeman signatures can be used to extract both the magnetic field direction and strength.
Zeeman signatures and the magnetic field components they are sensitive to.
2.1.2 Zeeman parameters
To complete our discussion of Eq. (4), we consider the Zeeman parameters in more detail. Each spectral line has three Zeeman parameters associated with it: the Zeeman coefficient z, which is on the order of kHz mG−1, and the dimensionless coefficients 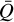 and ΔQ. The Zeeman coefficient z describes the relative offset of the σ±-transition groups per unit magnetic field strength. Transitions with large Zeeman coefficients have relatively strong circular polarization associated with them. The dimensionless Zeeman coefficients
and ΔQ. The Zeeman coefficient z describes the relative offset of the σ±-transition groups per unit magnetic field strength. Transitions with large Zeeman coefficients have relatively strong circular polarization associated with them. The dimensionless Zeeman coefficients 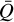 and ΔQ describe the intragroup broadening of the π0 and σ± transitions. For a J = 1−0 transition, the transition groups σ± and π0 are each associated with only one transition. Therefore, for J = 1−0 transitions, no additional broadening or linear polarization is produced due to intragroup broadening and the Zeeman broadening and linear polarization are perfectly described by the Zeeman coefficient:
and ΔQ describe the intragroup broadening of the π0 and σ± transitions. For a J = 1−0 transition, the transition groups σ± and π0 are each associated with only one transition. Therefore, for J = 1−0 transitions, no additional broadening or linear polarization is produced due to intragroup broadening and the Zeeman broadening and linear polarization are perfectly described by the Zeeman coefficient: 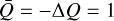 (see also Crutcher et al. 1993). However, for transitions of larger angular momentum, a multitude of transitions make up the σ± and π0 transition groups, and they may exhibit intragroup broadening. The intragroup broadening adds to the total broadening of the spectral line, and to its linear polarization. The parameters
(see also Crutcher et al. 1993). However, for transitions of larger angular momentum, a multitude of transitions make up the σ± and π0 transition groups, and they may exhibit intragroup broadening. The intragroup broadening adds to the total broadening of the spectral line, and to its linear polarization. The parameters 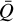 and ΔQ are multiplication factors that address the relative contribution of intragroup broadening to the total Zeeman broadening or linear polarization. They are large if the intragroup broadening exceeds the relative offset of the σ±-transition groups, whose effect is already captured by the Zeeman coefficient.
and ΔQ are multiplication factors that address the relative contribution of intragroup broadening to the total Zeeman broadening or linear polarization. They are large if the intragroup broadening exceeds the relative offset of the σ±-transition groups, whose effect is already captured by the Zeeman coefficient.
In anticipation of the simulations that are reported in Sect. 3, it is helpful to consider the spectral decomposition of Zeeman-split lines from the CN Band 3 transitions. In Fig. 3, we compare the Zeeman-split transitions of the v0 = 113.144 GHz, v0 = 113.191 GHz, and v0 = 113.170 GHz lines. These lines have different Zeeman effects and signatures. For the v0 = 113.144 line, σ±-transitions are shifted in frequency with respect to each other relatively strongly. This is why this transition exhibits strong circular polarization, reflected in its high z-parameter, while also having modest broadening or linear polarization, reflected in the 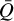 and ΔQ parameters approaching 1 and −1. The v0 = 113.191 GHz line has a large spread in its Zeeman-split transitions, even though the relative shift of the σ±-transitions is modest. This transition therefore exhibits relatively low circular polarization (low z-parameter), but strong broadening and linear polarization (high
and ΔQ parameters approaching 1 and −1. The v0 = 113.191 GHz line has a large spread in its Zeeman-split transitions, even though the relative shift of the σ±-transitions is modest. This transition therefore exhibits relatively low circular polarization (low z-parameter), but strong broadening and linear polarization (high 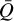 and ΔQ parameters). The line at v0 = 113.170 GHz shows generally weak Zeeman shifts in its magnetic sublevel transitions, which is why polarization and broadening is relatively weak for this line, reflected in its low z-,
and ΔQ parameters). The line at v0 = 113.170 GHz shows generally weak Zeeman shifts in its magnetic sublevel transitions, which is why polarization and broadening is relatively weak for this line, reflected in its low z-, 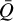 , and ΔQ parameters.
, and ΔQ parameters.
 |
Fig. 3 Stem plots of magnetic sublevel transitions of Band 3 CN hyperfine transitions. The individual magnetic sublevel transitions are indicated by a solid line, and grouped (π0, σ±) by color. The dotted lines indicate the average shift of the σ± groups. |
2.2 Zeeman effects for molecules excited in protoplanetary disks
In Sect. 3, we investigate the signature of the protoplanetary disk magnetic field in the spectral lines of CN. There we use proper 3D polarized radiative transfer simulations to study Zeeman broadening, linear polarization, and the emergence of circular polarization in a range of CN transitions. In anticipation of the discussion of these results, it is helpful to analyze some simple radiative transfer problems for optically thin Zeeman-split lines that will help in interpreting the more intricate 3D simulations.
Protoplanetary disks are permeated by a magnetic field which is commonly divided into its cylindrical components: radial, vertical, and toroidal. It is a reasonable approximation to assume that these components are axisymmetric (Béthune et al. 2017). The toroidal magnetic field component is likely dominant and, together with the radial magnetic field component, it changes sign between the two sides of the disk (Bai & Stone 2013; Lesur 2021, for more discussion, see text after Eq. (23)).
Using the Zeeman effect, the magnetic field of protoplanetary disks is most effectively traced by the paramagnetic molecule CN because CN exhibits a strong Zeeman effect and shows strong emission from an elevated emission surface at both sides of the disk (Cazzoletti et al. 2018). We constructed a simplified representation of the radiative transfer in a protoplanetary disk by dividing it into two propagations through optically thin isothermal slabs that correspond to the back and front side molecular emission surfaces of the disk. We account only for the toroidal and vertical components of the magnetic field as the radial component is assumed to be negligible.
We consider a disk with inclination ι and position angle ΦPA. The position angle is defined by the position angle of the disk redshifted semimajor axis. In the disk frame, where the x-axis is along its semimajor axis and the z-axis is the rotation axis of the disk, the line-of-sight direction toward the observer 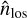 , and the northern and eastern directions in the plane of the sky
, and the northern and eastern directions in the plane of the sky 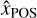 and
and 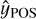 are
are
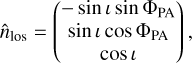 (11a)
(11a)
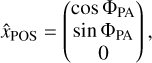 (11b)
(11b)
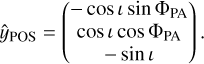 (11c)
(11c)
From these definitions, we can compute the projection of the magnetic field onto the line of sight. We consider an axisymmetric magnetic field with a toroidal and a vertical component: 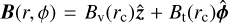 . The magnetic field strengths are dependent on the disk-frame cylindrical radius rc, and the unit vectors in the disk-frame are
. The magnetic field strengths are dependent on the disk-frame cylindrical radius rc, and the unit vectors in the disk-frame are ![$\hat z = \left[ {0,0,1} \right]$](/articles/aa/full_html/2023/10/aa45840-23/aa45840-23-eq57.png) and
and ![$\hat \phi = \left[ { - \sin \,\phi ,\cos \,\phi ,0} \right]$](/articles/aa/full_html/2023/10/aa45840-23/aa45840-23-eq58.png) , which are a function of the (disk-frame) azimuthal angle ϕ. The projection of the magnetic field onto the line of sight is then
, which are a function of the (disk-frame) azimuthal angle ϕ. The projection of the magnetic field onto the line of sight is then
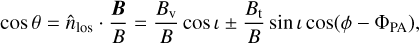 (12)
(12)
where ± is positive for the front and negative for the back side of the disk. We note that we assumed the toroidal component to be counter to and along the disk rotation direction for the front and back side of the disk, respectively. We suppressed the magnetic field strength dependence on the cylindrical radius in our notation. Hereafter we denote the azimuthal angle ϕ′ = ϕ – ΦPA with respect to the disk position angle. The magnetic field position angle η, which is relevant to evaluate the linear polarization Stokes parameters, can be evaluated from
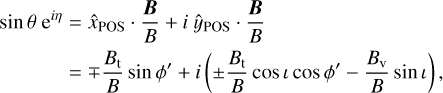 (13)
(13)
where the upper elements of ± and ∓ apply to the front side of the disk, while the lower elements apply to the back side of the disk.
2.2.1 Circular polarization
We put together Eqs. (7) and (12) to obtain the expected circular polarization fraction, emerging from the front and back side of the disk,
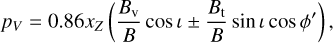 (14)
(14)
where ± corresponds to the front and back sides of the disk. The contributions of the vertical and toroidal magnetic field components to the total circular polarization signal are additive, 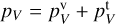 , so we can consider them separately.
, so we can consider them separately.
The vertical component of the magnetic field does not change sign across the disk midplane and the vertical projection does not depend on the azimuthal angle. The contribution of the vertical magnetic field to the circular polarization is thus 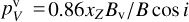 cos i for either side of the disk.
cos i for either side of the disk.
The toroidal magnetic field component changes sign through the midplane. Effectively, the circular polarization that is produced in the back side of the disk is then cancelled by the circular polarization produced in the front side of the disk. A net circular polarization is produced if (i) a velocity shift along the line of sight occurs between the front and back sides of the disk, (ii) the projected magnetic field varies between the two sides of the disk, or (iii) an optically thick dust layer that partially absorbs the emission emerging from the back side of the disk is present between the two emission layers (as can be seen in, e.g., Isella et al. 2018).
The recovery of circular polarization through a velocity shift between the emission surfaces and a difference in the projected magnetic fields of the two emission surfaces is proportional to the inclination. Of these two effects, we found that a velocity shift between the emission surfaces is most effective in negating the circular polarization cancellation. The velocity shift along the line of sight between the emission surfaces occurs for inclined disks with emission surfaces above the midplane. It can be larger than the line width at high inclinations ι ≳ 40°, and roughly follows an azimuthal profile ∝ sin 2ϕ′. In large parts of the disk two well-separated line profiles would emerge that do not interfere in each other’s (polarized) emission. For moderately inclined disks, ι ≲ 20°, the velocity shifts are generally smaller than the Doppler widths for all azimuthal angles. We can evaluate the impact of a velocity shift on the emergent circularly polarized emission. We let Δx = (υupper – υlower)/b denote the (Doppler normalized) velocity shift between the line-of-sight projected velocities of the emission emerging from the front and back sides of the disk. For Δx ≲ 0.3, the two-step (optically thin) radiative transfer with opposite magnetic fields permits us to find the solution for the circular polarization (see Appendix B for a derivation)
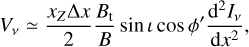 (15)
(15)
that yields a polarization fraction of
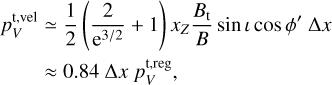 (16)
(16)
where 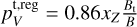 sin ι cos ϕ′ is the expected circular polarization fraction due to the toroidal magnetic field from the front side of the disk. Thus, some of the circular polarization due to the toroidal magnetic field that would have been cancelled through the magnetic field sign-flip is recovered when a velocity shift between the two emission surfaces is present. We note, however, that the line profile of the circular polarization in this special case is not the usual S -shaped profile as expected from the “regular” Zeeman effect, but rather a profile proportional to
sin ι cos ϕ′ is the expected circular polarization fraction due to the toroidal magnetic field from the front side of the disk. Thus, some of the circular polarization due to the toroidal magnetic field that would have been cancelled through the magnetic field sign-flip is recovered when a velocity shift between the two emission surfaces is present. We note, however, that the line profile of the circular polarization in this special case is not the usual S -shaped profile as expected from the “regular” Zeeman effect, but rather a profile proportional to 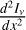 , as shown in Fig. 1. We show a comparison between the circular polarization profile due to the “regular” Zeeman effect and due to adversely Zeeman splitted emission with a velocity-shift in Fig. 4.
, as shown in Fig. 1. We show a comparison between the circular polarization profile due to the “regular” Zeeman effect and due to adversely Zeeman splitted emission with a velocity-shift in Fig. 4.
Another way to suppress the destructive interference of the toroidal magnetic field circular polarization is through an optically thick dust layer in the midplane. If absorption due to dust occurs between the back and front side emission surfaces, then the cancellation is partially suppressed. In this scenario the resulting circular polarization can be estimated as (see Appendix B for a derivation)
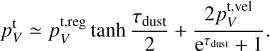 (17)
(17)
As an example, we estimate the effect of a dust layer on the circular polarization in a source such as TW Hya. Estimates of the TW Hya dust optical depth at 50 AU for a range of frequencies put these at τdust = 0.7 to 2 from ALMA Band 3 to Band 7 (Macías et id. 2021). That means that 33–76% (Band 3 – Band 7) of the 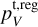 is recovered when the dust absorption is accounted for.
is recovered when the dust absorption is accounted for.
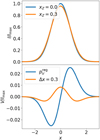 |
Fig. 4 Total (upper) and circularly polarized (lower) intensity of a Zeeman-split line. The intensities are normalized with respect to the unsplit (xZ = 0) intensity. The total intensity plots are for an unsplit (xZ = 0) and Zeeman-split (xZ = 0.3, |
2.2.2 Zeeman broadening
We combine Eqs. (9) and (12) to obtain the expected (Doppler normalized) Zeeman broadening emerging from the front and back sides of the disk,
![$\matrix{ {{{{\rm{\Delta }}{\upsilon _Z}} \over b} = 0.84x_Z^2\left[ {\bar Q - {\rm{\Delta }}Q\left( {{{B_{\rm{v}}^2} \over {{B^2}}}{{\cos }^2}\,\iota \, + {{B_t^2} \over {{B^2}}}{{\sin }^2}\iota } \right.} \right.} \hfill \cr {\left. {\left. {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times {{\cos }^2}\phi ' \pm {{{B_{\rm{v}}}{B_{\rm{t}}}} \over {{B^2}}}\sin 2i\sin \phi '} \right)} \right],} \hfill \cr } $](/articles/aa/full_html/2023/10/aa45840-23/aa45840-23-eq72.png) (18)
(18)
where ± corresponds to the front and back sides of the disk. We recognize from Eq. (18) that most of the Zeeman broadening is insensitive to the polarity of the magnetic field and is identical for the front and back sides of the disk. Only the cross-term BvBt, is explicitly dependent on the polarity of the toroidal magnetic field, which changes sign through the midplane. For weakly inclined disks the cross-term is minor compared to broadening terms that are invariant to the magnetic field polarity. The expression of the cross-term is therefore dependent on the presence of a dust layer and on the velocity shift between the front and back sides of the disk emission surfaces.
We previously pointed out that when considering inclined disks, a velocity shift arises between the back and front sides of the disk. For moderately inclined disks this velocity shift manifests in the total intensity profile of spectral lines as an additional broadening term. For a Doppler normalized velocity shift between the two emission surfaces of Δx, we note the additional broadening
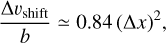 (19)
(19)
where the total broadening of a Zeeman-split line for a slightly inclined disk is the sum of the two broadening mechanisms, ΔυZ + Δυshit, if they are small compared to the line width. The Zeeman broadening can be disentangled from the broadening due to the velocity shift between the two emission surfaces by observing multiple spectral lines. While the ΔυZ contribution to the broadening is dependent on the Zeeman coefficient, which varies between transitions, the Δυshift contribution to the broadening is dependent on the system geometry and does not vary between transitions. The presence of an optically thick dust layer in the midplane will suppress the broadening due to the velocity shift between the two emission surfaces.
2.2.3 Linear polarization
The linear polarization of Zeeman-split spectral lines is quadratically dependent on the plane-of-the-sky component of the magnetic field (see also Eqs. (4b,c) and (13)). Linear polarization is observed through the Stokes Q and U parameters. The simultaneous observation of these parameters yields a two-dimensional quasi vector, which may be related to the magnetic field direction (but not its polarity) and strength projected onto the plane of the sky. We put together Eqs. (4b,c) and (13) to derive an expression for the linear polarization fractions, 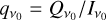 and
and 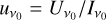 , at the line center, v0,
, at the line center, v0,
![$\matrix{ {{q_{{v_0}}} = - {{x_Z^2{\rm{\Delta }}Q} \over 2}\left( { - {{B_{\rm{v}}^2} \over {{B^2}}}{{\sin }^2}\,\iota \, - {{B_{\rm{t}}^2} \over {{B^2}}}} \right.} \hfill \cr {\left. {\left. {\,\,\,\,\,\,\,\,\,\,\,\,\, \times {{\cos }^2}\phi '} \right] \pm {{{B_{\rm{v}}}{B_{\rm{t}}}} \over {{B^2}}}\,\sin \,2\iota \,\cos \phi '} \right)} \hfill \cr } $](/articles/aa/full_html/2023/10/aa45840-23/aa45840-23-eq76.png) (20a)
(20a)
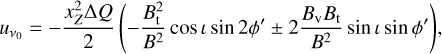 (20b)
(20b)
while the total linear polarization fraction at the line center, 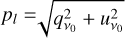 , is
, is
![$\matrix{ {{p_l} = - {{x_Z^2{\rm{\Delta }}Q} \over 2}\left( {{{B_{\rm{t}}^2} \over {{B^2}}}\left[ {{{\sin }^2}\phi ' + {{\cos }^2}\,\iota \,{{\cos }^2}\phi '} \right] + {{B_{\rm{v}}^2} \over {{B^2}}}{{\sin }^2}\iota } \right.} \hfill \cr {\left. {\,\,\,\,\,\,\,\,\,\,\, \mp {{{B_{\rm{t}}}{B_{\rm{v}}}} \over {{B^2}}}\sin 2\iota \,\cos \phi '} \right).} \hfill \cr } $](/articles/aa/full_html/2023/10/aa45840-23/aa45840-23-eq79.png) (20c)
(20c)
The ± sign applies to the front and back side of the disk. Just as for the Zeeman broadening, a polarity-dependent term arises in the expressions for the linear polarization. The manifestation of the cross-term is dependent on the presence of a dust layer and on the velocity shift between the front and back side of the disk emission surfaces, and is maximum at inclinations of 45°.
2.2.4 Azimuthal stacking of Zeeman signatures
We have seen that the Zeeman broadening and linear polarization are partially dependent on terms that change sign between the back and front sides of the disk. The polarity-dependent terms are maximum at a disk inclination of 45°, and require detailed knowledge of the continuum absorption or a velocity shift between the two emission surfaces along the line of sight in order for them to be modeled properly. In this way the interpretation of the Zeeman broadening or linear polarization measurements for their magnetic field information is, just as for the circular polarization observations, inherently associated with uncertainty. In order to remove this uncertainty, we take the axisymmetry of the disk magnetic field into consideration such that we may devise an averaging scheme that eliminates the polarity dependent term, similar to the technique employed in Teague et al. (2021). Specifically, when the Zeeman broadening is stacked over the range of deprojected azimuthal angles,
![$\matrix{ {{{\left\langle {{{{\rm{\Delta }}{\upsilon _Z}} \over b}} \right\rangle }_{\phi '}} = 0.84x_Z^2\left[ {\bar Q - {\rm{\Delta }}Q{{\left\langle {{{\cos }^2}\theta } \right\rangle }_{\phi '}}} \right]} \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 0.84x_Z^2\left[ {\bar Q - {{{\rm{\Delta }}Q} \over 2}\left( {{{B_{\rm{v}}^2} \over {{B^2}}}{{\cos }^2}\iota + {{B_{\rm{t}}^2} \over {{B^2}}}{{\sin }^2}\iota } \right)} \right],} \hfill \cr } $](/articles/aa/full_html/2023/10/aa45840-23/aa45840-23-eq80.png) (21)
(21)
then the resulting averaged quantity is insensitive to the polarity-dependent terms in cos2 θ. Similarly, we can exploit the axisym-metry of the disk to extract the different magnetic field components from the linear polarization by applying the weighted stacking,
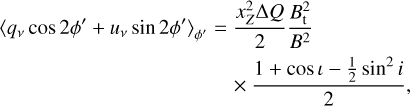 (22a)
(22a)
to extract the toroidal magnetic field component, and the weighting,
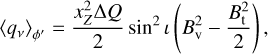 (22b)
(22b)
to obtain the vertical magnetic field component.
3 Simulations
In this section we study the signature of magnetic fields in CN lines excited in a TW Hya-like protoplanetary disk using full 3D radiative transfer simulations. We model the polarized radiative transfer using Eqs. (A.1)–(A.3), which are based on Eqs. (9.2–9.16) from Degl’Innocenti & Landolfi (2006). In this formalism, we rigorously model the propagation of radiation through a Zeeman split population by resolving the individual magnetic sublevel transitions within a line. A similar method is employed in the radiative transfer code POLARIS (Brauer et al. 2017).
We modeled the radiative transfer of CN in a TW Hya-like disk, at inclination ι = 6°, where we used the physical model of Calahan et al. (2021). In our models we assume CN to be excited in an emission surface located at z/r = 0.1 ± 0.025 or z/r = 0.3 ± 0.025. Of these emission surface heights, z/r ~ 0.3 is predicted by chemical models (Cazzoletti et al. 2018), while we include simulations with z/r ~ 0.1 in our analysis to analyze the sensitivity of our results to the emission height. According to the physical model we adopt, at cylindrical radius rc = 50 AU, emission from z/r = 0.3 is associated with 50 K gas, while emission from z/r = 0.1 is associated with 22 K gas. To cover a range of optical depths, corresponding roughly to τ ~ 0.1, 1, and 10, we adopted the emission surface abundances: xCN = 3 × 10−7, 3 × 10−8, and 3 × 10−9 for the z/r ~ 0.3 simulations, and xCN = 1 × 10−8, 1 × 10−9, and 1 × 10−10 for the z/r ~ 0.1 simulations. In order to evaluate the effects of dust absorption in the midplane, we performed simulations with and without a midplane layer of dust, with optical depth based on values from Macías et al. (2021), and a vertical profile where the dust scale height is set to 20% of the gas scale height.
We adopted a magnetic field based on the constraints of Vlemmings et al. (2019),
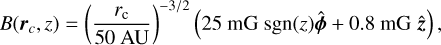 (23)
(23)
with components in the toroidal 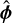 and vertical
and vertical 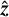 directions. It is commonly assumed that the radial and toroidal components of magnetic fields that permeate accretion disks exhibit a sign change crossing the midplane (Blandford & Payne 1982; Wardle & Koenigl 1993; Bai 2016). Such a magnetic field structure is expected from the advection of magnetic field lines throughout the star formation process. In the early evolutionary stages, field lines are dragged inward (Mouschovias & Ciolek 1999; Girart et al. 1999), creating a radial magnetic field of opposite polarity between the two sides of the midplane. Subsequently, Keplerian rotation of the accretion disk winds the radial field lines into a toroidal magnetic field with opposite polarity at the two sides of the midplane. Accordingly, this magnetic field configuration is required to magnetocentrifugally launch the often observed bipolar jets and winds associated with young stellar objects (Frank et al. 2014; Bjerkeli et al. 2019). Recent 3D magnetohydrody-namic simulations find that under specific conditions the usual symmetry of the magnetic field can be broken, specifically for disks where rotation is anti-aligned with the magnetic field; such disks will then have an associated dissymmetrical wind (Béthune et al. 2017; Bai 2017). Still, considering the magnetic field evolution and observational evidence in earlier stages of the star formation process, we adopt our simulations to the common expectation of a magnetic field that changes sign in its radial and toroidal components through the midplane.
directions. It is commonly assumed that the radial and toroidal components of magnetic fields that permeate accretion disks exhibit a sign change crossing the midplane (Blandford & Payne 1982; Wardle & Koenigl 1993; Bai 2016). Such a magnetic field structure is expected from the advection of magnetic field lines throughout the star formation process. In the early evolutionary stages, field lines are dragged inward (Mouschovias & Ciolek 1999; Girart et al. 1999), creating a radial magnetic field of opposite polarity between the two sides of the midplane. Subsequently, Keplerian rotation of the accretion disk winds the radial field lines into a toroidal magnetic field with opposite polarity at the two sides of the midplane. Accordingly, this magnetic field configuration is required to magnetocentrifugally launch the often observed bipolar jets and winds associated with young stellar objects (Frank et al. 2014; Bjerkeli et al. 2019). Recent 3D magnetohydrody-namic simulations find that under specific conditions the usual symmetry of the magnetic field can be broken, specifically for disks where rotation is anti-aligned with the magnetic field; such disks will then have an associated dissymmetrical wind (Béthune et al. 2017; Bai 2017). Still, considering the magnetic field evolution and observational evidence in earlier stages of the star formation process, we adopt our simulations to the common expectation of a magnetic field that changes sign in its radial and toroidal components through the midplane.
The nonlocal thermal equilibrium excitation analysis was performed using LIME1 (Brinch & Hogerheijde 2010). The excitation solutions were subsequently used in conjunction with the magnetic field model to ray-trace a (polarized) image using the above-mentioned formalism outlined in Degl’Innocenti & Landolfi (2006)2. We include in our analysis the nine strongest Band 3 transitions of CN which are part of a (hyper)fine manifold, and therefore lie close in frequency around 113.4 GHz. Due to the low inclination of the TW Hya-like disk that we model, line overlap within the manifold does not occur, but this may be a possibility in more strongly inclined disks. The energy levels, Einstein coefficients, and collision coefficients of CN were taken from the LAMDA database (Schöier et al. 2005; Kalugina & Lique 2015). The level specific g-factors of CN were evaluated using the method outlined in Appendix A of Vlemmings et al. (2019). We analyzed the (polarization) spectra and properties of the Band 3 transitions of CN emerging at deprojected distance rc = 50 AU (0.83″). We chose to analyze the Band 3 transitions as these exhibit the largest Doppler normalized Zeeman coefficients (see Table 1 and Eq. (2)). Around a deprojected distance of rc = 50 AU CN emission is observed to peak (Cazzoletti et al. 2018), while dust continuum remains important to the radiative transfer (Vlemmings et al. 2019; Macías et al. 2021).
3.1 Circular polarization
The spectral profiles of the circular polarization of the CN (N, J, F) → (N′, J′, F′) = (1,1/2,1/2) → (0,1/2,1/2) transition at rc = 50 AU are shown in Fig. 5 at a range of azimuthal angles ϕ′. Simulations were performed with and without an optically thick midplane dust layer, and a large difference between both simulations can be readily appreciated. The simulations without a midplane dust layer show an S -shaped spectral profile in the circular polarization, with a circular polarization fraction of ~1% that is weakly variable over the azimuthal angle. While also exhibiting S -shaped spectral profiles, the simulations that include an optically thick midplane dust layer show a variation in the circular polarization fraction in the range ~1%–2% for emission emerging from different azimuthal angles.
The variability of the circular polarization fraction with the azimuthal angle can be explained by the Zeeman effect due to the toroidal magnetic field. As discussed in Sect. 2.2.1, the circular polarization due to the toroidal magnetic field is affected by destructive interference between the emission from the front and back sides of the disk. The interference is suppressed by either a velocity shift between the two disk sides along the line of sight or through an optically thick layer of dust. The Zeeman effect due to the toroidal magnetic field component is most prominent in simulations with a midplane dust layer. For these simulations, strongest circular polarization is found at azimuthal angle ϕ′ = 0° as the toroidal magnetic field contributes maximally to the line-of-sight component of the magnetic field. In contrast, we find that the contribution to the circular polarization from the toroidal magnetic field component is almost completely suppressed for the simulations assuming optically thin dust. This may be explained by the small velocity shift between the two emission surfaces, Δx ~ 0.05, due to the low inclination adopted. The small variation in the circular polarization that is a result of the velocity shift between the back and front side emission surfaces is most strongly present around azimuthal angles of 45° as the velocity shift is greatest there.
For the optically thin simulations with the emission surface at z/r = 0.3, we plotted the variability of the circular polarization fraction, defined in Eq. (6), with the azimuthal angle in Fig. 6. We note for the simulations with τdust = 0.7 an enhanced polarization fraction for azimuthal angles <180°, while it is diminished for azimuthal angles >180º. Strikingly, the circular polarization that is predicted from our analytical modeling, pV = 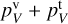 tanh
tanh 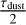 (see Eqs. (14)–(17) and Sect. 2.2.1), compares well to the simulation results. The variation in the τdust → 0 simulations is much weaker, due to the small velocity shift between the two sides of the disk.
(see Eqs. (14)–(17) and Sect. 2.2.1), compares well to the simulation results. The variation in the τdust → 0 simulations is much weaker, due to the small velocity shift between the two sides of the disk.
In Table 3, we list the circular polarization of the different CN Band 3 transitions we found in our simulations. The simulations show that the differently placed emission surfaces at z/r = 0.1 and z/r = 0.3 yield different circular polarization fractions for the same transition. This is the result of the different thermal line width for the two surfaces, with the higher surface tracing warmer gas resulting in enhanced thermal line widths. Between transitions, we also find strong variations in the circular polarization. The circular polarization is weakly dependent on the optical depth when lines are ≲1 in optical depth, and they increase slightly for τ ≳ 1, as the gradient toward the line wings increases (this effect was also seen in Mazzei et al. 2020).
 |
Fig. 5 Spectra of circularly polarized intensity of CN (N, J, F) → (N′, J′, F′) = (1,1 /2,1 /2) → (0,1 /2,1/2) transition excited in a TW Hya-like protoplanetary disk, in an emission surface around z/r = 0.3, with (lower row) and without (upper row) a layer of dust present between the emission surfaces. The spectra for different optical depths and position angles are given. |
 |
Fig. 6 Circular polarization fraction at deprojected distance rc = 50 AU as a function of the deprojected azimuthal angle ϕ′. Simulations with and without a dust layer are plotted inside the figure and the dashed line is a fitting function. |
3.2 Zeeman broadening
The broadening of spectral lines can be extracted from the total intensity profiles. We plot the total intensity spectra of the CN (N, J, F) → (N′, J′, F′) = (1,1/2,1/2) → (0,1/2,1/2) transition in Fig. 7, where we plot spectra for varying optical depths and azimuthal angles, and with and without the presence of an optically thick dust layer. Inside the figure we indicate with dashed lines the simulations assuming negligible magnetic fields, xZ → 0. Comparing these simulations to simulations with magnetic fields, we note a consistent broadening of the line profiles due to the Zeeman effect for the emission emerging from different azimuthal angles. The broadening is most noticeable for optically thin lines, where Zeeman broadened lines clearly show weaker signals, that accordingly have a broader FWHM. From inspection of the spectra, only a weak variation in the broadening with the azimuthal angle is observed. The simulations with the dust layers yield a lower total intensity, but the Zeeman broadening appears to have been affected only to a small degree. We explore this feature in more detail later on.
We extracted the Zeeman broadening, as defined in Eq. (8), from the total intensity spectra, and plotted it against the azimuthal angle for the optically thin simulations in Fig. 8. The azimuthal variability of the Zeeman broadening is relatively weak compared to the total broadening: about 5%. We note a different variability for the simulations with and without a dusty midplane layer. The difference is due to the cos2 θ term in Eq. (12) that is dependent on the product between the vertical Bv and toroidal Bt magnetic fields, and so depends on the polarity of the toroidal magnetic field that changes sign through the midplane. We plot Eq. (18), putting the polarity-dependent term at zero, in Fig. 8, where we observe an excellent agreement with the simulations that assume an optically thin dust layer. We acquire a good fit because the absence of a midplane dust layer suppresses the expression of the polarity-dependent term in the Zeeman broadening. The polarity-dependent term is expressed when a dust layer is present, but its precise effect is difficult to model. However, averaged over all azimuthal angles, as motivated in Sect. 2.2.4, the polarity-dependence is eliminated, regardless of the presence of a dust layer in the midplane.
In Table 3, we list the broadening of the different CN Band 3 transitions that we explored in our simulations. First, the simulations show that the differently placed emission surfaces at z/r = 0.1 and z/r = 0.3 show very different Zeeman broadening for the same transition. This is true because of the weaker thermal line broadening at the z/r = 0.1 surface, which is situated in cooler gas. Between transitions we find strong variance of the Zeeman broadening, which for the optically thin simulations of the z/r = 0.3 surface varies from 96 m s−1 to 6.4 m s−1. This is expected from the quadratic dependence of the broadening on the Zeeman shift, and the variation in the Zeeman splitting factor between the CN transitions. The predicted Zeeman broadening is weakly dependent on the optical depth when lines are ≲ 1 in optical depth. Our estimates of the Zeeman broadening increase for τ ≳ 1, but it is difficult to model them with the formalism we introduced in Sect. 2.
Summary of simulation results of the broadening and circular polarization of the N = 1–0 transitions of CN at deprojected distance rc = 50 AU and ϕ = 0° and ϕ = 90°.
 |
Fig. 7 Spectra of the total intensity of the CN (N, J, F) → (N′, J′, F′) = (1, 1/2, 1/2) → (0, 1/2, 1/2) transition excited in a TW Hya-like proto-planetary disk in an emission surface around z/r = 0.3, with (lower row) and without (upper row) a layer of dust present between the emission surfaces. In each panel the spectra for different optical depths (left to right) and azimuthal angles (different colors within the panels) are given. The dashed lines are from spectra assuming no magnetic field permeating the disk. |
 |
Fig. 8 Zeeman broadening at deprojected distance rc = 50 AU as a function of the azimuthal angle. Simulations with and without a dust layer are plotted and the dashed line is a fitting function (see text). |
3.3 Linear polarization
We plot the linear polarization spectra of the CN (N, J, F) → (N′, J′, F′) = (1, 1/2, 1/2) → (0, 1/2, 1/2) transition in Fig. 9. We plot the Stokes Q and U spectra, assuming an optically thin dust layer, for three azimuthal angles and a varying optical depth. While the Stokes U is almost completely suppressed at 0° and 90°, the Stokes Q is suppressed at 45°. From our simulations and Eq. (20), we note that the linearly polarized Stokes parameters change sign for ф′ → ф′ ± π/2. In addition, for simulations τ ≲ 1, the linear polarization spectra are characterized by a sign change toward the line wings. Therefore, both excellent angular and spectral resolutions are required to resolve the linear polarization signal. Optically thick spectral lines show strong signals toward their line wings, while toward the line center, no polarization is produced.
In Fig. 10, we plot the Stokes Qv and Uv linear polarization intensities at the line center, normalized with respect to the total intensity at the line center 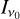 as a function of the azimuthal angle from the optically thin simulations. Simulations with and without a dust layer in the midplane are presented, but they differ only slightly. It is readily apparent that the dominant variation with the position angle in the Stokes
as a function of the azimuthal angle from the optically thin simulations. Simulations with and without a dust layer in the midplane are presented, but they differ only slightly. It is readily apparent that the dominant variation with the position angle in the Stokes 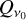 adheres to ∝ cos 2ф′, while for the Stokes
adheres to ∝ cos 2ф′, while for the Stokes 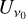 the variation is as ∝ sin 2ф′. We note that, assuming the polarity-dependent term to be zero, Eq. (20) describes the linear polarization with high precision. When we subtract Eq. (20) from our simulated results we are left with the contributions of the polarity-dependent terms to the linear polarization. We plot the residuals in the lower part of Fig. 10; we note that they are a fraction of the total signal and show different profiles between the simulations with and without a dusty midplane layer. Regardless of the presence of the dusty midplane layer, the residuals average to zero when using the weighting schemes outlined in Sect. 2.2.4.
the variation is as ∝ sin 2ф′. We note that, assuming the polarity-dependent term to be zero, Eq. (20) describes the linear polarization with high precision. When we subtract Eq. (20) from our simulated results we are left with the contributions of the polarity-dependent terms to the linear polarization. We plot the residuals in the lower part of Fig. 10; we note that they are a fraction of the total signal and show different profiles between the simulations with and without a dusty midplane layer. Regardless of the presence of the dusty midplane layer, the residuals average to zero when using the weighting schemes outlined in Sect. 2.2.4.
We computed the linear polarization fractions, using Eq. (10), of every CN Band 3 transition, for three optical depths; they are listed in Table 3. The linear polarization shows a dependence on the optical depth, where the strongest linear polarization is found for optically thin transitions and, above τ ~ 1, progressively diminishes with increasing optical depth. While this is indeed expected for the linear polarization at the line center, we find that the polarization in the line wings increases with the optical depth. For the optically thin simulations, the expected linear polarization fractions are between 0.0% and 13.0% for the z/r = 0.3 simulations, and about twice those estimates for the z/r = 0.1 simulations.
4 Discussion
4.1 Magnetic field detection in protoplanetary disks through spectral line observations
We studied the signature of the magnetic field in the Band 3 transitions of CN, excited in a protoplanetary disk. The signature of the magnetic field is manifested in the CN spectra through circular and linear polarization, and in the (Zeeman) broadening of the spectral lines. Each of these effects has a unique relation to the magnetic field of the region that the spectral lines trace. In the following we discuss how to characterize the underlying magnetic field from observations through each of these effects, and discuss their limitations and uncertainties.
4.1.1 Circular polarization
Extracting magnetic field information through circular polarization observations of the Zeeman effect of paramagnetic molecules is widely regarded as one of the most reliable ways to measure the magnetic field strength of astrophysical regions (Crutcher & Kemball 2019). The first attempts to characterize protoplanetary disk magnetic fields used this method, but to date observations have only been able to set upper limits on the magnetic field properties due to nondetections of the circular polarization (Vlemmings et al. 2019; Harrison et al. 2021).
The production of circular polarization in spectral lines scales with the Zeeman shift in Doppler units xZ, while the effects of Zeeman broadening and linear polarization scale with 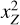 . Considering that for protoplanetary disks xZ < 1, we expect the circular polarization to be the most sensitive magnetic field tracer. However, the dominant toroidal (and radial) components of the magnetic field likely change sign across the disk midplane, and thus suppressing the circular polarization produced by these magnetic field components (also pointed out in Mazzei et al. 2020). Additionally, for weakly inclined disks, primarily the vertical component of the magnetic field is expressed in the circular polarization, which is expected to be a factor of ~ 10 weaker than the dominant toroidal magnetic field component (Béthune et al. 2017).
. Considering that for protoplanetary disks xZ < 1, we expect the circular polarization to be the most sensitive magnetic field tracer. However, the dominant toroidal (and radial) components of the magnetic field likely change sign across the disk midplane, and thus suppressing the circular polarization produced by these magnetic field components (also pointed out in Mazzei et al. 2020). Additionally, for weakly inclined disks, primarily the vertical component of the magnetic field is expressed in the circular polarization, which is expected to be a factor of ~ 10 weaker than the dominant toroidal magnetic field component (Béthune et al. 2017).
We considered two mechanisms through which the cancellation of circular polarization due to the midplane polarity change can be diminished. First, when a velocity shift between the two sides of the disk is present, the circular polarization profiles of the two disk sides are nonresonant and circular polarization is recovered in proportion to the size of the velocity shift. Second, with the presence of an optically thick dust layer in the mid-plane, a part of the circular polarization of the back side of the disk is absorbed and the cancellation of circular polarization is accordingly partially negated.
We apply our results to the existing circular polarization measurements of CN toward protoplanetary disks. Vlemmings et al. (2019) observed a subset of the Band 6 transitions of CN toward TW Hya using ALMA. They obtain the tightest constraints on the vertical magnetic field through performing of a stacking of the CN transitions in combination with an azimuthal stacking. The toroidal magnetic field component they extract through subtracting the stacked results between the red- and blueshifted parts of the major axis. We performed 3D polarized radiative transfer simulations of a TW Hya-like disk and found that the polarization fraction was reproduced excellently by Eq. (17). From this result, we have no comments on the method to estimate the vertical component of the magnetic field, but point out that the procedure meant to extract the toroidal magnetic field yields tanh 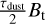 rather than Bt. With the current estimates of the dust opacity of TW Hya (Macías et al. 2021), we put tanh
rather than Bt. With the current estimates of the dust opacity of TW Hya (Macías et al. 2021), we put tanh 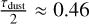 . On the basis of our comments on the extraction method and our radiative transfer simulations, we suggest updating the constraint of Vlemmings et al. (2019) of the toroidal magnetic field to Bф < 65 mG. Additionally, we point out that the procedure to extract the toroidal magnetic field strength using the stacking of spectral lines along the line of nodes can be improved by a positional angle stacking with the appropriate weighing of cos ф′ (see Eq. (14). This analysis will be undertaken in a future paper.
. On the basis of our comments on the extraction method and our radiative transfer simulations, we suggest updating the constraint of Vlemmings et al. (2019) of the toroidal magnetic field to Bф < 65 mG. Additionally, we point out that the procedure to extract the toroidal magnetic field strength using the stacking of spectral lines along the line of nodes can be improved by a positional angle stacking with the appropriate weighing of cos ф′ (see Eq. (14). This analysis will be undertaken in a future paper.
Harrison et al. (2021) observed a subset of CN Band 6 transitions toward AS 209 in search of circular polarization. Using a method similar to that in Vlemmings et al. (2019), stacking the transitions of the red- and blueshifted parts of the disk, they extract a toroidal magnetic field strength of <8.7 mG, but we note that this may be an underestimation due to cancellation effects. First, the method that Harrison et al. (2021) used to extract the toroidal magnetic field is by stacking the circularly polarized emission in either the red- or the blueshifted parts of the disk. According to Eq. (14), this procedure extracts 2/πBt times the toroidal magnetic field, while Harrison et al. (2021) assumed it extracted Bt. Therefore, their estimated toroidal magnetic field strength has to be raised by a factor of π/2. Additionally, the estimates of the toroidal magnetic field are impacted by cancellation effects. AS 209 is inclined at 35.3° (Fedele et al. 2018), and between the disk major- and minor-axes, a velocity shift on the order of the Doppler width is expected (Teague et al. 2018). For this velocity shift, only weak circular polarization cancellation effects are expected, but we note that around the major axes, where the toroidal projection is greatest, no velocity shift occurs. Toward the major axes, based on estimates of the dust optical depth (Pérez et al. 2012; Tazzari et al. 2016), we can put the relevant dust optical depth at τdust ~ 0.2, and find that dust absorption recovers ~10% of the circular polarization due to the toroidal magnetic field there. Based on these considerations, we conservatively estimate that about 40% of the circular polarization due to the toroidal magnetic field is recovered, and accordingly we suggest updating their constraint of the toroidal magnetic field strength to <35 mG.
We established that circular polarization observations can be reliably employed to extract information on the vertical magnetic fields of protoplanetary disks. However, the emergence of circular polarization due to the toroidal magnetic field is significantly affected by the sign change of the magnetic field between the two sides of the disk (see also Mazzei et al. 2020). Accordingly, the circular polarization due to the toroidal magnetic field is partially cancelled, and the interpretation of circular polarization signals for their magnetic field information is contingent on accurate knowledge of the dust optical depth in the disk, and on the velocity structure and emission surface. Unavoidably, this places large uncertainties on estimates of the toroidal magnetic field using circular polarization observations.
 |
Fig. 9 Spectra of the linearly polarized intensity of the CN (N, J, F) → (N′, J′, F′) = (1, 1 /2, 1 /2) → (0, 1/2, 1 /2) transition excited in a TW Hya-like protoplanetary disk, in an emission surface around z/r = 0.3. Top: stokes Q spectra; Bottom: stokes U spectra. |
 |
Fig. 10 Linear polarization emission of the CN (N, J, F) → (N′, J′, F′) = (1, 1 /2, 1 /2) → (0, 1 /2, 1 /2) transition at deprojected distance rc = 50 AU and as a function of the azimuthal angle ф′. Top: linear polarization from Stokes Q and U parameters at line center. Simulations with and without a dust layer are plotted inside the figure. Bottom: residuals from subtracting the fitting function (see text). |
4.1.2 Zeeman broadening
The splitting of spectral lines through the Zeeman effect also broadens them. We established that the Zeeman broadening is proportional to the square of the total magnetic field strength, in addition to the square of the line-of-sight component of the magnetic field. Each of these contributions is proportional to the factors 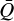 and ΔQ, which we list for the CN transitions in Table 1. We showed that Eq. (9) accurately describes the Zeeman broadening of weakly Zeeman split, optically thin emission lines, while for very optically thick lines or strong magnetic fields (xZ > 0.3), Eq. (9) tends to underestimate the broadening. In the case of TW Hya, Teague & Loomis (2020) estimated CN Band 3 transitions to have τ ≲ 1, while current magnetic field limits place the Zeeman splitting well under xZ < 0.3, so we can establish that Eq. (9) describes the Zeeman broadening of CN lines excited in this disk with high accuracy.
and ΔQ, which we list for the CN transitions in Table 1. We showed that Eq. (9) accurately describes the Zeeman broadening of weakly Zeeman split, optically thin emission lines, while for very optically thick lines or strong magnetic fields (xZ > 0.3), Eq. (9) tends to underestimate the broadening. In the case of TW Hya, Teague & Loomis (2020) estimated CN Band 3 transitions to have τ ≲ 1, while current magnetic field limits place the Zeeman splitting well under xZ < 0.3, so we can establish that Eq. (9) describes the Zeeman broadening of CN lines excited in this disk with high accuracy.
We showed that the position dependent Zeeman broadening is well described by Eq. (18) if we disregard the contribution to the Zeeman broadening due to the changing polarity of the toroidal magnetic field through the midplane. The contribution of the polarity dependent cross-term to the Zeeman broadening suggests that its interpretation, just as circular polarization observations, is contingent on accurate modeling of the disk radiative transfer. Strictly, if aiming for a resolved profile of the magnetic field of a strongly inclined disk, this is the case. However, taking into consideration the expected axisymmetry of the disk magnetic field, it is possible to devise averaging schemes that extract the axisymmetric magnetic field components, Bv and Bt, while eliminating any influence of the cross-terms on the averaged quantities. Our radiative transfer simulations confirmed Eq. (21), and showed that when we stack the Zeeman broadening over the range of position angles, then the resulting averaged quantity is insensitive to the polarity-dependent terms in cos2 θ, and is thus insensitive to any cancellation effects of the Zeeman broadening between the two sides of the disk. Thus, extracting magnetic field information from the Zeeman broadening in this way does not require knowledge of the continuum absorption or a velocity shift between the two emission surfaces along the line of sight. Moreover, the result of Eq. (21) retains its quality for disks with varying inclination.
In order to separate the Zeeman broadening from other broadening mechanisms, we need to observe a number of lines with varying Zeeman parameters simultaneously. A molecule such as CN, which exhibits several manifolds of transitions that lie relatively close in frequency, is ideally suited for this. Our simulations indicate that at a deprojected distance of rc = 50 AU, assuming an emission surface at z/r = 0.3 and a magnetic field such as Eq. (23), that the nine transitions of the N = 1−0 manifold vary in Zeeman broadening, from 6.4 m s−1 to 96 m s−1.
Detection of such a level of broadening should be possible with current facilities. This can be seen by considering the accuracy of Gaussian fits to noisy spectra described in Appendix B of Teague et al. (2022). The S/N values reported for CN N = 1−0 emission from TW Hya in Teague & Loomis (2020) vary from 2 to 50, depending on the specific hyperfine component. The sampling rate, defined as the ratio of the FWHM to the channel spacing, is ≈ 3, assuming a FWHM of 250 m s−1 and adopting the highest channel sampling of 30 kHz, or 80 m s−1 at the frequency of the N = 1-0 transition. Following Fig. 13 in Teague et al. (2022), this yields an accuracy on the line width of 50 m s−1 for the low S/N lines, and down to 13 m s−1 for the higher S/N lines. We note that while for an individual component this precision is insufficient to detect Zeeman broadening, measuring the line widths of the nine hyperfine components simultaneously will yield an improvement of 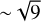 in the accuracy. This should be sufficient to detect the predicted broadening of between 6.4 m s−1 and 96 m s−1. Longer integrations than the 78 minute observations reported in Teague & Loomis (2020) would allow for smaller changes in line width, associated with weaker magnetic fields, to be detected. Looking to the future, the ALMA2030 Wideband Sensitivity Upgrade will achieve a velocity resolution of at least 10 m s−1 at 113 GHz (Carpenter et al. 2023), providing another improvement of a factor ~3 in the accuracy of line width measurements and opening up the study of Zeeman broadening to a wide variety of sources.
in the accuracy. This should be sufficient to detect the predicted broadening of between 6.4 m s−1 and 96 m s−1. Longer integrations than the 78 minute observations reported in Teague & Loomis (2020) would allow for smaller changes in line width, associated with weaker magnetic fields, to be detected. Looking to the future, the ALMA2030 Wideband Sensitivity Upgrade will achieve a velocity resolution of at least 10 m s−1 at 113 GHz (Carpenter et al. 2023), providing another improvement of a factor ~3 in the accuracy of line width measurements and opening up the study of Zeeman broadening to a wide variety of sources.
4.1.3 Linear polarization
Zeeman split lines produce linear polarization in proportion to the square of the plane-of-the-sky component of the magnetic field. To predict the total linear polarization fraction for the frequently observed CN transitions from protoplanetary disks, we derived Eqs. (10) and (20), which we showed compare well to full polarized radiative transfer simulations with optically thin emission. As the linear polarization is dependent on the plane-of-the-sky magnetic field, we predict that weakly inclined disks produce the strongest linear polarization because the dominant toroidal magnetic field is optimally oriented. We compute that the CN Band 3 transitions, assuming a TW Hya-like disk at deprojected distance of 50 AU and a magnetic field as in Eq. (23), exhibit polarization levels up to 10%, far exceeding the modeled ~1% polarization levels due to circular polarization.
Linear polarization observations commonly return the two Stokes parameters, Qv and Uv, which span a two-dimensional quasi vector on the plane of the sky and may be related to the magnetic field projected onto the plane of the sky. In Eqs. (20), we related the linear polarization fractions of both Stokes parameters to the magnetic field properties of the disk. We noted that both Stokes parameters have a dependence on the square of the vertical and toroidal components of the magnetic field, but also on their cross elements, BvBt, which change sign between the back and front sides of the disk. Our radiative transfer simulations indicate that the impact of the cross-terms on the linear polarization is difficult to estimate when an absorbing dust layer is present and when the disk is observed at high inclination.
For such sources, the interpretation of a resolved linear polarization mapping requires accurate modeling of the disk radiative transfer.
However, we can exploit the axisymmetry of the disk to extract different magnetic field components from the linear polarization data by applying the weighted stacking procedure outlined in Sect. 2.2.4 to obtain the 3D magnetic field components. Our modeling shows that the stacked quantities are insensitive to the polarity-dependent terms that require detailed modeling to be quantified. Thus, they provide for a robust procedure to extract magnetic field information from observations. We note that in order to perform the suggested azimuthal stacking, excellent spatial and spectral resolution is requried. Spatial resolution is an important factor as background gradients in the gas temperature and velocities can result in beam smearing, as discussed in Teague et al. (2016). A good rule of thumb is that the angular resolution must be such that all properties are expected to be broadly constant across the beam size. Spectral resolution is important as it allows the stacking to be performed, while correcting for the disk kinematics. It is for this reason that interferometers such as ALMA, which provide a combination of excellent angular and spectral resolution, are key to these observations.
The (sub)millimeter continuum emission emerging from protoplanetary disks is linearly polarized up to a few percent (Stephens et al. 2017; Vlemmings et al. 2019). The precise polarization mechanism is under active debate, and is dependent on the wavelength, dust and disk properties, and on the dust alignment mechanism (Kataoka et al. 2015, 2017; Stephens et al. 2017; Tazaki et al. 2017; Hoang et al. 2022). We estimate the impact of the continuum polarization on the emergent spectral line polarization by considering the polarization resolved emissivity and extinction properties of the midplane dust. First, we estimate the impact of the continuum emission on the spectral line polarization signal. The continuum emission is about ten times weaker than co-spatial CN emission toward the line center. In addition, the continuum emission that adds to the spectral line signal will be weakened by a factor of 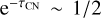 , due to absorption in the front side emission surface. Putting the continuum polarization fraction at 5%, we thus estimate its contribution to the spectral line linear polarization fraction to be 0.25%. The spectral line polarization can also be impacted through extinction in the midplane. The extinction properties of midplane dust include a conversion of Stokes I to Q, whose efficiency depends on the degree of alignment of the midplane dust (Andersson et al. 2015). If we take the conversion of Stokes I to Q to be ~1% of the total extinction, we can estimate the contribution of the converted back side CN emission to linearly polarized radiation as 1%/(
, due to absorption in the front side emission surface. Putting the continuum polarization fraction at 5%, we thus estimate its contribution to the spectral line linear polarization fraction to be 0.25%. The spectral line polarization can also be impacted through extinction in the midplane. The extinction properties of midplane dust include a conversion of Stokes I to Q, whose efficiency depends on the degree of alignment of the midplane dust (Andersson et al. 2015). If we take the conversion of Stokes I to Q to be ~1% of the total extinction, we can estimate the contribution of the converted back side CN emission to linearly polarized radiation as 1%/(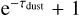 ) ~ 0.1–0.5%. However, since this polarized radiation will be subsequently absorbed in the front side emission surface, it will get suppressed by an additional factor
) ~ 0.1–0.5%. However, since this polarized radiation will be subsequently absorbed in the front side emission surface, it will get suppressed by an additional factor 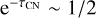 , to yield ~0.05−0.25%. In summary, we estimate an error of ~0.35% in the spectral line linear polarization fractions due to the polarized emission and absorption properties of the protoplanetary disk continuum.
, to yield ~0.05−0.25%. In summary, we estimate an error of ~0.35% in the spectral line linear polarization fractions due to the polarized emission and absorption properties of the protoplanetary disk continuum.
The observations of Vlemmings et al. (2019) and Harrison et al. (2021) were performed in ALMA full polarization mode, and also yielded linear polarization data. Both observations were performed in Band 6, where linear polarization levels are expected to be lower than for CN Band 3 transitions. Still, the linear polarization of the CN spectral lines may be advantageously used to constrain the magnetic field strength using the above-mentioned methods. We leave this analysis for a future publication.
4.2 Zeeman effect in spectral lines
The measurement of the Zeeman effect is widely recognized as one of the most reliable tracers of the magnetic field strength in astrophysics (Crutcher & Kemball 2019; Semel 1989). Circular polarization measurements to interstellar medium (ISM) molecules have allowed the measurement of the line-of-sight component of the magnetic field in star-forming regions (Crutcher & Kemball 2019), at a range of densities and scales from the diffuse ISM (Heiles & Troland 2005) to masers excited close to (massive) protostars (Vlemmings et al. 2006; Vlemmings 2008; Lankhaar et al. 2018). In this paper we placed particular emphasis on the linear polarization and line broadening that is associated with the Zeeman effect.
The linear polarization and broadening properties of Zee-man split spectral lines are often overlooked, as the Zeeman splitting of ISM spectral lines is generally weak compared to their line width (circular polarization fractions of pV ~ 0.01 are observed). Based on the discussion of Crutcher et al. (1993) about the radiative transfer of polarized radiation due to Zeeman effects, we expect the linear polarization and Zeeman broadening to be on the order of 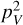 , which would yield no detectable signature. We note, however, that Crutcher et al. (1993) assume no intragroup spread of Zeeman shifts within the groups of σ±- and π0-transitions. This is a good approximation for transitions with low angular momentum (and perfect for F = 1−0 transitions), but becomes increasingly unreliable with increasing angular momentum of the quantum states associated with the transition. We showed in Sect. 2.1 that the intragroup spread in frequency of the individual magnetic sublevel transitions impacts the estimates for the linear polarization and Zeeman broadening significantly. This impact is conveniently represented by the factors ΔQ for the linear polarization and additionally the factor Q for the Zeeman broadening. In Fig. 3, we plotted transitions that exhibit a low and high intragroup spread in Zee-man shifts. For transitions with high angular momentum, the Q-factors can assume values >1000 (see Table 1). Accounting for the intragroup spread in Zeeman shifts significantly impacts the expected linear polarization and Zeeman broadening compared to estimates assuming no intragroup spread of frequencies (
, which would yield no detectable signature. We note, however, that Crutcher et al. (1993) assume no intragroup spread of Zeeman shifts within the groups of σ±- and π0-transitions. This is a good approximation for transitions with low angular momentum (and perfect for F = 1−0 transitions), but becomes increasingly unreliable with increasing angular momentum of the quantum states associated with the transition. We showed in Sect. 2.1 that the intragroup spread in frequency of the individual magnetic sublevel transitions impacts the estimates for the linear polarization and Zeeman broadening significantly. This impact is conveniently represented by the factors ΔQ for the linear polarization and additionally the factor Q for the Zeeman broadening. In Fig. 3, we plotted transitions that exhibit a low and high intragroup spread in Zee-man shifts. For transitions with high angular momentum, the Q-factors can assume values >1000 (see Table 1). Accounting for the intragroup spread in Zeeman shifts significantly impacts the expected linear polarization and Zeeman broadening compared to estimates assuming no intragroup spread of frequencies (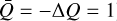 ).
).
Transitions that exhibit strong Zeeman broadening or linear polarization may be more sensitive tracers of the magnetic field strength than circular polarization. There are distinct advantages to using Zeeman broadening as a magnetic field strength tracer. First, full polarization observations are technically challenging; they require excellent weather conditions to be calibrated, often at the cost of other observational parameters such as the spectral resolution. Second, the Zeeman broadening and linear polarization are a direct probe of the magnetic energy of the probed region. Third, due to their quadratic dependence on the magnetic field, Zeeman broadening and linear polarization will not suffer from a loss of signal, as circular polarization would, under a variable magnetic direction along the line of sight; this is a favorable property when tracing magnetic fields in protoplanetary disks. In turbulent regions, such as molecular clouds, this is highly advantageous over circular polarization measurements. The observation of several Zeeman-induced effects is highly complementary, with the simultaneous observation of circular polarization and linear polarization yielding the 3D direction and strength of the magnetic field of the probed region.
5 Conclusions
The most reliable and direct method of magnetic field detection is through detection of the Zeeman effect in spectral lines. We have considered the detection of the Zeeman effect in the spectral lines of CN that are excited in protoplanetary disks using (polarized) radiative transfer modeling. While previous attempts to detect and characterize protoplanetary disk magnetic fields have been via circular polarization observations (Vlemmings et al. 2019; Harrison et al. 2021), we dedicated particular attention to the magnetic field signature in the Zeeman broadening and in the linear polarization of Zeeman split lines. In order to characterize the observability and robustness regarding magnetic field characterization of these observable features of the Zeeman effect, we performed both simplified and detailed modeling of the transfer of polarized radiation of Zeeman split CN spectral lines that are excited in protoplanetary disks.
We find that the magnetic field sign inversion through the disk midplane, characteristic of protoplanetary disks, significantly impacts the circular polarization signal. Because of the magnetic field inversion along the line of sight, much of the circular polarization that is due to the toroidal magnetic field is lost. The reduction in circular polarization can be partially suppressed through a velocity shift between the back and front side emission surfaces, or an optically thick dust layer. In addition to negatively impacting the observability, the resulting interpretation of circularly polarized signals for their magnetic field information is contingent on accurate modeling of these effects. Application of our results to the existing circular polarization observations of TW Hya (Vlemmings et al. 2019) and AS 209 (Harrison et al. 2021) suggests raising their upper limits on the toroidal magnetic field strength from 30 mG to 65 mG, and from 8.7 mG to 35 mG, respectively.
The production of linear polarization and Zeeman broadening scale quadratically with the magnetic field strength, while circular polarization scales linearly with the line-of-sight component of the magnetic field. From our radiative transfer simulations we found that for moderately inclined disks the observation of linear polarization and Zeeman broadening carry two advantages over circular polarization measurements. First, due to the quadratic dependence on the magnetic field strength, linear polarization and Zeeman broadening are only weakly affected by the magnetic field inversion along the line of sight. Second, linear polarization and Zeeman broadening are sensitive to the plane-of-the-sky magnetic field and the total magnetic field strength, respectively, meaning that they are sensitive to the toroidal magnetic field, which is expected to be the dominant component of the magnetic field.
We have presented a method to interpret and predict linear polarization and Zeeman broadening observations. Importantly, we introduced the coefficients  and ΔQ, which take into account the enhanced Zeeman broadening and linear polarization due to intragroup spread of Zeeman shifted transitions and which are omitted in the seminal work of Crutcher et al. (1993). With the
and ΔQ, which take into account the enhanced Zeeman broadening and linear polarization due to intragroup spread of Zeeman shifted transitions and which are omitted in the seminal work of Crutcher et al. (1993). With the 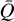 and ΔQ coefficients, simplified radiative transfer models could reproduce synthetic observations from full 3D polarized radiative transfer modeling with high fidelity. Conversely, the simplified radiative transfer models may thus be used in the interpretation of observations. From the simultaneous observation of the linear polarization, and the Zeeman broadening or circular polarization, the magnetic field strength and its 3D direction can be derived. We predict that such observations are feasible for a moderately inclined protoplanetary disk such as TW Hya.
and ΔQ coefficients, simplified radiative transfer models could reproduce synthetic observations from full 3D polarized radiative transfer modeling with high fidelity. Conversely, the simplified radiative transfer models may thus be used in the interpretation of observations. From the simultaneous observation of the linear polarization, and the Zeeman broadening or circular polarization, the magnetic field strength and its 3D direction can be derived. We predict that such observations are feasible for a moderately inclined protoplanetary disk such as TW Hya.
Acknowledgements
B.L. acknowledges support for this work from the Swedish Research Council (VR) under grant number 2021-00339. Simulations were performed on resources at the Chalmers Centre for Computational Science and Engineering (C3SE) provided by the Swedish National Infrastructure for Computing (SNIC). We thank the referee for comments that improved the quality of the paper.
Appendix A Polarized radiative transfer of Zeeman split lines
We consider the transfer of (polarized) radiation in a Zeeman split spectral line. We relate the polarized propagation properties of the Zeeman split spectral line to its propagation properties in the limit of no Zeeman splitting, where we let the absorption coefficient and source function be κv and 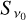 . We factorize the absorption coefficient
. We factorize the absorption coefficient 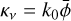 (x) in an absorption constant and a dimensionless line-profile, where we use Doppler-normalized units for the line-profile,
(x) in an absorption constant and a dimensionless line-profile, where we use Doppler-normalized units for the line-profile, 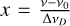 , with ν as the frequency, v0 as the frequency of the line center, and ΔvD as the Doppler broadening in frequency units. Even though we defined the line profile as a Gaussian in the main text, our following discussion is appropriate for any profile function, provided that
, with ν as the frequency, v0 as the frequency of the line center, and ΔvD as the Doppler broadening in frequency units. Even though we defined the line profile as a Gaussian in the main text, our following discussion is appropriate for any profile function, provided that 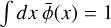 .
.
When a magnetic field is present, the spectral line under consideration splits into a multitude of transitions between the individual magnetic sublevels of the upper and lower state. As in the main text, we consider a transition between two states, with angular momenta F1 and F2 for the upper and lower states, respectively. Transitions between magnetic sublevels are shifted in frequency according to Eq. (1). Accordingly, the line profile of the transition |F1m1〉 → |F2m2〉 is Zeeman shifted: ![$\bar \phi \left( {x + {x_B}\left[ {{g_1}{m_1} - {g_2}{m_2}} \right]} \right) = {{\bar \phi }_{{m_1},{m_2}}}$](/articles/aa/full_html/2023/10/aa45840-23/aa45840-23-eq125.png) , where xB = µBB/hΔvD is the Zeeman shift term in Doppler units.
, where xB = µBB/hΔvD is the Zeeman shift term in Doppler units.
As discussed in the text, transitions between magnetic sub-levels can be divided into three groups, the π0 - and the σ± -transitions, which are associated with the Δm = 0 and Δm = ±1 transitions. The individual transition groups emit polarized emission and have opacities that are dependent on the angle between the propagation direction and the magnetic field that gives rise to Zeeman splitting (see also main text). We therefore define a total line profile per transition group,
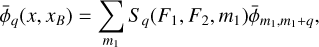 (A.1)
(A.1)
where Sq(F1, F2, m1) is the relative line strength of the |F1m1〉 → | F2m1 + q〉 transition (see also main text, and equation 3.16 in Degl’Innocenti & Landolfi 2006). We now cite the polarized radiative transfer equation over an incremental distance ds of a Zeeman split spectral line (Degl’Innocenti & Landolfi 2006; Rees et al. 1989),
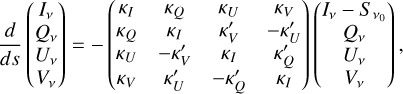 (A.2)
(A.2)
where the Stokes parameters are the same as those in the main text. The polarized absorption coefficients are
![${\kappa _I} = {{{k_0}} \over 2}\left[ {{{\bar \phi }_0}{{\sin }^2}\theta + {{{{\bar \phi }_1} + {{\bar \phi }_{ - 1}}} \over 2}\left( {1 + {{\cos }^2}\theta } \right)} \right],$](/articles/aa/full_html/2023/10/aa45840-23/aa45840-23-eq128.png) (A.3a)
(A.3a)
![${\kappa _Q} = {{{k_0}} \over 2}\left[ {{{\bar \phi }_0} - {{{{\bar \phi }_1} + {{\bar \phi }_{ - 1}}} \over 2}} \right]\,{\sin ^2}\theta \cos 2\eta ,$](/articles/aa/full_html/2023/10/aa45840-23/aa45840-23-eq129.png) (A.3b)
(A.3b)
![${\kappa _U} = {{{k_0}} \over 2}\left[ {{{\bar \phi }_0} - {{{{\bar \phi }_1} + {{\bar \phi }_{ - 1}}} \over 2}} \right]\,{\sin ^2}\theta \sin 2\eta ,$](/articles/aa/full_html/2023/10/aa45840-23/aa45840-23-eq130.png) (A.3c)
(A.3c)
![${\kappa _V} = {{{k_0}} \over 2}\left[ {{{\bar \phi }_1} - {{\bar \phi }_{ - 1}}} \right]\,\cos \theta ,$](/articles/aa/full_html/2023/10/aa45840-23/aa45840-23-eq131.png) (A.3d)
(A.3d)
and the κ′Q,U,V terms are transformation coefficients that are related to the κQ,U,V opacities through the Kramers-Kronig relations.
We now endeavor to obtain simplified polarized absorption coefficients. To this end, we represent the line profiles of the transition groups by a Taylor expansion,
![${\bar \phi _q} = \sum\limits_n {{{\left[ {{{{d^n}{{\bar \phi }_q}} \over {d{x_B}}}} \right]}_{{x_B} = 0}}} {{x_B^n} \over {n!}},$](/articles/aa/full_html/2023/10/aa45840-23/aa45840-23-eq132.png) (A.4)
(A.4)
around the Zeeman shift term, xB, where we recognize that this representation is best applied in the weak-field limit, to lines with xB < 1 (Degl’Innocenti & Landolfi 2006). We combine Eqs. (A.1) and (A.4):
![${\left[ {{{{d^n}{{\bar \phi }_q}} \over {dx_B^n}}} \right]_{{x_B} = 0}} = \sum\limits_{{m_1}} {{S_q}\left( {{F_1},{F_2},{m_1}} \right)} \,{\left[ {{{{d^n}{{\bar \phi }_{{m_1},{m_1} + q}}} \over {dx_B^n}}} \right]_{{x_B} = 0}}.$](/articles/aa/full_html/2023/10/aa45840-23/aa45840-23-eq133.png) (A.5)
(A.5)
From the definition of  , we recognize that we can substitute the differential dxB = dx′/[ɡ1m1 − ɡ2(m1 + q)], where x′ = x + xB[ɡ1m1 − ɡ2(m1 + q)]. Furthermore, x′ → x in the limit of xB → 0, and so
, we recognize that we can substitute the differential dxB = dx′/[ɡ1m1 − ɡ2(m1 + q)], where x′ = x + xB[ɡ1m1 − ɡ2(m1 + q)]. Furthermore, x′ → x in the limit of xB → 0, and so
![${\left[ {{{{d^n}{{\bar \phi }_{{m_1},{m_1} + q}}} \over {dx_B^n}}} \right]_{{x_B} = 0}} = {\left( {{g_1}{m_1} - {g_2}\left[ {{m_1} + q} \right]} \right)^n}{{{d^n}\bar \phi \left( x \right)} \over {d{x^n}}},$](/articles/aa/full_html/2023/10/aa45840-23/aa45840-23-eq135.png) (A.6)
(A.6)
where  is the n-th derivative of the unsplit line profile. We implement Eq. (A.6) in Eq. (A.5) to find
is the n-th derivative of the unsplit line profile. We implement Eq. (A.6) in Eq. (A.5) to find
![$\matrix{ {x_B^n{{\left[ {{{{d^n}{{\bar \phi }_q}} \over {dx_B^n}}} \right]}_{{x_B} = 0}} = x_B^n\sum\limits_{{m_1}} {{S_q}\left( {{F_1},{F_2},{m_1}} \right)} } \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times {{\left( {{g_1}{m_1} - {g_2}\left[ {{m_1} + q} \right]} \right)}^n}{{{d^n}\bar \phi } \over {d{x^n}}}} \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = G_q^{\left( n \right)}x_B^n{{{d^n}\bar \phi } \over {d{x^n}}},} \hfill \cr } $](/articles/aa/full_html/2023/10/aa45840-23/aa45840-23-eq137.png) (A.7)
(A.7)
and define g-factors,  , that encapsulate the effects of the Zee-man shifts on the line profile. Truncating the Taylor expansion at n = 2, while using that
, that encapsulate the effects of the Zee-man shifts on the line profile. Truncating the Taylor expansion at n = 2, while using that 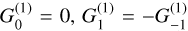 , and
, and 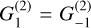 (relations that follow from the symmetry relations of the line strength factors; see also Degl’Innocenti & Landolfi 2006), we have for the transition group line profiles
(relations that follow from the symmetry relations of the line strength factors; see also Degl’Innocenti & Landolfi 2006), we have for the transition group line profiles
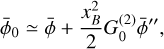 (A.8a)
(A.8a)
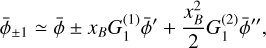 (A.8b)
(A.8b)
where we used the short-hand notation for the first and second derivatives. Using the approximate expressions for the line profiles in Eq. (A.3), we retrieve
![${{{\kappa _I}} \mathord{\left/ {\vphantom {{{\kappa _I}} {{k_0}}}} \right. \kern-\nulldelimiterspace} {{k_0}}} \simeq \bar \phi + x_B^2\left[ {{{G_0^{\left( 2 \right)} + G_1^{\left( 2 \right)}} \over 4} - {{G_0^{\left( 2 \right)} - G_1^{\left( 2 \right)}} \over 4}{{\cos }^2}\theta } \right]\,\bar \phi '',$](/articles/aa/full_html/2023/10/aa45840-23/aa45840-23-eq143.png) (A.9a)
(A.9a)
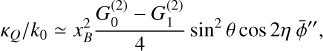 (A.9b)
(A.9b)
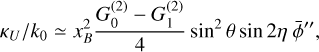 (A.9c)
(A.9c)
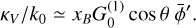 (A.9d)
(A.9d)
To correlate our discussion to the literature of radio-astronomical Zeeman observations, we related the proportionality constants to the relative production of circular polarization, through the parameter 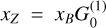 . Thus, we defined
. Thus, we defined 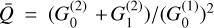 and
and 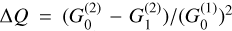 , which are the second-order g-factors normalized to the first-order g-factor. In Eq. (2) we give the definition of xZ, where we used the expression for
, which are the second-order g-factors normalized to the first-order g-factor. In Eq. (2) we give the definition of xZ, where we used the expression for 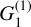 , while in Eqs. (5) we give isomorphic definitions of
, while in Eqs. (5) we give isomorphic definitions of 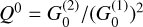 and
and 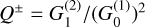 .
.
Using the approximate propagation coefficients of Eq. (A.9) in conjunction with the radiative transfer equation of Eq. (A.2) in the optically thin limit, we retrieve Eqs. (4).
Appendix B Detailed derivations of Eqs. (15) and (17)
To derive Eq. (15) we divide the radiative transfer through the disk into two optically thin propagations through the back and front sides of the disk emission surfaces. The emission surfaces have equal source function and optical depth 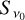 and
and 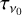 . We consider the case where
. We consider the case where  , and we consider a Doppler normalized velocity shift between the emission surfaces of Δx, where also (Δx)2 ≪ 1. The emergent total intensity is then
, and we consider a Doppler normalized velocity shift between the emission surfaces of Δx, where also (Δx)2 ≪ 1. The emergent total intensity is then
![$\matrix{ {{I_v} = {S_{{v_0}}}{\tau _{{v_0}}}\left[ {\bar \phi \left( {x - {{{\rm{\Delta }}x} \over 2}} \right) + \bar \phi \left( {x + {{{\rm{\Delta }}x} \over 2}} \right)} \right],} \hfill \cr {\,\,\,\,\, = 2{S_{{v_0}}}{\tau _{{v_0}}}\bar \phi \left( x \right) + {S_{{v_0}}}{\tau _{{v_0}}}} \hfill \cr {\,\,\,\,\, \times \left[ { - 2\bar \phi \left( x \right) + \bar \phi \left( {x - {{{\rm{\Delta }}x} \over 2}} \right) + \bar \phi \left( {x + {{{\rm{\Delta }}x} \over 2}} \right)} \right],} \hfill \cr {\,\,\,\,\, \simeq 2{S_{{v_0}}}{\tau _{{v_0}}}\bar \phi \left( x \right) + {S_{{v_0}}}{\tau _{{v_0}}}{{{{\left( {{\rm{\Delta }}x} \right)}^2}} \over 4}\bar \phi ''\left( x \right),} \hfill \cr {\,\,\,\,\, \simeq 2{S_{{v_0}}}{\tau _{{v_0}}}\bar \phi \left( x \right),} \hfill \cr } $](/articles/aa/full_html/2023/10/aa45840-23/aa45840-23-eq156.png) (B.1)
(B.1)
while the emergent circular polarization, due to the toroidal magnetic field, with a projection 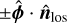 in the front and back side of the disk, respectively, is
in the front and back side of the disk, respectively, is
![$\matrix{ {{V_v} = - {S_{{v_0}}}{\tau _{{v_0}}}{x_Z}\left( {\hat \phi \cdot {{{\bf{\hat n}}}_{{\rm{los}}}}} \right)\left[ {\bar \phi '\left( {x - {{{\rm{\Delta }}x} \over 2}} \right) - \bar \phi '\left( {x + {{{\rm{\Delta }}x} \over 2}} \right)} \right],} \hfill \cr {\,\,\,\,\, \simeq {S_{{v_0}}}{x_Z}\left( {\hat \phi \cdot {{{\bf{\hat n}}}_{{\rm{los}}}}} \right){\rm{\Delta }}x{{d\bar \phi '\left( x \right)} \over {dx}}} \hfill \cr } $](/articles/aa/full_html/2023/10/aa45840-23/aa45840-23-eq158.png) (B.2)
(B.2)
By using the total intensity from Eq. (B.1) to substitute the lineprofile 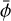 in Eq. (B.2), we retrieve Eq. (15).
in Eq. (B.2), we retrieve Eq. (15).
To derive Eq. (17) we divide the radiative transfer through the disk into three propagations. First, we have an optically thin propagation through the back side of the disk. This is followed by a propagation through a dusty midplane. Finally, we have a propagation through the optically thin front side of the disk. The emission surfaces have equal source function and optical depth 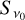 and
and 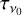 and the dusty midplane has an optical depth of τdust and a source function Sdust. It will later turn out that the our final result is independent of the dust source function. We consider the case where
and the dusty midplane has an optical depth of τdust and a source function Sdust. It will later turn out that the our final result is independent of the dust source function. We consider the case where 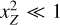 , and we consider a Doppler normalized velocity shift between the emission surfaces of Δx, where also (Δx)2 ≪ 1. The emergent total intensity is then
, and we consider a Doppler normalized velocity shift between the emission surfaces of Δx, where also (Δx)2 ≪ 1. The emergent total intensity is then
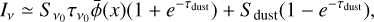 (B.3)
(B.3)
where we assumed the broadening due to the velocity shift to be zero, which we motivated in more detail in our derivation of Eq. (15). Emission from the back side is partially absorbed by the dusty midplane layer, while the emission from the dusty midplane has no significant absorption from the front side of the disk as we have assumed the emission surfaces to be optically thin. The emission from the dusty midplane is removed from the emergent line intensity, as we are interested in the continuum subtracted line intensity:
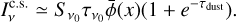 (B.4)
(B.4)
Taking into account both the midplane absorption and the velocity shift, the emergent circular polarization is
![$\matrix{ {{V_v} = - {S_{{v_0}}}{\tau _{{v_0}}}{x_Z}\left( {\hat \phi \cdot {{{\bf{\hat n}}}_{{\rm{los}}}}} \right)\left[ {\bar \phi '\left( {x - {{{\rm{\Delta }}x} \over 2}} \right){e^{ - {\tau _{{\rm{dust}}}}}} - \bar \phi '\left( {x + {{{\rm{\Delta }}x} \over 2}} \right)} \right],} \hfill \cr {\,\,\,\,\, = - {e^{ - {\tau _{{\rm{dust}}}}}}{S_{{v_0}}}{\tau _{{v_0}}}{x_Z}\left( {\hat \phi \cdot {{{\bf{\hat n}}}_{{\rm{los}}}}} \right)\left[ {\bar \phi '\left( {x - {{{\rm{\Delta }}x} \over 2}} \right) - \bar \phi '\left( {x + {{{\rm{\Delta }}x} \over 2}} \right)} \right]} \hfill \cr {\,\,\,\,\, + \left( {1 - {e^{ - {\tau _{{\rm{dust}}}}}}} \right){S_{{v_0}}}{\tau _{{v_0}}}{x_Z}\left( {\hat \phi \cdot {{{\bf{\hat n}}}_{{\rm{los}}}}} \right)\bar \phi '\left( {x + {{{\rm{\Delta }}x} \over 2}} \right),} \hfill \cr } $](/articles/aa/full_html/2023/10/aa45840-23/aa45840-23-eq165.png) (B.5)
(B.5)
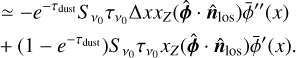 (B.6)
(B.6)
It can then be recognized that, due to the dusty midplane layer, the total intensity is adjusted to
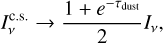 (B.7a)
(B.7a)
while the circular polarization due to the regular Zeeman effect and the velocity shift are adjusted to
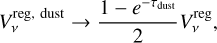 (B.7b)
(B.7b)
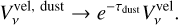 (B.7c)
(B.7c)
Adjusting the estimates for the emergent polarization fraction using these factors yields Eq. (17).
Appendix C Zeeman signatures of CN from a TW Hya-like disk in ALMA bands 3, 6, and 7
Estimates of Zeeman-induced circular polarization fractions, linear polarization fractions, and Zeeman broadening of CN transitions excited in a TW Hya-like disk, relevant to ALMA polarization measurements.
References
- Andersson, B., Lazarian, A., & Vaillancourt, J. E. 2015, ARA&A, 53, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Armitage, P. J. 2011, ARA&A, 49, 195 [Google Scholar]
- Armitage, P. J., & Kley, W. 2019, From Protoplanetary Disks to Planet Formation (Springer) [CrossRef] [Google Scholar]
- Bai, X.-N. 2016, ApJ, 821, 80 [Google Scholar]
- Bai, X.-N. 2017, ApJ, 845, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Bai, X.-N., & Stone, J. M. 2013, ApJ, 769, 76 [Google Scholar]
- Balbus, S. A., & Hawley, J. F. 1991, ApJ, 376, 214 [Google Scholar]
- Béthune, W., Lesur, G., & Ferreira, J. 2017, A&A, 600, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bjerkeli, P., Ramsey, J. P., Harsono, D., et al. 2019, A&A, 631, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blandford, R., & Payne, D. 1982, MNRAS, 199, 883 [CrossRef] [Google Scholar]
- Brauer, R., Wolf, S., Reissl, S., & Ober, F. 2017, A&A, 601, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brinch, C., & Hogerheijde, M. 2010, A&A, 523, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Calahan, J. K., Bergin, E., Zhang, K., et al. 2021, ApJ, 908, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Carpenter, J., Brogan, C., Iono, D., & Mroczkowski, T. 2023, in Physics and Chemistry of Star Formation: The Dynamical ISM Across Time and Spatial Scales, Proceedings of the 7th Chile-Cologne-Bonn Symposium, 304 [Google Scholar]
- Cazzoletti, P., Van Dishoeck, E., Visser, R., Facchini, S., & Bruderer, S. 2018, A&A, 609, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cleeves, L. I., Adams, F. C., & Bergin, E. A. 2013, ApJ, 772, 5 [Google Scholar]
- Crutcher, R. M., & Kemball, A. J. 2019, Front. Astron. Space Sci., 6, 66 [CrossRef] [Google Scholar]
- Crutcher, R., Troland, T., Goodman, A., et al. 1993, ApJ, 407, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Degl’Innocenti, M. L., & Landolfi, M. 2006, Polarization in Spectral Lines (Springer Science & Business Media), 307 [Google Scholar]
- Fedele, D., Tazzari, M., Booth, R., et al. 2018, A&A, 610, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Flaherty, K. M., Hughes, A. M., Rosenfeld, K. A., et al. 2015, ApJ, 813, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Flaherty, K. M., Hughes, A. M., Teague, R., et al. 2018, ApJ, 856, 117 [CrossRef] [Google Scholar]
- Frank, A., Ray, T., Cabrit, S., et al. 2014, Protostars and Planets VI (Tucson: University of Arizona Press), 451 [Google Scholar]
- Girart, J. M., Crutcher, R. M., & Rao, R. 1999, ApJ, 525, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Kylafis, N. D. 1981, ApJ, 243, L75 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, D. F. 1984, ApJ, 277, 640 [Google Scholar]
- Harrison, R. E., Looney, L. W., Stephens, I. W., et al. 2021, ApJ, 908, 141 [CrossRef] [Google Scholar]
- Heiles, C., & Troland, T. 2005, ApJ, 624, 773 [NASA ADS] [CrossRef] [Google Scholar]
- Hoang, T., Phan, V. H. M., Giang, N. C., et al. 2022, AJ, 164, 248 [NASA ADS] [CrossRef] [Google Scholar]
- Isella, A., Huang, J., Andrews, S. M., et al. 2018, ApJ, 869, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Kalugina, Y., & Lique, F. 2015, MNRAS, 446, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Kataoka, A., Muto, T., Momose, M., et al. 2015, ApJ, 809, 78 [Google Scholar]
- Kataoka, A., Tsukagoshi, T., Pohl, A., et al. 2017, ApJ, 844, L5 [Google Scholar]
- Kochukhov, O., Shultz, M., & Neiner, C. 2019, A&A, 621, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lankhaar, B., & Vlemmings, W. 2020a, A&A, 636, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lankhaar, B., & Vlemmings, W. 2020b, A&A, 638, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lankhaar, B., Vlemmings, W., Surcis, G., et al. 2018, Nat. Astron., 2, 145 [Google Scholar]
- Lankhaar, B., Vlemmings, W., & Bjerkeli, P. 2022, A&A, 657, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Larsson, R., Lankhaar, B., & Eriksson, P. 2019, JQSRT, 224, 431 [NASA ADS] [CrossRef] [Google Scholar]
- Lesur, G. R. 2021, A&A, 650, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lesur, G., & Papaloizou, J. C. 2010, A&A, 513, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Macías, E., Guerra-Alvarado, O., Carrasco-Gonzalez, C., et al. 2021, A&A, 648, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marcus, P. S., Pei, S., Jiang, C.-H., et al. 2015, ApJ, 808, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Mazzei, R., Cleeves, L. I., & Li, Z.-Y. 2020, ApJ, 903, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Mouschovias, T. C., & Ciolek, G. E. 1999, in The Origin of Stars and Planetary Systems (Springer), 305 [CrossRef] [Google Scholar]
- Nelson, R. P., Gressel, O., & Umurhan, O. M. 2013, MNRAS, 435, 2610 [Google Scholar]
- Pattle, K., Fissel, L., Tahani, M., Liu, T., & Ntormousi, E. 2023, ASP Conf. Ser., 534, 193 [NASA ADS] [Google Scholar]
- Pérez, L. M., Carpenter, J. M., Chandler, C. J., et al. 2012, ApJ, 760, L17 [CrossRef] [Google Scholar]
- Rees, D., Murphy, G., & Durrant, C. 1989, ApJ, 339, 1093 [NASA ADS] [CrossRef] [Google Scholar]
- Robinson, R. D., Jr. 1980, ApJ, 239, 961 [NASA ADS] [CrossRef] [Google Scholar]
- Rosén, L., Kochukhov, O., & Wade, G. A. 2015, ApJ, 805, 169 [Google Scholar]
- Schöier, F. L., van der Tak, F. F., van Dishoeck, E. F., & Black, J. H. 2005, A&A, 432, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Semel, M. 1989, A&A, 225, 456 [NASA ADS] [Google Scholar]
- Shakura, N., & Sunyaev, R. 1976, MNRAS, 175, 613 [NASA ADS] [CrossRef] [Google Scholar]
- Stephens, I. W., Yang, H., Li, Z.-Y., et al. 2017, ApJ, 851, 55 [Google Scholar]
- Stephens, I. W., Fernández-López, M., Li, Z.-Y., Looney, L. W., & Teague, R. 2020, ApJ, 901, 71 [CrossRef] [Google Scholar]
- Tazaki, R., Lazarian, A., & Nomura, H. 2017, ApJ, 839, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Tazzari, M., Testi, L., Ercolano, B., et al. 2016, A&A, 588, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Teague, R., & Loomis, R. 2020, ApJ, 899, 157 [Google Scholar]
- Teague, R., Guilloteau, S., Semenov, D., et al. 2016, A&A, 592, A49 [CrossRef] [EDP Sciences] [Google Scholar]
- Teague, R., Bae, J., Birnstiel, T., & Bergin, E. A. 2018, ApJ, 868, 113 [Google Scholar]
- Teague, R., Hull, C. L., Guilloteau, S., et al. 2021, ApJ, 922, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Teague, R., Bae, J., Andrews, S. M., et al. 2022, ApJ, 936, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Vlemmings, W. 2008, A&A, 484, 773 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vlemmings, W. H. T., Diamond, P. J., van Langevelde, H. J., & Torrelles, J. M. 2006, A&A, 448, 597 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vlemmings, W., Lankhaar, B., Cazzoletti, P., et al. 2019, A&A, 624, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wardle, M., & Koenigl, A. 1993, ApJ, 410, 218 [Google Scholar]
We used LIME version 1.9.5, available from https://github.com/lime-rt/lime
The source code for the polarized ray-tracing is available from https://github.com/blankhaar/zeeman_disk
All Tables
Zeeman parameters, frequencies, and Einstein coefficients of CN transitions relevant to ALMA polarization measurements.
Summary of simulation results of the broadening and circular polarization of the N = 1–0 transitions of CN at deprojected distance rc = 50 AU and ϕ = 0° and ϕ = 90°.
Estimates of Zeeman-induced circular polarization fractions, linear polarization fractions, and Zeeman broadening of CN transitions excited in a TW Hya-like disk, relevant to ALMA polarization measurements.
All Figures
 |
Fig. 1 Normalized Gaussian line profile and its first two derivatives plotted against the Doppler unit. |
| In the text | |
 |
Fig. 2 Zeeman broadening of a Zeeman-split line as a function of the Doppler normalized Zeeman shift xZ. The predicted Zeeman broadening between proper polarized radiative transfer simulations and the fitted Eq. (9) are compared. The radiative transfer equations are performed using |
| In the text | |
 |
Fig. 3 Stem plots of magnetic sublevel transitions of Band 3 CN hyperfine transitions. The individual magnetic sublevel transitions are indicated by a solid line, and grouped (π0, σ±) by color. The dotted lines indicate the average shift of the σ± groups. |
| In the text | |
 |
Fig. 4 Total (upper) and circularly polarized (lower) intensity of a Zeeman-split line. The intensities are normalized with respect to the unsplit (xZ = 0) intensity. The total intensity plots are for an unsplit (xZ = 0) and Zeeman-split (xZ = 0.3, |
| In the text | |
 |
Fig. 5 Spectra of circularly polarized intensity of CN (N, J, F) → (N′, J′, F′) = (1,1 /2,1 /2) → (0,1 /2,1/2) transition excited in a TW Hya-like protoplanetary disk, in an emission surface around z/r = 0.3, with (lower row) and without (upper row) a layer of dust present between the emission surfaces. The spectra for different optical depths and position angles are given. |
| In the text | |
 |
Fig. 6 Circular polarization fraction at deprojected distance rc = 50 AU as a function of the deprojected azimuthal angle ϕ′. Simulations with and without a dust layer are plotted inside the figure and the dashed line is a fitting function. |
| In the text | |
 |
Fig. 7 Spectra of the total intensity of the CN (N, J, F) → (N′, J′, F′) = (1, 1/2, 1/2) → (0, 1/2, 1/2) transition excited in a TW Hya-like proto-planetary disk in an emission surface around z/r = 0.3, with (lower row) and without (upper row) a layer of dust present between the emission surfaces. In each panel the spectra for different optical depths (left to right) and azimuthal angles (different colors within the panels) are given. The dashed lines are from spectra assuming no magnetic field permeating the disk. |
| In the text | |
 |
Fig. 8 Zeeman broadening at deprojected distance rc = 50 AU as a function of the azimuthal angle. Simulations with and without a dust layer are plotted and the dashed line is a fitting function (see text). |
| In the text | |
 |
Fig. 9 Spectra of the linearly polarized intensity of the CN (N, J, F) → (N′, J′, F′) = (1, 1 /2, 1 /2) → (0, 1/2, 1 /2) transition excited in a TW Hya-like protoplanetary disk, in an emission surface around z/r = 0.3. Top: stokes Q spectra; Bottom: stokes U spectra. |
| In the text | |
 |
Fig. 10 Linear polarization emission of the CN (N, J, F) → (N′, J′, F′) = (1, 1 /2, 1 /2) → (0, 1 /2, 1 /2) transition at deprojected distance rc = 50 AU and as a function of the azimuthal angle ф′. Top: linear polarization from Stokes Q and U parameters at line center. Simulations with and without a dust layer are plotted inside the figure. Bottom: residuals from subtracting the fitting function (see text). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.