| Issue |
A&A
Volume 677, September 2023
|
|
|---|---|---|
| Article Number | A9 | |
| Number of page(s) | 17 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/202346005 | |
| Published online | 25 August 2023 | |
IDEFIX: A versatile performance-portable Godunov code for astrophysical flows
Univ. Grenoble Alpes, CNRS, IPAG,
38000
Grenoble, France
e-mail: geoffroy.lesur@univ-grenoble-alpes.fr
Received:
27
January
2023
Accepted:
26
April
2023
Context. The exascale super-computers becoming available rely on hybrid energy-efficient architectures that involve an accelerator such as a graphics processing unit (GPU). Leveraging the computational power of these machines often means a significant rewrite of the numerical tools each time a new architecture becomes available.
Aims. We present IDEFIX, a new code for astrophysical flows that relies on the KOKKOS meta-programming library to guarantee performance portability on a wide variety of architectures while keeping the code as simple as possible to the user.
Methods. IDEFIX is based on a Godunov finite-volume method that solves the nonrelativistic hydrodynamical (HD) and magnetohy-drodynamical (MHD) equations on various grid geometries. IDEFIX includes a large choice of solvers and several additional modules (constrained transport, orbital advection, nonideal MHD), allowing users to address complex astrophysical problems.
Results. IDEFIX has been successfully tested on Intel and AMD CPUs (up to 131 072 CPU cores on Irene-Rome at TGCC) as well as NVidia and AMD GPUs (up to 1024 GPUs on Adastra at CINES). IDEFIX achieves more than 108 cell s−1 in MHD on a single NVidia V100 GPU and 3 × 1011 cell s−1 on 256 Adastra nodes (1024 GPUs) with 95% parallelization efficiency (compared to single node). For the same problem, IDEFIX is up to six times more energy efficient on GPUs compared to Intel Cascade Lake CPUs.
Conclusions. IDEFIX is now a mature exascale-ready open-source code that can be used on a large variety of astrophysical and fluid dynamics applications.
Key words: hydrodynamics / magnetohydrodynamics (MHD) / methods: numerical
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
The development of modern theoretical astrophysics relies heavily on numerical modeling because of the complex interplay between several, often nonlinear physical processes. This is especially true for many astrophysical flows ranging from stellar interiors to large-scale galaxy clusters, all of which rely on multiscale modeling of the plasma. Many techniques have been designed to model astrophysical flows, the most popular being based on a fixed grid approach: finite differences schemes, with codes such as ZEUS (Stone & Norman 1992) and its derivatives, such as FARGO (Masset 2000) or the PENCIL code (Pencil Code Collaboration 2021), finite volume and in particular Godunov-like shock-capturing schemes, such as RAMSES (Teyssier 2002; Fromang et al. 2006) ATHENA (Stone et al. 2008, 2020), PLUTO (Mignone et al. 2007), and NIRVANA (Ziegler 2008), and spectral methods often used in quasi-incompressible problems, such as MAGIC (Wicht 2002; Gastine & Wicht 2012), SNOOPY (Lesur & Longaretti 2007), or DEDALUS (Burns et al. 2020). All of these codes are widely used by the community and are usually written in Fortran or C for ease of use.
With a few exceptions, these codes are designed to run on CPU-based systems like ×86 machines, with typically a few tens of independent cores in each CPU, which are inter-connected with a high-bandwidth and low-latency network. The advent of exascale supercomputers and the requirement of energy sobriety in high-performance computing is now driving a shift towards hybrid machines. Clusters of CPUs are progressively replaced by energy-efficient architectures, often based on many-core systems such as graphics processing units (GPUs). In this approach, each GPU is made of thousands of cores all working synchronously following the single instruction multiple data (SIMD) paradigm. This change in hardware architecture means that codes should at the very least be ported to these new architectures. Making things even more complicated, each hardware manufacturer tends to push its own programming language or library for its own hardware, often as an extension of Fortran or C (NVidia Cuda, AMD HIP Rocm or Apple Metal to name a few).
This situation has a dramatic impact on the numerical astrophysics community. It is already a long process to write a new code, but support and maintenance are often scarce because of the limited staff available, and the low recognition of support activities. It is therefore almost impossible to develop and maintain n versions of a code for n architecture variants given the human resources available. Nevertheless, our community must find ways to exploit these architectures as they will dominate in the future, not only in exascale machines but also in university clusters because of the constraints imposed by energy sobriety.
To address some of these issues, we have developed a new code based on a high-order Godunov scheme that relies on the KOKKOS (Trott et al. 2022) metaprogramming library. This allows us to exploit a performance-portability approach, where a single source code can be compiled for a large variety of target architectures, with minimal impact on performance. While our original intention was to port the PLUTO code, we thought it more efficient in the long run to write a code from scratch using modern C++. This allowed us to leverage class encapsulation, polymorphism, exception handling, and C++ containers, which are all absent from the C standard. We present the main features of this code in this paper. We first introduce the basics of the algorithm with the various physical modules we have implemented in Sect. 2. We then focus on implementation details. The various standard tests used to validate the code are presented in Sect. 4. Finally, we discuss the code performances for various target architectures in Sect. 5, as well as future prospects for this tool.
2 Algorithm
2.1 Equations
In all generality, the dimensionless equations solved by IDEFIX read:
![${\partial _t}\rho + \nabla \cdot \left[ {\rho {\bf{\upsilon }}} \right] = 0,$](/articles/aa/full_html/2023/09/aa46005-23/aa46005-23-eq1.png) (1)
(1)
![${\partial _t}\left( {\rho {\bf{\upsilon }}} \right) + \nabla \cdot \left[ {\rho {\bf{\upsilon }} \otimes {\bf{\upsilon }} - {\bf{B}} \otimes {\bf{B}} + {\rm{PI}} + \overline{\overline {\rm{\Pi }}} } \right] = - \rho \nabla \psi ,$](/articles/aa/full_html/2023/09/aa46005-23/aa46005-23-eq2.png) (2)
(2)
![$\matrix{ {{\partial _t}{\bf{B}} + \nabla \times \left[ { - {\bf{\upsilon }} \times {\bf{B}} + {\eta _{\rm{{\rm O}}}}{\bf{J}} + } \right.{x_{\rm{H}}}{\bf{J}} \times {\bf{B}}} \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left. { - {x_{{\rm{AD}}}}\left( {{\bf{J}} \times {\bf{B}}} \right) \times {\bf{B}}} \right] = 0,} \hfill \cr } $](/articles/aa/full_html/2023/09/aa46005-23/aa46005-23-eq3.png) (3)
(3)
![$\matrix{ {{\partial _t}E + \nabla \cdot \left[ {\left( {E + {\rm{P}}} \right)} \right.{\bf{\upsilon }} - {\bf{B}}\left( {{\bf{B}} \cdot {\bf{\upsilon }}} \right) + \overline{\overline {\rm{\Pi }}} \cdot {\bf{\upsilon }}} \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + {\eta _{\rm{{\rm O}}}}{\bf{J}} \times {\bf{B}} + {x_{\rm{H}}}\left( {{\bf{J}} \times {\bf{B}}} \right) \times {\bf{B}}} \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\left. { - {x_{{\rm{AD}}}}\left[ {\left( {{\bf{J}} \times {\bf{B}}} \right) \times {\bf{B}}} \right] \times {\bf{B}} + \kappa \nabla T} \right] = - \rho {\bf{\upsilon }} \cdot \nabla \psi .} \hfill \cr } $](/articles/aa/full_html/2023/09/aa46005-23/aa46005-23-eq4.png) (4)
(4)
Equations (1) and (2) are the continuity and momentum equations, where ρ is the flow density, υ is the velocity, B is the magnetic field, 𝒫 = P + B2/2 is the generalized pressure with P the gas pressure, ψ is the gravitational potential, 𝕀 is the identity tensor, and 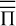 is the viscous stress tensor, defined as
is the viscous stress tensor, defined as
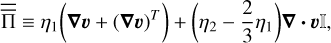 (5)
(5)
where η1 and η2 are the standard and bulk viscosities. In magnetohydrodynamics (MHD), this is complemented by the induction Eq. (3), where ηO is the Ohmic diffusivity, J = ∇ × B is the electrical current, xH is the Hall parameter, and xAD is the ambipolar diffusion parameter. This set of equations is completed by the total energy Eq. (4) where E is the total energy density
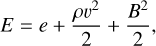 (6)
(6)
with e being the internal energy density, and κ the thermal diffusion coefficient (assumed to be a scalar).
We note that IDEFIX does not assume any explicit physical units. The user is free to choose the physical units depending on the problem at hand, keeping in mind that the equations effectively solved by the code are the ones shown above.
2.2 Method of solution
This set of conservative equations can be reformulated using a generalized vector of conserved quantities U = (ρ,ρυ, B, E) as
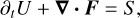 (7)
(7)
where F is the flux of conserved quantity U, and S is a source term that cannot be included in the divergence term. IDEFIX is fundamentally a Godunov-type finite-volume code designed to model astrophysical plasmas. Hence, IDEFIX primarily evolves the cell-averaged conserved quantities 〈U〉, which are computed using the face- and time-averaged fluxes 〈F〉 (Toro 2009). While we omit the 〈 〉 symbol in the remainder of the manuscript for simplicity, this distinction should be kept in mind. The algorithm is relatively standard and follows the reconstruct-solve-average (RSA) approach similar to other codes available, such as PLUTO, ATHENA, RAMSES, and NIRVANA to name a few. The implementation design of this algorithm in IDEFIX is intentionally close to that of the PLUTO code to simplify the portability of physical setups from one code to the other (see Sect. 3.2). Therefore, we do not go into the details of the algorithm, which may be found in the papers mentioned above, but instead focus on the main stages of the algorithms, and the differences with PLUTO. The full algorithm with its various steps and loops is represented graphically in Fig. 1 for reference.
2.3 Hyperbolic hydrodynamical terms
As with all Godunov codes, IDEFIX uses a strategy based on cell reconstruction followed by inter-cell flux computation using Riemann solvers to follow the evolution of U due to hyperbolic terms. In IDEFIX, the reconstruction to cell faces (step S2) is performed on the primitive variables (ρ, υ, B, P). In doing so, we avoid the decomposition in characteristics used in other codes while keeping the basic physical constraints (e.g., density and pressure positivity). Reconstruction can be performed using either a flat reconstruction (first-order accurate), piece-wise linear reconstruction using the van Leer slope limiter (second-order accurate), compact third-order reconstruction (up to forth-order accurate Čada & Torrilhon 2009), and piece-wise parabolic reconstruction using an extremum-preserving limiter (forth-order accurate on regularly spaced grids; Colella & Woodward 1984; Colella & Sekora 2008)1. The number of ghost cells is automatically adjusted to the requirements of the reconstruction scheme.
Once the reconstruction on cell faces is complete, a Riemann solver is used to compute the inter-cell flux (step S3). IDEFIX can use, ordered from most to least diffusive, the Lax-Friedrichs Russanov flux (Rusanov 1962), the Harten, Lax, and van Leer (HLL) approximate solver (Einfeldt et al. 1991), the HLLC solver (a version of the HLL solver that keeps the contact wave; Toro et al. 1994), and the approximate linear Roe Riemann solver (Cargo & Gallice 1997). In the MHD case, the HLLC solver is replaced by its magnetized HLLD counterpart (Miyoshi & Kusano 2005). These Riemann solvers can be chosen freely at run time, allowing the user to experiment with each of them. We note that, in contrast to PLUTO, which treats pressure gradients as a source term in the momentum equation, pressure in IDEFIX is included in the momentum flux, and hence solved for by the Riemann solver. This approach has the advantage of treating all of the variables equally but creates additional pressure source terms in non-Cartesian geometries, which are absent from PLUTO. As a consequence, the results of PLUTO and IDEFIX are expected to differ, even if the same algorithm combination is chosen.
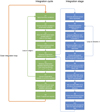 |
Fig. 1 Schematics of the integration algorithm in IDEFIX. |
2.4 Magnetohydrodynamics
When the MHD module is switched on, IDEFIX adds the induction Eq. (3) to the set of equations being solved, which can be written as
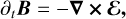 (8)
(8)
where ℰ is the induced electric field. In contrast to the discretization of Eq. (7), which uses cell-averaged quantities, the induction equation uses face-averaged magnetic field components B and evolves them using the constrained transport scheme (CT, Evans & Hawley 1988). In this approach, the electric field ℰ is discretized on cell edges, and a discrete version of Stokes theorem is used to evolve B from the contour integral of ℰ. This approach in principle allows us to keep ∇ · B = 0 at machine precision. However, we note that even with CT, roundoff errors can accumulate in B, leading to potentially significant ∇ · B. This can be encountered for particularly long simulations running for billions of time steps, and is even more prevalent when a Runge–Kutta-Legendre super-time-stepping scheme is used in conjunction with CT (see Sect. 2.8). Hence, IDEFIX allows the user to split the induction equation into two parts:
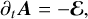 (9)
(9)
 (10)
(10)
By defining the vector potential A on cell edges, the resulting algorithm is mathematically equivalent to the original CT algorithm. However, it prevents roundoff errors from accumulating in ∇ · B, guaranteeing that the solenoidal condition is always satisfied, even at late times. The only drawback of this vector potential approach is the extra cost of storing A in memory, and the need to code an initial condition for A instead of B. As our gauge choice is so that A = ∫ ℰ dt, there is a possibility of overflowing the vector potential in physical problems where a large-scale constant EMF is present. While we have not encountered this difficulty in real-life applications, it is recommended to clean the vector potential periodically using an adequate gauge transformation if such a situation is expected to occur. Finally, we note that this vector potential formulation is always available, even when orbital advection, nonideal MHD, and/or super time-stepping is used.
The main difficulty with the CT scheme is to reconstruct ℰ on cell edges in a way that is numerically stable and mathematically consistent with steps S2–S4. Two classes of schemes in IDEFIX satisfy these requirements and are performed in S7: schemes that rely on the face-centered fluxes computed by the Riemann solvers in S3, following Gardiner & Stone (2005), and schemes that solve an additional 2D Riemann problem at each cell edge as proposed by Londrillo & del Zanna (2004). In the first category, IDEFIX can use the arithmetic average of fluxes, and the ℰ0 and ℰc schemes of Gardiner & Stone (2005). In the second category, IDEFIX can use the 2D HLL and HLLD 2D Riemann solvers following the method of Mignone & Del Zanna (2021). By default, IDEFIX uses the ℰc scheme – in a similar way to ATHENA – which is a good trade-off between accuracy, stability, and computing time. The choice of the ℰ reconstruction scheme can be changed at runtime.
2.5 Parabolic terms
Several parabolic terms have been implemented in IDEFIX: viscous diffusion, thermal diffusion, Ohmic diffusion, ambipolar diffusion, and the Hall effect. These terms are added to the hyperbolic fluxes in S4 so as not to break the numerical conservation of U. For MHD diffusive parabolic terms (Ohmic and ambipolar diffusion), we add their contribution using a centered finite-difference formula to ℰ before advancing B (or A) in S8. Finally, the Hall effect requires special treatment. This term is notoriously difficult to implement owing to its dispersive but nondissipative nature. In IDEFIX, we follow the approach presented in Lesur et al. (2014) and add the whistler speed to the Riemann fan of the HLL solver in S3. We further improve this approach by using the whistler wave speed only to evolve the magnetic field fluxes, and keep the usual ideal MHD wave speeds for the other components of F, following Marchand et al. (2019). This treatment reduces the numerical diffusion on nonmagnetic conserved quantities. Finally, ℰ is reconstructed on cell edges using an arithmetic average of F, as in Lesur et al. (2014). We tried modifying the ℰc reconstruction scheme to include the Hall term but found that this approach led to numerical instabilities. While known to be diffusive, our implementation of the Hall effect guarantees the stability of the resulting scheme.
2.6 Grid and geometry
IDEFIX can run problems in Cartesian, polar/cylindrical, and spherical geometry. In all of these geometries, the grid is rectilinear, but its spacing may be parameterized as piecewise functions of coordinates. While this approach is clearly not as flexible as adaptive mesh refinement, it allows refinement around regions of interest at a reduced computational cost and code complexity. In polar and spherical geometry, we choose the conserved quantity in the azimuthal direction to be the vertical component of the angular momentum. This guarantees the conservation of angular momentum to machine precision. Great care has been taken for spherical domains extending up to the axis. A special “axis” boundary condition is provided, which guarantees regularity of solutions around the axis, following Zhu & Stone (2018).
2.7 Time integrator
The outermost time integration loop is called a cycle. At each cycle n, the solution U(n) is advanced by a time step dt giving U(n+1). Within a cycle, several time-marching schemes can be invoked to evolve physical quantities, each of them possibly using several subcycles called stages. In IDEFIX, the default time-integrator is an explicit multistage scheme. To guarantee a given level of accuracy, IDEFIX supports several orders for this scheme, following the method of lines: Euler (first order in time) and total variation diminishing Runge–Kutta 2 and 3 (respectively second and third order; Gottlieb & Shu 1998).
Each explicit time-integration cycle starts with the solution at time t, U0 ≡ U(n). For each stage s, IDEFIX advances the previous stage Us−1 by dt using the algorithm described in Sects. 2.3–2.5 (steps S1–S10, which we note in a single operator 𝒮dt) and store it in U* = 𝒮dt(Us−1). This solution is then linearly combined with U0 to give Us. Formally, for each stage s ≥ 1, we compute
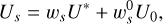 (11)
(11)
where ws and 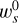 are fixed real coefficients (Table 1).
are fixed real coefficients (Table 1).
As the main time marching scheme in IDEFIX is explicit, a Courant–Friedrichs–Lewy (CFL, Courant et al. 1928) condition is needed to guarantee numerical stability. This constraint is computed as a generalization of Beckers (1992), Eq. (62):
![$${\rm{d}}t = {\sigma _{{\rm{CFL}}}}{\left( {\mathop {\max }\limits_v \left[ {\mathop \sum \limits_d {{{c_{\max ,d}}} \over {{\rm{d}}{\ell _d}}} + {{2{\eta _{\max }}} \over {{\rm{d}}\ell _d^2}}} \right]} \right)^{ - 1}},$$](/articles/aa/full_html/2023/09/aa46005-23/aa46005-23-eq17.png) (12)
(12)
where σCFL < 1 is a safety factor, cmax,d is the maximum signal speed in current cell in direction d (computed in the Riemann solver step S3), ηmax is the maximum diffusion coefficient in current cell, and dℓd is the current cell length in direction d. We note that the maximum in the above formula is taken over the entire integration volume 𝒱, while the summation is performed in all directions of integration d. Finally, we emphasize that our CFL condition is different from that of PLUTO (Mignone et al. 2012, Eq. (7)) in at least two ways: (1) we do not include any pre-factor on the number of dimensions, and therefore σCFL = D × Ca,PLUTO where D is the number of dimensions so that the stability condition is always σCFL < 1 in IDEFIX, and (2) our CFL condition combines the point-wise hyperbolic and parabolic constraints, while PLUTO computes a global dt for hyperbolic terms and parabolic terms separately. The end result is that dt computed by IDEFIX can be somewhat larger than the more restrictive time step from PLUTO, while still satisfying the Beckers (1992) constraint on a point-wise basis.
Weight coefficients for the time-integration schemes available in IDEFIX.
2.8 Super time-stepping: The Runge–Kutta–Legendre scheme
In some circumstances, for instance, in very diffusive plasmas, the CFL condition (12) on parabolic terms leads to prohibitively low dt. In such cases, it is recommended to use super time-stepping to specifically integrate this term and remove it from the standard explicit scheme. In IDEFIX, super time-stepping is implemented using the explicit Runge–Kutta–Legendre scheme (RKL) from Meyer et al. (2014) and Vaidya et al. (2017). The advantage of the RKL scheme over the usual super time-stepping based on Chebyshev polynomials (sometimes called RKC) is its increased accuracy and robustness, and the absence of any free “damping” parameter, as the method is intrinsically stable. In IDEFIX, we have implemented a second-order RKL scheme (a first-order scheme is also available for debugging purposes). Splitting the time-step (12) into a hyperbolic and parabolic part
![$${\rm{d}}{t_{{\rm{hyp}}}} = {\left( {\mathop {\max }\limits_\nu \left[ {\sum\limits_d {{{{c_{\max ,d}}} \over {{\rm{d}}{\ell _d}}}} } \right]} \right)^{ - 1}},$$](/articles/aa/full_html/2023/09/aa46005-23/aa46005-23-eq18.png) (13)
(13)
![$$d{t_{{\rm{par}}}} = {\left( {\mathop {\max }\limits_\nu \left[ {\sum\limits_d {{{2{\eta _{\max }}} \over {{\rm{d}}{\ell _d}}}} } \right]} \right)^{ - 1}},$$](/articles/aa/full_html/2023/09/aa46005-23/aa46005-23-eq19.png) (14)
(14)
then the RKL scheme saves computational time when dthyp ≫ dtpar. More precisely, the number of stages sRKL required by the second-order RKL scheme satisfies (Meyer et al. 2014):
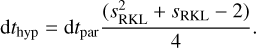 (15)
(15)
Therefore, when dthyp ≫ dtpar, 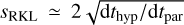 , which should be compared to 2dthyp/dtpar if the term had been integrated using the explicit RK2 scheme.
, which should be compared to 2dthyp/dtpar if the term had been integrated using the explicit RK2 scheme.
IDEFIX allows the user to activate the RKL scheme for viscosity, thermal diffusion, ambipolar diffusion, Ohmic diffusion, or a combination of these terms. When enabled, the RKL scheme directly calls the same routines, which are used to compute the parabolic terms in the main time integrator, so that no code is duplicated. Finally, in order to retain global second accuracy in time, the RKL stages are called alternatively before and after the main time integrator at each integration cycle.
While testing the RKL scheme for Ohmic and ambipolar diffusions, we noted that the roundoff error on ∇ · B tends to accumulate rapidly: while the standard explicit time integrator yields 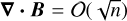 , with n the number of integration cycles, we find ∇ · B = 𝒪(n) with the RKL scheme. This issue can lead to relatively large values of ∇ · B for long simulations, which may become problematic. Hence, it is recommended to use the vector potential formulation of the induction Eq. (9) when using RKL on a parabolic MHD term to circumvent this problem.
, with n the number of integration cycles, we find ∇ · B = 𝒪(n) with the RKL scheme. This issue can lead to relatively large values of ∇ · B for long simulations, which may become problematic. Hence, it is recommended to use the vector potential formulation of the induction Eq. (9) when using RKL on a parabolic MHD term to circumvent this problem.
2.9 Orbital advection (Fargo-type scheme)
When working on cold Keplerian disks (i.e., when orbital velocity U is much larger than the other signal speeds involved in the system), orbital velocity is the limiting term in the CFL condition (12). A well-known procedure to speed up the time-integration in this case, initially proposed by Masset (2000) for the FARGO code, is to split the flux associated to the advection operator for every conserved quantity Q as
 (16)
(16)
where we assume ∇ · U = 0 and use δυ = υ − U. When U is known, the time evolution of ∂tQ + U ··∇Q = 0 is analytical, and so no explicit time-integration step is needed, nor any CFL condition. Hence, one splits the time integration of the full system into two stages: a numerical integration using the chosen time-marching scheme (Sect. 2.7) using ∇ · δυQ in the flux function, and an analytical advection stage using the prescribed orbital velocity U. The end result of this procedure is that the total velocity υ in the CFL condition is replaced by the residual velocity δυ, allowing for much larger time steps when δυ ≪ υ.
In IDEFIX, we have implemented the conservative orbital advection scheme of Mignone et al. (2012). This algorithm presents the advantage of retaining the conservation of mass, angular momentum, and magnetic flux by carefully formulating the source terms implied by the operator splitting. Our implementation is fully parallelized in 3D, and in particular, allows for domain decomposition along the toroidal direction.
3 Implementation
3.1 Performance portability using the KOKKOS library
IDEFIX was designed with performance portability in mind, which means that a single source code can be compiled on a wide variety of target architectures, with excellent performance being achieved on each of them. To this end, IDEFIX uses the KOKKOS library (Trott et al. 2022). KOKKOS sources are bundled as a git submodule by IDEFIX and are compiled alongside it. Hence, IDEFIX can be compiled and run out of the box.
Technically speaking, IDEFIX always assumes it is running on a machine that consists of a host and a device. The host is the CPU on which the code is launched, while the device can be any valid KOKKOS target: CPU, GPU, and so on. In special cases where no supported target is detected, the device code will be compiled as a host code, allowing IDEFIX to run seamlessly on systems without accelerators with very little overhead. For code portability constraints, it is always assumed that host and device memories are separated: memory owned by the host cannot be directly accessed from the device code, and vice versa. Hence, special constructs are needed to implement the algorithm described above.
IDEFIX provides two base constructs: arrays and parallel loops. Following the approach used in K-ATHENA (Grete et al. 2021), arrays are stored in IdefixArrayND2 where 1 < N < 4 is the number of dimensions of the array. Parallel loops are executed using idefix_for function, which acts similarly to for loops in C, and seamlessly encapsulates the SIMD execution paradigm on GPUs. Hence, a usual C loop written as
const int N = 10;
double array [N];
// initialise array to 1
for(int i = 0 ; i < N ;i++) {
array [ i ] = 1 . 0;
}
is written in IDEFIX as
const int N = 10;
IdefixArray 1D <double> array (“myArray” , N);
// initialise array to 1
idefix_for (“initLoop” , 0, N,
KOKKOS_LAMBDA(int i) {
array ( i ) = 1 . 0;
}
);
We note that the additional tag provided as the first argument to IdefixArraylD and idefix_for is only used for debugging and profiling purposes.
By construction, an IdefixArrayND is allocated in device space and all instructions within an idefix_for call are executed on the device. Hence, any access to elements of an IdefixArrayND needs to be done inside an idefix_for. IDEFIX also provides arrays allocated on the host (IdefixHostArrayND) which can be used in usual for loops, and are meant to mirror IdefixArrayND instances. Host arrays are useful for I/O routines and complex initial conditions.
IDEFIX is entirely written using these constructs, hence the algorithm described in Sect. 2 is running exclusively on the device, the host being used only for I/O, initial conditions, and handling exceptions (either triggered internally or by the user). This guarantees optimal acceleration for all combinations of algorithms provided.
3.2 Setup portability from PLUTO
The interface of IDEFIX is very close to that of PLUTO. Parameter files follow the same format and use identical keywords when possible. Variable names (grid variables, hydro variables), and several preprocessor macros have been kept to simplify the portability of PLUTO setups to IDEFIX as our research group has been using and developing physics setups for PLUTO for more than a decade. Similarly, outputs (VTK3 files) follow the same format and variable naming convention as PLUTO. However, we note that restart dumps are not compatible between the two codes. In addition, while PLUTO relies on C arrays, IDEFIX is based on C++ objects and uses C++ containers. This allows for more flexibility and simpler development of physics modules.
3.3 Inputs and outputs
IDEFIX uses a text input file – following the input file format of PLUTO – that is read at runtime. Most of the code options (time integrator, Riemann solvers, physical modules) are enabled in this input file.
IDEFIX outputs come in two formats: an internal dump file format that contains the raw data required to restart a simulation, and the VTK file format, which is used for visualization and analysis. The user can easily add new fields computed on the fly in IDEFIX VTK outputs to simplify visualization and post-processing. The VTK outputs produced by IDEFIX can be directly loaded in Paraview or Visit (Childs et al. 2012) for instantaneous visualization. Python routines are provided with the code to load IDEFIX VTK and dump files into numpy arrays. Both VTK and dump files can also be analyzed with the yt Python library (Turk et al. 2011) with the yt_idefix extension4. We note that the VTK file format imposes that data be written in single precision and only contain cell-averaged quantities (reconstructed from face-averaged quantities when storing B). This reduces storage requirements but also prevents the code from restarting from VTK files, hence the necessity for dump files.
Internally, IDEFIX relies on MPI I/O routines to write all of the data from all of the MPI processes to a single file (either VTK or dump). Therefore, no external I/O library is required to compile and run IDEFIX. We find this property useful when moving setups on different machines as it greatly simplifies the portability.
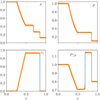 |
Fig. 2 Adiabatic hydrodynamical Sod (1978) shock test, at t = 0.2. Orange crosses: IDEFIX solution computed using the Roe solver with 500 points. Blue plain line: Analytical solution. |
3.4 Parallelism
When run in serial, IDEFIX starts a single process on the host and launches the computation kernels (the idefix_for) either on a single device (typically a GPU) or in the host process (when running without an accelerator). In addition, IDEFIX supports coarse-grained parallelism, as it can run on several processors or nodes using domain decomposition and the Message Passing Interface (MPI) library.
When MPI parallelization is enabled, IDEFIX decomposes the grid into subdomains of similar size and attaches each MPI host process to a different device. MPI is then used to exchange boundary elements directly between devices, using a GPu-aware implementation on GPUs. The MPI routines have been optimized to pack and unpack boundary elements in device space, and are based on MPI persistent communications to reduce latency. Therefore, if a direct connection is available between devices (such as NVlink), there is no host-to-device overhead induced by communications.
The boundary exchange routines in IDEFIX use a sequential dimension decomposition strategy. This means that we first exchange all of the boundary elements in the first dimension before starting to exchange in the second dimension and so on for the third dimension. This implies that in 3D, the exchange of ghost zones in the third dimension has to wait for the exchanges in the first and second dimensions. This choice was motivated by direct timing measures comparing the sequential implementation to the simultaneous implementation where the face, corner, and edge elements are all exchanged at the same time with the 26 neighbors in 3D (see e.g., the implementation in ATHENA, Stone et al. 2020). We chose the sequential implementation as it proved to be generally faster, especially on NVidia GPUs. However, we note that such a choice would not be suited to an AMR version of IDEFIX.
 |
Fig. 3 Double Mach reflection test computed at t = 0.2. Here, we represent the resulting density map for various combinations of algorithms with a 1920 × 480 resolution. |
 |
Fig. 4 Sedov-Taylor blast wave in Cartesian geometry at t = 0.1. Left panel: slice of the pressure field through z = 0. Right panel: pressure distribution as a function of the distance from the blast center. The inset shows a zoom onto the blast shock region. |
4 Tests
4.1 Hydrodynamical tests
Hydrodynamical Sod shock tube
A standard and simple 1D test for hydrodynamic codes, the Sod shock tube (Sod 1978) is made of two constant states separated by a discontinuity. Here we use ρL = 1.0, PL = 0.1 on the left of the discontinuity and ρR = 0.125, PR = 0.1 on the right, with υ = 0 in the entire domain initially. The test is performed with an ideal equation of state with γ = 1.4 and is integrated up to t = 0.2 using various combinations of Riemann solvers and time integrators. An example with the Roe Riemann solver, linear reconstruction, and RK2 time-integrator is reproduced in Fig. 2 and compared to the analytical solution.
Double Mach reflection test
A test introduced by Colella & Woodward (1984) in which the interaction between two shock waves forms a contact discontinuity and a small jet. The properties of this jet are known to depend strongly on numerical diffusion and in particular on the spatial reconstruction scheme and Riemann solver. The test presented here (Fig. 3) follows the initial conditions from Colella & Woodward (1984) and uses various combinations of reconstruction, Riemann solvers, and time integrator on a 1920 × 480 resolution grid. As expected, we find a more vigorous jet along with the beginning of Kelvin-Helmholtz rolls for the LimO3 and PPM reconstruction schemes, which are the least diffusive schemes in IDEFIX. This figure can be compared with Fig. 16 from Stone et al. (2008) and Fig. 2 from Mignone et al. (2007).
Sedov–Taylor blast wave
This test is designed to reproduce the Sedov (1946) and Taylor (1950) blast wave self-similar solution for infinitely compact explosions. In this test, we consider an initially stationary flow with ρ = 1, P = 10−2, and γ = 5/3. We initiate the explosion in the center of the domain by depositing an amount of energy 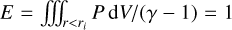 in a spherical subdomain of radius ri. The problem is then integrated up to t = 0. 1 using the HLL solver, RK2 time-integration, and linear reconstruction, at which point we compare the numerical solution to the analytical one. We perform two tests: one in Cartesian geometry with a resolution 5123 and a cubic box size L = 1 (Fig. 4), and one in spherical geometry (nr × nθ × nϕ = 256 × 256 × 512 with a domain size r ∊ [0.5, 1.5], θ ∊ [0, 0.7], ϕ ∊ [0, 2π]), where the explosion is initiated close to the polar axis (x = 0.1, y = 0, z = 1) so as to test the propagation of the blast wave through the axis (Fig. 5). In the Cartesian test, all three directions are assumed to be periodic, while in the spherical test, we use outflow boundary conditions in radius, the axis regularisation boundary condition in the θ direction, and periodic boundary conditions in azimuth.
in a spherical subdomain of radius ri. The problem is then integrated up to t = 0. 1 using the HLL solver, RK2 time-integration, and linear reconstruction, at which point we compare the numerical solution to the analytical one. We perform two tests: one in Cartesian geometry with a resolution 5123 and a cubic box size L = 1 (Fig. 4), and one in spherical geometry (nr × nθ × nϕ = 256 × 256 × 512 with a domain size r ∊ [0.5, 1.5], θ ∊ [0, 0.7], ϕ ∊ [0, 2π]), where the explosion is initiated close to the polar axis (x = 0.1, y = 0, z = 1) so as to test the propagation of the blast wave through the axis (Fig. 5). In the Cartesian test, all three directions are assumed to be periodic, while in the spherical test, we use outflow boundary conditions in radius, the axis regularisation boundary condition in the θ direction, and periodic boundary conditions in azimuth.
 |
Fig. 5 Sedov–Taylor blast wave in spherical geometry at t = 0.1. The blast is initialized slightly off the polar axis (at x = 0.1, z = 1). Left panel: slice of the pressure field through y = 0. The dashed white line represents the polar axis of the domain, which is regularized automatically by IDEFIX. Right panel: pressure distribution as a function of the distance from the blast center. The inset shows a zoom around the blast shock region. |
4.2 MHD tests
MHD shock tube
The Brio & Wu (1988) MHD shock tube test is the MHD equivalent of the Sod shock tube test in hydrodynamics. We use γ = 5/3 and an initial condition identical to Mignone et al. (2007). There is no analytical solution for this test, and so the reference solution is computed with Pluto 4.3 using a Roe solver and a grid of 8000 points (Fig. 6). We note that this test being 1D, it only validates the Riemann solvers but not the EMF reconstruction schemes that are used only in multidimensional tests. We observe excellent agreement with the high-resolution solution. We note a small-amplitude oscillation of the post-shock velocity, which is typical of the primitive variable reconstruction used in IDEFIX.
Linear MHD wave convergence
This test was designed by Gardiner & Stone (2005) and Stone et al. (2008) to recover the linear MHD eigenmodes on an inclined grid. The test consists of a rectangular box (Lx, Ly Lz) = (3.0, 1.5, 1.5) and a grid of 2N × N × N cells, which is assumed to be periodic with the three directions of space. The background flow is assumed to be stationary (except for the entropy wave) with ρ = 1 and P = γ−1 = 3/5. To fully characterize the initial condition, we use a coordinate system (x1, x2, x3) that is rotated with respect to the grid (x, y, z). In this rotated coordinate system, we use B1 = 1, B2 = 3/2, and υ1 = 1 (when testing the entropy mode), and υ1 = 0 otherwise. With this background state, the fast, Alfvén, and slow modes propagate respectively at cf = 2, cA = 1, and cs = .5 in the x1 direction, respectively, while the entropy mode propagates at υ1. To check the convergence of the code, we set up a small-amplitude (ϵ = 10−6) monochromatic wave along x1 for each eigenmode (see Stone et al. 2008 for the expression of the eigenmodes). We then compare the value of all of the fields after exactly one crossing time tc of the simulation domain and compute the error e as
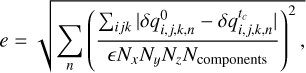 (17)
(17)
where Ncomponents is the number of nonzero components in the eigenmode and 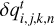 is the deviation from the background state at time t for component n at location (xi, yj, zk). We perform two kinds of linear convergence tests: We first compare the different Riemann solvers with linear reconstruction and second-order time integration (RK2; Fig. 7). This confirms that IDEFIX is overall second order for smooth problems, as expected. We next perform this test using different reconstruction schemes with the HLLD Riemann solver: linear (van Leer) with RK2 time-stepping and LimO3 and PPM in conjunction with RK3 time-stepping (Fig. 8). This demonstrates the superiority of LimO3 and PPM schemes, which overall have a lower diffusivity than linear (particularly notable for the entropy mode). However, we note that at high resolution, the PPM reconstruction scheme stops converging for this test. This is particularly stringent for the slow mode, which seems to be most sensitive to this effect (probably because it has the lowest wave speed and therefore requires longer integration times). We verified that this lack of convergence was also observed with more diffusive solvers (HLL), and is also present in other codes (notably ATHENA++ with primitive reconstruction, see Fig. 8), and is therefore not related to the PPM implementation used in IDEFIX. The error reached at very high resolution is about 10−2 for PPM, which is potentially problematic for sensitive applications. Overall, this indicates that the PPM scheme could produce low-level numerical artifacts in very high-resolution simulations and that the LimO3 scheme should be preferred, as it shows proper second-order convergence for all of the resolutions we have tested.
is the deviation from the background state at time t for component n at location (xi, yj, zk). We perform two kinds of linear convergence tests: We first compare the different Riemann solvers with linear reconstruction and second-order time integration (RK2; Fig. 7). This confirms that IDEFIX is overall second order for smooth problems, as expected. We next perform this test using different reconstruction schemes with the HLLD Riemann solver: linear (van Leer) with RK2 time-stepping and LimO3 and PPM in conjunction with RK3 time-stepping (Fig. 8). This demonstrates the superiority of LimO3 and PPM schemes, which overall have a lower diffusivity than linear (particularly notable for the entropy mode). However, we note that at high resolution, the PPM reconstruction scheme stops converging for this test. This is particularly stringent for the slow mode, which seems to be most sensitive to this effect (probably because it has the lowest wave speed and therefore requires longer integration times). We verified that this lack of convergence was also observed with more diffusive solvers (HLL), and is also present in other codes (notably ATHENA++ with primitive reconstruction, see Fig. 8), and is therefore not related to the PPM implementation used in IDEFIX. The error reached at very high resolution is about 10−2 for PPM, which is potentially problematic for sensitive applications. Overall, this indicates that the PPM scheme could produce low-level numerical artifacts in very high-resolution simulations and that the LimO3 scheme should be preferred, as it shows proper second-order convergence for all of the resolutions we have tested.
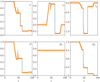 |
Fig. 6 Brio & Wu (1988) adiabatic MHD shock test. IDEFIX solution (orange cross) was computed using the Roe solver with 500 points and linear reconstruction while the reference solution (blue line) was computed with Pluto 4.3 using 8000 points. |
 |
Fig. 7 Convergence rate of the four linear wave types in adiabatic MHD for various Riemann solvers using linear reconstruction. The code exhibits second-order spatial convergence, as expected. |
Magnetised rotor test
This test is designed to test the propagation of strong torsional Alfvén waves (Balsara & Spicer 1999). It consists of a fast-rotating disk (the rotor) embedded in a light stationary fluid (the ambient medium). The whole domain is initially threaded by a homogeneous magnetic field directed in the x direction. We follow Mignone et al. (2007) to set up the problem, with a smooth transition for the angular velocity and density between the rotor and the ambient medium. In addition, we use two versions of the test in Cartesian and polar geometries to check the validity of our curvilinear implementation. The resulting tests are presented in Fig. 9. The Cartesian test is computed on a 5122 grid with a Roe Riemann solver, RK2 time integrator, a CFL parameter set to 0.2, and the ℰc EMF reconstruction scheme. The polar test is computed on a NR × Nφ = 256 × 1024 grid extending from R = 0.05 to R = 0.5 keeping the other parameters of the solver identical to the Cartesian setup. This test confirms that IDEFIX correctly handles curvilinear coordinates such as polar coordinates.
 |
Fig. 8 Convergence rate of the four linear wave types for various reconstruction techniques using the HLLD Riemann solver. The code exhibits a slightly higher convergence rate than second order for LimO3. However, we highlight the lack of convergence at high resolution for PPM, which is also observed in ATHENA++ (dashed lines). |
Orszag Tang vortex
A classic test of 2D MHD that consists in evolving an initially purely vortical flow threaded by a large-scale magnetic field (Orszag & Tang 1979). For this test, we use a periodic Cartesian domain of size Lx = Ly = 1 with constant initial pressure P = 5/(12π) and density ρ = 25/(36π). We add a velocity perturbation υ = − sin(2πy)ex + sin(2πx)ey and a magnetic perturbation B = −B0 sin(2πy)ex + B0 sin(4πx)ey with 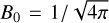 , both of which are initially divergence-free. We then evolve this initial condition up to t = 0.5 with a resolution of 1283, plus a reference case at 5123. Figure 10 presents the resulting pressure distribution using different combinations of Riemann solver, reconstruction scheme, and EMF implementation, while Fig. 11 shows a cut at y = 0.316 and y = 0.425 of the same pressure field. These figures confirm that the RK3+PPM+Roe combination is the most accurate solver for a given resolution, but other combinations also give the correct results at a reduced numerical cost. This test also validates our implementation of constrained transport, because we measure |∇ · B| ≪ 10−12 in all of these simulations.
, both of which are initially divergence-free. We then evolve this initial condition up to t = 0.5 with a resolution of 1283, plus a reference case at 5123. Figure 10 presents the resulting pressure distribution using different combinations of Riemann solver, reconstruction scheme, and EMF implementation, while Fig. 11 shows a cut at y = 0.316 and y = 0.425 of the same pressure field. These figures confirm that the RK3+PPM+Roe combination is the most accurate solver for a given resolution, but other combinations also give the correct results at a reduced numerical cost. This test also validates our implementation of constrained transport, because we measure |∇ · B| ≪ 10−12 in all of these simulations.
4.3 Additional modules
Orbital advection (Fargo-type) module
We test the orbital advection scheme in hydrodynamics by looking at the perturbation of an embedded planet in an inviscid gaseous disk solved in 2D polar coordinates. In this test, we set a planet with a planet-to-star mass ratio of q = 10−3 on a fixed circular orbit at R = 1 with a Plummer potential ψp = −q/(‖r − rp‖2 + a2)1/2, where a = 0.03 is the Plummer smoothing length. The resolution is set to (NR, Nϕ) = (256, 256) and we use the HLLC Riemann solver with linear reconstruction. Orbital advection is set to use a PPM reconstruction scheme (we note that a linear scheme is also available). The problem is then integrated for four planetary orbits. We compare the resulting density deviations (Fig. 12) and the radial velocity along the azimuthal direction at several radii (Fig. 13) using FARGO3D (Benítez-Llambay & Masset 2016) as a reference. The agreement between the two codes is excellent. We notice that FARGO3D produces more small-scale waves between the main spiral shocks launched from the planet.
Ambipolar diffusion isothermal C-shock
This test consists of a “shock” (which is actually continuous) and is driven by ambipolar diffusion. We follow Mac Low et al. (1995) and use a stationary shock with an upstream Mach number M = 50, an Alfvénic Mach Number A = 10, and an inclination angle of θ = π/4 (Fig. 14). The characteristic length of the shock is L ≡ ηA/υA where ηAD ≡ xADB2 is the ambipolar diffusivity and υA is the Alfvén speed. We find excellent agreement between the analytical solution (in black) and the various solutions computed with IDEFIX using either the explicit RK2 integrator or the second-order RKL time-integrator for parabolic terms, with an error of less than 2% when using two points per L. Also, the time to solution with the RKL scheme is about 10% of the explicit scheme in the high-resolution runs, indicating the very substantial gain brought by the RKL scheme.
 |
Fig. 9 Magnetic rotor test from Balsara & Spicer (1999), on the left using a Cartesian geometry and on the right using a polar geometry. We note the close resemblance of the iso-surfaces, indicating the excellent behaviour of the code in these two geometries. |
Hall-dominated shock
This test consists of a shock wave in a flow dominated by the Hall effect, but also involving Ohmic and ambipolar diffusivities. It was first introduced in the context of multi-fluid MHD by Falle (2003) to test the propagation of whistler waves in the pre-shock region of an MHD shock. Here, we follow the shock tube test A5 of González-Morales et al. (2018) by setting up an initial discontinuity at x = 0 with the left and right states in Table 2. The system is then evolved with all the nonideal MHD effects turned on explicitly and with η = 1, xA = 25, and xH = 500. The solver is set to RK2, CFL to 0.5, and we use the HLL Riemann solver (our only solver compatible with the Hall effect). We finally compare the final steady state obtained to a semi-analytical solution obtained by computing the steady state, numerically integrating the induction equations (Eqs. (50a) and (50b) in González-Morales et al. 20186). The results are presented in Fig. 15. We find the solution computed with IDEFIX to be in excellent agreement with the analytical solution. The relative error decreases by a factor of 3–4 by doubling the resolution, which indicates a convergence rate that is slightly lower than second order for this test, which is due to the high diffusivity induced by grid-scale whistler waves. We note that it is possible to strictly recover the second-order convergence using the LimO3 or PPM reconstruction schemes (not shown).
Left and right states for the Hall-dominated shock tube (González-Morales et al. 2018).
Shearing box
The shearing box is a well-known model of sheared flows that has been used extensively for the study of the magneto-rotational instability (MRI) in the context of accretion-disk physics (Balbus & Hawley 1991; Hawley et al. 1995). We implemented the shearing box specific shear-periodic boundary conditions in IDEFIX, both in hydro and MHD. This module is also compatible with the orbital advection module, allowing a significant speedup in large boxes, where the shear flow is largely supersonic. To test the implementation, we compare against the exact shearing wave solution of Balbus & Hawley (2006) in hydro, and against a generalized version of it for the MHD case. The setup consists of a cubic box of size 1 with a Keplerian rotation profile and a resolution of 2563. The initial configuration for the shearing wave is uR = ux = AR sin[2π(nRx + nϕy + nzz)], where we choose nR = 0, nϕ = 1, nz = 4, and an initial wave amplitude of AR = 10−5. Additionally, we set a uniform density and pressure ρ = 1 and P = 1/γ with γ = 5/3 assuming an ideal equation of state for the gas. Finally, in the MHD case, we add a mean toroidal and vertical magnetic field By0 = 0.02 and Bz0 = 0.05. We note that while the single shearing wave of Balbus & Hawley (2006) is an exact nonlinear solution of the incompressible equations of motion, it is not an exact nonlinear solution in the compressible regime modeled by IDEFIX. Therefore, we only recover the Balbus & Hawley (2006) solutions in the linear limit AR ≪ 1.
The system is then integrated using the HLLC (hydro) or HLLD (MHD) Riemann solvers using a linear reconstruction, RK2 time-stepping, and enabling orbital advection. We present the evolution of the velocity components of the hydro problem in Fig. 16 and the velocity and field components of the MHD problem in Fig. 17. The semi-analytical solutions are computed numerically by integrating the linearized equations of motion (Eqs. (6.25)–(6.29) in Lesur 2021). We find that the agreement between the numerical and analytical solution is excellent up to Ωt ≃ 10, where υz starts to diverge in the hydro case. This time corresponds to an effective radial wavenumber nr(t) = 3/2Ωt ~ 15, so that the wave is effectively resolved by about 17 points. Similar results were obtained with the ATHENA code using PPM reconstruction (Balbus & Hawley 2006), and so they are not necessarily surprising, but illustrate the difficulty of following shearing waves on long timescales, even at relatively high resolutions.
 |
Fig. 10 Orszag Tang vortex pressure distribution at t = 0.5 with different combinations of algorithms computed with 1282 points, except for the bottom-right plot, which is computed with 10242 points. |
 |
Fig. 11 Cut in the Orszag Tang vortex at y = 0.316 (top) and y = 0.425 (bottom) for selected algorithms from Fig. 10. Solutions were computed with 1282 points, while the reference was computed with 10242 points. |
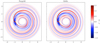 |
Fig. 12 Planet–disk interaction problem with orbital advection enabled at t = 4 planetary orbits. Comparison between FARGO3D and IDEFIX for the density deviation map in the planet–disk interaction problem with orbital advection enabled at t = 4 planetary orbits. We note the presence of small wave-like patterns in FARGO3D that are absent from IDEFIX. |
 |
Fig. 13 Planet–disk interaction problem with orbital advection enabled at t = 4 planetary orbits. Comparison between FARGO3D and IDEFIX of the radial velocity υR at R = 0.7 (plain line) and R = 1.3 (dashed line). |
5 Performance
In order to test the performances of the code on CPUs and on GPUs, we used an extension of the Orszag Tang problem in three dimensions. We consider a periodic Cartesian domain of size Lx = Ly = Lz = 1 with constant initial pressure P = 5/(12π) and density ρ = 25/(36π). We add a velocity perturbation υ = – sin(2πy)ex + [sin(2πx) + cos(2πz)]ey + cos(2πx)ez and a magnetic perturbation B = –B0 sin(2πy)ex + B0 sin(4πx)ey + B0[cos(2πx) + sin(2πy)]ez with 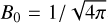 , both of which are initially divergence free. This physical setup is run until t = 1.0 and the result is compared to that obtained with PLUTO to check for convergence. The test is executed for both codes with the HLLD Riemann solver, second-order (linear) reconstruction, the ℰc EMF reconstruction scheme, and RK2 time-stepping in double precision.
, both of which are initially divergence free. This physical setup is run until t = 1.0 and the result is compared to that obtained with PLUTO to check for convergence. The test is executed for both codes with the HLLD Riemann solver, second-order (linear) reconstruction, the ℰc EMF reconstruction scheme, and RK2 time-stepping in double precision.
We ran this test problem on Intel Cascade Lake CPUs and NVidia V100 GPUs in the Jean Zay cluster hosted by IDRIS (CNRS); on AMD Rome CPUs in the Irene Rome cluster hosted by TGCC (CEA); and on AMD Mi250 GPUs in the Adastra cluster hosted by CINES. The details of the configuration and compilation options are given in Table 3. We note that we use the Intel compiler on CPUs, which allows us to benefit from auto-vectorization. An analysis of the executable file produced with Intel Vtune shows that more than 86% of the integration loops are being automatically vectorized with avx2 instructions.
We first present the single node performances in Table 4 along with an estimation of the energy efficiency. The code typically performs better than 10 Mcell s−1 on a single Intel 20-core CPU and 20 Mcell s−1 on a single AMD 64-core CPU, which is similar to other CPU codes available. When we compare Intel CSL nodes to GPU nodes, we find an acceleration of a factor 19.3 on NVidia V100 and 49.6 on AMD Mi250, demonstrating that performance portability is extremely good.
We then analyzed the parallelism efficiency of the code by running the same problem on up to 512 NVidia GPUs (128 nodes), 1024 AMD GPUs (256 nodes), and 131 072 CPU cores (1024 nodes). Measured performances are presented in Fig. 18 for various resolutions. On CPUs, we find that scaling and overall performance are very close to those of PLUTO. This is not surprising as the algorithms are similar. However, we note that IDEFIX performs slightly better beyond 10 000 cores, which is probably explained by the packing/unpacking strategy when exchanging boundary elements used in IDEFIX (see Sect. 3.4). On GPUs, IDEFIX exhibits an excellent scaling with above 80% parallelization efficiency with subdomains of 2563 on Nvidia V100 (Jean Zay), and remarkably above 95% on AMD Mi250 (Adastra), probably thanks to the AMD Slingshot interconnect used in the latter. We note that performances drop substantially for subdomains smaller than 643. This is because GPUs use a latency-hiding strategy, where memory accesses (which is slow) to some portion of an array are performed simultaneously with computations. This strategy is efficient if there are enough computations to be performed while fetching data in memory, which is not the case below 643 resolution on each GPU. Overall, IDEFIX achieves a peak performance of about 3 × 1011 cell s−1 on 1024 GPUs on Adastra, with sufficiently large subdomains.
In order to estimate the energy consumption of the node, we used the Thermal Design Power (TDP) published by the manufacturer of each CPU/GPU. For GPU nodes, we count both the GPU TDP and that of the host CPUs. We find that energy efficiency on CPUs is about 3 × 1010 cell kWh−1 while it reaches as high as 1.8 × 1011 cell kWh−1 on Mi250 GPUs. This demonstrates that for the same problem, IDEFIX can be up to six times more energy efficient on GPUs than on CPUs. We note that our approach is only a proxy for the real energy consumption of the node, as it does not include storage, network, or cooling in the energy budget. Moreover, this gain is observed for 2563 subdomain size, and drops severely as one reduces the domain size: for 323 domain size on GPUs, we get a similar efficiency between CPUs and GPUs. Therefore, from an energy sobriety standpoint, the use of GPUs only makes sense for subdomains larger than 643.
 |
Fig. 14 Ambipolar isothermal C-shock integrated at high resolution (HR, 2 points/L) and low resolution (LR, 1 point/L) and using the explicit or RKL second-order time integrators for parabolic terms. Top: Magnetic field, density, and velocity field across the shock (the black line denotes the analytical solution). Bottom: L1 error (in %) for each field. |
Configuration of the clusters used for the performance tests, and compilation options used to compile IDEFIX.
Single node performance and energy efficiency comparison on a variety of architectures.
6 Discussions and conclusions
In this paper, we present IDEFIX, a new performance-portable code for compressible magnetised fluid dynamics. The code follows a standard finite-volume high-order Godunov approach, where inter-cell fluxes are computed by dedicated Riemann solvers. For MHD problems, IDEFIX uses constraint transport to evolve the magnetic field components on cell faces, satisfying the solenoidal condition at machine precision. The code can handle Cartesian, polar, cylindrical, and spherical coordinate systems with variable grid spacing in every direction. It also features several time integrators including an explicit second- and third-order Runge–Kutta scheme and Runge–Kutta–Legendre super time-stepping for parabolic terms (viscosity, thermal, ambipolar, and ohmic diffusion). A conservative orbital-advection scheme (Fargo-type) is also implemented to accelerate the computation of rotation-dominated flows. The code is parallelized using domain decomposition and the MPI library. Finally, several additional physical modules are currently in development for IDEFIX, including a multigeometry self-gravity solver and a particle-in-cell module, which will be discussed in dedicated papers.
All features in IDEFIX are implemented in a performance-portable way, meaning that they are available for every target architecture supported by KOKKOS (CPU or GPU). In contrast to other codes where only a fraction of an algorithm is running on a GPU, the philosophy behind IDEFIX is that all data structures and loops live in device space, while the host system is only responsible for input and output operations. Benchmarks show that IDEFIX performs similarly to PLUTO and other similar Godunov codes on CPU architectures, with an efficiency of above 80% on up to 131 072 CPU cores. On GPU, the speed-up is significant (an AMD Mi250 node being 50 times faster than an Intel Cascade Lake CPU node), and the code is also significantly more energy efficient, that is, by up to a factor of about 6, comparing Intel Cascade Lake CPUs to AMD Mi 250 GPUs. However, these performances are only achievable for sufficiently large subdomains (typically more than 643), which is an intrinsic limitation of GPU architectures. Finally, IDEFIX reaches a peak performance of 3 × 1011 cell s−1 in MHD on AdAstra at Cines (1024 GPUs), with a parallelization efficiency of above 95%.
IDEFIX is not the only code that proposes performance portability. K-ATHENA (Grete et al. 2021) is similar to IDEFIX in terms of algorithm and also uses KOKKOS, but is limited to Cartesian and ideal-MHD problems. For these problems, the performances of IDEFIX and K-ATHENA are quantitatively similar, but IDEFIX allows the user to address more complex physics. PARTHENON (Grete et al. 2023) is a KOKKOS-based AMR framework on which several Godunov codes are being developed, including PKATHENA, which would be similar to IDEFIX. The performance of PARTHENON has only been reported for hydro problems, and is similar to that of IDEFIX. However, we note that PARTHENON provides an AMR framework that is not present in IDEFIX. It is not clear at this stage whether PARTHENON will support non-Cartesian geometry and all of the features present in IDEFIX in the future, but IDEFIX exhibits some clear advantages at the moment.
The current development of IDEFIX is tracked on a private git repository, from which a public version7 is forked. The public version is progressively enriched by new modules once they are published and is distributed under a CECILL license (French Open Source License). IDEFIX development is achieved in a collaborative way with modern versioning tools (git). The code master branches (public and private) are validated daily for CPU and GPU targets on a large number of tests (including the ones presented in this paper). Merge requests can be accepted only if the test pipeline fully succeeds, which helps preserve code quality and avoids regression. Finally, the online documentation is generated nightly from the code sources and is available from the code repositories (public and private). While IDEFIX was initially developed for our own needs in the ERC project “MHDiscs”, we believe that the code is now mature enough to be used more broadly and to benefit from external inputs.
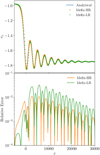 |
Fig. 15 Hall-dominated stationary shock at two different resolutions (the high-resolution test has twice the number of points as the low-resolution test). Top: normal velocity. The propagation of whistler waves in the pre-shock region (right state) is evident. Bottom: relative error between the numerical solution and the semi-analytical one. We observe a slightly lower convergence rate than second order in this case. |
 |
Fig. 16 Temporal evolution of the velocity components of the hydro Keplerian shearing wave problem of Balbus & Hawley (2006). The analytical solution is shown as a dashed line, while the IDEFIX solution computed with 2563 points is shown as a plain line. |
 |
Fig. 17 Temporal evolution of the velocity (top) and magnetic (bottom) components of the MHD Keplerian shearing wave problem of Balbus & Hawley (2006). The analytical solution is the dashed line, while the IDEFIX solution computed with 2563 points is shown as a plain line. |
 |
Fig. 18 Parallel efficiency (weak scaling) on AMD Rome CPUs (left), NVidia V100 GPUs (middle), and AMD Mi250 GPUs (right). The scaling of IDEFIX is above 80% efficiency on up to 131 072 CPU cores (1024 AMD Rome nodes) and reaches 95% on 1024 AMD Mi 250 GPUs (256 nodes). |
Acknowledgements
We wish to thank our referee, James Stone, for his valuable comments and suggestions that significantly improved the manuscript. We also thank Philipp Grete, Jeffrey Kelling, Rémi Lacroix, Thomas Padioleau and Simplice Donfack who mentored and helped us to improve IDEFIX during the 2021 hackathon organised by IDRIS and NVidia. Finally, we acknowledge the inspiring work of Pierre Kestener (CEA) on Kokkos-based Godunov methods. This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (Grant Agreement No. 815559 (MHDiscs)). This work was supported by the “Programme National de Physique Stellaire” (PNPS), “Programme National Soleil-Terre” (PNST), “Programme National de Hautes Energies” (PNHE) and “Programme National de Planétologie” (PNP) of CNRS/INSU co-funded by CEA and CNES. This work was granted access to the HPC resources of IDRIS and TGCC under the allocation 2022-A0120402231, and a grand challenge allocation at CINES made by GENCI. Some of the computations presented in this paper were performed using the GRICAD infrastructure (https://gricad.univ-grenoble-alpes.fr), which is supported by Grenoble research communities. Data analysis and visualisation in the paper were conducted using the scientific Python ecosystem, including numpy (Harris et al. 2020), scipy (Virtanen et al. 2020) and matplotlib (Hunter 2007).
References
- Balbus, S. A., & Hawley, J. F. 1991, ApJ, 376, 214 [Google Scholar]
- Balbus, S. A., & Hawley, J. F. 2006, ApJ, 652, 1020 [NASA ADS] [CrossRef] [Google Scholar]
- Balsara, D. S., & Spicer, D. S. 1999, J. Comput. Phys., 149, 270 [NASA ADS] [CrossRef] [Google Scholar]
- Beckers, J. M. 1992, SIAM J. Numer. Anal., 29, 701 [CrossRef] [Google Scholar]
- Benítez-Llambay, P., & Masset, F. S. 2016, ApJS, 223, 11 [Google Scholar]
- Brio, M., & Wu, C. C. 1988, J. Comput. Phys., 75, 400 [NASA ADS] [CrossRef] [Google Scholar]
- Burns, K. J., Vasil, G. M., Oishi, J. S., Lecoanet, D., & Brown, B. P. 2020, Phys. Rev. Res., 2, 023068 [NASA ADS] [CrossRef] [Google Scholar]
- Čada, M., & Torrilhon, M. 2009, J. Comput. Phys., 228, 4118 [Google Scholar]
- Cargo, P., & Gallice, G. 1997, J. Comput. Phys., 136, 446 [NASA ADS] [CrossRef] [Google Scholar]
- Childs, H., Brugger, E., Whitlock, B., et al. 2012, Visit: An End-User Tool For Visualizing and Analyzing Very Large Data [Google Scholar]
- Colella, P., & Sekora, M. D. 2008, J. Comput. Phys., 227, 7069 [NASA ADS] [CrossRef] [Google Scholar]
- Colella, P., & Woodward, P. R. 1984, J. Comput. Phys., 54, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Courant, R., Friedrichs, K., & Lewy, H. 1928, Math. Ann., 100, 32 [Google Scholar]
- Einfeldt, B., Roe, P. L., Munz, C. D., & Sjogreen, B. 1991, J. Comput. Phys., 92, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, C. R., & Hawley, J. F. 1988, ApJ, 332, 659 [Google Scholar]
- Falle, S. A. E. G. 2003, MNRAS, 344, 1210 [NASA ADS] [CrossRef] [Google Scholar]
- Fromang, S., Hennebelle, P., & Teyssier, R. 2006, A&A, 457, 371 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gardiner, T. A., & Stone, J. M. 2005, J. Comput. Phys., 205, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Gastine, T., & Wicht, J. 2012, Icarus, 219, 428 [Google Scholar]
- González-Morales, P. A., Khomenko, E., Downes, T. P., & de Vicente, A. 2018, A&A, 615, A67 [Google Scholar]
- Gottlieb, S., & Shu, C. W. 1998, Math. Comput., 67, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Grete, P., Glines, F. W., & O’Shea, B. W. 2021, IEEE Trans. Parallel Distrib. Syst., 32, 85 [CrossRef] [Google Scholar]
- Grete, P., Dolence, J. C., Miller, J. M., et al. 2023, Int. J. High Performance Comput. Applic., 0, 10943420221143775 [Google Scholar]
- Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Hawley, J. F., Gammie, C. F., & Balbus, S. A. 1995, ApJ, 440, 742 [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Lesur, G. R. J. 2021, J. Plasma Phys., 87 [Google Scholar]
- Lesur, G., & Longaretti, P.-Y. 2007, MNRAS, 378, 1471 [NASA ADS] [CrossRef] [Google Scholar]
- Lesur, G., Kunz, M. W., & Fromang, S. 2014, A&A, 566, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Londrillo, P., & del Zanna, L. 2004, J. Comput. Phys., 195, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Mac Low, M.-M., Norman, M. L., Konigl, A., & Wardle, M. 1995, ApJ, 442, 726 [NASA ADS] [CrossRef] [Google Scholar]
- Marchand, P., Tomida, K., Commerçon, B., & Chabrier, G. 2019, A&A, 631, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Masset, F. 2000, A&A, 141, 165 [NASA ADS] [Google Scholar]
- Meyer, C. D., Balsara, D. S., & Aslam, T. D. 2014, J. Comput. Phys., 257, 594 [NASA ADS] [CrossRef] [Google Scholar]
- Mignone, A., & Del Zanna, L. 2021, J. Comput. Phys., 424, 109748 [NASA ADS] [CrossRef] [Google Scholar]
- Mignone, A., Bodo, G., Massaglia, S., et al. 2007, ApJS, 170, 228 [Google Scholar]
- Mignone, A., Flock, M., Stute, M., Kolb, S. M., & Muscianisi, G. 2012, A&A, 545, A152 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miyoshi, T., & Kusano, K. 2005, J. Comput. Phys., 208, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Orszag, S. A., & Tang, C. M. 1979, J. Fluid Mech., 90, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Pencil Code Collaboration (Brandenburg, A., et al.) 2021, J. Open Source Softw., 6, 2807 [Google Scholar]
- Rusanov, V. 1962, USSR Comput. Math. Math. Phys., 1, 304 [CrossRef] [Google Scholar]
- Schroeder, W., Martin, K., & Lorensen, B. 2006, The Visualization Toolkit (Kitware) [Google Scholar]
- Sedov, L. I. 1946, J. Appl. Math. Mech., 10, 241 [Google Scholar]
- Sod, G. A. 1978, J. Comput. Phys., 27, 1 [CrossRef] [MathSciNet] [Google Scholar]
- Stone, J. M., & Norman, M. L. 1992, ApJS, 80, 753 [Google Scholar]
- Stone, J. M., Gardiner, T. A., Teuben, P., Hawley, J. F., & Simon, J. B. 2008, ApJS, 178, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Stone, J. M., Tomida, K., White, C. J., & Felker, K. G. 2020, ApJ, 249, 4 [NASA ADS] [Google Scholar]
- Taylor, G. 1950, Proc. Roy. Soc. Lond. A, 201, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Teyssier, R. 2002, A&A, 385, 337 [CrossRef] [EDP Sciences] [Google Scholar]
- Toro, E. F. 2009, Riemann Solvers and Numerical Methods for Fluid Dynamics (Berlin, Heidelberg: Springer) [CrossRef] [Google Scholar]
- Toro, E. F., Spruce, M., & Speares, W. 1994, Shock Waves, 4, 25 [Google Scholar]
- Trott, C. R., Lebrun-Grandié, D., Arndt, D., et al. 2022, IEEE Trans. Parallel Distrib. Syst., 33, 805 [CrossRef] [Google Scholar]
- Turk, M. J., Smith, B. D., Oishi, J. S., et al. 2011, ApJS, 192, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Vaidya, B., Prasad, D., Mignone, A., Sharma, P., & Rickler, L. 2017, MNRAS, 472, 3147 [NASA ADS] [CrossRef] [Google Scholar]
- Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Methods, 17, 261 [Google Scholar]
- Wicht, J. 2002, Phys. Earth Planet. Interiors, 132, 281 [CrossRef] [Google Scholar]
- Zhu, Z., & Stone, J. M. 2018, ApJ, 857, 34 [Google Scholar]
- Ziegler, U. 2008, Comput. Phys. Commun., 179, 227 [NASA ADS] [CrossRef] [Google Scholar]
Note however that the code is still at most globally second order, see Sect. 4.2.
Visualization Tool Kit (Schroeder et al. 2006).
We note that there is a typo in the last term of Eq. (50a) in González-Morales et al. (2018), which should read υzBy instead of υzBx.
All Tables
Left and right states for the Hall-dominated shock tube (González-Morales et al. 2018).
Configuration of the clusters used for the performance tests, and compilation options used to compile IDEFIX.
Single node performance and energy efficiency comparison on a variety of architectures.
All Figures
 |
Fig. 1 Schematics of the integration algorithm in IDEFIX. |
| In the text | |
 |
Fig. 2 Adiabatic hydrodynamical Sod (1978) shock test, at t = 0.2. Orange crosses: IDEFIX solution computed using the Roe solver with 500 points. Blue plain line: Analytical solution. |
| In the text | |
 |
Fig. 3 Double Mach reflection test computed at t = 0.2. Here, we represent the resulting density map for various combinations of algorithms with a 1920 × 480 resolution. |
| In the text | |
 |
Fig. 4 Sedov-Taylor blast wave in Cartesian geometry at t = 0.1. Left panel: slice of the pressure field through z = 0. Right panel: pressure distribution as a function of the distance from the blast center. The inset shows a zoom onto the blast shock region. |
| In the text | |
 |
Fig. 5 Sedov–Taylor blast wave in spherical geometry at t = 0.1. The blast is initialized slightly off the polar axis (at x = 0.1, z = 1). Left panel: slice of the pressure field through y = 0. The dashed white line represents the polar axis of the domain, which is regularized automatically by IDEFIX. Right panel: pressure distribution as a function of the distance from the blast center. The inset shows a zoom around the blast shock region. |
| In the text | |
 |
Fig. 6 Brio & Wu (1988) adiabatic MHD shock test. IDEFIX solution (orange cross) was computed using the Roe solver with 500 points and linear reconstruction while the reference solution (blue line) was computed with Pluto 4.3 using 8000 points. |
| In the text | |
 |
Fig. 7 Convergence rate of the four linear wave types in adiabatic MHD for various Riemann solvers using linear reconstruction. The code exhibits second-order spatial convergence, as expected. |
| In the text | |
 |
Fig. 8 Convergence rate of the four linear wave types for various reconstruction techniques using the HLLD Riemann solver. The code exhibits a slightly higher convergence rate than second order for LimO3. However, we highlight the lack of convergence at high resolution for PPM, which is also observed in ATHENA++ (dashed lines). |
| In the text | |
 |
Fig. 9 Magnetic rotor test from Balsara & Spicer (1999), on the left using a Cartesian geometry and on the right using a polar geometry. We note the close resemblance of the iso-surfaces, indicating the excellent behaviour of the code in these two geometries. |
| In the text | |
 |
Fig. 10 Orszag Tang vortex pressure distribution at t = 0.5 with different combinations of algorithms computed with 1282 points, except for the bottom-right plot, which is computed with 10242 points. |
| In the text | |
 |
Fig. 11 Cut in the Orszag Tang vortex at y = 0.316 (top) and y = 0.425 (bottom) for selected algorithms from Fig. 10. Solutions were computed with 1282 points, while the reference was computed with 10242 points. |
| In the text | |
 |
Fig. 12 Planet–disk interaction problem with orbital advection enabled at t = 4 planetary orbits. Comparison between FARGO3D and IDEFIX for the density deviation map in the planet–disk interaction problem with orbital advection enabled at t = 4 planetary orbits. We note the presence of small wave-like patterns in FARGO3D that are absent from IDEFIX. |
| In the text | |
 |
Fig. 13 Planet–disk interaction problem with orbital advection enabled at t = 4 planetary orbits. Comparison between FARGO3D and IDEFIX of the radial velocity υR at R = 0.7 (plain line) and R = 1.3 (dashed line). |
| In the text | |
 |
Fig. 14 Ambipolar isothermal C-shock integrated at high resolution (HR, 2 points/L) and low resolution (LR, 1 point/L) and using the explicit or RKL second-order time integrators for parabolic terms. Top: Magnetic field, density, and velocity field across the shock (the black line denotes the analytical solution). Bottom: L1 error (in %) for each field. |
| In the text | |
 |
Fig. 15 Hall-dominated stationary shock at two different resolutions (the high-resolution test has twice the number of points as the low-resolution test). Top: normal velocity. The propagation of whistler waves in the pre-shock region (right state) is evident. Bottom: relative error between the numerical solution and the semi-analytical one. We observe a slightly lower convergence rate than second order in this case. |
| In the text | |
 |
Fig. 16 Temporal evolution of the velocity components of the hydro Keplerian shearing wave problem of Balbus & Hawley (2006). The analytical solution is shown as a dashed line, while the IDEFIX solution computed with 2563 points is shown as a plain line. |
| In the text | |
 |
Fig. 17 Temporal evolution of the velocity (top) and magnetic (bottom) components of the MHD Keplerian shearing wave problem of Balbus & Hawley (2006). The analytical solution is the dashed line, while the IDEFIX solution computed with 2563 points is shown as a plain line. |
| In the text | |
 |
Fig. 18 Parallel efficiency (weak scaling) on AMD Rome CPUs (left), NVidia V100 GPUs (middle), and AMD Mi250 GPUs (right). The scaling of IDEFIX is above 80% efficiency on up to 131 072 CPU cores (1024 AMD Rome nodes) and reaches 95% on 1024 AMD Mi 250 GPUs (256 nodes). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


