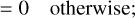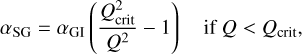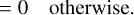| Issue |
A&A
Volume 676, August 2023
|
|
|---|---|---|
| Article Number | A124 | |
| Number of page(s) | 16 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202245757 | |
| Published online | 21 August 2023 | |
FU Orionis disk outburst: Evidence for a gravitational instability scenario triggered in a magnetically dead zone★
1
Max Planck Institute for Extraterrestrial Physics,
Giessenbachstr.1,
85748
Garching,
Germany
e-mail: bourdarot@mpe.mpg.de
2
Univ. Grenoble Alpes, CNRS, IPAG,
38000
Grenoble,
France
3
Univ. Grenoble Alpes, LIPHY,
38000
Grenoble,
France
4
Giant Magellan Telescope Organization,
465 N. Halstead St.,
Pasadena,
CA 91107,
USA
5
School of Physics, University College Dublin,
Belfield,
Dublin 4,
Ireland
6
Max-Planck-Institut für Astronomie,
Königstuhl 17,
69117
Heidelberg,
Germany
7
Department of Astronomy, University of Michigan,
Ann Arbor,
MI 48109,
USA
8
European Southern Observatory,
Casilla
19001,
Santiago 19,
Chile
9
University of Exeter, School of Physics and Astronomy, Astrophysics Group,
Stocker Road,
Exeter
EX4 4QL,
UK
10
I. Physikalisches Institut, Universität zu Köln,
Zülpicher Str. 77,
50937
Köln,
Germany
11
The University of North Carolina at Greensboro,
USA
Received:
21
December
2022
Accepted:
7
April
2023
Context. FUors outbursts are a crucial stage of accretion in young stars. However, a complete mechanism at the origin of the outburst still remains missing.
Aims. We aim to constrain the instability mechanism in the star FU Orionis itself by directly probing the size and evolution in time of the outburst region with near-infrared (NIR) interferometry, and to confront it with physical models of this region.
Methods. As the prototype of the FUors class of objects, FU Orionis has been a regular target of NIR interferometry. In this paper, we analyze more than 20 years of NIR interferometric observations to perform a temporal monitoring of the region of the outburst, and compare it to the spatial structure deduced from 1D magneto-hydrodynamic (MHD) simulations.
Results. We measure from the interferometric observations that the size variation of the outburst region is compatible with a constant or slightly decreasing size over time: -0.56-0.36+0.14 AU/100 yr and -0.30-0.19+0.19 AU/100 yr in the H and K bands, respectively. The temporal variation and the mean size probed by NIR interferometry are consistently reproduced by our 1D MHD simulations. We find that the most compatible scenario is a model of an outburst occurring in a magnetically layered disk, where a magneto-rotational instability (MRI) is triggered by a gravitational instability (GI) at the outer edge of a dead zone. The scenario of a pure thermal instability (TI) fails to reproduce our interferometric sizes because it can only be sustained in a very compact zone of the disk <0.1 AU. The comparison between the data and the MRI-GI models favors MHD parameters of αMRI = 10−2, TMRI = 800 K, and Σcrit = 10 g cm−2, with more work needed in terms of observations and modeling in order to improve the precision of these values. Locally, in the very inner part of the disk, TI can be triggered in addition to MRI-GI, which qualitatively better matches our observation but is not strongly constrained by the currently available data. The scenario of MRI-GI could be compatible with an external perturbation that enhances the GI, such as tidal interaction with a stellar companion, or a planet at the outer edge of the dead zone.
Conclusions. We favor a layered-disk model driven by MRI turbulence in order to explain the spatial structure and temporal evolution of the outburst region on FU Orionis. Understanding this phase will provide a crucial link between the early phase of disk evolution and the process of planet formation in the first inner astronomical units.
Key words: accretion, accretion disks / techniques: interferometric / protoplanetary disks / stars: variables: T Tauri, Herbig Ae/Be
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model.
Open Access funding provided by Max Planck Society.
1 Introduction
Young stellar objects (YSOs) are surrounded by circumstellar disks from which they accrete matter in their early phase of evolution. In the case of low-mass YSOs (M < 3 M⊙, T Tauri stars), it is now clear that, rather than being a steady process, accretion occurs through episodic events (Calvet et al. 2000), as the steady accretion rate deduced from observations of T Tauri is not sufficient to build up a star over timescales of a few million years (Kenyon & Hartmann 1990). Two families of YSOs gather such episodic events: EXor and FUor classes, the archetypical object of the latter being the star FU Orionis. The main characteristic of FUors is that they display a 4–6 mag luminosity outburst at visible wavelengths over short timescales, from a few months to a few years, followed by a decay in luminosity that lasts from several decades to hundreds of years (Herbig 1977). A large fraction of stars may therefore go through the FUor or EXor stage, and may do this several times during their early existence.
The first comprehensive view of the FUor stage of evolution was provided by Hartmann & Kenyon (1996), who explained this phenomenon as an accretion disk experiencing a massive instability episode, leading to a huge increase in accretion rate, from 10−7 M⊙ yr−1 to 10−4 M⊙ yr−1, and therefore a burst of luminosity. Spectroscopic observations show the presence of an infrared (IR) excess in the spectral energy distribution (SED) and of rotationally broadened absorption lines in FUors, providing convincing evidence in favor of a self-luminous accretion disk in rotation around the star.
Nevertheless, the exact instability mechanism at the origin of the outburst remains poorly understood, and several classes of solution are generally invoked (Audard et al. 2014). Thermal instability (TI, Bell & Lin 1994), in which the outburst is triggered by a thermal runaway of the disk as its temperature reaches ionized hydrogen temperature, was the first mechanism proposed (Bell & Lin 1994; Hartmann & Kenyon 1996), with discussions on the origin of the trigger of the instability, including external perturbation by an stellar companion (Bonnell & Bastien 1992) and internal perturbation by the presence of a planet (Lodato & Clarke 2004). The second possible mechanism is a limit cycle driven by the activation of the magneto-rotational instability (MRI; Balbus & Hawley 1998) when the ionization fraction becomes sufficient (Gammie 1996). The MRI scenario is known to affect larger disk regions because it starts at lower temperatures than TIs. However, MRI usually requires an external trigger, which is often assumed to be the gravitational instability (GI, Armitage et al. 2001), which starts when enough material has accumulated in the outer disk. This scenario in particular was confronted with observational data (SED) by Zhu et al. (2007, 2009), who found their results to favor this model. The last main scenario for the instability is disk fragmentation (Vorobyov & Basu 2005; Dong et al. 2016), in which large fragments migrate inwards as the deeply embedded disk becomes gravitationally unstable.
FUOrs outbursts are therefore intimately related to the process driving accretion in the disk. In that respect, they are particularly important manifestations for our understanding of the mechanisms at the origin of accretion and turbulence in this early phase of protoplanetary disks, and for characterizing the physical properties and structure of the disk. These reasons strongly motivate our search for a comprehensive understanding of the origin of the FU Orionis instability mechanism.
In the present study, we focus on the star FU Orionis itself (d = 407 pc (Gaia Collaboration 2021). The only technique able to spatially resolve the inner astronomical units (AU) of FU Orionis, where the outburst takes place, is near-infrared (NIR) interferometry. As a relatively bright object in the NIR, FU Orionis has been a prime target of interferometry, and was the first YSO to be spatially resolved (Malbet et al. 1998), which provided direct evidence of the presence of an accretion disk. The findings of this initial study were then confirmed and refined by Malbet et al. (2005), who provided a first estimation of the temperature profile of the disk, and explored the potential detection of an embedded hot spot. This estimation was recently complemented by Labdon et al. (2021) based in particular on J-band interferometric data obtained on CHARA/MIRC-X, which were used to confirm the T ∝ r−3/4 temperature profile of the accretion disk. In addition, the presence of an extended halo as a general feature of FUors in interferometric data, corresponding to the remnant of the infalling envelope, was first identified by Millan-Gabet et al. (2006) on a sample of three FUors. The properties of the dusty envelope of FU Orionis itself were examined in the mid-infrared (MIR) by Quanz et al. (2006), and more recently by Liu et al. (2019), through ALMA and GRAVITY data, with both studies inferring the presence of a cold envelope.
In this paper, we propose to take advantage of the unique temporal coverage accessible with 20 years of archival NIR interferometry, complemented with dedicated VLTI/PIONIER (ESO run ID 2102.C-5036(A) and VLTI/GRAVITY observations, in order to perform a temporal monitoring of the outbursting region of FU Orionis. The primary goal of this work is to put constraints on the typical size and variation of the outbursting region over time and to confront this evolution with the spatial structure deduced from a 1D magneto-hydrodynamic simulation in order to identify the mechanism at play in FU Orionis and potentially add preliminary constraints on its physical parameters. Section 2 describes the data set used in our study. The global geometrical modeling of FU Orionis and the methodology used to analyze our data sample and give a robust estimate of the quality and error bars are presented in Sect. 3. The results of this analysis are presented in Sect. 4. Section 5 provides a comparison of these results with the output of the MHD simulation and discusses the implications of our findings for the instability mechanism at play in this star.
2 Observations
We based our analysis on dedicated observations performed with PIONIER and GRAVITY instruments at VLTI obtained in February 2019 (ESO run 2102.C-5036, PI: G. Bourdarot) and January 2021 (ESO GTO run 106.212G.004) respectively, and on archival data available for these instruments. In addition, we benefited from the broad archive of observations in the H and K bands carried out from 1998 to 2005 and initially published in Malbet et al. (2005). These data are complemented with CHARA observations published in Labdon et al. (2021), acquired with CLIMB instruments in K band and MIRC-X data in H band. Given the heterogeneity of the dataset, we place specific emphasis on the examination of the data quality in order to identify potential sources of bias for each observation. The different pieces of information relative to the data and the acronyms by which we refer to them in the following are provided in Table 1. In the following, we give a description of the different instruments, data sets, and reduction tools used to homogeneously process our data.
2.1 Interferometric archival data
The most distant data in our data set originate from the legacy study of Malbet et al. (2005). This data set is essentially based on observations with the interferometers IOTA (Traub 1998) and PTI (Colavita et al. 1999). These instruments consist in two-telescope beam combiners with low spectral resolution in H and K bands. IOTA and PTI observations cover complementary spatial scales (respectively small baselines of ~30m and large baselines of ~120m). These observations were initially gathered as a unique temporal point in the original study of Malbet et al. (2005) in order to obtain the most complete coverage of the (u,υ) plane. In the present study, we have chosen to temporally separate the PTI observations for each year, and to gather them with IOTA data of the closest year, when available, in order to benefit simultaneously from constraints on small and high spatial scales. Given the specific format of these observations, the reduced data included in this analysis were provided by Regis Lachaume (pri. comm.).
In addition to IOTA and PTI observations, we include CHARA/CLIMB observations from three telescopes (PI: R. Millan-Gabet) conducted on two nights on 29 Nov. 2010 and 27 Oct. 2011, and initially published in Labdon et al. (2021). Due to the larger number of telescopes and the larger baselines, these observations offer a more complete sampling of the (u, υ) plane in a single observation. In the case of CLIMB10 data, a large dispersion can be seen in the visibility data, as well as a significant discrepancy at high spatial scales (low visibilities) for the same baselines with respect to CLIMB11 data. We keep CLIMB10 and CLIMB11 in our sample in the following as they enable us to constrain the disk around year 2010 in the K band; however, greater weight is given to CLIMB11 data in our analysis given the lower dispersion in visibility data. These observations were reduced using J.D. Monnier’s pipeline at the University of Michigan.
Finally, we also include two CHARA/MIRCX observations made with six telescopes conducted on 27 Nov. 2018 and 3 Oct. 2019, and initially published in Labdon et al. (2021). These data were reduced using the MIRC-X standard reduction pipeline1.
Logs of FU Orionis interferometric observations in H and K bands.
2.2 New data reduction on archival data
We also include additional archival data in our analysis, with which it was possible to perform a full new data reduction. In the H band, we include two PIONIER observations. PION10 originates from commissioning observations retrieved from the oidb service of the Jean-Marie Mariotti Center (JMMC)2. PIONIER 2017 data were retrieved from the publicly available ESO archive3 (ESO run ID 0100.C-0278(J)). We reduced both datasets using the standard pndгs pipeline (Le Bouquin et al. 2011). PION10 shows a relatively large dispersion, but visibility values consistent with other short-baseline observations such as IOTA. On the contrary, PION17 data are characterized by relatively low data dispersion and small error bars, and with significantly higher visibility values than similar observations on the Auxiliary Telescopes (ATs) with PIONIER. A careful inspection of the calibrators did not reveal anomalies in the calibration procedure. However, intermediate products of the data reduction highlight strong phase variations in this data set, which are likely to bias the visibility of the fringes. These variations could originate from a dome-seeing effect, which would explain such degradation in very good atmospheric conditions. In the following, we include the PION17 data set but we caution that these data may be biased.
In the K band, three additional archival data sets are included. We reduced VINCI observation originally included in Malbet et al. (2005) using the standard vndгs pipeline (Kervella et al. 2004). VINCI data were obtained on the Unitary Telescopes (UTs), for which the interferometric field of view is smaller than the ATs given the larger telescope diameter. The extended flux in this data set is therefore lower than the other data. We also reduced two GRAVITY datasets on the ATs. For both observations we used the fringe-tracker (FT) channel rather than the scientific (SCI) channel of GRAVITY. In the case of GRAVI17, we used the FT data only because of the insufficient signal-to-noise ratio (S/N) in the SCI channel in high-resolution mode (R ≈ 4000). Concerning GRAVI16, careful inspection of the intermediate products of data reduction reveals discrete phase fluctuations of the fringe tracker away from the zero optical path difference (OPD) reference. This perturbation potentially impacts the chromatic dependency seen in the visibilities: this point is discussed in more detail in Sect. 4.2.
Geometrical model used to fit FU Orionis visibility.
2.3 Dedicated interferometric observing programs
In order to add two contemporary reference observations in H and K bands, respectively, we performed two dedicated observations of FU Orionis with the PIONIER and GRAVITY instruments on VLTI. The PIONIER observation was obtained through a specific Director’s Discretionary Time (DDT) Proposals awarded in winter 2019 (PI/Bourdarot), which was conducted on the night of 20 Feb 2019 (ESO run 2102.C-5036). A PIONIER observation with the large configuration on the 1.8m ATs was specifically chosen in order to reach the highest angular resolution and to obtain the most complete (u, υ)-coverage on VLTI. Data were reduced using the standard pndrs pipeline (Le Bouquin et al. 2011) and exhibit good atmospheric conditions and low statistical dispersion. GRAVITY observations on unitary telescopes (UTs) were obtained during GRAVITY-GTO time (ESO run 106.212G.004) on the 8.2 m UTs and were reduced with the standard ESO pipeline, but these data only include three telescopes because of a technical problem on UT2 during that night.
2.4 Spectral energy distribution
In order to complement our analysis, we also provide a recent SED of FU Orionis using Gaia Data Releases 2 and 3 (DR2 and DR3), and TESS photometric data. The data originate from a limited time range (2015–2019) in order to avoid potential temporal variation.
3 Methodology
In this section, we describe our geometrical modeling of FU Orionis and the fitting strategy used for our temporal analysis. The final goal of this analysis is an estimation of the full width at half-maximum (FWHM) size of the outburst in time, together with a reliable estimation of the statistical and systematics errors in the data through bootstrap analysis.
3.1 Geometrical modeling of FU Orionis
In order to introduce our geometrical modeling of FU Orionis, we present one observation that exhibits the archetypal features of our sample. Three main components can be identified in the visibility, which we designate the inner disk (partially resolved), the central unresolved component, and the over-resolved structure. These components describe the general structure of FUors objects, as shown in Fig. 1. This model is also consistent with the common picture from NIR interferometric observations in Herbig Ae/Be stars (Lazareff et al. 2017; GRAVITY Collaboration 2019).
 |
Fig. 1 Visibility squared versus projected baseline of observations with the MIRCX instrument in H band in 2019 (see logs of Table 1). The red dashed line shows the minor and major axis of the Gaussian inner disk, while the black solid lines and black arrows show the contribution of the compact flux fc and of the over-resolved flux fe. |
3.1.1 Inner disk
The inner disk visible on the interferometric observations is a regularly decreasing visibility profile, the extent of which is inversely proportional to the typical size of the emission zone. This component is marginally resolved on spatial frequencies 45Mλ ≡ 100 m in K band, and we therefore model it as a Gaussian elongated disk Vd(α,β), with a being the FWHM of the Gaussian, θ the position angle of the disk, and i the inclination angle of the disk (cf. Table 2). In the geometrical model, this component is designated the resolved emission. In FU Orionis, this resolved component is associated with the inner disk surrounding FU Orionis that constitutes the brightest component of the object, where the instability at the origin of the outburst takes place. In this respect, the primary goal of the present study is to constrain the size of this emitting region as a function of time.
3.1.2 Extended structure
FU Orionis is embedded in a large source of extended emission (Millan-Gabet et al. 2006), also visible on high-contrast images at very large spatial scales (Takami et al. 2018). This emission corresponds to the large infalling envelope that feeds the disk in the classical picture of FUors (Hartmann & Kenyon 1996). In the case of interferometric observations, this extended flux fills the whole interferometric field of view, and its extension corresponds typically to the diffraction limit of one telescope, of the order of 250 mas ≡ 100 AU for an AT in H band. Finally, in the visibility space, the extended component corresponds to an object of low spatial frequency, which is fully resolved in our observations and is modeled as a dirac function with a certain amplitude, fe, centered on zero spatial frequency. In Fig. 1, this component indeed appears as an apparent offset between the maximum of the resolved visibility and the V2 = 1 visibility at null spatial frequency. Given the apparent spectral dependency visible in GRAVITY data, which was first reported by Liu et al. (2019), a polynomial dependency in wavelength is allowed for this over-resolved component (second-order polynomial), with coefficients (ƒ0,ƒ1,ƒ2).
3.1.3 Central unresolved component
The inner disk is marginally resolved on baselines of shorter than 100 m (spatial frequencies of 40 Mλ), and is resolved in H band with 300 m baselines (spatial frequencies of 180 Mλ), as shown on MIRC-X observations (see Fig. 1) in the H band, and CLIMB observations in the K-band. For the largest spatial frequencies, this resolved component leaves an unresolved component, which appears as a “floor” of visibility at high angular frequencies. This unresolved component corresponds to compact emission in the inner part of the disk, which is not resolved at the resolution of our NIR interferometric data, and is therefore encircled in <0.1 AU of the disk. In the following, we model this floor as a pure unresolved component in our geometrical model, that is, a constant in visibility ƒc (see Table 2).
Finally, the total visibility is written as the sum of the three individual components, normalized to 1:
The interferometric data considered in the following consist in the modulus squared of Eq. (1).
3.2 Fitting strategy
A major limiting factor of this study is the large heterogeneity of the dataset, and in some cases the sparsity of the uv-coverage of the oldest data also poses a problem (IOTA, PTI). These constraints call for a specific fitting strategy. We first present the global methodology used in this study to fit the interferometric data. We then provide details of this procedure for each particular data set in H and K bands. We used a Levenberg–Marquardt minimization over all steps to fit the model to the interferometric data.
Our fitting strategy is composed of three steps:
Initialization: We start the fitting by the observations that present the most complete (u, υ) coverage and the best data uncertainty at medium spectral resolution (R > 50), for which we fit all parameters for each observation independently. These observations are chosen among the second-generation instruments (PIONIER and MIRCX in H band, GRAVITY in K band). We then choose the observation that provides us with the estimate that is most robust to statistical errors (dispersion) and systematic errors (e.g., bi-modal distribution) in the H and K bands. The parameters of this observation are used as a reference set of parameters in Step 2 for the other, less complete observations.
Fit of the fixed observations: In the case of the oldest instruments, the complete set of parameters of the visibility model will be poorly constrained because of the limited number of visibility points in the (u, υ)-plane and the parameter degeneracy. On the other hand, several parameters of the model are considered constant over time: the position and inclination angles (θ and i), the spectral variation of the envelope (ƒ0, ƒ1, ƒ2), and the flux of the central unresolved component (ƒc). These parameters are fixed on the reference observations during the fit, and only a is left as a free parameter.
Error estimation: The error on the estimation of each parameter is then estimated using the bootstrap method (Efron 1982; Kervella et al. 2004; Lachaume et al. 2019). For each observation, we do a random sampling with replacement of the visibilities, with the total length of the output sample being equal to the number of visibilities available in the original observation. We then apply the fit to these points in the same order as described in Step 1 and Step 2. The fitted parameters are then registered, and the whole procedure (Steps 1 and 2) is repeated from the start over a large number of trials (typically 1000). The final parameters are estimated with the median value of the samples, and the 1σ upper and lower bars with the 84% and 16% percentiles of the distribution. This method also enables us to reconstruct the probability distribution of our fitted parameters and to evaluate their error bars without any assumptions as to their properties. In addition, it is possible to identify potential bimodal or multimodal results from the output probability distribution; these can be used to trace potential biases or local minima in our parameter estimation.
The list of the reference and fixed observations, as well as the different parameters fitted for each observation, are given in Table B.1. The peculiarities of the fit for each spectral band are described in detail in the following subsection.
3.2.1 Fit of the H band data set
All the parameters of the model are fitted in MIRCX19, PION19, MIRCX18, and PION17 (Step 1), considering the (u, υ) coverage and the spectral resolution available with this dataset. A bimodal distribution can be seen at the output of MIRCX19 bootstrap (Fig. A.1), which may originate from an issue with the calibrator, and so we preferred to select MIRCX18 as a reference for the value of ƒc ;nevertheless, the values of ƒc obtained with MIRCX19 and MIRCX18 are consistent with one another other. Given their limited baselines, PIONIER observations do not provide a reliable estimate the contribution of the unresolved component shown in Fig. 1, and so we fixed the ƒc parameter in PION19 and PION17 using MIRCX18. PION17 was tested with both independent and fixed parameters, but in both cases this fit does not enable us to obtain a reliable size estimation for reasons explained in Sect. 2. PION10, PTI00, and IOTA+PTI exhibit a sparse (u, υ) coverage, and so we fixed their parameters based on a reference observation (Step 2). Because of the lack of small baselines, the contribution of the extended envelope in PION10 and PTI00 was fixed based on PION19, and only the size a was fitted for these two observations. IOTA observations conducted in 1998 and PTI observations conducted in 1999 (Table 1) were combined in the same point IOTA+PTI, as they enable us to constrain both small and intermediate baselines, respectively, at the price of a relatively low decrease in time resolution, which enables us to provide independent estimations of a and ƒc. The results of the bootstrap (Step 3) are shown in Fig. A.1.
3.2.2 Fit of the K band data set
In the K band, GRAVITY and CLIMB data provide independent fits of each of the parameters of our model. The compact component is probed using CLIMB data but is less constrained compared to our constraint based on H band MIRC-X data because of the larger error bars and the smaller number of visibility points (smaller number of spectral channels and smaller number of baselines). For GRAVI21, GRAVI17, and GRAVI16, fc is not well constrained because of the shorter baselines compared to CHARA, and so we fixed this value to the that fitted with CLIMB (fc = 0.30). The parameters of PTI observations were fixed on GRAVI17, given the sparsity of these datasets, except a was left as a free parameter. GRAVI17 was preferred over GRAVI16 given the fringe-tracking issue in this latter observation (Sect. 2), and over GRAVI21 given that the field of view of the ATs are closer to the field of view of PTI and IOTA observations. For the same reason, GRAVI21 was chosen as a reference for VINCI data, which were obtained on the UTs. In a similar fashion to our treatment of data in H band, the IOTA and PTI observations conducted in 1998 were combined into a single point, which allows us to provide an estimation of both a and fe. The results of the bootstrap analysis are also shown in Fig. A.2.
 |
Fig. 2 Variation in time of the estimated FWHM of the outburst in FU Orionis in H band (left) and K band (right). The temporal slope is evaluated from a bootstrap analysis: each trial of the bootstrap is shown as a transparent solid line; the final result is the median of all trials, shown as a dashed line. |
4 Results
In this section, we present our estimation of the parameters through temporal fitting, and evaluate the range of validity of these results. The complete output of the fit is shown in Figs. A.1 and A.2.
4.1 Size estimate of the inner zone
The size a of the resolved emission as a function of time is shown in Fig. 2. On average, the mean size a over all the observations is 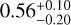 mas in the H band and
mas in the H band and 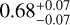 mas in the K band, which is consistent with previous estimates based on comparable models (Labdon et al. 2021). These measurements translate to
mas in the K band, which is consistent with previous estimates based on comparable models (Labdon et al. 2021). These measurements translate to 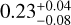 AU in the H band and
AU in the H band and 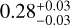 AU in the K band (Table 3), assuming a distance of d = 407 pc (Gaia Collaboration 2021).
AU in the K band (Table 3), assuming a distance of d = 407 pc (Gaia Collaboration 2021).
The error bars and the validity of each individual data point can be inspected through the output of the bootstrap in Figs. A.1 and A.2. The output of the bootstrap follows a Gaussian distribution in both H and K band overall, but this not the case for MIRCX19 and PION17 because of the above-mentioned observational biases. In the following, we discard PION17, given that this size estimate is clearly inconsistent with the rest of the sample and that an observational bias is identified for this point. From Fig. 2, the size estimate from the oldest data points in the early 2000s differs significantly from that deduced from the most recent points, in particular in K band. On the other hand, the error bars of IOTA and PTI points tend to be underestimated by the bootstrap analysis, given that only two parameters are fitted.
From this set of FWHM sizes, we estimate the temporal slope in H and K bands. The temporal slopes resulting from the bootstrap are respectively 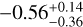 AU/100yr and
AU/100yr and 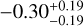 AU/100yr in H and K band (Table 3). These two values are consistent with a slowly decreasing or constant size over time. In addition, the temporal variations are consistent with each other to within 1σ. In H and K bands, the mean temporal slope is mostly constrained by the points with the smallest uncertainty, that is, MIRC-X and GRAVITY, respectively. Although the uncertainties on the first points in the 2000s are large, they contribute to the drawing of the uncertainty contours of the temporal estimate, and are important because they allow us to cover a large time span and to set upper and lower bounds on the size variation of the resolved emission. Finally, the overall consistency of this temporal slope with the mean estimate of a can be evaluated by comparing the points lying in the 1σ and 3σ estimate of the temporal slope in Fig. 2. In K band, the IOTA+PTI point lies outside the 3σ region, but might be affected by several factors, such as the estimation of the extended flux by combining IOTA and PTI data, or the large error in these data sets.
AU/100yr in H and K band (Table 3). These two values are consistent with a slowly decreasing or constant size over time. In addition, the temporal variations are consistent with each other to within 1σ. In H and K bands, the mean temporal slope is mostly constrained by the points with the smallest uncertainty, that is, MIRC-X and GRAVITY, respectively. Although the uncertainties on the first points in the 2000s are large, they contribute to the drawing of the uncertainty contours of the temporal estimate, and are important because they allow us to cover a large time span and to set upper and lower bounds on the size variation of the resolved emission. Finally, the overall consistency of this temporal slope with the mean estimate of a can be evaluated by comparing the points lying in the 1σ and 3σ estimate of the temporal slope in Fig. 2. In K band, the IOTA+PTI point lies outside the 3σ region, but might be affected by several factors, such as the estimation of the extended flux by combining IOTA and PTI data, or the large error in these data sets.
Estimation of the size and the temporal slope of the resolved emission.
4.2 Spectral variation and temperature of the extended envelope
The over-resolved component was first systematically revealed by Millan-Gabet et al. (2006) as a general feature of FUors observed with single-mode NIR interferometry. This feature is the signature of strong extended flux covering the interferometric field of view, in which FUors are still deeply embedded, and which is also clearly visible in AO images. The fit in the K band highlights a spectral dependency of the extended envelope on the GRAVI16 high-resolution data, as reported by Liu et al. (2019), who analyzed the same GRAVITY dataset. A certain amount of uncertainty remained in this dataset because strong OPD shifts could be seen in these observations, which could mimick this spectral dependency. We therefore also analyzed GRAVI21 and observed again this spectral dependency in the data, with a total extended flux contribution of smaller than that of GRAVI16. This smaller number is expected because the field of view of the UTs is smaller than that of the ATs by a factor 20 in surface, which matches the value fitted. This latter spectral dependency is shown in Fig. C.1. In addition, in the H band, we do not detect any significant chromatic effect of the envelope in MIRCX data (R = 50), which therefore tends to indicate a significantly red component.
Using both the nondetection in the H band and the spectral slope in the K band, we fitted a black body to the spectrum of the envelope, which by definition is the total spectrum multiplied by the proportion of the extended flux ƒe(λ). We fitted the spectrum of the envelop in GRAVI16 and GRAVI21 independently in order to quantify the error on this estimate. We obtain temperatures of TGRAVI16 = 580 K and TGRAVI21 = 280 K, respectively. This discrepancy can be attributed to (i) the fact that these two observations probe significantly different fields of view, and (ii) the accuracy with which we estimate the slope of this component in the fit process. We keep an approximate value of 300K-500K as an indication of the temperature of the envelope (Fig. 3). This observation could be compared with interferometric observations in the MIR in order to refine this estimation of the temperature of the halo (Lykou et al. 2022).
4.3 Unresolved flux
The unresolved flux of the disk is better estimated in the CHARA/MIRC-X H-band observations. The mean unresolved flux for these observations is 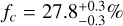 and
and 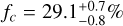 in the H band, respectively. This compact unresolved component therefore represents a significant proportion of the total flux: ~30%. All this flux should be encircled within a radius smaller than ~0.1 AU (i.e., within the inner disk) according to the maximum spatial frequency measured in the MIRC-X observation. This component could naturally arise from a power-law temperature profile, which we discuss in Sect. 5.2.
in the H band, respectively. This compact unresolved component therefore represents a significant proportion of the total flux: ~30%. All this flux should be encircled within a radius smaller than ~0.1 AU (i.e., within the inner disk) according to the maximum spatial frequency measured in the MIRC-X observation. This component could naturally arise from a power-law temperature profile, which we discuss in Sect. 5.2.
5 Discussion
In this section, we compare our interferometric observations to the outburst models of FUors. Two main models were put forward in the case of FU Orionis (Hartmann & Kenyon 1996; Hirose 2015): an outburst driven by TI (Bell & Lin 1994), and an outburst driven by MRI triggered by GI (MRI+GI) in a magnetically layered disk model (Armitage et al. 2001).
5.1 Thermal instability model
The first instability model proposed for FUors is an outburst driven by TI (Bell & Lin 1994): in this model, the outburst is triggered as the disk temperature increases up to the point where hydrogen is ionized, creating an abrupt change of opacity, which traps the thermal energy generated by the viscous disk and results in a thermal runaway of the disk. Once the matter has been accreted onto the star, the disk returns to its lower state, until a new cycle begins. We implemented the TI in a 1D numerical model, assuming an axisymmetric disk. The numerical model is based on the 1D disk instability model used by Scepi et al. (2019, 2020) in the context of cataclysmic variables, omitting magnetised winds. To sample both inner and outer regions, a logarithmic radial grid is used from 0 1 AU to 30 AU. We assume a star with a mass of M = 0.5 M⊙ (Hartmann & Kenyon 1996; Pérez et al. 2020). The opacities used in our model are based on the prescription described by Bell & Lin (1994). Angular momentum transport and accretion are solved in the α disk paradigm (Shakura & Sunyaev 1973) using a time-dependent continuity equation. In the TI models, α is assumed to have two values: one in the hot state and one in the cold state. The α values have to be as low as 10−3 in the hot state and 10−4 in the cold state in order to be compatible with the typical timescale of the eruption seen in FUors (Bell & Lin 1994). However, the exact physical justification of these particularly low values of α remains problematic in general (Hirose 2015).
The outburst predicted by TI models alone brings two main difficulties. First, the estimated FWHM of the disk emission from this model is <0.1 AU, which is three times smaller than the value of ~0.3 AU measured from our interferometric observations. This smaller predicted emission arises from the high temperature needed to ionize hydrogen, of namely ~5000 K, which can only be sustained in the innermost region of the disk. TI cannot sustain effective temperatures much higher than 5000K up to a maximum extent of ~0.01 AU. Second, without an external triggering event, the instability front propagates inside-out, starting at a few stellar radii where the temperature is high enough and increasing in size as the whole disk becomes unstable, up until the instability front stops its propagation and moves backwards onto the star. This should translate to increases in size and in visible magnitude over a few tens to one hundred years, followed by a decay over a similar timescale. This contradicts the pure decay in time observed in our interferometric sizes and in the light curves. In Sect. 5.3, we present the method we use to compare these simulations with the observations in more detail.
5.2 Magneto-rotational instability+gravitational instability in a layered disk model
The second model considered in this work is a magnetically layered disk driven by MRI-GI (Armitage et al. 2001; Armitage 2011). In the quiescent state, the disk is structured with a thin surface layer, in which accretion by MRI can be sustained by ionization from high-energy particles, and a dead zone from 0.1 AU to 2 AU (Gammie 1996), as shown in Fig. 3. As a magnetically inactive region, the dead zone cannot sustain MRI and is quiescent. On the contrary, the outer region of the disk is considered to be gravitationally unstable for radii larger than ~3 AU. Material from the outer part of the disk therefore flows inwards and piles up on the outer edge of the dead zone. As material accumulates, the temperature increases up to a point where it reaches the activation temperature of MRI (TMRI), thus triggering the instability. This instability front propagates inwards and places the entire disk in a hot turbulent state. After the outburst, as the matter has been drained from the disk, the inner disk returns to its initial quiescent state until a new cycle is triggered.
The main difference between the TI and MRI+GI scenarios is the threshold temperature for the outburst. In the TI case, the outburst is due to the sudden rise in opacity due to the ionization of hydrogen atoms, which starts at about 3000 K. In the MRI case, it is the ionization of alkali metals (above 800 K) that is sufficient to increase the ionization fraction above that required for MRI activity (Gammie 1996). The net result is that MRI outbursts start at larger radii (lower temperature), and therefore concern a wider fraction of the disk than TI outbursts. Moreover, as the typical accretion rates are comparable in the two kinds of outburst, MRI outbursts last longer than TI outbursts because it takes more time to empty the larger MRI-unstable disk.
However, we note that both outbursts can exist simultaneously: TI could locally be activated in the hottest and innermost region of the disk <0.1 AU, although this is not essential for triggering and sustaining the outburst (Armitage et al. 2001). We implemented the MRI+GI model in a 1D numerical simulation similar to the TI model (axisymmetric, logarithmic scale) and based on the model given in Martin & Lubow (2011).
In contrast to the TI model, α is in this case computed as the sum of several contributions:
where we identified three regimes of angular momentum transport: the dead zone, where the MRI is active only in the surface layer down to a column density Σcrit (Lesur et al. 2022);
which is the active zone where the MRI is activated in the entire disk column when T ≳ TMRI
and finally the self-gravitating regime, where angular momentum is driven by GI when the Toomre Q parameter (Toomre 1964) falls below a threshold Qcrit :
In the above definitions, we use the local disk surface density Σ, its central temperature T, and the Toomre parameter Q = csΩ/(πGΣ), where cs is the local sound speed, Ω is the local orbital angular velocity, and G is the gravitational constant. In the following, we set Qcrit = 2 and αGI = 10−2 while αMRI, TMRI, and Σcrit are allowed to vary.
For the disk cooling, we have two possible opacity tables. In the simplest case, we follow Martin & Lubow (2011) and assume κ = 0.02 T0.8 cm2 g−1. In this case, because the temperature dependence of the opacity is sublinear, the disk is stable for TI, and we label these models as “without TI”. In the more elaborated case, we use the full opacity fit of Armitage et al. (2001, see his Table 1), which includes a steep dependence of the opacity when H gets ionized (T>3000 K), and therefore leads to thermal cycles. These last models are therefore tagged as “with TI”.
The temperature profile of the MRI+GI instability is shown in Fig. 4. The result of the simulation is an effective temperature profile that varies in time and reproduces a radial temperature profile ∝ Teff ∝ r−3/4, as predicted for a standard accretion disk (Shakura & Sunyaev 1973). The instability front extends from the star up to ~3AU, where the MRI is sustained. Locally, in the innermost region up to ~0.3 AU, TI can be sustained and heats up the disk depending on the opacity law chosen for this model (“with TI” or “without TI”; see Table 4). Unlike the TI scenario, starting from a purely theoretical model, MRI+GI enables us to obtain solutions that are in agreement with our observations. The model allows us to retrieve the typical size of the outburst, and the compact unresolved emission that naturally arises from the peak of intensity of a power-law temperature profile in the inner region of the disk at <0.1 AU. In the following section, we present our comparison of the model and the data in more detail.
 |
Fig. 3 Observational results. Left: structure of FU Orionis as seen with the components of our NIR dataset. The outbursting region corresponds to the marginally resolved disk in the interferometric data. Right: (adapted from Armitage 2011): scenario of a FU Orionis outburst in the MRI-GI model. In the quiescent phase, the disk has a magnetically layered structure: material piles up at the outer edge of the dead zone due to GI. As it reaches a sufficient density and temperature to activate MRI, the full disk goes into outburst, which corresponds to the region seen in the NIR interferometric data. Locally, TI can be triggered very close to the star (<O.1 AU). |
 |
Fig. 4 Simulation of an FU Orionis eruption with a 1D MHD layered disk model. Left (upper): temperature profile in time from the 1D model (Simu 1); radial direction in x-axis and time in y-axis. Left (lower): temperature profile produced by the simulation for different epochs (solid colored lines); a T ∝ r−3/4 slope is shown for comparison (solid gray line); the uncorrected profile in the innermost region (~0.01 AU, see text) is shown as a dashed line. Right: spatial morphology of the disk deduced from simulated temperature profile and compared to interferometric observations in H band (1.65 µm) and K band (2.2 µm). |
 |
Fig. 5 Temporal evolution of the FWHM of the outbursting region deduced from the model (solid line) compared to the fit of the observations (points). H band observations agree well with the model; K band exhibits a good mean estimate but shows strong temporal variation for the oldest data points, which likely originates from instrumental factors. |
of the 1D numerical simulations for the outburst.
5.3 Parameters of the instability
We compared the size of the outburst obtained from interferometry with the output of the TI and the MRI-GI models, as shown in Fig. 5. Following the method of Malbet et al. (2005), we simulate the interferometric visibility and the SED for each time step by numerical integration of successive rings with infinitesimal radius, and an effective temperature given by the output of the MHD simulation. The SED was reddened following the prescription of Pueyo et al. (2012) using Aυ = 1.4, and the light curve is extracted from the SEDs computed at each time step. Our simulation does not allow us to faithfully simulate the inner few stellar radii of the disk, because this would require a dedicated treatment of the boundary layer (Popham et al. 1996), which is out of the scope of this work. Nonetheless, it could be reasonably approximated that the boundary layer follows a power-law temperature profile T ∝ r−q in the first 0.1 AU of FU Orionis, as also visible in Popham et al. (1996). In order to correct for the inner region, we set the (q, Tin, Rin) of the power-law profile of the effective temperature at < 0.1 AU on a joint fit of the SED and the MIRCX data, which accurately probe the inner region of the disk. The main parameters, which are the least constrained in the MRI-GI scenario, are TMRI, Σcrit, and αMRI. In the following, we provide a preliminary exploration of these parameters by comparing the simulations obtained with different values of these parameters. In addition, the runs are separated into pure TI (Simulation 8), pure MRI-GI (Simulations 3–7), and MRI-GI with TI (Simulations 1 and 2). In order to compare the simulation to our interferometric sizes, we fitted the same geometrical model to the interferometric visibility from the MHD simulation, adopting the fixed parameters of each respective band as described in Sect. 4. This method enables us to compare equivalent models of the spatial distribution, and to reduce the comparison with the MHD simulation to the evolution of one parameter (FWHM size) in time.
From the 1D model, we are able to retrieve the typical sizes of the outburst. We reproduce the general morphology of the disk, where the resolved component approximately corresponds to the contribution of the 0.1–1 AU inner region, which varies during the outburst, and the unresolved flux, which corresponds to the innermost region of 0.1 AU. The typical spatial extent of TI is limited to 0.1 AU, which is too small compared to the measured size. On the contrary, the simulation with MRI-GI with TI seems to provide the best match to the observed sizes and their temporal variation, while MRI-GI without TI seems to produce a disk extension and a temporal variation that are slightly too large during the outburst.
In the case of the MRI-GI with TI, the parameters that reproduce the instability are αMRI = 1 × 1010−2, TMRI = 800 K, which is the activation temperature of the MRI, and Σcrit = 10 g cm−2, the critical density of the disk. A higher value of αMRI = 2 × 10−2 seems unlikely in this run, as it would translate to an outburst of larger size (larger by almost a factor 2; Simulation 4). Based on the typical size and temporal variation, Simulations 1 and 2, which include TI in addition to MRI-GI, qualitatively better match the typical size of the outburst; however, this point is still loosely constrained by the currently available data. For Simulation 1, we obtain Tin = 5480 K and Rin = 5.3 R⊙, which is consistent with the Rin derived by Malbet et al. (2005). Finally, we can extract the SED and the light curve, which are shown in Fig. 6. The SED and the light curves also match the observation data, in particular the K magnitude and its temporal variation. Interestingly, in the case of the light curve, the simulation reproduces the small overshoot in B magnitude seen in the visible light curve (Herbig 1977). More work is needed to refine the simulated outburst. However, this approach clearly favors the MRI-GI scenario and its basic physics.
 |
Fig. 6 SED (left) and light curve (right) simulated from the MHD model and compared to the archival data of FU Orionis. |
5.4 What triggering event?
Different events have been proposed to trigger the instability in the outer edge of the outburst region (~3 AU) so that the instability can propagate outside-in and reproduce the visible light curve. The most notable scenario is an instability triggered by an external perturbation, which could be compatible with the presence of a stellar companion FU Ori S at large separation (Bonnell & Bastien 1992; Cuello et al. 2020), or by an internal perturbation, in particular a planet of a few Jupiter masses (Lodato & Clarke 2004). We note that in the case of MRI-GI, unlike in a single fly-by scenario, high temperatures of ~5000 K can naturally be sustained in the disk, and with multiple eruptions, as seen in some FUors (ZCMa), as long as the disk is replenished on the outer edge of the dead zone. The MRI-GI scenario does not exclude and could even be compatible with an enhancement of GI by an external perturber, which could favor these eruptions in multiple systems that are still deeply embedded in a reservoir of material. In the specific case of FU Orionis, further investigation of the impact of (i) the tidal interaction of FU Orionis S (projected separation of 227 AU) on the extended envelope, or (ii) the presence of a planet in the inner region of the disk on the outer edge of the dead zone, would be important in order to obtain a precise measurement of the impact of an external perturbation on the outburst and its dynamics.
6 Conclusion
We present a temporal monitoring of FU Orionis outbursts over 20 years of spatially resolved observations with NIR interferometry. We reduced and analyzed this dataset homogeneously in order to estimate the size of the outburst region over the time span covered by interferometric observations. We can draw the following conclusions from this analysis:
The typical structure of FU Orionis can be described by an outbursting region marginally resolved with interferometry, an extended envelope, and an unresolved compact flux in our interferometric data and originating from the inner region of the disk.
We constrain a typical FWHM size of the outbursting region of
 and
and 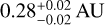 in the H- and K bands, respectively, and a temporal variation of
in the H- and K bands, respectively, and a temporal variation of 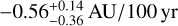 and
and 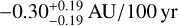 , respectively. This size variation is compatible with a constant or slowly decreasing size of the outbursting region.
, respectively. This size variation is compatible with a constant or slowly decreasing size of the outbursting region.The most consistent model is a scenario in which MRI is triggered by a GI instability at the outer-edge zone and occurs in a magnetically layered diskand consistently reproduces the interferometric sizes and visibilities, the SED, and the light curve observed in FU Orionis.
These preliminary 1D simulations are mostly compatible with αMRI = 1.10−2, TMRI = 800 K, and Σcrit = 10 g cm−2. Higher values of αMRI are less favored as they produce larger outburst regions. Further work is needed to confirm the values of these parameters, both with observations and models.
This scenario could be compatible with an external perturber enhancing GI at the outer edge of the dead zone; for example, through tidal interaction with a large-separation stellar companion or a planet at the outer edge of the dead zone.
Our study refines the scenario of FU Orionis outburst and highlights the unique potential of directly probing the inner AU of protoplanetary disks with spatially resolved observations in order to understand the process of planet formation.
Acknowledgements
We would like to thank the individuals who have built and contributed to develop during more than 20 years the generations of interferometric instruments whose data are included here. G.B. and J.-P.B. thank Regis Lachaume for having provided the PTI, IOTA and VINCI archival data, and Pierre Kervella for providing the data reduction software of VINCI. G.B. acknowledges funding from the Ecole Doctorale de Physique de l’Université Grenoble Alpes for this work. G.L has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (Grant Agreement No. 815559 (MHDiscs)). PIONIER was funded by the Université Joseph Fourier (UJF, Grenoble) through its Poles TUNES and SMING and the vice-presidency of research, the Institut de Planétologie et d’Astrophysique de Grenoble, the “Agence Nationale pour la Recherche” with the program ANR EXOZODI, and the Institut National des Science de l’Univers (INSU) with the programs PNPRS and PNP. GRAVITY has been developed in a collaboration by the Max Planck Institute for Extraterrestrial Physics, LESIA of Paris Observatory-PSL/CNRS/Sorbonne Université/Université Paris-Cité and IPAG of Université Grenoble Alpes/CNRS, the Max Planck Institute for Astronomy, the University of Cologne, the Centro Multidisciplinar de Astrofisica Lisbon and Porto, and the European Southern Observatory. We thank the anonymous referee for his/her comments that improved the manuscript. This research has benefited from the support of the Jean-Marie Mariotti Center (JMMC), and has made use of Aspro and Search Cal (http://www.jmmc.fr).
Appendix A Output of the bootstrap analysis in H and K band
 |
Fig. A.1 H band: Output of the fitting procedure of the interferometric observations. Left: Visibility model is represented as a dashed line; the minor axis of the Gaussian disk is associated with the upper visibility curve and the major axis with the lower visibility curve. Residuals are shown in red scattered points. Middle: Bootstrap values of the FWHM estimate. Right: (u,v) coverage associated with each observation. |
 |
Fig. A.2 K band: Output of the fitting procedure. See Fig. A.1 for details of the plot, and Fig. A.2 continued for the second part. |
Appendix B Fitted parameters
Fitted parameters of the geometrical modeling of FU Orionis. The reference datasets in each band, on which the sparse dataset (see text) is fixed, are indicated in bold (values without error bars).
Appendix C Extended flux
 |
Fig. C.1 Proportion of the flux of the extended envelope over the total flux measured in the interferometric field of view in K band. A chromatic dependency is visible in GRAVI21 and GRAVI16 data. The offset between these two curves is due to the smaller interferometric field of view in GRAVI21. |
References
- Armitage, P. J. 2011, ARA&A, 49, 195 [Google Scholar]
- Armitage, P. J., Livio, M., & Pringle, J. E. 2001, MNRAS, 324, 705 [NASA ADS] [CrossRef] [Google Scholar]
- Audard, M., Ábrahám, P., Dunham, M. M., et al. 2014, in Protostars and Planets VI, 387 [Google Scholar]
- Balbus, S. A., & Hawley, J. F. 1998, Rev. Mod. Phys., 70, 1 [Google Scholar]
- Bell, K. R., & Lin, D. N. C. 1994, ApJ, 427, 987 [NASA ADS] [CrossRef] [Google Scholar]
- Bonnell, I., & Bastien, P. 1992, ApJ, 401, L31 [Google Scholar]
- Calvet, N., Hartmann, L., & Strom, S. E. 2000, in Protostars and Planets IV, 377 [Google Scholar]
- Colavita, M. M., Wallace, J. K., Hines, B. E., et al. 1999, ApJ, 510, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Cuello, N., Louvet, F., Mentiplay, D., et al. 2020, MNRAS, 491, 504 [Google Scholar]
- Dong, R., Vorobyov, E., Pavlyuchenkov, Y., Chiang, E., & Liu, H. B. 2016, ApJ, 823, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Efron, B. 1982, The Jackknife, the Bootstrap and other resampling plans (Philadelphia (PA), USA: Society for industrial and applied mathematics) [CrossRef] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gammie, C. F. 1996, ApJ, 457, 355 [Google Scholar]
- GRAVITY Collaboration (Perraut, K., et al.) 2019, A&A, 632, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hartmann, L., & Kenyon, S. J. 1996, ARA&A, 34, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Herbig, G. H. 1977, ApJ, 217, 693 [NASA ADS] [CrossRef] [Google Scholar]
- Hirose, S. 2015, MNRAS, 448, 3105 [NASA ADS] [CrossRef] [Google Scholar]
- Kenyon, S. J., & Hartmann, L. W. 1990, ApJ, 349, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Kervella, P., Ségransan, D., & Coudé du Foresto, V. 2004, A&A, 425, 1161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Labdon, A., Kraus, S., Davies, C. L., et al. 2021, A&A, 646, A102 [EDP Sciences] [Google Scholar]
- Lachaume, R., Rabus, M., Jordán, A., et al. 2019, MNRAS, 484, 2656 [NASA ADS] [CrossRef] [Google Scholar]
- Lazareff, B., Berger, J. P., Kluska, J., et al. 2017, A&A, 599, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Le Bouquin, J. B., Berger, J. P., Lazareff, B., et al. 2011, A&A, 535, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lesur, G., Ercolano, B., Flock, M., et al. 2022, ArXiv e-prints [arXiv:2203.09821] [Google Scholar]
- Liu, H. B., Mérand, A., Green, J. D., et al. 2019, ApJ, 884, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Lodato, G., & Clarke, C. J. 2004, MNRAS, 353, 841 [NASA ADS] [CrossRef] [Google Scholar]
- Lykou, F., Ábrahám, P., Chen, L., et al. 2022, A&A, 663, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Malbet, F., Berger, J. P., Colavita, M. M., et al. 1998, ApJ, 507, L149 [NASA ADS] [CrossRef] [Google Scholar]
- Malbet, F., Lachaume, R., Berger, J. P., et al. 2005, A&A, 437, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martin, R. G., & Lubow, S. H. 2011, ApJ, 740, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Millan-Gabet, R., Monnier, J. D., Akeson, R. L., et al. 2006, ApJ, 641, 547 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez, S., Hales, A., Liu, H. B., et al. 2020, ApJ, 889, 59 [CrossRef] [Google Scholar]
- Popham, R., Kenyon, S., Hartmann, L., & Narayan, R. 1996, ApJ, 473, 422 [NASA ADS] [CrossRef] [Google Scholar]
- Pueyo, L., Hillenbrand, L., Vasisht, G., et al. 2012, ApJ, 757, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Quanz, S. P., Henning, T., Bouwman, J., Ratzka, T., & Leinert, C. 2006, ApJ, 648, 472 [NASA ADS] [CrossRef] [Google Scholar]
- Scepi, N., Dubus, G., & Lesur, G. 2019, A&A, 626, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scepi, N., Lesur, G., Dubus, G., & Jacquemin-Ide, J. 2020, A&A, 641, A133 [EDP Sciences] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Takami, M., Fu, G., Liu, H. B., et al. 2018, ApJ, 864, 20 [Google Scholar]
- Toomre, A. 1964, ApJ, 139, 1217 [Google Scholar]
- Traub, W. A. 1998, SPIE Conf. Ser., 3350, 848 [NASA ADS] [Google Scholar]
- Vorobyov, E. I., & Basu, S. 2005, ApJ, 633, L137 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, Z., Hartmann, L., Calvet, N., et al. 2007, ApJ, 669, 483 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, Z., Hartmann, L., Gammie, C., & McKinney, J. C. 2009, ApJ, 701, 620 [CrossRef] [Google Scholar]
All Tables
Fitted parameters of the geometrical modeling of FU Orionis. The reference datasets in each band, on which the sparse dataset (see text) is fixed, are indicated in bold (values without error bars).
All Figures
 |
Fig. 1 Visibility squared versus projected baseline of observations with the MIRCX instrument in H band in 2019 (see logs of Table 1). The red dashed line shows the minor and major axis of the Gaussian inner disk, while the black solid lines and black arrows show the contribution of the compact flux fc and of the over-resolved flux fe. |
| In the text | |
 |
Fig. 2 Variation in time of the estimated FWHM of the outburst in FU Orionis in H band (left) and K band (right). The temporal slope is evaluated from a bootstrap analysis: each trial of the bootstrap is shown as a transparent solid line; the final result is the median of all trials, shown as a dashed line. |
| In the text | |
 |
Fig. 3 Observational results. Left: structure of FU Orionis as seen with the components of our NIR dataset. The outbursting region corresponds to the marginally resolved disk in the interferometric data. Right: (adapted from Armitage 2011): scenario of a FU Orionis outburst in the MRI-GI model. In the quiescent phase, the disk has a magnetically layered structure: material piles up at the outer edge of the dead zone due to GI. As it reaches a sufficient density and temperature to activate MRI, the full disk goes into outburst, which corresponds to the region seen in the NIR interferometric data. Locally, TI can be triggered very close to the star (<O.1 AU). |
| In the text | |
 |
Fig. 4 Simulation of an FU Orionis eruption with a 1D MHD layered disk model. Left (upper): temperature profile in time from the 1D model (Simu 1); radial direction in x-axis and time in y-axis. Left (lower): temperature profile produced by the simulation for different epochs (solid colored lines); a T ∝ r−3/4 slope is shown for comparison (solid gray line); the uncorrected profile in the innermost region (~0.01 AU, see text) is shown as a dashed line. Right: spatial morphology of the disk deduced from simulated temperature profile and compared to interferometric observations in H band (1.65 µm) and K band (2.2 µm). |
| In the text | |
 |
Fig. 5 Temporal evolution of the FWHM of the outbursting region deduced from the model (solid line) compared to the fit of the observations (points). H band observations agree well with the model; K band exhibits a good mean estimate but shows strong temporal variation for the oldest data points, which likely originates from instrumental factors. |
| In the text | |
 |
Fig. 6 SED (left) and light curve (right) simulated from the MHD model and compared to the archival data of FU Orionis. |
| In the text | |
 |
Fig. A.1 H band: Output of the fitting procedure of the interferometric observations. Left: Visibility model is represented as a dashed line; the minor axis of the Gaussian disk is associated with the upper visibility curve and the major axis with the lower visibility curve. Residuals are shown in red scattered points. Middle: Bootstrap values of the FWHM estimate. Right: (u,v) coverage associated with each observation. |
| In the text | |
 |
Fig. A.2 K band: Output of the fitting procedure. See Fig. A.1 for details of the plot, and Fig. A.2 continued for the second part. |
| In the text | |
 |
Fig. C.1 Proportion of the flux of the extended envelope over the total flux measured in the interferometric field of view in K band. A chromatic dependency is visible in GRAVI21 and GRAVI16 data. The offset between these two curves is due to the smaller interferometric field of view in GRAVI21. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



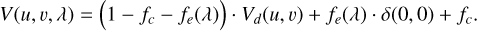
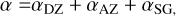
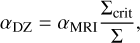
![$ \matrix{ {{\alpha _{{\rm{AZ}}}} = {\alpha _{{\rm{MRI}}}}{{\Sigma - {\Sigma _{{\rm{crit}}}}} \over \Sigma }\tanh \left[ {\left( {T - {T_{{\rm{MRI}}}}} \right)/150} \right]} & {{\rm{if}}\,T > {T_{{\rm{MRI}}}},} \cr } $](/articles/aa/full_html/2023/08/aa45757-22/aa45757-22-eq20.png)