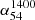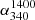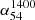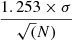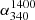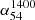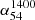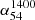EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 675 (July 2023) A&A, 675 (2023) L3 Full HTML
Open Access
Issue
A&A
Volume 675, July 2023
Article Number L3
Number of page(s) 7
Section Letters to the Editor
DOI https://doi.org/10.1051/0004-6361/202346593
Published online 04 July 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

Statistical variations in the radio spectral index (α; S ∝ να) of extragalactic radio sources with monochromatic radio luminosity (P) has been inferred in several studies, reaching back to works conducted more than five decades ago (Heeschen 1960; Kellermann et al. 1969; Bridle et al. 1972; Veron et al. 1972; MacLeod & Doherty 1972; Gopal-Krishna 1988; Blundell et al. 1999). A statistically more significant correlation was reported in Laing & Peacock (1980), modelled in terms of multiple shocks occurring within the hot spots (Gopal-Krishna & Wiita 1990). In an alternative claim, the correlation of spectral index with redshift, z, was posited to be more basic (Katgert-Merkelijn et al. 1980; Macklin 1982). Choosing between these two alternatives has remained difficult mainly because in a flux-limited sample, P and z are strongly correlated due to Malmquist bias (e.g., Singal 1993; Blundell et al. 1999). Another complicating factor is the statistical trend for the spectra of individual sources to be curved becoming progressively steeper between metre and centimetre wavelengths (Laing & Peacock 1980; Gopal-Krishna 1988; Blundell et al. 1999; Konar et al. 2006; Jamrozy et al. 2008; McKean et al. 2016). An attempt to resolve this degeneracy was made using two flux-limited samples selected at metre wavelengths, for which the radio spectrum of each source could be determined in the rest-frame; it was thus inferred that the correlation of α with P is likely to be primary (Gopal-Krishna 1988; also, Blundell et al. 1999). These above correlations involving α have a bearing on a number of important issues, such as the strong tendency (i) of high-z radio galaxies to exhibit a very steep radio spectrum (α < −1.1) at decimetre wavelengths (Tielens et al. 1979; Blumenthal & Miley 1979; Gopal-Krishna & Steppe 1981; De Breuck et al. 2000) and (ii) for the very steep spectra to remain straight at least up to ∼10 GHz (Mangalam & Gopal-Krishna 1995; Klamer et al. 2006).

Another well known statistical dependence of α is related to the radio flux density (S). The variation of α with flux density can be used to constrain models of cosmological evolution of extragalactic radio sources (Dagkesamanskii 1970; Laing & Peacock 1980; Condon 1984; Kulkarni et al. 1990; Calistro Rivera et al. 2017). For samples of sources selected at metre wavelengths, the statistical dependence of α on S was first pointed out almost five decades ago by Murdoch (1976). Using a complete sample of 133 sources above a limiting flux density of 0.97 Jy at 408 MHz, this author found the mean value of 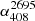α 408 2695 $ \alpha_{408}^{2695} $ to be −0.911±0.014, which is significantly steeper than the corresponding value of −0.816±0.018 found for the all-sky catalogue of Robertson (1973), a complete sample of sources stronger than 10 Jy at 408 MHz. For metre-wavelength selected sources, it demonstrated a 4.2σ level systematic spectral steepening between the strong and intermediate flux densities. This led to the obvious question regarding whether the steepening of α continues to lower flux levels (by e.g., an order of magnitude) or does it plateau or even reverse? This question was first investigated in a set of two papers on the ‘spectral index-flux density relation’ using metre-wavelength samples (Gopal-Krishna & Steppe 1982: GS82; Steppe & Gopal-Krishna 1984: SG84), spanning a wide range in flux density from S408 ∼ 25 Jy to ∼0.1 Jy, which is known to be dominated by distant extragalactic radio sources (Condon 1989). In these two papers (particularly the latter one in which the authors used their more accurate flux measurements of a complete sample of 212 sources, made with the 100-m Effelsberg radio telescope), it was shown that αmedian steepens from −0.815±0.02 at about S408 ∼ 15 Jy to −0.90±0.02 at intermediate flux levels (S408 ∼ 1 − 2 Jy); it thereafter flattens back to ∼ − 0.78 ± 0.03 by S408 ∼ 0.2 Jy, mirroring the differential source counts of radio sources selected at metre wavelengths. While this trend was confirmed by Windhorst et al. (1990) and Kapahi & Kulkarni (1986), later on Kulkarni et al. (1990) found the flattening of αmedian between S408 ∼ 2 Jy and ∼0.2 Jy to be roughly an order of magnitude smaller, thus, barely significant (see also Zhang et al. 2003). In yet another study, based on 1.5 GHz VLA imaging of 1103 sources from the Bologna B3 sample at 408 MHz (Ficarra et al. 1985), Vigotti et al. (1989) found that the steepening of α (mean) continues all the way down to S408 ∼ 0.1 Jy. Hence, whilst almost all the studies from 1975 to 1990 were consistent in finding for metre-wavelength samples a systematic steepening of α from high to intermediate (S408 ∼ 1 − 2 Jy) flux density levels, contradictory trends were claimed about the run of α towards a further order-of-magnitude lower flux densities. Over the past 5 years, this issue has been revisited by Tiwari (2019) and de Gasperin et al. (2018), using the 147 MHz survey TIFR GMRT SKY SURVEY Alternate Data Release 1 (TGSSADR1; Intema et al. 2017), by combining this database with the 1.4 GHz NRAO VLA Sky Survey catalogue (NVSS; Condon et al. 1998). Both these independent analyses confirm a significant spectral flattening occurring between the intermediate and lower flux densities, consistent with the results of GS82 and SG841. One may, however, recall that the spectral curvature of sources often becomes very significant at frequencies below ∼200 MHz, as underscored, for instance, in Laing & Peacock (1980) and this raises the possibility of bias getting introduced in the α − S relation determined in the above mentioned two recent studies which are based on TGSS-ADR1 survey made at 147 MHz. This has given us the impetus to verify the α − S relation using a similarly large metre-wavelength survey carried out at a somewhat higher frequency, namely, the recent VLITE2 Commensal Sky Survey Epoch 1 (‘VCSS1’) at 340 MHz. We refer to Polisensky et al. (2016) and Clarke et al. (2016) for further details. In addition, the recent release of the LOFAR LBA Sky Survey preliminary data (LoLSS-PDR de Gasperin et al. 2021) survey at 54 MHz has enabled us to extend the α − S relation to decametre wavelengths. The higher-frequency data have been taken from the 1.4 GHz NRAO VLA Sky Survey catalogue (NVSS; Condon et al. 1998)3. Our analysis procedure is described in Sect. 2 and the results, along with a brief discussion, are presented in Sect. 3. Our conclusions are summarised in Sect. 4.

2. The sample

In brief, VCSS was carried out at the central frequency of 340 MHz with a 33.6 MHz bandwidth, resulting in ∼15″ resolution images, with an average rms noise (σ) of ∼3 mJy beam−1. Peters et al. (2021) provided, with the VCSS epoch 1 data release, a bright source catalogue (VCSS4 henceforth) comprised of 52 844 sources covering 30 000 deg2 of the sky. The completeness of this VCSS catalogue is estimated to be ∼90% for sources with a total flux density exceeding 0.2 Jy at 340 MHz and the present analysis only considers the subset of 42 890 sources above this flux density.

As mentioned above, our decametric sample of sources has been extracted from the LoLSS-PDR survey at 54 MHz. The survey data release covers a sky area of ∼ 740 deg2, imaged with a circular beam of 47″, reaching a median rms noise level (σ) 5 mJy beam−1, and resulting in a catalogue of 25 247 sources. LoLSS is the first survey of such high quality, made at a very low frequency, as it provides an unprecedented combination of sensitivity and resolution. de Gasperin et al. (2021) estimated that the LoLSS-PDR catalogue is 90% complete for sources stronger than 40 mJy. In this analysis, we have only used the sources (7746) with an integrated flux density above 200 mJy at 54 MHz. As mentioned below, both our samples only consist of sources with structural codes S and M.

Here, it may be recalled that in these recent large surveys, the identification of individual discrete radio sources as well as their structural classification have been performed using an automated procedure that employs PyBDSF (Mohan & Rafferty 2015). Accordingly, a source is classified either as ‘single’ (type ‘S’, resolved or unresolved), or ‘multiple’ (type ‘M’, fitted with multiple Gaussian components). For both types, integrated flux densities are available in the published databases. For the present purpose, we have selected sources having either of these two structural codes, in order to arrive at samples that should be unbiased with respect to radio structural details. Thus, our 340 MHz sample consists of 42 890 S/M sources above the 200 mJy limit adopted here. Out of these, NVSS counterparts could not be found for 1272 (∼3%) sources (see below). Their numbers in different flux density bins are listed in Table 1. For our 54 MHz sample containing 7746 S/M class sources above the 200 mJy limit adopted here, NVSS counterparts could not be found for 1629 (∼21%) sources (see below). Their numbers in different flux density bins are listed in Table 2.

Table 1.

Overview of the analysis results for the VCSS_NVSS combination, for different flux density ranges or bins (Col. 1) whose median values (mJy) are shown in Col. 2.

Table 2.

Overview of the analysis results for the LoLSS_NVSS combination, for different flux density bins (Col. 1) whose median values (mJy) are shown in Col. 2.

The cross-matching of the above two samples defined at 340 MHz and 54 MHz, with the 1.4 GHz NVSS was done on the basis of positional coincidence for which we have adopted a search radius of 10″. This criterion could be more effectively applied for the LoLSS sample because the beam size of this 54 MHz survey (47″) is nearly identical to that of the NVSS (45″) and, consequently, the imaging responses to the source structure are expected to be very similar at the two frequencies. Thus, if an NVSS counterpart was not found for a source in our 54 MHz sample, we have (conservatively) assigned to its 1.4 GHz flux density an upper limit of 9 mJy, which is 20 times the typical rms error of 0.45 mJy in the NVSS.

On the other hand, the beam width of the 340 MHz VCSS is about three times smaller than that of the NVSS (45″). This large difference could engender substantially different imaging responses to the source structure at the two frequencies, potentially amplifying the offset between the positions of the same source measured in the two surveys. Consequently, not finding an NVSS counterpart within the 10″ search radius would not necessarily imply that the source is below the NVSS detection limit (taken here to be 9 mJy at 1.4 GHz, as mentioned above). Therefore, for the VCSS sources remaining unidentified in the NVSS catalogue (dubbed here as ‘NVSS-undetected’ or just ‘ND’) it would be unrealistic to use the 9 mJy limit for constraining 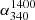α 340 1400 $ \alpha_{340}^{1400} $ and for such ND sources, 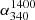α 340 1400 $ \alpha_{340}^{1400} $ has been taken here as unconstrained (see below). The numbers of ND sources in the different flux density ranges are given in Tables 1 and 2.

3. Results and discussion

In this section, we present the ‘αmedian − S’ relations derived for our above-defined source sample selected at 340 MHz and then also compare it with its counterpart, determined here at a much lower selection frequency of 54 MHz. As mentioned above, the present investigation is focused on the flux density range ∼0.2 < S340 < 2 Jy, which is dominated by intrinsically powerful, distant radio sources of synchrotron emission, having a median redshift of ∼1 (Condon 1989). For several classes of intrinsically weak radio sources, including radio-quiet quasars and starburst-dominated active galaxies, the dependence of radio spectral index on parameters such as Eddington luminosity and ionisation ratios (across the optical diagnostic diagrams) have been investigated recently by Laor et al. (2019) and Zajaček et al. (2019).

3.1. The α − S relation at 340 MHz

This frequency is close to the ones at which α − S relation has been commonly reported (Sect. 1) and, hence, the αmedian − S340 MHz relation determined here can be directly compared with them. We have divided our 340 MHz VCSS sample into 12 equally populated bins of S340 MHz (see Table 1 for details). Figure A.1 shows histogram of 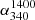α 340 1400 $ \alpha_{340}^{1400} $ for each of the 12 flux density bins and ranges. For each histogram we have estimated three values of 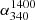α 340 1400 $ \alpha_{340}^{1400} $(median), listed in Table 1. The middle value was determined using only the sources (97%) for which an NVSS counterpart was found. In order to quantify the maximum impact on this estimate of 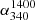α 340 1400 $ \alpha_{340}^{1400} $(median) due to the ND sources (for which 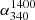α 340 1400 $ \alpha_{340}^{1400} $ is taken as unconstrained value, see above), we considered two extreme situations regarding their spectral indices. In the first instance, leading to 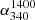α 340 1400 $ \alpha_{340}^{1400} $(median) minimum, we assumed all the ND sources to have 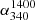α 340 1400 $ \alpha_{340}^{1400} $ values well below 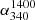α 340 1400 $ \alpha_{340}^{1400} $(median), say 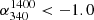α 340 1400 < − 1.0 $ \alpha_{340}^{1400} < -1.0 $. In the other extreme, leading to 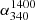α 340 1400 $ \alpha_{340}^{1400} $(median) maximum, we assumed all the ND sources to have 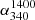α 340 1400 $ \alpha_{340}^{1400} $ well above 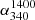α 340 1400 $ \alpha_{340}^{1400} $(median), say 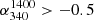α 340 1400 > − 0.5 $ \alpha_{340}^{1400} > -0.5 $. Table 1 gives all the three estimates of 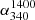α 340 1400 $ \alpha_{340}^{1400} $(median) for each flux density bin and the same are shown in Fig. 1a as the uncertainty in 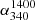α 340 1400 $ \alpha_{340}^{1400} $(median) estimated for each flux bin. Despite the maximum uncertainty of α(median) we have taken into consideration here, the overall trend is clear and it shows a progressive flattening of 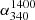α 340 1400 $ \alpha_{340}^{1400} $(median) towards lower flux densities, over the region of ∼0.2 Jy < S340 MHz < ∼2 Jy. This confirms the pattern first reported in GS82 and SG82 and also in some (though not all) subsequent studies (Sect. 1). Thus, the various claims to the contrary (see Sect. 1) are not supported by the much more extensive and sensitive data that have now become available, after the passage of a few decades. We note, however, that the plot in Fig. 1a does not extend much beyond the flux density corresponding to the peak of αmedian, somewhat limiting the scope for comparison with previous results that were extended to higher flux density ranges; although we note that at such higher flux density levels, most claims about α − S relation are still in any case, mutually consistent (see Sect. 1).

thumbnail Fig. 1.

‘Spectral index-flux density’ relation for two different frequency samples. (a): αmedian − S340 MHz plot (Sects. 2 and 3.1), with the data for each of the 12 flux density bins listed in Table 1. (b): αmedian − S54 MHz plot (Sects. 2 and 3.2), with the data for each of the eight flux density bins listed in Table 2.

3.2. The α − S relation for sources selected at 54 MHz

The distribution of 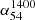α 54 1400 $ \alpha_{54}^{1400} $ for our 54 MHz sample containing 7746 sources is shown in Fig. 2. While the main hump (blue-shaded) is seen to drop to an insignificant level by 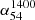α 54 1400 $ \alpha_{54}^{1400} $ ∼ − 1.3, the region at still steeper spectral indices (orange shaded) is populated by the ND sources (∼21%, Table 2). This secondary yet prominent population of very-steep-spectrum (VSS) sources is likely to be associated with clusters of galaxies, as inferred from decametric radio observations conducted over the past few decades (e.g., Baldwin & Scott 1973; Slingo 1974; Roland et al. 1976; Bagchi & Kapahi 1994; de Gasperin et al. 2017). Bearing this dichotomy in mind, we proceeded to estimate 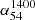α 54 1400 $ \alpha_{54}^{1400} $(median), using the entire set of sources falling in each flux density bin (Table 2; Fig. A.2), and plotted the same in Fig. 1b, along with the median error5. The trend of flattening of 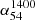α 54 1400 $ \alpha_{54}^{1400} $(median) with decreasing S54 MHz is present, although it is milder in comparison to that found for the 340 MHz sample (Fig. 1a) and confined to S54 MHz < ∼0.5 Jy. Conceivably, this difference could be due to the stronger presence of the VSS sources in the 54 MHz sample, as mentioned above. While this requires further investigation, we note that a similar onset of flattening of 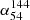α 54 144 $ \alpha_{54}^{144} $(median) near S54 MHz ∼ 0.5 Jy has been noticed in the deep LOFAR survey of a small field in Boötes, covering an area of ∼23.6 deg2, namely, ∼3% of the survey area used here (see Fig. 17 of Williams et al. 2021). It may also be noted that our plot shown in Fig. 1b extends only up to S54 MHz ∼ 3 Jy, which is roughly equivalent to S340 MHz ∼ 0.7 Jy. This is well below the peak of the αmedian established for metre-wavelengths samples (Fig. 1a). Therefore, a more detailed comparison is anticipated for future releases of LoLSS.

thumbnail Fig. 2.

α 54 1400 $ \alpha_{54}^{1400} $ values of orange shaded columns are upper limits (as they represent ND sources). The value of αmedian given inside the box is for the entire histogram.

4. Conclusions

By combining the recently released extensive high-quality database at 340 MHz (VCSS) with the NVSS at 1.4 GHz, we have revisited the spectral index–flux density relation for extragalactic radio sources selected at metre wavelengths. Here, we have focused on the flux density range below S340 MHz ∼ 1 Jy for which grossly divergent claims have been reported concerning the gradient of the αmedian − S relation. The present work demonstrates that αmedian becomes progressively flatter towards decreasing flux densities below S340 MHz ∼1–2 Jy, where αmedian has been known to attain its steepest value. This is in accord with the trend initially reported in the 1980s (Gopal-Krishna & Steppe 1982; Steppe & Gopal-Krishna 1984) and also seen in some recent studies (Tiwari 2019; de Gasperin et al. 2018) using the TGSS ADR1 survey at 147 MHz.

A novel development stemming from the present study is the determination of αmedian − S relation for extragalactic sources selected at decametre wavelengths. While this is broadly in agreement with the trend found for sources selected at metre wavelengths (Sect. 3.1), this relation shows a milder gradient and appears to be less sharply peaked. A possible contributor to the difference between the two α − S relations may be a distinctly stronger presence of very steep spectrum (VSS with 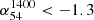α 54 1400 < − 1.3 $ \alpha_{54}^{1400} < -1.3 $) sources in the 54 MHz sample, where they account for about 9% of the sources. Such VSS sources have long been known to be associated with clusters of galaxies and are found conspicuously in decametric radio surveys. It should be possible to verify this different trend when the second (and subsequent) releases of the LoLSS 54 MHz survey become available in the coming years. Equally promising in this context is the ongoing 14–30 MHz LOFAR Decameter Sky Survey (LoDeSS; Groeneveld et al., in prep.).

A major advance in these studies would, of course, be achieved when it becomes possible to determine the αmedian–flux density relation using radio K-corrected values of α of individual sources (i.e., measured at the same frequency in the rest-frame). There has been little progress on this front since some initial attempts using metre-wavelength samples of radio sources that were comparatively small but had nearly complete redshift information (Gopal-Krishna 1988; Mangalam & Gopal-Krishna 1995; Blundell et al. 1999).

1

The sequence of data points defining the 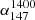α 147 1400 $ \alpha_{147}^{1400} $-S147 relation has a large gap near S147 ∼ 2 Jy (de Gasperin et al. 2018) where the relation is expected to peak (i.e., steepest α). Nonetheless, the trend indicated by their data points seems consistent with the expected peaking of α.

2

VLA Low-band Ionosphere and Transient Experiment (https://vlite.nrao.edu/).

3

We use the S ∝ να convention for calculating α 340 1400 $ \alpha_{340}^{1400} $ and α 54 1400 $ \alpha_{54}^{1400} $.

5

rms error of the estimated median value for a histogram = 1.253 × σ ( N ) $ \frac{1.253\times \sigma}{\sqrt(N)} $ (here, σ is the standard deviation of the histogram and N the total number of sources in it.)

Acknowledgments

The authors would like to thank an anonymous reviewer for helpful comments. GK thanks Indian National Science Academy for a Senior Scientist position. GK would like to dedicate this work to the memory of Dr Hans Steppe, jointly with whom the turnover in the spectral index–flux density relation was first found.

References

  1. Bagchi, J., & Kapahi, V. K. 1994, A&A, 15, 275 [Google Scholar]
  2. Baldwin, J. E., & Scott, P. F. 1973, MNRAS, 165, 259 [NASA ADS] [CrossRef] [Google Scholar]
  3. Blumenthal, G., & Miley, G. 1979, A&A, 80, 13 [NASA ADS] [Google Scholar]
  4. Blundell, K. M., Rawlings, S., & Willott, C. J. 1999, AJ, 117, 677 [Google Scholar]
  5. Bridle, A. H., Kesteven, M. J. L., & Guindon, B. 1972, ApJ, 11, 27 [Google Scholar]
  6. Calistro Rivera, G., Williams, W. L., Hardcastle, M. J., et al. 2017, MNRAS, 469, 3468 [Google Scholar]
  7. Clarke, T. E., Kassim, N. E., Brisken, W., et al. 2016, in Ground-based and Airborne Telescopes VI, eds. H. J. Hall, R. Gilmozzi, & H. K. Marshall, SPIE Conf. Ser., 9906, 99065B [NASA ADS] [CrossRef] [Google Scholar]
  8. Condon, J. J. 1984, ApJ, 287, 461 [Google Scholar]
  9. Condon, J. J. 1989, ApJ, 338, 13 [NASA ADS] [CrossRef] [Google Scholar]
  10. Condon, J. J., Cotton, W. D., Greisen, E. W., et al. 1998, AJ, 115, 1693 [Google Scholar]
  11. Dagkesamanskii, R. D. 1970, Nature, 226, 432 [NASA ADS] [CrossRef] [Google Scholar]
  12. De Breuck, C., van Breugel, W., Röttgering, H. J. A., & Miley, G. 2000, A&AS, 143, 303 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. de Gasperin, F., Intema, H. T., Shimwell, T. W., et al. 2017, Sci. Adv., 3, e1701634 [Google Scholar]
  14. de Gasperin, F., Intema, H. T., & Frail, D. A. 2018, MNRAS, 474, 5008 [Google Scholar]
  15. de Gasperin, F., Williams, W. L., Best, P., et al. 2021, A&A, 648, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Ficarra, A., Grueff, G., & Tomassetti, G. 1985, A&AS, 59, 255 [NASA ADS] [Google Scholar]
  17. Gopal-Krishna 1988, A&A, 192, 37 [NASA ADS] [Google Scholar]
  18. Gopal-Krishna, & Steppe, H. 1981, A&A, 101, 315 [NASA ADS] [Google Scholar]
  19. Gopal-Krishna, & Steppe, H. 1982, A&A, 113, 150 [NASA ADS] [Google Scholar]
  20. Gopal-Krishna, & Wiita, P. J. 1990, A&A, 236, 305 [NASA ADS] [Google Scholar]
  21. Heeschen, D. S. 1960, PASP, 72, 368 [NASA ADS] [CrossRef] [Google Scholar]
  22. Intema, H. T., Jagannathan, P., Mooley, K. P., & Frail, D. A. 2017, A&A, 598, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Jamrozy, M., Konar, C., Machalski, J., & Saikia, D. J. 2008, MNRAS, 385, 1286 [NASA ADS] [CrossRef] [Google Scholar]
  24. Kapahi, V. K., & Kulkarni, V. K. 1986, A&A, 165, 39 [NASA ADS] [Google Scholar]
  25. Katgert-Merkelijn, J., Lari, C., & Padrielli, L. 1980, A&AS, 40, 91 [NASA ADS] [Google Scholar]
  26. Kellermann, K. I., Pauliny-Toth, I. I. K., & Williams, P. J. S. 1969, ApJ, 157, 1 [NASA ADS] [CrossRef] [Google Scholar]
  27. Klamer, I. J., Ekers, R. D., Bryant, J. J., et al. 2006, MNRAS, 371, 852 [Google Scholar]
  28. Konar, C., Saikia, D. J., Jamrozy, M., & Machalski, J. 2006, MNRAS, 372, 693 [NASA ADS] [CrossRef] [Google Scholar]
  29. Kulkarni, V. K., Mantovani, F., & Pauliny-Toth, I. I. K. 1990, A&AS, 82, 41 [NASA ADS] [Google Scholar]
  30. Laing, R. A., & Peacock, J. A. 1980, MNRAS, 190, 903 [Google Scholar]
  31. Laor, A., Baldi, R. D., & Behar, E. 2019, MNRAS, 482, 5513 [NASA ADS] [CrossRef] [Google Scholar]
  32. Macklin, J. T. 1982, MNRAS, 199, 1119 [NASA ADS] [Google Scholar]
  33. MacLeod, J. M., & Doherty, L. H. 1972, Nature, 238, 88 [NASA ADS] [CrossRef] [Google Scholar]
  34. Mangalam, A. V., & Gopal-Krishna 1995, MNRAS, 275, 976 [NASA ADS] [CrossRef] [Google Scholar]
  35. McKean, J. P., Godfrey, L. E. H., Vegetti, S., et al. 2016, MNRAS, 463, 3143 [Google Scholar]
  36. Mohan, N., & Rafferty, D. 2015, Astrophysics Source Code Library [record ascl:1502.007] [Google Scholar]
  37. Murdoch, H. S. 1976, MNRAS, 177, 441 [NASA ADS] [CrossRef] [Google Scholar]
  38. Peters, W., Polisensky, E., Brisken, W., et al. 2021, Am. Astron. Soc. Meet. Abstr., 53, 211.06 [NASA ADS] [Google Scholar]
  39. Polisensky, E., Lane, W. M., Hyman, S. D., et al. 2016, ApJ, 832, 60 [NASA ADS] [CrossRef] [Google Scholar]
  40. Robertson, J. G. 1973, Aust. J. Phys., 26, 403 [NASA ADS] [CrossRef] [Google Scholar]
  41. Roland, J., Véron, P., Pauliny-Toth, I. I. K., Preuss, E., & Witzel, A. 1976, A&A, 50, 165 [NASA ADS] [Google Scholar]
  42. Singal, A. K. 1993, MNRAS, 263, 139 [NASA ADS] [CrossRef] [Google Scholar]
  43. Slingo, A. 1974, MNRAS, 168, 307 [NASA ADS] [CrossRef] [Google Scholar]
  44. Steppe, H., & Gopal-Krishna 1984, A&A, 135, 39 [NASA ADS] [Google Scholar]
  45. Tielens, A. G. G. M., Miley, G. K., & Willis, A. G. 1979, A&AS, 35, 153 [NASA ADS] [Google Scholar]
  46. Tiwari, P. 2019, RAA, 19, 096 [NASA ADS] [Google Scholar]
  47. Veron, M. P., Veron, P., & Witzel, A. 1972, A&A, 18, 82 [NASA ADS] [Google Scholar]
  48. Vigotti, M., Grueff, G., Perley, R., Clark, B. G., & Bridle, A. H. 1989, AJ, 98, 419 [NASA ADS] [CrossRef] [Google Scholar]
  49. Williams, W. L., de Gasperin, F., Hardcastle, M. J. H., et al. 2021, A&A, 655, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Windhorst, R., Mathis, D., & Neuschaefer, L. 1990, in Evolution of the Universe of Galaxies, ed. R. G. Kron, ASP Conf. Ser., 10, 389 [NASA ADS] [Google Scholar]
  51. Zajaček, M., Busch, G., Valencia, S. M., et al. 2019, A&A, 630, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Zhang, X.-Z., Reich, W., Reich, P., & Wielebinski, R. 2003, Chin. J. Astron. Astrophys., 3, 347 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Additional figures

thumbnail Fig. A.1.

Histogram of α 340 1400 $ \alpha_{340}^{1400} $ corresponding to only the NVSS detected sources, for each of the 12 flux-density bins (see Table 1). The three values of αmedian shown inside the box for each histogram are explained in Sect. 3.1.

thumbnail Fig. A.2.

Histogram of α 54 1400 $ \alpha_{54}^{1400} $ for each of the 8 flux-density bins. The α 54 1400 $ \alpha_{54}^{1400} $ for NVSS non-detections (ND) are shown in orange colour, and these are upper limits (Sect. 3.2). The median α 54 1400 $ \alpha_{54}^{1400} $ is indicated by the green dashed line, for each histogram (see Table 2).

All Tables

Table 1.

Overview of the analysis results for the VCSS_NVSS combination, for different flux density ranges or bins (Col. 1) whose median values (mJy) are shown in Col. 2.

In the text
Table 2.

Overview of the analysis results for the LoLSS_NVSS combination, for different flux density bins (Col. 1) whose median values (mJy) are shown in Col. 2.

In the text

All Figures

thumbnail Fig. 1.

‘Spectral index-flux density’ relation for two different frequency samples. (a): αmedian − S340 MHz plot (Sects. 2 and 3.1), with the data for each of the 12 flux density bins listed in Table 1. (b): αmedian − S54 MHz plot (Sects. 2 and 3.2), with the data for each of the eight flux density bins listed in Table 2.
In the text
thumbnail Fig. 2.

α 54 1400 $ \alpha_{54}^{1400} $ values of orange shaded columns are upper limits (as they represent ND sources). The value of αmedian given inside the box is for the entire histogram.
In the text
thumbnail Fig. A.1.

Histogram of α 340 1400 $ \alpha_{340}^{1400} $ corresponding to only the NVSS detected sources, for each of the 12 flux-density bins (see Table 1). The three values of αmedian shown inside the box for each histogram are explained in Sect. 3.1.
In the text
thumbnail Fig. A.2.

Histogram of α 54 1400 $ \alpha_{54}^{1400} $ for each of the 8 flux-density bins. The α 54 1400 $ \alpha_{54}^{1400} $ for NVSS non-detections (ND) are shown in orange colour, and these are upper limits (Sect. 3.2). The median α 54 1400 $ \alpha_{54}^{1400} $ is indicated by the green dashed line, for each histogram (see Table 2).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.