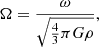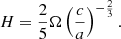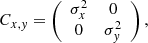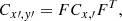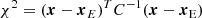EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 675 (July 2023) A&A, 675 (2023) L2 Full HTML
Open Access
Issue
A&A
Volume 675, July 2023
Article Number L2
Number of page(s) 5
Section Letters to the Editor
DOI https://doi.org/10.1051/0004-6361/202346206
Published online 03 July 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

The classical problem of equilibrium figures consists in finding the possible shapes of a self-gravitating, spatially isolated, hydrostatic, and solidly rotating celestial body. From a mathematical or numerical point of view, this question is not completely resolved. From an astronomical point of view, it is not always clear whether hydrostatic theory is suitable for a given object and, if not, which theory can be used to determine the shape of that object. In this Letter we focus mainly on hydrostatic equilibrium; we briefly discuss non-hydrostatic equilibrium shapes in the conclusion and defer a more in-depth discussion to a future paper.

There are some known solutions to the problem of hydrostatic equilibrium figures. For homogeneous bodies, an ellipsoid of revolution is a solution with a flattening controlled by its angular velocity (Maclaurin 1741); an ellipsoid with three different axes is also a solution if the axes obey a specific geometrical relation, as found by Jacobi (1834). Later, Liapounov (1884) and Poincaré (1885) found equilibrium figures close to Maclaurin and Jacobi ellipsoids. For heterogeneous bodies, only one mathematical equilibrium solution is known, for the case of slow rotation. It is a figure very close to a moderately flattened ellipsoid, which we, slightly inaccurately, call a ‘Clairaut ellipsoid’.

From the point of view of astronomy, planets and dwarf planets are nearly hydrostatic equilibrium figures, but questions remain as to which bodies are actually dwarf planets. A VLT/SPHERE observing programme has recently imaged the dwarf planet Ceres and 41 main-belt asteroids (for simplicity, we refer to these 42 objects as ‘asteroids’). By plotting the normalised angular velocity of these objects against their normalised angular momentum (Fig. 1), Vernazza et al. (2021) deduced that all but (216) Kleopatra are compatible with the Maclaurin ellipsoids. However, the statistical distribution of these asteroids around the homogeneous hydrostatic equilibrium remains up for discussion.

thumbnail Fig. 1.

Normalised angular velocity, Ω, as a function of the normalised angular momentum, H, for the 42 asteroids (see also Vernazza et al. 2021, Fig. 6). Predictions for the Maclaurin ellipsoids are shown in blue and those for Jacobi ellipsoids in red. The H = 0 value on the left corresponds to the sphere, and the very flattened objects are on the right. The shaded region corresponds to all ellipsoids with 0.5 ≤ c/a ≤ 1. Though this is a large aspect ratio interval, the region is narrow: this representation is not appropriate for evaluating the compatibility of asteroids with Maclaurin ellipsoids.

In this Letter we show that the angular velocity of our 42 asteroids does not globally match that of Maclaurin ellipsoids. We also show that the asteroids are not even axi-symmetric. Finally, we quantify the misfit between the asteroids and the Maclaurin and Jacobi ellipsoids by calculating their reduced chi-square statistics. A few asteroids might be in hydrostatic equilibrium with depth-dependent densities, but most show a significant deviation.

2. Asteroid rotation rate and flattening

For the 42 asteroids, Vernazza et al. (2021, Tables 1 and A.1) determined and listed the mean density, ρ, the lengths of the axes of the ellipsoids that best fit their shape, a > b > c, the sidereal period of rotation, which we converted into angular velocity, ω, and the uncertainties on these values.

Maclaurin ellipsoids are axi-symmetric (a = b) and are determined by a relationship between the aspect ratio c/a and the normalised angular velocity:

(1)

where G is the gravitational constant, and the Jacobi ellipsoids are determined by two relationships between Ω, c/a, and c/b (e.g., Bertotti et al. 2012, p. 78–82). Our own comparison between the Maclaurin ellipsoids and the asteroids in the (c/a, Ω) plane shows that all but ten of them do not match the Maclaurin sequence within the errors bars in this 2D graphic, and thus cannot be globally considered as Maclaurin ellipsoids (Fig. 2).

thumbnail Fig. 2.

Square of the normalised angular velocity of the 42 asteroids as a function of the aspect ratio c/a and their error bars. Predictions for the Maclaurin ellipsoids are shown in blue and those for the Jacobi ellipsoids in red. All error bars in the paper are at 1 sigma. The c/a = 1 value on the left corresponds to the sphere, and the very flattened objects are on the right. Even taking the large error bars into account, most asteroids are far from the curves of the Maclaurin and Jacobi ellipsoids. In the data published by Vernazza et al. (2021, Table A.1), two asteroids have axes b < c; we consider this to be an exchange of values between b and c.

A pitfall with Fig. 1 is that it represents Ω not as a function of c/a but as a function of the normalised angular momentum, H, which, for an ellipsoid of revolution, is expressed as

(2)

With c/a varying mainly between 0.5 and 1, all possible data deviate little from the straight line 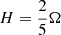and from the Maclaurin curve (Fig. 1). Therefore, this plot cannot distinguish Maclaurin shapes from other ellipsoidal shapes. We use the momentum of ‘axi-symmetric’ ellipsoids for an illustrative reason: it yields a simple relation (Eq. (2)) that more easily highlights the correlation between H and Ω. This choice implies that the abscissa of the points in Fig. 1 are slightly different from those of Vernazza et al. (2021, Fig. 6), who used the momentum of ‘triaxial’ ellipsoids. However, for most of the asteroids, the difference between the two calculations is very small: even in the large range 0.5 ≤ b/a ≤ 1, the relative difference is less than 5%, and in any case, it does not change the reasoning nor the results of this paper.

From a statistical point of view, data that differ significantly from a theory in a representation (Fig. 2) should also differ from it in another representation (Fig. 1). A second pitfall with using the variables in Fig. 1 would be encountered if the correlations between them are ignored when calculating the errors on H and Ω: most of the correlations are indeed close to one due to the abovementioned fact that 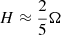. Since the rotation period and the shape parameters are largely determined using different observations, the data x = c/a and y = Ω2 in Fig. 2 are de-correlated, that is, their covariance is written as

(3)

where the σi denotes the standard deviations. A change in variables of the type x′=fx(x, y),y′=fy(x, y) implies the covariance matrix is propagated into the new variables. The covariance matrix in the new variables can be approximated as (Cowan 1998, Sect. 1.6)

(4)

where F denotes the Jacobian matrix of components Fij = ∂jfi. We performed this change in variables, with x′=H and y′=Ω, diagonalised the resulting covariance matrix, and plotted the corresponding error bars on the previous figure, thereby creating Fig. 3. As expected, one of the eigen-directions is almost orthogonal to the Maclaurin ellipsoid curve; the corresponding standard deviation is very small and does not intersect the model prediction. This confirms that, although the data seem to closely match the model, they remain statistically distant.

thumbnail Fig. 3.

Same as Fig. 1 but with the correlated error bars. They indicate that the points are statistically far from the curve despite being visually close.

3. Discussion

3.1. Tri-axiality of asteroids

One possible explanation for the difference between the angular velocity of Maclaurin ellipsoids compared to asteroids that are supposedly hydrostatic is that the shapes of the asteroids have been frozen from an earlier condition in which they were potentially much hotter and deformable and had a different angular velocity. In addition to finding a mechanism that would have decelerated so many asteroids, it would also be necessary to verify that they are rotationally symmetrical, as Maclaurin ellipsoids must be.

To check this, we plotted the ratios c/b vs. c/a (Figs. 4 and 5, top panels). We assumed that the errors on a, b, and c are de-correlated; then, as before, we computed the covariance matrix of c/a and c/b with Eq. (4), diagonalised it, and plotted the corresponding error bars. Figure 4 shows the general geometrical deviation of asteroids from the Maclaurin ellipsoids where a = b. These asteroids are close to neither the Maclaurin nor the Jacobi ellipsoids. Nevertheless, considering error bars in this 2D graphic, the compatibility of a small number of asteroids with these equilibrium figures is not excluded. As a dwarf planet, (1) Ceres is almost rotationally symmetrical. Other smaller bodies, such (24) Themis, (173) Ino, and (324) Bamberga, could also be axi-symmetric. Therefore, except for some bodies, a change in angular velocity cannot explain the difference highlighted in Sect. 2 between asteroids and Maclaurin ellipsoids.

thumbnail Fig. 4.

Aspect ratios of the asteroids. Shown are curves of the Maclaurin (blue) and Jacobi (red) ellipsoids. The c/a = 1 value on the left corresponds to the sphere, and the most flattened objects are on the right. The asteroids are not globally on the curve of the Maclaurin or Jacobi ellipsoids.

thumbnail Fig. 5.

Same as Figs. 4 (top) and 2 (bottom) but without error bars and with asteroid numbers. See Vernazza et al. (2021, Table 1) for the correspondences between numbers and asteroid names. The bottom panel shows a zoomed-in view of the x-axis to exclude the red point that corresponds to (216) Kleopatra, which has already been identified as a dumbbell body (Ostro et al. 2000). The asteroids closest to a Maclaurin ellipsoid are in blue, and those closest to a Jacobi ellipsoid are in red. This shows that the projections formed by these two figures can be misleading with respect to a 3D misfit. In the bottom panel, we have hatched the surface that corresponds to possible Clairaut ellipsoids (see Sect. 3.3).

3.2. Quantification of misfit

The distances between asteroids and hydrostatic ellipsoids, which we have thus far shown in two planes (Figs. 2 and 4), can be estimated in three dimensions in the (c/a, c/b, Ω2) space. We used

(5)

(Cowan 1998, Sects. 2.7 and 7.5) to quantify the distance between a measured position, x, in N dimensions (here N = 3), of covariance, C, and the closest position, xE, on the curves of the hydrostatic ellipsoids. Assuming x follows a Gaussian (which is only a crude approximation here), then χ2 follows a χ2 distribution with N degrees of freedom. Therefore, the reduced chi square, χ2/N, has an expectation of 1 and a median ≈1, and we define as ‘misfit’ its square root, 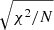, which measures the average number of standard deviations by which x and xE differ. Quantified in this way, six asteroids are closer to the Jacobi ellipsoid curve, while 36 asteroids are closer to the Maclaurin ellipsoid curve. These points are identified in Fig. 5.

The misfit 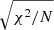varies between 0.4 for (324) Bamberga and 100 for (4) Vesta (Fig. 6). Again, the misfits must be estimated without ignoring the correlations in Eq. (5); taking these correlations into account, we get misfits close to one, greater than one, or much greater than one, which means that most of the asteroids do not match the Maclaurin or Jacobi sequences (a misfit of, for example, 5 has a probability of only ≈10−16 of occurring if the variable follows a χ2 law). Only 10 of the 42 asteroids have a misfit lower than or close to 1. Therefore, once again, we cannot exclude the possibility that a few asteroids have hydrostatic equilibrium figures.

thumbnail Fig. 6.

Misfit of asteroids with Maclaurin and Jacobi ellipsoids, ordered by increasing misfit. The asteroids closest to a Maclaurin ellipsoid are in blue, and those closest to a Jacobi ellipsoid are in red. The black dots represent the ordered medians for 42 random variables following a χ2 distribution. The green dot is the median for a single random variable following a χ2 distribution (it corresponds to the 21st asteroid and a misfit of 0.88). The misfits of the asteroids are well above the ordered medians, indicating that they are very unlikely to be Maclaurin or Jacobi ellipsoids overall. Individually, few asteroids have a misfit lower than the median of a single random variable, indicating that, even individually, few asteroids have a good probability of being Maclaurin or Jacobi ellipsoids.

However, this comparison must be expanded upon. The problem with comparing each individual misfit with 1 is that it does not take into account the increasing probability of having a false positive (i.e., having a small misfit by chance) when increasing the number of comparisons. Here, the probability that one of the 42 asteroids has the shape of a hydrostatic ellipsoid by chance is much higher than for a single asteroid. In statistics, this is known as a multiple comparison problem (Lehmann & Romano 2005), and it is taken into account by estimating a confidence level for the whole family of simultaneous tests (here the 42 tests). To do that, considering that the tests on asteroids are independent of one another, we computed the ordered medians of 42 random variables following a χ2 distribution (Fig. 6). All the asteroid misfits are above these random misfits. This means that, overall, the 42 asteroids do not match the sequence of Maclaurin or Jacobi ellipsoids.

Even restricted in the two dimensions c/a and c/b, the misfits (not given here) are important: the asteroids are not rotationally symmetric and do not have the axis ratios of Jacobi ellipsoids.

3.3. Asteroids are probably not hydrostatic

As a whole, asteroids observed by Vernazza et al. (2021) cannot be considered as Maclaurin or Jacobi ellipsoids. Not only does the relationship between their rotation rate and their shape not match that of a Maclaurin ellipsoid, but the asteroids have large deviations from axial symmetry.

There are at least three different possible reasons for this mismatch. The first is heterogeneity: a hydrostatic and radially ‘heterogeneous’ body takes a different shape than a Maclaurin or Jacobi ellipsoid. In this case, it is known that for low rotation rates, the aspect ratio c/a of the Clairaut ellipsoid is higher than that of a homogeneous body and is lower than that of a point mass (e.g., Tassoul 1978, p. 100 and Poincaré 1902, p. 73). This ratio interval corresponds to the hatched surface in Fig. 5 (bottom). For the very few asteroids that this applies to, the cause of the misfit may therefore be density stratification. This is typically the case for asteroid (31) Euphrosine, which could fit to a strongly heterogeneous hydrostatic figure (Yang et al. 2020), and for Ceres (Rambaux et al. 2015; Park et al. 2016), which is not far from rotational symmetry and has almost the angular velocity of a Maclaurin ellipsoid. The second and most common reason for the mismatch is that the asteroids are not in rotational hydrostatic equilibrium (even if they are ellipsoidal). The deviation from a hydrostatic shape is related to the existence of shear stresses. Such stresses are limited by the strength of the rocks but are also proportional to the weight of the topography (i.e., the height of the relief times gravity). As the topography features are limited by gravity, the largest celestial bodies have proportionally lower reliefs. On the contrary, small rocky bodies, typically with radii of less than a few hundred kilometres, generally do not have sufficient gravity to fracture rocks. If these bodies are made of coherent material, then they can have large topographies. This is why non-hydrostatic theories should be more suitable for small bodies such as asteroids (for non-hydrostatic studies, see e.g., Johnson & McGetchin 1973; Holsapple 2001, 2004, 2007; Richardson et al. 2005; Chambat & Valette 2008; Sharma et al. 2009; Al-Attar 2011). A few asteroids have a small misfit and could be investigated in more detail to determine if they are nearly homogeneous hydrostatic ellipsoids. For example, (324) Bamberga, (24) Themis, (187) Lamberta, (173) Ino, (88) Thisbe, (704) Interamnia, (10) Hygiea, (29) Amphitrite, and (354) Eleonora have misfits smaller than one.

In this Letter we have thus far considered asteroids as ellipsoids; more exactly, we have identified each asteroid with its best fitting ellipsoid as determined by Vernazza et al. (2021). However, the non-ellipsoidal topography is also a non-hydrostatic signature. We have not taken into account this third possible reason for a mismatch between asteroids and hydrostatic shapes. A major source of topography are impacts. For example, (2) Pallas or (4) Vesta have heavily cratered surfaces, probably linked to the origin of a collisional family (Karimi et al. 2017; Marsset et al. 2020; Vernazza et al. 2021). The deep depressions observed at their poles make them distinct from equilibrium figures.

Acknowledgments

We thank Keith Holsapple for the idea of the shaded region in Fig. 1 and for other useful remarks. We thank Emmanuel Lellouch for improvements of the manuscript.

References

  1. Al-Attar, D. 2011, PhD Thesis, Oxford University, UK [Google Scholar]
  2. Bertotti, B., Farinella, P., & Vokrouhlicky, D. 2012, in Physics of the Solar System: Dynamics and Evolution, Space Physics, and Spacetime Structure, (Dordrecht: Springer Science + Business Media), Astrophysics and Space Science Library, 293 [Google Scholar]
  3. Chambat, F., & Valette, B. 2008, J. Geophys. Res. Planets, 113, E02009 [NASA ADS] [CrossRef] [Google Scholar]
  4. Cowan, G. 1998, Statistical Data Analysis (Oxford: Oxford University Press) [Google Scholar]
  5. Holsapple, K. 2001, Icarus, 154, 432 [NASA ADS] [CrossRef] [Google Scholar]
  6. Holsapple, K. A. 2004, Icarus, 172, 272 [NASA ADS] [CrossRef] [Google Scholar]
  7. Holsapple, K. A. 2007, Icarus, 187, 500 [NASA ADS] [CrossRef] [Google Scholar]
  8. Jacobi, C. G. J. 1834, Poggendorf Annalen der Physik und Chemie, 33, 229 [NASA ADS] [CrossRef] [Google Scholar]
  9. Johnson, T., & McGetchin, T. 1973, Icarus, 18, 612 [NASA ADS] [CrossRef] [Google Scholar]
  10. Karimi, R., Ardalan, A. A., & Farahani, S. V. 2017, Earth Planet. Sci. Lett., 475, 71 [CrossRef] [Google Scholar]
  11. Lehmann, E., & Romano, J. 2005, Testing Statistical Hypotheses, 3rd edn. (New-York: Springer) [Google Scholar]
  12. Liapounov, A. 1884, Thesis translated in french in Annales de la Faculté des sciences de Toulouse: Mathématiques, 2e série, 1904, 6, 5 [Google Scholar]
  13. Maclaurin, C. 1741, Pièces qui ont remporté le prix de l’Académie royale des sciences en 1740 sur le flux et reflux de la mer (Paris: G. Martin, J.B. Coignard et Frères Guerin), 193 [Google Scholar]
  14. Marsset, M., Brož, M., Vernazza, P., et al. 2020, Nat. Astron., 4, 569 [NASA ADS] [CrossRef] [Google Scholar]
  15. Ostro, S. J., Scott, R., Nolan, M. C., et al. 2000, Science, 288, 836 [CrossRef] [Google Scholar]
  16. Park, R., Konopliv, A., Bills, B., et al. 2016, Nature, 537, 515 [NASA ADS] [CrossRef] [Google Scholar]
  17. Poincaré, H. 1885, Bull. Astron., 2, 109 [CrossRef] [Google Scholar]
  18. Poincaré, H. 1902, Figures d’équilibre d’une masse fluide (Paris: Gauthier Villars) [Google Scholar]
  19. Rambaux, N., Chambat, F., & Castillo-Rogez, J. 2015, A&A, 584, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. Richardson, D. C., Elankumaran, P., & Sanderson, R. E. 2005, Icarus, 173, 349 [NASA ADS] [CrossRef] [Google Scholar]
  21. Sharma, I., Jenkins, J. T., & Burns, J. A. 2009, Icarus, 200, 304 [NASA ADS] [CrossRef] [Google Scholar]
  22. Tassoul, J.-L. 1978, Theory of Rotating Stars (Princeton: Princeton University Press) [Google Scholar]
  23. Vernazza, P., Ferrais, M., Jorda, L., et al. 2021, A&A, 654, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Yang, B., Hanuš, J., Carry, B., et al. 2020, A&A, 641, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

All Figures

thumbnail Fig. 1.

Normalised angular velocity, Ω, as a function of the normalised angular momentum, H, for the 42 asteroids (see also Vernazza et al. 2021, Fig. 6). Predictions for the Maclaurin ellipsoids are shown in blue and those for Jacobi ellipsoids in red. The H = 0 value on the left corresponds to the sphere, and the very flattened objects are on the right. The shaded region corresponds to all ellipsoids with 0.5 ≤ c/a ≤ 1. Though this is a large aspect ratio interval, the region is narrow: this representation is not appropriate for evaluating the compatibility of asteroids with Maclaurin ellipsoids.
In the text
thumbnail Fig. 2.

Square of the normalised angular velocity of the 42 asteroids as a function of the aspect ratio c/a and their error bars. Predictions for the Maclaurin ellipsoids are shown in blue and those for the Jacobi ellipsoids in red. All error bars in the paper are at 1 sigma. The c/a = 1 value on the left corresponds to the sphere, and the very flattened objects are on the right. Even taking the large error bars into account, most asteroids are far from the curves of the Maclaurin and Jacobi ellipsoids. In the data published by Vernazza et al. (2021, Table A.1), two asteroids have axes b < c; we consider this to be an exchange of values between b and c.
In the text
thumbnail Fig. 3.

Same as Fig. 1 but with the correlated error bars. They indicate that the points are statistically far from the curve despite being visually close.
In the text
thumbnail Fig. 4.

Aspect ratios of the asteroids. Shown are curves of the Maclaurin (blue) and Jacobi (red) ellipsoids. The c/a = 1 value on the left corresponds to the sphere, and the most flattened objects are on the right. The asteroids are not globally on the curve of the Maclaurin or Jacobi ellipsoids.
In the text
thumbnail Fig. 5.

Same as Figs. 4 (top) and 2 (bottom) but without error bars and with asteroid numbers. See Vernazza et al. (2021, Table 1) for the correspondences between numbers and asteroid names. The bottom panel shows a zoomed-in view of the x-axis to exclude the red point that corresponds to (216) Kleopatra, which has already been identified as a dumbbell body (Ostro et al. 2000). The asteroids closest to a Maclaurin ellipsoid are in blue, and those closest to a Jacobi ellipsoid are in red. This shows that the projections formed by these two figures can be misleading with respect to a 3D misfit. In the bottom panel, we have hatched the surface that corresponds to possible Clairaut ellipsoids (see Sect. 3.3).
In the text
thumbnail Fig. 6.

Misfit of asteroids with Maclaurin and Jacobi ellipsoids, ordered by increasing misfit. The asteroids closest to a Maclaurin ellipsoid are in blue, and those closest to a Jacobi ellipsoid are in red. The black dots represent the ordered medians for 42 random variables following a χ2 distribution. The green dot is the median for a single random variable following a χ2 distribution (it corresponds to the 21st asteroid and a misfit of 0.88). The misfits of the asteroids are well above the ordered medians, indicating that they are very unlikely to be Maclaurin or Jacobi ellipsoids overall. Individually, few asteroids have a misfit lower than the median of a single random variable, indicating that, even individually, few asteroids have a good probability of being Maclaurin or Jacobi ellipsoids.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.