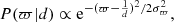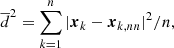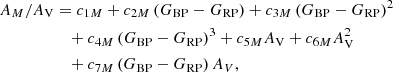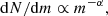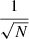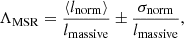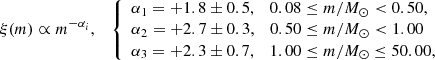| Issue |
A&A
Volume 675, July 2023
|
|
|---|---|---|
| Article Number | A67 | |
| Number of page(s) | 10 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/202244737 | |
| Published online | 03 July 2023 | |
Cluster aggregates surrounding Pismis 5 in the Vela molecular ridge⋆
1
Xinjiang Astronomical Observatory, Chinese Academy of Sciences, No. 150, Science 1 Stree, Urumqi, Xinjiang, 830011
PR China
e-mail: zhy@xao.ac.cn
2
School of Astronomy and Space Science, University of Chinese Academy of Sciences, 19 Yuquan Road, Shijingshan District, Beijing, 100049
PR China
3
School of Physical Science and Technology, Xinjiang University, No. 777, Huarui Street, Urumqi, Xinjiang, 830017
PR China
Received:
11
August
2022
Accepted:
31
March
2023
Context. In the Gaia era, the precision of astrometric data is unprecedented. High-quality data make it easier to find more cluster aggregates and gather further confirmation of these open clusters.
Aims. We use Gaia Data Release 3 (DR3) to redetermine the open clusters surrounding Pismis 5 in the Vela molecular ridge (VMR). We also investigate the basic properties of these clusters.
Methods. We applied two clustering algorithms (STARGO and pyUPMASK) to identify the open-cluster members in five-dimensional space with α, δ, ϖ, μαcos δ, and μδ.
Results. We identify eight open clusters surrounding Pismis 5 in the VMR. The open cluster QZ 1 is newly discovered. As a result of our investigation of the comprehensive properties of the clusters, we present one open binary cluster candidate (Alessi 43 and Collinder 197) and one triple open-cluster candidate (Pismis 5, Pismis 5A, and Pismis 5B).
Conclusions. We identify binary and triple open-cluster candidates as potential primordial aggregates based on their similar age, position, and motion. According to kinematic speculations, the two aggregate candidates will gradually separate, and their interiors will slowly disintegrate.
Key words: open clusters and associations: general / Galaxy: stellar content
The table of member candidates for eight open clusters is only available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/675/A67.
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Open clusters are gravitationally bound systems of stars that share a common heritage from the same progenitor molecular cloud, resulting in members with similar ages, distances, and metal abundances. In particular, young open clusters contain young stellar objects in various evolutionary states and they are essential testbeds for understanding star formation and evolution (Lada & Lada 2003). Most open clusters are found in the Galactic disk, and their spatial distributions play critical roles in the study of the Galactic structure.
The Vela molecular ridge (VMR;260°≲ℓ≲272°;|b|≲3°) identified by Murphy & May (1991) is a giant molecular cloud located in Vela and Puppis. Murphy & May (1991) split the VMR into four clouds (named A, B, C, and D) according to local CO peaks. VMR A, VMR C, and VMR D are situated at 700 ± 200 pc from the sun, while VMR B is located at about 2000 pc, which means VMR B is not related to the other clouds. Therefore, our research only refers to the open clusters in the VMR A, VMR C, and VMR D. In the following, all instances of VMR refer to VMR A, VMR C and VMR D.
Pismis 5 (also known as ESO 313-SC7, l = 259.355 deg, b = 0.905 deg), is situated in the VMR at a distance of 947.6 pc from the Sun (Cantat-Gaudin & Anders 2020). It is a young open cluster with an estimated age of 7.6 million years according to Dias et al. (2021). It is also a low-mass open cluster, with a flat mass function and an irregular radial density profile (Bonatto & Bica 2009). There are several known open clusters surrounding Pismis 5 in the VMR, for example, Collinder 197, Alessi 43, and BH 56. Collinder 197 (l = 261.517 deg, b = 0.956 deg), Alessi 43 (also known as ASCC 50; l = 262.546 deg, b = 1.501 deg), and BH 56 (l = 264.470 deg b = 1.548 deg) are located at about 940 pc, 940 pc, and 903 pc, respectively, from the Sun (Cantat-Gaudin & Anders 2020). Collinder 197 and Alessi 43 form a binary open-cluster candidate, and were recognized to do so in previous studies due to their identical movements and near spatial proximity (de La Fuente Marcos & de La Fuente Marcos 2009; Piecka & Paunzen 2021). Furthermore, Liu & Pang (2019) use the FOF algorithm for member-star determination, and Collinder 197, Alessi 43, and BH 56 are considered to be a cluster group. In this paper, we study the fundamental nature of these clusters as a step towards further understanding the VMR.
In this work, we aim to discover previously neglected clusters surrounding Pismis 5 in the VMR through the STARGO1 (Yuan et al. 2018) and pyUPMASK (Pera et al. 2021) algorithms. This paper is organized as follows. Section 2 describes the process of data processing and the selection of cluster members. Section 3 displays the spatial and proper-motion distribution of clusters, as well as assessments of cluster characteristics such as age, stellar mass function, level of mass segregation, and initial stellar mass function. Our discussion and summary are presented in Sects. 4 and 5, respectively.
2. Data and membership analysis
Gaia data release 3 (Gaia DR3, Gaia Collaboration 2016, 2023) provides a catalog of 1.8 billion sources brighter than 21 mag in the G band, including parallax and proper motion values. Gaia DR3 includes 34 months of observations, a 12 month increase over Gaia DR2, and extends two magnitudes fainter than Gaia DR2. Furthermore, Gaia DR3 also includes 33 812 183 sources with radial velocity (RV) determinations, where RVs have a median formal precision of 1.3 and 6.4 km s−1 at GRVS = 12 and GRVS = 14 mag, respectively. These sources form the cornerstone of studies of the three-dimensional kinematics of open clusters (Katz et al. 2023). However, the determination of RVs is incomplete and cannot be used for member-star selection. Therefore, we use highly accurate five-dimensional astrometric data (α, δ, ϖ, μαcos δ, and μδ) provided by Gaia DR3 as the initial data with which to investigate open clusters surrounding Pismis 5 in the VMR.
2.1. Data processing and analysis
Firstly, the data with a radius of 250 pc centered on the Galactocentric coordinates2 (X, Y, Z) = (−8474.93, −931.18, 42.54) pc of Pismis 5 were chosen in order to include as many open clusters surrounding Pismis 5 in the VMR as possible. The coordinates of Pismis 5 were transformed from the α, δ, and parallax values adopted from Cantat-Gaudin & Anders (2020) via the Astronomical Coordinate Systems module of the Astropy Python package (Astropy Collaboration 2013, 2018)3. We corrected the parallax zero-points of all the sources using the procedure described by Lindegren et al. (2021). To minimize the impact of data uncertainties, we applied a series of filters to exclude artifacts and low-quality sources. We removed stars with relative uncertainties in parallax and photometry greater than 10%. Additionally, we discarded stars with renormalized unit weight errors (RUWEs) exceeding 1.4 because they indicate a potentially problematic astrometric solution (Fabricius et al. 2021). The data were incomplete beyond 18 mag, because the distribution of the G-band of the data clearly shows a truncation at 18 mag.
High-quality data enable us to investigate the open clusters in the target area more thoroughly, despite the fact that our quality cut implies a certain level of incompleteness. We used a set of selection criteria to identify sources with a stellar density of greater than 50% in their proper-motion distribution in right ascension and declination. The selection criteria were −8.89 ≤ μαcos δ ≤ −1.86 mas yr−1 and 0.03 ≤ μδ ≤ 8.00 mas yr−1. The reason for applying these criteria was to exclude the majority of the field stars, which would not be relevant for the more detailed data processing that follows. A total of 158 593 sources met our selection criteria and were retained as Sample 1.
Secondly, we constructed a two-dimensional (2D) histogram of the spatial distribution (l − b) to restrict the Sample 1 in Fig. 1a. This diagram only represents bins with overdensities > 3σ in Sample 1, where σ is the standard deviation of all bins. The overdensity in the histogram signifies the clustering of stars. We therefore tried to include high-density areas for the next member star identification. There are three overdensities in Fig. 1a, and the cyan box contains NGC 2546, referred to here as Sample 2, the black box contains Pismis 5, referred to as Sample 3, and the magenta box contains Alessi 43, Collinder 197, and BH 56, referred to as Sample 4, as revealed by the cluster information provided by Cantat-Gaudin & Anders (2020). Despite the fact that NGC 2546 (l = 254.919 deg, b = −2.009 deg, the blue box region in Fig. 1a) is not our target object located in the VMR, it was included in our initial sample and subsequently subjected to analysis. The sides of cyan, black, and magenta boxes in the l − b plane are 4, 2, and 3 deg in length, respectively. These values are a compromise between keeping more member stars and removing more field stars.
 |
Fig. 1. Two-dimensional histogram of Sample 1 in l − b plane and the results from SOM. (a): 2D histogram of the spatial distribution (l − b) of Sample 1, which only shows the bins with overdensities > 3σ. The NGC 2546 region, Pismis 5 region, and Alessi 43 region are each represented by a box in cyan, black, or magenta, respectively. The sources in the cyan, black, and magenta boxes are referred to as Sample 2, Sample 3, and Sample 4. (b), (c), and (d): 2D neural network produced by SOM, showing the neurons with a u value below the 99.85th percentile of the u distribution. |
2.2. Membership selection
There are several robust algorithms available for determining the membership of stars, including DBSCAN (Ester et al. 1996), FoF (Liu & Pang 2019), STARGO (Yuan et al. 2018), pyUPMASK (Pera et al. 2021), and others. We combine STARGO and pyUPMASK to determine the open-cluster member stars.
2.2.1. STARGO
The Stars’ Galactic Origin (STARGO) clustering method, developed by Yuan et al. (2018) and based on the self-organizing map (SOM). This algorithm will build a neural network, where each neuron is represented by a weight vector that is consistent with the dimension of the input data. SOM maps multidimensional input data onto a two-dimensional neural network using weight vectors. For each star we input, the weight vector of all neurons on the neural network will be changed according to the input vector. The difference in weight vectors between adjacent neurons is represented by the u value; the smaller the u, the more similar the neurons are. Finally, the algorithm will return a series of u values. In the case of uniformly distributed stellar fields, the distribution of u values should conform to a normal distribution. However, if the input sample contains clusters, the distribution of u values will consist of two parts: a normal distribution representing field stars and a small series of u values representing clusters. Connected blocks with smaller u values indicate more similar neurons, representing a group of stars that share similarities in the input data dimension. These identified groups serve as potential open cluster candidates. The successful application of STARGO in several studies (e.g., Tang et al. 2019; Zhang et al. 2020; Pang et al. 2021, 2022) further supports its reliability and effectiveness as a clustering method.
Using 1/ϖ as distance, we computed Galactocentric Cartesian coordinates (X, Y, Z) for each source from Sample 2, Sample 3, and Sample 4. We generated a 120 × 120 network and then entered the data (X, Y, Z, μαcos δ, and μδ) for each star from Sample 2, Sample 3, and Sample 4, respectively. After 400 iterations, we obtained the values of u for three samples and selected the u that were smaller than the 99.85th percentile of the u distribution. Our selection was equal to deleting any values greater than upeak (the peak position of the u distribution), and u values that were less than upeak but within 3σ (σ was the standard deviation of the normal distribution). As a result, the field star distributions were almost entirely removed. Neurons that passed our filter requirements were displayed as transparent patches in Figs. 1b, c, and d. When the threshold of u was lowered, SOM displayed neurons that are more similar, which were the core structures inside the transparent patches. After calculating the smallest difference between neurons in the transparent patches and neurons in each core patch, transparent neurons were assigned to the closest core block. Their colors aligned with the colors of their core patches. Each color patch represented an open-cluster candidate. The member candidates of eight open clusters were obtained by associating the stars from the patches.
2.2.2. pyUPMASK
To reduce the contamination rate of member stars, we use pyUPMASK for member-star selection. pyUPMASK is a modified version of Unsupervised Photometric Membership Assignment in Stellar Clusters (UPMASK; Krone-Martins & Moitinho 2014), an open-source package written in the Python language. pyUPMASK uses clustering methods with a random initialization to identify clumps, followed by an assessment of their level of clustering relative to random distribution. To eliminate spurious clusters generated by chance, it uses the K-function introduced by Ripley (1976, 1979) to assess the authenticity of the identified clusters. To mitigate contamination from field stars, pyUPMASK employs a Gaussian uniform mixture model. Lastly, it assesses the probability of cluster membership using kernel density estimation (KDE). The reliability and effectiveness of pyUPMASK has been demonstrated by its successful applications in Bai et al. (2022) and Qin et al. (2023).
We calculated the member probabilities of the samples by applying the pyUPMASK algorithm on Sample 2, Sample 3, and Sample 4. We combined the member star candidates selected by STARGO and the results of pyUPMASK using member probabilities to obtain member star candidates. We identified the open cluster in the NGC 2546 region as NGC 2546 (pink). The Pismis 5 region contained Pismis 5 (blue), two neighboring clusters, and a separate cluster. We labeled these two clusters Pismis 5A (red) and Pismis 5B (green), respectively, and designated another open cluster QZ 1 (magenta). The clusters in the Alessi 43 region were Alessi 43 (orange), Collinder 197 (purple), and BH 56 (brown). In all the diagrams below, the blue, red, green, magenta, purple, orange, brown, and pink dots represent Pismis 5, Pismis 5A, Pismis 5B, QZ 1, Collinder 197, Alessi 43, BH 56, and NGC 2546, respectively.
2.2.3. Decontamination in CMD
Performing field-star decontamination in color–magnitude diagrams (CMD) is a crucial step in identifying and characterizing star clusters. To calculate the cluster main sequence lines and their corresponding error positions, we used the Gaussian process-based regression method provided by Li et al. (2020). Data points are considered outliers if they deviate from the main sequence band by more than 3σ, being either bluer than the main sequence line or redder than the equal-mass-binary curve, where σ is the uncertainty caused by photometric errors and main sequence line errors. We remove outliers on both sides of the main sequence band and obtain candidate member stars for eight clusters. The resulting CMDs exhibit a low-noise main sequence after decontamination. Numbers for the cluster members are displayed in the second column of Table 1.
Parameters of eight open clusters in this paper.
2.3. Comparison with previous catalogs
Cantat-Gaudin & Anders (2020) give the member candidates of 2017 open clusters based on Gaia DR2, all of which have member probabilities of greater than or equal to 0.7. To maintain the same contamination rate, we also restrict the probability of member stars from Cantat-Gaudin & Anders (2020) to be greater than or equal to 0.9. We performed a cross-match4 between our clusters and the open-cluster catalog given by Cantat-Gaudin & Anders (2020). We matched to 53, 0, 0, 0, 168, 119, 56, and 34 member stars for the clusters Pismis 5, Pismis 5A, Pismis 5B, QZ 1, Alessi 43, Collinder 197, BH 56, and NGC 2546, respectively. In the list of Cantat-Gaudin & Anders (2020), Pismis 5, Alessi 43, Collinder 197, BH 56, and NGC 2546 have 57, 196, 161, 62, and 35 member candidates, respectively. These parameters are listed in the third column of the Table 1. Comparing our member candidates to the member candidates given by Cantat-Gaudin & Anders (2020), we discover that there is good agreement between the two member-candidate lists. There are also member candidates found by Cantat-Gaudin & Anders (2020) that are not in our list. We find that the majority of these stars do not meet our criteria because of their inferior photometric quality.
The open clusters OC-0467, OC-0469, and OC-0472 discovered by Hao et al. (2022) are in the region of Pismis 5. After matching, Pismis 5A has 57 member stars that are members of OC-0467, 15 member stars of OC-0469, and 1 member star of OC-0472, whereas Pismis 5B has 7 member stars that are members of OC-0467, 1 member star of OC-0469, and 2 member stars of OC-0472. Even though we employ two clustering methods in our work, we are unable to find OC-0467, OC-0469, or OC-0472. We call these two star clusters Pismis 5A and Pismis 5B. We have not found any known clusters sharing members with QZ 1, and therefore consider it to be a new open cluster.
3. General properties
3.1. Spatial distribution
We present the spatial distribution and corresponding errors of eight open clusters in Fig. 2a. Pismis 5 (l = 259.36 deg, b = 0.92 deg), Pismis 5A (l = 259.90 deg, b = 0.41 deg), Pismis 5B (l = 260.19 deg, b = 0.54 deg), QZ 1 (l = 258.96 deg, b = 0.23 deg), Alessi 43 (l = 262.52 deg, b = 1.49 deg), Collinder 197 (l = 261.53 deg, b = 0.94 deg), and BH 56 (l = 264.48 deg, b = 1.60 deg) are located in the VMR. NGC 2546 (l = 254.91 deg, b = −1.98 deg) is situated outside the VMR. The member candidates of Pismis 5, Pismis 5A, Pismis 5B, and QZ 1 are indistinguishable in the l − b plane. Alessi 43 and Collinder 197 also have member candidates that are indistinguishable. Except for QZ 1, BH 56, and NGC 2546, other star clusters are mixed and difficult to distinguish in proper-motion space, as seen in Fig. 2b. The information above suggests that the five clusters are possibly a large cluster aggregate, in which Pismis 5, Pismis 5A, and Pismis 5B form one set of sub-aggregate candidates, and Alessi 43 and Collinder 197 form the other.
 |
Fig. 2. Spatial and proper motion distribution of eight open clusters. (a): Spatial distribution of open clusters in the Galactic coordinate system. (b): Distribution of proper motions of eight open clusters. (c): Spatial distribution of open clusters in the Galactocentric Cartesian coordinate system on the X − Y plane. The stars with distance correction are shown by color dots, whereas the position of the members without distance correction is shown by grey dots in the background. The direction of the line of sight is shown by the grey arrow. The error bars are depicted in the three diagrams by the grey lines. The data errors in position and proper motion space are much smaller than the scale of the cluster itself. The contribution of errors to cluster search and identification is negligible. |
We studied the distribution of clusters in 3D space, and Fig. 2c gives the distribution of clusters in the X − Y plane. Every open cluster shows an apparent elongation along the line of sight. The extension is an artificial one caused by directly inverting the parallaxes to obtain the distances. Because the parallax error has a symmetric distribution function, introducing a skewed distribution of errors on the distance obtained by taking the reciprocal leads to a bias in estimating the distance (Carrera et al. 2019; Zhang et al. 2020; Pang et al. 2021, 2022). To alleviate this artificial elongation, previous studies (e.g., Pang et al. 2021, 2022; Ye et al. 2021) have employed the Bayesian approach outlined in Bailer-Jones (2015) and Carrera et al. (2019). And we also follow their method and adopt the prior consist of the density of the field stars and the cluster members in Ye et al. (2021).
where d0 is the predicted mean distance of cluster members, adopted as the inverted median of clusters. σd is the deviation of the distances between mparallaxesember stars and their cluster center. The coefficient C is the contamination fraction. Under the assumption of the Gaussian parallax uncertainties, the likelihood is
where 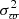 equals the quoted error bar on each parallax measurement, as used in Carrera et al. (2019). In Fig. 2c, the member stars with distance correction are more compactly distributed along the line of sight direction. Here we note that the distances through Bayesian parallax inversion effectively mitigate the elongation of open clusters. The median, 5%, and 95% quantiles of corrected distances for open clusters are listed in Table 1.
equals the quoted error bar on each parallax measurement, as used in Carrera et al. (2019). In Fig. 2c, the member stars with distance correction are more compactly distributed along the line of sight direction. Here we note that the distances through Bayesian parallax inversion effectively mitigate the elongation of open clusters. The median, 5%, and 95% quantiles of corrected distances for open clusters are listed in Table 1.
We get more precise 3D positions for the cluster member candidates after correcting for distance. Furthermore, we carry out Monte Carlo (MC) simulations to estimate the uncertainty in the 3D position transformed by α, δ, and distance. With the initial parameters serving as the mean and the associated uncertainties serving as the standard deviation, we resampled the α, δ, and distance of each source from a Gaussian distribution. We used 1000 resampled data to perform the coordinate conversion for each source, yielding 1000 3D positions for each star. The uncertainties of each star position were determined using the standard deviation of 1000 results. Due to the substantial distance uncertainties brought on by the parallax uncertainties, the uncertainties in the 3D position are greater than for the 2D ones.
In proper motion space, five open clusters are indistinguishable, but in the X − Y plane, we can see that the eight open clusters are distinct from one another. As a result, it can be inferred that Pismis 5, Pismis 5A, and Pismis 5B are three separate open clusters, and the overall region is a triple open-cluster candidate. Alessi 43 and Collinder 197 is also a binary open-cluster candidate.
3.2. Age determination
The CMD is also a common tool used to estimate the basic parameters of open clusters, including reddening, metallicity, and age. We present the CMDs of eight open clusters in Fig. 3. Only QZ 1 and NGC 2546 exhibit clear main sequence tracks; the other clusters have minor main sequence dispersion due to their location in molecular clouds, which are more extinct and younger.
 |
Fig. 3. CMDs of Pismis 5, Pismis 5A, Pismis 5B, QZ 1, Alessi 43, Collinder 197, BH 56, and NGC 2546. The solid lines are the isochrones from PARSEC and the corresponding parameters are marked in the figure. The dashed lines are the curve of equal-mass binaries. |
Gaia DR3 provides [Fe/H] values based on synthetic spectrum templates for main sequence stars of spectral types F-G-K. Therefore, we only use stars of spectral types F-G-K (effective temperatures between 3500 and 7500 K) as metallicity samples. We consider the medians of these samples to be the metallicity of the cluster for the isochrone fit. Table 1 provides the median, 5%, and 95% quantiles of metallicities. We use the PARSEC stellar evolution isochrones (Bressan et al. 2012; Chen et al. 2014) for the Gaia filters, to fit the isochrones of open clusters with an age range of 1 Myr to 1 Gyr, at steps of log age = 0.05. We use the following function (Liu & Pang 2019) to determine the best-fitting isochrone and obtain the value of AV:
where n is the number of members, and xk = [Gk + ΔG + AG, (GBP − GRP)k + (ABP − ARP)], xk, nn is the position of the kth member star and the nearest neighboring point to this star in the isochrone, respectively. The nearest neighboring point is searched for using the K–D Tree method.
The relations between AG, AGBP, and AGRP are calculated using the following formula:
where the subscript M indicates the G, GBP, and GRP band, and c1…7M belong to a set of coefficients defined in Table 1 of Gaia Collaboration (2018). We used these equations to get the square of the mean separation between each isochrone and its member stars. The Nelder-Mead algorithm, which is part of the “scipy” package (Virtanen et al. 2020), is used to determine the optimal age and AV. The isochrones are displayed in Fig. 3 and the corresponding parameters are listed in Table 1. The uncertainty in the fitted age for each cluster is considered to be twice the age step.
With the exception of NGC 2546 and QZ 1, the clusters are young and have similar ages. According to their ages, NGC 2546 is thought to have formed first, followed by QZ 1, Pismis 5, Collinder 197, BH 56, and Pismis 5B, with Pismis 5A and Alessi 43 forming last in that sequence. This phenomenon is called age spread (Lada & Lada 2003), and is due to the time needed for star formation and cluster gestation. The similar ages of Pismis 5, Pismis 5A, and Pismis 5B indicate that they are coeval. Pismis 5, Pismis 5A, and Pismis 5B have similar locations, kinematics, and metallicities, have young ages, and show little difference in age, implying that they are a primordial triple open-cluster candidate. Similarly, Alessi 43 and Collinder 197 are a primordial binary open-cluster candidate.
3.3. Mass function and mass segregation
3.3.1. Mass function
One of the most fundamental properties of an open cluster is its stellar mass. The stellar mass of members is estimated via the mass–magnitude relation of the PARSEC stellar-evolution isochrone, and we obtain stellar mass for each member candidate of eight open clusters. Table 1 also shows the total stellar mass of Pismis 5, Pismis 5A, Pismis 5B, QZ 1, Alessi 43, Collinder 197, BH 56, and NGC 2546. The mass function (MF) is the most basic distribution of clusters (Krumholz et al. 2019). The functional form of the mass function is:
where N is the number of member stars within the mass bin dm, and α is the slope of the mass function (Salpeter 1955). The members are incomplete beyond ∼18 mag. In order to obtain a more accurate mass function, we select stars with apparent magnitudes smaller than or equal to 18 mag. By using the linear least-squares fitting, we are able to determine the values of α for the mass functions shown in Fig. 4.
 |
Fig. 4. Present-day mass function of Pismis 5, Pismis 5A, Pismis 5B, QZ 1, Alessi 43, Collinder 197, BH 56, and NGC 2546. The stellar mass is assigned to each source by nearest-neighbor interpolation in the Gaia colour–magnitude space (BP − RP vs. MG) using the PARSEC isochrones. The Y-axis is shifted manually by 2 units so that the mass function of each cluster is visible. The dashed lines are the fitted mass functions and the quantity α is the fitted slope. The error bars represent Poissonian uncertainties ( |
The mass functions of the eight clusters exhibit varying degrees of smoothness, with NGC 2546 having the smoothest mass function, followed by BH 56, QZ 1, Pismis 5, Alessi 43, and Pismis 5A, while Collinder 197 and Pismis 5B have steeper mass functions. The proportion of low-mass stars decreases with a flatter mass function. On the one hand, we note that these clusters are far from the Sun and the low-mass stars may be too faint to be observed. As a result, the fraction of low-mass stars from clusters is affected by data incompleteness for the cluster. On the other hand, both internal and external forces have an impact on the loss of less massive stars. The less massive stars migrate to the outer regions of the cluster as they evolve due to internal relaxation, making them more vulnerable to being stripped away by Galactic tidal field.
The cluster NGC 2546, which is not part of the VMR, has the flattest mass function as many of its low-mass stars have already been lost to the Galactic tidal field. Similarly, BH 56, QZ 1, Pismis 5, and Alessi 43 are located at the periphery of the VMR region and have a flatter mass function in comparison to the clusters in the interior of the VMR (Pismis 5A, Pismis 5B, and Collinder 197), as they are more vulnerable to the loss of low-mass stars by external perturbations.
3.3.2. Mass segregation
Mass segregation is frequently observed in open clusters. We use the minimum spanning tree method provided by Allison et al. (2009) to measure the degree of mass segregation of eight open clusters. This method determines the length of the minimum spanning tree of the N most massive stars as lmassive, the average length of the minimum spanning tree of sets of N random stars as lnorm, and the standard deviation of the lengths lnorm as σnorm. Allison et al. (2009) define the “mass segregation ratio (MSR)” (ΛMSR) as the ratio between the average random path length and that of the massive stars:
where ΛMSR significantly > 1 indicated mass segregation, and ΛMSR ≤ 1 showed no mass segregation. To quantify the mass segregation of the 50 most massive members of the clusters, we divide these stars into five groups and use the Python package Minimum Spanning Trees (Mistree; Naidoo 2019) to calculate the mass segregation ratios of these five groups. The minimum spanning tree method is applied using the 3D positions of the members, and the results are displayed in Fig. 5. Only ten stars of Collinder 197 show mass segregation, but with large uncertainty, suggesting that mass segregation is not present in this cluster. Our analysis reveals that Pismis 5, Pismis 5A, Pismis 5B, Alessi 43, and BH 56 do not exhibit mass segregation. Therefore, among the eight target open clusters, only NGC 2546 and QZ 1 show significant evidence of mass segregation.
 |
Fig. 5. “Mass segregation ratio” (ΛMST) for the 50 most massive members with a bin size of 10 stars in the 3D spatial position of Pismis 5, Pismis 5A, Pismis 5B, QZ 1, Alessi 43, Collinder 197, BH 56, and NGC 2546. The dashed line (ΛMST = 1) indicates an absence of mass segregation. The increasing value of ΛMST indicates a more significant degree of mass segregation. The error bars indicate the uncertainties obtained from 100 realizations of lnormal. |
Mass segregation in star clusters may be either primordial or dynamical. The hierarchical formation scenario postulates that open clusters form in small clumps, which merge to form larger mass-segregated systems in young clusters. Dynamical mass segregation is the consequence of the equipartition of energy during the two-body encounters. N-body simulations suggest that mass segregation occurs on a timescale of a few million years (Tarricq et al. 2022). QZ 1 and NGC 2546 have ages of 56.23 and 112.20 Myr. It is very likely that they have lost the imprint of substructures from their parent molecular clouds. Therefore, the mass segregation of QZ 1 and NGC 2546 is probably caused by the equipartition of kinetic energy via two-body relaxation, which makes massive stars within clusters move toward their center, whereas lighter stars move toward the outskirts. The other clusters do not exhibit mass segregation, which is probably because they are younger and do not have enough time to dynamically evolve into a state of mass segregation.
3.3.3. Initial stellar mass
The evolution of a cluster is the result of cluster internal dynamics, gas expulsion, stellar evolution from a realistic initial stellar mass function, and the tidal field of the host galaxy (Dinnbier et al. 2022). Therefore, the initial stellar mass is an essential parameter for the cluster. We removed data beyond 18 mag to estimate the initial stellar mass of the cluster, because the data fainter than 18 mag are incomplete. As Pismis 5, Pismis 5A and Pismis 5B form a triple open-cluster candidate, we evaluate their initial stellar mass as a whole. Likewise, Alessi 43 and Collinder 197 are also considered as a whole. We use the initial mass function (IMF) given by Kroupa (2001). The multiple-part power-law IMF is represented by the following formula,
where ξ(m) dm is the number of stars in the mass interval m to m + dm, and α is the slope of the mass functions, the value of which varies with stellar mass. The lower and upper limits of the IMF are 0.08 M⊙ and 50 M⊙, respectively. We constructed mass-distribution histograms for the eight open clusters and used the IMF to create a series of mass histogram profiles with different initial masses, as shown in Fig. 6. BH 56 and QZ 1 have an initial stellar mass of about 500 M⊙, while the triple open-cluster candidate, the binary open-cluster candidate, and NGC 2546 all have an initial stellar mass of approximately 1000 M⊙.
 |
Fig. 6. Initial stellar mass estimation of the aggregate candidate Pismis 5, Pismis 5A, and Pismis 5B, (a) QZ 1; (b) aggregate candidate composed of Alessi 43 and Collinder 197; (c) BH 56 (d); and NGC 2546; (e) based on the IMF model (Kroupa 2001). The histograms, which are fitted with IMFs of varied total mass, show the observed mass distribution. |
We estimate that the triple and binary open-cluster candidates have lost roughly 54% and 36% of their stellar mass in comparison to the present-day stellar mass of clusters. The two older clusters, NGC 2546 and QZ 1, show significant mass segregation, losing mostly low-mass stars in the peripheral at moderate mass-loss rates of 48% and 41%, respectively. BH 56 has a stellar mass-loss rate of 56%, because it is situated at the boundary of the VMR in a complicated external environment that is prone to star loss. As these clusters reside in molecular clouds with significant extinction, the completeness of their member stars is greatly affected. The incompleteness of the member stars can lead to an underestimation of the initial mass. Therefore, the actual mass-loss rate ought to be higher than the one calculated now. Open clusters, as they evolve and keep losing stars, contribute to the field stellar populations; full disintegration happens when they can no longer be distinguished from the field in terms of stellar density.
4. Discussion
4.1. Kinematic analysis
We calculate the 3D velocities (U, V, W) in the Galactocentric Cartesian coordinates with Astropy using the proper motions and RVs from Gaia DR3. We take the median values of 3D velocities to represent the overall motion of the clusters. We utilize MC simulations (the same steps as procedures to estimate the uncertainties of the locations in Sect. 3.1) to estimate the uncertainties in the 3D velocities, and these are shown as gray error bars in Fig. 7a. The velocity errors are relatively small in the X and Z directions and large in the Y direction. But within the error range, the relative motion trend of the cluster remains unchanged.
 |
Fig. 7. Relative motions and orbits of eight open clusters. (a) The colored dots represent the members of eight open clusters and the larger dots represent the centers of the clusters. The directions of the arrows for Pismis 5A, Pismis 5B, QZ 1, and NGC 2546 indicate the direction of motion with respect to Pismis 5. The length of the arrows represents the magnitude of the velocity. The arrow directions for Alessi 43 and BH 56 represent the direction of movement relative to Collinder 197, and the length of the arrow represents the magnitude of the speed. The gray error bars represent the velocity uncertainties in the X, Y, and Z directions. (b) The orbits of eight open clusters. The stars display the position before 5 Myr, whereas the solid lines depict the orbits from before that time to the present. The cluster positions after 10 Myr are indicated by the squares, while the dotted lines depict the trajectory from the present to that point. The gray trajectory is the result of 1000 simulations, meaning the uncertainties of the orbit. |
We split the eight clusters into two groups in order to analyze the relative motion of the clusters. The first group includes Pismis 5, Pismis 5A, Pismis 5B, QZ 1, and NGC 2546, because QZ 1 and NGC 2546 are closer to the triple open cluster candidate. We obtain the relative motion of these four clusters with respect to Pismis 5. As shown in Fig. 7a, Pismis 5A, Pismis 5B, and QZ 1 will be far away from Pismis 5, indicating that members in the triple open-cluster candidate may gradually disperse. While NGC 2546 moves towards Pismis 5, it may gradually approach the triple open-cluster candidate in the future. The second group is made up of Alessi 43, Collinder 197, and BH 56. The motions of Alessi 43 and BH 56 relative to Collinder 197 are shown in Fig. 7a. Alessi 43 and BH 56 move away from Collinder 197, with BH 56 moving away from Collinder 197 more rapidly due to its higher velocity. The two aggregate candidates are also found to be separated from each other. The seven clusters in the VMR have a tendency to separate, and the NGC 2546 shows a trend towards moving closer to the VMR.
We use the Python galpy package (Bovy 2015)5 to calculate orbits of star clusters based on the data of position, proper motion, and RVs. As most of our open clusters are young, we backtrack their orbital motion by 5 Myr. In order to ensure the accuracy of the orbits, we only calculate the orbit of the next 10 Myr. To calculate the orbital uncertainty, we employ the MC simulation described in Sect. 3.1. As shown in Fig. 7b, the gray orbits represent the uncertainties in the cluster orbit.
After 10 Myr, BH 56 will be the cluster that is the furthest away from the other seven, possibly due to its high relative velocity. The NGC 2546 will be getting closer and closer to the binary and triple open-cluster candidates. Pismis 5, Pismis 5A, Pismis 5B, QZ 1, Alessi 43, and Collinder 197 have similar orbits. The separation between these six clusters is projected to gradually increase over the next 10 Myr. The members of the binary and triple open-cluster candidates are expected to progressively separate due to their orbital motions. This is in accordance with the star cluster kinematics tendency to move apart from one another.
4.2. Double/three or binary/triple?
Star clusters with slight angular separations are identified as double clusters. However, not all double clusters are binary clusters because a binary cluster means that the objects are gravitationally bound in a physical pair. The double clusters resulting from resonant trapping or hyperbolic encounters may share common kinematics or occupy a limited space but are not physical binary clusters.
There are several mechanisms for the formation of binary and multiple clusters. The cluster aggregates may have formed simultaneously in the same molecular cloud or stellar complex. Alternatively, the collapse of a nearby cloud induced by stellar winds or supernova shocks generated by one open cluster may trigger the formation of companion clusters, ultimately forming a cluster aggregate (Piecka & Paunzen 2021). These two processes create cluster aggregates, which are referred to as primordial cluster aggregates. Primordial cluster aggregates share similar spatial positions, kinematics, ages, and metallicities. Moreover, the cluster aggregates may also be formed completely separately and then be captured together by tidal forces. Generally, the captured cluster aggregates have similar spatial positions and kinematics but different ages and metallicities (de La Fuente Marcos & de La Fuente Marcos 2009).
We calculate the median of the RVs of each cluster to represent the overall RV of the cluster. And we compute 5% and 95% quantiles to provide the 90% central confidence interval for RVs in Table 1. The RVs for Pismis 5, Pismis 5A, and Pismis 5B are approximately 17.80 km s−1, 21.86 km s−1, and 17.29 km s−1, respectively, exhibiting slight variations among them. Combined with the proper motions, the three clusters have similar but not identical kinematics. In addition, these clusters exhibit a similar 3D spatial distribution, young ages, and a minimal difference in metallicity, and therefore they are a primordial triple open-cluster candidate. Similarly, the RVs of Alessi 43 and Collinder 197 are 17.96 and 25.20 km s−1, respectively. These two clusters are also a primordial binary open-cluster candidate.
According to the findings of the N-body simulation by de la Fuente Marcos & de la Fuente Marcos (2010), the evolution of the original binary cluster can come in one of three forms: merger, shredded secondaries, and separated twins. Darma et al. (2021) also prove that the proportion of binary and multiple clusters is higher in the Galactic environment at 20 Myr in N-body simulation. At 50 Myr, the proportion of merged clusters is higher. This demonstrates that the existence of binary and multiple star clusters is only temporary. Based on the kinematic analysis, we presume that the members of the binary and triple clusters will gradually separate. However, the gradual separation of multiple cluster members over the next 10 Myr does not mean they will become separate clusters. Priyatikanto et al. (2016) presented the orbits of the merging process of star clusters. Clusters can be separated from each other first then merge, or revolve and merge. Therefore, the cluster aggregate candidates in this work may merge, become separate clusters, or disintegrate.
4.3. Comparison with other works on VMR
The VMR is composed of three adjacent emission peaks, and it has been studied many times. Investigations of the VMR have focused on its young stellar objects (Pettersson & Reipurth 1994), the dense cores of Vela-D and Vela-C (Olmi et al. 2010; Massi et al. 2019), the H II regions (Prisinzano et al. 2018), and 3D structure (Hottier et al. 2021), most in association with an investigation of star formation in molecular clouds. The two investigations that are most relevant to our work are listed below.
Bonatto & Bica (2009) use data from the near-infrared Two-Micron All Sky Survey (2MASS)6 to identify member stars and investigate its age, radial density profile, mass function, and other properties. These authors estimated an age of 5 ± 4 Myr for the Pismis 5 main sequence stars, which is consistent with our result of 5 ± 0.6 Myr. They also obtained a mass function slope of −1.03 ± 0.19 for Pismis 5, while our result is −1.29 ± 0.17. There are differences between the parameters provided by Bonatto & Bica (2009) and those used here, which are most likely due to different initial data and different member star determination methods. While these latter authors use field decontamination, we use a clustering algorithm that combines STARGO and pyUPMASK. The triple cluster we find was discovered using 5D data, whereas Pismis 5A and Pismis 5B are not significantly clustered in 2D position space. Field decontamination might miss Pismis 5A and Pismis 5B in the RA − Dec plane. It is also possible to consider this triple open-cluster candidate as one cluster without considering other dimensions.
By cross-matching near-infrared 2MASS data with the Gaia DR2 catalog, Hottier et al. (2021) use the FEDReD (Field Extinction-Distance Relation Deconvolver) algorithm to unravel the 3D structure of Vela. These authors obtain a 3D cube of extinction density, as well as measurements of 14 dense extinction clouds and nine cavities. We compare the eight clusters to the structures they obtained and find that, except for NGC 2546, the remaining seven clusters are in density clump 1 and clump 3 obtained by Hottier et al. (2021). The center of clump 1 is l = 261.74, b = −0.75 deg, and the distance of it ranges from 750 to 3300 pc. The clump 1 contains Pismis 5, Pismis 5A, Pismis 5B, and QZ 1. The clump 3 is adjacent to clump 1 in l − b space and the center of clump 3 is l = 261.74, b = −0.75 deg. The distance from clump 3 to the Sun ranges from 470 to 1660 pc. The clump 3 contains Alessi 43, Collinder 197, and BH 56. The positions of our target clusters are consistent with the high-density clouds in their Fig. 4, which demonstrates the reliability of the clusters we identified.
5. Conclusions
Using highly precise astrometric data of Gaia DR3, we obtained eight clusters using STARGO and pyUPMASK with a membership probability of at least 90%. All open clusters are located in the VMR except for NGC 2546. One of the eight clusters is discovered by us for the first time, and we name it QZ 1. Pismis 5, Pismis 5A, and Pismis 5B are identified as a triple open-cluster candidate because of their close distribution in 3D space and their common kinematics. Alessi 43 and Collinder 197 are also recognized as a binary open-cluster candidate. With the exception of NGC 2546 and QZ 1, all clusters are relatively young and of similar age. Therefore, both triple and binary open-cluster candidates are primordial aggregate candidates. The NGC 2546 and QZ 1 have evolved mass segregation, which may be caused by dynamical evolution. The smoothest mass function of NGC 2546 may be caused by the loss of low-mass stars due to the external environment and the incompleteness of the data.
Through the relative motions of the clusters, we find that Pismis 5A, Pismis 5B, and QZ 1 have a tendency to move away from Pismis 5, whereas NGC 2546 is migrating toward the triple open-cluster candidate. Alessi 43 and BH 56 are moving away from Collinder 197, with BH 56 exhibiting a higher velocity. These motion trends suggest that the open clusters in the VMR are slowly separating from each other. Moreover, the orbital motions of the clusters confirm that the distance between them is gradually increasing. It is likely that the triple and binary open-cluster candidates may gradually separate or disintegrate in the future.
The origin of the Cartesian Galactocentric coordinate system is the Galactic center (l = 0° and b = 0°). The Galactocentric coordinates have a positive x direction pointing from the position of the Sun projected to the Galactic midplane to the Galactic center; the positive y-axis points toward l = 90° and the positive z-axis points toward b = 90°.
For the package, we adopted the values for the Galactocentric coordinate frame, namely: ICRS coordinates (α, δ) of the Galactic center = (266.4051, −28.936175) deg; Galactocentric distance of the Sun = 8.3 kpc, and the height of the Sun above the Galactic midplane = 27.0 pc (Tang et al. 2019).
Our cross-match bases on α and δ, and if the difference between the coordinates of the two stars is less than one arcsecond, then they are considered as the same star with TOPCAT (Taylor 2005).
The 2MASS, All Sky data release (Skrutskie et al. 2006) http://www.ipac.caltech.edu/2mass/releases/allsky/
Acknowledgments
The authors thank the reviewer for the very helpful comments and suggestions. The authors acknowledge the Chinese Academy of Sciences (CAS) “Light of West China” Program, No. 2022-XBQNXZ-013, the Natural Science Foundation of Xinjiang Uygur Autonomous Region, No. 2022D01E86, National Natural Science Foundation of China under grant U2031204, the National Key R & D program of China for Intergovernmental Scientific and Technological Innovation Cooperation Project under No. 2022YFE0126200 and the science research grants from the China Manned Space Project with NO. CMS-CSST-2021-A08. M.Q. thanks Ali Esamdin, Hubiao Nui, Xianhao Ye, Xiaokun Hou, and Guimei Liu for helpful discussions. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. All member stars of the cluster in this work will be released online. Software: Astropy (Astropy Collaboration 2013, 2018), Mistree (Naidoo 2019), galpy (Bovy 2015), Scipy (Virtanen et al. 2020), TOPCAT (Taylor 2005).
References
- Allison, R. J., Goodwin, S. P., Parker, R. J., et al. 2009, MNRAS, 395, 1449 [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Bai, L., Zhong, J., Chen, L., et al. 2022, RAA, 22, 055022 [NASA ADS] [Google Scholar]
- Bailer-Jones, C. A. L. 2015, PASP, 127, 994 [Google Scholar]
- Bisht, D., Yadav, R. K. S., Ganesh, S., et al. 2019, MNRAS, 482, 1471 [NASA ADS] [CrossRef] [Google Scholar]
- Bonatto, C., & Bica, E. 2009, MNRAS, 397, 1915 [CrossRef] [Google Scholar]
- Bovy, J. 2015, ApJS, 216, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Cantat-Gaudin, T., & Anders, F. 2020, A&A, 633, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carrera, R., Pasquato, M., Vallenari, A., et al. 2019, A&A, 627, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, Y., Girardi, L., Bressan, A., et al. 2014, MNRAS, 444, 2525 [Google Scholar]
- Darma, R., Arifyanto, M. I., & Kouwenhoven, M. B. N. 2021, MNRAS, 506, 4603 [NASA ADS] [CrossRef] [Google Scholar]
- de La Fuente Marcos, R., & de La Fuente Marcos, C. 2009, A&A, 500, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de la Fuente Marcos, R., & de la Fuente Marcos, C. 2010, ApJ, 719, 104 [CrossRef] [Google Scholar]
- Dias, W. S., Monteiro, H., Moitinho, A., et al. 2021, MNRAS, 504, 356 [NASA ADS] [CrossRef] [Google Scholar]
- Dinnbier, F., Kroupa, P., & Anderson, R. I. 2022, A&A, 660, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ester, M., Kriegel, H. P., Sander, J., & Xu, X. 1996, Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, KDD’96 (AAAI Press), 226 [Google Scholar]
- Fabricius, C., Luri, X., Arenou, F., et al. 2021, A&A, 649, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Drimmel, R., et al.) 2023, A&A, 674, A37 [CrossRef] [EDP Sciences] [Google Scholar]
- Hao, C. J., Xu, Y., Wu, Z. Y., et al. 2022, A&A, 660, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hottier, C., Babusiaux, C., & Arenou, F. 2021, A&A, 655, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Katz, D., Sartoretti, P., Guerrier, A., et al. 2023, A&A, 674, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krone-Martins, A., & Moitinho, A. 2014, A&A, 561, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., McKee, C. F., & Bland-Hawthorn, J. 2019, ARA&A, 57, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., & Lada, E. A. 2003, ARA&A, 41, 57 [Google Scholar]
- Lindegren, L., Hernández, J., Bombrun, A., et al. 2018, A&A, 616, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lindegren, L., Klioner, S. A., Hernández, J., et al. 2021, A&A, 649, A2 [EDP Sciences] [Google Scholar]
- Liu, L., & Pang, X. 2019, ApJS, 245, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Li, L., Shao, Z., Li, Z.-Z., et al. 2020, ApJ, 901, 49 [Google Scholar]
- Massi, F., Weiss, A., Elia, D., et al. 2019, A&A, 628, A110 [EDP Sciences] [Google Scholar]
- Murphy, D. C., & May, J. 1991, A&A, 247, 202 [NASA ADS] [Google Scholar]
- Naidoo, K. 2019, J. Open Source Softw., 4, 1721 [NASA ADS] [CrossRef] [Google Scholar]
- Olmi, L., Anglés-Alcázar, D., De Luca, M., et al. 2010, ApJ, 723, 1065 [NASA ADS] [CrossRef] [Google Scholar]
- Pang, X., Li, Y., Yu, Z., et al. 2021, ApJ, 912, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Pang, X., Tang, S.-Y., Li, Y., et al. 2022, ApJ, 931, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Pera, M. S., Perren, G. I., Moitinho, A., et al. 2021, A&A, 650, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pettersson, B., & Reipurth, B. 1994, A&AS, 104, 233 [NASA ADS] [Google Scholar]
- Piecka, M., & Paunzen, E. 2021, A&A, 649, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prisinzano, L., Damiani, F., Guarcello, M. G., et al. 2018, A&A, 617, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Priyatikanto, R., Kouwenhoven, M. B. N., Arifyanto, M. I., et al. 2016, MNRAS, 457, 1339 [NASA ADS] [CrossRef] [Google Scholar]
- Qin, S., Zhong, J., Tang, T., et al. 2023, ApJS, 265, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Ripley, B. D. 1976, J. Appl. Probab., 13, 255 [CrossRef] [Google Scholar]
- Ripley, B. D. 1979, J. R. Stat. Soc. Ser. B (Methodol.), 41, 368 [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Tarricq, Y., Soubiran, C., Casamiquela, L., et al. 2022, A&A, 659, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tang, S.-Y., Pang, X., Yuan, Z., et al. 2019, ApJ, 877, 12 [Google Scholar]
- Taylor, M. B. 2005, ASP Conf. Ser., 347, 29 [Google Scholar]
- Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Methods, 17, 261 [Google Scholar]
- Ye, X., Zhao, J., Zhang, J., et al. 2021, AJ, 162, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, Z., Chang, J., Banerjee, P., et al. 2018, ApJ, 863, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Y., Tang, S.-Y., Chen, W. P., et al. 2020, ApJ, 889, 99 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Two-dimensional histogram of Sample 1 in l − b plane and the results from SOM. (a): 2D histogram of the spatial distribution (l − b) of Sample 1, which only shows the bins with overdensities > 3σ. The NGC 2546 region, Pismis 5 region, and Alessi 43 region are each represented by a box in cyan, black, or magenta, respectively. The sources in the cyan, black, and magenta boxes are referred to as Sample 2, Sample 3, and Sample 4. (b), (c), and (d): 2D neural network produced by SOM, showing the neurons with a u value below the 99.85th percentile of the u distribution. |
| In the text | |
 |
Fig. 2. Spatial and proper motion distribution of eight open clusters. (a): Spatial distribution of open clusters in the Galactic coordinate system. (b): Distribution of proper motions of eight open clusters. (c): Spatial distribution of open clusters in the Galactocentric Cartesian coordinate system on the X − Y plane. The stars with distance correction are shown by color dots, whereas the position of the members without distance correction is shown by grey dots in the background. The direction of the line of sight is shown by the grey arrow. The error bars are depicted in the three diagrams by the grey lines. The data errors in position and proper motion space are much smaller than the scale of the cluster itself. The contribution of errors to cluster search and identification is negligible. |
| In the text | |
 |
Fig. 3. CMDs of Pismis 5, Pismis 5A, Pismis 5B, QZ 1, Alessi 43, Collinder 197, BH 56, and NGC 2546. The solid lines are the isochrones from PARSEC and the corresponding parameters are marked in the figure. The dashed lines are the curve of equal-mass binaries. |
| In the text | |
 |
Fig. 4. Present-day mass function of Pismis 5, Pismis 5A, Pismis 5B, QZ 1, Alessi 43, Collinder 197, BH 56, and NGC 2546. The stellar mass is assigned to each source by nearest-neighbor interpolation in the Gaia colour–magnitude space (BP − RP vs. MG) using the PARSEC isochrones. The Y-axis is shifted manually by 2 units so that the mass function of each cluster is visible. The dashed lines are the fitted mass functions and the quantity α is the fitted slope. The error bars represent Poissonian uncertainties ( |
| In the text | |
 |
Fig. 5. “Mass segregation ratio” (ΛMST) for the 50 most massive members with a bin size of 10 stars in the 3D spatial position of Pismis 5, Pismis 5A, Pismis 5B, QZ 1, Alessi 43, Collinder 197, BH 56, and NGC 2546. The dashed line (ΛMST = 1) indicates an absence of mass segregation. The increasing value of ΛMST indicates a more significant degree of mass segregation. The error bars indicate the uncertainties obtained from 100 realizations of lnormal. |
| In the text | |
 |
Fig. 6. Initial stellar mass estimation of the aggregate candidate Pismis 5, Pismis 5A, and Pismis 5B, (a) QZ 1; (b) aggregate candidate composed of Alessi 43 and Collinder 197; (c) BH 56 (d); and NGC 2546; (e) based on the IMF model (Kroupa 2001). The histograms, which are fitted with IMFs of varied total mass, show the observed mass distribution. |
| In the text | |
 |
Fig. 7. Relative motions and orbits of eight open clusters. (a) The colored dots represent the members of eight open clusters and the larger dots represent the centers of the clusters. The directions of the arrows for Pismis 5A, Pismis 5B, QZ 1, and NGC 2546 indicate the direction of motion with respect to Pismis 5. The length of the arrows represents the magnitude of the velocity. The arrow directions for Alessi 43 and BH 56 represent the direction of movement relative to Collinder 197, and the length of the arrow represents the magnitude of the speed. The gray error bars represent the velocity uncertainties in the X, Y, and Z directions. (b) The orbits of eight open clusters. The stars display the position before 5 Myr, whereas the solid lines depict the orbits from before that time to the present. The cluster positions after 10 Myr are indicated by the squares, while the dotted lines depict the trajectory from the present to that point. The gray trajectory is the result of 1000 simulations, meaning the uncertainties of the orbit. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} P\left( d \right) \propto C \cdot d^{2} \mathrm{e}^{-\frac{d}{8 \mathrm{[kpc]} }} + \left( 1-C \right) \cdot \frac{1}{\sqrt{2\pi \sigma _{d}^{2}}}\mathrm{e}^{-\frac{(d-d_{0})^2}{2 \sigma _{d}^{2}}}, \end{aligned} $$](/articles/aa/full_html/2023/07/aa44737-22/aa44737-22-eq1.gif)