EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 673 (May 2023) A&A, 673 (2023) A118 Full HTML
Open Access
Issue
A&A
Volume 673, May 2023
Article Number A118
Number of page(s) 8
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/202345854
Published online 17 May 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

Polycyclic aromatic hydrocarbons (PAHs) have attracted the attention of the astrochemistry community since the early 1980s when Leger & Puget (1984) proposed that the unidentified infrared (IR) emission from dust grains was due to the C-H stretching modes of the edge of hydrogenated graphite. Although there is observational evidence of the presence of these aromatic hydrocarbons, their identification is not robust yet. Indirect proof of the presence of PAHs is the detection of the fullerenes C60 and C70 in the ejecta of dying stars (Cami et al. 2010). However, the most intriguing issue is how PAHs form under interstellar conditions. Two approaches have traditionally been considered: top-down and bottom-up (Reizer et al. 2022). The top-down scenario assumes that PAHs form from the destruction of high-mass carbon allotropes like graphite and graphene. Several mechanisms has been proposed for the breaking off of such structures, such as the hydrogenation of graphene (Merino et al. 2014) or the photodissociation of large dust particles of graphite in photon-dominated regions (PDRs; Boersma et al. 2013, 2015). In contrast, the bottom-up scenario considers that PAHs are synthesised from the association of smaller molecules. The latter approach is supported by the recent discovery of highly abundant cyclic hydrocarbons in molecular dark clouds. Some aromatic and conjugated cycles such as indene (c-C9H8) and cyclopentadiene (c-C5H5) have recently been detected in the TMC-1 molecular cloud (Cernicharo et al. 2021b; McGuire et al. 2021), as have other cyclopentadiene derivatives such as two isomers of ethynyl cyclopentadiene (c-C5H5) and fulvenallene (c-C7H6; Cernicharo et al. 2021d, 2022). Simpler three-membered rings such as c-C3H2 (Turner et al. 2000; Fosse et al. 2001), ethynyl cyclopropenylidene (c-C3HCCH; Cernicharo et al. 2021b), and the cyclic c-C5H radical (Cabezas et al. 2022) have also been detected towards the same cloud. The relative abundance of these cyclic hydrocarbons with respect to H2 is high: 1.6 × 10−9 for indene, 1.2 × 10−9 for cyclopentadiene, 1.4 × 10−10 and 2.0 × 10−10 for 1- and 2-ethynyl cyclopentadiene, 2.7 × 10−10 for fulvenallene, 3.1 × 10−11 for ethynyl cyclopropenylidene, and 5.9 × 10−9 for the c-C5H radical. However, it is not known why and how these species can be formed and can reach such high abundances.

Numerous efforts have been made to try to explain the formation of naphthalene (c-C10H8), the simplest PAH. However, it has never been detected in the ISM. This pursuit has also been notable for indene; although not strictly a PAH, it shows the ideal chemical structure for a potential precursor. Frequently used precursors to explain the formation of complex polycyclic hydrocarbons are vinylacetylene (C4H4) and the propargyl radical (C3H3) due to their high abundances (1.2 × 10−9 and 8.7 × 10−9, respectively) in cold molecular clouds (Cernicharo et al. 2021a; Agúndez et al. 2021, 2022). The latter has demonstrated to play an important role in the formation of naphthalene in combustion and circumstellar envelope conditions (Mebel et al. 2017).

Taking into account the narrow variety of hydrocarbon radicals detected in the ISM, and the difficulty in finding a reaction that explains the formation of complex hydrocarbons in dark clouds, sometimes it might be necessary to resort to molecules not detected yet, which is the reason for choosing hydrocarbons such as styrene (c-C9H8) and the phenyl radical (c-C6H5) to explain the formation of indene (Doddipatla et al. 2021; Mebel et al. 2017). Or it might be necessary to resort to highly dehydrogenated benzenes to explain the formation of complex PAHs (Hanine et al. 2020). The incorporation of yet undetected simpler molecules such as the vinyl radical (C2H3) in astrochemical models is also needed to explain the abundances of more complex hydrocarbons (Cernicharo et al. 2021b,d,c). The formation of vinyl radical is expected to be viable under ISM conditions through reactions on dust grains of atomic hydrogen and hydroxyl radical with ethylene (Molpeceres & Rivilla 2022). Since the interstellar abundance of the species involved in the formation of C2H3 is likely high (Molpeceres & Rivilla 2022), it is expected that the abundance of C2H3 is high as well.

Another good candidate that may lead to PAHs is cyclopentadienyl radical (c-C5H5). Very recently, Kaiser et al. (2022) have demonstrated that the reaction between cyclopentadienyl radical and methyl radical yields benzene, and that the recombination of the former leads to naphthalene in typical conditions of circumstellar environments and combustion conditions. Unfortunately, the cyclopentadienyl radical has a very low dipole moment, and is very difficult to detect through rotational spectroscopy. Although this cyclic radical is a good candidate as intermediate reactive in the molecular growth processes of aromatic hydrocarbons, it has never been proposed in astrochemical codes describing the chemical evolution of molecular dark clouds. Cyclopentadienyl radical, could form via the reaction between benzene and excited nitrogen atoms (N(2D); see Chin et al. 2021 and references therein). Although from the mechanistic point of view this reaction could occur even at absolute zero, it is not a viable route of formation in cold molecular dark clouds since atomic nitrogen is expected to be mainly in its ground state (N(4S)).

With the aim of shedding light on the formation of PAHs and their precursors, we studied the reaction of propargyl radical (C3H3) with vinyl radical (C2H3) using state-of-the-art quantum chemical calculations. Our kinetic results show that this reaction gives cyclopentadienyl radical (C5H5) as the mayor product (~60–86%) in the typical conditions of the ISM. Our work provides theoretical predictions that can help future astrochemical modelling by expanding the database of reactions of astrochemical interest. Although we propose the formation of a molecular species that can hardly be detected in the ISM (i.e. cyclopentadienyl radical), we provide indirect ways to assess whether this species is indeed formed in molecular dark clouds. This species can be an essential piece in the puzzle of the bottom-up formation processes of PAHs in the ISM.

2 Computational details

2.1 Electronic structure calculations of the reaction C3H3 + C2H3

All the geometries were optimised without constraints at the hybrid meta-GGA functional M06-2X (Zhao & Truhlar 2008) with the Dunning’s triple-zeta correlation-consistent basis set jun-cc-pVTZ (Papajak et al. 2009; Dunning et al. 2001). All the stationary points have been characterised by frequency calculations at the above-mentioned level of theory, showing one and none imaginary frequencies for transition structures (TSs) and energy minima, respectively. All saddle points linking specific reactant and products through the reaction path were verified using intrinsic reaction coordinate (IRC) analysis. The stationary points TS15-6 and TSabs showed diradical character. Thus, the broken-symmetry wave function was used in order to destroy the α and β spatial symmetries. These calculations showed eigenvalues of total spin operator 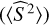(〈 S^2 〉)$\left( {\left\langle {{{\widehat S}^2}} \right\rangle } \right)$ between 0.9 and 1.1. Electronic energies (E) were refined by computing single points with the DLPNO-CCSD(T) method (TightPNO threshold; Riplinger et al. 2013; Riplinger & Neese 2013) on the M06-2X/jun-cc-pVTZ geometries. We also used the F12 correction (Pavosevic et al. 2016) in combination with the auxiliary and special orbital basis set cc-pVTZ-F12-CABS and cc-pVTZ-F12, respectively. As auxiliary basis set for the correlation calculations we increased the size of the basis functions by using the cc-pVQZ/C basis set. The T1 diagnostic (Lee & Taylor 1989) obtained for the singlet open-shell transition structures TS15-6 and TSabs with the above-mentioned method were 0.015 and 0.023. These values suggest that the single and double excitations augmented with perturbative triples cover the static correlation. However, the wave function calculated with DLPNO-CCSD(T)-F12 of TSabs is spin-contaminated. The minimum energy path that corresponds with the latter saddle point is very flat for S < 0. Single point calculations with DLPNO-CCSD(T)-F12 along the reaction coordinate showed species of multiconfigurational character that give energies above the saddle point. Considering also that the self-consistent field (SCF) convergence to the broken-symmetry wave function with the DLPNO-CCSD(T)-F12 method could give meaningless results (Neese 2012; Neese et al. 2020), we decided not to use DLPNO-CCSD(T)-F12 energies for TSabs. To validate our DFT calculations we optimised without restriction the TSabs with the double hybrid rev-DSD-PBEP86 (Kozuch & Martin 2011; Santra & Martin 2019) with the D3(BJ) corrections (Grimme et al. 2010, Grimme et al. 2011) in combination with the above-mentioned Dunning basis set. The electronic energy barrier obtained with the DFT and double hybrid methods were 3.5 and 4.5 kcal mol−1, respectively. Then, the method that we used to carry out the kinetic study for this reaction was M06-2X (see below). Due to the diradical character showed by TSabs, we also checked whether this reaction is possible in the triplet state. We were able to characterise the TSabs in the triplet state at the above-mentioned DFT level of theory; however, the energy gap that separates it from the singlet state is 30.5 kcal mol−1. Therefore, we did not explore this spin state further since the system cannot overcome this energy barrier under interstellar conditions.

Finally, anharmonic zero-point energy (ZPEAnh) corrections were evaluated at the M06-2X/jun-cc-pVTZ level within vibrational perturbative theory to second order VPT2 (Barone 2004). For the kinetics of all the barrierless processes we employed phase space theory (PST; see below). To do this, we computed relaxed scans of the two fragments from large distances (10 Å). The two entrance channels (i.e. the associations of the two hydrocarbons), were computed with the DFT method mentioned above. However, we were unable to converge the wave funtion at large distances for C–H dissociation with the DFT method. Thus, for these barrierless exit channels we used the complete active self-consistent method (CASSCF; Roos 1987) in combination with the cc-pVTZ basis set. To study the C–H dissociation we started with an optimisation at 10 Å constraining the C–H degree of freedom of interest. The choice of the active space was the π electrons and the half-filled molecular orbital of the hydrocarbon, and the 1s orbital of the hydrogen atom. For cyclic hydrocarbons, an active space of six electrons in six orbitals was employed. For linear hydrocarbons an additional orbital was used since we selected the two almost degenerate π orbitals of the triple bond, which left an (8,8) active space.

The DFT calculations were carried out with the Gaussian 16 (Frisch et al. 2016) program package. Coupled cluster and CASSCF calculations were carried out with ORCA 5.0 (Neese 2012; Neese et al. 2020). The images of the structures were done with the Cylview (Legault 2009) software.

2.2 Kinetics calculations

The PST was used to compute the rate constants for all barrier-less bimolecular reactions (Pechukas & Light 1965; Chesnavich 1986). The attractive potentials between the two fragments is described by the 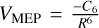VMEP=−C6R6${V_{{\rm{MEP}}}} = {{ - {C_6}} \over {{R^6}}}$ functional form. The long-range coefficient (C6) is obtained from a fit of the M06-2X/jun-cc-pVTZ or CASSCF/cc-pVTZ energies.

For reaction steps with well-characterised transition structures, unimolecular rate constants were computed using the Rice-Ramsperger-Kassel-Marcus (RRKM) theory within the rigid-rotor harmonic-oscillator (RRHO) approximation (Weston 1972). For each step, one-dimensional tunnelling corrections were computed using the Eckart model (Eckart 1930).

Pressure and temperature-dependant rate constants were calculated by resolving the one-dimensional master equation using the MESS software (Georgievskii et al. 2013). The rate constant of the individual product channels were computed in the 10—400 K temperature range and at a pressure of 1 × 10−7 atm.

The hydrogen abstraction reaction of the propargyl radical to the vinyl radical showed a transition state that is 2.88 kcal mol−1 above the reactants (with inclusive ZPEAnh). Then, to compute the rate constant of this reaction we used the canonical variational transition state theory (CVT) with the small curvature tunnelling approximation (SCT; Bao & Truhlar 2017). For submerged energy barriers in the low pressure limit quantum tunnelling is not always effective since the system is not thermalised and stays away from the vibrationally adiabatic potential (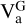VaG${\rm{V}}_{\rm{a}}^{\rm{G}}$, i.e. E + ZPE). However, for an energy barrier that is above the reactants, as in this case, a correct description of quantum tunnelling should be considered, especially at low temperatures. We did not find a pre-reactive complex for this reaction. However, this does not affect the rate constant of the individual product channels in the low pressure limit since the complex is never formed and the mechanism involves just one step, which is the transition state. The expression for the bimolecular rate constant is thus given by 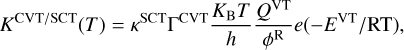KCVT/SCT(T)=κSCTΓCVTKBThQVTϕRe(−EVT/RT),${K^{{{{\rm{CVT}}} \mathord{\left/ {\vphantom {{{\rm{CVT}}} {{\rm{SCT}}}}} \right. \kern-\nulldelimiterspace} {{\rm{SCT}}}}}}\left( T \right) = {\kappa ^{{\rm{SCT}}}}{{\rm{\Gamma }}^{{\rm{CVT}}}}{{{K_{\rm{B}}}T} \over h}{{{Q^{{\rm{VT}}}}} \over {{\phi ^{\rm{R}}}}}e\left( {{{ - {E^{{\rm{VT}}}}} \mathord{\left/ {\vphantom {{ - {E^{{\rm{VT}}}}} {{\rm{RT}}}}} \right. \kern-\nulldelimiterspace} {{\rm{RT}}}}} \right),$(1)

where R is the ideal gas constant; κSCT is the small curvature multidimensional tunneling transmission coefficient; ΓCVT is the canonical variational transition state recrossing coefficient, which is given by KCVT/KTST, where KTST is the rate coefficient of the conventional transition state theory, and KCVT is the rate coefficient of the canonical variational transition state theory; kB is the Boltzmann constant and h is the Planck constant; ϕrmR is the product of the reactants’ partition functions; and EVT is the potential energy of the variational transition state with respect to the reactants. To give more accurate results for both the barrier and the 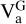VaG${\rm{V}}_{\rm{a}}^{\rm{G}}$, we multiplied the ZPE by a scaling factor (λ) computed as ZPEAnh/ZPEHar (Gao et al. 2018) at the above-mentioned DFT method for all the stationary points. We obtained scaling factors of 0.986, 0.995, 0.991, 0.995, and 0.994 for propargyl radical, vinyl radical, propargyl, acetylene, and TSabs, respectively. It should be noted that the scaling factor for TS is used along the reaction coordinate.

Finally, to describe the temperature dependence of the rate constant of the individual product channels and to provide kinetic data for astrochemical codes, we used the Arrhenius-Kooij formula (Kooij 1893) 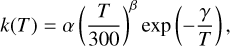k(T)=α (T300)β exp (−γT),$k\left( T \right) = \alpha \,{\left( {{T \over {300}}} \right)^\beta }\,\exp \,\left( { - {\gamma \over T}} \right),$(2)

where α, β, and γ are fitting parameters, determined using the computed rate coefficients at different temperatures.

3 Results

3.1 Reaction mechanism

Figure 1 shows the E + ZPEAnh profile for the reaction between the propargyl radical (C3H3; labelled (1) and vinyl radical (C2H3; labelled (2). This complex reaction shows three entrance and seven exit channels. We characterised 13 intermediates and 19 transition structures. All the geometries of the stationary points are shown in Fig. 2. The reaction starts with two highly exothermic barrierless association reactions that yield the intermediates 7a and 7b, which are 86.6 and 87.1 kcal mol−1 below the reactants. The two intermediates are connected through the transition structure TS7a-7b, which shows a very low submerged energy barrier (−84.6 kcal mol−1), and corresponds with the torsion of the newly formed C–C bond. Intermediates 7a and 7b could lose one hydrogen atom from the new sp3 carbon to give cis-C5H5 and trans-C5H5 + H through barrierless dissociation processes. These two exit channels show reaction energies of −9.7 and −10.2 kcal mol−1 for the formation of cis-C5H5 and trans-C5H5, respectively.

The intermediate 7b could evolve through three rearrangements. The minimum energy path leads to the intermediate 12 (−44.6 kcal mol−1) through the transition structure TS7b-12, which is 26.5 kcal mol−1 below the reactants. Along the reaction coordinate that corresponds with TS7b-12 there is first a Csp3−Csp bond breaking of the intermediate 7b before reaching the saddle point. Then there is a concerted addition of the carbene-like structure to the triple bond forming 12. The latter intermediate shows a three-centre two-electron (3c-2e) bond at the end of the chain. This unusual intermediate is formed along the reaction coordinate due to the migration of the Csp which makes it electron deficient. To counteract this electronic deficiency, the hydrogen of the neighbouring group migrates to stabilise this carbon, to then become a three-centre two-electron system. The intermediate 12 could evolve into the rotamer 11, which is 1.3 kcal mol−1 below 12, through the transition structure TS11-12 that shows an energy barrier of just 1.7 kcal mol−1 from 12. It could also evolve to cyclopentadiene (6) through TS12-6. In this TS, the 3c-2e bond is broken, leaving an electron-deficient carbon at the end of the chain that is inserted in one of the two C-H bonds of the CH2 at the other end of the chain, giving rise to the highly stable cyclopentadiene (6). This intermediate shows three C-H bond-types which could dissociate through barrier-less processes to give cyclopentadienyl radical (5), 3, and 4. The most favoured reaction pathway of these three competitive exit channels is the formation of 5, which is 32.2 and 34.8 kcal mol−1 below the products 4 and 3, respectively.

The intermediate 7b could also reach 6 through other reaction pathway that is below the reactants, but less favourable than the one previously described. Intermediate 7b evolves to 17 through TS7b-17 (−26.5 kcal mol−1), in which the two ends of the chain form a new C-C bond, whilst a hydrogen of the CH2 group migrates to the CH moiety. Later, one of the four hydrogens held by the two sp3 carbons of 17 migrates to the carbene yielding 6 through TS17-6 (−48.6 kcal mol−1).

The last rearrangement that 7b could suffer leads to the intermediate 8 through a very endothermic process (68.9 kcal mol−1 from 7b), which shows a high energy barrier (TS7b-8, 75.0 kcal mol−1 from 7b). This strained transition structure corresponds with a cyclisation process between the Csp that is linked to the Csp3 of 7b and the two carbons that form the double bond, giving rise to the unstable bicycle 8. This bicycle could return to 7b or rearrange to the bicycle 9 through TS8-9, which shows an energy barrier of 7.7 kcal mol−1 above the reactants. Thus, all subsequent transformations from 8 are not viable in the conditions of the ISM.

The intermediate 9 can isomerise to 14 through a positive energy barrier (4.0 kcal mol−1), which corresponds to TS9-14. In this step, there is a concerted hydrogen donation from the CH2 group of the cyclobutane moiety, while there is a bond breaking of the C–C bridge. The subsequent evolution of the strained intermediate 14 into the stable intermediate 16 (−92.4 kcal mol−1) is aring closure (TS14-16, −31.5 kcal mol−1) in which the carbene attacks one of the CH groups to form the four-membered ring derivative 16, which undergoes a retro-[2+2] cycloaddition to give acetylene (C2H2) and the allene propadiene (a-C3H4). This exit channel is one of the most favoured process from the thermodynamic point of view, with a reaction energy of −53.5 kcal mol−1. In addition, 14 could also isomerise into the bicycle-[2.1.0] 15 through TS14-15, which is 1.3 kcal mol−1 above the reactants. A ring-opening reaction of 15 in which the C–C bond bridge is broken (TS15-6, −48.0 kcal mol−1) also leads to cyclopentadiene (6).

The intermediate 6 could also come from the intermediate 9 passing through 13. The latter is formed from a concerted hydrogen transfer reaction summed to the C–C bond bridge breaking of 9 (TS9-13, −26.0 kcal mol−1). Then, the formation of 6 comes from a hydrogen donation of the CH2 group linked to the carbene through the TS13-6, which is 6.5 kcal mol−1 above 13.

Intermediate 9 also isomerises to 10 through a very low energy barrier, 0.7 kcal mol−1 (TS9-10), in which there is almost no change in geometry. In this case there is just a change in the C–C bridge of the bicycle that allows the system to decrease by 5.0 kcal mol−1. Intermediate 10 is connected to 11 (see above) through TS10-11 and also to 15 through TS10-15, which shows the highest energy barrier found for this mechanism (14.7 kcal mol−1 above the reactants). This transition structure corresponds with a hydrogen donation from the CH2 group to the carbene of 10.

Finally, the third entrance channel is a hydrogen abstraction reaction that is not connected to the other intermediates. In this process the carbon holding the unpaired electron of propargyl radical abstracts one of the two hydrogens of the CH2 group of vinyl radical, yielding two closed shell molecules: propargyl (p-C3H4) and acetylene (C2H2). We were unable to locate a pre-reactive complex in this reaction since the reaction coordinate is very flat in the entrance channel region (S < 0). In any case, this reaction does not compete with the barrierless processes followed by submerged barriers since the emerged energy barrier is high enough to make it a non-viable process under interstellar conditions.

thumbnail Fig. 1

E + ZPEAnh, energy profile for the reaction between propargyl radical (1) and vinyl radical (2). The dashed orange and blue profiles correspond to the formation of cis-C5H5 and trans-C5H5, respectively; the solid black and dashed yellow profiles correspond to the minimum energy paths for the formation of 5 and a-C3H4 + C2H2, respectively, and the dashed green and red lines correspond to the exit channels leading to 3 and 4, respectively. Energy values are given in kcal mol−1.
thumbnail Fig. 2

Optimised geometries of all the stationary points at the level of theory mentioned in Sect. 2.1.

3.2 Kinetics

Figure 3 shows the rate constant of the individual product channels for the reaction between 1 and 2 at 1 × 10−7 atm and in the temperature range 10–400 K. The solid black line in the left panel corresponds to the rate constants for the formation of cyclopentadienyl radical (5). In the same plot the dashed blue and orange lines correspond to the formation of the acyclic trans-C5H5 and cis-C5H5, respectively. In the middle panel, the red dashed line refers to the rate constants for the formation of 4, whilst the dashed green line is for its isomer 3. Finally, the right plot shows the rate constants for the formation of allene (a-C3H4) and propargyl (p-C3H4; + acetylene - C2H2), depicted as brown and purple dashed lines, respectively.

Of all the competitive reaction pathways, the formation of the cyclopentadienyl radical (5) is the fastest process, followed by the dissociation of the intermediates 7a and 7b into trans-C5H5 + H and cis-C5H5 + H. The last step in the formation of 5 is the loss of a hydrogen of the methylene group of cyclopentadiene (6) through a barrierless dissociation. There are several reaction pathways leading to 6; the most favoured one is the rearrangement of 7b to give 12, which evolves into 6 through the higher submerged barrier of this reaction pathway (solid black line of Fig. 1). The second most favoured pathway corresponds to the cyclisation of 7b into 17, which corresponds to the higher submerged barrier of this path. Subsequently, 17 leads to 6 through a fast hydrogen transfer process. The other reaction pathway leading to 6 involves the formation of the intermediate 9. To reach 9 the system should overcome an energy barrier of 7.7 kcal mol−1 (TS8-9) that makes the process non-viable under ISM conditions.

Therefore, considering all these reaction pathways, the rate-determining step of the whole process are the first barrierless association reactions between 1 and 2, again involving the intermediate 7b. This is reflected in the rate constant values in the whole range of temperatures studied here, presenting the typical rate constant values of a barrierless reaction. The formation of 5 follows an Arrhenius behaviour from 10 to ~200 K. When the temperature goes beyond 200 K, the reaction acquires a soft inverse temperature dependence. In contrast, the formation of the radicals C5H5, in cis (cis-C5H5) and in trans (trans-C5H5) conformations, only involves the first barrierless reactions and the post-barrierless dissociations after the formation of 7a and 7b. These two intermediates can isomerise through a very low submerged barrier (TS7a-7b) that makes the first barrierless associations the rate-determining step of the whole process, as inferred from the rate constant of the individual product channels values. These temperature-dependent rate constants show an Arrhenius behaviour from 35 to 400 K, but at 35 K there is an inflection point from which the rate of the reaction increases slightly to 10 K. The formation of cis-C5H5 and trans-C5H5 are both viable in the conditions of the ISM and the difference in the rate of formation between the two isomers is directly influenced by its energy difference (0.5 kcal mol−1).

The formation of the radicals 3 and 4 are significantly slower than the formation reactions of 5, trans-C5H5 and cis-C5H5, and follow a similar kinetic behaviour to the formation of trans-C5H5, but much more pronounced. In this case the Arrhenius behaviour is observed from ~70 to 400 K whereas for 4 it is observed from ~55 K. The marked increase in the rate constants at very low temperatures is probably due to the closeness in energy between the reactants and products. Since the formation of 3, 4, and 5 shares the same reaction pathway up to reaching cyclopentadiene (6), the competition between these pathways is ruled by the barrierless dissociation of the C-H bonds of 6 to give the three different isomers. Therefore, the determining point of the rate of formation for these compounds is given by its energy difference, which is markedly favoured for 5 by 32.2 and 34.8 kcal mol−1 relative to 4 and 3, respectively. Although all these processes are viable in the conditions of the ISM, the rate constant of the individual product channels obtained for the formation of 3 and 4 indicate that they are non-competitive processes when compared to the formation of 5, cis-C5H5 and trans-C5H5.

The slowest reaction found is the formation of allene (a-C3H4) + C2H2. The minimum energy pathway found for the formation of a-C3H4 + C2H2 shows that the rate-determining step of the whole process is TS8-9, which is 7.7 kcal mol−1 above the reactants. This very high energy barrier makes the process non-viable under interstellar conditions. This positive energy barrier induces a temperature dependence in the whole range of temperatures studied here, as can be seen from the yellow dotted line in Fig. 3.

The hydrogen abstraction reaction between 1 and 2 yielding propargyl radical (p-C3H4) and C2H2 shows a positive energy barrier (3.5 kcal mol−1) that prevents the process from occurring in the conditions of the ISM. Thus, this process is not competitive with those forming the C5H5 isomers. Although the reaction is slow, the rate is slightly higher at very low and high temperatures. At low temperatures there is an increase in the rate due to quantum tunnelling effects, whereas at higher temperatures there is enough thermal energy to overcome the energy barrier. The fitting parameters that describe the temperature dependence of all these rate constants are summarised in Table 1.

thumbnail Fig. 3

log10 of the temperature-dependant rate constant of the individual product channels for the reaction between propargyl radical (1) and vinyl radical (2) in the temperature range of 10–400 K.
Table 1

Arrhenius–Kooij parameters for the reaction between propargyl radical (1) and vinyl radical (2) in the range of temperatures 10–400 K.

4 Discussion

As mentioned in Sect. 1, although there are no unequivocal detections of PAHs in the ISM, there is strong observational evidence that points to the existence of these molecules in the universe. The detection of fullerenes in the ejecta of dying stars (Cami et al. 2010), the assignment of the unidentified IR emission from dust grains (Leger & Puget 1984), and the unequivocal detection of potential precursors of PAHs in cold cores suggest that these high-molecular-weight carbon derivatives are very likely key components of the ISM.

Within the bottom-up approach, the most studied formation route of PAHs in the ISM considers the increase in the molecular weight of fused aromatic rings by the combination between lower-mass hydrocarbons.

However, it is not known which hydrocarbons are the precursors of PAHs. The reactions between simple hydrocarbons should be possible in the extreme physical conditions of interstellar cold sources, that is, at temperatures close to absolute zero and at very low pressures. Given the extremely low collision frequency between molecules, however, interstellar conditions hinder reactions between non-activated species, such as closed shell compounds, requiring the participation of activated molecules, such as reactive radicals.

Large aromatic fused cycles like indene should not be formed in a single reaction step from radicals detected in cold clouds such as TMC-1. Considering that indene consists of nine carbons and eight hydrogens, the combination of different simple radical hydrocarbons detected in this source, seem unlikely. Thus, we should consider that its formation starts from more complex precursors than those of lower molecular weight.

Under this premise, we have studied the reaction between the highly abundant propargyl radical (1) and vinyl radical (2). The latter radical has not been detected in the ISM yet. However, it is likely very abundant in the ISM given that other unsaturated radical hydrocarbons of higher complexity than vinyl radical have been detected. Furthermore, in a recent theoretical study it has been demonstrated that the reaction of atomic hydrogen and/or hydroxyl radical with ethylene efficiently gives vinyl radical on the surface of dust grains (Molpeceres & Rivilla 2022).

In addition, the association between two molecules of carbene (CH2), which has been already detected in the ISM (Polehampton et al. 2005), should be barrierless and highly exothermic, forming ethylene. The latter, which likely does not get stabilised by collisions due to the low density of the ISM, could dissociate to give the radical C2H3 + H.

Our high-level quantum-chemical calculations show that the mechanism of the reaction between propargyl and vinyl radicals in the typical conditions of the ISM could lead to several reaction products. After the formation of the initial intermediates through barrierless reactions there are numerous rearrangements showing very high energy barriers, although most of them are submerged below the reactants. The low-pressure conditions of the ISM allow these submerged barriers to be overcome, leading finally to the formation of C5H5 isomers throughout exothermic processes. Of the seven exit channels found in this study, the formation of cyclopentadienyl radical is the most favoured process, showing a branching fraction at 10 K of 60.42%, followed by a 20.92% for trans-C5H5 and 18.66% for cis-C5H5. Table 2 shows the product branching ratios for the reaction of 1 and 2 in the temperature range of 10–400K. These results show that the formation of the open-chain unsaturated radicals cis-C5H5 and trans-C5H5 is non-negligible. This result invites us to try to look for these (so far) undetected species. The detection of these open-chain C5H5 isomers could be indicative of the presence of cyclopentadienyl radical in the TMC-1 molecular cloud.

Our work shows that cyclopentadienyl radical could be an essential ingredient in the formation of aromatic cycles and poly-cycles like benzene and naphthalene (Kaiser et al. 2022). In the future, we will explore whether the recombination of cyclopentadienyl radical leads to the formation of indene and methylene. In addition, reactions between cyclopentadienyl radical with ethylene or the recently detected benzine could yield indene and the byproducts H and C2H, respectively. This will be the topic of future work.

Table 2

Product branching ratios (%) for the reaction between 1 and 2.

5 Conclusions

In this work, we have carried out quantum-chemical calculations to study the reaction between the propargyl radical and vinyl radical. The former is one of the most abundant hydrocarbons in cold molecular clouds. The vinyl radical has not been reported in the ISM yet, but previous theoretical studies suggest it should be present.

Our kinetic study under interstellar conditions (i.e. at very low pressure and in the temperature range 10–400 K) show that this reaction likely takes place even at the low temperatures of the molecular dark clouds. Although we found seven exit channels, the only viable processes are the formation of the cyclopentadienyl radical (with a branching ratio of ~60%), followed by the formation of the unsaturated open chain hydrocarbons trans-C5H5 (~21%) and cis-C5H5 (~19%).

The detection of cyclopentadienyl radical in molecular dark clouds is challenging due to its very low dipole moment. Alternatively, our kinetic study demonstrates that the formation of cis-C5H5 and trans-C5H5 should also be sufficiently efficient. Thus, the detection of these two radical hydrocarbons could be proof of the presence of the cyclopentadienyl radical in the ISM. Previous studies suggest that the cyclopentadienyl radical is an important intermediate in the synthesis of PAHs. So including the formation and reactions involving this cyclic radical in astro-chemical models could help in understanding the observed high abundances of compounds such as indene and the formation of PAHs such as naphthalene.

Acknowledgements

J.G.d.l.C., I.J.-S., J.M.-P. and L.C. have received partial support from grant no. PID2019-105552RB-C41 by the Spanish Ministry of Science and Innovation/State Agency of Research MCIN/AEI/10.13039/501100011033 and by “ERDF A way of making Europe”. V.M.R. has received support from the Comunidad de Madrid through the Atraccion de Talento Investigador Modalidad 1 (Doctores con experiencia) Grant (COOL: Cosmic Origins Of Life; 2019-T1/TIC-5379), and from the project RYC2020-029387-I funded by MCIN/AEI/10.13039/501100011033. Computational assistance was provided by the Supercomputer facilities of LUSITANIA founded by Cenits and Computaex Foundation.

References

  1. Agúndez, M., Cabezas, C., Tercero, B., et al. 2021, A&A, 647, L10 [EDP Sciences] [Google Scholar]
  2. Agúndez, M., Marcelino, N., Cabezas, C., et al. 2022, A&A, 657, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Bao, J. L., & Truhlar, D. G. 2017, Chem. Soc. Rev., 46, 7548 [CrossRef] [Google Scholar]
  4. Barone, V. 2004, JChPh, 120, 3059 [NASA ADS] [Google Scholar]
  5. Boersma, C., Bregman, J. D., & Allamandola, L. J. 2013, ApJ, 769, 117 [NASA ADS] [CrossRef] [Google Scholar]
  6. Boersma, C., Bregman, J., & Allamandola, L. J. 2015, ApJ, 806, 121 [NASA ADS] [CrossRef] [Google Scholar]
  7. Cabezas, C., Agúndez, M., Fuentetaja, R., et al. 2022, A&A, 663, A2 [Google Scholar]
  8. Cami, J., Bernard-Salas, J., Peeters, E., & Malek, S. E. 2010, Science, 329, 1180 [NASA ADS] [CrossRef] [Google Scholar]
  9. Cernicharo, J., Agúndez, M., Cabezas, C., et al. 2021a, A&A, 647, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Cernicharo, J., Agúndez, M., Cabezas, C., et al. 2021b, A&A, 649, A15 [Google Scholar]
  11. Cernicharo, J., Agúndez, M., Kaiser, R. I., et al. 2021c, A&A, 652, A9 [Google Scholar]
  12. Cernicharo, J., Agúndez, M., Kaiser, R. I., et al. 2021d, A&A, 655, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Cernicharo, J., Fuentetaja, R., Agúndez, M., et al. 2022, A&A, 663, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Chesnavich, W. J. 1986, JChPh, 84, 2615 [NASA ADS] [Google Scholar]
  15. Chin, C.-H., Zhu, T., & Zhang, J. Z. H. 2021, Phys. Chem. Chem. Phys., 23, 12408 [NASA ADS] [CrossRef] [Google Scholar]
  16. Doddipatla, S., Galimova, G. R., Wei, H., et al. 2021, Sci. Adv., 7, eabd4044 [Google Scholar]
  17. Dunning, T. H., Peterson, K. A., & Wilson, A. K. 2001, J. Chem. Phys., 114, 9244 [NASA ADS] [CrossRef] [Google Scholar]
  18. Eckart, C. 1930, PhRv, 35, 1303 [NASA ADS] [Google Scholar]
  19. Fosse, D., Cernicharo, J., Gerin, M., & Cox, P. 2001, ApJ, 552, 168 [NASA ADS] [CrossRef] [Google Scholar]
  20. Frisch, M. J., Trucks, G. W., Schlegel, H. B., et al. 2016, Gaussian 16 Revision A.03 (Gaussian Inc. Wallingford CT) [Google Scholar]
  21. Gao, L. G., Fernández-Ramos, A., & Truhlar, D.G. 2018, J. Am. Chem. Soc., 140, 2906 [CrossRef] [Google Scholar]
  22. Georgievskii, Y., Miller, J. A., Burke, M. P., & Klippenstein, S. J. 2013, JPCA, 117, 12146 [NASA ADS] [CrossRef] [Google Scholar]
  23. Grimme, S., Antony, J., Ehrlich, S., & Krieg, H. 2010, J. Chem. Phys., 132, 154104 [Google Scholar]
  24. Grimme, S., Ehrlich, S., & Goerigk, L. 2011, J. Comput. Chem., 32, 1456 [Google Scholar]
  25. Hanine, M., Meng, Z., Lu, S., et al. 2020, ApJ, 900, 188 [NASA ADS] [CrossRef] [Google Scholar]
  26. Kaiser, R. I., Zhao, L., Lu, W., et al. 2022, J. Phys. Chem. Lett., 13, 208 [Google Scholar]
  27. Kooij, D. M. 1893, ZPhCh, 12, 155 [Google Scholar]
  28. Kozuch, S., & Martin, J.M.L. 2011, PCCP, 13, 20104 [CrossRef] [Google Scholar]
  29. Lee, T. J., & Taylor, P. R. 1989, Int. J. Quantum Chem., 36, 199 [Google Scholar]
  30. Legault, C. Y. 2009, http://www.cylview.org [Google Scholar]
  31. Leger, A., & Puget, J. L. 1984, A&A, 137, L5 [Google Scholar]
  32. McGuire, B. A., Loomis, R. A., Burkhardt, A. M., et al. 2021, Science, 371, 1265 [Google Scholar]
  33. Mebel, A. M., Landera, A., & Kaiser, R. I. 2017, J. Phys. Chem. A, 121, 901 [Google Scholar]
  34. Merino, P., Švec, M., Martinez, J. I., et al. 2014, Nat. Commun., 5, 3054 [NASA ADS] [CrossRef] [Google Scholar]
  35. Molpeceres, G., & Rivilla, V. M. 2022, A&A, 665, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Neese, F. 2012, WIREs: Comput. Mol., 2, 73 [CrossRef] [Google Scholar]
  37. Neese, F., Wennmohs, F., Becker, U., Riplinger, C. 2020, J. Chem. Phys., 152, 224108 [NASA ADS] [CrossRef] [Google Scholar]
  38. Papajak, E., Leverentz, H. R., Zheng, J., & Truhlar, D. G. 2009, J. Chem. Theory Comput., 5, 1197 [CrossRef] [Google Scholar]
  39. Pavosevic, F., Pinski, P., Riplinger, C., Neese, F., & Valeev, E. 2016, J. Chem. Phys., 144, 144109 [NASA ADS] [CrossRef] [Google Scholar]
  40. Pechukas, P., & Light, J. C. 1965, JChPh, 42, 3281 [NASA ADS] [Google Scholar]
  41. Polehampton, E. T., Menten, K. M., Brünken, S., Winnewisser, G., & Baluteau, J. P. 2005, A&A, 431, 203 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Reizer, E., Viskolcz, B., & Fiser, B. 2022, Chemosphere, 291, 132793 [NASA ADS] [CrossRef] [Google Scholar]
  43. Riplinger, C., & Neese, F. 2013, J. Chem. Phys., 138, 034106 [NASA ADS] [CrossRef] [Google Scholar]
  44. Riplinger, C., Sandhoefer, B., Hansen, A., & Neese, F. 2013, J. Chem. Phys., 139, 134101 [NASA ADS] [CrossRef] [Google Scholar]
  45. Roos, B. O. 1987, The Complete Active Space Self-Consistent Field Method and its Applications in Electronic Structure Calculations (John Wiley & Sons, Ltd), 399 [Google Scholar]
  46. Santra, G., Sylvetsky, N., & Martin, J. M. L. 2019, JPCA, 123, 5129 [NASA ADS] [CrossRef] [Google Scholar]
  47. Turner, B. E., Herbst, E., & Terzieva, R. 2000, ApJS, 126, 427 [Google Scholar]
  48. Weston, R. E., Schwartz, H. E. 1972, Chemical Kinetics (Englewood Cliffs, NJ: Prentice-Hall Inc.) [Google Scholar]
  49. Zhao, Y., & Truhlar, D. G. 2008, Theor. Chem. Acc., 120, 215 [CrossRef] [Google Scholar]

All Tables

Table 1

Arrhenius–Kooij parameters for the reaction between propargyl radical (1) and vinyl radical (2) in the range of temperatures 10–400 K.

In the text
Table 2

Product branching ratios (%) for the reaction between 1 and 2.

In the text

All Figures

thumbnail Fig. 1

E + ZPEAnh, energy profile for the reaction between propargyl radical (1) and vinyl radical (2). The dashed orange and blue profiles correspond to the formation of cis-C5H5 and trans-C5H5, respectively; the solid black and dashed yellow profiles correspond to the minimum energy paths for the formation of 5 and a-C3H4 + C2H2, respectively, and the dashed green and red lines correspond to the exit channels leading to 3 and 4, respectively. Energy values are given in kcal mol−1.
In the text
thumbnail Fig. 2

Optimised geometries of all the stationary points at the level of theory mentioned in Sect. 2.1.
In the text
thumbnail Fig. 3

log10 of the temperature-dependant rate constant of the individual product channels for the reaction between propargyl radical (1) and vinyl radical (2) in the temperature range of 10–400 K.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.