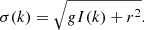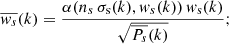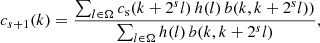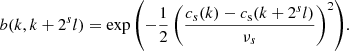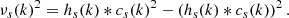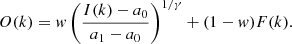| Issue |
A&A
Volume 670, February 2023
Solar Orbiter First Results (Nominal Mission Phase)
|
|
|---|---|---|
| Article Number | A66 | |
| Number of page(s) | 10 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/202245345 | |
| Published online | 06 February 2023 | |
Image enhancement with wavelet-optimized whitening⋆
Université Paris-Saclay, CNRS, Institut d’Astrophysique Spatiale, 91405 Orsay, France
e-mail: frederic.auchere@ias.u-psud.fr
Received:
31
October
2022
Accepted:
1
December
2022
Context. Due to its physical nature, the solar corona exhibits large spatial variations of intensity that make it difficult to simultaneously visualize the features present at all levels and scales. Many general-purpose and specialized filters have been proposed to enhance coronal images. However, most of them require the ad hoc tweaking of parameters to produce subjectively good results.
Aims. Our aim was to develop a general purpose image enhancement technique that would produce equally good results, but based on an objective criterion.
Methods. The underlying principle of the method is the equalization, or whitening, of power in the à trous wavelet spectrum of the input image at all scales and locations. An edge-avoiding modification of the à trous transform that uses bilateral weighting by the local variance in the wavelet planes is used to suppress the undesirable halos otherwise produced by discontinuities in the data.
Results. Results are presented for a variety of extreme ultraviolet (EUV) and white light images of the solar corona. The proposed filter produces sharp and contrasted output, without requiring the manual adjustment of parameters. Furthermore, the built-in denoising scheme prevents the explosion of high-frequency noise typical of other enhancement methods, without smoothing statistically significant small-scale features. The standard version of the algorithm is about two times faster than the widely used multiscale Gaussian normalization (MGN). The bilateral version is slower, but provides significantly better results in the presence of spikes or edges. Comparisons with other methods suggest that the whitening principle may correspond to the subjective criterion of most users when adjusting free parameters.
Key words: techniques: image processing / methods: numerical / Sun: corona / Sun: UV radiation / Sun: transition region
Movies associated to Figs. 3 and 5 are available at https://www.aanda.org.
The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1. Introduction
Modern image sensors, like those used in the Extreme Ultraviolet Imager (EUI, Rochus et al. 2020) on board the Solar Orbiter mission (Müller 2020), have dynamic ranges (ratio of the digital range to the read noise) of 212 or more. As long as the observed scenes use the entire detector range, the typical 28 dynamic of monitors is insufficient to display the recorded images unmodified without losing information (left panel of Fig. 1). Therefore, most of the time the intensity values are rescaled to 8 bits prior to display using a nonlinear function (or stretch), usually a power 1/γ < 1 (γ-stretch) or a logarithm of the intensity (middle panel of Fig. 1). It is worth noting that a square root transformation (γ = 2) is sometimes applied on board (e.g., on EUI) for it provides optimum intensity sampling for images dominated by Poisson statistics (Nicula et al. 2005). Nonlinear intensity transformations alone, however, are not sufficient to bring out all the information present in the data. Filtering and enhancement is a crucial step in the analysis of scientific images for it can reveal features and phenomena that would otherwise remain undetected.
 |
Fig. 1. Dynamic range and spatial scales in a solar EUV image. Left: fifteen-bit image taken by the Full Sun Imager (FSI) channel of EUI at 17.4 nm on 2022 March 17 at 06:00:45 UT, displayed in linear scale. Only the brightest features are visible. The profile is taken along the row marked by the side ticks. Middle: same image after logarithmic scaling. Faint off-limb details are revealed, but the local contrast is diminished. Right: Fourier power spectrum of the variance normalized image. The profile is that of the bottom row. The larger the spatial scale, the more power (and thus variability) in the image. |
As illustrated in the right column of Fig. 1, the Fourier power spectrum of a typical solar EUV image follows a power-law-like distribution, with more power at low frequencies and less power at high frequencies. As per Parseval’s theorem, the mean power of the Fourier spectrum is equal to the variance of the signal. Thus, the larger (respectively lower) Fourier power at lower (respectively higher) frequencies correspond to larger (respectively lower) signal variance at larger (respectively smaller) spatial scales. The middle column of Fig. 1, which is remapped using a logarithm intensity transformation, indeed shows that the largest intensity variations come from the global scales. However, while bringing out the faint large-scale features, this simple intensity remapping produces a washed out image with poor local contrast. Intensity variations in the active regions are mapped to a much smaller range of output values than with the linear scaling of the left column. This is why many enhancement methods are designed to reduce the signal variance at low frequencies and to increase it at high frequencies.
Specialized background subtraction methods (e.g., Morgan et al. 2006; Patel et al. 2022) can be used to this end, but they are typically limited to the off-disk emission. One of the earliest general-purpose methods, the unsharp mask, is a simple high-pass filter that was developed to improve the quality of photographic prints by analog composition of a negative with a blurred positive (Yule 1944; Schreiber 1970; Levi 1974). Numerically, the convolution kernel is generally taken to be Gaussian, but the frequency response of the filter can be tailored to arbitrary shapes in the Fourier space. However, Fourier filtering techniques are limited in that they ignore the local variations of the image properties, unless the input is segmented into independent tiles.
On the contrary, multiscale approaches are able to modify the spectral content differently at different positions in the input image. The detail layer of the multiscale Gaussian normalization (MGN, Morgan & Druckmüller 2014) is essentially a weighted sum of unsharp-masked images of increasing Gaussian kernel widths, normalized to their local standard deviations and remapped to the [−1, 1] range. MGN is successful in equalizing the variances over a range of scales, but also enhances the high-frequency noise in doing so (see right panel of Fig. 3 of Morgan & Druckmüller 2014), a common issue with image sharpening techniques.
The decomposition of images into scales using a wavelet transform offers the possibility to simultaneously denoise (Starck & Murtagh 1994; Murtagh et al. 1995) and modulate the output power spectrum. The wavelet packet equalization scheme of Stenborg & Cobelli (2003), Stenborg et al. (2008) consists in a two-level à trous wavelet decomposition, followed by local noise reduction and weighted synthesis.
Enhancement methods typically include free parameters that need to be adjusted by the user: the kernel width for the unsharp mask; the kernel widths, variance regularization function, and synthesis weights in MGN; and the noise threshold and synthesis weights in Stenborg & Cobelli (2003). This provides flexibility in tuning the output, with the drawback of subjectivity in deciding what good results are.
In the present article we propose a transform that whitens the power spectrum, resulting in equal variance at all spatial frequencies (Sect. 2). While not the only possible choice of normalization, a comparison of the results (Sect. 3) with other methods suggests that images considered to be well enhanced tend to have a white spectrum. We summarize our work in Sect. 4.
2. Method
2.1. À trous transform
We summarize below only those aspects of the à trous transform necessary to understand the proposed method. We refer the reader to Holschneider et al. (1989), Shensa (1992), Starck & Murtagh (2002) and references therein for material on wavelet theory and the à trous transform in particular. See also Stenborg & Cobelli (2003) for a concise introduction and application to images of the solar corona.
The wavelet transform of a discrete signal f(l) is defined by
where s is a scaling factor. In the case of the à trous transform, the real-valued wavelet ψ satisfies the relationship
with ϕ(x) a scaling function that obeys the dilation equation
where h is a low-pass filter kernel. We can then demonstrate (Shensa 1992) that the à trous wavelet transform can be computed by the following iteration, initialized with the input image I(k)=c0(k):
Here Ω denotes the support of the compact kernel h and the convolution product. The set {w1(k)…wS(k),cS(k)} forms the wavelet transform of the input image, with S the largest scale compatible with the data. At scale s, the data values weighted by h(l) are separated by 2s, which is equivalent to a convolution with a sparse (with holes, à trous in French) kernel hs(k). We note that this iteration lends itself naturally to an implementation in which successive scales are recursively computed by convolutions of the compact kernel with interleaved subsamplings of one point out of two on each axis.
The successive convolutions form increasingly smooth representations cs(k) of the data (left half images in the first two rows of Fig. 2). The input image c0(k) used in this example was acquired with the 17.4 nm high-resolution EUV channel of EUI (HRIEUV, top left panel of Fig. 3) on 2022 March 17 at 04:02:57 UT, when Solar Orbiter was at 0.38 AU from the Sun. It is the one closest in time to the FSI image of Fig. 1. Its wavelet transform with S = 8 is represented in the left half images of the third and fourth rows. The input image can be synthesized with
 |
Fig. 2. À trous wavelet transform and coefficients whitening. Two top rows: chained convolutions cs(k) of the input image c0(k) with à trous kernels dilated by a factor of two at each step. The left half of each panel corresponds to regular convolutions; the right half to bilateral filtering. Two middle rows: corresponding wavelet coefficients ws + 1(k)=cs(k)−cs + 1(k), that is the difference between successive convolutions or bilateral filterings. The last coefficient is the result of the last convolution or bilateral filtering. The original image (c0(k), left) is the sum of all coefficients. The bilateral transform preserves the edges in the coarse images (top rows). Two bottom rows: whitened coefficients, i.e., normalized to the local power. The filtered image (left) is the sum of all whitened coefficients. For visualization purposes, the convolutions and the coefficients are displayed using two different color scales. |
In the remainder of this paper we use a basic cubic spline for the scaling function ϕ, which corresponds (Eq. (3)) to the one-dimensional kernel h = [1,4,6,4,1]/16, its n-dimensional counterparts being obtained by iterating hTh. Other choices are possible, but the B3-spline is smooth, is continuously differentiable, and has minimum curvature and a compact support, which makes it both robust to oscillations and computationally efficient (see, e.g., Unser 1999). We use mirror boundary conditions so that c(k + N)=c(N − 1 − k) with N the number of pixels on a given axis.
The wavelet coefficients (third and fourth row of Fig. 2) can be manipulated to achieve a variety of results after synthesis. Denoising will be treated in Sect. 2.3. In the next section, we discuss multiscale contrast enhancement.
2.2. Whitening
It is possible to enhance features at a given scale, or more generally to modify the relative importance of different scales, by multiplying the corresponding coefficients  with ad hoc weights βs at the image synthesis stage, so that Eq. (6) becomes
with ad hoc weights βs at the image synthesis stage, so that Eq. (6) becomes
It is possible, for example, to suppress large-scale gradients by setting the last weight to zero. This approach is used in the wavelet packet equalization method of Stenborg & Cobelli (2003). While it yields interesting results, it also produces undesirable ringing around sharp and bright features (see, e.g., the right panel of their Fig. 4). Nonetheless, building on this idea, we wondered whether the weights, instead of being arbitrary, could be dictated by the data content to produce an optimal output. Figure 1 suggests that a possible scheme consists in equalizing the power at all scales (i.e., whitening the power spectrum). However, using one global weight per scale ignores the information contained in the spatial variations of power in the wavelet spectrum. In order to equalize the spectrum in both the spectral and spatial dimensions, we normalize the coefficients using an estimate of the local mean power  obtained by convolution of the wavelet power by the à trous kernel. The whitened coefficients
obtained by convolution of the wavelet power by the à trous kernel. The whitened coefficients 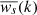 are given by
are given by
Unweighted synthesis of the whitened coefficients results in the wavelet-optimized whitening (WOW) enhanced image:
We note the similarity between Eq. (8) and Eqs. (1) and (2) of Morgan & Druckmüller (2014): both represent convolutions of the original image by variable-sized kernels normalized to a quantity analogous to a local standard deviation. However, the numerator in Eq. (1) of Morgan & Druckmüller (2014) is an unsharp mask (i.e., the difference between the original image and its convolution by a Gaussian), while in Eq. (8) it is an à trous wavelet coefficient (i.e., the difference between two successive chained convolutions by a scaling function). As we show in Sect. 3.2, this difference between the two methods results in significantly different output.
Figure 3 shows a γ-stretched high-resolution 17.4 nm EUI image (top left), and the corresponding output of the WOW process (top right). Only the brightest regions of the input image would be visible without γ-stretching, as in the left panel of Fig. 1. Multiscale whitening tends to equalize the variance at all spatial frequencies and locations, which attenuates the large-scale variations and comparatively reinforces the small-scale structures. The large-scale contrast is reduced, while the small-scale contrast is increased. The enlargement of the region in the white square shows that the noise, which behaves like a small-scale feature, is amplified in the process, especially in the originally faint regions where the noise contributes the most to the signal variance. However, the à trous wavelet transform offers a powerful framework for denoising.
 |
Fig. 3. Three levels of WOW processing. Top left: original γ-stretched (γ = 2.4) HRIEUV image. The inset (top left quarter) shows an enlargement of the area within the white square. Top right: output of the WOW algorithm. Bottom right: Same with added denoising. Bottom right: output of the edge-aware denoised version of the algorithm. For all images the gray scale maps to the central 99.8% of values. An animated version of this figure is available https://www.aanda.org/10.1051/0004-6361/202245345/olm. |
2.3. Denoising
The data can be denoised by attenuation of the wavelet coefficients that are not statistically significant, followed by synthesis (Starck & Murtagh 1994; Murtagh et al. 1995). This is achieved by comparing the ws(k) with the amplitudes expected in the presence of noise only. In the case of Gaussian white noise of unit standard deviation, the amplitudes at scale s are Gaussian-distributed with standard deviation 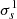 , which can easily be estimated numerically (Starck & Murtagh 2002). In the presence of noise of standard deviation σ, the significant coefficients are those for which
, which can easily be estimated numerically (Starck & Murtagh 2002). In the presence of noise of standard deviation σ, the significant coefficients are those for which
where ns sets the chosen significance level at scale s. The coefficients can then be weighted by a function α(ns σs, ws(k)) of their values relative to ns σs. Hard thresholding corresponds to
but tends to produce ringing in the synthesized image. There are several possibilities for smooth soft-thresholding functions. We chose to weight the coefficients by their probability of chance occurrence, so that
In addition to the Gaussian component corresponding to the read and thermal noises within the sensor, the data also contains the Poisson-distributed component of the photon shot noise. The variance of the Poisson component is proportional to the intensity and is thus variable across the image. In the case of pure Poisson statistics, the transform
results in data with Gaussian noise of unit variance (Anscombe 1948) for numbers of counts greater than about ten. It was generalized by Murtagh et al. (1995) for the presence of additional Gaussian noise in the input.
Following Starck et al. (1997), Stenborg & Cobelli (2003), the alternative approach adopted in this paper to account for the spatial dependence of the noise consists in replacing σs in Eqs. (10)–(12) by a spatially variable 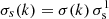 . The local standard deviation of the noise σ(k) can be estimated from the first wavelet coefficients (Starck et al. 1997; Stenborg & Cobelli 2003) or, preferably, if the detector gain g and read noise standard deviation r are known, with
. The local standard deviation of the noise σ(k) can be estimated from the first wavelet coefficients (Starck et al. 1997; Stenborg & Cobelli 2003) or, preferably, if the detector gain g and read noise standard deviation r are known, with
In the end, for combined denoising and whitening, Eq. (8) becomes
the expressions for 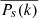 and the synthesis (Eq. (9)) remain unchanged.
and the synthesis (Eq. (9)) remain unchanged.
The bottom left panel of Fig. 3 shows the denoised whitening of the top left input image, to be compared with the regular whitening (Sect. 2.2) of the top right panel. The detector gain and read noise (Eq. (14)) for HRIEUV are given in Table 1. Noise being inherently high-frequency, it is usually significant only in the first few scales. In this example, we used ns = {5, 2, 1} for the first three scales and ns = 0 for the others. This choice is arbitrary; larger values yield smoother output at the expense of losing fainter details.
2.4. Edge-aware transform
In the à trous wavelet transform each convolution by the scaling function (Eq. (4)) produces halos around sharp peaks and edges. These halos are reinforced as genuine features by the whitening process, which tends to produce glows and/or gradient reversals. As proposed by Hanika et al. (2011), this unwanted side effect can be mitigated by replacing the convolution by bilateral filtering in Eq. (4). Range filtering is analogous to spatial filtering, but instead of being a function of spatial distance, the kernel weights are a function of the disparity of values. The bilateral filter (Tomasi & Manduchi 1998) combines both spatial and range filtering, so that Eq. (4) becomes
where the denominator ensures unit normalization. A classical choice for the range filter b is a Gaussian
Following the idea of equalization, we use for νs(k)2 the local variance at scale s, so that the range weights do not depend upon the absolute values of the wavelet coefficients. For computational efficiency, this is approximated by
The resulting edge-aware transform is illustrated in the right halves of the panels of Fig. 2. Compared to the regular transform, the edges are preserved in the coarse images (top two rows) by the bilateral filtering, and the power is correspondingly reduced in the coefficients (middle two rows). For denoising with the edge-aware transform, the corresponding standard deviations 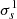 of Gaussian white noise were estimated numerically. The bottom right panel of Fig. 3 shows the output of the denoised edge-aware WOW algorithm for the top left input image. With the same set of significance levels ns as for the regular transform (bottom left panel), the output is sharper, but denoising is less pronounced. An animated version of Fig. 3 containing 899 frames acquired on 2022 March 17 from 03:18:00 to 04:02:57 UT is available online.
of Gaussian white noise were estimated numerically. The bottom right panel of Fig. 3 shows the output of the denoised edge-aware WOW algorithm for the top left input image. With the same set of significance levels ns as for the regular transform (bottom left panel), the output is sharper, but denoising is less pronounced. An animated version of Fig. 3 containing 899 frames acquired on 2022 March 17 from 03:18:00 to 04:02:57 UT is available online.
3. Results
3.1. Three examples
Figure 4 shows three examples of images processed with the edge-aware version of the WOW algorithm. The original γ-stretched (γ = 2.4) images are in the left column and the linearly stretched processed images, all obtained using the same denoising significance levels ns = {5, 3, 1}, are in the right column. The gain and read noise for the different detectors are given in Table 1. For all images, the black and white points of the linear grayscale are mapped respectively to the 0.1 and 99.9%. In the FSI 30.4 nm image (top row) the rapid off-disk intensity fall-off masks the faint outer coronal structures (see also Fig. 1). In the top right image, the whitening of the wavelet spectrum enhances the local contrast and reveals the fainter extensions. The method also accentuates imperfections in the calibration (vertical bands and pattern at the top and bottom edges) because they are spatially correlated, and therefore are not considered as noise by the algorithm. The Atmospheric Imaging Assembly (AIA, Lemen et al. 2012) image (middle row) can be compared to Fig. 2 of Druckmüller (2013) processed with noise adaptive fuzzy equalization (NAFE, see next section). The two images are visually similar, with WOW producing as sharp and contrasted an output without the ad hoc adjustment of parameters nor the addition of a γ-stretched component. In images from white-light coronagraphs (like that in the bottom left of Fig. 4, from LASCO C2, Brueckner et al. 1995), the dust corona and stray light form a diffuse background that dominates the K-corona. By equalizing the power across spatial frequencies, this component is attenuated with respect to smaller-scale features resulting, in the bottom right image, in the enhancement of the twisted filamentary structure of the erupting prominence. Comparison with the output of the wavelet packets equalization method (Fig. 4 of Stenborg & Cobelli 2003) shows that WOW avoids the ringing around the bright and sharp features, and also enhances the disturbances in the surrounding K-corona. As already mentioned, the algorithm treats coherent features irrespective of their solar or instrumental nature. For optimal results, artifacts like the inner diffraction rings or the long curved streaks should be either masked or calibrated out (Morgan 2015; Lamy et al. 2020, 2022) prior to enhancement.
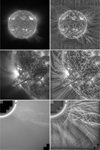 |
Fig. 4. Examples of WOW processed images. For each row, the left image is the original γ-stretched with γ = 2.4, the right image is the output of the edge-aware denoised version of the algorithm. Top: Crop of the 30.4 nm FSI image taken on 2022 March 21 at 06:30:15 UT. Middle: 17.1 nm AIA image taken on 2012 August 31 at 19:44:35 UT. Bottom: LASCO C2 image taken on 1998 June 2 at 13:31:06 UT. |
3.2. Comparison with NAFE and MGN
We chose to compare the output of WOW with that of NAFE (Druckmüller 2013) and MGN (Morgan & Druckmüller 2014), two algorithms commonly used in the solar physics community. The output O(k) of both NAFE and MGN is the weighted sum of the γ-stretched input I(k) and of the filtered image F(k) proper:
Here a0 and a1 are respectively the minimum and maximum input values considered, and w is a user-defined weight set by default to 0.2 for NAFE and 0.7 for MGN. In order to have comparable output, we set γ = 2.4 for both NAFE and MGN. The detail layers F(k) of NAFE and MGN depend on additional arbitrary parameters. For NAFE we use the width N of the neighborhood for local histogram equalization and the denoising coefficient σ (set to 129 and 12 respectively in the following). For MGN we use the scaling parameter k of the arctan function, the synthesis weights (all set to 1 by default), the number of scales (6 by default), and the widths of the Gaussian kernels, which by default follow a geometric progression, similarly to the à trous transform. Conversely, in WOW, the values of most parameters are dictated by either the use of the à trous transform (the progression of scales) or the whitening principle (the number of scales, the absence of synthesis weights). The only free parameters are the denoising significance levels.
As a test case, we picked an HRIEUV image recorded on 2022 April 2 at 09:30:55 UT while Solar Orbiter was at 0.38 AU from the Sun. The γ-stretched layer (γ = 2.4) of NAFE and MGN is shown in the top left panel of Fig. 5. An animated version containing 450 frames acquired from 09:19:15 to 10:34:05 UT is available online. For NAFE (middle row) and MGN (bottom row), the output is on the left, and the corresponding detail layer on the right. WOW does not have a γ-stretched layer, and thus its output (top right panel) must be compared with the detail layers of NAFE and MGN (right column). For all images the gray scale maps to the central 99.8% of values.
 |
Fig. 5. Comparison of the WOW, NAFE, and MGN algorithms. Top left: original γ-stretched (γ = 2.4) HRIEUV image. The inset (top left quarter) shows an enlargement of the area within the white square. Top right: output of the edge-aware denoised version of the algorithm. Middle row: NAFE (left) and corresponding detail layer (right). Bottom row: MGN (left), and corresponding detail layer (right). In NAFE and MGN, the γ-stretched original image (top left) is added to their respective detail layers (right column). The left column thus corresponds to: no enhancement, added NAFE detail layer, added MGN detail layer. The standard WOW output does not include an arbitrary γ-stretched component. An animated version of this figure is available https://www.aanda.org/10.1051/0004-6361/202245345/olm. |
NAFE and MGN produce a somewhat similar output, with NAFE being more contrasted and MGN emphasizing the small scales to a greater degree. The detail layer of MGN presents the typical dark fringes around bright features produced by unsharp masking. Despite the similarities mentioned in Sect. 2, WOW produces a significantly more contrasted output than MGN and no ringing, with notably less noise. Judgment of the merits of the enhancement methods can be subjective when free parameters are involved. The output of WOW is both as sharp as MGN and as contrasted as NAFE, which suggests that the whitening principle may correspond to what is qualitatively considered to be good results.
3.3. Performance
WOW was implemented in Python using open-cv bindings to compute the convolutions; the code is available on GitHub1. We compare the performance to a parallelized NAFE implementation in Python2 validated by comparison with the original implementation, and to the sunkit-image3 implementation of MGN. The results of performance tests on a 2.40 GHz Intel Xeon Silver 4214R CPU are summarized in Table 2. The execution time of WOW and MGN depends on the number of scales, which is set to six by default in MGN. In WOW, the number of scales is set to be ln(N)/ln(2). For comparison with MGN, we therefore also include execution times for the edge-aware version of WOW limited to six scales. The operations required by the two algorithms are very similar, hence the similar performance. However, the bilateral filter makes the edge-aware version of WOW significantly slower than the standard one. Compared to NAFE, it is much faster in all cases while providing equivalent results.
Comparison of execution times (in seconds) for NAFE (on 48 cores), MGN, and WOW, for the images presented in this paper.
3.4. Back to subjectivity
WOW was developed to identify an objective criterion for image enhancement that leads to a method free of arbitrary parameters. While the approach seems successful, the whitening of the power spectrum is not necessarily the unique viable choice. In addition, manual adjustment of the output may be desirable. Naturally, a weighted γ-stretched input image can be added to the WOW image, as in NAFE and MGN. However, any other transfer function can be used to rescale the large dynamic range of the input onto a restricted range of output values. A logarithmic scaling is commonly used for solar EUV images. Lupton et al. (2004) proposed to stretch the data using arcsinh(x/β), which is linear for x ≪ 1 and logarithmic for x ≫ 1, with β a free parameter. Synthesis weights can also be applied at each scale (Eq. (7)) to provide enhanced control over the result.
4. Summary
We introduced a new image enhancement algorithm that produces sharp and contrasted outputs from a variety of images, without arbitrarily determined coefficients nor the addition of a γ-stretched image. While it is possible to introduce ad hoc parameters at both the decomposition and the synthesis stages, the power spectrum whitening principle at the heart of the method, although arbitrary in itself, dictates that these parameters be set to one, yielding an optimum parameter-free scheme. The optional denoising step still requires significance levels to be set manually; however, based on the work of Batson & Royer (2019), it may be possible to determine optimal values automatically. The regular variant is significantly faster than MGN and produces more contrasted results. The sensitivity of the nominal scheme to spikes and edges is mitigated in the edge-aware variant, which is significantly slower, but remains practical on a typical laptop computer.
Movies
Movie 1 associated with Fig. 3 (animated_figure3) Access here
Movie 2 associated with Fig. 5 (animated_figure5) Access here
sunkit-image (https://docs.sunpy.org/projects/sunkit-image/) is a SunPy (The SunPy Community 2020) affiliated package.
Acknowledgments
Solar Orbiter is a space mission of international collaboration between ESA and NASA, operated by ESA. The EUI instrument was built by CSL, IAS, MPS, MSSL/UCL, PMOD/WRC, ROB, LCF/IO with funding from the Belgian Federal Science Policy Office (BELSPO/PRODEX PEA C4000134088); the Centre National d’Études Spatiales (CNES); the UK Space Agency (UKSA); the Bundesministerium für Wirtschaft und Energie (BMWi) through the Deutsches Zentrum für Luft- und Raumfahrt (DLR); and the Swiss Space Office (SSO). AIA is an instrument on board SDO, a mission for NASA’s Living With a Star program. SOHO/LASCO data are produced by a consortium of the Naval Research Laboratory (USA), Max-Planck-Institut für Aeronomie (Germany), Laboratoire d’Astronomie (France), and the University of Birmingham (UK). SOHO is a project of international cooperation between ESA and NASA. Gabriel Pelouze’s work was supported by a CNES post-doctoral grant. This work used data provided by the MEDOC data and operations centre (CNES / CNRS / Université Paris-Saclay), http://medoc.ias.u-psud.fr/.
References
- Anscombe, F. J. 1948, Biometrika, 35, 246 [Google Scholar]
- Batson, J., & Royer, L. 2019, in Proceedings of the 36th International Conference on Machine Learning, eds. K. Chaudhuri, & R. Salakhutdinov, Proceedings of Machine Learning Research, 97, 524 [Google Scholar]
- Boerner, P., Edwards, C., Lemen, J., et al. 2012, Sol. Phys., 275, 41 [Google Scholar]
- Brueckner, G. E., Howard, R. A., Koomen, M. J., et al. 1995, Sol. Phys., 162, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Druckmüller, M. 2013, ApJS, 207, 25 [CrossRef] [Google Scholar]
- Hanika, J., Dammertz, H., & Lensch, H. 2011, Comput. Graph. Forum, 30, 1879 [CrossRef] [Google Scholar]
- Holschneider, M., Kronland-Martinet, R., Morlet, J., & Tchamitchian, P. 1989, in Wavelets. Time-Frequency Methods and Phase Space, eds. J.-M. Combes, A. Grossmann, & P. Tchamitchian, 286 [Google Scholar]
- Lamy, P., Llebaria, A., Boclet, B., et al. 2020, Sol. Phys., 295, 89 [CrossRef] [Google Scholar]
- Lamy, P. L., Gilardy, H., & Llebaria, A. 2022, Space Sci. Rev., 218, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Lemen, J. R., Title, A. M., Akin, D. J., et al. 2012, Sol. Phys., 275, 17 [Google Scholar]
- Levi, L. 1974, Comput. Graph. Image Proces., 3, 163 [CrossRef] [Google Scholar]
- Lupton, R., Blanton, M. R., Fekete, G., et al. 2004, PASP, 116, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Morgan, H. 2015, ApJS, 219, 23 [CrossRef] [Google Scholar]
- Morgan, H., & Druckmüller, M. 2014, Sol. Phys., 289, 2945 [Google Scholar]
- Morgan, H., Habbal, S. R., & Woo, R. 2006, Sol. Phys., 236, 263 [Google Scholar]
- Müller, D., St Cyr, O. C., Zouganelis, I., et al. 2020, A&A, 642, A1 [Google Scholar]
- Murtagh, F., Starck, J. L., & Bijaoui, A. 1995, A&AS, 112, 179 [Google Scholar]
- Nicula, B., Berghmans, D., & Hochedez, J.-F. 2005, Sol. Phys., 228, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Patel, R., Majumdar, S., Pant, V., & Banerjee, D. 2022, Sol. Phys., 297, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Rochus, P., Auchère, F., Berghmans, D., et al. 2020, A&A, 642, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schreiber, W. F. 1970, Pattern Recogn., 2, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Shensa, M. J. 1992, IEEE Trans. Signal Proces., 40, 2464 [CrossRef] [Google Scholar]
- Starck, J.-L., & Murtagh, F. 1994, A&A, 288, 342 [NASA ADS] [Google Scholar]
- Starck, J.-L., & Murtagh, F. 2002, Astronomical Image and Data Analysis (Berlin: Springer-Verlag) [Google Scholar]
- Starck, J.-L., Siebenmorgen, R., & Gredel, R. 1997, ApJ, 482, 1011 [NASA ADS] [CrossRef] [Google Scholar]
- Stenborg, G., & Cobelli, P. J. 2003, A&A, 398, 1185 [CrossRef] [EDP Sciences] [Google Scholar]
- Stenborg, G., Vourlidas, A., & Howard, R. A. 2008, ApJ, 674, 1201 [Google Scholar]
- The SunPy Community (Barnes, W. T., et al.) 2020, ApJ, 890, 68 [Google Scholar]
- Tomasi, C., & Manduchi, R. 1998, Sixth International Conference on Computer Vision (IEEE Cat No.98CH36271), 839 [CrossRef] [Google Scholar]
- Unser, M. 1999, IEEE Signal Proces. Mag., 16, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Yule, J. 1944, Photogr. J., 84, 321 [Google Scholar]
All Tables
Comparison of execution times (in seconds) for NAFE (on 48 cores), MGN, and WOW, for the images presented in this paper.
All Figures
 |
Fig. 1. Dynamic range and spatial scales in a solar EUV image. Left: fifteen-bit image taken by the Full Sun Imager (FSI) channel of EUI at 17.4 nm on 2022 March 17 at 06:00:45 UT, displayed in linear scale. Only the brightest features are visible. The profile is taken along the row marked by the side ticks. Middle: same image after logarithmic scaling. Faint off-limb details are revealed, but the local contrast is diminished. Right: Fourier power spectrum of the variance normalized image. The profile is that of the bottom row. The larger the spatial scale, the more power (and thus variability) in the image. |
| In the text | |
 |
Fig. 2. À trous wavelet transform and coefficients whitening. Two top rows: chained convolutions cs(k) of the input image c0(k) with à trous kernels dilated by a factor of two at each step. The left half of each panel corresponds to regular convolutions; the right half to bilateral filtering. Two middle rows: corresponding wavelet coefficients ws + 1(k)=cs(k)−cs + 1(k), that is the difference between successive convolutions or bilateral filterings. The last coefficient is the result of the last convolution or bilateral filtering. The original image (c0(k), left) is the sum of all coefficients. The bilateral transform preserves the edges in the coarse images (top rows). Two bottom rows: whitened coefficients, i.e., normalized to the local power. The filtered image (left) is the sum of all whitened coefficients. For visualization purposes, the convolutions and the coefficients are displayed using two different color scales. |
| In the text | |
 |
Fig. 3. Three levels of WOW processing. Top left: original γ-stretched (γ = 2.4) HRIEUV image. The inset (top left quarter) shows an enlargement of the area within the white square. Top right: output of the WOW algorithm. Bottom right: Same with added denoising. Bottom right: output of the edge-aware denoised version of the algorithm. For all images the gray scale maps to the central 99.8% of values. An animated version of this figure is available https://www.aanda.org/10.1051/0004-6361/202245345/olm. |
| In the text | |
 |
Fig. 4. Examples of WOW processed images. For each row, the left image is the original γ-stretched with γ = 2.4, the right image is the output of the edge-aware denoised version of the algorithm. Top: Crop of the 30.4 nm FSI image taken on 2022 March 21 at 06:30:15 UT. Middle: 17.1 nm AIA image taken on 2012 August 31 at 19:44:35 UT. Bottom: LASCO C2 image taken on 1998 June 2 at 13:31:06 UT. |
| In the text | |
 |
Fig. 5. Comparison of the WOW, NAFE, and MGN algorithms. Top left: original γ-stretched (γ = 2.4) HRIEUV image. The inset (top left quarter) shows an enlargement of the area within the white square. Top right: output of the edge-aware denoised version of the algorithm. Middle row: NAFE (left) and corresponding detail layer (right). Bottom row: MGN (left), and corresponding detail layer (right). In NAFE and MGN, the γ-stretched original image (top left) is added to their respective detail layers (right column). The left column thus corresponds to: no enhancement, added NAFE detail layer, added MGN detail layer. The standard WOW output does not include an arbitrary γ-stretched component. An animated version of this figure is available https://www.aanda.org/10.1051/0004-6361/202245345/olm. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



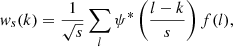
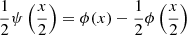
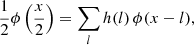
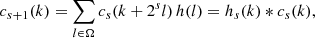
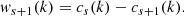
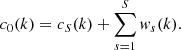
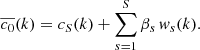
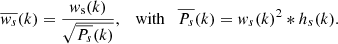
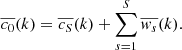
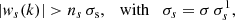
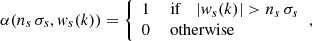
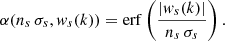
![$$ \begin{aligned} T[I(k)] = \sqrt{I(k) + \frac{3}{8}} \end{aligned} $$](/articles/aa/full_html/2023/02/aa45345-22/aa45345-22-eq17.gif)