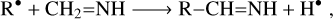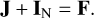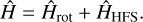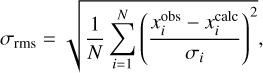EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 669 (January 2023) A&A, 669 (2023) A93 Full HTML
Open Access
Issue
A&A
Volume 669, January 2023
Article Number A93
Number of page(s) 11
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/202244618
Published online 17 January 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe-to-Open model.

Open access funding provided by Max Planck Society.

1 Introduction

To date, about 280 molecules have been detected in the interstellar medium (ISM) in a wide variety of environments, spanning from molecular clouds to late-type stars (see e.g., Endres et al. 2016)1. In recent years, the number of comparatively large species increased, and complex organic molecules (COMs, Herbst & van Dishoeck 2009) have generated a substantial amount of interest because their presence in the ISM suggests that chemical complexity starts already in the earliest stages of star formation. Furthermore, the discovery of many amino acids in carbonaceous chondrites (Snyder et al. 2005; Aponte et al. 2020) and the identification of glycine, the simplest member this molecular family, through in situ measurements in the 67P/Churyumov–Gerasimenko comet (Altwegg et al. 2016), has triggered an intense debate on their chemical origin, with many hypotheses on possible formation pathways, precursors, and intermediates (e.g. Theule et al. 2011; Koch et al. 2008; Woon 2002; Aponte et al. 2017).

Laboratory studies on interstellar ice analogues indicate that amino acids can form via hydration of an aminonitrile compound (H2N–CHR–CN, Koch et al. 2008), which in turn may be generated under astrophysical conditions in two ways. One pathway, driven by photochemistry, consists in the addition of ammonia to the corresponding nitrile (R–CN, Danger et al. 2011); alternatively, the formation can proceed through the Strecker synthesis, a reaction scheme that has been demonstrated to take place not only in solution, but also in the solid phase (Bossa et al. 2009). This process starts from the condensation of ammonia with an aldehyde (R–CHO, see Rimola et al. 2010) and involves imines (RCH=NH) as reactive intermediates (Walch et al. 2001).

Imines are a class of nitrogen-bearing molecules that have a good record of detection in the ISM. Methanimine (CH2=NH), the simplest member, was revealed in the ISM in 1973 by Godfrey et al.. Subsequently, other more complex species were identified: ethanimine (CH3CH=NH, Loomis et al. 2013), C-cyanomethanimine (NC-CH-NH, Zaleski et al. 2013; Rivilla et al. 2019), and propargylimine (HC≡C–CH=NH, Bizzocchi et al. 2020). More recently, ketenimine (CH2=C=NH, Lovas et al. 2006) has been tentatively detected and an upper limit has been reported for propanimine (CH3CH2CHNH, Margulès et al. 2022).

Formation routes of imines via tautomerisation (Lovas et al. 2006) or partial hydrogenation on the dust grain surface (Theule et al. 2011; Krim et al. 2019) of nitriles have been put forth in the past. More recently, a promising hypothesis points to the role of methanimine as the progenitor of complex imines upon the addition or elimination of reactive radicals. Theoretical studies showed that gas-phase reactions of the CN and CCH radicals with CH2=NH are exothermic and barrierless, leading to C-cyanomethanimine (Vazart et al. 2015) and propargylimine (Lupi et al. 2020), respectively. Generalising this idea, we can speculate that more complex members of the same chemical family are produced in the cold ISM through the process Puzzarini (2022)

R•+CH2=NH→R-CH=NH+H•${{\rm{R}}^ \bullet } + {\rm{C}}{{\rm{H}}_{\rm{2}}} = {\rm{NH}} \to {\rm{R - CH = NH + }}{{\rm{H}}^ \bullet }$(1)

where R• is a generic small radical. Following this scheme, the species allylimine (CH2 = CH–CH=NH, also known as 1-aza-1, 3-butadiene) is an interesting candidate for generation through the above reaction with R• being the vinyl radical (CH2 =CH•), which is likely to be abundant in the interstellar gas. Many vinyl-containing compounds have been detected so far: CH2 = CHCN, (Gardner & Winnewisser 1975), CH2=CHOH (Agúndez et al. 2021), CH2=CHCHO (Hollis et al. 2004), CH2=CHNH2 Zeng et al. 2021, CH2=CH=CCH (Cernicharo et al. 2021), and CH2 = CH–C3N (Kelvin Lee et al. 2021).

To date, allylimine has not been effectively searched for in space as it lacked a satisfactory spectroscopic characterisation. To the best of our knowledge, only two earlier and rather out-dated studies are present in the literature. The first laboratory investigation was published by Penn (1978), who recorded the microwave spectra of two structural isomers of this molecule in the 8–26 GHz frequency range using a Stark-modulation spectrometer. A few years later, Brown et al. (1981) investigated a few rotational transitions at centimetre (cm) wavelengths and determined the 14N-quadrupole coupling constants. Both of these studies are based on a very limited data set; the spectroscopic analyses are thus incomplete and lack an accurate treatment of the centrifugal distortion effects.

For the reasons above, we carried out a detailed laboratory investigation of the rotational spectra of the most stable isomers of allylimine extending the frequency coverage well into the millimetre (mm) domain. The goal is to obtain an accurate centrifugal distortion analysis and to generate an improved line catalogue for radio astronomical purposes. Guided by the new laboratory data, we performed a search for allylimine towards the quiescent G+0.693-0.027 molecular clouds (hereafter G+0.693), located at the central molecular zone (CMZ) in the inner ~500 pc of our Galaxy. In this object, methanimine, cyanomethanimine, and propargylimine have recently been detected (Zeng et al. 2018; Rivilla et al. 2019; Bizzocchi et al. 2020), together with many other molecular species, including several first detections in the ISM (Jiménez-Serra et al. 2020, 2022; Rivilla et al. 2020, 2021b,a, 2022a,b,c; Rodriguez-Almeida et al. 2021a,b; Zeng et al. 2021; Colzi et al. 2022).

The paper is structured as follows. The experimental procedure is described in Sect. 2. A concise account of the molecular properties of allylimine and the theoretical calculations performed to support the data analysis is given in Sect. 3. The spectral analysis is described in Sect. 4, and the astronomical observations in Sect. 5. In Sect. 6 we discuss the results, and in Sect. 7 we draw our conclusions.

2 Experimental details

The rotational spectrum of allylimine has been investigated using two millimetre-wave spectrometers located at the Center for Astrochemical Studies at the Max-Planck-Institut für extrater-restrische Physik in Garching (Germany) and at the Department of Chemistry of the University of Bologna (Italy). In the following we provide a brief description of the two experimental set-ups.

2.1. CASAC spectrometer

The Center for Astrochemical Studies Absorption Cell (CASAC) was employed to record the spectrum of allylimine in the 80–240 GHz range. The instrument has been described comprehensively elsewhere (Bizzocchi et al. 2017) and only a few details relevant for the present study are reported here. The instrument uses an active multiplier chain (Virginia Diodes) as the primary source of millimetre radiation in the 82–125 GHz band. This device is fed by a 9–15 GHz synthesizer locked to a Rb atomic clock for accurate frequency and phase stabilisation. Further multiplier stages, applied in cascade, allow a frequency coverage up to ~1.1THz. A closed-cycle He-cooled InSb hot electron bolometer operating at 4 K is used as a detector. The frequency-modulation technique is employed to improve the signal-to-noise ratio (S/N): the source is sine-wave modulated at 50 kHz and the detector output is demodulated at twice this frequency (2f detection) by a lock-in amplifier, so that the second derivative of the actual absorption profile is recorded by the computer-controlled acquisition system.

The same absorption cell and pyrolysis system used to study propargylimine (Bizzocchi et al. 2020) were adopted for this experiment. Allylimine was produced as described by Penn (1978). Diallylamine vapours were flowed through a 1 cm diameter quartz tube heated to 800°C with a typical pressure of 180 mTorr (24 Pa). The pyrolysis products were directly flowed through the absorption cell, which was continuously pumped and kept at a pressure of about 4 mTorr (0.5 Pa).

2.2. Bologna millimetre spectrometer

Rotational spectra between 240 and 310 GHz were recorded using the frequency-modulation millimetre/submillimetre-wave spectrometer located in Bologna (Melosso et al. 2019a,b). A Gunn diode working in the W band (80–115 GHz) coupled to a passive frequency multiplier (WR3.4x3, Virginia Diodes Inc.) was used as the main radiation source, whose frequency is stabilised and controlled through a phase-lock-loop (PLL). A frequency-modulated 75 MHz signal, coming from a centimetre-wave synthesizer (HP8642A), was used as intermediate frequency in the PLL. All the electronics are referenced to a Rb atomic clock. The detection system is composed of a zero-bias detector (WR3.4ZBD, Virginia Diodes Inc.) operating in the 220–330 GHz range and a lock-in amplifier. The latter has the twofold purpose of demodulating the output signal using the 2f detection scheme and filtering out some background noise as a resistor-capacitor circuit.

The measurements were performed in a quartz absorption cell surrounded by a 90 cm long tubular oven, using the same set-up recently described by Jiang et al. (2021). The optical elements of the spectrometer were arranged in a double-pass configuration (for further details, see e.g. Melosso et al. 2020a,b) in order to reach an absorption path-length of ~3 m. Allylimine was produced directly inside the absorption cell by heating diallylamine vapours at a temperature of 500°C. Differently from what was observed in the past for other imines, for which the flash vacuum pyrolysis was performed externally to the absorption cell (Melosso et al. 2018; Melli et al. 2018, 2020), good signals of allylimine were already obtained at 100°C. The working temperature of 500° C was chosen with the unique purpose of obtaining stable experimental conditions since the ON/OFF control of the oven causes some oscillation at lower temperatures.

thumbnail Fig. 1

Isomers of allylamine.

3 Molecular properties

Allylimine can be conveniently illustrated as an iminic moiety –CH=NH connected to a vinyl group CH2=CH–by a single C–C bond. Depending on the relative orientation of these two sub-units, four geometrical isomers can be defined. The prefixes cis - (C) and trans - (T) are used to identify the position of the two constituents with respect to the central C–C bond, respectively on the same and on the opposite side; the labels syn - (s) and anti-(a) define the position of the iminic H with respect to C=C. The resulting four geometric isomers are depicted in Fig. 1 and are denoted Ta, Ts, Ca, and Cs. All forms but Cs have a planar structure with Cs symmetry. In the Cs form, owing to the repulsion between the iminic H and one terminal vinyl H, the molecular backbone is tilted and the molecular symmetry is C1, in analogy to trans-butadiene (Baraban et al. 2018) and azabutadiene (Jiang et al. 2022).

The molecular and spectroscopic properties of the four allylimine isomers were evaluated by means of state-of-the-art computational methodologies. Equilibrium structures (and their corresponding energies), which straightforwardly provide equilibrium rotational constants, were computed by exploiting the so-called CCSD(T)/CBS+CV composite scheme (Heckert et al. 2005a,b). This approach is based on the CCSD(T) method (i.e. coupled cluster singles and doubles approximation augmented by a perturbative treatment of triple excitations; Raghavachari et al. 1989) and accounts for the extrapolation to the complete basis set (CBS) limit and core-valence (CV) correlation effects. Vibrational corrections to equilibrium rotational constants, evaluated at a lower level of theory, were incorporated to predict ground-state rotational constants. Quartic and sextic centrifugal distortion parameters as well as first-order molecular properties (dipole moments and nuclear quadrupole coupling constants) were accurately predicted by exploiting CCSD(T) calculations. For nuclear quadrupole coupling constants, vibrational corrections to the equilibrium values were also considered. A detailed account on the quantum-chemical calculations performed is provided in Appendix A.

The relative energies and the electric dipole moments of the four allylimine isomers are reported in Table 1. Our calculations indicate that the Ta isomer is the most stable, Ts is relatively close at E/k = 403.5 K, while the Ca and Cs species have higher energies, E/k > 1400 K. In the present investigation, we focus on the Ta and Ts isomers, which are the only two species detected in our laboratory experiments. Both are nearly prolate asymmetric top rotors (κ ~ –0.98); their dipole moments are rather similar (|μ| ≈ 2 D), but they differ in the corresponding principal axis projections. As Table 1 shows, the spectrum of the Ts isomer is dominated by a-type transitions, whereas the Ta species has almost equally strong a- and b-type spectra.

Table 1

Computed relative energies (CCSD(T)/CBS+CV level of theory) of the four allylimine isomers and their dipole moment components (ae-CCSD(T)/ccpCVQZ level of theory).

4 Spectral analysis and results

The rotational spectra of the Ta and Ts allylimine isomers have been recorded in selected frequency regions from 84 to 307 GHz. Two portions exhibiting typical a- and b-type patterns are shown in Fig. 2. In line with a nearly prolate rotor and the dipole components of Table 1, the Ts spectrum presents strong 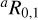aR0,1$^a{R_{0,1}}$2 branch transitions spaced by Δν ≈ (B + C). For the Ta isomer, instead, 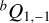bQ1,−1$^b{Q_{1, - 1}}$ branch band heads spaced by Δν ≈ 2A – B – C dominate the spectrum, leading to a more complicated pattern.

From the computed relative energy (see Table 1), a relative [Ta]/[Ts] isomer abundance of 3.8 can be estimated at 300 K (4.4 × 1017 at 10 K). From the relative intensity comparison of two closely spaced Ta and Ts lines recorded under the same experimental conditions (source power, sample pressure, temperature, and modulation depth) we derived [Ta]/[Ts] = 3.3 ± 0.8, in good agreement with the theoretical findings. Therefore, regarding the CASAC experiment, although allylimine is generated at high temperatures, a complete thermalisation is readily achieved in the room temperature absorption cell. On the contrary, the same does not apply to the Bologna experiment, which is characterised by a different set-up.

Owing to the presence of the 14N nucleus with spin I = 1 in the molecule, its non-zero nuclear quadrupole moment interacts with the molecular electric field gradient at the nucleus, giving rise to the hyperfine structure of the rotational spectrum. The interaction between the rotational angular momentum J and the nitrogen nuclear spin IN is described by the standard vector coupling scheme:

J + IN= F.${\rm{J}}\,{\rm{ + }}\,{{\rm{I}}_{\rm{N}}}{\rm{ = }}\,{\rm{F}}.$(2)

As a result, each rotational level with J > 0 splits into three hyperfine sub-levels labelled with the total angular quantum number F, where F = J – 1, J, J + 1. Therefore, the corresponding transitions are split into several components according to the ΔF = 0, ±1 selection rules, with the strongest features having ΔF = ΔJ. An example of these hyperfine patterns is given in Fig. 3.

A total of 617 and 470 lines were recorded for Ta- and Ts-allylimine, respectively, of which 293 and 65 exhibited resolvable hyperfine features that allowed their components to be assigned. For transitions with unresolved hyperfine structure, the intensity-averaged calculated frequency was instead compared with the recorded line. A few transitions (22 and 10 for Ta and Ts, respectively) taken from the literature (Penn 1978) were also included in the final data sets. To account for the different measurement precision (σ) of the two experimental sub-sets of data recorded with the CASAC and Bologna spectrometer, distinct statistical weights ω = 1/σ2 were assigned. The corresponding values are σ = 15 kHz and σ = 25–30 kHz (depending on experimental conditions).

The analysis was performed using a Hamiltonian composed of a purely rotational and a hyperfine term:

H^=H^rot+H^HFS.$\hat H = {\hat H_{{\rm{rot}}}} + {\hat H_{{\rm{HFS}}}}.$(3)

Here Ĥrot is the S -reduced Watson-type rotational Hamiltonian in its Ir representation (Watson 1977) including the centrifugal distortion up to sextic terms, whereas the hyperfine-structure Hamiltonian ĤHFS describes the 14N-quadrupole interaction making use of the traceless tensor χ, which has χaa and χbb – χcc as determinable coefficients. No 14N or H spin-rotation coupling effects were revealed; therefore, the corresponding interaction terms have been neglected in the present analysis.

The spectral analyses were carried out using the CALPGM program suite (Pickett 1991). Transitions with the J quantum number as high as 52 and 46 are included for the Ta and Ts species, respectively, whereas the maximum Ka value reached is 18 and 22, respectively. The spectroscopic constants determined from the fits are collected in Table 2, together with the corresponding computed values. The quality of the fits is expressed by the weighted root mean square σrms:

σrms=1N∑i=1Nxiobs−xicalcσi2,${\sigma _{{\rm{rms}}}} = \sqrt {{1 \over N}\sum\limits_{i = 1}^N {{{\left( {{{x_i^{{\rm{obs}}} - x_i^{{\rm{calc}}}} \over {{\sigma _i}}}} \right)}^2},} } $(4)

where xi denotes the N data, and σi the corresponding assumed uncertainties. For Ta- and Ts-allylimine, values of 1.03 and 1.00 were obtained for σrms, respectively, thus indicating that, on average, the data sets have been reproduced within the experimental uncertainties.

Owing to the new extensive data set, the spectroscopic characterisation of allylimine is considerably improved. Compared to the previous results reported by Penn (1978), the uncertainty of the rotational constants A, B, and C is reduced by three orders of magnitude (a factor of ~350 for the Ts isomer). Additionally, a complete set of quartic centrifugal distortion constants (with a precision of ~0.1%) plus four sextic terms (two for the Ts isomer) are provided for the first time. To give an example of the improvement accomplished, the JKa,Kc = 200,20 – 190,19 transition, expected to lie at 170.730 GHz with a log I of –3.82 nm2 MHz by Penn (1978), is now predicted at 170.726 GHz with a log I of –3.90 nm2 MHz, with an offset of 4 MHz between the two sets of data.

The comparison with the computed spectroscopic parameters (also reported in Table 2) points out a very good agreement for the rotational constants, which differ, on average, by only 0.07% from the experimental counterparts. The quartic centrifugal distortion constants, except for the DJK of Ta, also compare well with the experimental values, showing an average relative deviation of 3% for the two isomers. It was also possible to constrain the sextic centrifugal distortion constants to a partial set of sextic parameters: HJK, HKJ, HK, h1 for the Ta isomer and HJK, HKJ for the Ts isomer, with the remaining sextic terms kept fixed at the computed values. For the quadrupole coupling constants the agreement is on average within 1.1%.

From the improved spectroscopic constants determined in the present work, two collections of rest frequencies were produced for each isomer, and are accessible at CDMS3 (Müller et al. 2005; Endres et al. 2016); the <X>allylimine.cat catalogue list of pure rotational transitions extends up to 300 GHz, whereas the hfs_<X>allylimine.cat catalogue is limited to the 3 mm band (ν < 120 GHz), but contains all hyperfine components. The symbol <X> in the file names reads as <Ta-> or <Ts-> for the corresponding isomers. The catalogues were generated with the SPCAT routine (Pickett 1991) and their format matches that of the CDMS and JPL (Pickett et al. 1998) catalogues, thus allowing their straightforward use in astronomic line-analysis tools, such as MADCUBA (Martín et al. 2019), CASSIS (Vastel et al. 2015) and MADEX (Cernicharo, J. 2012).

A selection of rotational (Qrot), hyperfine (QHFS), and vibrational (Qvib) partition functions for Ta- and Ts-allylimine is given in Table 3. The values were computed for the 3–1000 K temperature interval and were obtained by direct summation over the rotational or hyperfine levels, whose energies have been accurately determined from the spectral analysis. The vibrational partition functions Qvib were computed using harmonic frequencies at the CCSD(T)/CBS+CV level, which were obtained as explained in Appendix A.

thumbnail Fig. 2

Portions of the experimental spectrum (in black) showing both a- and b-type spectral features (blue lines for Ts-allylimine and red lines for Ta-allylimine). Intensity is in arbitrary units.
thumbnail Fig. 3

Recordings of two b-type transitions of Ta-allylamine. The nitrogen quadrupole coupling splitting is evident (each hyperfine component has a F’ – F label). Left panel: Jka,ka 171,16 ← 170,17; right panel: Jka,ka = 42,2 ← 51,5.
Table 2

Spectroscopic constants determined for the Ta and Ts isomers of allylimine.

Table 3

Partition function values and abundance ratios at different temperatures for allylimine isomers.

5 Interstellar search towards the G+0.693 molecular cloud

We searched for the Ta and Ts allylimine isomers towards the G+0.693 molecular cloud, which is located in the SgrB2 N complex of the CMZ of our Galaxy. This region is thought to be affected by a cloud-cloud collision (Zeng et al. 2020) that produced large-scale shocks that sputtered the interstellar dust grains, thus releasing into the gas phase multiple molecules formed on the dust surfaces. This explains the extremely rich chemistry of G+0.693, where many complex organic molecules have been detected.

We exploited a sensitive unbiased spectral survey performed with the Yebes 40 m (Guadalajara, Spain) and the IRAM 30 m (Granada, Spain) telescopes. In both surveys, we used the position switching mode pointed towards α(J2000.0)= 17h47m22s, δ(J2000.0)= –28°21'27". We used Yebes 40m observations from 31.075 GHz to 50.424 GHz, and IRAM 30m observations for the 71.770–116.720 GHz, and 124.77–175.5 GHz frequency ranges. More detailed information of the observational survey, including noise levels and spectral resolutions, are available in Rivilla et al. (2021a,b).

We implemented the spectroscopy parameters presented in this work into the MADCUBA package4; version 11/03/2022; (Martín et al. 2019). Using the Spectral Line Identification and Modeling (SLIM) tool of MADCUBA, we generated synthetic spectra of the two lowest energy isomers of allylimine (Ta and Ts) under the assumption of local thermodynamic equilibrium (LTE) to be compared with the observed spectra.

Figure 4 shows the brightest transitions of the Ta form that, according to the LTE synthetic spectra, appear unblended or slightly blended with emission from other species already identified in this source, which contributes to reproducing the observed spectra well. The spectroscopic information for these Ta-allylimine transitions is shown in Table 4 and in Fig. 4. We note that all the remaining transitions of Ta-allylimine predicted within the LTE approximation are heavily contaminated by stronger emission from other species, and that there are no missing lines in the data.

To derive the column density, we used the AUTOFIT tool of SLIM (see Martín et al. 2019), which finds the best fit between the simulated LTE model and the observed spectra. We also considered the contribution to the emission from other molecules. The excitation temperature (Tex) found for most of the molecules detected towards this molecular cloud is low, typically in the range 5–20 K (see e.g. Zeng et al. 2019). This Tex is significantly lower than the kinetic temperature of the cloud (~150K) because the molecules are sub-thermally excited, due to the relatively low density of the cloud (~104– 105 cm–3, Zeng et al. 2020). For this reason, we used the Tex value of 8K derived for a very similar species, propargylimine (Bizzocchi et al. 2020), with a FWHM of 20km s–1 and velocity υLSR = 69kms–1. We obtained N=(1.5±0.6)×1013 cm–2, which implies a molecular abundance compared to molecular hydrogen of ~4x10–11, using N(H2)=1.35x1023 cm–2 (Martín et al. 2008).

Similarly, several transitions of the Ts species are tentatively detected, as shown in Fig. 5 (see Table 4 for their spectro-scopic information). In this case, the AUTOFIT algorithm did not converge, so we changed the value of N (leaving the other parameters fixed) until we found a good correspondence with the observed spectrum. We obtained N ~ 0.5×1013 cm–2, a factor of ~3 less abundant that the Ta isomer. This is in good agreement with the results found for other isomers, for which the most stable species is the most abundant, for example cyanomethanimine and propargylimmine (Rivilla et al. 2019; Bizzocchi et al. 2020, respectively).

The tentative detections of both forms of allylimine presented here confirm that these species are less abundant than others imines detected towards G+0.693. The Ta isomer is a factor of ~36, ~13, and ~1.6 less abundant than methanimine (CH2NH, Zeng et al. 2019), Z-cyanomethanimine (Z-HNCHCN, Rivilla et al. 2019), and Z-propargylimine (Z-HCCCHNH, Bizzocchi et al. 2020), respectively. This confirms a clear trend of decreasing molecular abundance with increasing imine complexity, similarly to what is found for other chemical families towards G+0.693, such as alcohols (Jiménez-Serra et al. 2022), isocyanates (Rodríguez-Almeida et al. 2021b), aldehydes (Sanz-Novo et al. 2022), and thiols (Rodríguez-Almeida et al. 2021a).

thumbnail Fig. 4

Ta-allylimine transitions tentatively detected towards G+0.693. The observed spectrum is shown in grey histograms. The simulated LTE spectrum of Ta-allylimine using the parameters explained in the text (Sect. 5) is indicated by the red curve. The blue curve denotes the contribution of all the species identified in G+0.693, including allylimine. The quantum numbers of the Ta-allylimine transitions are provided in each panel.
thumbnail Fig. 5

Ts-allylimine transitions tentatively detected towards G+0.693. The observed spectrum is shown in grey histograms. The simulated LTE spectrum of Ts-allylimine using the parameters explained in the text (Sect. 5) is indicated by the red curve. The blue curve denotes the contribution of all the species identified in G+0.693, including allylimine. The quantum numbers of the Ts-allylimine transitions are indicated in each panel.

6 Discussion

The analysis of the transitions tentatively assigned to allylim-ine in G+0.693 yielded a plausible estimate of its abundance, in line with the trend established by the other detected members of the same class. Starting from methanimine (RCH=NH, with R=H), an inverse relation between the observed abundance and the complexity of the R moiety is highlighted. Recent the oretical investigations on imine formation routes suggest that methanimine may actually act as the main progenitor (Lupi et al. 2020; Puzzarini & Barone 2020), and the processes leading to the various species are substantially influenced by the abundances of the R radicals that take part in the relevant reaction. The column density of allylimine estimated in this work (0.15 × 1014 cm–2, Ta isomer) is less than that derived for propar-gylimine (0.24 × 1014 cm–2, Z-isomer, Bizzocchi et al. 2020), thus suggesting a consistent relationship between the CCH and CH2=CH species. To date, no estimates of the vinyl radical column density are available, but the abundance ratio of the corresponding cyanides, [HC3N]/[CH2=CHCN] ~ 8 (Bizzocchi et al. 2020), points in that direction.

The [E]/[Z] isomeric ratio of imines in the ISM is a topic that has recently attracted some attention (see e.g. Rivilla et al. 2019 and reference therein). Generally speaking, the observed geometrical isomer ratio can be attributed to the combined effects of formation and destruction processes (Vazart et al. 2015; Shingledecker et al. 2020). An alternative hypothesis, which has been recently put forth, suggests that the conversion from the least stable isomer to the most stable one is feasible even at very low temperatures via quantum tunnelling (García de la Concepción et al. 2021). In this framework, the isomeric abundances of imines are governed solely by thermodynamics, and the observed [E]/[Z] ratios should be interpreted in terms of their relative stability. This scenario has had some success in reproducing the isomeric ratios observed in G+0.693 for cyanomethanimine ([Z]/[E] ~ 6), ethanimine ([Z]/[E] = 10–15), and propargylimine ([Z]/[E] > 2), when assuming a kinetic temperature Tkin = 150 K. For allylimine, by inserting the energy difference between Ts and Ta isomers, ΔΕ/k = 403.5 K, in Eq. (5) of Garcia de la Concepción et al. (2021), one gets an isomeric ratio [Ta/Ts] ~ 15, which is higher than the (tentatively) observed value of ~3. This would suggest that there is an extra abundance of the less stable Ts isomer with respect to that predicted by thermochemistry. This would also be in contrast relative dipole principle (RDP) proposed by Shingledecker et al. (2020), which postulates an anti-correlation between the relative isomer abundance and the magnitude of their permanent dipole moments (μTa = 2.05 D and μTs = 2.56 D). Therefore, either the formation of Ts-allylimine is kinetically favoured or the two isomers originate from distinct chemical routes.

Table 4

Tentatively observed rotational transitions of both allylimine isomers.

7 Conclusions

This paper reports on an extensive spectroscopic characterisation of allyllimine, CH2 =CH–CH=NH, a species that represents a higher level of complexity compared to the previous members of the same chemical class already detected in the ISM. Measurements have been performed between 84 and 300GHz, with the recording of 617 and 470 new rotational transitions for the two most stable Ta and Ts isomers, respectively. The resulting data sets were analysed using an S -reduced rotational Hamilto-nian, yielding a very precise set of rotational constants, a full set of quartic coefficients, and some sextic centrifugal distortion coefficients. A number of lines showed resolvable hyperfine structure due to the quadrupole interaction of the14 N nucleus with molecular rotation. For these transitions, each hyperfine component was accurately measured and analysed to determine the corresponding coupling coefficients. High-level theoretical calculations were performed to assist the spectral assignment and the analysis of the laboratory data. In particular, ab initio values were used as suitable constraints for the Hamiltonian coefficients which could not be adjusted in the least-squares fit. Overall, the agreement between experimentally derived constants and the corresponding theoretical prediction is very good.

The new extensive set of spectroscopic parameters (see Table 2) was employed to generate catalogues of highly precise rest frequencies for the Ta and Ts isomers at millimetre wavelengths. These data were used to perform a search for allylimine emission lines in a spectral survey of the molecular cloud G+0.693 located in the CMZ. Eight transitions for each isomers have been tentatively assigned, leading to the derivation of the column densities N = (1.5 ± 0.6) × 1013 cm–2 for Ta and N ~ 0.5 × 1013 cm–2 for Ts. These values are lower than those of the simpler related species cyanomethanimine and propargylimine, in agreement with the expected trend. The resulting [Ta]/[Ts] isomer ratio is ~3, much lower than the value of ~15 that can be estimated on the basis of thermodynamic considerations.

Acknowledgements

We thank the Max Planck society for the financial support. The work at Bologna University was supported by RFO funds and MIUR (PRIN Grant Number 202082CE3T). We are grateful to the IRAM 30 m and Yebes 40 m telescope staff for help during the different observing runs. IRAM is supported by the National Institute for Universe Sciences and Astronomy/National Center for Scientific Research (France), Max Planck Society for the Advancement of Science (Germany), and the National Geographic Institute (IGN) (Spain). The 40m radio telescope at Yebes Observatory is operated by the IGN, Ministe– rio de Transportes, Movilidad y Agenda Urbana. V.M.R. has received support from the Comunidad de Madrid through the Atracción de Talento Investigador Modalidad 1 (Doctores con experiencia) Grant (COOL:Cosmic Origins of Life; 2019-T1/TIC-5379), and the Ayuda RYC2020-029387-I funded by MCIN/AEI /10.13039/501100011033. A.P.C. gratefully acknowledges the super-computing facilities of CINECA (project “CINEMA”, grant HP10C2QE6F) and SCSCF (“Sistema per il Calcolo Scientifico di Ca’ Foscari”, a multiprocessor cluster system owned by Università Ca’ Foscari Venezia).

Appendix A Details of the theoretical calculations

As mentioned in the main text, equilibrium geometries (and the corresponding energies) were evaluated using the CCSD(T)/CBS+CV composite scheme. The extrapolation to the CBS limit was performed considering Hartree–Fock Self Consistent Field (HF-SCF) and CCSD(T) correlation energy separately. For HF-SCF, the three-point exponential extrapolation formula by Feller (1992) was used in conjunction with the cc-pVnZ basis sets, with n=T,Q,5. For CCSD(T), the n–3 formula by Helgaker et al. (1997) and the cc-pVTZ and cc-pVQZ basis sets were employed. The CV contribution was computed as the difference between the all-electron (ae) computation and the corresponding frozen–core (fc) computation at the CCSD(T)/cc-pCVTZ level (Woon & Dunning 1995).

Equilibrium geometries straightforwardly provided equilibrium rotational constants that were corrected for vibrational effects. The corresponding corrections were determined within vibrational perturbation theory to second order (VPT2) (Mills 1972) and required anharmonic force field calculations, which were performed at the fc-CCSD(T)/cc-pVTZ level. These computations also provided, as a by-product, sextic centrifugal distortion constants. The CCSD(T)/CBS+CV composite scheme has also been employed for harmonic force field calculations, which led to the determination of the harmonic vibrational frequencies collected in Table A.1 and, as a by-product, the quartic centrifugal distortion constants. Nuclear quadrupole coupling constants were computed at the CCSD(T)/cc-pCVQZ level correlating all electrons because, as is well known from the literature (Puzzarini et al. 2010), they require a basis set of at least quadruple-zeta quality and the correlation of core electrons. Furthermore, for quantitative predictions, vibrational corrections need to be incorporated (Puzzarini et al. 2009), that were evaluated using second-order M0ller-Plesset perturbation theory (MP2; Møller & Plesset (1934)) in conjunction with the cc-pCVTZ basis set. The CFOUR quantum chemistry package (Matthews et al. 2020) was employed for all CCSD(T) calculations, while the Gaus-sian16 software (Frisch et al. 2016) was used for MP2 computations. Sextic centrifugal distortion constants were obtained with an in-house program (Pietropolli Charmet & Cornaton 2018).

Table A.1

Harmonic vibrational frequencies.

References

  1. Agúndez, M., Marcelino, N., Tercero, B., et al. 2021, A&A, 649, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Altwegg, K., Balsiger, H., Bar-Nun, A., et al. 2016, Sci. Adv., 2, e1600285 [NASA ADS] [CrossRef] [Google Scholar]
  3. Aponte, J. C., Elsila, J. E., Glavin, D. P., et al. 2017, ACS Earth Space Chem., 1, 3 [NASA ADS] [CrossRef] [Google Scholar]
  4. Aponte, J. C., Elsila, J. E., Hein, J. E., & Dworkin, J. P. 2020, Meteor. Planet. Sci., 55, 2422 [NASA ADS] [CrossRef] [Google Scholar]
  5. Baraban, J., Martin-Drumel, M. A., Changala, P. B., et al. 2018, Angew. Chem. Int. Ed., 57, 1821 [CrossRef] [Google Scholar]
  6. Bizzocchi, L., Lattanzi, V., Laas, J., et al. 2017, A&A, 602, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Bizzocchi, L., Prudenzano, D., Rivilla, V. M., et al. 2020, A&A, 640, A98 [EDP Sciences] [Google Scholar]
  8. Bossa, J. B., Theule, P., Duvernay, F., & Chiavassa, T. 2009, ApJ, 707, 1524 [Google Scholar]
  9. Brown, R. D., Godfrey, P. D., & Winkler, D. A. 1981, Chem. Phys., 59, 243 [NASA ADS] [CrossRef] [Google Scholar]
  10. Cernicharo, J. 2012, EAS Publ. Ser., 58, 251 [Google Scholar]
  11. Cernicharo, J., Agúndez, M., & Cabezas. 2021, A&A, 647, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Colzi, L., Martín-Pintado, J., Rivilla, V. M., et al. 2022, ApJ, 926, L22 [NASA ADS] [CrossRef] [Google Scholar]
  13. Danger, G., Bossa, J.-B., de Marcellus, P., et al. 2011, A&A, 525, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Endres, C. P., Schlemmer, S., Schilke, P., Stutzki, J., & Müller, H. S. P. 2016, J. Mol. Spectrosc., 327, 95 [NASA ADS] [CrossRef] [Google Scholar]
  15. Feller, D. 1992, J. Chem. Phys., 96, 8 [NASA ADS] [Google Scholar]
  16. Frisch, M. J., Trucks, G. W., Schlegel, H. B., et al. 2016, Gaussian 16 Revision C.01 (Wallingford, CT: Gaussian Inc.) [Google Scholar]
  17. García de la Concepción, J., Jiménez-Serra, I., Carlos Corchado, J., Rivilla, V. M., & Martín-Pintado, J. 2021, ApJ, 912, L6 [CrossRef] [Google Scholar]
  18. Gardner, F. F., & Winnewisser, G. 1975, ApJ, 195, L127 [NASA ADS] [CrossRef] [Google Scholar]
  19. Godfrey, P. D., Brown, R. D., Robinson, B. J., & Sinclair, M. W. 1973, ApJL, 13, 119 [Google Scholar]
  20. Gordy, W., & Cook, R. L. 1984, Microwave Molecular Spectra, 3rd edn. (Wiley New York), 929 [Google Scholar]
  21. Heckert, M., Kállay, M., & Gauss, J. 2005a, Mol. Phys., 103, 2109 [NASA ADS] [CrossRef] [Google Scholar]
  22. Heckert, M., Kállay, M., Tew, D. P., Klopper, W., & Gauss, J. 2005b, J. Chem. Phys., 125, 044108 [Google Scholar]
  23. Helgaker, T., Klopper, W., Koch, H., & Noga, J. 1997, J. Chem. Phys., 106, 9639 [NASA ADS] [CrossRef] [Google Scholar]
  24. Herbst, E., & van Dishoeck, E. F. 2009, ARA&A, 47, 427 [NASA ADS] [CrossRef] [Google Scholar]
  25. Hollis, J. M., Jewell, P. R., Lovas, F. J., Remijan, A., & Møllendal, H. 2004, ApJ, 610, L21 [Google Scholar]
  26. Jiang, N., Melosso, M., Tamassia, F., et al. 2021, Front. Astron. Space Sci., 8, 29 [NASA ADS] [CrossRef] [Google Scholar]
  27. Jiang, N., Melosso, M., Bizzocchi, L., et al. 2022, J. Phys. Chem. A, 126, 1881 [NASA ADS] [CrossRef] [Google Scholar]
  28. Jiménez-Serra, I., Martín-Pintado, J., Rivilla, V. M., et al. 2020, Astrobiology, 20, 1048 [Google Scholar]
  29. Jiménez-Serra, I., Rodriguez-Almeida, L. F., Martin-Pintado, J., et al. 2022, A&A 663, A181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Kelvin Lee, K. L., Loomis, R. A., Burkhardt, A. M., et al. 2021, ApJL, 908, L11 [NASA ADS] [CrossRef] [Google Scholar]
  31. Koch, D. M., Toubin, C., Peslherbe, G. H., & Hynes, J. T. 2008, J. Phys. Chem. C, 112, 2972 [Google Scholar]
  32. Krim, L., Guillemin, J.-C., & Woon, D. E. 2019, MNRAS, 485, 5210 [Google Scholar]
  33. Loomis, R. A., Zaleski, D. P., Steber, A. L., et al. 2013, ApJ, 765, L9 [Google Scholar]
  34. Lovas, F. J., Hollis, J. M., Remijan, A. J., & Jewell, P. R. 2006, ApJ, 645, L137 [NASA ADS] [CrossRef] [Google Scholar]
  35. Lupi, J., Puzzarini, C., & Barone, V. 2020, ApJ, 903, L35 [NASA ADS] [CrossRef] [Google Scholar]
  36. Margulès, L., Remijan, A., Belloche, A., et al. 2022, A&A, 663, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Martín, S., Requena-Torres, M. A., Martín-Pintado, J., & Mauersberger, R. 2008, ApJ, 678, 245 [CrossRef] [Google Scholar]
  38. Martín, S., Martín-Pintado, J., Blanco-Sánchez, C., et al. 2019, A&A, 631, A159 [Google Scholar]
  39. Matthews, D. A., Cheng, L., Harding, M. E., et al. 2020, J. Chem. Phys., 152, 214108 [NASA ADS] [CrossRef] [Google Scholar]
  40. Melli, A., Melosso, M., Tasinato, N., et al. 2018, ApJ, 855, 123 [NASA ADS] [CrossRef] [Google Scholar]
  41. Melosso, M., Melli, A., Puzzarini, C., et al. 2018, A&A, 609, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Melosso, M., Bizzocchi, L., Tamassia, F., et al. 2019a, Phys. Chem. Chem. Phys., 21, 3564 [NASA ADS] [CrossRef] [Google Scholar]
  43. Melosso, M., Conversazioni, B., Degli Esposti, C., et al. 2019b, JQSRT, 222, 186 [CrossRef] [Google Scholar]
  44. Melli, A., Potenti, S., Melosso, M., et al. 2020, Chem. Eur. J., 26, 15016 [NASA ADS] [CrossRef] [Google Scholar]
  45. Melosso, M., Achilli, A., Tamassia, F., et al. 2020a, JQSRT, 248, 106982 [NASA ADS] [CrossRef] [Google Scholar]
  46. Melosso, M., Dore, L., Gauss, J., & Puzzarini, C. 2020b, J. Mol. Spectrosc., 111291 [NASA ADS] [CrossRef] [Google Scholar]
  47. Mills, I. 1972, in Molecular Spectroscopy: Modern Research, eds. K. N. Rao, & C. W. Matthews (Academic Press), 115 [CrossRef] [Google Scholar]
  48. Møller, C., & Plesset, M. S. 1934, Phys. Rev., 46, 618 [Google Scholar]
  49. Müller, H. S. P., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Struct., 742, 215 [Google Scholar]
  50. Penn, R. E. 1978, J. Mol. Spectrosc., 69, 373 [NASA ADS] [CrossRef] [Google Scholar]
  51. Pickett, H. M. 1991, J. Mol. Spectrosc., 148, 371 [Google Scholar]
  52. Pickett, H. M., Poynter, R. L., Cohen, E. A., et al. 1998, J. Quant. Spec. Radiat. Transf., 60, 883 [Google Scholar]
  53. Pietropolli Charmet, A., & Cornaton, Y. 2018, J. Mol. Struct., 1160, 455 [NASA ADS] [CrossRef] [Google Scholar]
  54. Puzzarini, C. 2022, Front. Astron. Space Sci., 8, 811342 [NASA ADS] [CrossRef] [Google Scholar]
  55. Puzzarini, C., & Barone, V. 2020, Phys. Chem. Chem. Phys., 22, 6507 [NASA ADS] [CrossRef] [Google Scholar]
  56. Puzzarini, C., Cazzoli, G., Harding, M. E., Vázquez, J., & Gauss, J. 2009, J. Chem. Phys., 131, 234304 [NASA ADS] [CrossRef] [Google Scholar]
  57. Puzzarini, C., Stanton, J. F., & Gauss, J. 2010, Int. Rev. Phys. Chem., 29, 273 [NASA ADS] [CrossRef] [Google Scholar]
  58. Raghavachari, K., Trucks, G. W., Pople, J. A., & Head-Gordon, M. 1989, CPL, 157, 479 [NASA ADS] [CrossRef] [Google Scholar]
  59. Rimola, A., Sodupe, M., & Ugliengo, P. 2010, Phys. Chem. Chem. Phys., 12, 5285 [NASA ADS] [CrossRef] [Google Scholar]
  60. Rivilla, V., Martín-Pintado, J., Jiménez-Serra, I., et al. 2019, MNRAS Lett., 483, L114 [NASA ADS] [CrossRef] [Google Scholar]
  61. Rivilla, V. M., Martín-Pintado, J., Jiménez-Serra, I., et al. 2020, ApJ, 899, L28 [Google Scholar]
  62. Rivilla, V. M., Jiménez-Serra, I., Martín-Pintado, J., et al. 2021a, Proc. Natl. Acad. Sci. U.S.A., 118, 2101314118 [NASA ADS] [CrossRef] [Google Scholar]
  63. Rivilla, V. M., Jiménez-Serra, I., García de la Concepción, J., et al. 2021b, MNRAS, 506, L79 [NASA ADS] [CrossRef] [Google Scholar]
  64. Rivilla, V. M., Colzi, L., Jiménez-Serra, I., et al. 2022a, ApJ, 929, L11 [NASA ADS] [CrossRef] [Google Scholar]
  65. Rivilla, V. M., García De La Concepción, J., Jiménez-Serra, I., et al. 2022b, Front. Astron. Space Sci., 9, 829288 [NASA ADS] [CrossRef] [Google Scholar]
  66. Rivilla, V. M., Jiménez-Serra, I., Martín-Pintado, J., et al. 2022c, Front. Astron. Space Sci., 9, 876870 [NASA ADS] [CrossRef] [Google Scholar]
  67. Rodríguez-Almeida, L. F., Jiménez-Serra, I., Rivilla, V. M., et al. 2021a, ApJ, 912, L11 [Google Scholar]
  68. Rodríguez-Almeida, L. F., Rivilla, V. M., Jiménez-Serra, I., et al. 2021b, A&A, 654, L1 [CrossRef] [EDP Sciences] [Google Scholar]
  69. Sanz-Novo, M., Belloche, A., Rivilla, V. M., et al. 2022, A&A 666, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Shingledecker, C. N., Molpeceres, G., Rivilla, V. M., Majumdar, L., & Kästner, J. 2020, ApJ, 897, 158 [NASA ADS] [CrossRef] [Google Scholar]
  71. Snyder, L. E., Lovas, F. J., Hollis, J. M., et al. 2005, ApJ, 619, 914 [CrossRef] [Google Scholar]
  72. Theule, P., Borget, F., Mispelaer, F., et al. 2011, A&A, 534, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  73. Vastel, C., Bottinelli, S., Caux, E., et al. 2015, SF2A-2015: Proceedings of the Annual meeting of the French Society of Astronomy and Astrophysics [Google Scholar]
  74. Vazart, F., Latouche, C., Skouteris, D., Balucani, N., & Barone, V. 2015, ApJ, 810, 111 [NASA ADS] [CrossRef] [Google Scholar]
  75. Walch, S. P., Bauschlicher, C. W., Ricca, A., & Bakes, E. L. O. 2001, Chem. Phys. Lett., 333, 1524 [Google Scholar]
  76. Watson, J. K. G. 1977, in Vibrational Spectra and Structure, ed. J. Durig, (Amsterdam: Elsevier), 6, 1 [Google Scholar]
  77. Woon, D. E. 2002, ApJ, 571, L177 [NASA ADS] [CrossRef] [Google Scholar]
  78. Woon, D. E., & Dunning, Thom H. J. 1995, J. Chem. Phys., 103, 4572 [NASA ADS] [CrossRef] [Google Scholar]
  79. Zaleski, D. P., Seifert, N. A., Steber, A. L., et al. 2013, ApJ, 765, L10 [Google Scholar]
  80. Zeng, S., Jiménez-Serra, I., Rivilla, V. M., et al. 2018, MNRAS, 478, 2962 [Google Scholar]
  81. Zeng, S., Quénard, D., Jiménez-Serra, I., et al. 2019, MNRAS, 484, L43 [Google Scholar]
  82. Zeng, S., Zhang, Q., Jiménez-Serra, I., et al. 2020, MNRAS, 497, 4896 [NASA ADS] [CrossRef] [Google Scholar]
  83. Zeng, S., Jiménez-Serra, I., Rivilla, V. M., et al. 2021, ApJ, 920, L27 [NASA ADS] [CrossRef] [Google Scholar]
1

See also the updated list presented at this URL: http://www. astrochymist.org/astrochymist_ism.html

2

The symbol 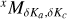xMδKa,δKc,$^x{M_{\delta {K_{a,}}\delta {K_{c,}}}}$ is used to identify the transition type of an asymmetric rotor: x stands for the dipole moment component involved; M = P, Q, R for the transitions with Δ J = –1,0, +1, respectively; δΚα and δΚc for the (signed) change of the ka and Kc pseudo quantum numbers (Gordy & Cook 1984).

4

Madrid Data Cube Analysis on ImageJ is a software developed at the Center of Astrobiology (CAB) in Madrid; http://cab.inta-csic.es/madcuba/

All Tables

Table 1

Computed relative energies (CCSD(T)/CBS+CV level of theory) of the four allylimine isomers and their dipole moment components (ae-CCSD(T)/ccpCVQZ level of theory).

In the text
Table 2

Spectroscopic constants determined for the Ta and Ts isomers of allylimine.

In the text
Table 3

Partition function values and abundance ratios at different temperatures for allylimine isomers.

In the text
Table 4

Tentatively observed rotational transitions of both allylimine isomers.

In the text
Table A.1

Harmonic vibrational frequencies.

In the text

All Figures

thumbnail Fig. 1

Isomers of allylamine.
In the text
thumbnail Fig. 2

Portions of the experimental spectrum (in black) showing both a- and b-type spectral features (blue lines for Ts-allylimine and red lines for Ta-allylimine). Intensity is in arbitrary units.
In the text
thumbnail Fig. 3

Recordings of two b-type transitions of Ta-allylamine. The nitrogen quadrupole coupling splitting is evident (each hyperfine component has a F’ – F label). Left panel: Jka,ka 171,16 ← 170,17; right panel: Jka,ka = 42,2 ← 51,5.
In the text
thumbnail Fig. 4

Ta-allylimine transitions tentatively detected towards G+0.693. The observed spectrum is shown in grey histograms. The simulated LTE spectrum of Ta-allylimine using the parameters explained in the text (Sect. 5) is indicated by the red curve. The blue curve denotes the contribution of all the species identified in G+0.693, including allylimine. The quantum numbers of the Ta-allylimine transitions are provided in each panel.
In the text
thumbnail Fig. 5

Ts-allylimine transitions tentatively detected towards G+0.693. The observed spectrum is shown in grey histograms. The simulated LTE spectrum of Ts-allylimine using the parameters explained in the text (Sect. 5) is indicated by the red curve. The blue curve denotes the contribution of all the species identified in G+0.693, including allylimine. The quantum numbers of the Ts-allylimine transitions are indicated in each panel.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.