| Issue |
A&A
Volume 669, January 2023
|
|
|---|---|---|
| Article Number | A28 | |
| Number of page(s) | 7 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202243841 | |
| Published online | 03 January 2023 | |
Three-dimensional reconstruction of type U radio bursts: a novel remote sensing approach for coronal loops
1
Istituto Nazionale di Astrofisica, Osservatorio Astrofisico di Torino, Via Osservatorio 20, Pino Torinese 10025, Italy
e-mail: salvatore.mancuso@inaf.it
2
Università degli Studi di Torino – Dipartimento di Fisica, Via Pietro Giuria 1, Torino (TO), Italy
Received:
22
April
2022
Accepted:
11
November
2022
Type U radio bursts are impulsive coherent radio emissions produced by the Sun that indicate the presence of subrelativistic electron beams propagating along magnetic loops in the solar corona. In this work, we present the analysis of a type U radio burst that was exceptionally imaged on 2011 March 22 by the Nançay Radioheliograph (NRH) at three different frequencies (298.7, 327.0, and 360.8 MHz). Using a novel modelling approach, we show for the first time that the use of high-resolution radio heliograph images of type U radio bursts can be sufficient to both accurately reconstruct the 3D morphology of coronal loops (without recurring to triangulation techniques) and to fully constrain their physical parameters. At the same time, we can obtain unique information on the dynamics of the accelerated electron beams, which provides important clues as to the plasma mechanisms involved in their acceleration and as to why type U radio bursts are not observed as frequently as type III radio bursts. We finally present plausible explanations for a problematic aspect related to the apparent lack of association between the modeled loop as inferred from radio images and the extreme-ultraviolet (EUV) structures observed from space in the same coronal region.
Key words: Sun: corona / Sun: magnetic fields / Sun: particle emission / Sun: radio radiation
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1. Introduction
Solar type U radio bursts, first discovered by Maxwell & Swarup (1958), represent rare spectral features characterized by an inverted-U shape on radio dynamic spectra. The emission mechanism is supposed to be similar to that responsible for the emission of the more commonly observed type III radio bursts previously reported by Wild & McCready (1950). The latter is the most common coherent solar radiation produced via plasma emission at the fundamental and/or second harmonic by subrelativistic energetic beams of electrons that travel along open magnetic field lines at distances up to 1 AU. The basic mechanism for type III radio emission, originally proposed by Ginzburg & Zhelezniakov (1958), involves wave–wave processes with ion-sound waves for the fundamental emission, and with oppositely directed Langmuir waves for second harmonic emission (see the recent review from Reid 2020). As these high-energy electron beams propagate through the coronal plasma with decreasing background electron densities, and hence decreasing plasma frequency, they emit type III radio emission at correspondingly decreasing radio frequencies. Their analysis can therefore provide useful insight into the astrophysical processes pertaining to the acceleration and transport of energetic charged particles of solar origin and also to the physical properties of the plasma through which they propagate. On the other hand, not all electron beams that generate type III radio bursts are able to escape into the solar wind. Some of them are compelled to travel along confined coronal magnetic loops, thus forming inverted U shapes in radio dynamic spectra. Moreover, being constrained by the loop’s magnetic field, the electron beams, after reaching the top of the loop, travel down the opposite leg through an increasing plasma density, thus producing a positively drifting frequency rate. Inverted type U bursts are therefore bounded by the turning frequencies reached at the apex of the loop that might occur at MHz (Stone & Fainberg 1971) or even GHz frequencies (Wang et al. 2001). As most of the solar magnetic flux in the corona has a closed-loop configuration, it is somewhat surprising that type U radio bursts are not observed as frequently as type III radio bursts. This could be related to the peculiar mechanism that limits the production of type U radio bursts with respect to type III radio bursts. According to Reid & Kontar (2017), the rarity of type U bursts could be due to the fact that the accelerated electron beams need to travel a certain distance along the loop to become unstable to Langmuir waves, which in most cases is greater than the linear length of the loops. In some cases, the descending branch of type U radio bursts presents an abrupt interruption, resulting in type J radio bursts: this could be a consequence of the energy loss of the emitting beam before covering the descending portion of the coronal loop (Fokker 1970). Type U radio burst analyses are therefore a powerful and unique remote sensing diagnostic tool for characterizing both the dynamics of the exciting electron beams and the confined magnetized plasma they travel through.
The present paper is structured as follows: in Sect. 2, we describe the observations of a type U radio burst that was detected by ground-based radio dynamic spectra and imaged by a radio heliograph at three different frequencies, with spatial and temporal resolving powers able to separate both its ascending and descending branches. In Sect. 3, we present a novel 3D modeling approach to reconstructing the loop morphology on the basis of the observed radio signatures. The results from this section are then used to characterize the physical properties of the coronal loop and to further constrain the characteristics of the accelerated electron beam that produced the observed coherent radio emission. Finally, in Sect. 4, we discuss the results and draw our conclusions.
2. Observations
The type U radio burst was detected in the dynamic spectral data obtained by the Compact Astronomical Low-cost Low-frequency Instrument for Spectroscopy and Transportable Observatory (CALLISTO) BLEN radio spectrograph1 (170–870 MHz with a cadence of 0.25 s). The dynamic radio spectrum related to this event, taken on 2011 March 22 over a time interval of about 6 s between 11:28:14 UT and 11:28:20 UT, is shown in the bottom panel of Fig. 1. The type U radio burst started at about 11:28:15 UT and lasted for nearly 3 s, occurring at frequencies between about 300 and 370 MHz.
 |
Fig. 1. Spectral data collected by the e-CALLISTO-BLEN radio spectrometer during the type U emission (bottom) together with temporal profiles of the radio brightness temperature TB based on NHR observations (top). The vertical lines denote the time of the NRH images corresponding to intensity maxima at each frequency. |
The propagation of the type U radio emission was simultaneously imaged by the Nançay Radioheliograph (NRH; Kerdraon & Delouis 1997), apparently originating above active region NOAA 11176, which at the time of the radio emission was near the eastern limb of the Sun. The NRH is a synthesis instrument that provides 2D Stokes I and V images of the Sun with subsecond time resolution. On that day, the NRH made observations of the Sun at all ten operating frequencies (445.0, 432.0, 408.0, 360.8, 327.0, 298.7, 270.6, 228.0, 173.2, and 150.9 MHz) with a cadence of 0.25 s. The NRH data were obtained from the Solar Radio Data Base website2, which provides free access to the radio observations of the Sun obtained by the NRH Radioheliograph and the two spectrographs ORFEES and NDA at the Nançay radioastronomy station in France. The data are distributed as binary files in a Nançay proprietary format, which contain the visibilities measured by NRH that were processed using the NRH widget of the Solarsoft system (SSW; Freeland & Handy 1998). The processed data contain measurements of both the Stokes I (total intensity) and V (circular polarization) components of the radio emission, recorded as brightness temperature TB and measured in Kelvin. The standard technique within the SSW software was used to synthesize the time series of the 2D radio intensity maps from the NRH visibilities of 128 × 128 pixels with the pixel size of 30″ for each NRH frequency. At 11:28 UT, the beam size (full width at half maximum) at the three observation frequencies (298.7, 327.0, and 360.8 MHz) was 78″, 71″, and 64″ along the major axes, and 63″, 58″, and 53″ along the minor axes, respectively. The beam was almost circular due to the fact that the event time was favorable to precise observations with NRH during the day, because of minimal zenith distance of the Sun.
The radio burst was imaged at three frequencies (298.7, 327.0, and 360.8 MHz). The top panel of Fig. 1 shows the temporal profiles of TB maxima and circular polarization levels (i.e., Stokes I and Stokes V) observed by NRH from 11:28:14 UT to 11:28:20 UT. Both the ascending and descending branches of the type U radio bursts have the same sign of polarization. This can be interpreted in terms of mode coupling, which supposes the existence of the quasi-transverse region in the overlying loop systems (Benz et al. 1977). The fractional circular polarization, ρ = V/I, is about 10% throughout the event. The weak polarization observed for this event is expected because it occurred near the limb (e.g., Dulk & Suzuki 1980). Moreover, this is consistent with previous observations of type U bursts, which revealed that the degree of polarization is generally low (Benz et al. 1977; Aschwanden et al. 1992; Aurass & Klein 1997). In Fig. 2, we show an extreme ultraviolet (EUV) intensity map taken at 171 Å by the Atmospheric Imaging Assembly (AIA; Lemen et al. 2012) on board the Solar Dynamics Observatory (SDO; Pesnell et al. 2012) superposed with the contours of the NRH radio brightness temperature (TB) of the radio burst obtained at about the same time. Radio source positions at the intensity peaks observed at the three frequencies listed above are delineated by colored contours that represent 99%, 99.5%, and 99.9% of the corresponding maximum. As a final remark, we point out that the type U radio burst investigated in this work is not associated with solar eruptive phenomena, implying that the energetic electrons emitting the coherent radio emission are most probably accelerated by nonflaring processes. However, a weak small-scale brightening was detected in SDO/AIA images at 304 Å at the southeast limb, peaking around the time of the type U burst, just above the position of the modeled loop (see Fig. 3).
 |
Fig. 2. SDO/AIA image taken at 171 Å on 2011 March 22 at 11:28 UT showing the coronal configuration during the type U radio emission. The radio source positions were imaged by the NRH at the intensity peaks at 298.7, 327.0, and 360.8 MHz. The colored contours represent 99.0%, 99.5%, and 99.9% of the corresponding intensity maximum and the three frequencies are plotted in blue, green, and red, respectively. The black solid curve represents the modeled loop, while the black filled circle indicates the apex of the loop. |
 |
Fig. 3. Running difference image from SDO/AIA at 304 Å taken at 11:28 UT showing a brightening at the southeast limb, peaking around the time of the type U burst, just above the position of the modeled loop. The inset shows the temporal behavior of the maximum EUV intensity at this wavelength from about 11:24 to 11:33 UT taken in the area specified by the red square. |
3. Data analysis and results
3.1. Coronal loop morphology
In general, the reconstruction of the geometry of coronal loops is not a straightforward task since they present a variety of shapes and orientations with respect to the line of sight and are often inclined with respect to the radial direction. On the other hand, as a good approximation, loops are expected to present a semi-elliptical shape (e.g., Reale 2014). In this work, we adopt a novel technique to infer the 3D morphology of the coronal loop (given the observed type U signature) and the dynamics of the electron beam responsible for the coherent radio emission without utilizing triangulation techniques. In particular, we adopt a semi-ellipse 3D loop modeling approach to match the morphology of the loop as observed by NRH in the plane of the sky.
A generic rotation in 3D of an inclined semi-elliptical loop is described by the product of successive rotations around the principal axes of the Cartesian coordinates as a rotation matrix:
where
give the rotations on the x, y, and z axes, respectively; α, β, and γ are the Euler’s angles, and δ is the inclination of the loop with respect to the radial direction. The six free parameters are the semi-minor and semi-major axes of the elliptical loop (ao and bo), the spherical coordinates (θo and ϕo) defining the center of the ellipse, δ, and one of the three Euler angles (γ). An important assumption is that the location of the radio source emitting at the minimum frequency (298.7 MHz) corresponds to the top of the loop. To satisfy the above condition, one of the two Euler angles was constrained by the requirement that β = θo. As for α, this Euler’s angle was simply given by ϕo. The six best-fit parameters were obtained by simultaneously minimizing the model parameters over their entire range of variability with respect to the positions of the radio sources. We adjusted these parameters until the best-fit loop model matched the morphology of the observed loop (as imaged by NRH) in projection on the plane of the sky. Further requirements were that the locations of the radio sources from which the other two frequencies (327.0 and 360.8 MHz) were emitted along the loop were symmetrical with respect to the vertical semi-axis of the semi-ellipse. This allowed us to better constrain the shape of the loop.
The best-fit parameters we obtained with the above model are ao = 0.218 R⊙, bo = 0.202 R⊙, δ = 3.6°, γ = 30.7°, θo = −21.4°, and ϕo = −205.0°. The values of θo and ϕo refer, respectively, to the latitude of the center of the ellipse with respect to the solar equator and to its longitude with respect to the central meridian as seen from Earth at the time of the event. The location on the solar surface of the reconstructed loop through which the type U radio burst propagated is shown in Fig. 2 superposed on a simultaneous SDO/AIA image taken at 171 Å and in the left panel of Fig. 4 as seen from the perspective of Earth. Although the fitting procedure yielded a clear minimum in the least-square procedure, an ambiguity still remains along the line of sight such that the minimum can be obtained by also imposing γ → −γ and θo → −θo. On the other hand, it is reasonable to assume, as also expected for type III radio burst emission, that the high degree of directivity of the subrelativistic electron beams inside the loop favors emission toward the observer. Under this plausible assumption, it is possible to completely disentangle the above ambiguity and conclusively derive the actual topology of the coronal loop above the disk. The right panel of Fig. 4 shows the location of the loop above the solar disk under a different perspective, that is, with the Sun rotated by 90° to the west. Figure 5 displays a schematic view of the loop model as seen from the front view (left panel), corresponding to the perpendicular direction to the plane of the loop, and from the side view (right panel), corresponding to the parallel direction to the plane of the loop.
 |
Fig. 4. Schematic view of the coronal loop model as seen from the perspective of Earth (left panel) and rotated by 90° to the west (right panel). The small colored circles on the loop yield a 3D view of the positions of the radio sources along the loop as seen by NRH (see also Fig. 2). |
 |
Fig. 5. Schematic view of the coronal loop model together with the radio source positions as detected by the NRH. The left panel shows the front view, corresponding to the perpendicular direction to the plane of the loop, while the right panel shows the side view, corresponding to the parallel direction to the plane of the loop. |
3.2. Physical properties of the coronal loop
As already discussed in Sect. 1, type U radio bursts represent a subclass of the most common type III radio bursts in that they are produced via coherent emissions induced by energetic electron beams propagating along closed magnetic coronal loops from one foot point to the other. However, type U radio bursts are not observed as frequently as type III radio bursts, even though most of the coronal magnetic flux is contained in closed-loop configurations. It is therefore important to identify the peculiar mechanism underlying their unexpected limited production.
Assuming electron beam acceleration with a power-law energy spectrum (e.g., Holman et al. 2011), the electron beams confined in the coronal loop are known to undergo an initial period of propagation before their distribution function becomes unstable (as an effect of a positive gradient in velocity space) to Langmuir waves so that it produces coherent radio emission (Ginzburg & Zhelezniakov 1958) at the fundamental or second harmonic of the plasma frequency fpe, which is related to the electron density ne by the simple relation ![$ f_{\mathrm{pe}}\,[\mathrm{MHz}] \approx 0.009 \sqrt{n_{\mathrm{e}}\, [\mathrm{cm}^{-3}]} $](/articles/aa/full_html/2023/01/aa43841-22/aa43841-22-eq4.gif) . The electron density ne inside the loop can therefore easily be obtained, apart from a generally unknown factor of two related to the uncertainty in identifying the correct harmonic from the observed radio dynamic spectrum. In the following discussion, we provide evidence that the observed radiation is indeed due to second harmonic emission, meaning that f = 2fpe, thus providing a sound estimate for the electron density ne near the top of the loop.
. The electron density ne inside the loop can therefore easily be obtained, apart from a generally unknown factor of two related to the uncertainty in identifying the correct harmonic from the observed radio dynamic spectrum. In the following discussion, we provide evidence that the observed radiation is indeed due to second harmonic emission, meaning that f = 2fpe, thus providing a sound estimate for the electron density ne near the top of the loop.
Electromagnetic waves are absorbed in a plasma, because electrons oscillating in the wave fields collide and lose a part of the energy of the waves. Collisional damping reduces the intensity of transverse waves particularly if radiated near the plasma frequency fpe. The effect of the so-called free–free absorption of radiation between source and observer can be estimated for radiation of frequency f emitted in an exponential atmosphere of scale height H. The optical depths of the fundamental (τF) and harmonic (τH) components for free–free absorption (Robinson & Benz 2000) are given, respectively, by
This implies that the collisional absorption depends on the observed emission frequency f relative to the plasma frequency fpe and that the observable fundamental emission is strongly suppressed above a few hundred MHz, while harmonic emission is suppressed above roughly 1 GHz. By using typical coronal temperatures of Te ≈ 1 − 2 × 106 K and a typical scale height H = 0.2 R⊙, as obtained for example by adopting the coronal density model of Newkirk (1961), we find τF ≈ 20 − 60 and τH ≈ 0.5 − 1.5 near the top of the loop. Harmonic emission is therefore much less affected than fundamental radiation, because little radiation emerges from τ > 3 (e.g., Benz 2002). As a consequence, the flux of the fundamental emission is significantly lower than that of harmonic emission and is expected to be below the lower thresholds of typical radio instruments, irrespective of whether damping by scattering off density fluctuations is important or not. Finally, the polarization degree of the second harmonic plasma emission is generally low, as also found for this event. We therefore assume throughout the paper that the observed emission mechanism is the second harmonic plasma emission, 2fpe, meaning that, for example, the density at the top of the loop (where f = fH = 2fpe ≈ 300 MHz) is estimated at about ne = (fpe[MHz]/0.009)2 ≈ (150/0.009)2 ≈ 3.0 × 108 cm−3.
For the coronal plasma in the loop to be magnetically confined, the following requirement for the plasma β parameter, representing the ratio of thermal pressure P = nekBT to magnetic pressure PB,
must be satisfied. In static loop models, it is assumed that the volumetric heating rate is balanced by the conductive and radiative loss rate. Assuming hydrostatic equilibrium, it is possible to apply the Rosner et al. (1978) scaling law to estimate the temperature maximum at the apex of a quasi-stationary loop structure. This scaling law provides a unique relation between the loop maximum temperature T, the pressure P, and the size L, given by
in cgs units. According to the above relation, as L ≈ roπ/2 = 0.33 R⊙ (ro = 0.21 R⊙ is the radius of the loop) and ne ≈ 3.0 × 108 cm−3 at the top of the loop, we obtain Tmax ≈ 1.6 × 106 K. According to the classification of coronal loops given in the review of Reale (2014), the physical parameters inferred for this loop are typical of warm giant arches.
It is known that it is very difficult to measure magnetic fields in the corona, and this can be done only in very special conditions, such as in very strong local fields (White et al. 1991), flare-induced coronal loop oscillations (Nakariakov & Ofman 2001), type II radio emission from shocks driven by coronal mass ejections (e.g., Mancuso & Garzelli 2013b; Mancuso et al. 2019), or using Faraday rotation techniques (e.g., Mancuso & Spangler 2000; Mancuso & Garzelli 2013a). Using Eq. (4), we find that in order to confine the plasma contained in the loop, the magnetic field strength B must largely exceed at least ≈1.3 G near the top of the loop.
3.3. Electron beam characteristics
If a distribution function has more particles at higher velocities than at lower velocities in some region of phase space, this distribution will be unstable to waves that are in resonance with the particles. Due to this effect, known as bump-on-tail instability, a beam of electrons with velocities vb much higher than the thermal speed vth of electrons in the plasma causes the exponential growth in amplitude of Langmuir waves, which can then undergo wave–wave processes to nonlinearly excite and emit electromagnetic radiation near the local plasma frequency and its second harmonic (e.g., Ginzburg & Zhelezniakov 1958; Melrose 1980; Cairns & Robinson 1987; Robinson et al. 1993). The energy for the Langmuir waves to grow comes from the accelerated electron beams. Quasi-linear theory predicts that the system evolves to a state in which two-thirds of the initial beam kinetic energy goes to the waves, while one-third of it is retained by the electrons, whose distribution function is flattened into a plateau in velocity space (Melrose 1985) so that the growth rate for Langmuir waves is deemed to vanish. This energy extraction causes a lower kinetic energy with consequent deceleration, until the beam velocity vb reaches a threshold of about 4vth for Langmuir waves (e.g., Benz 2002; Aschwanden 2005). Moreover, Landau damping inhibits the growth of Langmuir waves with velocities below about four times the ambient electron thermal velocity, and so we expect vb ≳ 4vth. Another important aspect is the level of density fluctuations: when the average level of density fluctuations becomes of the order of or larger than about 3(vth/vb)2, the dynamics of the system is strongly influenced by the scattering of the waves on the density inhomogeneities (see discussion in Krafft et al. 2015). In particular, compared to the homogeneous plasma case, the rate of growth of the Langmuir wave energy emitted during the bump-on-tail instability is decreased. Therefore, the influence of density fluctuations inside the loop on the nonlinear dynamics of waves during Langmuir turbulence is also important and should, in principle, be considered as well.
If we assume semi-relativistic electron beam acceleration injected with a power-law energy spectrum, we find that the beam is subject to an initial time interval of propagation in which it is not unstable to Langmuir wave production. On the other hand, above a given instability distance, the electron beams develop the bump-on-tail velocity distribution required for the generation of Langmuir waves. According to quasi-linear simulations (Reid et al. 2011), this distance depends on the electron beam velocity spectral index γ, the size d of the acceleration site, and the temporal injection profile. For the type U radio burst observed in this study, its starting height, and therefore the instability distance, is at least 0.2 R⊙. This distance depends largely on the spectral index of the injected electron beam and the longitudinal extent of the acceleration region (Reid et al. 2011, 2014). Assuming a typical acceleration region size of d = 0.015 R⊙ and an acceleration region height of hacc = 0.07 R⊙ (e.g., Reid & Kontar 2017), in case of instantaneous injection we expect the radio emission to start at h = dγ + hacc ≈ 0.2 R⊙, thus yielding γ ≈ 9. On the other hand, the latter can only be considered as an upper limit. In fact, the instability distance is also governed by the temporal injection profile that plays a significant role if vbτinj > d, where τinj is the injection time, in which case h = (d + vbτinj)γ + hacc.
A rough lower limit to the electron beam velocity vb can be estimated by considering the deflection time τD by Coulomb collisions with thermal particles (e.g., Hughes & Harkness 1963; Elgaroy & Lyngstad 1972), which is given by
in cgs units. Given the total duration of the type U radio burst (≈2.5 s), and assuming ne ≈ 3 × 108 cm−3 from its turnover frequency (see Fig. 5), the minimum velocity of the electron beam obtained with the above formula is vb ≈ 0.1c, where c is the speed of light. If we take into account the correct geometry of the loop as determined from our model and the electron beam velocity as derived from the radio observations, by fitting the result with an exponential decay to a constant level, we obtain the speed of the exciter as
which appears to be, as expected, above the estimated lower limit. Figure 6 shows how Coulomb collisions with thermal electrons rapidly affect, with an e-folding time of 0.40 s, the propagation of the electron beam inside the loop.
 |
Fig. 6. Temporal dependence of the electron beam speed inside the loop. The solid curve is the best-fit exponential decay to a constant level. |
Considering the maximum loop temperature Tmax determined in the previous analysis (Tmax ≈ 1.6 × 106 K), corresponding to an electron thermal velocity 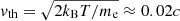 , this would imply a ratio vb/vth decreasing from about 19 to 6, that is, just above the threshold velocity needed for the generation of Langmuir waves. The corresponding electron energies therefore decrease from about 60 keV to 5 keV after 2 s. Assuming d = 0.015 R⊙, for vb ≈ 0.45c the injection time can be as low as τinj < d/vb ≈ 0.07 s, implying an even lower spectral index (γ ≈ 5) than the one previously determined. As a consequence, our analysis clearly supports the evidence that the type U radio burst extinguished because the electron beams related to this coherent radio emission traveled through a denser plasma in the coronal loop, thus tending to be isotropized faster by Coulomb collisions, until they reached a threshold velocity that did not meet the necessary criterion for beam-driven plasma emission (that is vB ≳ 4vth) due to bump-on-tail instability.
, this would imply a ratio vb/vth decreasing from about 19 to 6, that is, just above the threshold velocity needed for the generation of Langmuir waves. The corresponding electron energies therefore decrease from about 60 keV to 5 keV after 2 s. Assuming d = 0.015 R⊙, for vb ≈ 0.45c the injection time can be as low as τinj < d/vb ≈ 0.07 s, implying an even lower spectral index (γ ≈ 5) than the one previously determined. As a consequence, our analysis clearly supports the evidence that the type U radio burst extinguished because the electron beams related to this coherent radio emission traveled through a denser plasma in the coronal loop, thus tending to be isotropized faster by Coulomb collisions, until they reached a threshold velocity that did not meet the necessary criterion for beam-driven plasma emission (that is vB ≳ 4vth) due to bump-on-tail instability.
4. Discussion and conclusions
It has been suggested that for radio emission to be generated on closed magnetic fields, the loop needs to be long enough for a power-law-accelerated electron beam to become unstable to Langmuir waves (see Reid & Kontar 2017). It follows that the type U radio emission is supposed to occur far away from the beam injection region, so that the accelerated electrons actually trace the upper part of coronal loops. Moreover, the higher density and lower density gradient of the plasma inside the loop concur in reducing the growth rate of the Langmuir wave. As a consequence, the beam needs to be dense enough for the timescale of Langmuir wave growth and its successive conversion to radio waves to be shorter than the electron propagation timescale. The above conditions therefore result in a stringent set of preconditions for both the propagating electron beams and the background loop plasma parameters in order to produce type U radio emission over the more common type III radio emission. This also implies that small loops should not have sufficient heights for the required instability to occur.
In this study, we present the analysis of a type U radio burst observed on 2011 March 22 by the CALLISTO ground-based radio spectrograph. Radio imaging data from the NRH at three different frequencies (298.7, 327.0, and 360.8 MHz) were used in conjunction with a novel modeling approach to infer the 3D topology of the loop inside which the subrelativistic electron beams propagated, producing the coherent radio emission. The confined coronal structure is identified as an almost vertical and semi-circular inclined coronal loop with a height of about 0.21 R⊙ located behind the eastern solar limb as seen from Earth. The velocity of the exciting electron beam is found to be decreasing with a power-law trend from ≈c/2 to c/7, consistent with the interpretation of electron beams being instantaneously injected with a spectral index γ ≈ 9, decelerated, and losing their energy with an e-folding time of 0.40 s, and therefore being isotropized along the way due to Coulomb collisions in the loop. Assuming hydrostatic equilibrium, we were also able to constrain the maximum loop temperature (Tmax ≈ 1.6 × 106 K), while in order to confine the plasma contained in the loop, the magnetic field strength B was constrained to largely exceed at least ≈1.3 G near the top of the loop.
Our analysis supports the view that the type U radio burst extinguished because the injected electron beams related to this coherent radio emission traveled through a denser plasma in the coronal loop, thus tending to be isotropized faster by Coulomb collisions, until they reached a threshold velocity that did not meet the necessary criterion for beam-driven plasma emission (that is, vb ≳ 4vth) due to bump-on-tail instability. The size of the loop as inferred in this work should imply, in light of the findings of previous studies, that its dimensions could have been just sufficient to excite the observed type U radio burst and that some other major unknown factor may actually concur in the ignition of coherent radiation from a small loop.
Finally, we would like to point out that although several coronal loops of various shapes, heights, and orientations are visible in the vicinity of the coronal region under study (see Fig. 2), we were not able to reliably identify an exact counterpart of the modeled loop as outlined by the NRH radio sources in any of the available SDO/AIA EUV channels. This is problematic, but could be attributed to a selection effect due to the fact that the low density of the confined plasma in this loop could be difficult to detect (see Reale 2014) and that the presence of denser foreground coronal structures might have hindered its detection. On the other hand, as the modeled loop was positioned behind the east limb, as indicated from Fig. 4, the presence of strong refraction and scattering due to tangential propagation of the radio waves through the intervening dense inhomogeneous structures along the line of sight to the observer is another concrete possibility. In fact, it is known that in general, due to refraction in the corona, the apparent location of radio sources near the limb tends to be shifted toward the solar disk center, while scattering tends to shift their positions farther than the disk center. Anisotropic scattering from nonradial structures can further contribute in an effective manner to nonradial shifts in the observed positions of the radio sources. Indeed, Sharma & Oberoi (2020) found clear evidence for the presence of significant propagation effects, including anisotropic scattering, in their radio observations with the Murchison Widefield Array up to 240 MHz. Moreover, wave ducting can cause shifts in the radio source position under specific conditions of the emission angle with the coronal loop boundaries (Duncan 1979). Notwithstanding the above caveats, at the relatively high NRH radio frequencies considered in this work, we still expect the adverse contribution from scattering or refraction to play, in general, a less important role than observed. However, taking into account the much lower spatial resolution of NRH with respect to the SDO/AIA instrument and the recent findings of Sharma & Oberoi (2020), it is still possible that radio wave propagation effects have somehow hindered the correct identification of the loop in the EUV images.
In summary, we show that the analysis of type U radio bursts is a powerful remote sensing diagnostic tool for both the electron beams and the confined arched plasma structures they travel through. We demonstrate that the use of high-resolution radio heliograph images of type U radio bursts in conjunction with their radio dynamic spectra can be used to reconstruct the 3D morphology of the coronal loop inside which they propagate, alleviating the need for triangulation techniques. Moreover, the analysis of such events is a powerful and unique remote sensing diagnostic tool for constraining both the dynamics of the exciting electron beams and the physical parameters of the coronal loops in which they propagate.
Acknowledgments
We thank the referee for carefully reading our paper and providing useful comments and suggestions. We also thank the NRH and SDO teams, and the e-CALLISTO network for providing open data access. The NRH is supported by the Observatoire de Paris, CNRS and Région Centre. F. F. is supported through the Metis programme funded by the Italian Space Agency (ASI) under the contracts to the co-financing National Institute of Astrophysics (INAF): Accordo ASI-INAF n. 2018-30-HH.0.
References
- Aschwanden, M. J. 2005, Physics of the Solar Corona. An Introduction with Problems and Solutions, 2nd edn. (New York: Springer) [Google Scholar]
- Aschwanden, M. J., Bastian, T. S., Benz, A. O., & Brosius, J. W. 1992, ApJ, 391, 380 [CrossRef] [Google Scholar]
- Aurass, H., & Klein, K. L. 1997, A&AS, 123, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benz, A. 2002, Plasma Astrophysics, 2nd edn., (Dordrecht: Kluwer Academic Publishers), 279 [CrossRef] [Google Scholar]
- Benz, A. O., Berney, M., & Santin, P. 1977, A&A, 56, 123 [NASA ADS] [Google Scholar]
- Cairns, I. H., & Robinson, R. D. 1987, Sol. Phys., 111, 365 [Google Scholar]
- Dulk, G. A., & Suzuki, S. 1980, A&A, 88, 203 [NASA ADS] [Google Scholar]
- Duncan, R. A. 1979, Sol. Phys., 63, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Elgaroy, O., & Lyngstad, E. 1972, A&A, 16, 1 [NASA ADS] [Google Scholar]
- Fokker, A. D. 1970, Sol. Phys., 11, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Freeland, S. L., & Handy, B. N. 1998, Sol. Phys., 182, 497 [Google Scholar]
- Ginzburg, V. L., & Zhelezniakov, V. V. 1958, Soviet Ast., 2, 653 [NASA ADS] [Google Scholar]
- Holman, G. D., Aschwanden, M. J., Aurass, H., et al. 2011, Space Sci. Rev., 159, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Hughes, M. P., & Harkness, R. L. 1963, ApJ, 138, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Kerdraon, A., & Delouis, J. M. 1997, in Coronal Physics from Radio and Space Observations, ed. G. Trottet (Berlin: Springer), Lecture Notes in Physics, 483, 192 [Google Scholar]
- Krafft, C., Volokitin, A. S., & Krasnoselskikh, V. V. 2015, ApJ, 809, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Lemen, J. R., Title, A. M., Akin, D. J., et al. 2012, Sol. Phys., 275, 17 [Google Scholar]
- Mancuso, S., & Garzelli, M. V. 2013a, A&A, 560, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mancuso, S., & Garzelli, M. V. 2013b, A&A, 553, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mancuso, S., & Spangler, S. R. 2000, ApJ, 539, 480 [NASA ADS] [CrossRef] [Google Scholar]
- Mancuso, S., Frassati, F., Bemporad, A., & Barghini, D. 2019, A&A, 624, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maxwell, A., & Swarup, G. 1958, Nature, 181, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Melrose, D. B. 1980, Space Sci. Rev., 26, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Melrose, D. B. 1985, in Plasma Emission Mechanisms, eds. D. J. McLean, & N. R. Labrum, 177 [Google Scholar]
- Nakariakov, V. M., & Ofman, L. 2001, A&A, 372, L53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Newkirk, G., Jr 1961, ApJ, 133, 983 [NASA ADS] [CrossRef] [Google Scholar]
- Pesnell, W. D., Thompson, B. J., & Chamberlin, P. C. 2012, Sol. Phys., 275, 3 [Google Scholar]
- Reale, F. 2014, Liv. Rev. Sol. Phys., 11, 4 [Google Scholar]
- Reid, H. A. S. 2020, Front. Astron. Space Sci., 7, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, H. A. S., & Kontar, E. P. 2017, A&A, 606, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reid, H. A. S., Vilmer, N., & Kontar, E. P. 2011, A&A, 529, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reid, H. A. S., Vilmer, N., & Kontar, E. P. 2014, A&A, 567, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Robinson, P. A., & Benz, A. O. 2000, Sol. Phys., 194, 345 [NASA ADS] [CrossRef] [Google Scholar]
- Robinson, P. A., Willes, A. J., & Cairns, I. H. 1993, ApJ, 408, 720 [NASA ADS] [CrossRef] [Google Scholar]
- Rosner, R., Tucker, W. H., & Vaiana, G. S. 1978, ApJ, 220, 643 [Google Scholar]
- Sharma, R., & Oberoi, D. 2020, ApJ, 903, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Stone, R. G., & Fainberg, J. 1971, Sol. Phys., 20, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, M., Fu, Q., Xie, R., & Duan, C. 2001, A&A, 380, 318 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- White, S. M., Kundu, M. R., & Gopalswamy, N. 1991, ApJ, 366, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Wild, J. P., & McCready, L. L. 1950, Aust. J. Sci. Res. A Phys. Sci., 3, 387 [Google Scholar]
All Figures
 |
Fig. 1. Spectral data collected by the e-CALLISTO-BLEN radio spectrometer during the type U emission (bottom) together with temporal profiles of the radio brightness temperature TB based on NHR observations (top). The vertical lines denote the time of the NRH images corresponding to intensity maxima at each frequency. |
| In the text | |
 |
Fig. 2. SDO/AIA image taken at 171 Å on 2011 March 22 at 11:28 UT showing the coronal configuration during the type U radio emission. The radio source positions were imaged by the NRH at the intensity peaks at 298.7, 327.0, and 360.8 MHz. The colored contours represent 99.0%, 99.5%, and 99.9% of the corresponding intensity maximum and the three frequencies are plotted in blue, green, and red, respectively. The black solid curve represents the modeled loop, while the black filled circle indicates the apex of the loop. |
| In the text | |
 |
Fig. 3. Running difference image from SDO/AIA at 304 Å taken at 11:28 UT showing a brightening at the southeast limb, peaking around the time of the type U burst, just above the position of the modeled loop. The inset shows the temporal behavior of the maximum EUV intensity at this wavelength from about 11:24 to 11:33 UT taken in the area specified by the red square. |
| In the text | |
 |
Fig. 4. Schematic view of the coronal loop model as seen from the perspective of Earth (left panel) and rotated by 90° to the west (right panel). The small colored circles on the loop yield a 3D view of the positions of the radio sources along the loop as seen by NRH (see also Fig. 2). |
| In the text | |
 |
Fig. 5. Schematic view of the coronal loop model together with the radio source positions as detected by the NRH. The left panel shows the front view, corresponding to the perpendicular direction to the plane of the loop, while the right panel shows the side view, corresponding to the parallel direction to the plane of the loop. |
| In the text | |
 |
Fig. 6. Temporal dependence of the electron beam speed inside the loop. The solid curve is the best-fit exponential decay to a constant level. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



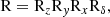
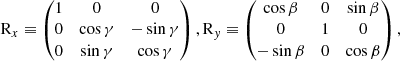
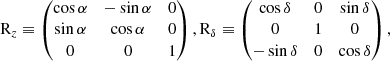
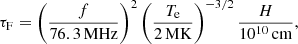
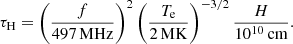
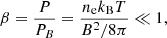
![$$ \begin{aligned} T_{\rm max} = 6.154 \times 10^{-4} \sqrt{n_{\rm e} L}\,[\mathrm{K}], \end{aligned} $$](/articles/aa/full_html/2023/01/aa43841-22/aa43841-22-eq8.gif)
![$$ \begin{aligned} \tau _{\rm D} = 3.1 \times 10^{-20} {{v}_{\rm b}^3 \over n_{\rm e}} \,[\mathrm{s}], \end{aligned} $$](/articles/aa/full_html/2023/01/aa43841-22/aa43841-22-eq9.gif)
![$$ \begin{aligned} {v}_{\rm b}(t) = \left[0.14+21.87\cdot \mathrm{exp}(-t/0.40)\right]c, \end{aligned} $$](/articles/aa/full_html/2023/01/aa43841-22/aa43841-22-eq10.gif)