| Issue |
A&A
Volume 668, December 2022
|
|
|---|---|---|
| Article Number | C1 | |
| Number of page(s) | 1 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201628955e | |
| Published online | 09 December 2022 | |
Evolution of protoplanetary discs with magnetically driven disc winds (Corrigendum)
1
School of Arts & Sciences, University of Tokyo,
3-8-1, Komaba, Meguro,
Tokyo
153-8902, Japan
e-mail: stakeru@ea.c.u-tokyo.ac.jp
2
Department of Physics, Nagoya University,
Nagoya, Aichi
464-8602, Japan
3
Laboratoire Lagrange, Université Côte d’Azur, Observatoire de la Côte d’Azur, CNRS Bvd de l’Observatoire,
CS 34229,
06304
Nice Cedex 4, France
4
Division of Theoretical Astronomy, National Astronomical Observatory of Japan,
2-21-1, Osawa, Mitaka,
Tokyo
181-8588, Japan
5
Institut Universitaire de France,
103 bd Saint Michel,
75005
Paris, France
Key words: accretion / accretion disks / ISM: jets and outflows / magnetohydrodynamics (MHD) / protoplanetary disks / stars: winds / outflows / errata / addenda
In the last paragraph of Sect. 2.5 of the original paper, the treatment of the boundary condition was incorrectly described. In the original paper, we stated that  was imposed at the inner and outer boundaries, r = rin = 0.01 au and = rout = 104 au, and that this condition corresponds to the zero-torque boundary condition. However, this statement and explanation were incorrect. The actual boundary condition implemented in our calculations was to impose
was imposed at the inner and outer boundaries, r = rin = 0.01 au and = rout = 104 au, and that this condition corresponds to the zero-torque boundary condition. However, this statement and explanation were incorrect. The actual boundary condition implemented in our calculations was to impose  at r = rin and = rout.
at r = rin and = rout.
This is consistent with the zero-torque boundary condition,  (
( for a constant
for a constant  and
and  ; see Eqs. (10) and (A.5)) → 0 at the centre, r → 0. The physical meaning of
; see Eqs. (10) and (A.5)) → 0 at the centre, r → 0. The physical meaning of  at r = rin and = rout is to impose a constant mass accretion rate induced by the rϕ stress for a constant
at r = rin and = rout is to impose a constant mass accretion rate induced by the rϕ stress for a constant 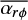 and
and  (Eq. (33)) across the boundary. All of the results presented in the original paper remain unchanged.
(Eq. (33)) across the boundary. All of the results presented in the original paper remain unchanged.
© T. K. Suzuki et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


