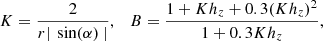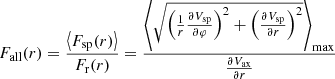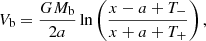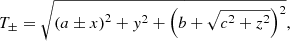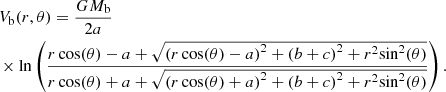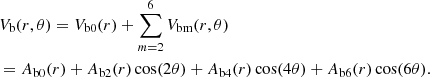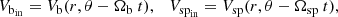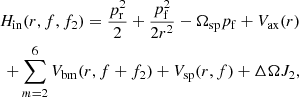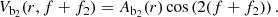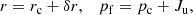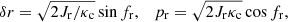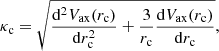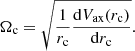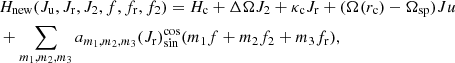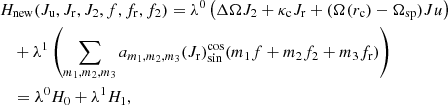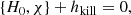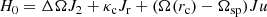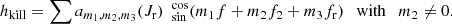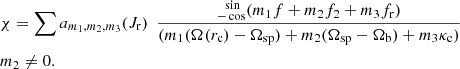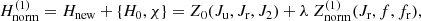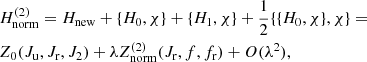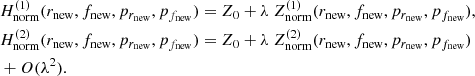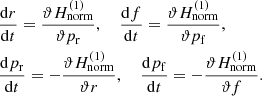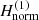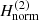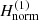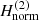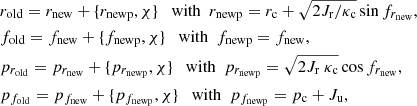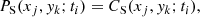| Issue |
A&A
Volume 667, November 2022
|
|
|---|---|---|
| Article Number | A33 | |
| Number of page(s) | 9 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/202244049 | |
| Published online | 01 November 2022 | |
Perturbed precessing ellipses as the building blocks of spiral arms in a barred galaxy with two pattern speeds
1
Research Center for Astronomy and Applied Mathematics, Academy of Athens, Soranou Efessiou 4, 115 27 Athens, Greece
e-mail: mharsoul@academyofathens.gr; gcontop@academyofathens.gr
2
Department of Mathematics, Tullio Levi-Civita, University of Padua, Via Trieste, 63, 35121 Padova, Italy
e-mail: cefthim@academyofathens.gr
Received:
18
May
2022
Accepted:
13
September
2022
Observations and simulations of barred spiral galaxies have shown that, in general, the spiral arms rotate at a different pattern speed to that of the bar. The main conclusion from the bibliography is that the bar rotates faster than the spiral arms with a double or even a triple value of angular velocity. The theory that prevails in explaining the formation of the spiral arms in the case of a barred spiral galaxy with two pattern speeds is the manifold theory, where the orbits that support the spiral density wave are chaotic, and are related to the manifolds emanating from the Lagrangian points L1 and L2 at the end of the bar. In the present study, we consider an alternative scenario in the case where the bar rotates fast enough in comparison with the spiral arms and the bar potential can be considered as a perturbation of the spiral potential. In this case, the stable elliptical orbits that support the spiral density wave (in the case of grand design galaxies) are transformed into quasiperiodic orbits (or 2D tori) with a certain thickness. The superposition of these perturbed preccesing ellipses for all the energy levels of the Hamiltonian creates a slightly perturbed symmetrical spiral density wave.
Key words: Galaxy: kinematics and dynamics
© M. Harsoula et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1. Introduction
There are two main theories that prevail nowadays concerning the building blocks of the spiral arms in galaxies. In the case of grand design galaxies, the “density wave” theory remains a valid dynamical model with which the spiral structure of many disk galaxies can be described. The density wave theory fits the description of spiral arms better when the spiral amplitude does not exceed a value of 10%–20% over a few pattern rotations. This theory was first developed by Lindblad (1940, 1961), and it was extended by Lin & Shu (1964, 1966). Lindblad (1955) pioneered the orbital description of spiral density waves. In the density wave theory, the periodic orbits are close to precessing ellipses that support the shape of the spiral structure. Many papers have studied these periodic orbits, in models of grand design galaxies. It has been shown that these orbits can collaborate so that the imposed model matches with the response model of spiral arms (see Contopoulos 1970, 1971, 1975; Berman & Mark 1977; Monet & Vandervoort 1978; Contopoulos & Grosbøl 1986; Patsis et al. 1991; Harsoula et al. 2021).
On the other hand, in the case of barred spiral galaxies, where the perturbation of the bar component is large enough and introduces chaos near corotation, the prevailing theory for the spiral arms is the “manifold theory” (Danby 1965; Voglis et al. 2006; Romero-Gomez et al. 2006, 2007; Tsoutsis et al. 2008, 2009; Athanassoula et al. 2009a,b; Athanassoula 2012; Harsoula et al. 2016). This theory predicts bisymmetric spirals emanating from the ends of galactic bars as a result of the outflow of matter connected with the unstable dynamics around the bar’s Lagrangian points L1 and L2. In this case the spiral arms are supported by chaotic orbits having initial conditions along the unstable manifolds emanating from L1 and L2. More recently, Efthymiopoulos et al. (2020) found empirically that the manifold spirals, which are computed in an N-body simulation by momentarily “freezing” the potential and making all calculations in a frame that rotates with the instantaneous pattern speed of the bar, reproduce the time-varying morphology of the N-body spirals rather well. In that simulation it was also found that multiple patterns are demonstrably present. Observations of barred spiral galaxies have shown that the existence of two different pattern speeds for the spiral arms and the bar is a very possible scenario (Moore & Gottesman 1995; Boonyasait et al. 2005; Meidt et al. 2009; Speights & Westpfahl 2012; Speights & Rooke 2016; Font et al. 2019). The same conclusion emerges from simulations (Sellwood & Sparke 1988; Rautiainen & Salo 1999; Quillen 2003; Quillen et al. 2011; Roca-Fàbrega et al. 2013; Font et al. 2014). A brief review of the different methods used to determine the pattern speeds of the Galactic bar and spiral arms of the Milky Way was given in Gerhard (2011). In most cases the ratio of the two pattern speeds is 1:2 or 1:3, with the spiral arms always having the lowest value. In Efthymiopoulos et al. (2020) it has been shown that, in a Milky Way-like model with two different pattern speeds for the bar and the spiral arms, the manifold theory can still be valid if the spiral potential is considered as a perturbation of the bar’s potential. As a consequence, the unstable Lagrangian points L1 and L2 of the pure bar model are continued in the full model as periodic orbits, or as epicyclic “Lissajous-like” unstable orbits.
In the present paper we reverse the idea of Efthymiopoulos et al. (2020) and we consider the potential of the bar as a perturbation of the spiral potential. An important quantity in this connection is the Q-strength, which gives an estimate of the relative importance of the bar’s and the spirals’ non-axisymmetric force perturbations. The Q-strength at fixed radius r (e.g., Buta et al. 2009) is defined for the bar as
where 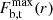 is the maximum tangential force generated by the potential term of the bar Vbar at the distance r, with respect to all azimuths ϕ. Moreover, ⟨F(r)⟩ is the average radial force at the same distance, with respect to ϕ, generated by the total potential Vax + Vbar + Vsp. The Q-strength of the bar is always much larger than the one of the spiral arms (Buta et al. 2005, 2009; Durbala et al. 2009). However, the Q-strength alone is not sufficient to state the importance of the bar’s perturbation in relation to the spiral perturbation. In the case where the bar rotates much faster that the spiral arms, an observer rotating with the spiral arms would see the bar as a kind of a bulge (an average axisymmetric component). In such a case, the potential of the bar can be considered as a perturbation of the potential of the spiral arms. Therefore, in such a case, a generalization of the density wave theory can be considered. Under this assumption, we construct a semianalytical algorithm, with the help of a normal form algorithm, with the aim of eliminating time dependence from the Hamiltonian (due to the difference in the pattern speeds). Then, in this new Hamiltonian, the precessing ellipses that support the spiral structure in the case of grand design galaxies is transformed into quasiperiodic orbits forming ellipses with a certain thickness. When we superimpose all of them at different energy levels, we can again extract a spiral density wave by calculating the isodensities, using an image processing method described below (Sect. 3.2).
is the maximum tangential force generated by the potential term of the bar Vbar at the distance r, with respect to all azimuths ϕ. Moreover, ⟨F(r)⟩ is the average radial force at the same distance, with respect to ϕ, generated by the total potential Vax + Vbar + Vsp. The Q-strength of the bar is always much larger than the one of the spiral arms (Buta et al. 2005, 2009; Durbala et al. 2009). However, the Q-strength alone is not sufficient to state the importance of the bar’s perturbation in relation to the spiral perturbation. In the case where the bar rotates much faster that the spiral arms, an observer rotating with the spiral arms would see the bar as a kind of a bulge (an average axisymmetric component). In such a case, the potential of the bar can be considered as a perturbation of the potential of the spiral arms. Therefore, in such a case, a generalization of the density wave theory can be considered. Under this assumption, we construct a semianalytical algorithm, with the help of a normal form algorithm, with the aim of eliminating time dependence from the Hamiltonian (due to the difference in the pattern speeds). Then, in this new Hamiltonian, the precessing ellipses that support the spiral structure in the case of grand design galaxies is transformed into quasiperiodic orbits forming ellipses with a certain thickness. When we superimpose all of them at different energy levels, we can again extract a spiral density wave by calculating the isodensities, using an image processing method described below (Sect. 3.2).
This paper contains the following: In Sect. 2 we give a description of the galactic model that we use in our study. In Sect. 3 we quote the normal form construction of the Hamiltonian corresponding to the galactic model and describe the way of locating the stable periodic orbits that are responsible for the spiral density way. We also plot these orbits in the old variables before the normal form transformation in order to see how the precessing ellipses have been deformed and if we can still detect a spiral density wave. In Sect. 4 we make a parametric study in order to see how the mass and the pattern speed of the bar affects the outcome of the spiral density wave derived from the procedure described in Sect. 3. Finally, in Sect. 5 we summarize the conclusions of our study.
2. The model
We consider a model of a Milky Way-like spiral galaxy that contains a combination of a bar, an axisymmetric, and a spiral potential used in Pettitt et al. (2014):
The axisymmetric potential Vax is composed of a disk, a halo, and the axisymmetric part of the bar’s potential, which plays the role of a central bulge:
For the disk potential Vd, we use a Miyamoto–Nagai model (Miyamoto & Nagai 1975) given by the relation
where Md = 8.56 × 1010 M⊙ is the total mass of the disk, ad = 5.3 kpc, and bd = 0.25 kpc. In order to have a 2D disk model, we take z = 0 and 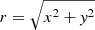 .
.
The halo potential is a γ-model (Dehnen 1993) with parameters as in Pettitt et al. (2014),
where rh, max = 100 kpc, γ = 1.02, Mh, 0 = 10.7 × 1010 M⊙, and Mh(r) is given by the function:
The spiral potential is given by the value Vsp (for z = 0) of the 3D logarithmic spiral model Vsp(r, ϕ, z) introduced by Cox & Gomez (2002; see Formula (19) in Efthymiopoulos et al. 2020):
where
and C = 8/(3π), hz = 0.18 kpc, r0 = 8 kpc, Rs = 7 kpc, and a = −13° is the pitch angle of the spiral arms. The function G(r) plays the role of a smooth envelope determining the radius beyond which the spiral arms are important. We adopt the form G(r) = b − carctan(Rs0 − r), with Rs0 = 6 kpc, b = 0.474, and c = 0.335. The spiral density is ρ0 = 15 × 107 M⊙ kpc−3 in the model under study. This value of the spiral density is chosen so as to yield a spiral F-strength value of 15%, consistent with those reported in the literature for the case of an intermediate spiral perturbation (see Patsis et al. 1991; Grosbøl et al. 2004) for grand design galaxies, and Sarkar & Jog (2018) and Pettitt et al. (2014) for the Milky Way. The F-strength value is given by the ratio of the maximum total force of the spiral perturbation over the radial force of the axisymmetric background:
(see Fig. 1 and corresponding text of Harsoula et al. 2021 for a detailed explanation of the role of the F-strength value).
The bar’s potential potential is as in Long & Murali (1992):
with
where Mb is the mass of the bar. In our study we use three different values of Mb, namely Mb = (6.25, 3, 1)×1010 M⊙, where M⊙ is the solar mass, a = 5.25 kpc, b = 2.1 kpc, and c = 1.6 kpc. The values of a and b set the bar’s length along the major and minor axes in the disk plane (x and y, respectively), while c sets the bar’s thickness in the z-axis (see Gerhard 2002; Rattenbury et al. 2007; Cao et al. 2013). These values are chosen so as to bring the bar’s corotation (for Ωb = 45 km s−1 kpc−1) to the value (specified by the L1, 2 points distance from the center) RL1, 2 = 5.4 kpc. Assuming corotation to be at 1.2 − 1.3 times the bar length, as seen in the literature, the latter turns to be about 4 Kpc with the adopted parameters. We set z = 0, because we deal with the 2D model, and finally, Eq. (10) in polar coordinates (r, θ), in the inertial frame of reference, takes the form
We now make a Taylor expansion of Eq. (12) with respect to cos(θ) and rewrite the bar’s potential as the sum of cos(mθ) terms, where m = 0, 2, 4, 6. Then, Eq. (12) takes the form
The bar’s and the spiral’s potential, in the inertial frame of reference and in polar coordinates (r, θ), are given by the following relations:
where Ωb is the pattern speed of the bar and Ωsp is the pattern speed of the spiral arms in the inertial frame of reference. The Hamiltonian of the total potential, in the rotating frame of reference of the spiral potential, is then written in the form
where pr is the radial velocity per unit mass, pf is the angular momentum of the unit mass in the rest frame of reference, f = θ − Ωspt, f2 = ΔΩt = (Ωsp − Ωb) t, and J2 is the canonically conjugate action of the angle f2. The axisymmetric part of the potential Vax(r), as given by Eq. (3), includes the axisymmetric part of the bar’s potential Vb0(r), while the non-axisymmetric part of the bar’s potential Vbm(r, f + f2) includes, in a first approximation, only the m = 2 terms of the bar’s potential, in order to facilitate the construction of the normal form:
3. Normal form construction
We now make a Taylor expansion of the bar’s potential Vb2(r, f, f2) around the radius of the circular orbit rc and the corresponding angular momentum pc, up to the second order, making the following replacements:
where δr is a small perturbation of the radius in relation to the radius of the circular orbit rc and Ju is a small perturbation of the angular momentum in relation to the angular momentum of the circular orbit pc. Finally, we make a canonical transformation in action-angle variables (δr, pr)→(Jr, fr):
where kc(rc) is the epicyclic frequency at r = rc, given by the relation
Moreover, pc is related to the angular velocity Ω(rc) of the star with the relation 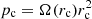 . The angular velocity Ω(rc), under the action of the axisymmetric potential only, is given by the relation
. The angular velocity Ω(rc), under the action of the axisymmetric potential only, is given by the relation
Then, the Hamiltonian (15) takes the following form:
where m1, m2, m3 can take the values 0, ±1, ±2. The notation 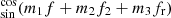 in the summation of Eq. (21) means that there are both terms with sin(m1f + m2f2 + m3fr) and cos(m1f + m2f2 + m3fr). ΔΩ = Ωsp − Ωb and Hc is a constant term that can be omitted.
in the summation of Eq. (21) means that there are both terms with sin(m1f + m2f2 + m3fr) and cos(m1f + m2f2 + m3fr). ΔΩ = Ωsp − Ωb and Hc is a constant term that can be omitted.
We now want to construct a normal form of the Hamiltonian (21) in order to eliminate the terms that contain the angle f2 = ΔΩt and make the Hamiltonian nonautonomous (for a tutorial on the normal form construction, see Efthymiopoulos 2012). We introduce a formal notation to account for this consideration: in front of every term in Eq. (21), we introduce a factor, λs, hereafter called the “book-keeping parameter”, which is a constant with a numerical value equal to λ = 1, while s is a positive integer exponent whose value, for every term in Eq. (21), is selected so as to reflect our consideration regarding the order of smallness we estimate a term to be of in the Hamiltonian. Thus, considering the leading terms ΔΩJ2 + κcJr + (Ω(rc)−Ωsp)Ju to be of order zero, we put λ0 in front of them. On the other hand, considering the remaining terms to be of a similar order of smallness (i.e., first order), we put a factor, λ1, in front of them. Then Eq. (21) becomes
where H0 is the integrable part of the Hamiltonian depending only on actions, and H1 is the part depending on action Jr as well as on all the angles f, f2, and fr.
In order to construct the normal form of the Hamiltonian (22) and eliminate the dependence on f2, we find the corresponding generating function χ using the homological equation
where { } defines the Poisson bracket and
is the integrable part of the Hamiltonian (21) containing the three basic frequencies ΔΩ, κc, and Ω(rc)−Ωsp. The term hkill is the part of the Hamiltonian (21) that contains the angle f2 that we want to eliminate:
Solving Eq. (23) we find the generating function χ, which is of the form
The first-order normal form of the Hamiltonian (21) is found by the relation
where Z0 = H0 and 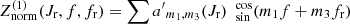 .
.
The second-order normal form of the Hamiltonian (21) is found by the relation
where Z0 = H0, 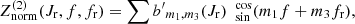 and
and 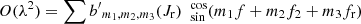 . The Hamiltonian (27) and the zero- and first-order terms of the Hamiltonian (28) (in the book keeping parameter λ) are now transformed in the new variables (rnew, fnew, prnew, pfnew) using Eqs. (17) and (18):
. The Hamiltonian (27) and the zero- and first-order terms of the Hamiltonian (28) (in the book keeping parameter λ) are now transformed in the new variables (rnew, fnew, prnew, pfnew) using Eqs. (17) and (18):
We find the main families of stable and unstable periodic orbits by the Hamiltonian 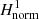 of Eq. (29) using the method described in Harsoula et al. (2021). The main family of stable periodic orbits that has the form of precessing ellipses and supports the spiral density wave is named x1 orbit after Contopoulos (1975), who introduced the nomenclature of the families of periodic orbits in a spiral galaxy. The other two families of periodic orbits are named x2 (stable periodic orbits) and x3, (unstable periodic orbit) and do not support the spiral density waves.
of Eq. (29) using the method described in Harsoula et al. (2021). The main family of stable periodic orbits that has the form of precessing ellipses and supports the spiral density wave is named x1 orbit after Contopoulos (1975), who introduced the nomenclature of the families of periodic orbits in a spiral galaxy. The other two families of periodic orbits are named x2 (stable periodic orbits) and x3, (unstable periodic orbit) and do not support the spiral density waves.
3.1. Finding the x1 stable periodic orbits
The stable periodic orbits of the x1 family correspond to the continuation of the circular orbits of the axisymmetric part of the potential Vax (Eq. (3)) into the region of the 2:1 resonance (inner Lindblad resonance).
The method of finding these orbits is thus: we fix a radius of a circular orbit rc and for this specific radius, we calculate the first order normal form 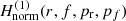 (we eliminate the subscript “new” for brevity) of Eq. (29) following the procedure described in the previous section.
(we eliminate the subscript “new” for brevity) of Eq. (29) following the procedure described in the previous section.
Then, we find the x1 stable periodic orbit, corresponding to this specific radius rc, by the use of a stroboscopic Poincaré section (r, pr) for f = 2κπ. The Poincaré section of Fig. 1a corresponds to the radius rc = 7 kpc and the central point (rx1, prx1) corresponds to the stable periodic orbit of the x1 family. The curves around the stable periodic orbit x1 correspond to quasiperiodic orbits. Using a Newton Rapshon iterative method, we locate the periodic orbit x1, selecting as initial condition the center of the island of stability (rx1, fx1, prx1, pfx1). Then we integrate these initial conditions using a Runge Kutta method of integration and the Hamilton equations of motion:
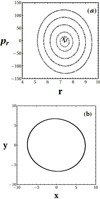 |
Fig. 1. (a) Stroboscopic Poincaré section (r, pr) for f = 2κπ and rc = 7.0, Mb = 6.25 × 1010 M⊙, Ωb = 45 km s−1 kpc−1, and Ωsp = 15 km s−1 kpc−1. (b) The stable periodic orbit of the x1 family. |
The orbit derived corresponds to the x1 family and has an approximately elliptic shape (Fig. 1b). We repeat this procedure for all the radii rc between 4.4 kpc and 10 kpc with a length step dr = 0.2 kpc, and superimpose the elliptical orbits in Fig. 2a. We observe that these precessing ellipses form a spiral density wave located between their apocenters and pericenters.
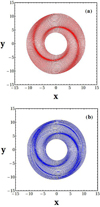 |
Fig. 2. (a) The spiral density wave derived from the periodic orbits of the x1 family for the normal form Hamiltonian (29) of first order |
If we repeat the procedure described above for the second-order normal form 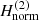 of Eq. (29), we derive a similar spiral density wave with almost no differences from the one derived from the first-order normal form (see Fig. 2b). In fact, the orbits corresponding to the same radius rc derived by the first- and the second-order normal forms almost coincide, except for a small range of radii around rc = 9.4 kpc and up to rc = 9.6 kpc, where there is a small deviation between them. We see that this small deviation results in the appearance of some weak secondary spiral structures, seen as bifurcations from the main spiral, which is something that one can observe in real galaxies. In Fig. 3 we plot a part of the orbits corresponding to the radius rc = 9.4 kpc derived from the first-order normal form
of Eq. (29), we derive a similar spiral density wave with almost no differences from the one derived from the first-order normal form (see Fig. 2b). In fact, the orbits corresponding to the same radius rc derived by the first- and the second-order normal forms almost coincide, except for a small range of radii around rc = 9.4 kpc and up to rc = 9.6 kpc, where there is a small deviation between them. We see that this small deviation results in the appearance of some weak secondary spiral structures, seen as bifurcations from the main spiral, which is something that one can observe in real galaxies. In Fig. 3 we plot a part of the orbits corresponding to the radius rc = 9.4 kpc derived from the first-order normal form 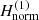 (in red) and from the second order normal form
(in red) and from the second order normal form 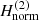 (in blue). For this specific radius, we observe the maximum deviation between the two cases.
(in blue). For this specific radius, we observe the maximum deviation between the two cases.
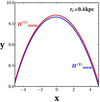 |
Fig. 3. Difference between the periodic orbits of the x1 families derived by the first-order normal form |
In general, the spiral density wave derived from the precessing ellipses of the x1 family, in both cases, is well defined. So, we can now continue with the transformation of the coordinates of the elliptical orbits of the x1 family to the old variables (rold, fold, prold, pfold) (before the normal form construction) using the orbits derived from the first-order normal form Hamiltonian 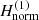 , in order to see how these ellipses are deformed.
, in order to see how these ellipses are deformed.
3.2. Transformation to the old variables
A back transformation to the old variables (rold, fold, prold, pfold) corresponding to the initial, time-dependent Hamiltonian (15), is necessary in order to see how the precessing ellipses forming a well-defined spiral density wave are deformed (from the first- and the second-order normal form constructions) for Ωb = 45 km s−1 kpc−1 and Ωsp = 15 km s−1 kpc−1.
We make the back transformation of the spiral density wave derived from the first-order normal form 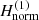 in the old variables, that correspond to the Hamiltonian (15), which includes the time-dependent angle f2 = ΔΩt. This transformation is made using the generating function χ. Using the new variables of each periodic orbit x1 in polar coordinates, (rnew, fnew, prnew, pfnew), and for a specific radius of the circular orbit rc, we find the old variables (rold, fold, prold, pfold) using the following relations:
in the old variables, that correspond to the Hamiltonian (15), which includes the time-dependent angle f2 = ΔΩt. This transformation is made using the generating function χ. Using the new variables of each periodic orbit x1 in polar coordinates, (rnew, fnew, prnew, pfnew), and for a specific radius of the circular orbit rc, we find the old variables (rold, fold, prold, pfold) using the following relations:
where χ is the solution of Eq. (23), 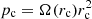 , and { } defines the Poisson bracket. Using Eq. (18), we can replace cos frnew, sin frnew, and Jr in the relations in Eq. (31) as follows:
, and { } defines the Poisson bracket. Using Eq. (18), we can replace cos frnew, sin frnew, and Jr in the relations in Eq. (31) as follows: 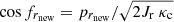 ,
, 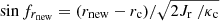 , and
, and 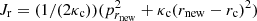 . Using Eq. (31), we find the perturbed precessing ellipse for each radius rc of the circular orbit, which includes the information of the second pattern speed of the bar Ωb in cartesian coordinates (xold = rold cos(fold), yold = rold sin(fold)).
. Using Eq. (31), we find the perturbed precessing ellipse for each radius rc of the circular orbit, which includes the information of the second pattern speed of the bar Ωb in cartesian coordinates (xold = rold cos(fold), yold = rold sin(fold)).
Figure 4 shows the perturbed precessing ellipses for the radii of Fig. 2, derived using the relations in Eq. (31). In particular, Fig. 4a consists of orbits integrated for a short time, namely for ten epicyclic periods (t = 10 Tepi), and Fig. 4b consists of orbits integrated for a longer time, namely for 20 epicyclic periods (t = 20 Tepi), where Tepi = 2π/κc and κc is the epicyclic frequency given by Eq. (19) for each radius rc.
 |
Fig. 4. Perturbed precessing ellipses of Fig. 2: (a) for a short integration time corresponding to ten epicyclic periods; and (b) a longer integration time corresponding to 20 epicyclic periods (see text) for Mb = 6.25 × 1010 M⊙ (a strong bar), Ωb = 45 km s−1 kpc−1, and Ωsp = 15 km s−1 kpc−1. |
In Fig. 4a it is quite difficult to distinguish the hidden spiral density wave, while in Fig. 4b it is impossible to distinguish any pattern at all. For this reason we used an image processing method in order to recognize the hidden pattern of Figs. 4a,b. The method is described as follows: let G be a grid of L × L square cells (with L = 300) that covers the dimensions of the galactic model (i.e., −12 ≤ x ≤ 12 kpc and −12 ≤ y ≤ 12 kpc). If S = [x(ti),y(ti)] is a time series of a single star trajectory on the configuration space, with ti = iΔt, i = 0, 1, 2, …, I, collected with a time step Δt = 10−4 (2π/κc) (where κc is the epicyclic frequency of each orbit given by Eq. (19)) and t = tI is the total time of the integration of the orbit, then we define the “single star trajectory distribution” Ps(xj, yk; ti) over G around the points (xj, yk) = (jΔx, kΔy) with j, k = −N, −N + 1, …, N − 1, N, where N = |xmax/Δx|=|ymax/Δy| and xmax = ymax = 12 kpc, as:
where CS is the number of points of the sample S inside the square cell defined by xj − Δx/2 ≤ x < xj + Δx/2, yk − Δy/2 ≤ y < yk + Δy/2. Therefore, Cs(xj, yk; ti) is the “single star trajectory occupation number” of the cell (xj, yk) from t = 0 up to t = tI.
The above considerations are easily extended in the case of an ensemble of M trajectories evolved up to t = tI.
In Fig. 5 we see the result of the processing of Fig. 4b with the method described above. The hidden spiral structure is revealed to be well defined and intense, but slightly deformed in relation to the one of Fig. 2.
 |
Fig. 5. Processed image of Fig. 2b using the method described in the text. A well-defined and intense spiral density wave is presented. |
4. Parametric study
The shape of the hidden density wave and how well the spiral structure is maintained in a galactic model containing two different pattern speeds, depend on several parameters, such as the mass of the bar Mb in Eq. (10) and the pattern speed of the bar Ωb. The perturbation of the precessing ellipses of Fig. 2 depends on the generating function given by Eq. (26). While the mass of the bar Mb affects the coefficients am1, m2, m3 of Eq. (26), the pattern speed of the bar Ωb is found in the denominator of Eq. (26) in the term ΔΩ = Ωsp − Ωb. Therefore, the perturbation of the precessing ellipses becomes greater for greater values of Mb and for smaller absolute values of ΔΩ = Ωsp − Ωb, in other words smaller values of Ωb.
We now make a parametric study for different values of Mb and ΔΩ in order to test the limits inside which the spiral density wave is still detectable.
4.1. The role of the mass of the bar
In order to test the effect of the mass of the bar, we use two smaller values of the value Mb, namely Mb = 3 × 1010 M⊙ and Mb = 1 × 1010 M⊙, and repeat the procedure described above.
We plot the processed images of the spiral density waves, derived after the transformation to the old variables, for the values of the mass of the bar Mb = 3 × 1010 M⊙ in Fig. 6a and Mb = 1 × 1010 M⊙ in Fig. 6b. The main observation is that the smaller the mass of the bar, the less intense the spiral density wave of the spiral arms, something that was expected since the coefficients am1, m2, m3(Jr) of the generating function χ in Eq. (26) depend on the mass Mb of the bar. However, one important remark is that the spirals are well defined and present no breaks, as in the case of the Fig. 5, with the greater value of the bar’s mass Mb. It is now obvious that for even smaller values than Mb = 1 × 1010 M⊙, the spiral density wave will gradually disappear.
 |
Fig. 6. Processed image of the spiral density wave for: (a) Mb = 3 × 1010 M⊙, and (b) Mb = 1 × 1010 M⊙. In both cases Ωb = 45 km s−1 kpc−1 and Ωsp = 15 km s−1 kpc−1. |
4.2. The role of the pattern speed of the bar
In order to investigate the role of the pattern speed in the normal form construction of the time-dependent Hamiltonian (15), we repeat the study of the previous subsection but for different values of the pattern speed of the bar Ωb. We now want to test a slower bar, namely Ωb = 20 km s−1 kpc−1, and a faster one, namely Ωb = 60, keeping the bar’s mass constant to Mb = 6.25 × 1010 M⊙ as in Fig. 5. Observing in more detail Eq. (26) of the generating function χ, through which the transformation of the normal form is made, we see that the denominator includes the three basic frequencies, namely ΔΩ = Ωsp − Ωb, κc, and Ω(rc)−Ωsp. If we reduce the absolute value of ΔΩ = Ωsp − Ωb by using a smaller value of the pattern speed of the bar Ωb, the perturbation in the normal form construction is greater (a greater value of the generating function χ) and this is reflected in the orbits having a greater deviation from the elliptical form.
We construct the first-order normal form 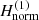 of Eq. (29) for Ωb = 20 km s−1 kpc−1 (much slower bar rotation) and for Ωb = 60 km s−1 kpc−1 (faster bar rotation), and then we repeat the procedure described in Sect. 3.2 in order to reveal the hidden structure of the superposition of the deformed precessing ellipses corresponding to the x1 periodic families. The spiral density waves derived are shown in Fig. 7. Figure 7a corresponds to Ωb = 20 km s−1 kpc−1, while Fig. 7b correpsonds to Ωb = 60 km s−1 kpc−1. We observe that for the case of the slower bar (Ωb = 20 km s−1 kpc−1), the spiral density wave derived is much less intense compared with Fig. 5, and less well defined as the spiral arms seem to be broken at several radii. On the other hand, in Fig. 7b, where the pattern speed of the bar has a much greater value (Ωb = 60 km s−1 kpc−1), the spiral density wave seems to be more intense but again it is much less well defined than in Fig. 5. So, there are some upper and lower limits in the value of the pattern speed of the bar in order to have an intense and well-defined spiral density wave structure in a galactic model with two different pattern speeds.
of Eq. (29) for Ωb = 20 km s−1 kpc−1 (much slower bar rotation) and for Ωb = 60 km s−1 kpc−1 (faster bar rotation), and then we repeat the procedure described in Sect. 3.2 in order to reveal the hidden structure of the superposition of the deformed precessing ellipses corresponding to the x1 periodic families. The spiral density waves derived are shown in Fig. 7. Figure 7a corresponds to Ωb = 20 km s−1 kpc−1, while Fig. 7b correpsonds to Ωb = 60 km s−1 kpc−1. We observe that for the case of the slower bar (Ωb = 20 km s−1 kpc−1), the spiral density wave derived is much less intense compared with Fig. 5, and less well defined as the spiral arms seem to be broken at several radii. On the other hand, in Fig. 7b, where the pattern speed of the bar has a much greater value (Ωb = 60 km s−1 kpc−1), the spiral density wave seems to be more intense but again it is much less well defined than in Fig. 5. So, there are some upper and lower limits in the value of the pattern speed of the bar in order to have an intense and well-defined spiral density wave structure in a galactic model with two different pattern speeds.
 |
Fig. 7. The spiral density wave derived from the periodic orbits of the x1 family for the normal form Hamiltonian (29) of first order, for: (a) a pattern speed of the bar Ωb = 20 km s−1 kpc−1, and (b) a pattern speed of the bar Ωb = 60 km s−1 kpc−1. Both figures have Mb = 6.25 × 1010 M⊙ (a strong bar). |
All the calculations were performed on the “superpc” computer with ten CPU cores and 20 threads at the Research Center for Astronomy and Applied Mathematics of the Academy of Athens.
5. Conclusions
In the present paper, we consider a galactic potential of a barred spiral galaxy with two different pattern speeds (for the bar and the spiral arms) and we eliminate the dependence on time of the potential by considering the bar as a perturbation of the spiral potential, in the case where the bar rotates much faster that the spiral arms. The idea is to see how the precessing ellipses that support the spiral structure in the case of a grand design galaxy will be deformed and whether a spiral density wave can still be detected. We use a Milky Way-like model with parameters chosen from Pettitt et al. (2014) and construct a normal form Hamiltonian in first- and second-order approximations, eliminating the time dependence due to the difference between the two pattern speeds.
We find the stable periodic orbits of the x1 family in this new normal form Hamiltonian and construct the spiral density wave made out of the approximately elliptical orbits of this family. Using the generating function χ, we make a back transformation of these orbits to their original variables where the time is involved. The elliptical periodic orbits are deformed in elliptical rings having a certain thickness. However, if we superimpose all the orbits corresponding to several radii, and using an image processing method, we reveal a slightly deformed spiral density wave that still survives. This result proves that in barred spiral galaxies where the bar rotates much faster that the spiral arms, the spiral structure can be supported by deformed precessing ellipses, such as in the case of grand design galaxies.
We make a parametric study for the values of the bar’s mass and pattern speed. By reducing the bar’s mass, we find less intense but better defined spiral arms. A lower limit of the bar’s mass is approximately the value Mb = 1 × 1010 M⊙. By reducing the bar’s pattern speed, we again find less intense spiral density waves and breaks in the spiral arms. Breaks in the spiral density wave appear also in the case of an extremely fast rotating bar (compared with the pattern speed of the spiral arms). The best, well-defined and intense, spiral density wave appears for a ratio of pattern speeds 3 : 1 and a strong bar (Mb = 6.25 × 1010 M⊙).
In the case where Ωb = Ωsp, the bar can no longer be considered as a perturbation of the spiral potential. This case has been already studied in the framework of the “manifold theory” in a series of papers, as mentioned in the introduction. According to this theory, in the case of barred spiral galaxies with one pattern speed, chaotic orbits with initial conditions along the unstable asymptotic manifolds, emanating from the Lagrandian points L1 and L2, as well as nearby sticky chaotic orbits, can support the spiral structures for a long time.
This study is an alternative scenario to the manifold theory, where the spiral potential is considered as a perturbation of the bar potential (see Efthymiopoulos et al. 2020) in the case of a barred spiral galactic model having two different pattern speeds. Here, in contrast, we consider the bar potential as a perturbation of the spiral potential in the case where the bar rotates fast enough, compared with the pattern speed of the spiral arms. This is a proposed scenario for cases of barred spiral galaxies where the spiral arms have a well-defined symmetric shape, such as the one proposed for the Milky Way. In Gerhard (2011), which is a review of the pattern speeds of the Milky Way, the author concludes that the bar of the Milky way is a fast rotator having between double and triple the speed of the spiral arms. In our study we adopt values for the pattern speeds of the bar and the spiral arms that are suggested in Gerhard’s review paper. In the cases where the bar rotates much faster than the spiral arms, as in the case of the Milky Way, the arms in general seem more symmetrical and well defined, having almost the same pitch angle along the entire radius of the galaxy (see also Font et al. 2019 where they give the pattern speeds of the bar and the spiral arms of a fairly large sample of barred spiral galaxies). This image of spiral arms can be supported by ordered elliptical orbits. This is a scenario that is consistent with the density wave theory. Font et al. (2019) also found that the longer the bars (and as a consequence slower), the smallest the differences between the pattern speeds. Thus, the spiral arms, which are most likely bar driven, seem less symmetric with variable pitch angle, while some other features appear such as gaps, bridges, and bifurcations. This image is more consistent with the scenario of chaotic orbits along unstable manifolds supporting the spiral structures. Further numerical investigation is needed in order to confirm such a statement.
So, in conclusion, for the case where the bar rotates much faster than the spiral arms, we suggest an alternative scenario to the “manifold theory” for supporting the spiral structures of the galaxy, which is, in fact, a generalization of the density wave theory.
References
- Athanassoula, E. 2012, MNRAS, 426, L46 [NASA ADS] [Google Scholar]
- Athanassoula, E., Romero-Gómez, M., & Masdemont, J. J. 2009a, MNRAS, 394, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Athanassoula, E., Romero-Gómez, M., Bosma, A., & Masdemont, J. J. 2009b, MNRAS, 400, 1706 [NASA ADS] [CrossRef] [Google Scholar]
- Berman, R. H., & Mark, J. W. K. 1977, ApJ, 216, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Boonyasait, V., Patsis, P. A., & Gottesman, S. T. 2005, NYASA, 1045, 203 [NASA ADS] [Google Scholar]
- Buta, R., Vasylyev, S., Salo, H., & Laurikainen, E. 2005, AJ, 130, 506 [NASA ADS] [CrossRef] [Google Scholar]
- Buta, R. J., Knapen, J. H., Elmegreen, B. G., et al. 2009, AJ, 137, 4487 [NASA ADS] [CrossRef] [Google Scholar]
- Cao, L., Mao, S., Nataf, D., Rattenbury, N. J., & Gould, A. 2013, MNRAS, 434, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Contopoulos, G. 1970, Proceedings of IAU. Symposium No 38 (Dordrecht: D. Reidel Publishing Co) [Google Scholar]
- Contopoulos, G. 1971, ApJ, 163, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Contopoulos, G. 1975, ApJ, 201, 566 [NASA ADS] [CrossRef] [Google Scholar]
- Contopoulos, G., & Grosbøl, P. 1986, A&A, 155, 11 [NASA ADS] [Google Scholar]
- Cox, D. P., & Gomez, G. C. 2002, ApJS, 142, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Danby, J. M. A. 1965, AJ, 70, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Dehnen, W. 1993, MNRAS, 265, 250 [NASA ADS] [CrossRef] [Google Scholar]
- Durbala, A., Buta, R., Sulentic, J. W., & Verdes-Montenegro, L. 2009, MNRAS, 397, 1756 [NASA ADS] [CrossRef] [Google Scholar]
- Efthymiopoulos, C. 2012, in Third La Plata Internat. School on Astron. Geophys., eds. P. M. Cincotta, C. M. Giordano, & C. Efthymiopoulos (La Plata: Asociación Argentina de Astronomía) [Google Scholar]
- Efthymiopoulos, C., Harsoula, M., & Contopoulos, G. 2020, A&A, 636, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Font, J., Beckman, J. E., Querejeta, M., et al. 2014, ApJS, 210, 2 [Google Scholar]
- Font, J., Beckman, J. E., James, P. A., & Patsis, P. A. 2019, MNRAS, 482, 5362 [NASA ADS] [CrossRef] [Google Scholar]
- Gerhard, O. 2002, in The Dynamics, Structure and History of Galaxies: A Workshop in Honour of Professor Ken Freeman, eds. G. S. Da Costa, E. M. Sadler, & H. Jerjen, ASP Conf. Ser., 73 [Google Scholar]
- Gerhard, O. 2011, Mem. Soc. Astron. It. Sup., 18, 185 [Google Scholar]
- Grosbøl, P., Patsis, P. A., & Pompei, E. 2004, A&A, 423, 849 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harsoula, M., Efthymiopoulos, C., & Contopoulos, G. 2016, MNRAS, 459, 3419 [NASA ADS] [CrossRef] [Google Scholar]
- Harsoula, M., Zouloumi, K., Efthymiopoulos, C., & Contopoulos, G. 2021, A&A, 655, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lin, C., & Shu, F. 1964, ApJ, 140, 646 [Google Scholar]
- Lin, C., & Shu, F. 1966, Proc. Natl. Acad. Sci., 55, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Lindblad, B. 1940, ApJ, 92, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Lindblad, B. 1955, Stockholm Obs. Ann., 18, 6 [Google Scholar]
- Lindblad, B. 1961, Stockholm Obs. Ann., 21, 8 [NASA ADS] [Google Scholar]
- Long, K., & Murali, C. 1992, ApJ, 397, L44 [NASA ADS] [CrossRef] [Google Scholar]
- Meidt, S. E., Rand, R. J., & Merrifield, M. R. 2009, ApJ, 702, 277 [Google Scholar]
- Miyamoto, M., & Nagai, R. 1975, Publ. Astron. Soc. Japan, 27, 533 [Google Scholar]
- Monet, D. G., & Vandervoort, P. O. 1978, ApJ, 221, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Moore, E. M., & Gottesman, S. T. 1995, ApJ, 447, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Patsis, P. A., Contopoulos, G., & Grosbøl, P. 1991, A&A, 243, 373 [NASA ADS] [Google Scholar]
- Pettitt, A. R., Dobbs, C. L., Acreman, D. M., & Price, D. J. 2014, MNRAS, 444, 919 [NASA ADS] [CrossRef] [Google Scholar]
- Quillen, A. C. 2003, ApJ, 125, 785 [CrossRef] [Google Scholar]
- Quillen, A. C., Dougherty, J., Bagley, M. B., Minchev, I., & Comparetta, J. 2011, MNRAS, 417, 762 [NASA ADS] [CrossRef] [Google Scholar]
- Rattenbury, N. J., Mao, S., Sumi, T., & Smith, M. C. 2007, MNRAS, 378, 1064 [NASA ADS] [CrossRef] [Google Scholar]
- Rautiainen, P., & Salo, H. 1999, A&A, 348, 737 [NASA ADS] [Google Scholar]
- Roca-Fàbrega, S., Valenzuela, O., Figueras, F., et al. 2013, MNRAS, 432, 2878 [Google Scholar]
- Romero-Gomez, M., Masdemont, J. J., Athanassoula, E., & Garcia-Gomez, C. 2006, A&A, 453, 39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Romero-Gomez, M., Athanassoula, E., Masdemont, J. J., & Garcia-Gomez, C. 2007, A&A, 472, 63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sarkar, S., & Jog, C. J. 2018, A&A, 617, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Speights, J. C., & Westpfahl, D. J. 2012, ApJ, 752, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Sellwood, J. A., & Sparke, L. S. 1988, MNRAS, 231, 25 [Google Scholar]
- Speights, J. C., & Rooke, P. 2016, ApJ, 826, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Tsoutsis, P., Efthymiopoulos, C., & Voglis, N. 2008, MNRAS, 387, 1264 [NASA ADS] [CrossRef] [Google Scholar]
- Tsoutsis, P., Kalapotharakos, C., Efthymiopoulos, C., & Contopoulos, G. 2009, A&A, 495, 743 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Voglis, N., Tsoutsis, P., & Efthymiopoulos, C. 2006, MNRAS, 373, 280 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1. (a) Stroboscopic Poincaré section (r, pr) for f = 2κπ and rc = 7.0, Mb = 6.25 × 1010 M⊙, Ωb = 45 km s−1 kpc−1, and Ωsp = 15 km s−1 kpc−1. (b) The stable periodic orbit of the x1 family. |
| In the text | |
 |
Fig. 2. (a) The spiral density wave derived from the periodic orbits of the x1 family for the normal form Hamiltonian (29) of first order |
| In the text | |
 |
Fig. 3. Difference between the periodic orbits of the x1 families derived by the first-order normal form |
| In the text | |
 |
Fig. 4. Perturbed precessing ellipses of Fig. 2: (a) for a short integration time corresponding to ten epicyclic periods; and (b) a longer integration time corresponding to 20 epicyclic periods (see text) for Mb = 6.25 × 1010 M⊙ (a strong bar), Ωb = 45 km s−1 kpc−1, and Ωsp = 15 km s−1 kpc−1. |
| In the text | |
 |
Fig. 5. Processed image of Fig. 2b using the method described in the text. A well-defined and intense spiral density wave is presented. |
| In the text | |
 |
Fig. 6. Processed image of the spiral density wave for: (a) Mb = 3 × 1010 M⊙, and (b) Mb = 1 × 1010 M⊙. In both cases Ωb = 45 km s−1 kpc−1 and Ωsp = 15 km s−1 kpc−1. |
| In the text | |
 |
Fig. 7. The spiral density wave derived from the periodic orbits of the x1 family for the normal form Hamiltonian (29) of first order, for: (a) a pattern speed of the bar Ωb = 20 km s−1 kpc−1, and (b) a pattern speed of the bar Ωb = 60 km s−1 kpc−1. Both figures have Mb = 6.25 × 1010 M⊙ (a strong bar). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



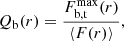
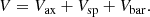
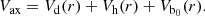
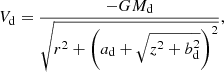
![$$ \begin{aligned} V_{\mathrm{h}}=\frac{-GM_{\mathrm{h(r)}}}{r}-\frac{-GM_{\mathrm{h,0}}}{\gamma r_{\mathrm{h}}} \left[-\frac{\gamma }{1+(r/r_{\mathrm{h}})^\gamma }+\ln \left(1+\frac{r}{r_{\mathrm{h}}}\right)^\gamma \right]_{\rm r}^{r_{\rm h,max}} ,\end{aligned} $$](/articles/aa/full_html/2022/11/aa44049-22/aa44049-22-eq7.gif)
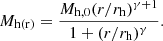
![$$ \begin{aligned} V_{\mathrm{sp}}= 4 \pi G h_{z} \rho _{0}\ G(r)\ \exp \left(- \left(\frac{r- r_{\mathrm{0}}}{ R_{\mathrm{s}}} \right) \right) {\frac{C}{K B}}\ \cos \left[ 2 \left(\varphi -\frac{\ln (r/ r_{0} )}{\tan (\alpha )} \right) \right] ,\end{aligned} $$](/articles/aa/full_html/2022/11/aa44049-22/aa44049-22-eq9.gif)