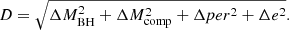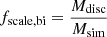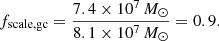| Issue |
A&A
Volume 667, November 2022
|
|
|---|---|---|
| Article Number | A55 | |
| Number of page(s) | 10 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/202141992 | |
| Published online | 04 November 2022 | |
Testing the presence of a dormant black hole inside HR 6819
Nicolaus Copernicus Astronomical Center, The Polish Academy of Sciences, ul. Bartycka 18, 00-716 Warsaw, Poland
e-mail: amedeoromagnolo@gmail.com
Received:
9
August
2021
Accepted:
22
August
2022
Context. HR 6819 was recently reported to be a triple system with a non-accreting black hole (BH). The inner binary system was defined as a B3 III type star (a 5 − 7 M⊙ star estimated to be at the end of its main sequence) and a dormant BH (> 4.2 M⊙). The period of the inner binary was estimated to be ∼40 days with an eccentricity in the range 0.02 − 0.04. As the inner binary is not resolved, the third component may actually just be spatially coinciding with the inner binary.
Aims. In this study we test whether the system’s inner binary can be reconstructed using the isolated binary evolution in the Galactic field or through the dynamical evolution within globular star clusters. Our goal is to understand the formation of the HR 6819 inner binary.
Methods. To simulate the inner binary evolution we assumed that the influence of the third body on the inner binary is negligible. We created synthetic populations of BH-main sequence binaries for the Galactic disc and the Galactic globular clusters to compare to the reported parameters of the HR 6819 inner binary. We have adopted very optimistic input physics, in terms of common envelope evolution and BH formation, for the formation of binaries similar to the reported inner HR 6819 binary.
Results. Despite our optimistic assumptions we cannot form systems like the inner HR 6819 binary in globular clusters. Even with our extreme assumptions, the formation of an HR 6819-like binary in the Galactic field population is not expected.
Conclusions. We argue that if a dormant BH actually exists in the reported configuration inside HR 6819, its presence cannot easily be explained by our models based on isolated and dynamical binary evolution.
Key words: binaries: close / stars: black holes / stars: massive / stars: statistics
© A. Romagnolo et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1. Introduction
Black holes (BHs) in binary systems are predicted to be around 10% of the whole Milky Way BH population, and most of them are BH-BH systems (Olejak et al. 2020a). Black holes with non-compact companions can be detected through interactions with them, but they are possibly a very small fraction of the total Galactic population. So far only ∼20 Galactic BH systems have been detected (Casares 2007; Casares & Jonker 2014)1. Most of them are close X-ray binary systems transferring matter through an accretion disc. A recent review on stellar-origin BHs is provided in Bambi (2018). Black holes may also be detected as gravitational wave signal emitters (Abbott et al. 2016) and in non-interacting binaries using astrometric and spectroscopic observations of their companion stars. Single BHs can potentially also be detected through microlensing (e.g., Wyrzykowski et al. 2016; Wiktorowicz et al. 2019), self-lensing (Wiktorowicz et al. 2021) or while accreting from the interstellar medium (Tsuna et al. 2018). Theoretically Hawking radiation (Hawking 1974) may possibly allow for a detection of thermal radiation from the immediate vicinity of a BH.
According to recent simulations (Sukhbold et al. 2016; Patton & Sukhbold 2020) stellar-origin BHs could either form from supernova events or from the direct collapse of the stellar progenitor without any emission of mass besides the neutrino emission. There is no hard line in terms of initial mass alone to whether an explosion or an implosion can happen, since this is rather dependent on factors such as the carbon-oxygen core mass and its initial uniform composition of carbon and oxygen, which in turn depend on the winds, mass loss, rotation, mixing effects, binary interactions and nuclear reaction rates during the early stages of stellar evolution (up to the core-helium burning phase; Patton & Sukhbold 2020). These simulations suggest that direct BH collapse is a very frequent phenomenon, more importantly for massive carbon-oxygen or iron cores and in general for stars between 10 and 30 M⊙ at the zero-age main sequence (ZAMS).
HR 6819 is reported to be a triple system harbouring a BH candidate (Rivinius et al. 2020). The BH candidate mass was estimated on the basis of radial motions of the visible star in the inner binary. The spectral type of the companion star has been classified as B3 III. Using single-star evolutionary tracks (Ekström et al. 2012) and observational data (Hohle et al. 2010), the most likely range for the star was estimated to be between 5 and 7 M⊙ and the star was estimated to be at the end of its main sequence (MS). The lower limit for the BH candidate mass was set at 4.2 M⊙. The star was reported to be roughly 1 M⊙ more massive than its unseen companion, while the inner binary is supposed to have a period of 40.333 ± 0.004 and an eccentricity of 0.03 ± 0.01. The outer orbit with the Be star (with a mass of ∼6 M⊙) is instead unconstrained. On top of that, the outer star does not show any significant RV variation and may actually be just spatially coinciding with the inner binary. Neither the Fiber-fed Extended Range Optical Spectrograph (FEROS; Rivinius et al. 2020), nor Gaia have a sufficient resolution to resolve the full triple system. The age of the whole triple system was estimated to be between 15 and 75 Myr.
Other possible interpretations of the observational data cannot be excluded. For instance, spectral features of HR 6819 may also be explained by a close binary in a 4-day period, composed of two A0 stars of ∼2.3 M⊙ each with no BH (Mazeh & Faigler 2020). In an independent analysis of the system spectrum, El-Badry & Quataert (2021) also propose the absence of a dormant BH. In their interpretation HR 6819 would be composed of two optical components: the B3 star and its Be stellar companion. Also Bodensteiner et al. (2020) propose a similar solution. According to their study HR 6819 could be a binary hosting a stripped B-type star and a rapidly rotating Be companion. Post-interaction lower-mass stars (exposed hot cores) can also mimic higher-mass isolated stars. The temperature of a B-type subdwarf can be higher than 20 000 K despite having a mass of ≲1 M⊙ (e.g., Heber 2009).
Safarzadeh et al. (2020) also argue for the unlikelihood of a dormant BH inside the HR 6819 inner binary. Their work was based on three different considerations: (i) the small probability of having such a triple system configuration in terms of mass and spectral type in the Galactic population of stars, (ii) the extremely narrow range of orbital separations (both for the inner and the outer orbit) for the system to be dynamically stable, and (iii) the very narrow set of BH kicks and ejected mass at the BH formation that fits the observational constraints in terms of the orbital parameters for the inner binary. Additionally, they show that a chance alignment between a B III star and a Be star could be a potential explanation for the observational data.
Stevance et al. (2022) pointed out, in their Letter regarding the potential existence of a dormant BH in NGC 1850, that the study of binary evolution in stellar populations can be beneficial for testing the strength of any claim regarding the presence of an unseen BH in binary systems. In our study we therefore try to reproduce the originally reported orbital parameters of HR 6819 within the framework of isolated binary evolution and dynamical formation in globular clusters (GCs). In both cases we test very optimistic models that can maximise the likelihood of reconstructing the reported parameters of the HR 6819 inner binary. In this way we will either set a best-case scenario (despite being unorthodox in terms of input physics) if we find any evolutionary solution for the reported parameters, or we will provide additional support for the absence of a dormant BH in HR 6819 in the case of no evolutionary solution. We assumed that HR 6819 is a triple system with the third component either unbound to the inner binary or with the outer orbit so wide that it does not affect its evolution. We consequently adopted the estimates from Rivinius et al. (2020) as reference parameters of the HR 6819 inner binary.
If we consider the influence of a third outer body, the inner binary might be gravitationally perturbed by the outer star during its evolution. Through the Kozai-Lidov mechanism (Kozai 1962; Lidov 1962), the two orbits can exchange orbital momentum (but not energy) and reciprocally alter their eccentricity and inclination. This effect could also produce highly eccentric inner binaries that could even merge before producing compact objects (Naoz 2016). Essentially, adding the outer star to the evolution of the system in our population study would result in a different eccentricity distribution as well as fewer BH-MS inner binaries arising due to the increased possibility of an early merger event.
2. Method
2.1. StarTrack
In our study we used the STARTRACK2 population synthesis code (Belczynski et al. 2002, 2008), which allows the user to simulate the isolated binary evolution of the system with a wide variety of initial conditions and physical parameters. The most up-to-date description of STARTRACK’s standard physical parameters and approaches, as well as the adopted model for star formation rates and the metallicity distribution of the Universe, can be found in Belczynski et al. (2020), with two updates in Sect. 2 of Olejak et al. (2020b).
We introduced a significant modification compared to the standard StarTrack assumptions, which is that all BHs (regardless of their mass) are formed via direct collapse without asymmetric mass ejection in supernova explosions. In such scenario, BHs do not receive natal kicks except for the ones due to asymmetric neutrino emission. The mass of the resulting compact object is equal to the mass of the pre-collapse star minus the emitted neutrino mass. This approach has also been adopted in Zapartas et al. (2019), where every single star beyond 20 M⊙ at ZAMS was assumed to not initiate a supernova event. We discriminate between whether the resulting compact object is a neutron star or a BH based on its final mass: if it is ≤2.5 M⊙, the compact object will be a neutron star, otherwise we will have a BH.
In our simulations we tested several scenarios with different values of metallicity Z (see Table 1), neutrino mass loss during BH collapse Floss (in terms of percentage of total mass loss), efficiency of orbital energy loss for common envelope (CE) ejections, α, the initial system semi-major axis, a0, and the stellar masses of progenitors at ZAMS, respectively MZAMS, a and MZAMS, b.
Tested parameter space for the isolated binary evolution of HR 6819.
2.2. MOCCA
To investigate a possible influence of dynamical interactions on the formation of HR 6819 within Galactic globular star clusters we used the numerical simulations performed with the MOCCA code3. It is currently one of the most advanced codes to simulate full stellar and dynamical evolution of real-size star clusters (Giersz et al. 2014; Hypki & Giersz 2013; Giersz 1998). MOCCA is already used in a wide number of projects to investigate the evolution of compact binaries, for example BHs binaries (Hong et al. 2020). Moreover, it is able to closely follow N-body codes and provides almost as much information about stars and binary stars (Wang et al. 2016). The strong dynamical interactions are performed with the FEWBODY code (Fregeau et al. 2004).
In order to increase the reliability of the results from the possible dynamical channel, the MOCCA code was fully integrated with the STARTRACK code. Now, MOCCA follows all the stellar and binary evolution processes with STARTRACK as was done with SSE/BSE4(Hurley et al. 2000, 2002, 2013) codes in previous MOCCA studies. In total 120 numerical simulations of GCs were performed. In each simulation a cluster began its evolution with 6 × 105 initial objects (binaries and single stars), a 95% binary fraction was assumed, and a metallicity of Z = 0.0105 was adopted, with a 60 pc tidal radius and a 2 pc half-mass radius. Every simulation was started with a unique ’seed’ value to generate different realisations of the initial conditions. The reason behind choosing one mass and one concentration was just simplicity. The goal was to check if the binary resembling HR 6819 can be formed with the help of dynamical interactions, which are characteristic of GCs (collisional systems). For that we decided to use a relatively massive initial cluster, with high density, in order to provoke various dynamical interactions. If the dynamical interactions could actually create many HR-like binaries, we would need to carefully select a broader range of initial conditions in order to find out in which GCs such systems are being preferentially formed. On the contrary, if dynamical interactions were shown to not have a role in the formation of a binary resembling HR 6819, there would not be the need to broaden the range of initial conditions.
All GC models were evolved with the same input stellar and binary physics (see Sect. 4) that increases possibility of HR 6819 inner binary formation (see Sect. 3.1). However, each model was a different realisation of the initial parameters for stars and binaries within their adopted initial distributions (star masses, binary orbits, initial positions, and velocities within a given cluster). This was done to ensure that we will not miss any potential HR 6819 formation channel due to poor statistics.
3. Isolated binary evolution
In order to reconstruct the HR 6819 inner binary, we had to recover some scenarios that, similarly to Rivinius et al. (2020), gave a BH-MS binary with component masses > 4.2 M⊙ for the BH and 5 − 7 M⊙ for the B star (the BH inner binary orbit companion). Additionally the two objects are supposed to differ in mass by ∼1 M⊙ (the BH being less massive). Finally, the observational constraints require an orbital period of 40.3 days and an eccentricity of ∼0.03. From now on we will refer to the BH progenitor as the primary star and its B companion as the secondary star.
3.1. Simulation
In isolated binary evolution calculations we can make an educated guess as to how we need to push evolutionary parameters to maximise the chance of formation of a binary similar to that of the inner binary of HR 6819. Our guess was based on several hundred trials of running evolution of massive binaries. We find that BH formation, CE evolution and the metallicity of a binary are important factors in the formation of BH-MS binaries with parameters resembling the reported architecture of HR 6819. We allow for some extreme changes in several parameters not excluded on theoretical grounds. Metallicity is allowed to change in the range Z = 0.01 − 0.02 allowed for the Galactic disc, neutrino mass loss during BH formation is allowed to change in the range Floss = 1 − 20%, and the efficiency of conversion of orbital energy into the ejection of the stellar envelope during the CE evolution in the range α = 0.5 − 5. We tested the combination for all the initial conditions described in Table 1 to see if any of the retrieved BH-MS fits is similar to the reported HR 6819 configuration. To do so, we compute the Euclidean distance in the multi-dimesional space MBH, MMS, e and per by taking the HR 6819 observational constraints into account (BH mass 4.2 − 6 M⊙, B star companion 5 − 7 M⊙, orbital period 30 − 50 days5, eccentricity 0.02 − 0.04). This distance was calculated as the modulus of the normalised difference vector [ΔMBH, ΔMcomp, Δper, Δe] between the simulated BH-MS binary and the reported HR 6819 parameters. The components of the aforementioned vector are equal to 0 if they are within their respective observational ranges. Otherwise, we took the absolute difference between the simulated parameter and the closest extreme in the observed range and divided it by the range of the observed quantity (1.8 M⊙ for the BH mass, 2 M⊙ for the companion mass, 20 days for the orbital period and 0.02 for the orbital eccentricity). For example, if MBH were 5 M⊙, then ΔMBH would be 0 because MBH is between 4.2 and 6 M⊙; if it were instead 3 M⊙, it would be closer to 4.2 M⊙ (the observed minimum) rather than 6 M⊙ (the observed maximum) and therefore ΔMBH = |3–4.2|/1.8 ∼ 0.7, while if it were 13 M⊙, then ΔMBH = |13–6|/1.8 ∼ 3.9. In the following equations this procedure is explicitly shown:
The Euclidean distance from HR 6819 for a specific system will therefore be
Out of the 336000 tested binaries with different initial conditions, the Euclidean distance to HR 6819 of the ones that form a BH-MS binary at any point in their life and that have at least one of the four parameters within Rivinius et al. (2020) observational ranges are plotted in Fig. 1. This difference can go up to 1.2 × 106. For the sake of an understandable visualisation only the ones within a Euclidean difference of 15 are shown in the histogram.
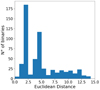 |
Fig. 1. Histogram of the Euclidean distance distribution between the test binaries and the HR 6819 observational constraints with D < 15. Only two binaries have D = 0. |
Among them, only two have D = 0. They both have ZAMS masses of 24 M⊙ (primary) and 7 M⊙, Z = 0.0105, α = 5 (as already used in other population studies, e.g., Santoliquido et al. 2020). One has Floss = 7%, and the other Floss = 6%.
Such a high CE efficiency does not imply energy that conservation has been violated, but rather that external energy sources that are not implemented in StarTrack contribute to the energy balance. This can be explained as a contribution of the recombination energy of the envelope, which was shown to account for a fraction of the binding energy (Kruckow et al. 2016; Fragos et al. 2019). It can also be due to a different prescription for the core–envelope boundary of the star just prior to the CE phase. The CE λ prescription in StarTrack comes from the so-called Nanjing λ procedure (Dominik et al. 2012), which comes from the Xu & Li (2010) models. For evolutionary stages beyond the MS, these models are based on the assumption that the core–envelope boundary is located deep down in the star at the point where the hydrogen mass fraction, XH, falls below 0.15 (the fits from Hurley et al. (2000) are instead based on the detailed simulations from Pols et al. (1998), where the boundary is set at XH = 0.1). Instead, if the envelope were in reality on a shallower position, as suggested by Fragos et al. (2019) and Marchant et al. (2021) (XH = 0.3), it would mean that the StarTrackλ factor in the CE prescription has been underestimated. If the λ prescription is kept fixed from the Nanjing λ models, this underestimation can be replicated by setting α > 1.
We chose the initial setup with Floss = 7% for our population study. We evolved N = 107 massive binaries, in which the primary mass (the initially more massive binary component) is taken from the initial mass function three-part broken power law within a mass range of 18 − 150 M⊙. The secondary component mass was instead taken from a flat distribution of mass ratio (secondary to primary) within the mass range 0.08 − 150 M⊙. The orbital period was taken from de Mink & Belczynski (2015). We then scaled the total mass from our simulations to account for the whole 0.08 − 150 M⊙ mass range for the primary stars by extending the initial mass function power law to primary stars between 0.08 and 18 M⊙ at ZAMS (the secondary star mass is still taken from the flat distribution of mass ratio).
We can now select BH-MS binaries that resemble the reported inner binary in HR 6819. For this purpose we adopted the same Euclidean distance method that was described in Sect. 3.1. In our simulations we find no binary (D = 0) resembling the reported parameters of the HR 6819 inner binary.
3.2. Calibration to the Milky Way
In our simulations we retrieved a number of BH-MS binaries equal to 2.4 × 106 and a total simulated ZAMS mass of 5.9 × 106 M⊙. We then extrapolated our results to correspond to the entire Milky Way disc (isolated binary evolution). The disc mass was estimated by Licquia & Newman (2015) to be 5.17 ± 1.11 × 1010 M⊙. We therefore adopted a star formation rate of ∼5 M⊙ yr−1 and assumed that it has been constant in the disc over the last 10 Gyr. We needed to scale up (multiply) our results with the factor
where Mdisc = 5 × 1010 M⊙ is the total stellar mass of the Milky Way disc and, after being scaled to take into account the whole 0.08 − 150 M⊙ mass range for primary stars, Msim ∼ 4.2 × 109 M⊙ is the total simulated stellar mass in the case of 100% binarity, and Msim ∼ 6.9 × 109 M⊙ in the case of 50% binarity (i.e. two out of three stars in binary systems).
The above calibration results in a total number of BH-MS binaries that were formed in the Galactic disc over 10 Gyr: 2.9 × 107 for 100% binarity and 1.8 × 107 for 50% binarity. Now we can distribute all BH-MS binaries uniformly over 10 Gyr of disc evolution, and, knowing (from population synthesis calculation) each system BH-MS lifetime, we can estimate the current number of BH-MS binaries present in the Galactic disc: 427464 for 100% binarity and 249134 for 50% binarity. Neither of the two binarity cases shows any BH-MS system matching the reported HR 6819 configuration, which is expected since none of the evolved BH-MS binaries in our simulated population fit the observational constraints in the first place. As a reference for potential studies to test the reliability of our results, we also show in Fig. 2 a corner plot that includes the correlations between BH mass, MS companion mass, orbital period (within ∼28 × 103 years for better visualisation) and orbital eccentricity for the generated binaries at 100% binarity, along with their distribution. Fig. 3 illustrates the current Galactic population of BH-MS binaries for 100% binarity and their Euclidean distances from the reported HR 6819 binary parameters. For the sake of easy visualisation only the binaries at D < 15 are shown in the histogram.
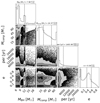 |
Fig. 2. Corner plot of the correlations and predicted distributions of Galactic disc BH-MS binaries at 100% binarity in terms of BH mass, MS companion mass, orbital period (within ∼28 × 103 years for better visualisation) and orbital eccentricity. The vertical dashed lines in the histograms show the 0.16, 0.5 and 0.84 quantiles for each parameter. |
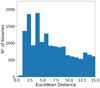 |
Fig. 3. Current predicted population of Galactic disc BH-MS binaries and their Euclidean distance (in terms of orbital parameters) for 100% binarity from the reported parameters of the HR 6819 inner binary (Rivinius et al. 2020). No BH-MS binary out of 427464 binaries resembles the HR 6819 inner binary to the point of having a Euclidean distance = 0. |
3.3. Statistical significance of the formation of the HR 6819 inner binary
Although we can find an evolutionary solution for the formation of the reported HR 6819 inner binary here we show that it is highly unlikely that such a binary would be expected in the current population of observed Galactic BH binaries. As pointed out in Sect. 3.2 we predicted up to 427464 ≈ 4 × 105 BH-MS binaries currently present in the Galactic disc, with none resembling the reported HR 6819 inner binary. Additionally, our estimate is done for very optimistic evolutionary assumptions on isolated binary evolution. We conclude that finding a binary similar to the reported inner HR 6819 binary in the current sample of Galactic BH systems is not expected.
Despite the fact that we do not consider it likely that such a system would form in the Galactic disc, in Appendix A we describe for completeness how such a system could have possibly formed and evolved in the framework of the isolated binary evolution.
4. Globular cluster evolution
After performing all 120 GC simulations we find the formation of 89817 BH-MS binaries. We find no BH-MS binary resembling the reported inner HR 6819 binary. The best candidate has a BH mass of 4.5 M⊙, a companion MS star with mass of 6.7 M⊙, an orbital period of 27.5 days (a = 120 R⊙), and an eccentricity of e = 0.014. The GC estimate ends here. We conclude that according to our models Galactic GCs do not form binaries resembling the reported inner binary of HR 6819. However, for consistency with the binary evolution estimate, we proceeded with an estimate of the current GC population of BH-MS binaries.
We calibrated and extrapolated our results to represent the entire population of Milky Way clusters. The current total mass of the Milky Way GCs is based on GC mass estimates from Baumgardt (2017)6 and equal to 3.7 × 107 M⊙. Mass loss of the star clusters through the Hubble time depends on many factors (e.g., Meiron et al. 2021). For the sake of simplicity, we assumed that half of the star mass of clusters was lost in their evolution. Thus, we arrive at an initial mass for Milky Way GCs of 7.4 × 107 M⊙. On the other hand the stellar mass included in our 120 GC simulation was 8.1 × 107 M⊙. Therefore the multiplication factor to our results is
This gives us 8.2 × 104 BH-MS binaries formed by GCs in the Milky Way. However, only a fraction of them will survive until the present time, as GCs are old and most BH-MS stars that formed long ago are already gone or are no longer BH-MS binaries.
Star formation in the GCs was taking place at large redshifts, z > 2 (Katz & Ricotti 2013). We, conservatively (in the context of survival of BH-MS binaries with rather massive MS stars), assumed that all stars in Galactic GCs formed at z = 2, so t ∼ 10 Gyr ago. Since we know BH-MS lifetimes from our GC simulations, we can remove BH-MS binaries that do not survive to the present time. The corner plot in Fig. 4 shows the correlation between the current BH mass (within 20 M⊙ for better visualisation), MS companion mass, orbital period (within ∼28 × 103 years) and orbital eccentricity in Galactic GCs. On the contrary, in the case of field binaries, the BH masses, the MS companion masses, and the orbital eccentricity are mainly localised within specific margins.
 |
Fig. 4. Corner plot of the correlations and predicted distributions of Galactic GC BH-MS binaries in terms of BH mass, MS companion mass, orbital period, and orbital eccentricity. The vertical dashed lines in the histograms show the 0.16, 0.5, and 0.84 quantiles for each parameter. |
In Fig. 5 we show the current population of GC BH-MS binaries. We see that there is no system resembling the reported HR 6819 inner binary (D = 0) and that there are very few systems with low Euclidean distance in orbital parameters from HR 6819. The main reason why it is hard to find dynamical candidates for the HR 6819 system in GCs comes from the fact that possible candidates can be found only at the very beginning of the star cluster evolution. Stars as massive as the companion to a BH (> 5 M⊙) only live for very short time (≲150 Myr) and cannot contribute to the current GC (old) stellar populations. Even if a GC produced an HR 6819-like system, such a binary would be long gone. Thus, dynamical origin for a potential HR 6819-like system is highly unlikely.
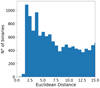 |
Fig. 5. Current predicted population of Galactic GC BH-MS binaries and their Euclidean difference (in terms of orbital parameters) from the reported parameters of the HR 6819 inner binary (Rivinius et al. 2020). |
5. Selection effects
We analysed if the HR 6819 inner binary, despite its extremely low likelihood of arising through both isolated and dynamical binary evolution, could be more easily detected than other BH-MS binaries and therefore somehow compensate for the low formation probability.
So far, 69 electromagnetic BH binaries have been detected (from the BlackCAT catalogue7: Corral-Santana et al. 2016), which is not yet a large enough sample from which to start statistical considerations. The problem becomes even more severe if we consider the BH discovery method. The majority of BH binaries are discovered through X-ray observations. Only five (plus the recent system in NGC 1850; Saracino et al. 2021) have been discovered via RV measurements of the optical companion, which is the same method by which the HR 6819 BH was hypothesised to be found. On top of that, we cannot even be sure that NGC 1850 hosts a dormant BH, since El-Badry & Burdge (2022) suggest that NGC 1850-BH1 is likely a stripped star and not a compact object. The first obvious conclusion here is that observations are more biased towards X-ray binaries than systems with dormant BHs, which therefore reduces the likelihood of HR-like systems being detected. In Table 2 we show the RV semi-amplitudes K1 for all the (hypothesised or confirmed) observed dormant BH-MS binaries. This was done to check whether HR 6819 has a considerably higher K1 that could compensate for an extremely low formation probability for isolated and dynamical binary evolution.
RV semi-amplitudes for the observed BH-MS binaries.
We also analysed the RV semi-amplitudes from our predicted current population of BH-MS binaries in the Galactic disc. Figure 6 shows the K1 distribution for such binaries and the position of the HR 6819 inner binary.
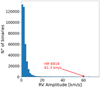 |
Fig. 6. Current predicted RV semi-amplitudes for dormant BHs in the Galactic disc, with the observed HR 6819 K1 at 61.3 km s−1. For the sake of easy visualisation the plot has been kept within semi-amplitudes of 80 km s−1. |
All the observed dormant BH-MS binaries (be they confirmed or not) have a higher amplitude when compared with the average predicted distribution in the Galactic disc, which is understandable since they are therefore more likely to be detected with a high K1. To be more precise, 93% of the binaries in our sample have a semi-amplitude below 60 km/s (roughly the semi-amplitude of HR 6819). Additionally, there was already admittedly an initial selection effect from the observations since HR 6819, among all the systems, was selected due to its line emission being similar to the one from LB-1 (Rivinius et al. 2020), which is another system claimed to be a hierarchical triple system with a dormant BH in its inner binary (Liu et al. 2019; El-Badry & Quataert 2021). This shows that there are indeed some selection effects that can contribute to increasing the detectability of HR-like systems, thought there are also some that would decrease it.
6. Conclusion
For the two major Galactic BH-MS formation channels, we adopted evolutionary physics that increases the possibility of formation of a system resembling the parameters of the HR 6819 inner binary reported by Rivinius et al. (2020). We tested several different types of initial input physics to retrieve the one that can maximise the possibility of an HR-like binary existing and therefore being detected. The evolution of stars in Galactic GCs does not allow for any avenues for creating such binaries. The Galactic disc also is a highly unlikely site for the formation of such binaries via isolated evolution.
We conclude that, even if a dormant BH existed in a triple system in a configuration similar to what has been proposed by Rivinius et al. (2020), its existence would be hard to explain with our models based on isolated and dynamical binary evolution. We nevertheless acknowledge that, despite the extremely low formation probability in our evolutionary channels, selection effects (both positive and negative) could alter the likelihood of such a system being detected.
We set an arbitrary confidence range of 10 days around the observed value, despite this not corresponding to the actual margin of error (0.004 days) reported by Rivinius et al. (2020).
Acknowledgments
A.R., A.O., A.H. and K.B. acknowledge support from the Polish National Science Center (NCN) grant Maestro (2018/30/A/ST9/00050). AH was also supported partially by Polish National Science Center grant 2016/23/B/ST9/02732.
References
- Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2016, Phys. Rev. X, 6, 041015 [Google Scholar]
- Bambi, C. 2018, Ann. Phys., 530, 1700430 [NASA ADS] [CrossRef] [Google Scholar]
- Baumgardt, H. 2017, MNRAS, 464, 2174 [Google Scholar]
- Belczynski, K., Kalogera, V., & Bulik, T. 2002, ApJ, 572, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Belczynski, K., Kalogera, V., Rasio, F. A., et al. 2008, ApJS, 174, 223 [Google Scholar]
- Belczynski, K., Klencki, J., Fields, C. E., et al. 2020, A&A, 636, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bodensteiner, J., Shenar, T., Mahy, L., et al. 2020, A&A, 641, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casares, J. 2007, in Black Holes from Stars to Galaxies - Across the Range of Masses, eds. V. Karas, & G. Matt, IAU Symp., 238, 3 [NASA ADS] [Google Scholar]
- Casares, J., & Jonker, P. G. 2014, Space Sci. Rev., 183, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Casares, J., Negueruela, I., Ribó, M., et al. 2014, Nature, 505, 378 [Google Scholar]
- Corral-Santana, J. M., Casares, J., Muñoz-Darias, T., et al. 2016, A&A, 587, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Mink, S. E., & Belczynski, K. 2015, ApJ, 814, 58 [Google Scholar]
- Dominik, M., Belczynski, K., Fryer, C., et al. 2012, ApJ, 759, 52 [Google Scholar]
- Ekström, S., Georgy, C., Eggenberger, P., et al. 2012, A&A, 537, A146 [Google Scholar]
- El-Badry, K., & Burdge, K. B. 2022, MNRAS, 511, 24 [NASA ADS] [CrossRef] [Google Scholar]
- El-Badry, K., & Quataert, E. 2021, MNRAS, 502, 3 [Google Scholar]
- Fragos, T., Andrews, J. J., Ramirez-Ruiz, E., et al. 2019, ApJ, 883, L45 [Google Scholar]
- Fregeau, J. M., Cheung, P., Portegies Zwart, S. F., & Rasio, F. A. 2004, MNRAS, 352, 1 [CrossRef] [Google Scholar]
- Giersz, M. 1998, MNRAS, 298, 1239 [NASA ADS] [CrossRef] [Google Scholar]
- Giersz, M., Leigh, N., Marks, M., Hypki, A., & Askar, A. 2014, ArXiv e-prints [arXiv:1411.7603] [Google Scholar]
- Hawking, S. W. 1974, Nature, 248, 30 [CrossRef] [Google Scholar]
- Heber, U. 2009, ARA&A, 47, 211 [Google Scholar]
- Hohle, M. M., Neuhäuser, R., & Schutz, B. F. 2010, Astron. Nachr., 331, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Hong, J., Askar, A., Giersz, M., Hypki, A., & Yoon, S.-J. 2020, MNRAS, 498, 4287 [NASA ADS] [CrossRef] [Google Scholar]
- Hurley, J. R., Pols, O. R., & Tout, C. A. 2000, MNRAS, 315, 543 [Google Scholar]
- Hurley, J. R., Tout, C. A., & Pols, O. R. 2002, MNRAS, 329, 897 [Google Scholar]
- Hurley, J. R., Pols, O. R., & Tout, C. A. 2013, {SSE: SingleStar Evolution}, Astrophysics Source Code Library [record ascl:1303.015] [Google Scholar]
- Hypki, A., & Giersz, M. 2013, MNRAS, 429, 1221 [NASA ADS] [CrossRef] [Google Scholar]
- Katz, H., & Ricotti, M. 2013, MNRAS, 432, 3250 [Google Scholar]
- Khokhlov, S. A., Miroshnichenko, A. S., Zharikov, S. V., et al. 2018, ApJ, 856, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Kozai, Y. 1962, AJ, 67, 591 [Google Scholar]
- Kruckow, M. U., Tauris, T. M., Langer, N., et al. 2016, A&A, 596, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Licquia, T. C., & Newman, J. A. 2015, ApJ, 806, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Lidov, M. L. 1962, Planet Space Sci., 9, 719 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, J., Zhang, H., Howard, A. W., et al. 2019, Nature, 575, 618 [Google Scholar]
- Marchant, P., Pappas, K. M. W., Gallegos-Garcia, M., et al. 2021, A&A, 650, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mazeh, T., & Faigler, S. 2020, MNRAS, 498, L58 [NASA ADS] [CrossRef] [Google Scholar]
- Meiron, Y., Webb, J. J., Hong, J., et al. 2021, MNRAS, 503, 3000 [NASA ADS] [CrossRef] [Google Scholar]
- Naoz, S. 2016, ARA&A, 54, 441 [Google Scholar]
- Olejak, A., Belczynski, K., Bulik, T., & Sobolewska, M. 2020a, A&A, 638, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Olejak, A., Fishbach, M., Belczynski, K., et al. 2020b, ApJ, 901, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Patton, R. A., & Sukhbold, T. 2020, MNRAS, 499, 2803 [NASA ADS] [CrossRef] [Google Scholar]
- Pols, O. R., Schröder, K.-P., Hurley, J. R., Tout, C. A., & Eggleton, P. P. 1998, MNRAS, 298, 525 [Google Scholar]
- Rivinius, T., Baade, D., Hadrava, P., Heida, M., & Klement, R. 2020, A&A, 637, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Safarzadeh, M., Toonen, S., & Loeb, A. 2020, ApJ, 897, L29 [CrossRef] [Google Scholar]
- Santoliquido, F., Mapelli, M., Bouffanais, Y., et al. 2020, ApJ, 898, 152 [Google Scholar]
- Saracino, S., Kamann, S., Guarcello, M. G., et al. 2021, MNRAS, 511, 2914 [Google Scholar]
- Stevance, H. F., Parsons, S. G., & Eldridge, J. J. 2022, MNRAS, 511, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Sukhbold, T., Ertl, T., Woosley, S. E., Brown, J. M., & Janka, H.-T. 2016, ApJ, 821, 38 [Google Scholar]
- Thompson, T. A., Kochanek, C. S., Stanek, K. Z., et al. 2019, Science, 366, 637 [NASA ADS] [CrossRef] [Google Scholar]
- Tsuna, D., Kawanaka, N., & Totani, T. 2018, MNRAS, 477, 791 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, L., Spurzem, R., Aarseth, S., et al. 2016, MNRAS, 458, 1450 [Google Scholar]
- Wiktorowicz, G., Wyrzykowski, Ł., Chruslinska, M., et al. 2019, ApJ, 885, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Wiktorowicz, G., Middleton, M., Khan, N., et al. 2021, MNRAS, 507, 374 [NASA ADS] [CrossRef] [Google Scholar]
- Wyrzykowski, Ł., Kostrzewa-Rutkowska, Z., Skowron, J., et al. 2016, MNRAS, 458, 3012 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, X.-J., & Li, X.-D. 2010, ApJ, 716, 114 [Google Scholar]
- Zapartas, E., de Mink, S. E., Justham, S., et al. 2019, A&A, 631, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Example of formation of HR 6819 inner binary in the framework of the isolated binary evolution
Here we present an example of one evolutionary scenario in the isolated binary evolution framework (Fig. A.1) that we find leads to the formation of a binary that matches the observational constraints from Rivinius et al. (2020). Initially the system consists, at ZAMS, of two stars with masses of 24.0 M⊙ and 7 M⊙. All the input physics corresponds to our population synthesis.
 |
Fig. A.1. Formation of a system resembling the reported HR 6819 inner binary in the isolated binary evolution framework. It starts with two massive stars at metallicity Z = 0.0105. While the companion star remains in its MS, the more massive star initiates a CE phase after ∼8.2 Myr and shortly after it collapses into a BH. |
At the beginning the two stars are on a very wide, circular orbit (period ∼2.6 × 103 days, e = 0.0). At 8 Myr, the primary evolves off its MS, expands and evolves into a core-helium-burning giant. It initiates a CE phase, after which the orbital period is reduced to about 30 days and the giant star loses its envelope. We then assume a direct collapse of the primary star into a BH. Due to the neutrino emission, the eccentricity of the system slightly increases to e = 0.035. We note the formation of a BH-MS binary. The evolution of the orbital period and eccentricity of this binary is shown in Fig. A.2. During the whole BH-MS phase (between ∼10 − 50 Myr after system formation), the orbital period is ∼36 d, which is close to the reported value of 40.3 d. The eccentricity during the BH-MS phase, e = 0.035, is in the observed [0.02; 0.04] range.
 |
Fig. A.2. Evolution of the binary period (blue) and eccentricity (purple) of the binary that forms a reported HR 6819 inner-binary-like system in the isolated binary evolution framework. The CE phase (red) takes place at ∼8.2 Myr and was initiated by the primary star, which collapses shortly thereafter into a BH. A BH-MS system (similar to HR 6819) phase is noted for ∼40 Myr (∼10 − 50 Myr after ZAMS). We also show the evolution of this binary beyond the BH-MS phase with two stable RLOF events (at ∼49 Myr and ∼61 Myr since ZAMS) initiated by an expanding secondary. |
The mass evolution of both components of this binary is shown in Fig. A.3. During the BH-MS phase, the BH mass is 6.1 M⊙ and its MS companion’s mass is 7.0 M⊙. Both masses are within the range of observational estimates from Rivinius et al. (2020). During the BH-MS phase, the difference in mass between the BH and its companion is ΔM = 0.9 M⊙, which is consistent with the estimated value ΔM ∼ 1 M⊙ for HR 6819.
 |
Fig. A.3. Evolution of mass of the two components of the binary that forms reported HR 6819 inner-binary-like system in the isolated binary evolution framework. The primary (green line) loses most of its mass during the CE phase (red line) and collapses into a BH at 8.6 Myr after ZAMS. The secondary star (blue line) remains in its MS with almost constant mass for 50 Myr. Then it loses most of its mass during two stable RLOF events (grey lines). |
In Fig. A.4 we show the temporal evolution of the radii of the two components for this binary in comparison with their Roche lobe radii. We note that during the BH-MS stage (the time between 8.6 and 49.8 Myr) there is no Roche lobe overflow (RLOF) event and that the wind mass loss from the secondary star (Ṁ < 10−7 M⊙ yr−1) is too weak to produce any significant X-ray emission at the orbital separation found for this system (a ∼108 R⊙) during this stage. The BH in our example is thus dormant and in agreement with the observational data.
 |
Fig. A.4. Radial evolution of the two components of the binary that forms a reported HR 6819 inner-binary-like system in the isolated binary evolution framework. After the formation of a BH, the secondary is well within its Roche lobe during its entire MS lifetime (< 50 Myr). |
In Figs. A.2, A.3, and A.4 we also include predictions for the future evolution of this binary system. During the whole BH-MS phase, parameters of this binary remain almost unchanged, the only exception being the radius of the secondary star, which increases from ∼3 R⊙ to ∼6 R⊙ as it evolves through its MS. The secondary leaves the MS at ∼50 Myr and begins a rapid expansion that eventually leads to a RLOF phase. The system then enters a stable mass transfer phase that lasts for ∼0.1 Myr. After the secondary loses its H-rich envelope (the BH does not accrete any significant amount of mass as accretion proceeds on a fast thermal timescale), it becomes a naked He star with a mass of 1.37 M⊙. The RLOF and associated mass and angular momentum loss from the binary leads to significant orbital expansion to an orbital period of ∼103 days (a ∼2.3 × 104 R⊙) and the orbit becomes circularised. The low-mass helium star then undergoes expansion during shell He-burning and initiates a second stable RLOF at ∼61 Myr since ZAMS. The loss of angular momentum again expands the orbit to an orbital period of 1279 days (∼2.1 × 105 R⊙). By the end of both RLOF episodes the secondary star has lost more than 80% of its mass and has cooled to become a carbon-oxygen white dwarf. We note the formation of a wide (coalescence time much larger than Hubble time) BH-white dwarf binary.
All Tables
All Figures
 |
Fig. 1. Histogram of the Euclidean distance distribution between the test binaries and the HR 6819 observational constraints with D < 15. Only two binaries have D = 0. |
| In the text | |
 |
Fig. 2. Corner plot of the correlations and predicted distributions of Galactic disc BH-MS binaries at 100% binarity in terms of BH mass, MS companion mass, orbital period (within ∼28 × 103 years for better visualisation) and orbital eccentricity. The vertical dashed lines in the histograms show the 0.16, 0.5 and 0.84 quantiles for each parameter. |
| In the text | |
 |
Fig. 3. Current predicted population of Galactic disc BH-MS binaries and their Euclidean distance (in terms of orbital parameters) for 100% binarity from the reported parameters of the HR 6819 inner binary (Rivinius et al. 2020). No BH-MS binary out of 427464 binaries resembles the HR 6819 inner binary to the point of having a Euclidean distance = 0. |
| In the text | |
 |
Fig. 4. Corner plot of the correlations and predicted distributions of Galactic GC BH-MS binaries in terms of BH mass, MS companion mass, orbital period, and orbital eccentricity. The vertical dashed lines in the histograms show the 0.16, 0.5, and 0.84 quantiles for each parameter. |
| In the text | |
 |
Fig. 5. Current predicted population of Galactic GC BH-MS binaries and their Euclidean difference (in terms of orbital parameters) from the reported parameters of the HR 6819 inner binary (Rivinius et al. 2020). |
| In the text | |
 |
Fig. 6. Current predicted RV semi-amplitudes for dormant BHs in the Galactic disc, with the observed HR 6819 K1 at 61.3 km s−1. For the sake of easy visualisation the plot has been kept within semi-amplitudes of 80 km s−1. |
| In the text | |
 |
Fig. A.1. Formation of a system resembling the reported HR 6819 inner binary in the isolated binary evolution framework. It starts with two massive stars at metallicity Z = 0.0105. While the companion star remains in its MS, the more massive star initiates a CE phase after ∼8.2 Myr and shortly after it collapses into a BH. |
| In the text | |
 |
Fig. A.2. Evolution of the binary period (blue) and eccentricity (purple) of the binary that forms a reported HR 6819 inner-binary-like system in the isolated binary evolution framework. The CE phase (red) takes place at ∼8.2 Myr and was initiated by the primary star, which collapses shortly thereafter into a BH. A BH-MS system (similar to HR 6819) phase is noted for ∼40 Myr (∼10 − 50 Myr after ZAMS). We also show the evolution of this binary beyond the BH-MS phase with two stable RLOF events (at ∼49 Myr and ∼61 Myr since ZAMS) initiated by an expanding secondary. |
| In the text | |
 |
Fig. A.3. Evolution of mass of the two components of the binary that forms reported HR 6819 inner-binary-like system in the isolated binary evolution framework. The primary (green line) loses most of its mass during the CE phase (red line) and collapses into a BH at 8.6 Myr after ZAMS. The secondary star (blue line) remains in its MS with almost constant mass for 50 Myr. Then it loses most of its mass during two stable RLOF events (grey lines). |
| In the text | |
 |
Fig. A.4. Radial evolution of the two components of the binary that forms a reported HR 6819 inner-binary-like system in the isolated binary evolution framework. After the formation of a BH, the secondary is well within its Roche lobe during its entire MS lifetime (< 50 Myr). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} \Delta M_{\rm comp}&= {\left\{ \begin{array}{ll} 0&\text{ if } 5 < M_{\rm comp}< 7\\ \min [|M_{\rm comp}-5|; |M_{\rm comp}-7|]/2,&\text{ otherwise}\end{array}\right.} \end{aligned} $$](/articles/aa/full_html/2022/11/aa41992-21/aa41992-21-eq1.gif)
![$$ \begin{aligned} \Delta M_{\rm BH}&= {\left\{ \begin{array}{ll} 0&\text{ if } 4.2 < M_{\rm BH}< 6\\ \min [|M_{\rm BH}-4.2|; |M_{\rm BH}-6|]/1.8,&\text{ otherwise}\end{array}\right.} \end{aligned} $$](/articles/aa/full_html/2022/11/aa41992-21/aa41992-21-eq2.gif)
![$$ \begin{aligned} \Delta per&= {\left\{ \begin{array}{ll} 0&\text{ if } 30 < per< 50\\ \min [|per-30|; |per-50|]/20,&\text{ otherwise}\end{array}\right.} \end{aligned} $$](/articles/aa/full_html/2022/11/aa41992-21/aa41992-21-eq3.gif)
![$$ \begin{aligned} \Delta e&= {\left\{ \begin{array}{ll} 0&\text{ if } 0.02 < e< 0.04\\ \min [|e-0.02|; |e-0.04|]/0.02,&\text{ otherwise}\end{array}\right.}. \end{aligned} $$](/articles/aa/full_html/2022/11/aa41992-21/aa41992-21-eq4.gif)