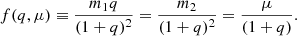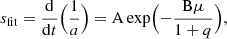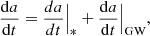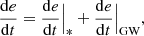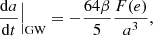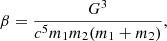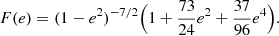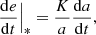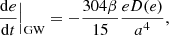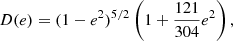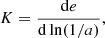EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 665 (September 2022) A&A, 665 (2022) A86 Full HTML
Open Access
Issue
A&A
Volume 665, September 2022
Article Number A86
Number of page(s) 7
Section Astrophysical processes
DOI https://doi.org/10.1051/0004-6361/202244354
Published online 13 September 2022

© P. Berczik et al. 2022

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.

1. Introduction

According to the hierarchical structure formation scenario in the Λ cold dark matter (ΛCDM) paradigm, bright massive galaxies are supposed to form through mergers and the accretion of smaller galaxies. Supermassive black holes (SMBHs) are commonly observed at the centres of most galaxies, and their mass correlates to several properties of their host galaxy, such as bulge mass (Ho & Kim 2014) or central velocity dispersion (see e.g., Gültekin et al. 2009). Therefore, if the majority of galaxies harbour an SMBH in their centres, SMBH binaries (SMBHBs) should represent an unavoidable outcome of the hierarchical formation scenario (Begelman et al. 1980).

Several examples of resolved SMBHBs with a separation of less than 1 kpc are known. The tightest resolved binary is settled in galaxy 0402+379 and was identified via radio observations achieved with the Very Long Baseline Interferometer (VLBI; Rodriguez et al. 2006; Bansal et al. 2017). It contains an SMBH pair candidate with a total mass ∼108 M⊙ and a separation of 7.3 pc. The most reliable and intensively observed SMBHB candidate was placed in a nearby ultraluminous infrared galaxy NGC 6240 (Komossa et al. 2003). Two components (South and North) were resolved in X-ray at a separation of 750 pc. High-resolved observations with the MUSE instrument revealed the possibility of the third smallest component presence at south nuclei (Kollatschny et al. 2020; for the discussion, see Fabbiano et al. 2020). Using the MBH − σ relation, BHs with masses of 3.6 ± 0.8 × 108 M⊙, 7.1 ± 0.8 × 108 M⊙, and 9.0 ± 0.7 × 107 M⊙ were obtained for North, South 1, and South 2 components, respectively. The recent optically and spectroscopically resolved binary in galaxy NGC 7727 has a separation of 500 pc and BH masses of 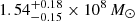1 . 54 − 0.15 + 0.18 × 10 8 M ⊙ $ 1.54^{+0.18}_{-0.15}\times10^{8}\,M_{\odot} $ and 6 . 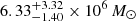33 − 1.40 + 3.32 × 10 6 M ⊙ $ 6.33^{+3.32}_{-1.40}\times10^{6}\,M_{\odot} $ (Voggel et al. 2022). The OJ287 is an SMBHB candidate detected via quasi-periodic outbursts for which it has been possible to model the binary separation (∼0.05 pc), eccentricity (∼0.6), and spin (modelled taking even the spin-orbit interaction into account, see Valtonen 2007; Valtonen et al. 2010a,b).

The relativistic in-spiral and final coalescence are driven by gravitational wave (GW) emission, making SMBHBs among the strongest sources to be measured with future GW space satellite missions, such as the Laser Interferometer Space Antenna (LISA; Gong et al. 2011; Amaro-Seoane et al. 2013, 2017), or the TianQin (Luo et al. 2016), Taiji (Ruan et al. 2020), or μAres (Sesana et al. 2021) space detectors. It is therefore of paramount importance to understand the astrophysical processes that drive SMBHBs from the unbound, pre-merger state, into the relativistic regime and their associated efficiency. This information can be used to place robust, and physically motivated, constraints on the merger rate of these GW sources and provide a test bed for GW signal templates to be compared with future observations.

However, the large number of existing works focussed on full numerical simulations of SMBHs pairing and evolution have not fully covered all the important parameters’ space yet. In particular, within the hierarchical galaxy formation scenario, the range of mass ratios in galaxy mergers can hugely vary from 1:1 (major mergers) to 1:3, down to minor mergers, that is with mass ratios even below 1:10 (cf. e.g., Naab et al. 2006, 2009). Given the correlations between galaxies and SMBHs masses, it is thus expected that also SMBHBs should form with a wide range of mass ratios. However, the majority of numerical studies based on N-body models have mostly focussed on nearly equal mass binaries. Moreover, the galactic nucleus produced in a galaxy merger event is expected to preserve a non-negligible rotation due to the global angular momentum conservation. The collective motion of stars affected by the rotation of the galactic nucleus can have a non-trivial effect on the SMBHB evolution. In this paper, we expand the simulations presented in Berczik et al. (2006) and Wang et al. (2014) by exploring a wider range of mass ratios, 0.01 − 1, and by also taking the rotating nuclei into account.

Furthermore, the new simulations are based on our improved φ-GPU N-body code (Berczik et al. 2013b; Sobolenko et al. 2021), which implements general relativity effects in the form of post-Newtonian corrections to the equations of motion (Sobolenko et al. 2017; Khan et al. 2016). This will enable us to follow the SMBH binary evolution as a result of the simultaneous action of stellar hardening and GW emission all the way to final coalescence and allow us to model the GW signal during the final inspiral (Khan et al. 2018, 2013; Sobolenko et al. 2017).

The paper is structured as follows. In Sect. 2 we describe the initial conditions adopted in our N-body simulations; in Sect. 3 we describe how the modelled SMBHB hardening rate varies across the parameter space explored; and in Sect. 4 we summarize and discuss the main conclusions of our paper.

2. Units and initial conditions

We analysed a suite of 68 N-body simulations comprised of N = 25k, 50k, 100k, 200k, 400k, 1M particles, modelling the evolution of an SMBHB embedded in a rotating galactic nucleus, so as to reproduce the typical environment of the inner regions of a post-merged galaxy. Details about these simulations are provided in Berczik et al. (2006), Berentzen et al. (2009), and Wang et al. (2014). In this work, we focus on the shrinking of the SMBHB as it interacts with surrounding stars. Because the small N runs (namely 25k and 50k) have a larger uncertainty in the hardening results, we exclude them from the discussion of the further results. We can briefly summarize the main features of our models as follows.

The simulations presented in this work have been carried out using the direct N-body φ-GPU code. Our N-body package uses a high order Hermite integration scheme and individual block time steps (the code supports time integration of particle orbits with fourth, sixth, and even eighth order schemes). We refer the more interested readers to a general discussion about different N-body codes and their implementation in Berczik et al. (2011); Berczik et al. (2013a). The φ-GPU code is fully parallelized using the MPI library. This code has been newly rewritten in C++ and based on the earlier CPU serial N-body code (YEBISU; Nitadori & Makino 2008). The MPI parallelization was done in the same ‘j’ particle parallelization mode as in the earlier φ-GRAPE code (Harfst et al. 2007).

The current version of the φ-GPU1 code uses native GPU support and direct code access to the GPU using the NVIDIA native CUDA library. The code is designed to use different softening parameters for the gravity calculation (if it is required) for different astrophysical components in our simulations, such as SMBHs, dark matter, or stars particles. More details about the public version of the φ-GPU code and its performance are presented in Berczik et al. (2011); Berczik et al. (2013a). The present code has been thoroughly tested and has already been used to obtain important results in our earlier large-scale (up to a few million body) simulations (Khan et al. 2018; Zhong et al. 2014; Li et al. 2012; Just et al. 2012).

All simulations are initially scaled by applying the standard strategy for N-body normalization2 (Aarseth et al. 1974), according to which both the gravitational constant and the total mass of the stellar systems are set to unity, G = M = 1, and the total energy of the system is set to E = −1/4. The galactic nucleus initially follows a rotating King distribution function (see, e.g., Einsel & Spurzem 1999, and references therein). We set the dimensionless potential well (King parameter) and rotation parameters to W0 = 6 and ω0 = 1.8, respectively, in all of our models. At the centre of the nucleus, we placed two SMBHs initially unbound with a primary mass m1 = (1 − 4)×10−2 times the nucleus mass and the mass ratio q = 10−4 − 1. The corresponding range of reduced mass adopted is thus μ ≡ m1m2/(m1 + m2) = 9.9 × 10−3 − 2. The total angular momentum vector of both the stellar nucleus and the SMBHs are aligned with the z axis of our coordinate frame. We placed the two SMBHs in the z = 0 mid-plane with initial coordinate components x1, 2 = 0 and y1, 2 = ±0.3, where the subscripts denote the two SMBHs. It is important to note that the coordinates of SMBHs are given in N-body units and the distance from the centre of the SMBHs’ particles roughly corresponds to the influence radius of models in which the SMBHB has a total mass of 2 × 10−2. In all the tables and figures, we use these normalized N-body units (if not specified directly).

The initial velocities for the two SMBHs are oriented along the x axis and set to vx; 1, 2 = ±Vcirc, where Vcirc is the circular velocity within the stellar background model of nuclei. We note that our choice of initial parameters and scaling implies a circular velocity Vcirc ≈ 0.7 in N-body units at the initial SMBH positions.

We complement our database of simulations with an extra set of four further models in which we assume for the SMBH the initial velocity vx; 1, 2 = Vred = ±0.1Vcirc ≈ 0.07. This choice implies that the SMBHs initially move on more eccentric orbits compared to the other simulations, thus allowing them to pair in a shorter timescale. All the main features of our models are summarized in Table 1.

Table 1.

Set of parameters of our model runs.

3. Results and discussion

Due to the initial rotation, the stellar distribution undergoes a strong initial bar instability and later forms a rotating triaxial nucleus, as has been discussed in our previous works (Berczik et al. 2006; Berentzen et al. 2009; Wang et al. 2014). The two SMBHs migrate inwards due to the dynamical friction until the point at which they become gravitationally bound.

After the SMBHB formation, continuous interactions with the surrounding field stars cause the shrinking of the orbit, that is to say there is a progressive decrease in the binary semi-major axis a. The semi-major axis evolution can be divided into two phases: one during which the binary orbit evolution is driven by both dynamical friction and stellar hardening and, another, dominated by stellar encounters during which the binary shrinking proceeds at a nearly constant rate. This process in basic steps was described and studied in previous classical works (Mikkola & Valtonen 1992; Makino & Funato 2004). The work of the highly eccentric SMBHB dynamical evolution in the environment of ‘field stars’ presented and described in Iwasawa et al. (2011) was especially important; it was shown that the eccentricity increase in SMBH binaries is driven by a combination of a secular effect impinged by the overall nucleus tidal field and a cumulative effect coming from the star-SMBHB scattering in a prograde configuration. In our simulations, these two effects are likely mixed, thus making it hard to discern between them. We postpone any analysis on the binary eccentricity evolution to a forthcoming paper, and we point the interested reader to our previous works for Newtonian simulations (Berentzen et al. 2009).

3.1. Hardening rate

Figure 1 shows the time evolution of the inverse of the binary semi-major axis (1/a) in the case of a set of models characterized by m1:m2 = 0.01:0.002, assuming N = 100k, 200k, 400k, and 1M. The plot outlines that the hardening follows a nearly linear trend, regardless of the number of particles. Therefore the slope of the 1/a curve provides us with an estimate of the binary hardening rate, s(t) = d(1/a)/dt. The black dashed line in Fig. 1 represents the best-fitting linear relation calculated for the time interval t = 50 − 150 (N-body units). Coupling the hardening rate with the extra hardening triggered by GW emission enables us to infer the binary merger time (e.g., Gualandris & Merritt 2012; Arca-Sedda & Gualandris 2018; Gualandris et al. 2022).

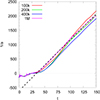thumbnail Fig. 1.

Inverse of the binary’s semi-major axis a as a function of time for the four different particles’ numbers N = 100k, 200k, 400k, 1M model with an SMBH mass ratio of m1:m2 = 0.01:0.002. The black dashed line shows the common corresponding linear fit between the time interval t = 50 − 150.

Figure 2 shows the dimensionless hardening rate for SMBHBs with different mass ratios q ≡ m2/m1 as a function of the binary total mass M12 = m1 + m2 for models with different particle numbers N (see Table 1) and different values for the mass of the primary SMBH. The plot outlines how, at a fixed SMBHB total mass, a heavier primary – that is to say a lower mass ratio – determines larger hardening. Similarly, at a fixed primary mass, we see that heavier binaries – that is to say heavier companions – are associated with a smaller hardening rate. This implies that the efficiency of stellar hardening is maximized for low-mass-ratio SMBHBs with a heavy primary mass. This result holds regardless of the number of particles used, thus confirming that is a physical effect rather than a numerical one.

thumbnail Fig. 2.

Hardening rate for SMBH binaries with different mass ratios q = m2/m1 (it is important to note m1 ≥ m2) as a function of the binaries’ total mass M12 = m1 + m2. Different symbols represent models with different particle numbers N (see Table 1), respectively. The open triangle is a parameter H0 (see Table 1 in Quinlan 1996). The colours are used to indicate the primary SMBH mass m1.

Taking advantage of scattering experiments, Rasskazov & Merritt (2017) and Rasskazov et al. (2019) recently showed that for low mass ratios (q < 10−2), the hardening rate is proportional to (1 + q)2/q. We find a similar dependence in our full N-body models, namely that the hardening is tightly linked to a simple combination of the binary primary mass and mass ratio defined as follows:

f ( q , μ ) ≡ m 1 q ( 1 + q ) 2 = m 2 ( 1 + q ) 2 = μ ( 1 + q ) . $$ \begin{aligned} f(q,\mu ) \equiv \frac{m_1 q}{(1+q)^2} = \frac{m_2}{(1+q)^2} = \frac{\mu }{(1+q)}. \end{aligned} $$(1)

Figure 3 shows the relation between the hardening rate and the μ/(1 + q) quantity. We find that this relation is well fitted by the following simple exponential formula:

s fit = d d t ( 1 a ) = A exp ( − B μ 1 + q ) , $$ \begin{aligned} s_{\rm fit} = \frac{\mathrm{d}}{\mathrm{d}t}\Bigl (\frac{1}{a}\Bigr ) = \mathrm{A} \exp \Bigl (-\frac{\mathrm{B}\mu }{1+q}\Bigr ), \end{aligned} $$(2)

thumbnail Fig. 3.

Hardening rate as a function of the ratio between the reduced mass and the mass ratio, μ/(1 + q). Colour coding marks the mass of the primary component, whereas different symbols refer to different N models. The open triangle is a parameter H0 (see Table 1 in Quinlan 1996). The hardening rate was fitted by Eq. (2).

with A = 17.5 ± 0.3 and B = 186.7 ± 8.8. We note that this relation implies that the secondary mass and the total mass ratio play the most effective role in shaping the SMBHB evolution. Also we fitted the data from Table 1 (Quinlan 1996) for systems with masses of m1 = 0.01, 0.02, and 0.04 and obtained B0.01 = 88.6, B0.02 = 44.3, and B0.04 = 22.1 accordingly when A = 23.0 for all models.

The fitting formula provided above enables us to link the binary hardening rate to the masses of the binary components. Figure 3 compares our fitting formula with the simulated data for the 52 largest N models considered here. We see that in passing from μ/(1 + q) = 10−4 to 10−2, the hardening rate decreases by a factor of 5. At a fixed primary mass, this implies that highly asymmetric binaries (q ≪ 1) tend to be characterized by a more effective hardening compared to the case of nearly equal mass SMBHBs. This might crucially affect the merger efficiency of SMBHBs in minor galaxy mergers, which are expected to be the main contributors to the population of SMBHBs with a mass ratio from 1:10 to 1:3, especially at high redshift (e.g., Callegari et al. 2011). Our results might have interesting consequences for GW astronomy since primary SMBHs with a mass from 106 − 107 M⊙ merging with a small companion might be bright GW sources for LISA (Amaro-Seoane et al. 2017) and similar space-based detectors such as TianQin (Luo et al. 2016), Taiji (Ruan et al. 2020), or μAres (Sesana et al. 2021).

3.2. Merger efficiency

We can use these results to place constraints on the SMBH merger efficiency. The long-term evolution of an SMBH binary can be written as follows (e.g., Gualandris & Merritt 2012; Arca-Sedda & Gualandris 2018; Gualandris et al. 2022):

d a d t = da dt | ∗ + d a d t | GW , $$ \begin{aligned}&\frac{\mathrm{d}a}{\mathrm{d}t} = \frac{da}{dt}\Big |_{*} + \frac{\mathrm{d}a}{\mathrm{d}t}\Big |_{\rm GW},\end{aligned} $$(3)

d e d t = d e d t | ∗ + d e d t | GW , $$ \begin{aligned}&\frac{\mathrm{d}e}{\mathrm{d}t} = \frac{\mathrm{d}e}{\mathrm{d}t}\Big |_{*} + \frac{\mathrm{d}e}{\mathrm{d}t}\Big |_{\rm GW}, \end{aligned} $$(4)

where the asterisk identifies stellar hardening, whereas GW refers to the hardening driven by GW emission.

While the stellar hardening term in our simulations is a direct consequence of continuous star-SMBHB interactions and can be described through the adimensional hardening rate described in the previous section, the GW term for the evolution of semi-major axes is given by the following (Peters & Mathews 1963; Peters 1964a,b):

d a d t | GW = − 64 β 5 F ( e ) a 3 , $$ \begin{aligned}&\frac{\mathrm{d}a}{\mathrm{d}t}\Big |_{\rm GW} = -\frac{64\beta }{5}\frac{F(e)}{a^3},\end{aligned} $$(5)

β = G 3 c 5 m 1 m 2 ( m 1 + m 2 ) , $$ \begin{aligned}&\beta = \frac{G^3}{c^5 m_1m_2(m_1+m_2)}, \end{aligned} $$(6)

F ( e ) = ( 1 − e 2 ) − 7 / 2 ( 1 + 73 24 e 2 + 37 96 e 4 ) . $$ \begin{aligned}&F(e) = (1 - e^2)^{-7/2}\Bigl (1+\frac{73}{24}e^2 + \frac{37}{96}e^4\Bigr ). \end{aligned} $$(7)

The eccentricity evolution regulated by stellar encounters and GW emission, respectively, is given by the following:

d e d t | ∗ = K a d a d t , $$ \begin{aligned}&\frac{\mathrm{d}e}{\mathrm{d}t}\Big |_{*} = \frac{K}{a}\frac{\mathrm{d}a}{\mathrm{d}t}, \end{aligned} $$(8)

d e d t | GW = − 304 β 15 e D ( e ) a 4 , $$ \begin{aligned}&\frac{\mathrm{d}e}{\mathrm{d}t}\Big |_{\rm GW} = -\frac{304\beta }{15}\frac{e D(e)}{a^4},\end{aligned} $$(9)

D ( e ) = ( 1 − e 2 ) 5 / 2 ( 1 + 121 304 e 2 ) , $$ \begin{aligned}&D(e) = (1-e^2)^{5/2}\left(1+\frac{121}{304}e^2\right), \end{aligned} $$(10)

K = d e d ln ( 1 / a ) , $$ \begin{aligned}&K = \frac{\mathrm{d}e}{\mathrm{d}\ln (1/a)}, \end{aligned} $$(11)

where K is the eccentricity growth rate (Quinlan 1996). As shown in several recent works, the K parameter depends, non-trivially, on the MBH masses and the environment (see e.g., Wang et al. 2014; Bonetti et al. 2020). Due to this, in the following we neglect Eq. 8, thus implicitly assuming that the star-SMBHB interaction does not alter the binary eccentricity significantly (see e.g., Fig. 3 in Wang et al. 2014).

We solved the system of differential Eqs. (5)–(11) numerically. We also adopted the scaling relation obtained for the adimensional hardening rate derived in Eq. (2), integrating the evolution of SMBH binaries down to the merger.

To obtain clues about the role played by our stellar hardening recipe on the formation of SMBH mergers, we created a sample of 2000 SMBH binary mergers as follows. Firstly, we selected the primary and companion SMBH mass between 104 − 109 M⊙, adopting a uniform distribution in logarithmic values. We assumed that the SMBH host nucleus has a mass extracted from between 101.5 and 104 times the SMBH mass (the values are in the range from the Milky Way to the classical bulges; Kormendy & Ho 2013), also adopting a uniform distribution in logarithmic values in this case.

In the Fig. 4, we show the random realizations SMBH individual masses m1, 2. As we can see, our random sampling thoroughly cover the observed range of SMBHs. This implies nuclei with masses in the range Mb = (3.5 × 105 − 1013) M⊙. For each pair, we calculated the hard-binary semi-major axis ah = G(m1 + m2)/2σ2, evaluating the galaxy velocity dispersion from the MSMBH − σ relation (Gültekin et al. 2009; Kormendy & Ho 2013). We started our integration assuming that the binary semi-major axis equals the hard-binary separation and we drew the eccentricity from a thermal distribution3 (Jeans 1919; Ambartsumian 1937; Heggie 1975; Kroupa et al. 2008).

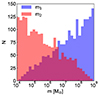thumbnail Fig. 4.

Distribution of the random realization component masses m1, 2 (m2 ≥ m1) for merging systems (Sect. 3.2). The mass range in the middle (cherry colour) shows the overlapping masses.

In Fig. 5, we show Tmerge as a function of the μ/[Mb(1 + q)] parameter (varying the binary mass ratio and primary mass) and the individual masses of the SMBHB. Looking at the two panels in the figure highlights the role of stellar hardening in the SMBHB evolution, leading the actual merger time to the range of ∼107 yr, which is many orders of magnitude larger as a simple merger timescale estimation based on the Peters–Mathews formalism (Peters & Mathews 1963; Peters 1964a,b). At a fixed SMBH primary mass, our results show that the minimization of the merger time is achieved for binaries with lighter SMBH companions, thus with lower mass ratios. This is due to the fact that lower mass ratios imply lower values for the μ/[Mb(1 + q)] parameter, which in turn implies a larger hardening in terms of absolute values. The efficient hardening driven by the rotating nucleus thus enables SMBHBs with mass ratios of q = 10−4 − 1 and component masses of m1, 2 = 104 − 9 M⊙ (Fig. 4) to merge over timescales, that is Tmerge ≈ 103 − 107 yr.

thumbnail Fig. 5.

Top panel: merger time Tmerge as a function of the μ/[Mb(1 + q)] parameter conveniently scaled to the galaxy nucleus mass Mb. The colour coding identifies the binary mass ratio. Bottom panel: merger time Tmerge as a function of the primary mass m1, where colour coding identifies the secondary mass m2.

4. Summary

We have presented a systematic study of the evolution of asymmetric SMBH binaries harboured in a non-axisymmetric, dense stellar galactic nucleus. To be able to perform this large systematic set of direct N-body simulations, we have developed a new high-performance computing code φ-GPU that enables one to fully exploit current and next generations high-performance GPU clusters.

Our simulations suggest that the binary hardening rate for unequal mass SMBHBs does not depend on the number of particles N, at least in the regime investigated here. The stellar hardening in our modelled SMBHBs is sufficiently effective to drive the SMBHB towards coalescence in a short timescale of about a gigayear (Berentzen et al. 2009).

For a fixed mass of the primary SMBH, that is the more massive one, we find a significant increase in the hardening rate for smaller masses of the secondary (i.e., lighter) SMBH. On the other hand, for a fixed mass of the secondary SMBH, we find the hardening rate to be proportional to the primary’s mass.

We find a tight relation between the hardening rate and the binary total mass M12 and reduced mass μ, which suggests that the SMBHB shrinkage process can be described by a two-parameters’ relation. Smaller values of M12 and μ result in an increase in the hardening rate. The hardening rates in our models support predictions of three-body scatter experiments (see e.g., Hills & Fullerton 1980; Hills 1983; Rasskazov & Merritt 2017; Rasskazov et al. 2019), which suggests a scaling between the hardening rate and binary mass ratio.

3

We also tried to use a uniform distribution and found no significant differences in the results.

Acknowledgments

We thank our colleagues Andreas Just, Christian Boily and Long Wang for their significant help and fruitful discussions during the preparation of the present work. This work was supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) Project-ID 138713538, SFB 881 (“The Milky Way System”) and by the Volkswagen Foundation under the grant No. 97778. We thank the Gauss Centre for Supercomputing e.V. (www.Gauss-centre.eu) for providing computing time through the John von Neumann Institute for Computing (NIC) on the GCS Supercomputers JUWELS and JUWELS-Booster (JSC; Jüich Supercomputing Centre 2021) in Germany. PB and MI acknowledge the support from the Ministry of Education and Science of Ukraine under the Ukrainian – French collaborative grant M/2-16.05.2022. PB and MI thanks the Partenariats Hubert Curien and Campus France for financial support through the DNIPRO programme No. 46814ZL, and the College de France for the award of a PAUSE short-term visiting scholarship tenable at the Observatorie astronomique at the Universite de Starsbourg. We also thanks its Director, Pierre-Alain Duc, for making our stay in Observatorie astronomique de Strasbourg possible, during which this work was being finalized. PB, MI, MS, and OS acknowledges by support under the special programme of the NRF of Ukraine “Leading and Young Scientists Research Support” – “Astrophysical Relativistic Galactic Objects (ARGO): life cycle of active nucleus”, No. 2020.02/0346. The work of PB was also supported by the Volkswagen Foundation under the special stipend No. 9B870 (2022). MS acknowledges the support under the Fellowship of the National Academy of Sciences of Ukraine for young scientists 2020–2022. MAS acknowledges financial support from the Alexander von Humboldt Foundation and the Federal Ministry for Education and Research for the research project “The evolution of black holes from stellar to galactic scales”, and funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No. 101025436 (project GRACE-BH, PI: Manuel Arca Sedda). RS and PB cordially acknowledge hospitality and support by National Astronomical Observatories of Chinese Academy of Sciences in Beijing, China.

References

  1. Aarseth, S. J., Henon, M., & Wielen, R. 1974, A&A, 37, 183 [NASA ADS] [Google Scholar]
  2. Amaro-Seoane, P., Aoudia, S., Babak, S., et al. 2013, GW Notes, 6, 4 [Google Scholar]
  3. Amaro-Seoane, P., Audley, H., Babak, S., et al. 2017, ArXiv e-prints [arXiv:1702.00786] [Google Scholar]
  4. Ambartsumian, V. A. 1937, AZh, 14, 207 [NASA ADS] [Google Scholar]
  5. Arca-Sedda, M., & Gualandris, A. 2018, MNRAS, 477, 4423 [Google Scholar]
  6. Bansal, K., Taylor, G. B., Peck, A. B., Zavala, R. T., & Romani, R. W. 2017, ApJ, 843, 14 [NASA ADS] [CrossRef] [Google Scholar]
  7. Begelman, M. C., Blandford, R. D., & Rees, M. J. 1980, Nature, 287, 307 [Google Scholar]
  8. Berczik, P., Merritt, D., Spurzem, R., & Bischof, H.-P. 2006, ApJ, 642, L21 [Google Scholar]
  9. Berczik, P., Nitadori, K., Zhong, S., et al. 2011, International Conference on High Performance Computing, HPC-UA 2011, 8 [Google Scholar]
  10. Berczik, P., Spurzem, R., & Wang, L. 2013a, Third International Conference on High Performance Computing, HPC-UA 2013, 59 [Google Scholar]
  11. Berczik, P., Spurzem, R., Zhong, S., et al. 2013b, in Procs. of 28th Intl. Supercomputing Conf. ISC 2013, Leipzig, Germany, June 16–20, 2013, eds. J. M. Kunkel, T. Ludwig, & H. Meuer (Berlin: Springer), Lecture Notes in Computer Science, 7905, 13 [Google Scholar]
  12. Berentzen, I., Preto, M., Berczik, P., Merritt, D., & Spurzem, R. 2009, ApJ, 695, 455 [NASA ADS] [CrossRef] [Google Scholar]
  13. Bonetti, M., Rasskazov, A., Sesana, A., et al. 2020, MNRAS, 493, L114 [Google Scholar]
  14. Callegari, S., Kazantzidis, S., Mayer, L., et al. 2011, ApJ, 729, 85 [NASA ADS] [CrossRef] [Google Scholar]
  15. Einsel, C., & Spurzem, R. 1999, MNRAS, 302, 81 [NASA ADS] [CrossRef] [Google Scholar]
  16. Fabbiano, G., Paggi, A., Karovska, M., Elvis, M., Nardini, E., & Wang, J. 2020, ApJ, 902, 49 [NASA ADS] [CrossRef] [Google Scholar]
  17. Gong, X., Xu, S., Bai, S., et al. 2011, Class. Quant. Grav., 28, 094012 [NASA ADS] [CrossRef] [Google Scholar]
  18. Gualandris, A., & Merritt, D. 2012, ApJ, 744, 74 [NASA ADS] [CrossRef] [Google Scholar]
  19. Gualandris, A., Khan, F. M., Bortolas, E., et al. 2022, MNRAS, 511, 4753 [NASA ADS] [CrossRef] [Google Scholar]
  20. Gültekin, K., Richstone, D. O., Gebhardt, K., et al. 2009, ApJ, 698, 198 [Google Scholar]
  21. Harfst, S., Gualandris, A., Merritt, D., et al. 2007, New Astron., 12, 357 [Google Scholar]
  22. Heggie, D. C. 1975, MNRAS, 173, 729 [NASA ADS] [CrossRef] [Google Scholar]
  23. Hills, J. G. 1983, AJ, 88, 1269 [NASA ADS] [CrossRef] [Google Scholar]
  24. Hills, J. G., & Fullerton, L. W. 1980, AJ, 85, 1281 [NASA ADS] [CrossRef] [Google Scholar]
  25. Ho, L. C., & Kim, M. 2014, ApJ, 789, 17 [NASA ADS] [CrossRef] [Google Scholar]
  26. Iwasawa, M., An, S., Matsubayashi, T., Funato, Y., & Makino, J. 2011, ApJ, 731, L9 [NASA ADS] [CrossRef] [Google Scholar]
  27. Jeans, J. H. 1919, MNRAS, 79, 408 [NASA ADS] [CrossRef] [Google Scholar]
  28. Jüich Supercomputing Centre 2021, J. Large-scale Res. Facilit., 7 [Google Scholar]
  29. Just, A., Yurin, D., Makukov, M., et al. 2012, ApJ, 758, 51 [NASA ADS] [CrossRef] [Google Scholar]
  30. Khan, F. M., Holley-Bockelmann, K., Berczik, P., & Just, A. 2013, ApJ, 773, 100 [Google Scholar]
  31. Khan, F. M., Fiacconi, D., Mayer, L., Berczik, P., & Just, A. 2016, ApJ, 828, 73 [Google Scholar]
  32. Khan, F. M., Capelo, P. R., Mayer, L., & Berczik, P. 2018, ApJ, 868, 97 [Google Scholar]
  33. Kollatschny, W., Weilbacher, P. M., Ochmann, M. W., et al. 2020, A&A, 633, A79 [EDP Sciences] [Google Scholar]
  34. Komossa, S., Burwitz, V., Hasinger, G., et al. 2003, ApJ, 582, L15 [NASA ADS] [CrossRef] [Google Scholar]
  35. Kormendy, J., & Ho, L. C. 2013, ARA&A, 51, 511 [Google Scholar]
  36. Kroupa, P. 2008, in The Cambridge N-Body Lectures, eds. S. J. Aarseth, C. A. Tout, & R. A. Mardling (Berlin: Springer-Verlag), Lecture Notes in Physics, 760, 181 [NASA ADS] [CrossRef] [Google Scholar]
  37. Li, S., Liu, F. K., Berczik, P., Chen, X., & Spurzem, R. 2012, ApJ, 748, 65 [Google Scholar]
  38. Luo, J., Chen, L.-S., Duan, H.-Z., et al. 2016, Class. Quant. Grav., 33, 035010 [NASA ADS] [CrossRef] [Google Scholar]
  39. Makino, J., & Funato, Y. 2004, ApJ, 602, 93 [NASA ADS] [CrossRef] [Google Scholar]
  40. Mikkola, S., & Valtonen, M. J. 1992, MNRAS, 259, 115 [NASA ADS] [CrossRef] [Google Scholar]
  41. Naab, T., Jesseit, R., & Burkert, A. 2006, MNRAS, 372, 839 [NASA ADS] [CrossRef] [Google Scholar]
  42. Naab, T., Johansson, P. H., & Ostriker, J. P. 2009, ApJ, 699, L178 [Google Scholar]
  43. Nitadori, K., & Makino, J. 2008, New Astron., 13, 498 [NASA ADS] [CrossRef] [Google Scholar]
  44. Peters, P. C. 1964a, PhD Thesis, California Institute of Technology [Google Scholar]
  45. Peters, P. C. 1964b, Phys. Rev., 136, 1224 [Google Scholar]
  46. Peters, P. C., & Mathews, J. 1963, Phys. Rev., 131, 435 [Google Scholar]
  47. Quinlan, G. D. 1996, New Astron., 1, 35 [Google Scholar]
  48. Rasskazov, A., & Merritt, D. 2017, ApJ, 837, 135 [Google Scholar]
  49. Rasskazov, A., Fragione, G., Leigh, N. W. C., et al. 2019, ApJ, 878, 17 [Google Scholar]
  50. Rodriguez, C., Taylor, G. B., Zavala, R. T., et al. 2006, ApJ, 646, 49 [Google Scholar]
  51. Ruan, W.-H., Guo, Z.-K., Cai, R.-G., & Zhang, Y.-Z. 2020, Int. J. Mod. Phys. A, 35, 2050075 [NASA ADS] [CrossRef] [Google Scholar]
  52. Sesana, A., Korsakova, N., Sedda, M. A., et al. 2021, Experimental Astronomy, 51, 1333 [NASA ADS] [CrossRef] [Google Scholar]
  53. Sobolenko, M., Berczik, P., Spurzem, R., & Kupi, G. 2017, Kinemat. Phys. Celest. Bodies, 33, 21 [NASA ADS] [Google Scholar]
  54. Sobolenko, M., Berczik, P., & Spurzem, R. 2021, A&A, 652, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Valtonen, M. J. 2007, ApJ, 659, 1074 [NASA ADS] [CrossRef] [Google Scholar]
  56. Valtonen, M. J., Mikkola, S., Lehto, H. J., et al. 2010a, Celest. Mech. Dyn. Astron., 106, 235 [NASA ADS] [CrossRef] [Google Scholar]
  57. Valtonen, M. J., Mikola, S., Merritt, D., et al. 2010b, ApJ, 709, 725 [NASA ADS] [CrossRef] [Google Scholar]
  58. Voggel, K. T., Seth, A., Baumgardt, H., et al. 2022, A&A, 658, A152 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  59. Wang, L., Berczik, P., Spurzem, R., & Kouwenhoven, M. B. N. 2014, ApJ, 780, 164 [Google Scholar]
  60. Zhong, S., Berczik, P., & Spurzem, R. 2014, ApJ, 792, 137 [Google Scholar]

All Tables

Table 1.

Set of parameters of our model runs.

In the text

All Figures

thumbnail Fig. 1.

Inverse of the binary’s semi-major axis a as a function of time for the four different particles’ numbers N = 100k, 200k, 400k, 1M model with an SMBH mass ratio of m1:m2 = 0.01:0.002. The black dashed line shows the common corresponding linear fit between the time interval t = 50 − 150.
In the text
thumbnail Fig. 2.

Hardening rate for SMBH binaries with different mass ratios q = m2/m1 (it is important to note m1 ≥ m2) as a function of the binaries’ total mass M12 = m1 + m2. Different symbols represent models with different particle numbers N (see Table 1), respectively. The open triangle is a parameter H0 (see Table 1 in Quinlan 1996). The colours are used to indicate the primary SMBH mass m1.
In the text
thumbnail Fig. 3.

Hardening rate as a function of the ratio between the reduced mass and the mass ratio, μ/(1 + q). Colour coding marks the mass of the primary component, whereas different symbols refer to different N models. The open triangle is a parameter H0 (see Table 1 in Quinlan 1996). The hardening rate was fitted by Eq. (2).
In the text
thumbnail Fig. 4.

Distribution of the random realization component masses m1, 2 (m2 ≥ m1) for merging systems (Sect. 3.2). The mass range in the middle (cherry colour) shows the overlapping masses.
In the text
thumbnail Fig. 5.

Top panel: merger time Tmerge as a function of the μ/[Mb(1 + q)] parameter conveniently scaled to the galaxy nucleus mass Mb. The colour coding identifies the binary mass ratio. Bottom panel: merger time Tmerge as a function of the primary mass m1, where colour coding identifies the secondary mass m2.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.