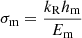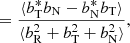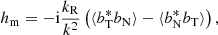EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 664 (August 2022) A&A, 664 (2022) L8 Full HTML
Open Access
Issue
A&A
Volume 664, August 2022
Article Number L8
Number of page(s) 4
Section Letters to the Editor
DOI https://doi.org/10.1051/0004-6361/202244314
Published online 12 August 2022

© T. Alberti et al. 2022

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.

1. Introduction

Understanding the magnetic helicity density A ⋅ B (hereafter simply the magnetic helicity) and its transport processes in the heliosphere will likely result in a breakthrough in the research areas of space and astrophysical plasma turbulence. From the theoretical point of view, the magnetic helicity is an invariant in the ideal magnetohydrodynamic (MHD) system when integrated over the volume bounded by the magnetic surface. The magnetic helicity is considered as an important control or constraint parameter of plasma turbulence such as evolution into helical or nonhelical turbulence (Biskamp 2003). The magnetic helicity density is accessible both by theoretical and observations means. The magnetic helicity content of the large-scale Parker field was theoretically calculated with a sign reversal between the northern and the southern hemispheres (Bieber et al. 1987a), and the large-scale helicity has impacts on the solar modulation of cosmic rays (Bieber et al. 1987b). Flux tubes closer to the solar surface have a helicity organization, by hemisphere, that parallels what is seen in the solar wind (Rust & Kumar 1994). The helicity connection between the two regions (near-surface region and heliosphere) shows the hemispheric segregation of the magnetic filaments (Bieber & Rust 1995; Rust & Kumar 1996).

Helicity studies are being recognized as one of most the powerful analysis tools to reveal the magnetic field structures in heliospheric physics. For example, the helicity of flux ropes can be directly determined in the spatial domain (Pecora et al. 2021), using an adaptation of the method introduced by Matthaeus et al. (1982). Yet, from the observational point of view, proper helicity measurements in space (in particular in the solar wind) remain a challenge. Most of the magnetic field data are provided by the single-point observations, and the helicity study is limited to the analysis of the field rotation sense around the radial direction from the Sun, assuming Taylor’s frozen-in flow hypothesis (Taulor 1938). This makes a marked difference to the numerical simulations in which the magnetic helicity can unambiguously be determined in the extended spatial domain.

The advent of the inner heliospheric probes performed by Parker Solar Probe (PSP), BepiColombo, and Solar Orbiter gives us a variety of observational opportunities by combining the data of two or three spacecrafts. The evolution or the transport process of the magnetic helicity can then be tracked from one region to another. Here we present a radial alignment study of the magnetic helicity from a heliocentric distance of 0.17 astronomical units (AU; below the distance of Mercury’s orbit of 0.3 AU) to 0.58 AU (below the distance of Venus’ orbit of 0.7 AU). The radial alignment of PSP and BepiColombo was achieved in September 2020 (Alberti et al. 2022). Our helicity study logically extends the helicity evolution study by Telloni et al. (2015) to even closer to the Sun.

Observationally speaking, the outer domain (Earth’s orbit and beyond) of the heliosphere in the ecliptic plane exhibits a reduced magnetic helicity with (i) random oscillation with zero-mean on the MHD scales up to about 0.1 Hz in the spacecraft frame (Matthaeus et al. 1982; Smith 2003), and (ii) a systematic trend toward a nonzero value in the ion-kinetic range at about 1 Hz and higher (Leamon et al. 1998; Podesta 2013). The aforementioned observations have undoubtedly contributed in our better understanding of the overall helicity density behavior. However, the lack of a systematic approach in the analysis of multipoint observations (also due to the design and operations of the related space missions) results in our still limited understanding of the helicity evolution in the inner heliosphere. We address the question if the empirical picture of helicity described above is inherited from the helicity profile in the innermost area of the heliosphere (below 0.58 AU, previous studies were devoted to larger distances Telloni et al. 2015), or if the helicity is actively evolving with generation, dissipation, or transport over different scales.

2. Radial alignment event study

2.1. Data set and analysis

We used measurements provided by the PSP and the BepiColombo spacecraft when they were radially aligned and orbiting near 0.17 AU and 0.58 AU, respectively. PSP magnetic field observations were taken from the FIELDS fluxgate magnetometer (MAG) (Bale et al. 2016) and were averaged to 1-s cadence from their native four samples per cycle cadence (see also Alberti et al. 2020). BepiColombo magnetic field data were obtained by the fluxgate magnetometer on board the MPO spacecraft (Glassmeier et al. 2010; Heyner et al. 2021) with its boom already having been deployed during cruise.

The interplanetary magnetic field data were analyzed in the Radial-Tangential-Normal (RTN) coordinate system in which R is pointing toward the Sun, T is tangential to the spacecraft orbit, and N is normal to the R − T plane (Fränz & Harper 2002). The time interval corresponding to the radial alignment is the same as in Alberti et al. (2022) and it is reported in Fig. 1. As shown in Alberti et al. (2022), the radial alignment between PSP and BepiColombo occurred for the time intervals 04:00–06:00 UT on 25 September 2020 for PSP, and 15:00–17:00 UT on 28 September 2020 for BepiColombo. These two intervals have been obtained by assuming that a plasma parcel is rigidly transported by the solar wind from the PSP to BepiColombo orbit. This clearly depends on the measured solar wind speed at the PSP orbit, thus determining the effective travel time to reach the BepiColombo orbit. As shown in Alberti et al. (2022), since VSW = 240 km s−1 and the spacecraft separation is Δr = 0.4775 AU, the corresponding travel time τ is about 3.5 days.

thumbnail Fig. 1.

Interplanetary magnetic field data in the RTN reference frame: 25 September 2020 04:00–06:00 UT for PSP (a) and 28 September 2020 15:00–17:00 UT for BepiColombo (b).

The method of reduced magnetic helicity σm was used in the data analysis, and constructed as follows (cf., Matthaeus & Smith 1981; Matthaeus & Goldstein 1982; Narita et al. 2009; Brandenburg et al. 2011; Narita 2022):

(1)

(2)

where kR is the radial component of the wavevector (from the Sun), hm is the one-component magnetic helicity density in the spectral domain defined as

(3)

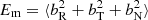is the spectral energy estimated by the trace of the spectral matrix of the fluctuating magnetic field, and “*” refers to the complex conjugate. The angular bracket ⟨…⟩ denotes the averaging over different realizations (over the time subintervals in our work). The essence of the reduced helicity is to extract the information on the spatial field rotation sense around the direction of interest (the radial direction from the Sun in our case) in a dimensionless form by normalizing to the fluctuation energy. Equation (3)) highlights the physical meaning of the magnetic helicity: it is a measure of the asymmetric part of the covariance matrix. These are the missing elements when only estimating the spectral density, corresponding to the diagonal elements of the covariance matrix.

The observational studies show that the helicity values can be both positive and negative (around the flow direction), and even oscillate between the two signs in a wider range of frequencies. The helicity magnitude declines as a function of the frequencies. Generally speaking, when one applies the inertial-range energy spectrum for isotropic, homogeneous turbulence, to the off-diagonal element of the spectral matrix, that is 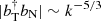, the helicity magnitude falls off as |hm|∼k−8/3, which is steeper than the inertial-range energy spectrum. Since we dealt with single-point measurements, previous findings were recovered in the frequency domain, yet in the spatial one by assuming Taylor’s frozen-in flow hypothesis (Taulor 1938) as in the present analysis.

The Fourier spectra were computed via the standard fast Fourier transform (FFT) method performed using a windowed approach consisting of a discrete spheroidal sequence with a time-bandwidth product NW = 4 (Percival & Walden 1993). The spectra were then smoothed by means of convolution with a Papoulis window function with a bandwidth of Δf, such that Δf/f = 7% (Percival & Walden 1993; Podesta & Gary 2011). This operation ensures that the smoothed spectrum over a uniformly spaced frequency grid matching that used to compute the spectrum is evaluated.

2.2. Results

Figure 2 reports the helicity spectrum hm(fsc) at both PSP and BepiColombo locations. An interesting feature emerging by comparing both locations is a clear, different scaling exponent. While close to the Sun hm ∼ f−5/2, far away (around 0.6 AU), it behaves as hm ∼ f−8/3. These features seem to be in agreement with recent works (e.g., Chen et al. 2020; Alberti et al. 2020) in which has been noted for the first time that the energy spectral exponent, that is to say the one associated with the symmetric part of the covariance matrix, moves from −3/2 to −5/3 when moving away from the Sun, with the transition occurring near 0.4 AU. By simple dimensional analysis, we can easily find that our observations on the reduced helicity match those in the power spectral density behavior. This is, to our knowledge, the first time we observed this feature.

thumbnail Fig. 2.

Spectral features of magnetic field observations. Upper panel: trace of the Fourier power spectral densities (PSDs) for PSP (black line) and BepiColombo (red line) orbits. The PSD at the PSP orbit follows the Iroshnikov-Kraichnan scaling of MHD turbulence f−3/2, while at the BepiColombo orbit, the Kolmogorov scaling of fluid turbulence f−5/3 is observed. Lower panel: helicity spectrum hm at both PSP (a) and BepiColombo (b) locations, respectively. At the PSP orbit, hm follows a f−5/2 power-law, while at the BepiColombo orbit, a f−8/3 scaling is observed. The gray lines are the 95% confidence intervals for both panels.

By looking at the behavior of the normalized helicity σm (see Fig. 3), other interesting features emerge. First of all, close to the Sun, σm fluctuates between positive and negative values, while at the BepiColombo orbit, it is almost positive. Second, approaching the inertial range break (around fsc ∼ 0.1 − 1 Hz), it seems that at the PSP orbit, larger fluctuations are found with respect to those at BepiColombo (almost zero). These findings both suggest that a common feature at 1 AU in which σm tends to nonzero in the ion-kinetic range (around 0.1 or 1 Hz) has not appeared. Furthermore, as one can note, the helicity oscillates around the zero mean at frequencies around 1 Hz, suggesting the absence of signatures of kinetic Alfven waves (KAWs) at both PSP and BepiColombo locations. This implies the presence of nonzero helicity waves at lower frequencies, such as the ion cyclotron wave (propagating parallel or antiparallel to the large-scale magnetic field) first predicted by Marsch & Tu (1990) using Helios particle data.

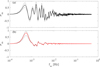thumbnail Fig. 3.

Reduced helicity for (upper panel) PSP and (lower panel) BepiColombo. The gray lines are the 95% confidence intervals.

Looking at the lowest frequencies (≤10−2 Hz), the following features are obtained. First, the reduced helicity reaches a peak of 70% positive polarization in the lowest frequency domain at about 5 × 10−4 Hz at both locations. This might represent a large-scale helical sense of the solar atmosphere or coronal field transported primarily by the solar wind advection. There is a moderate peak frequency shift from 5.0 × 10−4 Hz (PSP) to 5.5 × 10−4 Hz (BC), but the significance of the shift cannot be judged in the data resolution analyzed. Second, the reduced helicity exhibits larger fluctuations between positive values and negative values at PSP, reaching 40% negative polarization and 70% positive polarization in the intermediate frequency range up to 10−2 Hz. In contrast, the reduced helicity shows only moderate fluctuations, below 20% polarization in the intermediate frequency range. Some wave activities are expected at PSP locations such as the excitation of ion-cyclotron mode (Marsch & Tu 1990). The Helios proton velocity distribution functions can be well fitted by the scenario of pitch angle scattering by the ion-cyclotron waves (Marsch & Tu 1990). The current analysis shows that the wave activity almost rests at the BC location. Finally, the reduced helicity remains nearly zero-mean in the higher frequency range (approaching 1 Hz). The oscillation is also moderate. This feature makes a marked difference to the reduced helicity profile observed at Earth’s orbit (1 AU) such that the helicity shows a systematic trend and deviates from the zero mean.

3. Conclusions and outlook

Though limited in the frequency range, the radial alignment event achieved by PSP and BC offers an opportunity of tracking the magnetic helicity in the plasma parcel in the inner heliosphere. The helicity spectra exhibit the features that the solar wind develops into turbulence by convecting large-scale helicity components on the one hand and creating and annihilating helical wave components on the other hand. Excitation of waves can alter the helicity profile in the inner heliosphere. By comparing our findings with the typical helicity spectra at a distance of 1 AU (that is, randomly oscillating the helicity sign in the intermediate frequency range up to about 1 Hz), the helicity evolution approaches an asymptotic state at the Venus orbit (about 0.7 AU) and beyond.

The PSP-BC radial alignment in the inner heliosphere, extending from 0.17 AU to 0.58 AU, enabled us to track the evolution of the helical sense of the magnetic field around the radial direction from the Sun. The reduced magnetic helicity shows three main features: (i) a coherent major peak (highly helical component) at the lowest frequency (at about 5 × 10−4 Hz) on the analyzed time interval, (ii) damping helicity oscillation in the intermediate frequencies (10−3–10−2 Hz) when observed at 0.58 AU, and (iii) a coherent nonhelical component in the ion-kinetic range (frequencies 0.1 − 1 Hz) at the BepiColombo location (0.58 AU). The reduced helicity at Earth’s orbit often exhibits a different spectrum characterized by zero-mean, random oscillations at lower frequencies (where the MHD picture is valid) and a systematic trend to nonzero helicity at higher frequencies (the ion-kinetic range) interpreted as a sign of KAW excitation.

To conclude our work, a magnetic helicity evolution scenario is proposed as follows.

3.1. Large-scale helicity advection

The main novelty of our study is that the large-scale helicity is mainly transported by solar wind advection. Indeed a coherence major peak at 5 × 10−4 Hz is observed at both the PSP and BepiColombo orbit, thus suggesting an underlying transport mechanism primarily related to solar wind advection. This can be interpreted as a signature of processes related to solar wind heating and acceleration via linear resonance and instabilities in the solar corona that propagate through the inner heliosphere (e.g., Gary & Borovsky 2004; Podesta & Gary 2011). Thus, a possible source of helicity in the solar atmosphere include instabilities, while the observed weak radial scaling of the helicity peak and frequency location could indicate that waves are likely generated through in situ processes (Bowen et al. 2020).

3.2. Mid-frequency waves

The helicity sign shows a systematic trend in both the positive and negative senses in the range 10−3–10−2 Hz with waves being damped by the time the solar wind reaches the BepiColombo orbit (about 0.58 AU). Based on our frequency resolution (1 Hz), we cannot explore the possibility of occurrence of ion-cyclotron or whistler waves, mainly centered in the 1–10 Hz range at the PSP location (Bowen et al. 2020; Verniero et al. 2020). The observed damping of waves in the intermediate frequency range could be due to the interaction with the turbulent cascade. This scenario seems to be supported by the evolution of the nature of the inertial-range dissipation mechanisms at the PSP and BepiColombo orbits (e.g., Alberti et al. 2022). Indeed, a different role of large and small field gradients could produce damping mechanisms in terms of helicity properties. While large field gradients are needed to dissipate energy via the turbulent cascade close to the Sun, small fluctuations are primarily responsible for the energy transfer rate far away. This is reflected in large amplitude fluctuations in the reduced helicity at PSP with respect to those observed at BepiColombo. Thus, damping mechanisms could be searched in the interaction with inertial range physics (avalanching nonmultiplicative versus multiplicative processes, Alberti et al. 2022).

3.3. Ion-kinetic candidate waves

Short-wavelength or ion-kinetic waves, in the proper sense of KAWs, that is as a deviation from MHD Alfvén waves, occurring at about the ion gyroradius rgi (Narita et al. 2020), cannot be directly investigated due to our frequency resolution. Huang et al. (2020) reported the signature of the KAW in the range 2–26 Hz. Assuming that at these frequencies the linear-mode picture is valid, we can conjecture on the existence of some modes, such as (i) the ion cyclotron mode changing into kinetic Alfvén mode, (ii) the whistler mode which splits into ion Bernstein modes, or (iii) the slow mode with kinetic extension (e.g., Narita et al. 2020). Unfortunately, the mode(s) cannot be unambiguously identified, requiring a more dedicated analysis method which is beyond the scope of our study here. Of course, the above scenario is drawn from one radial alignment event, and the question is valid as to its statistical significance. Yet, the scenario can be used as a reference model, and it is useful in the theoretical modeling of solar wind turbulence.

Acknowledgments

The Parker Solar Probe (PSP) data used in this study are available at the NASA Space Physics Data Facility (SPDF), https://spdf.gsfc.nasa.gov/index.html. The FIELDS experiment on the Parker Solar Probe spacecraft was designed and developed under NASA contract NNN06AA01C. We acknowledge the contributions of the FIELDS team to the Parker Solar Probe mission. T. Alberti and A. Milillo acknowledge the support by the ASI-SERENA contract no. 2018-8-HH.O Partecipazione scientifica alla missione BEPICOLOMBO SERENA Fase E and the ESA contract (RFP/NC/ IPL-PSS/JD/258.2016) Expert Support to SERENA Science Operations. D. Heyner was supported by the German Ministerium für Wirtschaft und Energie and the German Zentrum für Luftund Raumfahrt under contract 50 QW 1501. The authors warmly acknowledge fruitful suggestions from an anonymous reviewer.

References

  1. Alberti, T., Laurenza, M., Consolini, G., et al. 2020, ApJ, 902, 84 [NASA ADS] [CrossRef] [Google Scholar]
  2. Alberti, T., Milillo, A., Heyner, D., et al. 2022, ApJ, 926, 174 [NASA ADS] [CrossRef] [Google Scholar]
  3. Bale, S. D., Goetz, K., Harvey, P. R., et al. 2016, Space Sci. Rev., 204, 49 [Google Scholar]
  4. Bieber, J. W., & Rust, D. M. 1995, ApJ, 453, 911 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bieber, J. W., Evenson, P. A., & Matthaeus, W. H. 1987a, ApJ, 315, 700 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bieber, J. W., Evenson, P. A., & Matthaeus, W. H. 1987b, Geophys. Res. Lett., 14, 864 [NASA ADS] [CrossRef] [Google Scholar]
  7. Biskamp, D. 2003, Magnetohydrodynamic Turbulence (Cambridge: Cambridge University Press) [Google Scholar]
  8. Bowen, T. A., Mallet, A., Huang, J., et al. 2020, ApJS, 246, 53 [Google Scholar]
  9. Brandenburg, A., Subramanian, K., Balogh, A., et al. 2011, ApJ, 734, 9 [NASA ADS] [CrossRef] [Google Scholar]
  10. Chen, C. H. K., Bale, S. D., Bonnell, J. W., et al. 2020, ApJS, 246, 53 [Google Scholar]
  11. Fränz, M., & Harper, D. 2002, Planet. Space Sci., 50, 217 [Google Scholar]
  12. Gary, S. P., & Borovsky, J. E. 2004, J. Geophys. Res., 109, A06105 [NASA ADS] [Google Scholar]
  13. Glassmeier, K.-H., Auster, H.-U., Heyner, D., et al. 2010, Planet. Space Sci., 58, 287 [NASA ADS] [CrossRef] [Google Scholar]
  14. Heyner, D., Auster, H.-U., Fornaçon, K.-H., et al. 2021, Space Sci. Rev., 217, 52 [CrossRef] [Google Scholar]
  15. Huang, S. Y., Zhang, J., Sahraoui, F., et al. 2020, ApJ, 897, L3 [NASA ADS] [CrossRef] [Google Scholar]
  16. Leamon, R. J., Smith, C. W., Ness, N. F., Matthaeus, W. H., & Wong, H. K. 1998, J. Geophys. Res., 103, 4775 [NASA ADS] [CrossRef] [Google Scholar]
  17. Marsch, E., & Tu, C.-Y. 1990, J. Geophys. Res., 95, 821 [Google Scholar]
  18. Matthaeus, W. H., & Goldstein, M. L. 1982, J. Geophys. Res., 87, 6011 [Google Scholar]
  19. Matthaeus, W. H., & Smith, C. W. 1981, Phys. Rev. A, 24, 2135 [CrossRef] [Google Scholar]
  20. Matthaeus, W. H., Goldstein, M. L., & Smith, C. 1982, Phys. Rev. Lett., 48, 1256 [Google Scholar]
  21. Narita, Y. 2022, in AGU book "Helicities in Geophysics, Astrophysics and Beyond", eds. S. Rodion, N. Valery, K. Kuzanyan, & N. Yokoi (John Wiley& Sons) [Google Scholar]
  22. Narita, Y., Kleindienst, G., & Glassmeier, K.-H. 2009, Ann. Geophys., 27, 3967 [NASA ADS] [CrossRef] [Google Scholar]
  23. Narita, Y., Roberts, O. W., Vörös, Z., & Hoshino, M. 2020, Front. Phys., 8, 166 [NASA ADS] [CrossRef] [Google Scholar]
  24. Pecora, D., Servidio, S., Greco, A., & Matthaeus, W. H. 2021, A&A, 650, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Percival, D. B., & Walden, A. T. 1993, Spectral Analysis for Physical Applications (Cambridge: Cambridge University Press) [CrossRef] [Google Scholar]
  26. Podesta, J. J. 2013, Sol. Phys., 286, 529 [NASA ADS] [CrossRef] [Google Scholar]
  27. Podesta, J. J., & Gary, S. P. 2011, ApJ, 734, 15 [NASA ADS] [CrossRef] [Google Scholar]
  28. Rust, D. M., & Kumar, A. 1994, Sol. Phys., 155, 69 [NASA ADS] [CrossRef] [Google Scholar]
  29. Rust, D. M., & Kumar, A. 1996, ApJ, 464, L199 [NASA ADS] [CrossRef] [Google Scholar]
  30. Smith, C. W. 2003, AdSpR, 32, 1971 [NASA ADS] [Google Scholar]
  31. Taulor, G. I. 1938, Proc. Roy. Soc. London Ser. A, 164, 476 [NASA ADS] [Google Scholar]
  32. Telloni, D., Bruno, R., & Trenchi, L. 2015, ApJ, 805, 46 [NASA ADS] [CrossRef] [Google Scholar]
  33. Verniero, J. L., Larson, D. E., Livi, R., et al. 2020, ApJS, 248, 5 [Google Scholar]

All Figures

thumbnail Fig. 1.

Interplanetary magnetic field data in the RTN reference frame: 25 September 2020 04:00–06:00 UT for PSP (a) and 28 September 2020 15:00–17:00 UT for BepiColombo (b).
In the text
thumbnail Fig. 2.

Spectral features of magnetic field observations. Upper panel: trace of the Fourier power spectral densities (PSDs) for PSP (black line) and BepiColombo (red line) orbits. The PSD at the PSP orbit follows the Iroshnikov-Kraichnan scaling of MHD turbulence f−3/2, while at the BepiColombo orbit, the Kolmogorov scaling of fluid turbulence f−5/3 is observed. Lower panel: helicity spectrum hm at both PSP (a) and BepiColombo (b) locations, respectively. At the PSP orbit, hm follows a f−5/2 power-law, while at the BepiColombo orbit, a f−8/3 scaling is observed. The gray lines are the 95% confidence intervals for both panels.
In the text
thumbnail Fig. 3.

Reduced helicity for (upper panel) PSP and (lower panel) BepiColombo. The gray lines are the 95% confidence intervals.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.