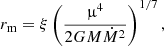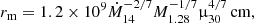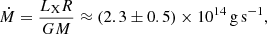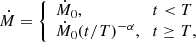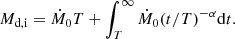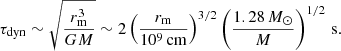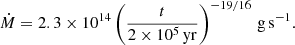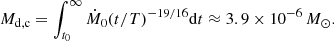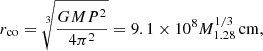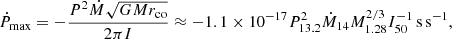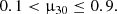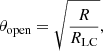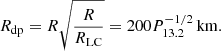EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 662 (June 2022) A&A, 662 (2022) A79 Full HTML
Open Access
Issue
A&A
Volume 662, June 2022
Article Number A79
Number of page(s) 5
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/202243536
Published online 21 June 2022

© W.-C. Chen 2022

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.

1. Introduction

HD 49798/RX J0648.0−4418 is a peculiar binary, comprised of a hot subdwarf of O spectral type and a compact companion in an orbit with an orbital period Porb = 1.55 days (Thackeray 1970; Kudritzki & Simon 1978). When this source was discovered, it was the brightest hot subdwarf detected (Jaschek & Jaschek 1963), and is still one of the brightest hot subdwarfs so far (Mereghetti et al. 2011). Bisscheroux et al. (1997) suggested that an intermediate-mass star that entered into a common envelope while in the early AGB stage is the most likely progenitor of HD 49798.

Israel et al. (1995, 1997) detected a 13.2 s period X-ray pulse, which probably originated from the spin period (P) of a magnetic compact object accreting from the weak wind of a subdwarf, in which the wind loss rate is about 3 × 10−9 M⊙ yr−1 (Hamann 2010). XMM-Newton data from 2002 to 2014 were used to derive a relatively low X-ray luminosity of LX ≈ (1.3 ± 0.3) × 1032(d/520 pc)2 erg s−1 (d is the distance of the source, Mereghetti et al. 2016). Comparing the observed X-ray luminosity with the accretion luminosity estimated by the wind capture rate of the compact object, Israel et al. (1997) proposed that the X-ray pulsator is a neutron star (NS) rather than a white dwarf (WD). However, a very soft blackbody of temperature (kT ∼ 30 eV), a hard power-law tail, and a large emitting area radius (RBB ∼ 32(d/520 pc) km) derived from the blackbody spectral fit suggested a WD compact object (Mereghetti et al. 2009, 2011). Most recently, a relatively precise parallax obtained with Gaia EDR3 was used to measure the distance of this source to be 521 ± 14 pc (Gaia Collaboration 2020).

Based on data from the XMM-Newton satellite, Mereghetti et al. (2009) obtained an X-ray mass function and an orbital plane inclination angle (79°–84°) by detecting an eclipse in the X-ray light curve, and constrained the mass of the X-ray pulsator to be 1.28 ± 0.05 M⊙, and the mass of the hot subdwarf to be 1.50 ± 0.05 M⊙. Adopting the optically thick wind assumption, Wang & Han (2010) proposed that HD 49798/RX J0648.0−4418 could produce a type Ia supernova by accretion of a carbon oxygen (CO) WD in the future. Recently, Liu et al. (2015) argued that the X-ray pulsar companion of HD 49798 is a CO WD rather than an oxygen neon (ONe) WD according to a binary population synthesis simulation. If HD 49798 is accompanied by a NS, this source will appear as an ultraluminous X-ray source by the mass transfer triggered by Roche lobe overflow in the future, and will eventually evolve into a wide intermediate-mass binary pulsar (Brooks et al. 2017). Wu & Wang (2019) found that the WD would experience an off-center C burning and form a NS via iron core collapse supernova if the compact companion of HD 49798 is a CO WD. However, this source is unlikely to form a NS from an accretion-induced-collapse process if the compact object is a ONe WD (Liu et al. 2018).

Whether the X-ray pulsator companion of HD 49798 is a NS or a WD remains controversial. Mereghetti et al. (2016) performed a phase-connected timing analysis for XMM-Newton, Swift, and ROSAT data spanning more than 20 yr, and obtained a spin-period derivative of the X-ray pulsator of Ṗ = (−2.15 ± 0.05) × 10−15 s s−1. Recently, the compact companion was reported to be still spinning up at a steady rate of Ṗ = (−2.17 ± 0.01) × 10−15 s s−1 according to the new XMM-Newton data (Mereghetti et al. 2021). In principle, the accretion process of a compact object can result in a steady spin-up rate. The orbital separation of HD 49798 is about 8.0 R⊙ (Mereghetti et al. 2009), and the effective Roche-lobe radius of the donor star can be estimated to be ∼3.1 R⊙ (Eggleton 1983). The radius of the subdwarf is 1.05 ± 0.06 R⊙ (Krtika et al., 2019), and therefore it is impossible to transfer material by the Roche-lobe overflow. However, this source is a member of the few hot subdwarfs showing obvious evidence of stellar wind (Hamann et al. 1981; Hamann 2010). The observed spin-up rate favors a NS accreting from the wind of the hot subdwarf. However, if the compact companion of HD 49798 is a NS, there still exist three puzzles in the NS model: first, the inferred low magnetic field (∼1010 G) is unusual for a NS without a millisecond period (Mereghetti et al. 2016); second, it is impossible to obtain such a large emitting area (RBB ∼ 32 km) fitted by the blackbody spectral; third, such a steady spin-up rate is difficult to interpret for a NS accreting from the stellar winds, in which variations of wind accretion rate captured by the NS would cause changes in accretion torque, and influence its spin period (Mereghetti et al. 2021).

If the compact companion of HD 49798 is a WD, it is very difficult to produce the observed spin-up rate by stellar wind accretion, unless disk accretion occurs (Mereghetti et al. 2016). Population synthesis simulations on hot subdwarf binaries also show that there are many more systems hosting WDs than systems hosting NSs (Yungelson & Tutukov 2005; Wu et al. 2018). Recently, Popov et al. (2018) provided a novel model, in which the contraction of a young WD with an age of ∼2 Myr can successfully explain the observed spin-up rate. However, the wind accretion model predicated an X-ray luminosity of LX = 1.3 × 1031 erg s−1 (Krtika et al., 2019)1, which is one order of magnitude lower than the observed value LX, obs ≈ (1.3 ± 0.3) × 1032 erg s−1 (Mereghetti et al. 2016). Therefore, the nature of this peculiar X-ray source remains a puzzle. In this work, we propose an alternative model, invoking a debris disk to account for the observed X-ray luminosity.

2. Debris disk accretion model

Some hot WDs have been discovered to be surrounded by a debris disk; for example SDSS 1228+1040 (Gänsicke et al. 2006; Manser et al. 2019), SDSS J1043+0855 (Gänsicke et al. 2007), SDSS J0845+2257 (Wilson et al. 2015), and SDSS J1344+0324 (Li et al. 2017). Recently, the WD G29-38 was reported to be currently accreting planetary material from a debris disk based on X-ray observations by Chandra X-ray Observatory (Cunningham et al. 2022). Although the compact companion of HD 49798 is in a binary system, we assume that it was surrounded by a debris disk similar to these latter, isolated WDs.

The magnetic accretion process of the WD from a debris disk is tightly related to the magnetospheric (Alfvén) radius rm, at which the ram pressure of the infalling material is balanced with the magnetic pressure. The magnetospheric radius can be written as (Davidson & Ostriker 1973)

r m = ξ ( μ 4 2 G M M ˙ 2 ) 1 / 7 , $$ \begin{aligned} r_{\rm m}=\xi \left(\frac{\upmu ^{4}}{2GM\dot{M}^{2}}\right)^{1/7}, \end{aligned} $$(1)

where G is the gravitational constant, ξ a dimensionless parameter of the order unity, M the WD mass, Ṁ the mass inflow rate at rm in the debris disk, and μ = BpR3/2 (Bp is the surface dipole magnetic field), which is the dipolar magnetic momentum of the WD.

Taking ξ = 0.52 for the disk accretion case (Ghosh & Lamb 1979), and inserting some typical parameters in Eq. (7):

r m = 1.2 × 10 9 M ˙ 14 − 2 / 7 M 1.28 − 1 / 7 μ 30 4 / 7 cm , $$ \begin{aligned} r_{\rm m}=1.2\times 10^{9} \dot{M}^{-2/7}_{14}M^{-1/7}_{1.28}\upmu ^{4/7}_{30}\,\mathrm{cm}, \end{aligned} $$(2)

where Ṁ14 is in units of 1014 g s−1, M1.28 is in units of 1.28 M⊙, and μ30 is in units of 1030 G cm3.

The observed X-ray luminosity of HD 49798 is LX ≈ (1.3 ± 0.3) × 1032(d/520 pc)2 erg s−1 (Mereghetti et al. 2016). Ignoring the X-ray luminosity produced by the stellar wind accretion, the accretion rate (i.e., the mass inflow rate at the inner edge of the debris disk) of the accreting WD in HD 49798 can be estimated to be

M ˙ = L X R GM ≈ ( 2.3 ± 0.5 ) × 10 14 g s − 1 , $$ \begin{aligned} \dot{M}=\frac{L_{\rm X}R}{GM}\approx (2.3\pm 0.5)\times 10^{14}\,\mathrm{g\,s^{-1}}, \end{aligned} $$(3)

where R is the WD radius. In this work, we take R = 3000 km.

Whether a debris disk around the WD could provide such an accretion rate is unclear. After a debris disk forms, the accretion rate should decrease self-similarly in accordance with Ṁ ∝ t−α due to the influence of viscous processes (Cannizzo et al. 1990). In our debris disk model, an evolutionary law of the accretion rate similar to that of Chatterjee et al. (2000) is adopted as follows:

M ˙ = { M ˙ 0 , t < T M ˙ 0 ( t / T ) − α , t ≥ T , $$ \begin{aligned} \dot{M}= \left\{ \begin{array}{l@{\quad }l} \dot{M}_{0},&t < T \\ \dot{M}_{0}(t/T)^{-\alpha } ,&t\ge T, \\ \end{array}\right. \end{aligned} $$(4)

where T is of the order of the dynamical timescale in the inner regions of the debris disk, and Ṁ0 is a constant accretion rate. The initial mass of the disk can be written as

M d , i = M ˙ 0 T + ∫ T ∞ M ˙ 0 ( t / T ) − α d t . $$ \begin{aligned} M_{\rm d,i}=\dot{M}_{0}T+\int _{T}^{\infty }\dot{M}_{0}(t/T)^{-\alpha }\mathrm{d}t. \end{aligned} $$(5)

Therefore, we have Ṁ0 = (α−1)Md,i/(αT) if α >  1 (Chatterjee et al. 2000). The dynamical timescale in the inner regions of the debris disk is given by

τ dyn ∼ r m 3 GM ∼ 2 ( r m 10 9 cm ) 3 / 2 ( 1.28 M ⊙ M ) 1 / 2 s . $$ \begin{aligned} \tau _{\rm dyn}\sim \sqrt{\frac{r_{\rm m}^{3}}{GM}}\sim 2\left(\frac{r_{\rm m}}{10^{9}\,\mathrm {cm}}\right)^{3/2}\left(\frac{1.28\,M_{\odot }}{M}\right)^{1/2}\,\mathrm{s}. \end{aligned} $$(6)

In the following calculations, we take T = 1 s and α = 19/16, meaning that the opacity is dominated by electron scattering (Cannizzo et al. 1990).

To account for the observed spin-up rate, Popov et al. (2018) proposed that the compact companion of HD 49798 is a contracting WD with a cooling age of ∼2 Myr. Similar to G29-38, we also assume that RX J0648.0–4418 experienced accretion for 10% of the cooling age (Jura 2003b), that is, the age of the debris disk is t0 = 2 × 105 yr. To explain the observed X-ray luminosity, the accretion rate from the debris disk should be Ṁ = 2.3 × 1014 g s−1 when t = t0 = 2  ×  105 yr, hence the evolution of the accretion rate when t ≥ T satisfies

M ˙ = 2.3 × 10 14 ( t 2 × 10 5 yr ) − 19 / 16 g s − 1 . $$ \begin{aligned} \dot{M}=2.3\times 10^{14}\left(\frac{t}{2\times 10^{5}\,\mathrm{yr}}\right)^{-19/16}\,\mathrm{g\,s^{-1}}. \end{aligned} $$(7)

This yields Ṁ0 = 3.6 × 1029 g s−1 from Eqs. (4) and (7), and the initial mass of the debris disk is estimated to be Md, i ≈ 0.001 M⊙ according to Eq. (5). The current mass of the debris disk is derived to be

M d , c = ∫ t 0 ∞ M ˙ 0 ( t / T ) − 19 / 16 d t ≈ 3.9 × 10 − 6 M ⊙ . $$ \begin{aligned} M_{\rm d,c}=\int _{t_{0}}^{\infty }\dot{M}_{0}(t/T)^{-19/16}\mathrm{d}t\approx 3.9\times 10^{-6}\,M_{\odot }. \end{aligned} $$(8)

If the gas-to-dust ratio is 100 (Jura 2003a), the current dust mass of the debris disk is Mdust ≈ 3.9 × 10−8 M⊙.

For reference, we also calculate the debris-disk mass of G29-38 using this model. The current accretion rate of G29-38 is about 1.63 × 109 g s−1 (Cunningham et al. 2022), and it has been actively accreting for 4  ×  107 yr, that is, t0 ≈ 40 Myr (Jura 2003b). Therefore, the accretion rate from the debris disk is Ṁ = 1.63 × 109(t/40 Myr)−19/16 g s−1. Similar to Eq. (8), the current debris-disk mass can be estimated to be 5.5 × 10−9 M⊙, which is not in contradiction with the minimum disk mass of ∼10−10 M⊙ estimated by Jura (2003b). Based on three-dimensional radiation-hydrodynamics stellar-atmosphere models, Cunningham et al. (2021) roughly estimated the debris-disk lifetimes around WDs to be log(t/yr) = 6.1 ± 1.4. Therefore, the debris-disk age of G29-38 is probably overestimated. If so, the current disk mass predicted by our model will correspondingly decline.

Taking M = 1.28 M⊙ and R = 3000 km, the X-ray luminosity of the WD accreting from the debris disk can be derived from LX = GMṀ/R and Eq. (7). Figure 1 plots the evolution of X-ray luminosity (we ignore the radius change of the WD in the contraction stage). It is clear that a WD accreting from a nascent debris disk can appear as a luminous X-ray source (∼1038 erg s−1) with a lifetime of up to 2 yr, which is similar to a black hole accreting from the fallback disk in ultraluminous X-ray sources (Li 2003). However, its maximum X-ray luminosity is difficult to exceed ∼1039 erg s−1 due to the Eddington luminosity LEdd = 1.9 × 1038 erg s−1 (if the accreting material is hydrogen, King & Lasota 2019). With the decline in the mass inflow rate, the magnetospheric radius will firstly exceed the corotation radius, and the accreting WD transitions to a low X-ray state that lacks X-ray pulsation (Campana et al. 2016). Subsequently, the magnetospheric radius will exceed the light cylinder radius (Rlc = cP/2π), and produce radio emission (Illarionov & Sunyaev 1975; Campana et al. 1998). According to the critical luminosity of WDs transitioning from accretion to the propeller regime, as determined by Campana et al. (2018), the accreting WD of HD 49798 will transition to the propeller phase if the accretion luminosity declines to the limiting luminosity 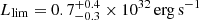L lim = 0 . 7 − 0.3 + 0.4 × 10 32 erg s − 1 $ L_{\mathrm{lim}}=0.7^{+0.4}_{-0.3}\times10^{32}\,\mathrm{erg\,s^{-1}} $, which depends on the dipolar magnetic momentum of the accreting WD2.

thumbnail Fig. 1.

X-ray luminosity produced by accretion from a debris disk as a function of the debris-disk age t. We take M = 1.28 M⊙ and R = 3000 km. The horizontal dashed line represents the observed X-ray luminosity range LX = (1.0−1.6) × 1032 erg s−1.

Similar to NSs, the spin evolution of WDs depends on the interaction between magnetic field lines and disk plasma, which can give rise to a continuous exchange of angular momentum between the WD and the disk. If the magnetospheric radius is smaller than the corotation radius (at which the Keplerian angular velocity is equal to the spin angular velocity of the WD),

r co = G M P 2 4 π 2 3 = 9.1 × 10 8 M 1.28 1 / 3 cm , $$ \begin{aligned} r_{\rm co} =\root 3 \of {\frac{GMP^{2}}{4\pi ^{2}}}=9.1\times 10^{8}M_{1.28}^{1/3}\,\mathrm{cm}, \end{aligned} $$(9)

the WD accretes the specific angular momentum of material at rm.

The maximum accretion torque receiving by the WD is 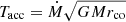T acc = M ˙ G M r co $ T_{\mathrm{acc}}=\dot{M}\sqrt{GMr_{\mathrm{co}}} $. Therefore, the maximum spin-up rate of the WD due to accretion from a debris disk can be expressed as

P ˙ max = − P 2 M ˙ G M r co 2 π I ≈ − 1.1 × 10 − 17 P 13.2 2 M ˙ 14 M 1.28 2 / 3 I 50 − 1 s s − 1 , $$ \begin{aligned} \dot{P}_{\rm max}=-\frac{P^{2}\dot{M}\sqrt{GMr_{\rm co}}}{2\pi I}\approx -1.1\times 10^{-17}P_{13.2}^{2}\dot{M}_{14}M_{1.28}^{2/3}I_{50}^{-1}\,\mathrm{s\,s^{-1}}, \end{aligned} $$(10)

where I50 is the moment of inertia of the WD in units of 1050 g cm2, P13.2 = P/13.2 s. For some typical parameters, the maximum spin-up rate produced by accretion from the debris disk is between one and two orders of magnitude lower than the observed value. Therefore, accretion from a debris disk can indeed account for the observed X-ray luminosity, while it cannot produce the detected spin-up rate of HD 49798/RX J0648.0−4418.

Figure 2 shows the evolution of the spin-period derivative produced by the accretion from the debris disk. According to our assumption, the debris disk should exist when the WD age is in the range of 1.8 Myr–2.0 Myr. Comparing with Fig. 2 in Popov et al. (2018), Ṗ produced by the debris disk is smaller than that resulting from the WD contraction for the debris-disk age t = 5000−2 × 105 yr. However, a young (with an age of less than 5000 yr) debris disk plays an important role in influencing the spin evolution of the WD.

thumbnail Fig. 2.

Evolution of the spin period derivative (Ṗ) of the WD accreting from a debris disk as a function of debris-disk age. We ignore the influence of the spin-period change on Ṗ. The horizontal dotted line represents the observed spin-up rate Ṗ = (−2.17 ± 0.01) × 10−15 s s−1.

To support a steady accretion, the inner radius of the debris disk (i.e., the magnetospheric radius rm) should satisfy the following relation:

R < r m ≤ r co . $$ \begin{aligned} R < r_{\rm m}\le r_{\rm co}. \end{aligned} $$(11)

Taking M1.28 = 1 and Ṁ14 2.3, the dipolar magnetic momentum of the WD can be constrained to

0.1 < μ 30 ≤ 0.9 . $$ \begin{aligned} 0.1 < \upmu _{30}\le 0.9. \end{aligned} $$(12)

Therefore, the surface dipolar magnetic field of the WD is in the range of (0.7−7) × 104 G.

For a magnetic WD, the accretion flow along the magnetic field lines would form an accretion column inside the polar cap (Shapiro & Teukolsky 1983). The polar cap opening angle of the last open field line is (Ruderman & Sutherland 1975)

θ open = R R LC , $$ \begin{aligned} \theta _{\rm open}=\sqrt{\frac{R}{R_{\rm LC}}}, \end{aligned} $$(13)

where RLC = cP/2π is the radius of the light cylinder. Therefore, we can estimate the polar cap radius of the WD in HD 49798 to be

R dp = R R R LC = 200 P 13.2 − 1 / 2 km . $$ \begin{aligned} R_{\rm dp}=R\sqrt{\frac{R}{R_{\rm LC}}}=200P_{13.2}^{-1/2}\,\mathrm{km}. \end{aligned} $$(14)

This radius is six times as large as the observed radius of the emitting area RBB ≈ 32(d/520pc) km at a distance of 520 pc (Mereghetti et al. 2016; Gaia Collaboration 2020).

Although the estimated polar cap radius is larger than the radius of the emitting zone derived from the black body spectral fit, it is already noted that the radius Rdp of the conventional polar cap is ten times larger than that of the radiation area in the neutron star field (Hermsen et al. 2013; Szary et al. 2017; Geppert 2017). Strong and small-scale local magnetic field structures in the polar cap surface were thought to be responsible for the small radius Rpc of the polar cap (Szary et al. 2015; Sznajder & Geppert 2020). According to the magnetic flux conservation law, if the magnetic field at the polar cap of the WD Bs ≃ 36Bp = (2.5−25) × 105 G, the small radius of the emitting zone can be easily understood.

3. Summary and Discussion

Stellar wind accretion from the hot subdwarf is insufficient to produce the observed X-ray luminosity of HD 49798 (Krtika et al., 2019). In this work, we propose an alternative model to account for the observed X-ray luminosity of HD 49798. If the compact companion of HD 49798 is a WD surrounded by a debris disk, by the interaction between the magnetic field and the debris disk, the accretion flow along the magnetic field lines could produce an accretion column on the polar cap of the WD, thereby naturally resulting in the observed X-ray pulses. Based on the model of time-varying accretion from a debris disk given by Chatterjee et al. (2000) and the observed X-ray luminosity, the initial mass and the current mass of the debris disk are constrained to be ∼0.001 M⊙ and 3.9 × 10−6 M⊙, respectively. Based on the accretion theory, the surface magnetic field of the WD is constrained to be Bp = (0.7−7) × 104 G, while the small polar cap zone requires a relatively strong local magnetic field (Bs = (2.5−25) × 105 G) to account for a small emitting area. The accretion torque exerted by the proposed debris disk can only influence the spin evolution of the WD when the debris-disk age is less than 5000 yr, and its affect is obviously smaller than that caused by the contraction of the WD in the current stage. Therefore, the debris disk cannot spin the accreting WD up to the observed rate in the current stage, which should arise from a change of the moment of inertia of the WD at the contraction stage (Popov et al. 2018).

The black body spectral fit for HD 49798 infers a radius of the emitting area of RBB ≈ 32(d/520 pc) km (Mereghetti et al. 2016). This emitting area should be the real polar cap zone resulting from the accretion column on the surface of the WD. However, our calculated polar cap radius is 200 km. The difference between the real polar cap zone and the theoretical value probably originates from strong and small-scale local magnetic field structures in the polar cap surface (Szary et al. 2015; Sznajder & Geppert 2020).

The debris disks around some isolated WDs probably originate from the tidal disruption of either comets (Debes & Sigurdsson 2002) or asteroids (Jura 2003b). Our scenario predicts a heavy debris disk with a mass of ∼10−6 M⊙, which is four orders of magnitude higher than that in the WD G29-38 (Jura 2003b). This mass discrepancy should arise from the different origins of the debris disks. As HD 49798 may experience a common envelope evolutionary phase (Bisscheroux et al. 1997), the debris disk around the WD may originate from the engulfment of the progenitor envelop of the hot subdwarf. For example, the engulfment of a low-mass companion star of HD 233517 when it evolved into a red giant resulted in a heavy debris disk of ∼0.01 M⊙ (Jura 2003a). However, it is challenging to confirm the debris disk by detecting the infrared excess from RX J0648.0–4418 as in G29-38. First, the distance of RX J0648.0–4418 is greater than that of G29-38 by a factor of 40; second, the detected radiation flux from the debris disk should be low due to a large orbital plane inclination angle3 (79°–84° , Mereghetti et al. 2009). On the other hand, a low X-ray state of RX J0648.0–4418 or a spin-down rate, if detected in the future, could be used to confirm the existence of a debris disk. We expect that further multiband observations of this source could help us to confirm or rule out the existence of a debris disk.

1

It is worth emphasizing that the wind accretion rate strongly depends on the wind velocity at the vicinity of the accreting WD (Krtika et al., 2019). Moreover, the effect of ionization by the X-ray flux might decrease the wind velocity, thus increasing the accretion rate (Sander et al. 2018; Krtika et al., 2018).

2

We take μ30 = 0.8; see also Eq. (7) of Campana et al. (2018).

3

The debris disk should be in the same plane as the orbital plane if it comes from the engulfment of the progenitor envelop of the hot subdwarf in the common envelope stage.

Acknowledgments

We cordially thank the anonymous referee for deep and constructive comments improving this manuscript. This work was partly supported by the National Natural Science Foundation of China (under grant numbers 11573016, 11733009), Natural Science Foundation (under grant number ZR2021MA013) of Shandong Province.

References

  1. Bisscheroux, B. C., Pols, O. R., Kahabka, P., Belloni, T., & van den Heuvel, E. P. J. 1997, A&A, 317, 815 [NASA ADS] [Google Scholar]
  2. Brooks, J., Kupfer, T., & Bildsten, L. 2017, ApJ, 847, 78 [NASA ADS] [CrossRef] [Google Scholar]
  3. Campana, S., Colpi, M., Mereghetti, S., Stella, L., & Tavani, M. 1998, A&ARv, 8, 279 [NASA ADS] [CrossRef] [Google Scholar]
  4. Campana, S., Coti Zelati, F., Papitto, A., et al. 2016, A&A, 594, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Campana, S., Stella, L., Mereghetti, S., & de Martino, D. 2018, A&A, 610, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Cannizzo, J. K., Lee, H. M., & Goodman, J. 1990, ApJ, 351, 38 [NASA ADS] [CrossRef] [Google Scholar]
  7. Chatterjee, P., Hernquist, L., & Narayan, R. 2000, ApJ, 534, 373 [NASA ADS] [CrossRef] [Google Scholar]
  8. Cunningham, T., Tremblay, P.-E., Bauer, E. B., et al. 2021, MNRAS, 503, 1646 [NASA ADS] [CrossRef] [Google Scholar]
  9. Cunningham, T., Wheatley, P. J., Tremblay, P.-E., et al. 2022, Nature, 602, 219 [NASA ADS] [CrossRef] [Google Scholar]
  10. Dall’Osso, S., Perna, R., & Stella, L. 2015, MNRAS, 449, 2144 [CrossRef] [Google Scholar]
  11. Davidson, K., & Ostriker, J. P. 1973, ApJ, 179, 585 [NASA ADS] [CrossRef] [Google Scholar]
  12. Debes, J. H., & Sigurdsson, S. 2002, ApJ, 572, 556 [NASA ADS] [CrossRef] [Google Scholar]
  13. Eggleton, P. P. 1983, ApJ, 268, 368 [Google Scholar]
  14. Gaia Collaboration (Brown, A. G. A., et al.) 2020, A&A, 649, A1 [Google Scholar]
  15. Gänsicke, B. T., Marsh, T. R., Southworth, J., & Rebassa-Mansergas, A. 2006, Science, 314, 1908 [Google Scholar]
  16. Gänsicke, B. T., Marsh, T. R., & Southworth, J. 2007, MNRAS, 380, L35 [NASA ADS] [CrossRef] [Google Scholar]
  17. Geppert, U. 2017, JApA, 38, 46 [NASA ADS] [Google Scholar]
  18. Ghosh, P., & Lamb, F. K. 1979, ApJ, 232, 259 [Google Scholar]
  19. Hamann, W.-R. 2010, Ap&SS, 329, 151 [NASA ADS] [CrossRef] [Google Scholar]
  20. Hamann, W., Gruschinske, J., Kudritzki, R. P., & Simon, K. P. 1981, A&A, 104, 249 [NASA ADS] [Google Scholar]
  21. Hermsen, W., Hessels, J. W. T., Kuiper, L., et al. 2013, Science, 339, 436 [NASA ADS] [CrossRef] [Google Scholar]
  22. Illarionov, A. F., & Sunyaev, R. A. 1975, A&A, 39, 185 [NASA ADS] [Google Scholar]
  23. Israel, G. L., Stella, L., Angelini, L., White, N. E., & Giommi, P. 1995, IAUC, 6277, 1 [NASA ADS] [Google Scholar]
  24. Israel, G. L., Stella, L., Angelini, L., et al. 1997, ApJ, 474, L53 [NASA ADS] [CrossRef] [Google Scholar]
  25. Jaschek, M., & Jaschek, C. 1963, PASP, 75, 365 [NASA ADS] [CrossRef] [Google Scholar]
  26. Jura, M. 2003a, ApJ, 582, 1032 [Google Scholar]
  27. Jura, M. 2003b, ApJ, 584, L91 [Google Scholar]
  28. King, A. R., & Lasota, J.-P. 2019, MNRAS, 485, 3588 [NASA ADS] [CrossRef] [Google Scholar]
  29. Krtička, J., Kubát, J., & Krtičková, I. 2018, A&A, 620, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Krtička, J., Janík, J., Krtičková, I., et al. 2019, A&A, 631, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Kudritzki, R. P., & Simon, K. P. 1978, A&A, 70, 653 [NASA ADS] [Google Scholar]
  32. Li, X.-D. 2003, ApJ, 596, L199 [NASA ADS] [CrossRef] [Google Scholar]
  33. Li, L., Zhang, F., Kong, X., Han, Q., & Li, J. 2017, ApJ, 836, 71 [NASA ADS] [CrossRef] [Google Scholar]
  34. Liu, D.-D., Zhou, W.-H., Wu, C.-Y., & Wang, B. 2015, Res. Astron. Astrophys., 15, 1813 [CrossRef] [Google Scholar]
  35. Liu, D.-D., Wang, B., Chen, W.-C., Zuo, Z.-Y., & Han, Z.-W. 2018, MNRAS, 477, 384 [NASA ADS] [CrossRef] [Google Scholar]
  36. Manser, C. J., Gänsicke, B. T., Eggl, S., et al. 2019, Science, 364, 66 [Google Scholar]
  37. Mereghetti, S., Tiengo, A., Esposito, P., et al. 2009, Science, 325, 1222 [NASA ADS] [CrossRef] [Google Scholar]
  38. Mereghetti, S., La Palombara, N., Tiengo, A., et al. 2011, ApJ, 737, 51 [NASA ADS] [CrossRef] [Google Scholar]
  39. Mereghetti, S., La Palombara, N., Tiengo, A., et al. 2013, A&A, 553, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Mereghetti, S., Pintore, F., Esposito, P., et al. 2016, MNRAS, 458, 3523 [NASA ADS] [CrossRef] [Google Scholar]
  41. Mereghetti, S., Pintore, F., Rauch, T., et al. 2021, MNRAS, 504, 920 [NASA ADS] [CrossRef] [Google Scholar]
  42. Mineshige, S., Nomura, H., Hiros, M., Nomoto, K., & Suzuki, T. 1997, ApJ, 489, 227 [NASA ADS] [CrossRef] [Google Scholar]
  43. Mukai, K. 2017, PASP, 129 [Google Scholar]
  44. Popov, S. B., Mereghetti, S., Blinnikov, S. I., Kuranov, A. G., & Yungelson, L. R. 2018, MNRAS, 474, 2750 [NASA ADS] [Google Scholar]
  45. Ruderman, M. A., & Sutherland, P. G. 1975, ApJ, 196, 51 [Google Scholar]
  46. Sander, A. A. C., Fürst, F., Kretschmar, P., et al. 2018, A&A, 610, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Shapiro, S. L., & Teukolsky, S. A. 1983, Black Holes, White Dwarfs, and Neutron Stars (New York: John Wiley& Sons) [CrossRef] [Google Scholar]
  48. Szary, A., Melikidze, G. I., & Gil, J. 2015, MNRAS, 447, 2295 [NASA ADS] [CrossRef] [Google Scholar]
  49. Szary, A., Gil, J., Zhang, B., et al. 2017, ApJ, 835, 178 [NASA ADS] [CrossRef] [Google Scholar]
  50. Sznajder, M., & Geppert, U. 2020, MNRAS, 493, 3770 [NASA ADS] [CrossRef] [Google Scholar]
  51. Thackeray, A. D. 1970, MNRAS, 150, 215 [NASA ADS] [CrossRef] [Google Scholar]
  52. Wang, B., & Han, Z.-W. 2010, Res. Astron. Astrophys., 10, 681 [CrossRef] [Google Scholar]
  53. Wickramasinghe, D. T., & Ferrario, L. 2000, PASP, 112, 873 [NASA ADS] [CrossRef] [Google Scholar]
  54. Wilson, D. J., Gänsicke, B. T., Koester, D., et al. 2015, MNRAS, 451, 3237 [NASA ADS] [CrossRef] [Google Scholar]
  55. Wu, C., & Wang, B. 2019, MNRAS, 486, 2977 [NASA ADS] [CrossRef] [Google Scholar]
  56. Wu, Y., Chen, X., Li, Z., & Han, Z. 2018, A&A, 618, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Yungelson, L. R., & Tutukov, A. V. 2005, Astron. Rep., 49, 871 [NASA ADS] [CrossRef] [Google Scholar]

All Figures

thumbnail Fig. 1.

X-ray luminosity produced by accretion from a debris disk as a function of the debris-disk age t. We take M = 1.28 M⊙ and R = 3000 km. The horizontal dashed line represents the observed X-ray luminosity range LX = (1.0−1.6) × 1032 erg s−1.
In the text
thumbnail Fig. 2.

Evolution of the spin period derivative (Ṗ) of the WD accreting from a debris disk as a function of debris-disk age. We ignore the influence of the spin-period change on Ṗ. The horizontal dotted line represents the observed spin-up rate Ṗ = (−2.17 ± 0.01) × 10−15 s s−1.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.