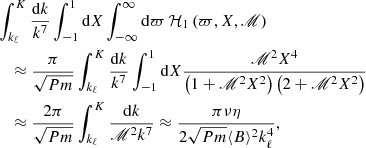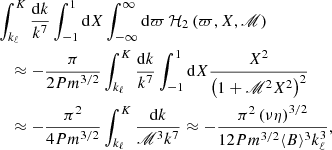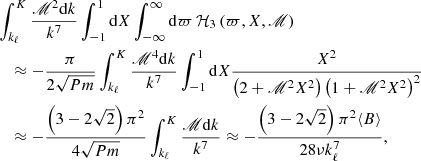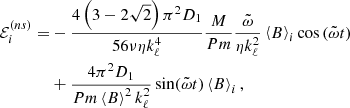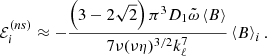| Issue |
A&A
Volume 660, April 2022
|
|
|---|---|---|
| Article Number | A110 | |
| Number of page(s) | 5 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/202142488 | |
| Published online | 22 April 2022 | |
Dynamo effect caused by non-stationary turbulence in strongly magnetized, hot, low-density plasma
Department of Magnetism, Institute of Geophysics, Polish Academy of Sciences, ul. Ksiecia Janusza 64, 01-452 Warsaw, Poland
e-mail: kamiz@igf.edu.pl
Received:
20
October
2021
Accepted:
10
March
2022
Context. The large-scale hydromagnetic dynamo mechanism is often assumed to rely on the existence of a resistive phase shift between the kinetic and magnetic components of waves. It is not clear how this mechanism could effectively operate in hot, low-density plasma, where the electrical resistivity is extremely low.
Aims. We show that non-stationarity, a common factor in plasma turbulence (e.g., in the interstellar medium caused by random supernova explosions), allows inducing a strong large-scale electromotive force (EMF) by the plasma flow and significantly enhances the dynamo effect.
Methods. We adopted the simplest approximation in which plasma evolution is modelled with a set of incompressible magnetohydrodynamic equations with a random, Gaussian, and non-stationary forcing to explicitly demonstrate the role of non-stationarity in the large-scale dynamo process. The EMF was calculated analytically in the limit of large magnetic Prandtl numbers (low magnetic diffusion in comparison with plasma viscosity) and strong magnetic fields for the non-stationary turbulence and the standard diffusive mechanism.
Results. We show that the EMF induced by the effects of non-stationarity can typically be expected to dominate the dynamo mechanism (over the diffusive phase shift generation) by several orders of magnitude. This is confirmed by the explicit calculation in two example cases for the interstellar medium in the Milky Way galaxy and hot accretion disks such as those of active galactic nuclei.
Key words: magnetohydrodynamics (MHD) / turbulence / ISM: magnetic fields / dynamo / magnetic fields / galaxies: nuclei
© ESO 2022
1. Introduction
The effect of a hydromagnetic dynamo, that is, the spontaneous generation of magnetic fields by plasma flow, is commonly invoked in the dynamical pictures of astrophysical systems, in particular in the cases of magnetized hot accretion disks or the interstellar medium (ISM). The flow can be driven for instance by supernova bursts, as in the case of galaxies (cf. Ferrière 1992; Brandenburg & Subramanian 2005) or by the development of violent instabilities such as the magneto-rotational instability in accretion disks (cf. Balbus & Hawley 1991a,b). The conditions for energy transfer from the kinetic energy of the turbulent plasma flow to the magnetic energy at large scales require a lack of reflexional symmetry in the flow (cf. e.g., Steenbeck et al. 1966; Roberts 1994; Moffatt & Dormy 2019), which in natural systems is satisfied by differential rotation. The turbulent mechanism of dynamo action, which is typically thought to be responsible for the generation of large-scale fields, is the so-called α-effect, which is based on non-linear interactions of the small-scale fluctuating components of the turbulent state that generate the large-scale electromotive force (EMF). However, in the standard approaches, this mechanism relies on the phase shift between the kinetic and magnetic components of turbulent fluctuations, which is generated by plasma resistivity. In other words, this mechanism becomes ineffective in low-resistivity plasma, and typically, only the small-scale dynamo is invoked (cf. e.g., Schekochihin et al. 2002, 2004a,b although it is known that large-scale dynamo action is not excluded and evidence for the possibility of large-scale dynamos even for stationary flows exists (cf. e.g., Alexakis 2011; Brandenburg & Subramanian 2005).
In hot plasma, the density ρ is extremely low and thus the kinematic viscosity ν = μ/ρ is high because the dynamic viscosity μ is almost independent of density in the limit ρ → 0, as already recognized by Maxwell (1867). It follows that η ≪ ν is satisfied, or that the magnetic Prandtl number Pm = ν/η ≫ 1 is large. It is the aim of this short paper to clearly demonstrate that the non-stationarity is capable of significantly enhancing the α-effect, that is, generating the large-scale EMF from small-scale fluctuations. The model considered here is very simple, based on incompressible magnetohydrodynamics (MHD), with a random, Gaussian, non-stationary forcing, which is a great simplification with respect to the real flows, which feature differential rotation, density stratification, self-gravity, and so on. This allows us to obtain analytic results. Nevertheless, despite the great simplifications, the result is generic in the sense that small-scale turbulence, which exhibits chirality and non-stationarity, induces an efficient large-scale dynamo process. Non-stationarity has already been shown to be a dynamically significant factor in the interstellar plasma turbulence for example by Korpi et al. (1999) and even for turbulent dynamo action (Mizerski 2018a,b, 2020). However, the former study was purely numerical and did not involve dynamo action, whereas the latter studies contain a limiting assumption of weak magnetic fields (small Hartmann numbers) and hence weak Lorentz force, which is mostly irrelevant in the case of hot, low-density turbulent plasma. In contrast, we consider here the opposite limit of strong magnetic fields. The effect of the Lorentz force is therefore strongly pronounced in the dynamo process. Explicit analytic results are rather rare, especially in the non-linear limit of a strong magnetic field. Even in the stationary case, the calculated EMF is therefore a new result.
2. Mathematical formulation
The evolution of the magnetic fields induced by the complex flow of an incompressible conducting fluid is governed by the following dynamical equations:
where the velocity field of the fluid flow is denoted by U(t, x), the magnetic field by B(t, x), and the total pressure Π = p/ρ + B2/2, and without loss of generality, we assume ∇ ⋅ f = 0; ν and η denote the viscosity and magnetic diffusivity (proportional to the electrical resistivity) of the fluid, respectively. For the sake of simplicity, we rescaled the magnetic field in the following way: 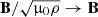 , so that the factor of
, so that the factor of 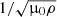 is lost, where ρ denotes the fluid density, and μ0 is the magnetic permeability of vacuum.
is lost, where ρ denotes the fluid density, and μ0 is the magnetic permeability of vacuum.
Next, denoting by angular brackets ⟨⋅⟩ the ensemble mean, we assume that the forcing f is homogeneous and isotropic but chiral (helical) and Gaussian with zero mean, ⟨f⟩ = 0 and is fully defined by the following correlation function:
where the function 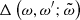 describes its statistical temporal properties,
describes its statistical temporal properties,
and is chosen in such a way that in the non-stationary case, the correlations in real space have a simple sinusoidal time dependence 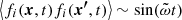 . Moreover, D0 and D1 are constants, the upper hat denotes a Fourier transform (cf. Eq. (4) below), and Pij(k) = δij − kikj/k2 is the projection operator on a plane perpendicular to the wave vector k; δij is the Kronecker delta, that is, the unity matrix, and ϵijk is the Levi-Civita symbol. The D1 term is the helical part of the forcing, introducing chirality into the flow. It can be easily shown that D0 > 0 and D1 ≤ kD0 for all k (cf. e.g., Moffatt & Dormy 2019 and Mizerski 2021a).
. Moreover, D0 and D1 are constants, the upper hat denotes a Fourier transform (cf. Eq. (4) below), and Pij(k) = δij − kikj/k2 is the projection operator on a plane perpendicular to the wave vector k; δij is the Kronecker delta, that is, the unity matrix, and ϵijk is the Levi-Civita symbol. The D1 term is the helical part of the forcing, introducing chirality into the flow. It can be easily shown that D0 > 0 and D1 ≤ kD0 for all k (cf. e.g., Moffatt & Dormy 2019 and Mizerski 2021a).
The non-helical part of the correlation function is inversely proportional to the third power of the wave number. This scaling exponent was shown by Yakhot & Orszag (1986) to correspond to the Kolmogorov-type turbulence in the absence of a magnetic field. Similar arguments can be put forward to show that the helical part must be inversely proportional to the fifth power of the wave number in order to reproduce the helicity spectrum for an isotropic, homogeneous, and stationary turbulence (cf. Brissaud et al. 1973; Chen et al. 2003; Mizerski 2021a).
Furthermore, we assume that the turbulence is forced only at small scales, that is, within the wave number band k > kℓ = 2π/ℓ, where ℓ denotes the size of the most energetic turbulent eddies, in other words, the forcing does not possess a large-scale component,
We consider the situation in which U, B and p are turbulent fields, spatially homogeneous on scales ≤ℓ. We introduce the following standard decomposition for turbulent flows into the mean and fluctuating parts:
and assume scale separation between the mean and fluctuating quantities. Therefore we treat the mean fields such that ⟨U⟩, ⟨B⟩, and ⟨p⟩ are locally uniform, but vary weakly on scales much greater than ℓ, that is, greatly exceeding the scales of the vigorous background turbulence.
The mean induction equation takes the form
and we identify the term ℰ = ⟨u×b⟩ as the large-scale electromotive force (EMF). We adopt the “first-order smoothing approximation” (FOSA; cf. Moffatt & Dormy 2019), in which squares and products of fluctuating quantities are ignored, and for clarity, we neglect all effects associated with the mean flow ⟨U⟩ in order to concentrate solely on the influence of the non-stationarity of turbulence on the α-effect. A consequence of the scale separation is that the gradients of means in the equations for fluctuations are negligible, thus the equations for the Fourier transforms of the turbulent fluctuations 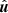 and
and  can be written in the form (cf. Moffatt & Dormy 2019)
can be written in the form (cf. Moffatt & Dormy 2019)
with
and we have eliminated the pressure from the Fourier transformed velocity equation with the use of the projection operator Pij(k) defined below (3c). We also introduced a short four-component notation q = (ω, k). Scale separation assumption, although common in mean field dynamo theory, eliminates shearing instabilities, since the effect of the mean velocity shear on the dynamics of fluctuations is eliminated. Hence turbulence is driven solely by the forcing. In addition, the shear-current effect (Krause & Rȧdler 1980; Rogachevskii & Kleeorin 2004), the so-called cross-helicity dynamo (Yokoi 2013), and the cross-helicity effect coupled with the mean magnetic strain (Yoshizawa 1990; Yokoi 2013) are also excluded by the scale separation assumption, likewise the effects of turbulent diffusion. Especially the latter can be important, as turbulent diffusion could account for an enhancement in the shift between the kinetic and magnetic components of waves and thus induction of the large-scale magnetic field via the standard, well-known mechanism or vivid amplification of magnetic energy via non-linear effects associated with the action of the Lorentz force (cf. Mizerski 2021a,b). Nevertheless, we concentrate here on the α-effect, as it is proportional to the lowest-order derivative of the mean magnetic field, and in this sense, may be expected to be dominant in many situations (cf. Moffatt & Dormy 2019). As mentioned in the introduction, the FOSA assumption allows us to obtain analytic results in the limit of strong magnetic fields, which are rather rare in the dynamo theory, and thus a clear estimation of the relative strength of the dynamo effect generated by non-stationarity.
Substitution for  from the first equation in Eq. (7) into the second one allows us to express the fluctuational magnetic field
from the first equation in Eq. (7) into the second one allows us to express the fluctuational magnetic field 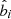 by the forcing
by the forcing 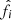 in an explicit way. Consequently, the large-scale EMF can be expressed in the following way:
in an explicit way. Consequently, the large-scale EMF can be expressed in the following way:
where in the second expression, we used a short notation for 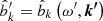 and similarly for
and similarly for 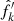 .
.
Hot, low-density plasma such as the ISM or plasma in some accretion disks is characterized by high values of the magnetic Prandtl number,
In the following, the mean EMF is explicitly calculated in the asymptotic limit defined by Eq. (10). In addition, strong magnetic fields, that is, large Hartmann numbers,
are assumed (for details, see the Appendix A). In many astrophysical applications, the Hartmann numbers 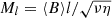 are still large for a wide range of dynamical length scales l ≪ ℓ; cf. Sect. 4 and estimates for the ISM and hot accretion disks.
are still large for a wide range of dynamical length scales l ≪ ℓ; cf. Sect. 4 and estimates for the ISM and hot accretion disks.
3. Stationary, high-Pm turbulence
In stationary turbulence, the force correlations Eq. (2) are given by (cf. also Eqs. (3a) and (3b))
We now introduce the latter formula into Eq. (9a), which yields
where we have made use of the fact that for any even function of ω, for instance, fe(ω), the integral 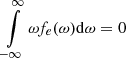 vanishes. Introducing new variables
vanishes. Introducing new variables
and using the relation
with 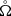 denoting the solid angle and θ the meridional angle in spherical coordinates (k, θ, φ), one can express the EMF in the following way:
denoting the solid angle and θ the meridional angle in spherical coordinates (k, θ, φ), one can express the EMF in the following way:
where
In the above we also introduced the upper cut-off K for the Fourier spectra, which in natural systems appears due to enhanced dissipation of energy at small scales; in particular, viscous dissipation of kinetic energy in Kolmogorov-type turbulence introduces the cut-off K = 2π(U/ν)3/4L−1/4, with L being the size of the entire system and U the large-scale velocity magnitude, hence typically kℓ ≪ K and the resistive cut-off, associated with magnetic diffusion, at Pm ≫ 1 exceeds K by several orders of magnitude. In the asymptotic limit Pm ≫ ℳ2 ≫ 1, which we assume to be satisfied for all kℓ ≤ k ≤ K in order to make analytical progress, one obtains
On defining the α(s) coefficient
we finally obtain for the case of stationary, high-Pm, strongly magnetized turbulence
An interesting observation can be made based on the fact that the α-effect is known to consist of two main contributions from the kinetic and magnetic helicities, that is, α ∼ ⟨ − u ⋅ ∇ × u + b ⋅ ∇ × b⟩ (cf. Pouquet et al. 1976; Yokoi 2013). In an analogous way as above, both contributions can be evaluated in the considered high-Pm limit, and the contribution from the magnetic helicity
turns out to dominate the kinetic helicity contribution, which is of the same sign, but 𝒪(Pm−1) times weaker. This emphasizes the fact that in the studied limit, the fluctuational Lorentz force, which plays a crucial part in the dynamo process, leads to the so-called essentially nonlinear dynamo (cf. Tobias et al. 2011; Mizerski 2021b).
4. Non-stationary, high-Pm turbulence
The real astrophysical turbulence is practically never stationary. As a first step towards more realistic models, we therefore consider the non-stationary forcing in a simple form defined by
with the function 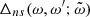 given in Eq. (3c). Introduction into Eq. (9a) leads to
given in Eq. (3c). Introduction into Eq. (9a) leads to
The latter integral is evaluated in the Appendix A in the asymptotic limit of large Pm and strong magnetic fields Pm ≫ ℳ2 ≫ 1 with the additional simplifying assumption
and by the use of Eq. (15), which yields
The assumption in Eq. (24) on the one hand ensures that the evolution of the mean EMF is very slow, much slower than the turbulent fluctuations, but on the other hand, it implies weak non-stationarity. Nevertheless, even in this restrictive limit (the timescale of magnetic diffusion is extremely long), the α-effect induced by non-stationarity in high-Pm, strongly magnetized plasma is likely to be significantly stronger than the stationary, diffusive one since the ratio
exceeds unity when
The latter is, in fact, a rather mild restriction, since by assumption, M ≫ 1 and even 106M−3 < 1 is typically satisfied in hot, low-density plasma. For example, in the case of the ISM of the Milky Way galaxy, with the aid of Beck et al. (1996) and Brandenburg & Subramanian (2005), we can take the following characteristic values:
which lead to PmISM ≈ 1014 ≫ 1, MISM ≈ 1012, and hence 5 × 105M−3 ≈ 5 × 10−31 for the ISM; ℓISM was taken as the supernova scale at which the turbulence is stirred (cf. also Schekochihin et al. 2004a). A second example involves active galactic nuclei (AGN), that is, hot accretion disks around the supermassive central black holes in spiral galaxies, for which we take the following characteristic values (cf. Brandenburg & Subramanian 2005; Modjaz et al. 2005):
This leads to PmAGN ≈ 104 ≫ 1, MAGN ≈ 104, and hence 5 × 105M−3 ≈ 5 × 10−7 for the AGNs.
In both example cases, that is, for the ISM and for the AGN, the particular assumption Pm ≫ ℳ2 made in order to facilitate and explicitly calculate the Fourier integrals is not strictly satisfied for all values of the wave number k. Nevertheless, the result highlights the importance of non-stationarity of turbulent magnetized plasma, since even weak non-stationarity leads to a significant enhancement of the α-effect.
5. Conclusions
The most important disadvantage of our theory is naturally the simplification of the physical model, the assumptions of isotropy, and the homogeneity of the turbulent flow, which are necessary in order to provide explicit analytic results. Real turbulence in natural hot, low-density plasma is anisotropic and inhomogeneous due to the action of differential rotation, gravity, density stratification, and so on. Nevertheless, despite the great simplification, our analysis clearly showed the importance of non-stationarity of the high-Pm turbulence in the large-scale dynamo process, which could easily dominate the standard α-effect based on the creation of a phase shift between the velocity and magnetic turbulent fluctuations by the very weak magnetic diffusion. It follows that non-stationarity should never be neglected in investigations of the high-Pm plasma, where the standard diffusive α-effect mechanism is weak.
Acknowledgments
This work was financed by the Polish National Science Centre (Grant No 2017/26/E/ST3/00554) and from the subvention of the Ministry of Science and Higher Education in Poland (statutory activity).
References
- Alexakis, A. 2011, Phys. Rev. E, 83, 036301 [NASA ADS] [CrossRef] [Google Scholar]
- Balbus, S. A., & Hawley, J. F. 1991a, ApJ, 376, 214 [Google Scholar]
- Balbus, S. A., & Hawley, J. F. 1991b, ApJ, 376, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, R., Brandenburg, A., Moss, D., Shukurov, A., & Sokoloff, D. 1996, ARA&A, 34, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Brandenburg, A., & Subramanian, K. 2005, Phys. Rep., 417, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Brissaud, A., Frisch, U., Léorat, J., Lesieur, M., & Mazure, A. 1973, Phys. Fluids, 16, 1366 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, Q., Chen, S., Eyink, G. L., & Holm, D. D. 2003, Phys. Rev Lett., 90, 214503 [NASA ADS] [CrossRef] [Google Scholar]
- Ferrière, K. 1992, ApJ, 389, 286 [CrossRef] [Google Scholar]
- Korpi, M. J., Brandenburg, A., Shukurov, A., Tuominen, I., & Nordlund, Å. 1999, ApJ, 514, L99 [NASA ADS] [CrossRef] [Google Scholar]
- Krause, F., & Rȧdler, K.-H. 1980, Mean-field Magnetohydrodynamics and Dynamo Theory (Oxford: Pergamon Press) [Google Scholar]
- Maxwell, J. C. 1867, Philos. Trans. R. Soc. London, 157, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Modjaz, M., Moran, J. M., Kondratko, P. T., & Greenhill, L. J. 2005, ApJ, 626, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Moffatt, H. K., & Dormy, E. 2019, Self-exciting Fluid Dynamos (Cambridge: Cambridge University Press) [CrossRef] [Google Scholar]
- Mizerski, K. A. 2018a, SIAM J. Appl. Math. (SIAP), 78, 1402 [CrossRef] [Google Scholar]
- Mizerski, K. A. 2018b, J. Plasma Phys., 84, 735840405 [NASA ADS] [CrossRef] [Google Scholar]
- Mizerski, K. A. 2020, ApJS, 251, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Mizerski, K. A. 2021a, J. Fluid Mech., 926, A13 [NASA ADS] [CrossRef] [Google Scholar]
- Mizerski, K. A. 2021b, Phys. Rev. E, 104, L053102 [NASA ADS] [CrossRef] [Google Scholar]
- Pouquet, A., Frisch, U., & Léorat, J. 1976, J. Fluid Mech., 77, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Roberts, P. H. 1994, Fundamentals of Dynamo Theory. eds. M. Proctor, & A. Gilbert, Lectures on Solar and Planetary Dynamos (Cambridge: Cambridge University Press), 1 [Google Scholar]
- Rogachevskii, I., & Kleeorin, N. 2004, Phys. Rev. E, 70, 046310 [NASA ADS] [CrossRef] [Google Scholar]
- Schekochihin, A. A., Cowley, S. C., Hammett, G. W., Maron, J. L., & McWilliams, J. C. 2002, New J. Phys., 4(84), 1 [NASA ADS] [CrossRef] [Google Scholar]
- Schekochihin, A. A., Cowley, S. C., Taylor, S. F., Maron, J. L., & McWilliams, J. C. 2004a, ApJ, 612, 276 [NASA ADS] [CrossRef] [Google Scholar]
- Schekochihin, A. A., Cowley, S. C., Taylor, S. F., et al. 2004b, Phys. Rev. Lett., 92, 084504 [NASA ADS] [CrossRef] [Google Scholar]
- Steenbeck, M., Krause, F., & Radler, K. H. 1966, Z. Naturforsch. 21a, 369 [English translation: Roberts & Stix (1971), pp. 29–47] [NASA ADS] [CrossRef] [Google Scholar]
- Tobias, S. M., Cattaneo, F., & Brummel, N. 2011, ApJ, 728, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Yakhot, V., & Orszag, S. A. 1986, J. Sci. Comp., 1, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Yokoi, N. 2013, Geophys. Astrophys. Fluid Dyn., 107, 114 [Google Scholar]
- Yoshizawa, A. 1990, Phys. Fluids B, 2, 1589 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Calculation of the (23) integral
Using the assumption 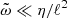 , the large-scale EMF in non-stationary turbulence (23) can be expressed as follows:
, the large-scale EMF in non-stationary turbulence (23) can be expressed as follows:
Next, using the variables (14) and the formula (15) integration over the azimuthal angle in the wave vector space leads to
where
and we have recognized the last integral in Eq. (A.1) next to 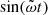 as the same as Eq. (13), hence the result in Eq. (16) with the function 𝒢(ϖ,X,ℳ) defined in Eq. (17) was used. We now evaluate each of the integrals in Eq. (A.2) separately, in the limit Pm ≫ ℳ2 ≫ 1,
as the same as Eq. (13), hence the result in Eq. (16) with the function 𝒢(ϖ,X,ℳ) defined in Eq. (17) was used. We now evaluate each of the integrals in Eq. (A.2) separately, in the limit Pm ≫ ℳ2 ≫ 1,
and the 𝒢-integral is the same as in the stationary case; cf. Sect. 3. It is now a straightforward task to write down the leading order form of the EMF,
hence at the leading order for small 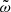 (for times
(for times 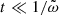 ),
),
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



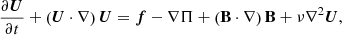
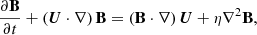

![$$ \begin{aligned}&\left\langle \hat{f}_{i}(\boldsymbol{k},\omega )\hat{f}_{j}(\boldsymbol{k^\prime },\omega^\prime )\right\rangle \nonumber \\&\qquad =\left[\frac{D_{0}}{k^3}P_{ij}(\boldsymbol{k})+{i}\frac{D_1}{k^5}\epsilon _{ijk}k_k\right]\delta (\boldsymbol{k}+\boldsymbol{k^\prime })\Delta \left(\omega ,\omega^\prime ;\tilde{\omega }\right), \end{aligned} $$](/articles/aa/full_html/2022/04/aa42488-21/aa42488-21-eq6.gif)
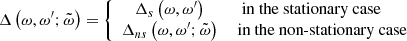
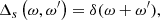
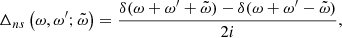
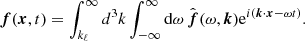
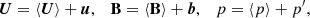
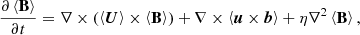
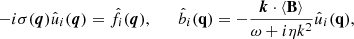
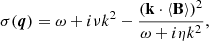
![$$ \begin{aligned}&\mathcal{E} _{i}= \epsilon _{ijk}\left\langle u_{j} b_{k}\right\rangle \nonumber \\&\quad = \epsilon _{ijk}\int \mathrm{d} ^{4}q\int \mathrm{d} ^{4}q^\prime \left\langle \hat{u}_{j}(\boldsymbol{q})\hat{b}_{k}(\boldsymbol{q^\prime })\right\rangle \mathrm{e} ^{\mathrm{i} \left[\left(\mathbf k +\boldsymbol{k^\prime }\right)\cdot \boldsymbol{x}-\left(\omega +\omega^\prime \right)t\right]}\end{aligned} $$](/articles/aa/full_html/2022/04/aa42488-21/aa42488-21-eq22.gif)
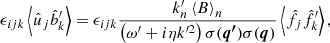
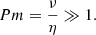
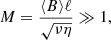
![$$ \begin{aligned}&\left\langle \hat{f}_{i}(\boldsymbol{k},\omega )\hat{f}_{j}(\boldsymbol{k^\prime },\omega^\prime )\right\rangle \nonumber \\&\quad =\left[\frac{D_{0}}{k^3}P_{ij}(\boldsymbol{k})+{i}\frac{D_1}{k^5}\epsilon _{ijk}k_k\right]\delta (\boldsymbol{k}+\boldsymbol{k^\prime })\delta (\omega +\omega^\prime ). \end{aligned} $$](/articles/aa/full_html/2022/04/aa42488-21/aa42488-21-eq29.gif)
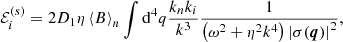
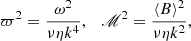
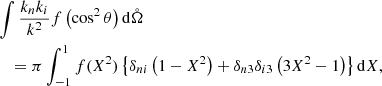
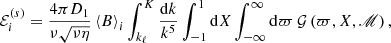
![$$ \begin{aligned}&\mathcal{G} \left(\varpi ,X,\fancyscript {M}\right)\nonumber \\&\quad =\frac{X^{2}}{\varpi ^{4}+\varpi ^{2}\left[\left(Pm+Pm^{-1}\right)-2\fancyscript {M}^{2}X^{2}\right]+\left(1+\fancyscript {M}^{2}X^{2}\right)^{2}}. \end{aligned} $$](/articles/aa/full_html/2022/04/aa42488-21/aa42488-21-eq36.gif)
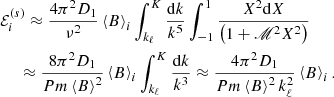
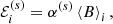
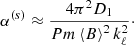
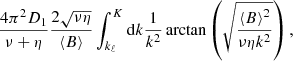
![$$ \begin{aligned}&\left\langle \hat{f}_{i}(\boldsymbol{k},\omega )\hat{f}_{j}(\boldsymbol{k^\prime },\omega^\prime )\right\rangle \nonumber \\&\quad =\left[\frac{D_{0}}{k^3}P_{ij}(\boldsymbol{k})+{i}\frac{D_1}{k^5}\epsilon _{ijk}k_k\right]\delta (\boldsymbol{k}+\boldsymbol{k^\prime })\Delta _{ns}\left(\omega ,\omega^\prime ;\tilde{\omega }\right), \end{aligned} $$](/articles/aa/full_html/2022/04/aa42488-21/aa42488-21-eq41.gif)
![$$ \begin{aligned}&\mathcal{E} _{i}^{(ns)}= D_{1}\left\langle B\right\rangle _n \int \mathrm{d} ^{4}q\frac{k_n k_{i} }{k^{5}}\left[\frac{ \mathrm{e} ^{-\mathrm{i} \tilde{\omega }t} }{\left(-\omega +\tilde{\omega }+\mathrm{i} \eta k^{2}\right)\sigma (\boldsymbol{k},-\omega +\tilde{\omega })\sigma (\mathbf k ,\omega )}\right.\nonumber \\&\qquad \quad \left.-\frac{ \mathrm{e} ^{{i}\tilde{\omega }t} }{\left(-\omega -\tilde{\omega }+{i}\eta k^{2}\right)\sigma (\boldsymbol{k},-\omega -\tilde{\omega })\sigma (\boldsymbol{k},\omega )}\right]. \end{aligned} $$](/articles/aa/full_html/2022/04/aa42488-21/aa42488-21-eq43.gif)
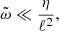
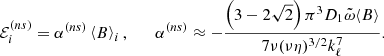
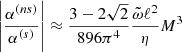
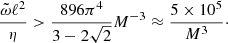
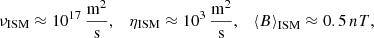
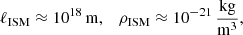
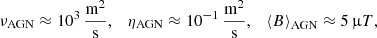
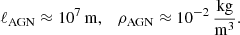
![$$ \begin{aligned} \mathcal{E} _{i}^{(ns)}=&2D_{1}\tilde{\omega }\cos \left(\tilde{\omega }t\right)\left\langle B\right\rangle _{m}\int \mathrm{d} ^{4}q\frac{k_{m}k_{i}}{k^{5}}\frac{1}{\left|\sigma (\mathbf q )\right|^{2}\left(\omega -\mathrm{i} \eta k^{2}\right)^{2}}\left[{0cm}{0.8cm}1+\right.\nonumber \\&\qquad \qquad \qquad \qquad \qquad \left.\sigma (\mathbf q )\frac{\left(\omega -\mathrm{i} \eta k^{2}\right)^{2}+\left(\mathbf k \cdot \left\langle \mathbf B \right\rangle \right)^2}{\left|\sigma (\mathbf q )\right|^{2}\left(\omega -\mathrm{i} \eta k^{2}\right)}\right]\nonumber \\&+2D_{1}\eta \sin \left(\tilde{\omega }t\right)\left\langle B\right\rangle _{n}\int \mathrm{d} ^{4}q\frac{k_{n}k_{i}}{k^{3}}\frac{1}{\left(\omega ^{2}+\eta ^{2}k^{4}\right)\left|\sigma (\mathbf q )\right|^{2}}. \end{aligned} $$](/articles/aa/full_html/2022/04/aa42488-21/aa42488-21-eq53.gif)
![$$ \begin{aligned} \mathcal{E} _{i}^{(ns)}&\nonumber \\&=\frac{4\pi D_1}{(\nu \eta )^{3/2}}\tilde{\omega }\cos \left(\tilde{\omega }t\right)\left\langle B\right\rangle _{i}\int _{k_{\ell }}^{K}\frac{\mathrm{d} k}{k^{7}}\int _{-1}^{1}\mathrm{d} X\int _{-\infty }^{\infty }\mathrm{d} \varpi \left[\mathcal{H} _1\left(\varpi ,X,\fancyscript {M}\right)\right.\nonumber \\&\qquad \qquad \qquad \qquad \left.+\mathcal{H} _2\left(\varpi ,X,\fancyscript {M}\right)+\fancyscript {M}^2\mathcal{H} _3\left(\varpi ,X,\fancyscript {M}\right)\right]\nonumber \\& \quad +\frac{4\pi D_{1}}{\nu \sqrt{\nu \eta }}\sin (\tilde{\omega }t)\left\langle B\right\rangle _{i}\int _{k_{\ell }}^K\frac{\mathrm{d} k}{k^{5}}\int _{-1}^{1}\mathrm{d} X\int _{-\infty }^{\infty }\mathrm{d} \varpi \,\mathcal{G} \left(\varpi ,X,\fancyscript {M}\right), \end{aligned} $$](/articles/aa/full_html/2022/04/aa42488-21/aa42488-21-eq54.gif)
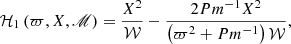
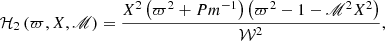
![$$ \begin{aligned} \mathcal{H} _3\left(\varpi ,X,\fancyscript {M}\right)&\nonumber \\&=\frac{\left[ \varpi ^{4}-\varpi ^{2}\left(3Pm^{-1}+3+\fancyscript {M}^{2}X^{2}\right)+Pm^{-1}\left(1+\fancyscript {M}^{2}X^{2}\right)\right] X^{4}}{\left(\varpi ^{2}+Pm^{-1}\right)\mathcal{W} ^{2}}, \end{aligned} $$](/articles/aa/full_html/2022/04/aa42488-21/aa42488-21-eq57.gif)
![$$ \begin{aligned} \mathcal{W} = \varpi ^{4}+\varpi ^{2}\left[\left(Pm+Pm^{-1}\right)-2\fancyscript {M}^{2}X^{2}\right]+\left(1+\fancyscript {M}^{2}X^{2}\right)^{2},\nonumber \\ \end{aligned} $$](/articles/aa/full_html/2022/04/aa42488-21/aa42488-21-eq58.gif)