| Issue |
A&A
Volume 659, March 2022
|
|
|---|---|---|
| Article Number | A54 | |
| Number of page(s) | 14 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/202142705 | |
| Published online | 04 March 2022 | |
Astrochemical significance and spectroscopy of tetratomic [H, P, S, O]
1
Department of Chemistry, University of Pennsylvania,
Philadelphia,
PA
19104-6243,
USA
e-mail: vje12@sas.upenn.edu, frjoseph@sas.upenn.edu
2
Department of Earth and Environment Science, University of Pennsylvania,
Philadelphia,
PA
19104-6243,
USA
e-mail: trabelsi@sas.upenn.edu
Received:
19
November
2021
Accepted:
18
January
2022
Context. Phosphorus is integral to life on Earth, and its role in the chemistry of the interstellar medium is highly debated and unknown. Only a handful of phosphorus-bearing species have been detected thus far, with the most recent confirmed detection taking place in 2014. The simultaneous detection of molecules such as PO, SH, and OH indicate the possibility of reactive intermediate species existing in the interstellar medium and circumstellar envelopes of evolved stars. To explore this possibility, the [H, P, S, O] tetratomic isomer family was characterized using high level ab initio methods.
Aims. The aim of this study is to provide rotational, vibrational, and electronic spectroscopic data to drive experimental and observational detection of new phosphorus and sulfur-bearing molecules. Additionally, chemical pathways are explored to explain possible reservoirs for the as of yet undetected PH and PS diatomic molecules.
Methods. Coupled cluster quantum chemistry methods were used to calculate the equilibrium electronic structure followed by the anharmonic treatment of the cubic and quartic force fields to obtain accurate rotational and vibrational data. Møller–Plesset perturbation theory in conjunction with coupled cluster methods were used to explore bimolecular reaction pathways. Multi-reference methods were then used to characterize the photochemical pathways of the excited electronic states and simulate the electronic absorption spectrum.
Results. The reaction between detected molecules SH and PO is highly exothermic and forms the HSPO isomer. Deeply submerged transition state barriers allow for facile isomerization to other isomers, especially HOPS. The dominant photochemical process predicted for HOPS is dissociation to form OH + PS, while that of HSPO is a combination of photodissociation to form H + SPO and SH + PO, depending on the wavelength of light absorbed. If PH and PS are formed in the early outflows from evolved stars, bimolecular reactions may act as a reservoir and partially account for their lack of detection to date. The electronic absorption spectrum is predicted to be congested in the 175–200 nm region for both HOPS and HSPO. Differentiating peaks exist >400 nm, which can be used for spectral assignment. Vibrationally corrected rotational constants and anharmonic vibrational frequencies were calculated to assist in the laboratory and observation identification of the most stable molecules. The PO stretch is predicted to be the most intense vibrational mode in both HOPS isomers, and a frequency difference of 20 cm−1 may prove to help differentiate the conformers in an experimental spectrum.
Key words: astrochemistry / techniques: spectroscopic / molecular data / circumstellar matter / ISM: molecules / ultraviolet: ISM
© ESO 2022
1 Introduction
Phosphorus is considered an essential element in biogenic processes due to its important roles in living systems (i.e., deoxyribonucleic acid (DNA), ribonucleic acid (RNA), and adenosine triphosphate (ATP)) (Powner et al. 2009). For instance, it plays a critical role in cell development and may be linked to the origin of life on Earth (Maciá et al. 1997). From an astrobiological point of view, phosphorus may serve as an important marker for life on temperate bodies (Hinkel et al. 2020).
Astrochemically, the number of detected phosphorus-bearing molecules in the interstellar medium (ISM) or circumstellar envelopes (CSEs) of various stars is relatively small compared to organic molecules or those containing oxygen or sulfur (Endres et al. 2016). The lack of detection of phosphorus-bearing molecules in the ISM results from the low cosmic abundance of phosphorus relative to hydrogen and the production of phosphorus only coming from large stars (Sonneborn et al. 2006; Maciá 2005). This low abundance may decrease the probability of phosphorus-bearing molecular formation via various mechanisms, such as reactive collision. Alternatively, the existence of undetected small phosphorus-bearing molecules is hypothesized and debated. From a chronological point of view, the number of detected P-bearing molecules has increased as (i) the amount of theoretical and experimental spectroscopic data increases and (ii) the sensitivity of space telescopes escalates.
The formation of such molecules in circumstellar envelopes is likely due to photodissociation processes, shock-initiated reactions, and thermodynamically controlled synthesis. For instance, in the gas phase, PO is formed via the reaction P + OH → PO + H, while the formation of PN depends on the abundance of PO through N + PO → PN + O (Jiménez-Serra et al. 2018; García de la Concepción et al. 2021). The CP radical is the daughter of HCP (Namai et al. 2009; Agúndez et al. 2007), that is HCP + hν → CP + H following the photodesorption of HCP from the surface of dust grains. Other P-bearing molecules may exist, especially those containing PO, PN, or PS bonds. Such examples include the OPCN and SPCN molecules, which could be intermediate complexes during the bimolecular reactions of the detected diatomics PO, PN, CO, SN, CP, CS, and CN (Tenenbaum et al. 2007; Yamaguchi et al. 2011; Ziurys 1987; Ziurys et al. 2018; Gottlieb et al. 1975; Milam et al. 2008; Guelin et al. 1990). Recently, exploration of the P + SO → PO + S reaction showed that this reaction is overwhelmingly bimolecular with a predicted rate of 2.1 × 10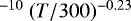 cm3 molecule−1 s−1 at pressures relevant to the ISM (Trabelsi et al. 2021).
cm3 molecule−1 s−1 at pressures relevant to the ISM (Trabelsi et al. 2021).
There is a current dearth of information on molecular reaction studies involving the PS diatomic and spectroscopic data of molecules containing a PS bond. This void in knowledge surrounding PS may explain why its lack of detection remains an open question. It is well known that mass loss from evolved stars results in the formation of complex chemical environments (Ziurys 2006). Therefore, the CSEs surrounding these evolved stars are excellent bench tests to understand many processes in space, such as chemical synthesis or photodissociation processes. Among the species that may exist in a CSE or serve as intermediates in chemical reactions includes [H, P, S, O]. This molecular system is isoelectronic to the well-known nitrous acid (HONO) (Ramazan et al. 2004), metaphosphorous acid (HOPO) (Bell et al. 2000; Chu et al. 2020), and thionitrous acid or S-nitrosothiol [H, S, N, O] (Filipovic et al. 2012), which play important roles in atmospheric and biological medium. For example, the hydrolysis of NO2 is a major source of HONO and subsequently OH radicals in polluted urban areas (Ramazan et al. 2004).
Previously, Mathieu et al. (1989) used SCF and configuration interaction methods to explore the geometry and bonding properties of some [H, P, S, O] isomers. Later, Yu-Juan et al. (2010) studied the structures and stabilities of the isoelectronic HNOS to understand the bonding nature of HNO2 and HNS2. Further, Brinkmann & Carmichael (2004) used B3LYP to determine the electronic structure of another isoelectronic molecule, HOPO. Later, Begue et al. (2006) utilized DFT methods to predict the photoelectron spectrum of HPO2 isomers. To date, there have been no publications using high-level theoretical methods to address the astrochemical impact of the tetratomic molecular system containing the elements [H, P, S, O] despite the importance of all four elements in the formation of life. The thermodynamics and spectroscopy of the included triatomic systems are well known, such as PSO (Trabelsi et al. 2021), HPO (Francisco 2003; Puzzarini 2006; Kitchens & Fortenberry 2016), HSO (Cazzoli et al. 2016), and the tetratomic system may be regarded as atom + triatom reaction (e.g., H + PSO or S + HPO) or diatom + diatom reaction (e.g., PH + SO, SP + OH or SH + PO). Many of these diatomic species involving sulfur and phosphorus atoms have been detected in space, including PO, PN, SO, and SH. However, the lack of detection of molecules such as PH and PS is currently an unresolved problem requiring exploration of the possible formation and isomerization mechanisms as well as the properties of the involved intermediate species.
In this paper, [H, P, S, O] isomers are treated in the gas-phase by means of ab initio methodology. The calculations presented here offer deep insights on the structure, thermochemistry, and spectroscopy of these isomers and will aid in the detection of this astrochemically-relevant species in the laboratory and in space.
2 Computational methods
Exploration of the stationary points of the [H, P, S, O] molecular system was initially carried out using Møller–Plesset second order Perturbation Theory (MP2) (Møller & Plesset 1934; Frisch et al. 1990a,b; Head-Gordon & Head-Gordon 1994; Head-Gordon et al. 1988; Sæbø & Almlöf 1989) with the 6-311++G(d, p) basis set (McLean & Chandler 1980; Krishnan et al. 1980). Following the initial survey, transition state structures connecting various isomers of [H, P, S, O] were located using MP2/6-311++G(d, p) and confirmed via an intrinsic reaction coordinate (IRC) calculation. To achieve a quantitative picture of the ground state potential energy surface, coupled cluster theory with single, double, and perturbative triple excitations [CCSD(T)] (Knowles et al. 1993, 2000) single point calculations employing the aug-cc-pV(Q+d)Z basis set were performed at the MP2 equilibrium geometries. Entrance channel pathways were explored via relaxed scans and individual searches for transition states. Following this, higher level calculations on the electronic structure, rotational constants, and harmonic vibrational frequencies of each isomer were performed using CCSD(T) together with the Dunning basis sets aug-cc-pV(X+d)Z (X = T, Q, 5) (Dunning 1989; Woon & Dunning 1993; Kendall et al. 1992), including additional tight d functions on the sulfur and phosphorous atoms (Dunning et al. 2001). CCSD(T) including all electrons was then performed using the second order Douglas-Kroll–Hess Hamiltonian in conjunction with the contracted relativistic Douglas–Kroll aug-cc-pwCVTZ-DK basis set to correct for scalar relativistic and core-correlation effects (Jorge et al. 2009). The aforementioned combinationof level of theory and basis set will be referred to as CCSD(T)-AE/TZ-DK. Finally, explicit correlation of the electrons was included using the CCSD(T)-F12b method (Werner et al. 2011) with the Dunning basis sets aug-cc-pVXZ (X = T, Q, 5). Single-reference character of the wavefunction was confirmed via single-state complete active spaceself-consistent field theory in addition to the coupled cluster T1 diagnostic. Energies and geometry parameters were then extrapolated to the complete basis set limit using the two-point (Q, 5) extrapolation scheme E(x)= ECBS + AX−3, where E(x) is the value calculated using the basis set of cardinal number X, ECBS is the extrapolated energy, and A is a parameter fit in the least-squares fitting procedure. Mulliken population analysis was performed on cis-HOPS using MOLPRO. Corrections to the rotational constants, spectroscopic data, and anharmonic vibrational data were calculated for the four lowest energy isomers at the CCSD(T)/aug-cc-pV(T+d)Z level of theory using CFOUR (Matthews et al. 2020; Stanton et al. 2019). Permanent dipole moments for each isomer were calculated using the finite field method (field strengths of 0, 0.005, and −0.005 au) as implemented in MOLPRO.
Vertical excitation energies were calculated in the Cs symmetry group using the multireference configuration interaction method including the Davidson correction to the energy (MRCI+Q) (Knowles & Werner 1992, 1988; Szalay & Bartlett 1993) as well as equation-of-motion coupled cluster including single and double excitations (EOM-CCSD) (Korona & Werner 2003). The MRCI calculations are based on a state-averaged complete active space self-consistent field (SA-CASSCF) (Knowles & Werner 1985; Werner & Knowles 1985) reference wavefunction employing a full valence active space of 18 electrons in 13 orbitals, including 10 A′ and 3 A′′ orbitals. The state-averaged wavefunction includes 4 A′ and 4 A′′ states in each calculation, for a total of eight equally weighted states. The aug-cc-pV(T+d)Z and 6-311++G(d, p) basis sets were used for the MRCI and EOM-CCSD methods, respectively. Transition dipole moments (μ) were calculated using MRCI and were utilized to calculate oscillator strengths of each electronic transition via Eq. (1):
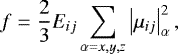 (1)
(1)
where Eij is the vertical excitation energy between initial and final electronic states i and j calculated at each level of theory. Following this, the adiabatic potential energy surfaces along various bond coordinates were constructed using the MRCI+Q method in conjunction with the aug-cc-pV(T+d)Z basis set.
Finally, to simulate the electronic absorption spectrum of cis-HOPS and cis-HSPO, the ground state geometry was optimized and normal mode analysis was performed at the CCSD(T) level of theory with the aug-cc-pV(Q+d)Z basis set. Following this, a set of initial geometries was obtained using a Wigner distribution based on the ground state harmonic frequencies calculated at the CCSD(T)/aug-c-pV(Q+d)Z level of theory. At each Wigner geometry, vertical excitation energies were calculated using the SS-SR-CASPT2 method (Celani & Werner 2000; Werner 1996) and transition dipole moments with the CASSCF method, both employing the aug-cc-pV(T+d)Z basis set. In these calculations, the CASSCF reference wavefunction was state averaged over the lowest eight singlet states and utilized the same active space as the MRCI calculations. Using the SArCASM package (Karsili et al. 2018), the excitation energy dependent photoabsorption cross section P(E) was determined via Eq. (2):
![\begin{equation*}P(E) = \frac{\pi e^2}{2{m_{\textrm{e}}\textrm{c}}\epsilon_0}\sum^M_{j=1}\left[\frac{1}{N_{\textrm{tot}}}\sum^{N_{\textrm{tot}}}_{N=1}f_{ij}^N g\left(E-\Delta E^N_{ij},\delta\right)\right],\end{equation*}](/articles/aa/full_html/2022/03/aa42705-21/aa42705-21-eq3.png) (2)
(2)
where g is a Lorentzian line shape function given by Eq. (3):
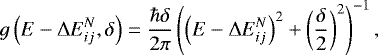 (3)
(3)
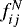 is the oscillator strength calculated via Eq. (1) at each point N, me and e are the mass and charge of an electron, respectively, and c is the speed of light. The internal sum in Eq. (2) is over the total number of Wigner geometries (Ntot = 106) while the external sum includes transitions from the initial state i to final states j. δ is a broadening factor which is arbitrarily set to 0.1 eV. The Wigner points were generated using Newton-X (Barbatti et al. 2014, 2018), and all calculations were performed in the C1 symmetry group.
is the oscillator strength calculated via Eq. (1) at each point N, me and e are the mass and charge of an electron, respectively, and c is the speed of light. The internal sum in Eq. (2) is over the total number of Wigner geometries (Ntot = 106) while the external sum includes transitions from the initial state i to final states j. δ is a broadening factor which is arbitrarily set to 0.1 eV. The Wigner points were generated using Newton-X (Barbatti et al. 2014, 2018), and all calculations were performed in the C1 symmetry group.
The MP2 calculations were performed using Gaussian 16 (Frisch, et al. 2016) and all CASSCF, MS-CASPT2, MRCI, and CCSD(T) calculations were carried out using MOLPRO 2019 (Werner et al. 2019).
3 Results and discussion
3.1 Ground state potential energy surface
To explore the [H, P, S, O] system, preliminary calculations were performed at the MP2/6-311++G(d, p) level of theory, and 16 distinct isomers were found. The isomers can be separated into three groups: HOPS and HSPO which interconvert and correlate with the SH+ PO and PS + OH asymptotes, HPSO and HOSP which interconvert and correlate with the PS + OH and PH + SO asymptotes, and high energy isomers HPOS and HSOP. Transition states (TSs) connect isomers within the various groups, providing isomerization pathways along the ground state potential energy surface shown in Fig. 1. All entrance channel pathways were found to be barrierless. The energy at each stationary point was evaluated with the CCSD(T)/aug-cc-pV(Q+d)Z level of theory at the MP2 optimized geometry and includes MP2 zero-point energy. Each isomer is identified by name and number according to stability for ease of reference.
The first pathway for this system begins with the reaction between SH + PO, two molecules detected in space, to form either HSPO or HSOP depending on angle of attack. The reaction to form HSOP species is endothermic by ~11–12 kcal mol−1 and will not participate in the low temperature and pressure environment of the ISM. The formation of HSPO is much more likely. The reaction to form cis-HSPO (4) is highly exothermic by 72.8 kcal mol−1, indicating a large amount of internal energy will be partitioned into rotation and vibration of the molecule due to the low molecular density in space. This value (72.8 kcal mol−1) also represents the bond dissociation energy (BDE) for cis-HSPO (4) to form SH + PO if beginning from a thermalized molecule. The transition state connecting cis-HSPO (4) to trans-HSPO (3), rotation around the PS bond, is 17.2 kcal mol−1 above cis-HSPO (4) and is deeply submerged below the reactant energy (−55.6 kcal mol−1). Interconversion between the cis- and trans-HSPO species is expected to occur readily.
The other potentially more interesting transition state leading from cis-HSPO (4) results in the formation of cis-HOPS (1), the ground state isomer of this system. Cis-HOPS (1) is predicted to be 6.6 kcal mol−1 more stable than cis-HSPO (4). The transition state barrier connecting these molecules, which involves an H-atom transfer from the sulfur atom to the terminal oxygen, lies 22.2 kcal mol−1 above cis-HSPO but is deeply submerged below the reactant energy (−50.6 kcal mol−1), indicating facile isomerization. This transition state is characterized by a large imaginary frequency (1656i), the presence of which signifies a tight transition state and the propensity for tunneling to further accelerate this isomerization process.
Continuing along the isomerization pathway from cis-HOPS (1), rotation around the PO bond to form trans-HOPS(2) is energetically favorable. The transition state leading to trans-HOPS (2) lies approximately 8.6 kcal mol−1 above cis-HOPS (1). This rotational transition state barrier is lower than that of HSPO due to the single-bond nature of the P–O bond in the HOPS isomer, whereas the S–P bond in HSPO is of higher bond order. Interconversion between cis-HOPS (1) and trans-HOPS (2) will occur easily unless a cooling process (such as collisional stabilization) locks the molecule into a specific conformation. Cis-HOPS (1) and trans-HOPS (2) both correlate with the PS + OH dissociation asymptote, corresponding to a BDE of 101.0 and 98.3 kcal mol−1, respectively.
The four most stable isomers have large BDEs relative to the final dissociation pathway that forms H + SPO. Dissociation to form H + SPO will occur at an energy of 89.9, 82.2, 78.9, and 78.3 kcal mol−1, respectively.
The second group of molecules also correlates with the PS + OH asymptote but connects on the other side with the PH + SO asymptote (the PS + OH asymptote lies below the PH + SO asymptote by 6.2 kcal mol−1). Both asymptotes include one molecule that has been detected in the ISM (OH and SO) and one that has not (PS and PH). The more energetically favorable of which is the PH + SO reaction that may produce cis-HPSO (8) or trans-HPSO (6). This reaction to form trans-HSPO (6) and cis-HPSO (8) is exothermic by 58.3 and 56.7 kcal mol−1, respectively. The transition state barrier to rotation between these two isomers is large, requiring 43.2 and 41.6 kcal mol−1 depending on direction, although, this TS barrier is submerged below the PH + SO reactants, so interconversion will occur spontaneously. A transition state was also found between trans-HPSO (6) and cyc-SOP(H) (7) that is predicted to be 37.2 kcal mol−1 relative to trans-HPSO (6); this TS is also submerged below the starting reactants.
Cis-HPSO (8) is connected to cis-HOSP (9) via a 29.6 kcal mol−1 transition state barrier. This H-atom transfer TS is characterized by the largest imaginary frequency found for this group of molecules (1749i), indicating a tight transition state where tunneling will play a large role. Despite the high barrier, this TS is submerged below both asymptotes and isomerization will occur if either cis-HOSP (9) or cis-HPSO (8) are formed via reaction of PS + OH or PH + SO. A transition state via rotation around the PO bond connects cis-HOSP (9) and trans-HOSP (10).
The third and final reaction pathway connects the SH + PO and PH + SO asymptotes via the HPOS and HSOP intermediates. This pathway is only feasible through the PH + SO reaction as it is exothermic by ~27 kcal mol−1 in this direction. The transition state connecting trans-HPOS (12) and cis-HPOS (11) occurs through the POS bending motion (imaginary frequency 802i) and has an energy of 7.5 kcal mol−1 relative to trans-HPSO (12). The H-atom transfer TS barrier from cis-HPSO (11) to HSOP (14) is nearly isoenergetic with the starting PH + SO reactants, with an energy lower by 0.8 kcal mol−1. Following isomerization to form cis-HSOP (14), there is enough energy in the system to either interconvert with trans-HSOP (15) or dissociate into SH + PO.
Isomers 1–5 are expected to exist following the formation of any single isomer. Due to the detection of SH and PO in the ISM and CSE of various stars, among other molecules, entrance channels for this tetratomic group of molecules are expected to be through trans-HSPO (3) and cis-HSPO (4), via the reaction SH + PO. This prediction follows from the highly exothermic nature of the adduct formation compared to the separated reactants, along with the deeply submerged transition state barriers for all isomerization processes. Based on thermodynamics alone, all of these isomers may exist in the ISM.
Following the formation of cis-HSPO (4) or trans-HSPO (3), with no additional energy added to the system, dissociation to form PS + OH, H + SPO, or S + HOP (not shown, high energy) is not possible in the assumed low pressure and temperature environment of the ISM due to a dissociation limit of 21.6, 5.5, and 48.9 kcal mol−1 above the starting SH + PO reactants, respectively. The formation of H + SPO products is a potentially feasible process in warm regions of space. Alternatively, if PS is initially formed by some means in the space, the bimolecular reaction with OH may be a sink for this molecule, leading to dissociation to form SH + PO or H + SPO, possibly explaining its lack of detection to date. Detection of any of isomers 1–5 would provide evidence for the possible existence of PS. Similarly, if PH is formed in the ISM, an exothermic reaction with SO to form cis-HPOS (11) and trans-HPOS(12) or cis-HPSO (8) and trans-HPSO (6) could be a possible sink. The route via HPSO formation has submerged transition state barriers that lead to the formation of PS + OH. Otherwise, the formation of HPOS would result in isomerization and fragmentation into SH + PO. These sinks are unlikely to regenerate PH following a reaction.
Figure 1 provides some insight into the observational question of PH and PS non-detection. Gas-phase reactions between diatomic pairs may act as a sink for PS and PH in the ISM and CSEs. The low-density environment of the ISM precludes collisional stabilization of the reactive intermediates, leading to dissociation following formation. If the reactions were to happen on the surface of dust grains followed by desorption, the stabilized tetratomic isomers may exist in space and be readily detectable.
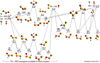 |
Fig. 1 Ground state potential energy surface for the [H, P, S, O] species. Relative energies (in kcal mol−1) are calculated at the CCSD(T)/aug-cc-pV(Q+d)Z // MP2/6-311++G(d, p) level of theory and are relative to the SH + PO asymptote. MP2 zero-point vibrational energy is included in the relative energies. Isomer numbering is shown in bold. |
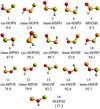 |
Fig. 2 Structures of the [H, P, S, O] isomers and their relative energies (in kcal mol−1) calculated at the CCSD(T)/CBS level of theory. |
3.2 Electronic structure
The ground state potential energy surface described in Fig. 1 points to [H, P, S, O] species as potential conduits for the removal of PH and PS from the ISM. Due to this fact, all isomers have been characterized with high-level ab initio methods. In the following sections, the spectroscopic parameters of the most stable of these molecules have been calculated to facilitate laboratory and observational searches.
The coupled cluster equilibrium geometries for the ground electronic state singlet [H, P, S, O] isomers along with their relative energies, including zero-point vibrational energy correction (ZPE), are listed in Table A.1, and their structures and relative energies are shown in Fig. 2. The energies and electronic structure of this system will be discussed in the text using the CCSD(T)/CBS values. Calculations performed including all electrons with the core-valence, scalar relativistic basis set aug-cc-pwCVTZ-DK show a negligible effect on the energies and rotational constants compared to the frozen-core CCSD(T) methods, as seen in Tables A.2 and A.3. For this reason, the methods accessible with large basis sets are recommended for future studies.
Cis-HOPS (1) is the global minimum of the potential energy surface and therefore the most thermodynamically stable species. Trans-HOPS (2) is 2.9 kcal mol−1 higher in energy than cis-HOPS (1). Population analysis of cis-HOPS (1) shows partial charges of +0.22e and −0.30e on the hydrogen and sulfur atoms, respectively. Charge-charge interaction and hydrogen bonding are the stabilizing forces that cause the cis conformer to be lower in energy, stabilizing it relative to the trans isomer.
The ground state of cis-HOPS (1) is characterized by a single-reference wave function, indicating that the CCSD(T) methods capture the true electronic structure well. The T1 diagnostic for this isomer at the CCSD(T)-F12/5Z level of theory was 0.017, while the dominant configuration for the ground state at the CASSCF/aug-cc-pV(T+d)Z level is:
(0.922) x [core](10a′)2(11a′)2(12a′)2(13a′)2(3a′′)2(14a′)2 (15a′)2(4a′′)2(16a′)2 X1 A′.
The PS bond in cis-HOPS (1) and trans-HOPS (2) are 1.9107 Å and 1.8987 Å, respectively. Both isomers have a PS bond length slightly longer than the prototypical PS diatomic bond length of 1.900 Å (Huber & Herzberg 1979). The P–O bond lengths for cis-HOPS (1) and trans-HOPS (2) are 1.6116 Å and 1.6241 Å, respectively. Both isomers contain longer PO bond lengths when compared to the PO diatomic of 1.475 Å (Huber & Herzberg 1979). In addition, both cis-HOPS (1) and trans-HOPS (2) are planar molecules, exhibiting a dihedral angle of 0.0 and 180.0°, respectively.
The ground state of cis-HSPO (4) shows even stronger single-reference character than cis-HOPS (1). Trans-HSPO (3) and cis-HSPO (4) have energies 5.6 kcal mol−1 and 6.3 kcal mol−1 above that of cis-HOPS (1). The trans-HSPO (3) P–O bond length is predicted to be 1.4711 Å while the cis-HSPO (4) P–O bond length equals 1.4727 Å. Therefore, each isomer has an almost identical PO bond length when compared to the free diatomic (1.475 Å) (Huber & Herzberg 1979). In addition, the trans-HSPO (3) and cis-HSPO (4) isomers have P-S bond lengths of 2.1038 Å and 2.1098 Å, respectively, indicating a longer bond distance when compared to the free diatomic (1.900 Å). The internal location of this PS bond causes elongation, whereas in the HOPS isomers, the terminal nature of the PS bond shows a closer structure to the free diatomic. Like the HOPS isomers, both cis-HSPO (4) and trans-HSPO (3) are planar.
SP(O)H (5) is predicted to lie 8.3 kcal mol−1 above the ground state isomer. This isomer exhibits a trigonal planar geometry with a phosphorous central atom and contains a P–O bond length of 1.4609 Å, slightly shorter than in the free diatomic PO. The P–S bond (1.8807 Å) in SP(O)H (5) is slightly shorter than in diatomic PS, indicating a strong PS bond in SP(O)H (5). Finally, the PH bond length of 1.4028 Å is 0.02 Å shorter than the same bond in the PH diatomic (1.4223 Å) (Huber & Herzberg 1979). Again, this molecule is planar with a dihedral angle of 0.0°. The terminal nature of each bond leads to the similar bond lengths when compared to the free diatomic species.
Following SP(O)H (5), there is a large jump in energy, with the next stable isomer, trans-HPSO (6), located 47.9 kcal mol−1 above the ground state cis-HOPS (1). The trans-HPSO (6) and cis-HPSO (8) isomers both exhibit PS bond lengths longer than the experimentally determined diatomic PS bond length of 1.900 Å (Huber & Herzberg 1979). Similar to the HSPO isomers, the internal PS bond shows elongation due to the bonding nature of the molecule. The SO bond lengths of 1.4728 Å and 1.4750 Å are both shorter than the corresponding bond length of 1.4810 Å in the SO diatomic (Huber & Herzberg 1979). This is a continuation of the pattern of a terminal bond exhibiting a shorter length than a free diatomic in this group of molecules.
The HOSP isomers, 9 and 10, with a terminal PS bond, show PS bond lengths slightly shorter than that of the diatomic PS. The OH bond in these two isomers is equal and larger in magnitude than the free OH diatomic, respectively. These two isomers lie 52.0 and 54.1 kcal mol−1 above the ground state isomer. The only isomer that is not planar (i.e., 0° or 180° dihedral angle) is cyc-SPO(H) (7), which has a dihedral angle of 92.7° and lies 50.1 kcal mol−1 above the ground state isomer. Isomers 11–16 will not be discussed in detailed because they are unstable relative to the various dissociation asymptotes and are predicted to not be relevant in space environments.
Rotational constants (A, B, C in MHz), permanent dipole moments (μ in Debye), centrifugal distortion parameters (DJ, DK, DJK in MHz), and harmonic and anharmonic frequencies (cm−1) with fundamental intensities in parentheses (km mol−1) for cis/trans HOPS and cis/trans HSPO isomers.
3.3 Rotational and vibrational spectroscopy
Higher order rotational and vibrational parameters for the four lowest energy isomers are presented in Table 1. These calculations were performed at the CCSD(T)/aug-cc-pV(T+d)Z level of theory due to the large computational cost of calculating the cubic and quartic force fields. Although this is a slightly smaller basis set than described in the previous section, the higher order corrections provide more accuracy for these parameters, especially vibrational correction to the rotational constants. These values along with the centrifugal distortion constants for each isomer give an accurate description of expected rotational spectra in order to facilitate laboratory detection of the [H, P, S, O] species. All four species possess an appreciable permanent dipole moment, with trans-HOPS (2) and trans-HSPO (3) having vibrationally averaged dipole moments of 2.6132 D and 2.8765 D, respectively. These dipole moments are similar or larger in magnitude when compared to other species detected in the interstellar medium (e.g., HSCN [3.5 D], Halfen et al. 2009; and H2 CCS [1.02 D], Cernicharo et al. 2021), meaning the intrinsic intensity of the lines will not be the limiting factor in detection. The ca. 1500 MHz difference in the A0 rotational constant between cis-HOPS (1) and trans-HOPS (2) and the 3× larger dipole moment for trans-HOPS (2) should aid in differentiating these two conformers in a spectrum.
Harmonic and anharmonic vibrational wavenumbers were calculated for each species using second order vibrational perturbation theory (VPT2) in order to drive experimental infrared (IR) characterization of these molecules. Mode descriptions for each normal mode, as well as harmonic frequencies calculated at the CCSD(T)-AE/TZ-DK level of theory and intensities at the MP2 level of theory are available in Table A.4. Large anharmonicity is seen for various modes of each species, especially ν1 of cis-HOPS (1). This mode represents the PH stretch and a decrease of ca. 200 cm−1 to 3518 cm−1 is seen when applying VPT2. Mode ν2 shows slightly less anharmonicity; however, there is still a 4.4% decrease in the frequency to 974 cm−1 upon VPT2 treatment. Normal modes ν3 –ν6 of cis-HOPS (1) show smaller changes and are well described by harmonic treatment.
Mode ν3, the PO stretch, is predicted to have the largest intensity of any mode for both HOPS isomers. There is a 20 cm−1 difference in predicted frequency for this mode, so it may prove to be the best chance to detect and differentiate each isomer in an experimental spectrum. Additionally, modes ν1, the PH stretch, and ν5, the out-of-plane OH wag, can also be used to differentiate cis-HOPS (1) from trans-HOPS (2) due to the respective 60.8 cm−1 and 77.6 cm−1 difference in frequency between the two isomers.
Trans-HSPO (3) is reasonably well described via harmonic frequency analysis, with the only mode showing an appreciable decrease in frequency with anharmonic treatment being ν1, the SH stretch. A 3.9% decrease from 2662 cm−1 to 2556 cm−1 is observed. All other modes show minor changes in magnitude with the VPT2 method. Mode ν2, the PO stretch, exhibits the largest intensity and is expected to be the transition with the largest signal in an experiment; however, the small difference in predicted frequency between the cis-HSPO (4) and trans-HSPO (3) isomers may make differentiating them difficult.
3.4 Electronic spectroscopy and photochemistry
The electronic spectroscopy of the four most stable isomers was investigated to explore whether photochemical processes will compete with the isomerization pathways described above. As cis-HOPS (1) is the most stable isomer, the photochemistry and the stability of its low-lying electronic state were studied. Cis-HSPO (4) was chosen to compare isomers in the same conformation. Usually, cis and trans conformers exhibit the same behavior in evolution of the low-lying excited states (Trabelsi et al. 2019), with differences seen in the vertical excitation energy and oscillator strengths. Vertical excitation energies, transition dipole moments, and oscillator strengths to the low-lying singlet states are given in Table 2, and adiabatic potential energy surfaces of the low-lying singlet and triplet states along the H–O and O–P bond coordinates of cis-HOPS (1) and H–S and S–P bond coordinates of cis-HSPO (4) are shown in Fig. 3. These bond scans were performed in the Cs symmetry group with all other coordinates fixed at their equilibrium geometry. Following this, the electronic absorption spectra were simulated for both isomers.
The ground state (X 1 A′) of cis-HOPS(1) is characterized by a deep potential well along both the O–H and O–P bond coordinates, as shown in Figs. 3a and b. In both cases, the ground state correlates adiabatically to ground electronic state products. Focusing on Fig. 3a, all states exhibit a minima in their potential energy profile along the O–H bond length. Many avoided crossings arise in the ROH ~1.5–2.0 Å region, most notably between the 3 1 A′′ and 2 1 A′′ states. The vertical transition to the 3 1 A′′ state at 7.063 eV (175.5 nm) has an oscillator strength of 0.031, indicating probability of populating this state. If the molecule can overcome the small barrier near the Franck–Condon region, bond elongation via internal conversion to the 2 1 A′′ state is possible, followed by further internal conversion to the 1 1 A′′ state. This would lead to electronically excited H + OPS products. This is the only obvious photodissociation pathway along the O–H bond, with the other states exhibiting minima too deep to lead to dissociation. Excitation to these states would lead to fluorescence. Based on the barrier in the Franck-Condon region, production of SPO is not likely via photochemical pathways.
Photodissociation of cis-HOPS (1) is more likely to occur along the O-P bond due to the shallower bound states and presence of repulsive states, as seen in Fig. 3b. The excitation to the 2 1 A′ state at 4.821 eV (257.1 nm), which has an oscillator strength of 0.058, will lead to the formation of ground state OH (X 2 Π) + PS (X 2 Π). Detection of OH via laser induced fluorescence would confirm the formation of the PS diatomic. Photochemical production of the yet undetected PS may be more favorable than ground state dissociation predicted in Fig. 1 due to the non-negligible oscillator strength, a small barrier to dissociation on the 2 1 A′ excited state surface, and a large bond dissociation energy in the ground state. In cis-HOPS (1), maximum absorption will take place on the 4 1 A′ ← X 1 A′ transition at 174.5 nm due to a very large oscillator strength of 0.200. This region is fairly congested, with three electronic states within a few nm of each other. Fluorescence studies may be possible after excitation to the 4 1 A′ state because it is bound in both coordinates that were studied. The avoided crossing between the 4 1 A′ and 3 1 A′ states at ROP ~ 1.75 Å will lead to a fairly large Stokes shift for the fluorescence radiation, simplifying detection. Depending on route of formation (e.g., gas-phase or grain surface), cis-HOPS (1) is expected to either dissociate to form ground state OH (X 2 Π) + PS (X 2 Π) or be present in the ISM due to its thermodynamic stability.
The adiabatic potential energy surfaces for cis-HSPO (4) along the H–S and S–P coordinates are displayed in Figs. 3c and d, respectively. Again, the ground state (X 1 A′) adiabatically correlates to ground electronic state products in both cases. There are large differences in the potential energy surfaces in cis-HSPO (4) compared to those for cis-HOPS (1) that present new photochemical pathways. The major differences to note are the shallower wells along the H–S bond coordinate and the repulsive states along the S–P coordinate. First looking at Fig. 3c, the H–S coordinate, the major decay pathway will proceed through electronic excitation to the 3 1 A′ state followed by rapid dissociation to the first excited state H + SPO products. The 3 1 A′ ← X 1 A′ transition has a vertical excitation energy of 6.185 eV (200.5 nm) and a large oscillator strength of 0.124. The 3 1 A′ state adiabatically correlates with a highly excited dissociation asymptote but is repulsive in the diabatic representation. Internal conversion to the 2 1 A′ state would lead to the formation of first singlet excited state products H + SPO.
Figure 3d depicts the adiabatic potentials along the S–P bond of cis-HSPO (4). Along this coordinate, the low-lying excited states are either weakly bound or show repulsive character. The 2 1 A′ ← X 1 A′ transition has an oscillator strength of 0.060, smaller than that of the 3 1 A′ ← X 1 A′ transition, but still appreciable. Excitation into the 2 1 A′ state would lead to prompt and direct dissociation along the S-P bond, leading to formation of ground state SH (X 2 Π) + PO (X 2 Π) products. The H–S bond coordinate is bound and will not participate in photodissociation following direct excitation to the 2 1 A′ state. Based on the excited state studies shown here, cis-HSPO (4) is expected to be a transient intermediate species in the ISM due to its facile photodissociation pathways, with the formation of H + SPO dominating due to the very large oscillator strength of the 3 1 A′ ← X 1 A′ transition.
In order to aid in experimental detection of cis-HOPS (1) and cis-HSPO (4), the electronic absorption spectra were simulated for both isomers, and are shown in Fig. 4. Panel 4a displays the simulated spectrum for cis-HOPS (1), where there are two broad, strongly absorbing peaks. The lower energy peak is centered at 270 nm and spans from ~250 nm to 350 nm with a predicted peak absorption cross section of 1.5 × 10−17 cm2 molecule−1. This peak consists mostly of transition to the 3 1A state, with minor contribution from the 2 1A state on the long wavelength side. The larger peak centered at 200 nm is made up of four different overlapping transitions; the strongest of which is the 6 1 A ← X 1 A transition. In an experimental setting, the congested nature of the spectrum in this region would preclude assignment of any specific transitions. The transition at 200 nm is extremely strong: more than double that of the peak at 270 nm.
The simulated absorption spectrum for cis-HSPO is shown in Fig. 4b and is similarly congested in the shorter wavelength region, but with less intensity distributed across all states. The broad peak centered at 210 nm is mainly comprised of the 6 1 A ← X 1 A transition, with minor contributions from the 3 1 A ← X 1 A and 4 1 A ← X 1 A transitions. An almost equally intense feature with a double peak structure is located at 281 nm and corresponds solely to the 2 1 A ← X 1 A transition. In addition to these two peaks, there is a small high-energy feature with two maxima at 183 nm and 191 nm arising from the 5 1 A ← X 1A transition.
Both of these molecules exhibit extremely strong absorptions. The peaks ~200 nm in both molecules are almost 3 times stronger than SO2 (σ(E) = 1 × 10−17 cm2 molecule−1) (Ahmed & Kumar 1992) and an order of magnitude stronger than HONO (σ(E) = 2 × 10−18 cm2 molecule−1) (Atkinson et al. 2004) at the same wavelength. Unfortunately, the overlap between the two spectra in the 150–350 nm region makes isomer assignment difficult depending on the method of experimental production. If excess energy is present, isomerization is possible, although the ~30 kcal mol−1 barrier may be prohibitive in an experimental setting, locking in an isomer following synthesis. If both isomers are indeed present, the small peaks in the 350–500 nm region (insets in Figs. 4a and b) can be used to differentiate them. Both isomers have a weak 1 1 A ← X 1 A transition, with the maximum in cis-HOPS (1) occurring at 440 nm and the maximum in cis-HSPO (4) occurring at 385 nm. These features are spaced far enough apart to be discernable in an experimental spectrum even with possible deviation from the computational predictions.
Vertical electronic excitation energies (VEE, in eV (nm)) calculated at the MRCI+Q and EOM-CCSD levels of theory along with transition dipole moments (μij, in Debye) andoscillator strengths (f) for each transition.
 |
Fig. 3 One-Dimensional cuts of the adiabatic potential energy surface of cis-HOPS along the (a) RH–O and (b) RO–P bond coordinates and cis-HSPO along the (c) RH–S and (d) RS–P bond coordinates at the MRCI+Q/aug-cc-pV(T+d)Z level of theory. All other coordinates are held fixed at their equilibrium geometry. |
 |
Fig. 4 Simulated electronic absorption spectrum of (a) cis-HOPS and (b) cis-HSPO. The total spectrum is shown in black, with individual contributions shown arising from transitions from the ground stateto the 1 1A (gray), 2 1A (red), and 3 1A (orange), 4 1A (green), 5 1A (dark blue), 6 1A (light blue), and 7 1A (purple) states. |
4 Conclusions
Ab initio calculations reveal the potential for production and/or suppression of diatomic PS and PH in the interstellar medium via the formation of [H, P, S, O] tetratomic intermediates. If PS is formed in the early outflows of the circumstellar envelopes of stars, the reaction PS + OH to form cis- or trans-HOPS (2) and subsequent dissociation to form SH + PO may serve as a sink for PS, partially explaining the lack of detection to date. Similarly, the reaction of PH + SO can lead to either PS + OH via HPSO and HOSP, or SH + PO via HPOS and HSOP. If diatomic reaction occurs on the surface of dust grains, stabilized [H, P, S, O] isomers may exist in space and be detectable. Detection of any [H, P, S, O] isomer in the ISM would indicate the potential presence of other phosphorus-bearing molecules, namely PS or PH, and would designate the detection source as a good place to search for signs of PS or PH. Due to the thermodynamic stability of these tetratomic species, highly accurate equilibrium geometries, vibrationally-corrected rotational constants, and anharmonic vibrational frequencies were calculated to assist in laboratory and observational studies of these molecules. The PO stretch is predicted to be the most intense vibrational mode for both HOPS isomers, and a 20 cm−1 difference in predicted frequency can prove to differentiate isomers in an experimental spectrum.
Electronic excitation of cis-HOPS (1) in the 250 nm region is predicted to result in photodissociation to form ground state OH (X 2Π) + PS (X 2 Π), while excitation to the strongly absorbing 4 1 A′ state will lead to highly Stokes-shifted fluorescence. The former may be a photochemical pathway to the production of PS in space. Electronic excitation in cis-HSPO (4) is expected to lead to dissociation in both H-S and S-P coordinates due to steep repulsive states with large oscillator strengths. Excitation to the strongly absorbing 3 1 A′ state, followed by internal conversion to the 2 1 A′ state, will lead to formation of electronically excited H + SPO products. If cis-HSPO (4) absorbs lower energy light in the 260 nm region, excitation to the 2 1 A′ state will cause prompt dissociation to form SH (X 2Π) + PO (X 2Π) products.
Finally, the electronic absorption spectrum of cis-HOPS (1) and cis-HSPO (4) is expected to be congested in the 175–200 nm region. Many overlapping transitions lead to a large absorption cross section for both molecules. The 1 1 A ← X 1 A transition can be used as a differentiating factor in a convoluted spectrum of the two isomers. Due to the large permanent dipole moments and electronic absorption cross sections for this group of molecules, rotational and electronic spectroscopy are recommended as the most likely means of experimental detection and characterization.
Acknowledgements
This material is based upon work supported by the National Science Foundation Graduate Research Fellowship Program under Grant No. DGE-1845298 (VJE).
Appendix A High level electronic structure data for all isomers
Equilibrium geometries (bond lengths in Å and angles in deg) and energy relative to the lowest energy isomer (ΔE, in kcal mol−1) for [H, P, S, O] isomers calculated at various levels of theory.
Zero-point vibrational energy (in kcal mol−1) calculated at the MP2/6-311++G(d, p) and CCSD(T)-AE/aug-cc-pwCVTZ-DK levels of theory and core-valence correction calculated with the CCSD(T)-AE method.
Equilibrium rotational constants (in MHz) calculated at the CCSD(T)-AE/aug-cc-pwCVTZ-DK and CCSD(T)/aug-cc-pV(T+d)Z level of theory.
Harmonic frequencies, mode descriptions and zero-point vibrational energy (in cm−1) calculated at the CCSD(T)-AE/aug-cc-pwCVTZ-DK level of theory. MP2/6-311++G(d, p) harmonic infrared intensities (in km mol−1) are included in parenthesis.
References
- Agúndez, M., Cernicharo, J., & Guélin, M. 2007, ApJ, 662, L91 [CrossRef] [Google Scholar]
- Ahmed, S. M., & Kumar, V. 1992, J. Quant. Spec. Rad. Trans., 47, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Atkinson, R., Baulch, D. L., Cox, R. A., et al. 2004, Atmos. Chem. Phys., 4, 1461 [NASA ADS] [CrossRef] [Google Scholar]
- Barbatti, M., Ruckenbauer, M., Plasser, F., et al. 2014, WIREs Comp. Mol. Sci., 4, 26 [CrossRef] [Google Scholar]
- Barbatti, M., Granucci, G., Ruckenbauer, M., et al. 2018, NEWTON-X: A Package for Newtonian Dynamics Close to the Crossing Seam, 2018 [Google Scholar]
- Begue, D., Sotiropoulos, J.-m., Pouchan, C., & Zhang, D. Y. 2006, Can. J. Chem., 84, 5 [Google Scholar]
- Bell, I. S., Ahmad, I. K., Hamilton, P. A., & Davies, P. B. 2000, CPL, 320, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Brinkmann, N. R., & Carmichael, I. 2004, JPCA, 108, 9390 [NASA ADS] [CrossRef] [Google Scholar]
- Cazzoli, G., Lattanzi, V., Kirsch, T., et al. 2016, A&A, 591, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Celani, P., & Werner, H.-J. 2000, JCP, 112, 5546 [Google Scholar]
- Cernicharo, J., Cabezas, C., Agúndez, M., et al. 2021, A&A, 648, L3 [EDP Sciences] [Google Scholar]
- Chu, X., Qian, W., Lu, B., et al. 2020, Angew. Chem., 132, 22133 [NASA ADS] [CrossRef] [Google Scholar]
- Dunning, T. H. 1989, JCP, 90, 1007 [Google Scholar]
- Dunning, T. H., Peterson, K. A., & Wilson, A. K. 2001, JCP, 114, 9244 [Google Scholar]
- Endres, C. P., Schlemmer, S., Schilke, P., Stutzki, J., & Müller, H. S. P. 2016, J. Mol. Spectr., 327, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Filipovic, M. R., Miljkovic, J. L., Nauser, T., et al. 2012, J. Am. Chem. Soc., 134, 12016 [CrossRef] [Google Scholar]
- Francisco, J. S. 2003, Chem. Phys., 287, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Frisch, M. J., Trucks, G. W., Schlegel, H. B., et al. Gaussian, 2016, 16 [Google Scholar]
- Frisch, M. J., Head-Gordon, M., & Pople, J. A. 1990a, CPL, 166, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Frisch, M. J., Head-Gordon, M., & Pople, J. A. 1990b, CPL, 166, 281 [NASA ADS] [CrossRef] [Google Scholar]
- García de la Concepción, J., Puzzarini, C., Barone, V., Jiménez-Serra, I., & Roncero, O. 2021 ApJ, 922, 169 [CrossRef] [Google Scholar]
- Gottlieb, C. A., Ball, J. A., Gottlieb, E. W., Lada, C. J., & Penfield, H. 1975, ApJ, 200, L147 [NASA ADS] [CrossRef] [Google Scholar]
- Guelin, M., Cernicharo, J., Paubert, G., & Turner, B. E. 1990, A&A, 230, L9 [NASA ADS] [Google Scholar]
- Halfen, D. T., Ziurys, L. M., Brünken, S., et al. 2009, ApJ, 702, L124 [NASA ADS] [CrossRef] [Google Scholar]
- Head-Gordon, M., & Head-Gordon, T. 1994, CPL, 220, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Head-Gordon, M., Pople, J. A., & Frisch, M. J. 1988, CPL, 153, 503 [NASA ADS] [CrossRef] [Google Scholar]
- Hinkel, N. R., Hartnett, H. E., & Young, P. A. 2020, ApJ, 900, L38 [NASA ADS] [CrossRef] [Google Scholar]
- Huber, K. P., & Herzberg, G. 1979, Molecular Spectra and Molecular Structure. IV. Constants of Diatomic Molecules (Van Nostrand Reinhold) [CrossRef] [Google Scholar]
- Jiménez-Serra, I., Viti, S., Quénard, D., & Holdship, J. 2018, ApJ, 862, 128 [CrossRef] [Google Scholar]
- Jorge, F. E., Canal Neto, A., Camiletti, G. G., & Machado, S. F. 2009, JCP, 130, 064108 [Google Scholar]
- Karsili, T. N. V., Thodika, M., Nguyen, L., & Matsika, S. 2018, Chem. Phys., 515, 434 [NASA ADS] [CrossRef] [Google Scholar]
- Kendall, R. A., Dunning, T. H., & Harrison, R. J. 1992, JCP, 96, 6796 [Google Scholar]
- Kitchens, M. J. R., & Fortenberry, R. C. 2016, Chem. Phys., 472, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Knowles, P. J., & Werner, H.-J. 1985, CPL, 115, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Knowles, P. J., & Werner, H.-J. 1988, CPL, 145, 514 [NASA ADS] [CrossRef] [Google Scholar]
- Knowles, P. J., & Werner, H.-J. 1992, Theoret. Chim. Acta, 84, 95 [Google Scholar]
- Knowles, P. J., Hampel, C., & Werner, H.-J. 1993, JCP, 99, 5219 [Google Scholar]
- Knowles, P. J., Hampel, C., & Werner, H.-J. 2000, JCP, 112, 3106 [Google Scholar]
- Korona, T., & Werner, H.-J. 2003, JCP, 118, 3006 [Google Scholar]
- Krishnan, R., Binkley, J. S., Seeger, R., & Pople, J. A. 1980, JCP, 72, 650 [Google Scholar]
- Maciá, E. 2005, Chem. Soc. Rev., 34, 691 [CrossRef] [Google Scholar]
- Maciá, E., Hernández, M. V., & Oró, J. 1997, Orig. Life Evol. Biosph., 27, 459 [CrossRef] [Google Scholar]
- Mathieu, S., Navech, J., & Barthelat, J. C. 1989, Inorg. Chem., 28, 3099 [Google Scholar]
- Matthews, D. A., Cheng, L., Harding, M. E., et al. 2020, JCP, 152, 214108 [Google Scholar]
- McLean, A. D., & Chandler, G. S. 1980, JCP, 72, 5639 [Google Scholar]
- Milam, S. N., Halfen, D. T., Tenenbaum, E. D., et al. 2008, ApJ, 684, 618 [NASA ADS] [CrossRef] [Google Scholar]
- Møller, C., & Plesset, M. S. 1934, Phys. Rev., 46, 618 [Google Scholar]
- Namai, M., Sasaki, T., Ishikawa, H., Morikuni, H., & Mikami, N. 2009, JPCA, 113, 13081 [NASA ADS] [CrossRef] [Google Scholar]
- Powner, M. W., Gerland, B., & Sutherland, J. D. 2009, Nat., 459, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Puzzarini, C. 2006, J. Mol. Struct., 780–781, 238 [CrossRef] [Google Scholar]
- Ramazan, K. A., Syomin, D., & J. Finlayson-Pitts, B. 2004, PCCP, 6, 3836 [NASA ADS] [CrossRef] [Google Scholar]
- Sæbø, S., & Almlöf, J. 1989, CPL, 154, 83 [CrossRef] [Google Scholar]
- Sonneborn, G., Moos, H. W., & Andersson, B.-G. 2006, Astrophysics in the Far Ultraviolet: Five Years of Discovery with FUSE, 348 [Google Scholar]
- Stanton, J. F., Gauss, J., Cheng, L., et al. 2019, CFOUR, Coupled-Cluster techniques for Computational Chemistry, a quantum-chemical program package [Google Scholar]
- Szalay, P. G., & Bartlett, R. J. 1993, CPL, 214, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Tenenbaum, E. D., Woolf, N. J., & Ziurys, L. M. 2007, ApJ, 666, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Trabelsi, T., Mahjoubi, K., Mehnen, B., Hochlaf, M., & Francisco, J. S. 2019, JPCA, 123, 463 [NASA ADS] [CrossRef] [Google Scholar]
- Trabelsi, T., Plane, J. M. C., & Francisco, J. S. 2021, ApJ, 909, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Werner, H.-J. 1996, Mol. Phys., 89, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Werner, H.-J., & Knowles, P. J. 1985, JCP, 82, 5053 [Google Scholar]
- Werner, H.-J., Knizia, G., & Manby, F. R. 2011, Mol. Phys., 109, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Werner, H.-J., Knowles, P. J., Knizia, G., et al. 2019, MOLPRO, version 2019.1, a package of ab initio programs [Google Scholar]
- Woon, D. E., & Dunning, T. H. 1993, JCP, 98, 1358 [Google Scholar]
- Yamaguchi, T., Takano, S., Sakai, N., et al. 2011, PASJ, 63, L37 [NASA ADS] [Google Scholar]
- Yu-Juan, C., Hai-Tao, Y., Hong-Gang, F., et al. 2010, Chin. J. Chem., 21, 30 [CrossRef] [Google Scholar]
- Ziurys, L. M. 1987, ApJ, 321, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Ziurys, L. M. 2006, PNAS, 103, 12274 [CrossRef] [Google Scholar]
- Ziurys, L. M., Schmidt, D. R., & Bernal, J. J. 2018, ApJ, 856, 169 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Rotational constants (A, B, C in MHz), permanent dipole moments (μ in Debye), centrifugal distortion parameters (DJ, DK, DJK in MHz), and harmonic and anharmonic frequencies (cm−1) with fundamental intensities in parentheses (km mol−1) for cis/trans HOPS and cis/trans HSPO isomers.
Vertical electronic excitation energies (VEE, in eV (nm)) calculated at the MRCI+Q and EOM-CCSD levels of theory along with transition dipole moments (μij, in Debye) andoscillator strengths (f) for each transition.
Equilibrium geometries (bond lengths in Å and angles in deg) and energy relative to the lowest energy isomer (ΔE, in kcal mol−1) for [H, P, S, O] isomers calculated at various levels of theory.
Zero-point vibrational energy (in kcal mol−1) calculated at the MP2/6-311++G(d, p) and CCSD(T)-AE/aug-cc-pwCVTZ-DK levels of theory and core-valence correction calculated with the CCSD(T)-AE method.
Equilibrium rotational constants (in MHz) calculated at the CCSD(T)-AE/aug-cc-pwCVTZ-DK and CCSD(T)/aug-cc-pV(T+d)Z level of theory.
Harmonic frequencies, mode descriptions and zero-point vibrational energy (in cm−1) calculated at the CCSD(T)-AE/aug-cc-pwCVTZ-DK level of theory. MP2/6-311++G(d, p) harmonic infrared intensities (in km mol−1) are included in parenthesis.
All Figures
 |
Fig. 1 Ground state potential energy surface for the [H, P, S, O] species. Relative energies (in kcal mol−1) are calculated at the CCSD(T)/aug-cc-pV(Q+d)Z // MP2/6-311++G(d, p) level of theory and are relative to the SH + PO asymptote. MP2 zero-point vibrational energy is included in the relative energies. Isomer numbering is shown in bold. |
| In the text | |
 |
Fig. 2 Structures of the [H, P, S, O] isomers and their relative energies (in kcal mol−1) calculated at the CCSD(T)/CBS level of theory. |
| In the text | |
 |
Fig. 3 One-Dimensional cuts of the adiabatic potential energy surface of cis-HOPS along the (a) RH–O and (b) RO–P bond coordinates and cis-HSPO along the (c) RH–S and (d) RS–P bond coordinates at the MRCI+Q/aug-cc-pV(T+d)Z level of theory. All other coordinates are held fixed at their equilibrium geometry. |
| In the text | |
 |
Fig. 4 Simulated electronic absorption spectrum of (a) cis-HOPS and (b) cis-HSPO. The total spectrum is shown in black, with individual contributions shown arising from transitions from the ground stateto the 1 1A (gray), 2 1A (red), and 3 1A (orange), 4 1A (green), 5 1A (dark blue), 6 1A (light blue), and 7 1A (purple) states. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


