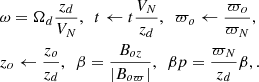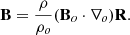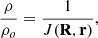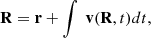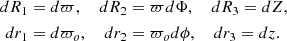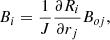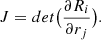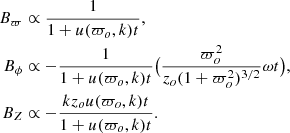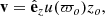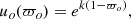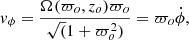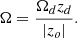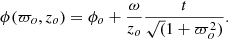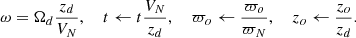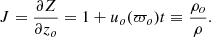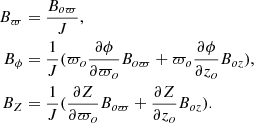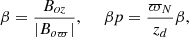| Issue |
A&A
Volume 658, February 2022
|
|
|---|---|---|
| Article Number | A101 | |
| Number of page(s) | 7 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202142330 | |
| Published online | 07 February 2022 | |
Galactic magnetic X fields
Dept. of Physics, Engineering Physics & Astronomy, Queen’s University, Kingston, Ontario K7L 3N6, Canada
e-mail: henrikr@queensu.ca
Received:
29
September
2021
Accepted:
9
December
2021
Aims. Or aim in this note is to compare a recent explanation of the galactic X pattern in Faraday rotation to the pattern produced by the advection part of the classical dynamo.
Methods. We find that the characteristic X magnetic field polarization in the plane of the sky, found in edge-on spiral galaxies, can develop magnetohydromagnetically from an initial disk magnetic field combined with wind and rotation. The rotation measure develops a corresponding X distribution in sign, but this distribution is not a universal behavior because it depends primarily on the velocity field. We use Cauchy evolution of an initial magnetic field to find the field at some later time.
Results. A battery mechanism that requires the current to always flow out of a galaxy has been recently suggested. This contrasts with the conclusions of this paper.
Conclusions. Either explanation has significant consequences for the structure of a spiral galaxy. If the battery mechanism applies, then we have a new method of producing a magnetic field independent of the traditional dynamo. If, however, the flow mechanism applies, then constraints concerning the presence and nature of a galactic wind, together with the signature of the mean radial magnetic field, can be inferred.
Key words: magnetohydrodynamics (MHD) / methods: analytical / galaxies: magnetic fields / techniques: interferometric / galaxies: jets
© ESO 2022
1. Introduction
Recent work by the CHANG-ES collaboration (Krause et al. 2020) has demonstrated, by stacking the maps of the sample galaxies, a certain universality of the X magnetic field topology in edge-on spiral galaxies. This X topology refers to the polarization structure in the plane of the sky, which forms an X centered on the galactic center. This result has been expanded in an interesting paper (Myserlis & Contopoulos 2021) that has presented evidence for an X-type pattern in the sign of the Faraday rotation measure (XRM)1. The sense of the implied toroidal magnetic field is such as to give outward current along the axis of a galaxy. The authors interpret this in terms of a battery mechanism, introduced in Contopoulos & Kazanas (1998), rather than as the result of a magnetohydrodynamic (MHD) dynamo. The mechanism produces current parallel to the galaxy rotation velocity, that is, always outward from the galaxy.
The observational evidence Myserlis & Contopoulos (2021), although indicative, is not yet definitive Beck (2021, priv. comm.). For example, it would be better not to mix rotation measures (RM) in L band with those measured in C band when performing the stacking. The signal-to-noise ratio of the field polarization for each of the galaxies should be taken into account. The inclusion of galaxies possessing a strong central radio source favors the new mechanism, but may also reduce sensitivity to the weaker structure. It would be better to have a larger sample because the evidence for this new result depends strongly on only a few galaxies. For these reasons, we present in this note an alternative explanation for the XRM pattern, based on advection of a magnetic field produced by a fast dynamo.
Because the battery mechanism depends on radiation from a central source interacting with electrons in an accretion disk, we may expect it to be most effective in the central regions of the galaxy. This is roughly in accord with the findings reported in Myserlis & Contopoulos (2021), although the effect seems to persist out to nearly half the radius of the galactic disk. In this same region of an edge-on galaxy, an X magnetic field structure and X structure are frequently found in the XRM, which is entirely due to dynamo theory, as described by Henriksen & Irwin (2016), Henriksen (2017), and Woodfinden et al. (2019). These papers may be said to predict an XRM behavior, although it is not universal in the sense of Myserlis & Contopoulos (2021).
There are various combined effects included in the general dynamo theory such as advection, rotation, diffusion, and a subscale fast dynamo (α effect; Steenbeck et al. 1966). It is our intention in this paper to reduce these effects to the bare minimum necessary for the X magnetic field and the XRM configurations. We show that with these minimal elements, a similar region of the galaxy can show both configurations.
In detail, we show that an advecting and rotating flow, working in MHD on an α dynamo disk magnetic field Butsky et al. (2017) that we assume, can produce the same X topology both in the polarization and in the RM. The X field structure and the toroidal field were already apparent in Henriksen & Irwin (2016), who used a self-similar model of galactic outflow. However, unlike the case with the battery mechanism, the sense of the toroidal field and hence of the axial current can vary, because it depends on two incidental factors.
One factor is the sign of the radial component of the initial disk magnetic field. In particular, we find that it is necessary that the sign of this component change on crossing the disk in order to establish the XRM topology. Such field components may arise in axially symmetric dynamo theory Klein & Fletcher (2015), Henriksen & Irwin (2021). The second factor is the sense and radial variation of the galactic rotation. These two factors interact.
In our example we have used left-handed galactic rotation and a positive radial magnetic field above (i.e., where the angular velocity vector points out of the disk). This gives the same RM distribution as suggested in Myserlis & Contopoulos (2021). However, the same topology arises with right-handed rotation and a negative radial field above the disk. If only one of the rotation or the radial field is reversed, then the sense of the toroidal field is such as to have inward-flowing current.
In addition to the wind velocity increasing with radius, the X field behavior depends on the angular velocity decreasing with radius as in Eq. (A.11). Therefore we exclude a region of rigid-body rotation in favor of differential rotation, which restricts our model to intermediate scales. One can change the sense of the toroidal field in the modeled region by changing the sign of either the radial field or the angular velocity.
Should we have right-handed rotation together with a disk radial field positive above the disc, then we predict the RM to be wholly positive on one side of the axis and wholly negative on the other, so that there is no XRM configuration, although there is likely still X magnetic field. The left and right signs are interchanged given left-handed rotation and an inward radial field in the disk.
Hence, our model requires that there should not be universality of the sense of the XRM topology and hence of the current direction on intermediate (i.e., kiloparsec) galactic scales. Smaller scales (perhaps at less than 1 kpc) may be more subject to the battery mechanism, although we would expect the jet of an active galactic nucleus to produce a similar topology Henriksen & Irwin (2021).
In this note we make use of the Cauchy integral for the magnetic field as a function of time and current location given an initial magnetic field and a prescribed wind and rotation, each with a spatial gradient. Such an advected magnetic field is only one element of a classical magnetic dynamo (e.g., Steenbeck et al. 1966; Moffat 1978; Brandenburg & Subramanian 2005; Klein & Fletcher 2015), and it cannot by itself be regarded as a self-sustaining dynamo because of the assumed lack of back-reaction on the flow due to induced currents. However, given an initial magnetic field and a velocity field of high magnetic Mach number, the Cauchy solution describes the exact transitory development of the magnetic field until energy equipartition with the flow is achieved.
An initial magnetic field implies a preexisting field source, probably a subscale turbulent (i.e., an α dynamo) dynamo (e.g., Butsky et al. 2017 for a supernova-driven turbulent dynamo). We assume an initial field that is parallel to the galactic disk and radial, for clarity in following the advected development. This does not exclude the presence of other components of the field in a realistic initial condition. It should be noted that the turbulence in the α dynamo is below the scale on which the global field appears. The global behavior is due to the assumed smooth variation of the α parameter function.
This description would cease to apply in a closed system as the magnetic field energy came into equipartition with the flow energy. In an open system, such as may be a galactic halo, the magnetic flux can be steadily lost to the intergalactic medium. It might be replenished by the α dynamo in the disk faster than it is advected away. This would depend on the supernova rate and on the wind transit time.
If the flow has internal spatial gradients, these act to create a new magnetic field in a kind of advection dynamo. A simple example of amplification or dilution behavior in time and space for each field component is given briefly in Appendix A. This accounts for the increasing field strength in our models with height and time. Once again, this must stop once the field energy density begins to dominate the flow energy density.
We remove the technical details, including definitions and physical laws, to the appendix. There, the Cauchy integral for an accelerated vertical wind with rotation is used in cylindrical coordinates based on the galactic axis. This integral follows from the continuity equation plus the usual MHD equation that assumes zero resistivity. Because it is a Lagrangian method, it allows the advected magnetic field to be found once the displacement field is given. No integration of the differential equations is required. The advection also occurs in classical dynamo theory in combination with the α effect and diffusion. This dynamo component gives the α/Ω effect when differential rotation exists. We ignore diffusion in favor of galactic wind and assume that the α effect has produced our initial field.
2. Examples
Scales in space and time are used in Appendix A and appear as {VN, Ωd, ϖN, zd}, which may be freely chosen. The height zd is a vertical scale in terms of which all other heights are measured. The velocity VN is the wind velocity at cylindrical radius scale ϖN, and Ωd is the angular velocity of a particle initially at z = zd. The height zd is roughly the height at which the wind begins. Together, these define the time from the initial configuration, the wind and angular velocities, and the spatial scales in height and radius. The subscript N suggests bulge values, while zd is essentially half the thickness of the galactic disk.
Additional constants are defined in the appendix, but for convenience, they are
In addition, the field strength is given in terms of the initial value of the radial magnetic field Bϖ(0). The subscript o indicates a value at an initial position in the rotating outflow, namely at {ϖo, zo}. We take Boz = 0 for simplicity in this example, although this is not necessary for the conclusion. There is an additional parameter k that defines how fast the radial velocity at an initial point falls off with radius, given in Eq. (A.10). In addition to the initial field strength, numerical values in our calculations require the numerical assignment of the constant VN for the velocity, ϖN for the radius, zd for the halo scale, and Ωd for the angular velocity. These can be chosen appropriately for any galaxy of interest.
Figure 1 shows an evolved magnetic field above and below the galactic disk, provided the radial field changes sign across the disk. The figure is axially symmetric in cylindrical coordinates, but Cartesian components are shown. The principal message from the upper panels of this figure is the spiral nature of the field in this cross cut, whose winding sense reverses across the equatorial plane. The panels show the {x, y} planes at z = ±1. The observer is looking perpendicular to the z -axis so that when a number of these planes are stacked in z, an extended line-of-sight (briefly los) magnetic field appears that reverses direction above and below the plane and across the axis. This reversal of field direction below the plane and across the axis corresponds to the reversing RM pattern shown in Figs. 2 and 3. This field evolution uses the flow field described in Fig. A.2.
 |
Fig. 1. Cartesian components of the magnetic field that is axially symmetric in cylindrical coordinates. Upper left panel: magnetic field in the {x, y} plane cut at z = +1. Upper right panel: {x, y} plane at z = −1. Lower left panel: {y, z} poloidal plane at x = 1. The lower right panel is a 3D view of the field above and below the plane. The parameters used in the figure are {k, s, β, βp, ω, t}={−0.03, 1, 0, 0, −2, 4}. The scales are ϖN for the radius and zd along the axis. The arrows show the direction of the field at the end point of the arrow, but the field strength in the first three figures has been adjusted so as to show the outer arrows clearly. The fourth figure shows each arrow length as a fraction of the maximum value. |
The lower left panel shows the {y, z} plane in a cut at x = 1. The strength of the field falls off faster from the axis than is indicated by the length of the arrows. Such a field projected onto the sky will show an X field about the axis, due to polarization generated mainly where the field is most transverse to the (los). The field closer to being along the los will generate the characteristic RM pattern or its negative.
Finally, the panel at lower right shows the local directions of the field in a full 3D space. The coordinates are also Cartesian, but the field strength is a fraction of the maximum, as indicated by the length of the arrows. Near the plane, the sense of field rotation and the sign of the radial field component are seen to reverse.
Figure 2 illustrates the XRM pattern produced by the toroidal component of the field for the same parameters as in the upper row of Fig. 1. We are still looking along the negative y-axis as defined in Fig. 1, so x increases positively to the left and negatively to the right. This X pattern in the RM signature evolves from the initially radial field that changes sign across the galactic disk. If the initial radial field does not change sign on crossing the disk, the pattern would be wholly negative on one side of the axis and wholly positive on the side across the axis.
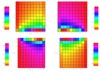 |
Fig. 2. Distribution of the integrated line-of-sight RM in the four quadrants on the sky determined by the galactic edge-on disk and the positive rotation axis. We are looking along the negative y-axis relative to Fig. 1. The parameters of the magnetic field and of the flow field including rotation are as in the upper row of Fig. 1. Upper right and lower left images contain only negative RM values, while those at upper left and lower right are positive. The sign changes across the disk and across the axis to give the characteristic X configuration in the RM. The positive behavior is at upper left and lower right, while the negative behavior is at upper right and lower left. |
The signs of the RM in the pattern can be interchanged either by reversing the sign of the radial field component above and below the disk, or by reversing the sense of the galactic rotation. We have used left-handed rotation about the z-axis in these examples.
It should be emphasized that this XRM pattern is the inevitable result of an α small-scale turbulent fast dynamo plus a galactic wind and halo rotation. The same behavior may be demonstrated if the wind moves in spherical radius with a cos(θo) colatitude dependence. A supernova-driven nuclear wind was already studied in Chevalier (1985).
The wind and rotation together cause the small-scale magnetic field to be expanded in scale. The advection is a kind of macroscopic diffusion. The importance of the advection confirms a recent conclusion Henriksen & Irwin (2021) based on scale-invariant dynamo theory.
Our RM is calculated as the line integral of the line-of-sight magnetic field in each quadrant, using the convention of positive field toward the observer. Only the signs plus relative values are therefore significant. It should be noted that a similar pattern is quoted for the Milky Way in Oppermann et al. (2012). The inferred quadrupole does possess the pattern required in Myserlis & Contopoulos (2021), but it is on a very large scale.
In Fig. 3 a discrete block diagram of the RM values in the second quadrant is shown. The values are the same in the other quadrants, but for a negative sign in the first and third quadrants. The height of the diagram in each block gives the mean RM value in the block. The blocks correspond to the grid divisions in Fig. 2, where the values are smoothed. The label ‘row’ stands for 11 − x, and ‘column’ stands for z.
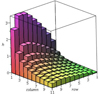 |
Fig. 3. Diagram showing the value on each patch of the RM in the second quadrant of our example. Other quadrants are the same except for sign. The color is merely shading and has no physical significance. To ensure that we are looking along the negative y-axis across the positive x-axis, the row is 11 − x, and the column is the z-axis. The observer is looking down from the left. |
3. Discussion and conclusions
In this paper we have identified a flow field and an initial magnetic field that together produce the characteristic X magnetic field that has proven common in edge-on spiral galaxies (see, e.g., Krause et al. 2020 and references therein). The basic requirement is an initial magnetic field that has a radial component that changes sign across the disk2, plus a galactic wind that increases outward.
To achieve the characteristic X distribution of the RM, the wind must have rotation. We have allowed this rotation to have a lag and the vertical velocity to accelerate. Both of these effects enhance the strength of the magnetic field, but are not essential for the two X behaviors.
It is interesting to note that these elements are present in recent series of studies on the asymptotic galactic dynamo (see, e.g., Henriksen & Irwin 2021) and references therein), which also produce the X-field topology. The fast subscale dynamo (α effect) is also present in those studies, as is also diffusion in some cases. However, the α effect is primarily only necessary for the self-consistent production of the field on which the flow works. The field relaxation produced by diffusion is dominated by a galactic outflow when present.
Our important conclusion relative to the literature is that, unlike the recent interesting suggestion by Myserlis & Contopoulos (2021), the sense of the X pattern in the Faraday rotation is not necessarily such that current flows outward along the axis of the galaxy. By changing the sense of galactic rotation, or by reversing the sign of the radial magnetic field, our mechanism produces a pattern that corresponds either to outward or inward axial current flow. Should the sign of the radial field be the same on both sides of the disk, then the X RM pattern disappears in favor of a simple sign change across the disk.
The two possibilities admitted by this paper are shown, in terms of the sign of the RM in each quadrant, in the left column of the sketch in Fig. 4. The upper left implies current flowing outward along the axis, while the lower left has inward-flowing current. We admit both possibilities in this paper, while only the upper left is possible with the battery mechanism. At right, the projected X polarization is sketched. The signs indicate the position angle relative to the rotation axis, measured positively counterclockwise.
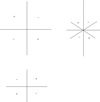 |
Fig. 4. Left: two possibilities for the RM signature in each quadrant. A plus sign indicates a field approaching the observer. Hence the upper image indicates outward current along the rotation axis, and the lower image indicates inward current. The sketch at right shows the projected polarization that comprises an X field. The signs indicate the position angle relative to the rotation axis, if the angle is measured positively counterclockwise. The actual angles vary considerably both in theory and observation. |
This means that we have a clear contrast between our radially increasing wind with rotation acting on a radial field component and the battery mechanism of Myserlis & Contopoulos (2021). The stacked RM for magnetized spiral galaxies should not, according to our advection mechanism, show a strong tendency to the configuration given by outward axial current. In Myserlis & Contopoulos (2021), evidence was presented that such a stacked image does yield the electromagnetic current outflow configuration required by the battery mechanism. We must await a definitive conclusion when improvements mentioned previously are included, however. This model can also be tested in individual galaxies (even for the Milky Way; Oppermann et al. 2012) by measuring both the angular velocity and the RM in four quadrants, but we do not predict stacking of the RM to show any strong residual signal. More studies of this type can only be anticipated before a conclusive answer will be available. It is rare to have such a conclusive test of two contrasting possibilities.
Acknowledgments
This paper has had the advice of my wife Judith Irwin, for which I am grateful. The referee, Rainer Beck, provided much constructive criticism.
References
- Brandenburg, A., & Subramanian, K. 2005, Phys. Rep., 417, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Butsky, I., Zrake, J., Ji-hoon, K., et al. 2017, ApJ, 843, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Chevalier, R. 1985, Nature, 317, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Contopoulos, I., & Kazanas, D. 1998, ApJ, 508, 859 [Google Scholar]
- Heald, G. 2009, in Cosmic Magnetic Fields, eds. K. G. Strassmeier, A. G. Kosovichev, & J. E. Beckman, IAU Symp., 259, 591 [NASA ADS] [Google Scholar]
- Henriksen, R. N. 2017, MNRAS, 469, 4806 [Google Scholar]
- Henriksen, R. N., & Irwin, J. A. 2016, MNRAS, 458, 4210 [NASA ADS] [CrossRef] [Google Scholar]
- Henriksen, R. N., & Irwin, J. A. 2021, ApJ, 920, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Henriksen, R. N., Woodfinden, A., & Irwin, J. A. 2018, MNRAS, 476, 635 [NASA ADS] [CrossRef] [Google Scholar]
- Klein, U., & Fletcher, A. 2015, Galactic and Intergalactic Magnetic Fields (Springer) [Google Scholar]
- Krause, M., Irwin, J., Schmidt, P., et al. 2020, A&A, 639, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moffat, H. K. 1978, Magnetic Field Generation in Electrically Conducting Fluids (Cambridge, U.K.: Cambridge University Press) [Google Scholar]
- Myserlis, I., & Contopoulos, I. 2021, A&A, 649, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oppermann, N., Junklewitz, H., Robbers, G., et al. 2012, A&A, 542, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rand, R. 2000, ApJ, 537, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Steenbeck, M., Krause, F., & Rädler, K. H. 1966, Naturforschung, 21a, 369 [CrossRef] [Google Scholar]
- Woodfinden, A., Henriksen, R. N., Irwin, J. A., & Mora-Partiarroyo, S. C. 2019, MNRAS, 487, 1498 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Basic theory
A.1. Basic assumptions
We recall that formally, the Cauchy solution for the magnetic field given a velocity field is
Here the subscript o indicates values at an initial point in the flow. The gas density is ρ, B is the vector magnetic field, and R(r, t) is the current location of the initial point. The current density is given in terms of the initial density by
where J is the Jacobian between the new (R) and old (r) coordinate locations. We calculate R in appropriate coordinates generally as
but we will choose a simpler form for the velocity field than this expression assumes.
In Cartesian coordinates, the meaning of these various expressions is clear, but in curvilinear coordinates, a little care is required. We let the physical increments along the current and initial curvilinear axes to be designated dRi and dri respectively. In cylindrical coordinates {ϖ,Φ, Z}≡{1, 2, 3} with the three axis coincident with the rotation axis of the galaxy, these become
This allows us to write the solution (A.1) in a practical form for curvilinear coordinates,
where the summation convention is used. The Jacobian becomes in these terms
Equation (A.5) gives each field component in terms of a stretching matrix (∂Ri/∂rj) operating on the initial magnetic field multiplied by the change in density. This operation amplifies the field in an accelerating wind, or under differential rotation, provided that the density does not fall off too rapidly (cf. equation A.6). It is well known and can be found as equation (3.28) in Brandenburg & Subramanian (2005).
The simplest example of combining our flow field with equation (A.5) gives a mixture of amplification and dilution. Thus, a field at a current position that began at {ϖo, zo} will have after a time t the components (the radial velocity u is given by equation (A.10) below)
The proportional sign allows for an arbitrary strength of the initial radial magnetic field so the quantities on the right are local amplification or dilution factors. We see that due to the density dilution, the radial field decreases in time and with increasing radius. The azimuthal field stabilizes in time at ω/(u(ϖo, k)zo), but decreases with radius and height. The vertical field stabilizes in time and radius, and increases with height. The flow field of the following section can be used to convert from initial position into current position.
Once we insert into these formulae a suitable form from equation (A.3), the magnetic field is known as a function of time and the initial coordinates. For this we must choose the form of the velocity flow field that establishes the coordinate transformation R(r, t). This is the subject of the next section.
A.2. Flow field
We treat the simplest possible wind in cylindrical coordinates. Throughout, we assume axial symmetry. The wind outflow takes the form
so that it is purely vertical and a function of its initial radius and height. We consider it to be established as a constant quantity by the galaxy. We choose the wind velocity to be proportional to the initial height zo rather than to the current height Z. Therefore each Lagrangian wind element labelled zo moves with a constant velocity, whose value is fixed by the velocity at the initial height of the element. This initial velocity increases linearly with zo (taking the time derivative of equation A.9).
Consequently, we have the transformation from initial vertical coordinates of a flow element to current vertical coordinates of the flow element as
where VN is the amplitude of u(ϖo). The scale velocity uo(ϖo) is dimensionless. We take this radial function to be
where ϖo is now measured in units of a radial scale ϖN, at which radius the vertical velocity is equal to VN. The numerical constant k allows the scale of the exponential decline in outflow to be adjusted. If this value is close to 1, and if ϖo is small, this form may imitate the rapid decline from a nuclear jet. However, a key result of this paper is that k should be negative and small in order to produce a definite X field. This describes a wind velocity that increases with cylindrical radius in the galaxy.
The rotation velocity is taken to have the form
where ẋ ≡ dx/dt. The radius ϖo does not change during the flow, but we allow for a moderate halo lag Rand (2000), Heald (2009) as the flow element moves vertically by taking
Here the constant Ωd is equal to Ω at zo = zd and t = 0. We choose the halo lag to depend on the initial vertical location of the wind element because we take this to be set by the larger galaxy. This gives a rotation angle that varies linearly in time. The form (A.11) gives a flat galactic rotation velocity at large ϖo and a linear rise at small ϖo. We note that the angular velocity 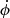 increases to smaller ϖo.
increases to smaller ϖo.
Equations (A.9), (A.11), and (A.12) can now be combined to give
We have defined the dimensionless quantities
Using the definition (A.6) and the mappings (A.9) (scaled by zd), (A.13), and ϖ = ϖo, we find that
Equation (A.5) gives finally the magnetic field as a function of time in the explicit form for cylindrical coordinates {ϖ,ϕ, z} as
The necessary derivatives follow from equations (A.13) and (A.9) plus the choice of u(ϖo) in equation (A.10).
We can use these equations to find the magnetic field development as a function of time over any {ϖo, zo} meridian plane. This development is studied in the text.
We scale the magnetic field strength by |Boϖ| in our sample calculations. Because this equals A/ϖo for some constant A, the calculated fields must be multiplied by A/ϖo. This assumes that the initial field is replenished by the galaxy on a timescale that is short compared to the advection time. This can be altered by taking the initial field to depend on ϖ(ϖo, t) so that the outflow is no longer cylindrical, but that is another model.
Because of the modulus, if the initial radial field (i.e., a split monopole) reverses direction across the galactic plane, Boϖ should be replaced by signum(zo) in equations (A.16). The length and time scalings are as discussed above. The derivative ∂ϕ/∂zo generally requires a signum(zo) factor at zo < 0 so that ϕ may decline with increasingly negative zo. If we take the initial magnetic field to lie wholly in the meridional plane, then Boϖ ∝ 1/ϖo and Boz must be constant in z for the field divergence to vanish. In fact, Boz = 0 in our simple model.
Formally, we introduce constants βp and β given by
but in this study they are both set equal to zero.
We have reduced the model to a toy model by our assumptions, in order that one principal effect (edge-on X magnetic field) of a radially varying galactic disk wind and galactic rotation should be isolated.
All Figures
 |
Fig. 1. Cartesian components of the magnetic field that is axially symmetric in cylindrical coordinates. Upper left panel: magnetic field in the {x, y} plane cut at z = +1. Upper right panel: {x, y} plane at z = −1. Lower left panel: {y, z} poloidal plane at x = 1. The lower right panel is a 3D view of the field above and below the plane. The parameters used in the figure are {k, s, β, βp, ω, t}={−0.03, 1, 0, 0, −2, 4}. The scales are ϖN for the radius and zd along the axis. The arrows show the direction of the field at the end point of the arrow, but the field strength in the first three figures has been adjusted so as to show the outer arrows clearly. The fourth figure shows each arrow length as a fraction of the maximum value. |
| In the text | |
 |
Fig. 2. Distribution of the integrated line-of-sight RM in the four quadrants on the sky determined by the galactic edge-on disk and the positive rotation axis. We are looking along the negative y-axis relative to Fig. 1. The parameters of the magnetic field and of the flow field including rotation are as in the upper row of Fig. 1. Upper right and lower left images contain only negative RM values, while those at upper left and lower right are positive. The sign changes across the disk and across the axis to give the characteristic X configuration in the RM. The positive behavior is at upper left and lower right, while the negative behavior is at upper right and lower left. |
| In the text | |
 |
Fig. 3. Diagram showing the value on each patch of the RM in the second quadrant of our example. Other quadrants are the same except for sign. The color is merely shading and has no physical significance. To ensure that we are looking along the negative y-axis across the positive x-axis, the row is 11 − x, and the column is the z-axis. The observer is looking down from the left. |
| In the text | |
 |
Fig. 4. Left: two possibilities for the RM signature in each quadrant. A plus sign indicates a field approaching the observer. Hence the upper image indicates outward current along the rotation axis, and the lower image indicates inward current. The sketch at right shows the projected polarization that comprises an X field. The signs indicate the position angle relative to the rotation axis, if the angle is measured positively counterclockwise. The actual angles vary considerably both in theory and observation. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.