EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 658 (February 2022) A&A, 658 (2022) A60 Full HTML
Free Access
Issue
A&A
Volume 658, February 2022
Article Number A60
Number of page(s) 6
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/202141850
Published online 01 February 2022

© ESO 2022

1 Introduction

Although particles in supernova remnants (SNRs) can be efficiently accelerated up to about PeV energy through the diffusive shock acceleration (DSA) mechanism (Ptuskin et al. 2010), no direct observational evidence for the acceleration of PeV Galactic cosmic rays in SNRs has been reported so far. As cosmic rays (CR) are deflected by Galactic magnetic fields, it is difficult for us to trace their sources. However, GeV-TeV gamma-ray emission can be produced through relativistic protons interacting with gas and/or a molecular cloud (MC) near the SNRs (e.g., Aharonian 2001; Gabici et al. 2007; Ohira et al. 2011). At least two SNRs (IC 443 and W 44) appear to have the characteristic pion bump feature in the gamma-ray spectra (Ackermann et al. 2013), helping us to understand the particle acceleration mechanism.

A large number of SNRs have been detected in the gamma-ray band, but none of these SNRs has been shown to emit gamma-rays to hundreds of TeV, that is, a PeV particle accelerator (or PeVatron) has not yet been confirmed experimentally. Recently, HAWC, ASγ, and LHAASO experiments1 have reported a gamma-ray spectrum of SNR G106.3+2.7 above 40 TeV, indicating that SNR G106.3+2.7 is a promising PeVatron candidate (Albert et al. 2020; Cao et al. 2021). Observation of gamma-ray emission from SNR G106.3+2.7 above 10 TeV, even up to a few 100 TeV, has also been reported (Tibet ASg Collaboration 2021), indicating that the very high-energy (VHE) gamma-ray emission above 10 TeV is well correlated with an MC rather than with the pulsar PSR J2229+6114. This morphological feature favors a hadronic origin of the VHE emission.

Recently, Xin et al. (2019) argued that the pure leptonic model for the γ-ray emission can be ruled out based on the X-ray and TeV data from SNR G106.3+2.7. According to the current understanding of acceleration and escaping processes, Bao & Chen (2021) explored a new scenario to explain the γ-ray spectrum for this source. They considered the hadronic γ-ray spectrum dominating the emission above 10 TeV to be due to the accelerated protons escaping and interacting with MCs.

The CR particles in SNRs can been accelerated through the DSA mechanism (e.g., Kang & Jones 2006; Caprioli et al. 2008; Zirakashvili & Ptuskin 2012; Telezhinsky et al. 2012a; Ferrand et al. 2014). They escape from SNRs at the so-called free escape boundary (e.g., Ellison & Bykov 2011; Telezhinsky et al. 2012b; Kang et al. 2013).

In this paper, a theoretical model is developed to explain the multiband emission from SNR G106.3+2.7, in particular, GeV to ~ 100 TeV emission. In our model, the particles are accelerated inside an SNR through DSA with Bohm-like type diffusion. Then the accelerated particles propagate outward into a different region with Galactic diffusion outside the free escape boundary. These escaped particles can produce ≳ 100 TeV photons through π0 decay when they encounter dense MCs. Therefore, the multiband emission from the SNR G106.3+2.7 can be consistently reproduced.

2 Modeling multiband emission from SNR G106.3+2.7

2.1 Basic properties of observed multiband emission

Supernova remnant G106.3+2.7 has been observed at radio, X-ray, and γ-ray bands. Its basic features are as follows: (i) At the radio band, a brighter head and an extended tail region are evident. The overall spectral index is ~0.57, and the tail region has a slightly steeper spectrum than that in the head region (Pineault & Joncas 2000). (ii) At the X-ray band, the observational data of Suzaku targeting the SNR and adjacent pulsar PSR J2229+6114 indicate that the diffusive X-ray emission is nonthermal and originates from leptonic synchrotron emission with a photon index of ~ 2.2 (Fujita et al. 2021). (iii) At the γ-ray band, a detailed analysis of GeV emission near VER J2227+608 with ten years of Fermi-LAT Pass 8 data was performed (Xin et al. 2019). Significant TeV γ-ray emission from the elongated radio extension of SNR G106.3+2.7 was detected by VERITAS (Acciari et al. 2009). In this region, emission with tens of TeV was also detected by Milagro (Abdo et al. 2007, 2009). Multi-TeV emission coincident with G106.3+2.7 has also been detected by HAWC, and the joint VERITAS-HAWC spectrum is well fitted by a power law from 900 GeV to 180 TeV (Albert et al. 2020). Recently, ≳ 100 TeV photons from the direction of SNR G106.3+2.7 were detected by ASγ experiment and LHAASO (Tibet ASg Collaboration 2021; Cao et al. 2021). Observationally, the spectral energy distribution between ~ 1 GeV and ~10 TeV at first appears as an increasing trend, then decreases sharply, extending to ≳ 100 TeV. Therefore, SNR G106.3+2.7 is a new potential Galactic PeVatron.

The age of SNR G106.3+2.7 still remains uncertain, with several speculations: ~ 1 kyr (Albert et al. 2020; Bao & Chen 2021), or about 104 yr in comparison with the characteristic age of PSR J2229+6114. Here we adopt an age of 2000 yr to match the radius (~ 5.7 pc at a distance of 800 pc) of the SNR evolution with reasonable parameters (the explosion energy Esn = 1050 erg and ejecta mass Mej = 1.4 M⊙). With the adiabatic model of Kothes et al. (2001) (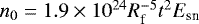n0=1.9×1024Rf−5t2Esn$n_0=1.9\times10^{24}R_{\textrm{f}}^{-5} t^2 E_{\textrm{sn}}$, and Rf is the shock radius), the ambient medium number density is estimated as n0 ~ 0.2 cm−3.

2.2 Modeling and results

As mentioned in Sect. 1, we assumed that the multiband nonthermal emission stems from two different regions, namely the acceleration region and the escaping region. These two regions, separated by the free escape boundary Resc, retain different diffusion coefficients. Inside the radius of Resc, the actual diffusion resembles a Bohm-like type, while outside the radius, Galactic diffusion dominates. For this purpose, the numerical nonlinear diffusive shock acceleration (NLDSA) model developed in Zirakashvili & Ptuskin (2012, hereafter ZP2012 model) was adopted, as it could naturally extend from the Bohm-like diffusion region to the Galactic diffusion region (Yang et al. 2015; Tang et al. 2015).

The main content of our NLDSA model is solving the hydrodynamic equations numerically for gas density ρ(r, t), gas velocity u(r, t), and gas pressure Pg(r, t) and the equation for the quasi-isotropic particle momentum distribution N(r, t, p) (see Eqs. (1)–(4) of ZP2012). We extended the ZP2012 model to the Galactic diffusion region and explained TeV emission from two TeV sources in our previous work (Tang et al. 2015).

In the acceleration region, the magnetic field above the radius Rc of the contact discontinuity (CD) is given by ZP2012, and the pressure and energy flux of the magnetic field are introduced in the dynamical equation (Zirakashvili et al. 2014). In the ZP2012 model, the coordinate dependences of the magnetic field are shown as follows: 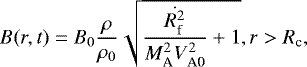B(r,t)=B0ρρ0Rf2.MA2VA02+1,r>Rc,\begin{equation*}B(r,t)=B_0 \frac{\rho}{\rho_0}\sqrt{\frac{\dot{R_{\textrm{f}}^2}}{M_{\textrm{A}}^2V_{\textrm{A0}}^2}+1}, r > R_{\textrm{c}}, \end{equation*}(1)

where ρ0 and 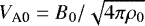VA0=B0/4πρ0$V_{\textrm{A0}}=B_0/\sqrt{4\pi\rho_0}$ are the gas density and the Alfvén velocity of the circumstellar medium; MA determines the value of the magnetic field amplification, and for young SNRs MA, it is about 23 (ZP2012); Rf is the radius of the forward shock (FS). However, in the region of ≤ Rc, the magnetic field is 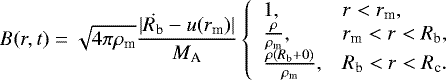B(r,t)=4πρm|Rb.−u(rm)|MA{1,r<rm,ρρm,rm<r<Rb,ρ(Rb+0)ρm,Rb<r<Rc. \begin{equation*}B(r,t)=\sqrt{4\pi\rho_{\textrm{m}}}\frac{|\dot{R_{\textrm{b}}}-u(r_{\textrm{m}})|}{M_{\textrm{A}}}\left\{ \begin{array}{ll} 1, & r<r_{\textrm{m}}, \\ \frac{\rho}{\rho_{\textrm{m}}}, & r_{\textrm{m}} <r<R_{\textrm{b}},\\ \frac{\rho(R_{\textrm{b}}+0)}{\rho_{\textrm{m}}},& R_{\textrm{b}}<r<R_{\textrm{c}}. \end{array} \right. \end{equation*}(2)

Here rm < Rb is the radius where the ejecta density has a minimum and equals ρm. The particlediffusion in the acceleration region is assumed to be a Bohm-like type, and the diffusion coefficient is given by D = ηBDB, where ηB = 2 represents the possible deviations of diffusion coefficient from the typical Bohm value in a high-velocity shock, DB = vpc∕3qB is the Bohm diffusion coefficient (also see ZP2012 for details).

In the escaping region, the magnetic field is assumed to be the classical Galactic magnetic field, and the diffusion coefficient can be expressed as 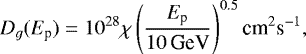Dg(Ep)=1028χ(Ep10 GeV)0.5cm2s−1,\begin{equation*}D_g(E_{\textrm{p}})=10^{28}\chi \left(\frac{E_{\textrm{p}}}{10 \,\textrm{GeV}}\right)^{0.5} \textrm{cm}^2\textrm{s}^{-1}, \end{equation*}(3)

where Ep is the accelerated proton energy, and the modification factor of χ = 10−3 is for slow diffusion and is much lower than that of the averaged Galactic diffusion (χ ~ 1), which indicates that the diffusion is suppressed by a factor of 100 or more near SNRs (Fujita et al. 2009). According to 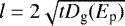l=2tDg(Ep)$l=2\sqrt{tD_{\textrm{g}}(E_{\textrm{p}})}$ (Atoyan et al. 1995), we have l ~ 5 pc for a 100 TeV in a diffusing particle of 2000 yr. The escaped particles with a few hundred TeV remain in the interacting region with the nearby MC.

In our calculations, the SNR shock propagates in the ambient medium with an average hydrogen number density of n0 = 0.2 cm−3, a magnetic field strength of B0 = 5 μG, a temperature of T = 104 K, an index of the ejecta velocity distribution of k = 7, and an initial forward-shock velocity of 2.9 × 104 km s−1. The injection efficiency of thermal protons and electrons is assumed to be ηf = ηb = 10−4 and ηf = ηb = 10−7 at FS (f) and RS (b), respectively.

In this case, the changes in shock radii Rf and Rb, the forward- and reverse-shock velocities Vf and Vb, and the ratio of CR energy to SN explosion energy (Ecr∕Esn) with time are shown in Fig. 1. The calculations were performed until t = 2000 yr, when the value of the forward-shock velocity drops down to Vf = 1384 km s−1 and the forward-shock radius is Rf = 5.70 pc. At the Sedov stage, the reverse-shock velocity quickly decreases to 78 km s−1 after ~ 1000 yr. Moreover, at 2000 yr, Ecr∕Esn ≈ 12%, approaching Ecr ~ 1049 erg. Considering the gas density n0 = 0.2 cm−3, the total CR energy is 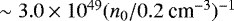~3.0×1049(n0/0.2 cm−3)−1$\sim 3.0\times 10^{49} (n_0/0.2\ \textrm{cm}^{-3})^{-1}$, which can reproduce the ~ GeV gamma-ray observation (Xin et al. 2019) for this source.

The profiles of the gas, CR pressure, and magnetic pressure at the radial distance at 2000 yr are shown in the top panel of Fig. 2, where the value of CR pressure is much lower than that of the gas pressure at the forward-shock position. The spatially integrated spectrum of accelerated protons and electrons is shown in the bottom panel of Fig. 2. On the one hand, because of the severe synchrotron losses in strong magnetic field, the spectrum of the accelerated electrons appears to have an obvious break. They are cut off at a few TeV. On the other hand, the proton spectrum can be approximated as a power law with a spectral index of ~ 2 below a break energy Ecut, and it decreases exponentially above Ecut. The protons inside the SNR can be accelerated up to ~PeV, and the escaped protons mainly stem from the high-energy region with energy between ~ Ecut to Emax (see the dashed line in the bottom panel of Fig. 2).

For the maximum energy Emax of the accelerated protons, a simple estimate is as follows. Because of the free-escape boundary at the Resc = ξRf, maximum energy particles with distances greater than Resc cannot diffuse back to the shock, and then the instantaneous maximum energy can be estimated by using D(pmax)∕Vf = (ξ − 1)Rf (e.g., Caprioli et al. 2010; Morlino & Caprioli 2012), where D(p) is the diffusion coefficient. Here ξ = 1.2 is used, which corresponds to a diffusing distance of 0.2Rf upstream of the shock. The maximum energy for the Bohm-like diffusion is then approximated as 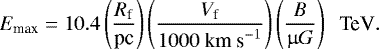Emax=10.4(Rfpc)(Vf1000 km s−1)(B\upmuG)  TeV.\begin{equation*}E_{\textrm{max}}=10.4 \left(\frac{R_{\textrm{f}}}{\textrm{pc}}\right)\left(\frac{V_{\textrm{f}}}{1000~\textrm{km~s}^{-1}}\right)\left(\frac{B}{\upmu G}\right)\;\;\textrm{TeV}. \end{equation*}(4)

At the age of 2000 yr in our calculations, Rf ~ 5.7 pc and Vf ~ 1384 km s−1, and for the instantaneous maximum magnetic field B ~ 50 μG in the FS upstream, the estimated Emax ~ 2 PeV. The magnetic field strength would fall back to the background magnetic field (5μG) as it is away from the immediate shock front (see the top panel of Fig. 2). Therefore, the value of Emax estimated in Eq. (4) is an upper limit. On the other hand, the value of Emax can be roughly estimated as follows. Because the escape particles consist of those with maximum energies in different shock positions, their spectrum has a Gauss-like distribution, as shown in Fig. 2. If Nesc(ppeak) represents the peak number density of the escape particles with ppeak, then we can define a parameter f = Nesc(p ≥ ppeak)∕Nesc(ppeak). For a given value of f, the change in corresponding p with time can be calculated. The results for f = 1,  0.5,  0.1, and 0.01 are shown in Fig. 3, and the maximum energy Emax = pmaxc can reach ~ PeV when f ≈ 0.01. Therefore, the maximum energy of accelerated particles is ~1−~ 2 PeV. The values of the resulting step shape are only approximate because the momentum grid numbers are far lower than the time steps in our calculations.

In our calculations, a low injection efficiency (ηf = ηb = 10−4) is adopted to reproduce the radio and GeV observation. If the injection efficiency for protons is high (e.g., ηf = ηb = 10−2), then the Ecr ∕Esn can be approximately 70% after 1000 yr in ZP2012, and the total energy of the accelerated protons would be close to the energy of a supernova explosion. This high ratio (Ecr∕Esn ~ 70%) is higher than our result here (Ecr∕Esn = 10%). As a consequence, the produced GeV flux would exceed the observed flux for this source.

To characterize the regions in which the escaped protons interact with the MC in the shell with a solid angle of Ω and a radius from Resc to Resc,out (the accelerated CR particles begin to run away from SNRs at the boundary (Resc = ξRf)), we set the value of Resc,out as 10 pc to match the high-energy gamma ray observation. We introduced a parameter of ncloudΩ∕4π = 50 cm−3 to describe the number density of the MC, where the ncloud is the number density of the MC. It is worth mentioning that ncloud cannot be determined separately because of the relation to the size of radiation region (e.g., Ω =π∕3, ncloud ~ 1500 cm−3; Ω =4π, ncloud ~ 50 cm−3). In addition, its typical density is about 100 cm−3, wherein the cloud could host clumps with a density of 103−104 cm−3 (Owen et al. 2021). The total mass of the MC in the interacting region is 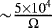~5×104Ω${\sim} \frac{5\times 10^4}{\Omega}$ M⊙ by integrating the density from 1.2Resc to 10 pc.

The particle (both the leptonic and hadronic) acceleration can be calculated by coupling hydrodynamic process and the evolution of the magnetic field (including the feedback between the magnetic field and the accelerated protons) inside the SNR, as well as the extension to the escaped particle diffusion outside the SNR (Tang et al. 2015). For a given SNR, the spectra of accelerated particles and escaped particles can therefore be calculated naturally at any time t. Generally, the radio and X-ray photons originate from the leptonic synchrotron emission, and the high-energy gamma-rays are produced by the proton-proton interaction process (hadronic scenario) or the inverse-Compton (IC) process (leptonic scenario). Here the seed photons consist of 2.7 K microwave background light with an energy density of 0.25eV cm−3, and a 25 K far-infrared radiation field with anenergy density of 0.2eV cm−3. Specifically, we used the emissivity formula developed by Blumenthal & Gould (1970) for the leptonic component, while the proton-proton (pp) interaction process can be calculated by analytic approximation of Kelner et al. (2006), where the hadronic scenario contains the intrinsic emission inside an SNR and the emission from its escaped protons colliding with a nearby MC.

The calculated spectral energy distribution (SED) of G106.3+2.7 with an estimated age of 2000 yr is shown in Fig. 4. From radio to X-ray band, the photons are produced through the synchrotron emission of energetic electrons in the magnetic field with a strength of ~50 μG at the FS position (also see the evolution of magnetic field of Fig. 1). Thus, the resulting IC flux is very low due to severe radiative cooling in the strong magnetic field. Xin et al. (2019) also argued that the radio flux gives a magnetic field strength of ~ 50μG and a corresponding Ecut ~ TeV of the accelerated electrons in a hadronic scenario. The gamma-ray emission mainly originates from the hadronic component, and the Fermi data can be fit by the accelerated protons inside the SNR together with the escaped protons outside the SNR interacting with the nearby MC. A clearer picture is presented in Fig. 5. Our results indicate that the spectrum of high-energy gamma-rays is dominated by the hadronic component, and the overall gamma-ray flux can naturally be explained by our model.

thumbnail Fig. 1

Dependences on time of the forward-shock radius Rf (thin solid line), the reverse-shock radius Rb (thin dashedline), the forward-shock velocity Vf (thick solid line), the reverse-shock velocity |Vb| (thick dashed line), the ratio of CR energy and energy of supernova explosion Ecr ∕Esn (thick dotted line), and the magnetic field strength (thick dash-dotted line) in the shock radius (r = Rf).
thumbnail Fig. 2

Radial profiles of relevant physical quantities and spectra of particles produced in SNR. Top panel: Radial dependence of the gas pressure (solid line), the CR pressure (dotted line), and the magnetic field pressure (dashed line) at the epoch of t = 2000 yr. Bottom panel: Spectra of particles produced in the whole SNR (space integrating) at the epoch of t = 2000 yr. The spectra of protons include the intrinsic proton spectrum (solid line) and the electron spectrum (dotted line) inside the SNR, and escaped spectra (dashed line) integrated from Resc = 1.2Rf to Resc,out = 10 pc.
thumbnail Fig. 3

Change of the energy E of accelerated particles with time for f = 1 (red line), f = 0.5 (green line), f = 0.1 (blue line), and f = 0.01 (yellow line).The definition of f is described in text.
thumbnail Fig. 4

Multiwave band spectra of G106.3+2.7. The red line shows synchrotron (dashed line), inverse Compton (dot-dashed line), and pp interaction (solid line) inside the SNR. The dotted blue line represents the high-energy emission from the escapedprotons interacting with the MC, and the black line shows the overall VHE emission (pp interaction). Radio data of the tail region are from Pineault & Joncas (2000). The statistical uncertainties of the tail region of XMM-Newton are from Ge et al. (2021), and of the whole region of Suzaku, they are from Fujita et al. (2021). The Fermi-LAT data are from Xin et al. (2019), the VERITAS data are from Acciari et al. (2009), the Milagro data are from Abdo et al. (2007, 2009), the statistical uncertainties of HAWC are from Albert et al. (2020), the ASγ data are from Tibet ASg Collaboration (2021), and the LHAASO data are from Cao et al. (2021).

3 Summary and discussion

The multiband photon emission from SNR G106.3+2.7 (a potential Galactic PeVatron) was studied here. The results show that photons with energy of Eγ ≳ 1 GeV favor a hadronic origin, where the photons in the energy range of ~ 1 GeV to ~1 TeV are produced inside the SNR through proton-proton interaction, and photons with Eγ ≳ 1 TeV originate from the interaction of escaped protons with a dense molecular cloud.

In our model, the magnetic field plays a dynamical role. Magnetic pressure and magnetic energy flux are taken into account in the shock. The amplified effects and the spatial distribution of the magnetic field were assumed using a simple parameterized description in the following. The parameter MA and the plasma density determine the value of the amplified magnetic field strength for r > Rc (see Eq. (1)). In the vicinity of the CD, the plasma flow is strongly influenced by the Rayleigh-Taylor instability and results in the generation of magnetohydrodynamic (MHD) turbulence in this region. Equation (2) is assumed to describe the amplification of the downstream magnetic field of the reverse shock. However, one important mechanism for generatingan amplified magnetic field is the plasma instabilities driven by CR streaming (Bell et al. 2013; Caprioli et al. 2009), which in turn leads to a more efficient particle acceleration. In particular, the shock permeating into the dense medium is able to excite nonresonant streaming instabilities, and efficiently accelerates particles to the PeV range in the early stages (Cristofari et al. 2020a). It is noteworthy that the nonresonant growth of instabilities is expected to lead to the PeV range in only very few cases (Bell et al. 2013; Schure & Bell 2013; Cristofari et al. 2020b). For instance, based on the analysis of the nonresonant instability, Schure & Bell (2013) reported that, in the context of SNR shocks, only young SNRs in a dense environment are plausible candidates to accelerate CRs to PeV energies under some conditions (see also Cristofari et al. 2020b for a more recent discussion). Therefore, a further investigation of MHD effects at astrophysical shocks is necessary.

In the escaping region, parameter χ of the diffusion coefficient in Eq. (3) is taken as 0.001 to fit the TeV gamma-ray spectra observed by LHAASO, which is much lower than its counterpart in the Galaxy. Near the SNR, the diffusion coefficient can be suppressed by a factor of 100 or more compared to the Galaxy (Fujita et al. 2009). In addition, we calculated the gamma-ray emission spectra for different χ values (see Fig. 6). The results indicate that the diffusion coefficient greatly affects the high-energy tail of gamma-rays.

We set the age of the SNR to 2000 yr to reproduce the high-energy data. Figure 3 shows that the maximum energy of acceleration particles decreases rapidly at a late stage, and an older age (e.g., 104 yr) makes it harder to fit the high-energy data. On the other hand, the energetic escaped particles accelerated at an early stage should not reside in the interacting region with the MC.

The typical explosion energy for a thermonuclear supernova is Esn= 1051 erg. Regarding the age of SNR G106.3+2.7 (2000 yr) and the discussion in Sect. 2.1, the ambient medium number density is about 2 cm−3. The total CR energy is 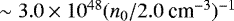~3.0×1048(n0/2.0 cm−3)−1$\sim 3.0\times 10^{48} (n_0/2.0\ \textrm{cm}^{-3})^{-1}$, which leads to Ecr ∕Esn ~ 0.1% for a medium number density of 2 cm−3 with an explosion energy Esn = 1051 erg. Therefore, the insufficient acceleration of CR protons in the shock is invoked. Everything we know about DSA suggests that young, strong SNR shocks are intrinsically much more efficient than our case here, for instance, Ecr ∕Esn ~ 10%. It is very difficult to produce TeV photons via DSA with this low acceleration efficiency. Hence, the explosion energy adopted here is Esn= 1050 erg, while the estimated ambient medium number density is n0 ~ 0.2 cm−3 (Kothes et al. 2001).

Here, the evolution and particle acceleration only consider type Ia SNR. However, ignoring other types is probably too simple for this specific SNR, as the actual types of the parent supernova explosion and the progenitor star are still undetermined. For type Ia SNRs, the matter distribution in the circumstellar medium (CSM) and interstellar medium (ISM) is less affected by the activities of the progenitor stars, which may result in a statistically more spherical shape. For core-collapse SNRs, however, the stellar winds blown by progenitor stars would have modified the CSM and ISM matter distribution prior to the explosion. As a consequence, the hadronic processes are affected as the matter distribution varies. A more detailed numerical simulation of particle acceleration in four types of SNRs has been conducted by Ptuskin et al. (2010). Their results indicated that the maximum energy of accelerated particles in all stages can be different for various types.

Bao & Chen (2021) have studied the hard γ-ray SED of SNR G106.3+2.7 and pointed out that the radio to X-ray band and the Fermi gamma-rays can originate from the synchrotron emission and inverse Compton of the energetic electrons, respectively. Above 10 TeV, gamma-ray emission arises from the contribution of escaped particles that interact with the MC. However, the differences between their model and our model are as follows. The acceleration and propagation of the particles are self-consistently considered through the ZP2012 model in the acceleration region with its extension (Tang et al. 2015) to escaping regions, and the hadronic contribution from two regions is predicted in our model. Moreover, the resulting IC flux with Eγ ≳ 100 MeV is much lower than that produced in proton-proton interaction inside the SNR because of the energetic electron cooling in a strong magnetic field.

Finally, although the gamma-ray emission can be produced via high-energy particles accelerated by the shock of the SNR G106.3+2.7 (Albert et al. 2020; Liu et al. 2020), with hadronic processes dominating the photon spectrum extending to at least 400 TeV (Xin et al. 2019; Tibet ASg Collaboration 2021), it should be pointed out that a leptonic origin of VHE γ-rays is also possible, such as in pulsar wind nebulae (Albert et al. 2020). Therefore, deeper observations are required.

thumbnail Fig. 5

Spectra of particles produced in SNR G106.3+2.7 as well as the multiwave band spectra. Top panel: same as the bottom panel of Fig. 2, but the value of the escape particle spectra is magnified by an order of magnitude. Bottom panel: same as Fig. 4.
thumbnail Fig. 6

Interaction of gamma-rays from the escaped protons with the same density of the MC for χ = 0.1 (solid line), 0.01 (dashed line), and 0.001 (dotted line), where the gamma-ray flux maximum value is normalized to 1.

Acknowledgements

This work is partially supported by National Key R & D Program of China under grant No. 2018YFA0404204, and the National Natural Science Foundation of China U1738211. C.Y. Yang is partially supported by the National Natural Science Foundation of China U2031111, U1931204, 11673060.

References

  1. Abdo, A. A., Allen, B., Berley, D., et al. 2007, ApJ, 664, L91 [NASA ADS] [CrossRef] [Google Scholar]
  2. Abdo, A. A., Allen, B. T., Aune, T., et al. 2009, ApJ, 700, L127 [CrossRef] [Google Scholar]
  3. Acciari, V. A., Aliu, E., Arlen, T., et al. 2009, ApJ, 703, L6 [NASA ADS] [CrossRef] [Google Scholar]
  4. Ackermann, M., Ajello, M., Allafort, A., et al. 2013, Science, 339, 807 [NASA ADS] [CrossRef] [Google Scholar]
  5. Aharonian, F. A. 2001, Space Sci. Rev., 99, 187 [CrossRef] [Google Scholar]
  6. Albert, A., Alfaro, R., Alvarez, C., et al. 2020, ApJ, 896, L29 [NASA ADS] [CrossRef] [Google Scholar]
  7. Atoyan, A. M., Aharonian, F. A., & Völk, H. J. 1995, Phys. Rev. D, 52, 3265 [NASA ADS] [CrossRef] [Google Scholar]
  8. Bao, Y. W., & Chen, Y. 2021, ApJ, 919, 32 [NASA ADS] [CrossRef] [Google Scholar]
  9. Bell, A. R., Schure, K. M., Reville, B., et al. 2013, MNRAS, 431, 415 [NASA ADS] [CrossRef] [Google Scholar]
  10. Blumenthal, G. R., & Gould, R. J. 1970, Rev. Mod. Phys., 42, 237 [Google Scholar]
  11. Cao, Z., Aharonian, F. A., An, Q., et al., 2021, Nature, 594, 33 [NASA ADS] [CrossRef] [Google Scholar]
  12. Caprioli, D., Blasi, P., Amato, E., & Vietri, M. 2008, ApJ, 679, L39 [Google Scholar]
  13. Caprioli, D., Amato, E., Blasi, P., & Vietri, M 2009, MNRAS, 395, 895 [NASA ADS] [CrossRef] [Google Scholar]
  14. Caprioli, D., Amato, E., & Blasi, P., 2010, Astropart. Phys. 33, 307 [NASA ADS] [CrossRef] [Google Scholar]
  15. Cristofari, P., Renaud, M., Marcowith, A., Dwarkadas, V. V., & Tatischeff, V. 2020a, MNRAS, 494, 2760 [NASA ADS] [CrossRef] [Google Scholar]
  16. Cristofari, P., Blasi, P., Amato, E. 2020b, Astropart. Phys., 123, 102492 [NASA ADS] [CrossRef] [Google Scholar]
  17. Ellison, D. C., & Bykov, Andrei M. 2011, ApJ, 731, 87 [NASA ADS] [CrossRef] [Google Scholar]
  18. Ferrand, Gilles, Decourchelle, Anne, & Safi-Harb, Samar 2014, ApJ, 789, 49 [NASA ADS] [CrossRef] [Google Scholar]
  19. Fujita, Y., Ohira, Y., Tanaka, S. J., & Takahara, F. 2009, ApJ, 707, L179 [NASA ADS] [CrossRef] [Google Scholar]
  20. Fujita, Y., Bamba, A., Nobukawa, K. K., et al. 2021, ApJ, 912, 133 [NASA ADS] [CrossRef] [Google Scholar]
  21. Gabici, S., Aharonian, F.A., & Blasi, P. 2007, Ap&SS, 309, 365 [CrossRef] [Google Scholar]
  22. Ge, C., Liu, R.-Y., Niu, S., et al. 2021, The Innovation, 2, 100118 [NASA ADS] [CrossRef] [Google Scholar]
  23. Kang, H., & Jones, T. W. 2006, Astropart. Phys., 25, 246 [NASA ADS] [CrossRef] [Google Scholar]
  24. Kang, Hyesung, Jones, T. W., & Edmon, Paul P. 2013, ApJ, 777, 25 [CrossRef] [Google Scholar]
  25. Kelner, S. R., Aharonian, F. A., & Bugayov, V. V. 2006, Phys. Rev. D, 74, 034018 [Google Scholar]
  26. Kothes, R., Uyaniker, B., & Pineault, S. 2001, ApJ, 560, 236 [NASA ADS] [CrossRef] [Google Scholar]
  27. Liu, S., Zeng, H., Xin, Y., et al. 2020, ApJ, 897, L34 [NASA ADS] [CrossRef] [Google Scholar]
  28. Morlino, G., & Caprioli, D. 2012, A&A, 538, 81 [Google Scholar]
  29. Ohira, Y., Murase, K., & Yamazaki, R. 2011, MNRAS, 410, 1577 [NASA ADS] [Google Scholar]
  30. Owen, E. R., On, A. Y. L., Lai, S.-P., & Wu, K. 2021, ApJ, 913, 52 [NASA ADS] [CrossRef] [Google Scholar]
  31. Pineault, S., & Joncas, G. 2000, AJ, 120, 3218 [NASA ADS] [CrossRef] [Google Scholar]
  32. Ptuskin, V., Zirakashvili, V., & Seo, E. 2010, ApJ, 718, 31 [NASA ADS] [CrossRef] [Google Scholar]
  33. Schure, K. M., & Bell, A. R., 2013, MNRAS, 435, 1174 [NASA ADS] [CrossRef] [Google Scholar]
  34. Tang, Y. Y., Yang, C. Y., Zhang, L., & Wang, J. C. 2015, ApJ, 812, 32 [NASA ADS] [CrossRef] [Google Scholar]
  35. Telezhinsky, I., Dwarkadas, V. V., & Pohl, M. 2012a, Astropart. Phys., 35, 300 [NASA ADS] [CrossRef] [Google Scholar]
  36. Telezhinsky, I., Dwarkadas, V. V., & Pohl, M. 2012b, A&A, 541, 153 [Google Scholar]
  37. Tibet ASg Collaboration (Amenomori, M., et al.) 2021, Nat. Astron., 5, 460 [NASA ADS] [CrossRef] [Google Scholar]
  38. Xin, Y., Zeng, H., Liu, S., et al. 2019, ApJ, 885, 162 [NASA ADS] [CrossRef] [Google Scholar]
  39. Yang, C. Y., Zhang, L., & Wang, J. C. 2015, MNRAS, 448, 3423 [NASA ADS] [CrossRef] [Google Scholar]
  40. Zirakashvili, V. N., & Ptuskin, V. S. 2012, Astropart. Phys., 39, 12 [Google Scholar]
  41. Zirakashvili, V. N., Aharonian, F. A., Yang, R., Oña-Wilhelmi, E., & Tuffs, R. J. 2014, ApJ, 785, 130 [NASA ADS] [CrossRef] [Google Scholar]
1

HAWC: the High-Altitude Water Cherenkov Gamma-Ray Observatory. ASγ: Tibet air shower experiment. LHAASO: large High Altitude Air Shower Observatory.

All Figures

thumbnail Fig. 1

Dependences on time of the forward-shock radius Rf (thin solid line), the reverse-shock radius Rb (thin dashedline), the forward-shock velocity Vf (thick solid line), the reverse-shock velocity |Vb| (thick dashed line), the ratio of CR energy and energy of supernova explosion Ecr ∕Esn (thick dotted line), and the magnetic field strength (thick dash-dotted line) in the shock radius (r = Rf).
In the text
thumbnail Fig. 2

Radial profiles of relevant physical quantities and spectra of particles produced in SNR. Top panel: Radial dependence of the gas pressure (solid line), the CR pressure (dotted line), and the magnetic field pressure (dashed line) at the epoch of t = 2000 yr. Bottom panel: Spectra of particles produced in the whole SNR (space integrating) at the epoch of t = 2000 yr. The spectra of protons include the intrinsic proton spectrum (solid line) and the electron spectrum (dotted line) inside the SNR, and escaped spectra (dashed line) integrated from Resc = 1.2Rf to Resc,out = 10 pc.
In the text
thumbnail Fig. 3

Change of the energy E of accelerated particles with time for f = 1 (red line), f = 0.5 (green line), f = 0.1 (blue line), and f = 0.01 (yellow line).The definition of f is described in text.
In the text
thumbnail Fig. 4

Multiwave band spectra of G106.3+2.7. The red line shows synchrotron (dashed line), inverse Compton (dot-dashed line), and pp interaction (solid line) inside the SNR. The dotted blue line represents the high-energy emission from the escapedprotons interacting with the MC, and the black line shows the overall VHE emission (pp interaction). Radio data of the tail region are from Pineault & Joncas (2000). The statistical uncertainties of the tail region of XMM-Newton are from Ge et al. (2021), and of the whole region of Suzaku, they are from Fujita et al. (2021). The Fermi-LAT data are from Xin et al. (2019), the VERITAS data are from Acciari et al. (2009), the Milagro data are from Abdo et al. (2007, 2009), the statistical uncertainties of HAWC are from Albert et al. (2020), the ASγ data are from Tibet ASg Collaboration (2021), and the LHAASO data are from Cao et al. (2021).
In the text
thumbnail Fig. 5

Spectra of particles produced in SNR G106.3+2.7 as well as the multiwave band spectra. Top panel: same as the bottom panel of Fig. 2, but the value of the escape particle spectra is magnified by an order of magnitude. Bottom panel: same as Fig. 4.
In the text
thumbnail Fig. 6

Interaction of gamma-rays from the escaped protons with the same density of the MC for χ = 0.1 (solid line), 0.01 (dashed line), and 0.001 (dotted line), where the gamma-ray flux maximum value is normalized to 1.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.