EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 657 (January 2022) A&A, 657 (2022) A66 Full HTML
Free Access
Issue
A&A
Volume 657, January 2022
Article Number A66
Number of page(s) 14
Section Numerical methods and codes
DOI https://doi.org/10.1051/0004-6361/202141763
Published online 11 January 2022

© ESO 2022

1. Introduction

The characterisation of stellar spectra is of great importance to modern astrophysics. It marks the cornerstone for different fields including exoplanets (see Valenti & Fischer 2005; Santos et al. 2013; Brewer et al. 2016), nearby field cosmology (e.g., De Silva et al. 2015; Buder et al. 2021), or even resolved stellar populations in nearby galaxies (see Davies et al. 2017). Moreover, the use of automated methods to infer their stellar atmospheric parameters, including effective temperature Teff, surface gravity log g, and metallicity [Fe/H], allows large surveys to release large databases comprising thousands of stars. Among these surveys are the APO Galactic Evolution Experiment (APOGEE, Dawson et al. 2013), the GALactic Archaeology with HERMES (GALAH, De Silva et al. 2015), the LAMOST Experiment for Galactic Understanding and Exploration (LEGUE, Deng et al. 2012), the RAdial Velocity Experiment (RAVE, Kunder et al. 2017), the Sloan Extension for Galactic Understanding and Exploration (SEGUE, Lee et al. 2008), the Gaia-ESO Survey (GES, Gilmore et al. 2012), the WHT Enhanced Area Velocity Explorer (WEAVE, Dalton et al. 2018), and the 4-metre Multi-Object Spectroscopic Telescope (4MOST, de Jong et al. 2019).

In parallel, the census of stars harbouring exoplanets has been steadily increasing over the last decades thanks to the space missions like CoRoT (Convection, Rotation and planetary Transits, Auvergne et al. 2009), Kepler (Koch et al. 2010; Borucki et al. 2010), and TESS (Transiting Exoplanet Survey Satellite, Ricker et al. 2015), as well as to the ground-based instruments like the High-Accuracy Radial velocity Planet Searcher (HARPS, Mayor et al. 2003), HARPS North (HARPS-N, Cosentino et al. 2012), the Calar Alto high-Resolution search for M dwarfs with Exoearths with Near-infrared and optical Echelle Spectrographs (CARMENES, Quirrenbach et al. 2020), and the Echelle Spectrograph for Rocky Exoplanet and Stable Spectroscopic Observations (ESPRESSO, Pepe et al. 2021). The determination of stellar parameters is also of great interest to exoplanetary science because the masses and radii of the host stars are key to characterising the planets orbiting around them (see, e.g., Torres et al. 2012; Santos et al. 2013; Brewer et al. 2016; Sousa et al. 2018; Schweitzer et al. 2019; Brucalassi et al. 2021). Moreover, they are critical to the high-resolution transmission spectroscopy since they are employed to model the centre-to-limb variation, the limb-darkening, and the Rossiter-McLaughlin effect (see, e.g., Czesla et al. 2015; Hoeijmakers et al. 2018; Casasayas-Barris et al. 2020).

Broadly speaking, the computation of the stellar atmospheric parameters of FGKM-type stars by means of spectroscopic data can be performed via two different methods: equivalent width (EW) and spectral synthesis. On the one hand, the EW method uses the strength of several spectral lines to calculate the stellar atmospheric parameters. It employs the standard technique based on the ionisation and excitation balance, taking advantage of the sensitivity of the EWs of Fe I and Fe II lines to the stellar atmospheric parameters (see, e.g., Ghezzi et al. 2010; Tabernero et al. 2012; Santos et al. 2013). On the other hand, the spectral synthesis method relies on synthetic spectra used to reproduce the observations using χ2 fitting algorithms (e.g., Valenti & Fischer 2005; García Pérez et al. 2016; Tsantaki et al. 2018). The synthetic spectra, all of which might be divided into spectral regions of interest (see e.g., Tsantaki et al. 2014; Brewer et al. 2016), are finally compared to observations to find the atmospheric model that reproduces the data.

These two methods have been extensively reviewed in the literature (see, e.g., Allende Prieto 2016; Nissen & Gustafsson 2018; Jofré et al. 2019; Blanco-Cuaresma 2019; Marfil et al. 2020). In fact, open-source implementations of both methods are available to the astronomical community. Regarding the spectral synthesis method, we find the APOGEE Stellar Parameter and Chemical Abundance Pipeline (ASCAP, García Pérez et al. 2016), FERRE (Allende Prieto et al. 2006), MINESweeper (Cargile et al. 2020), MyGIsFOS (Sbordone et al. 2014), The Payne (Ting et al. 2019), and Spectroscopy Made Easy (SME, Piskunov & Valenti 2017; Valenti & Piskunov 1996), whereas the EW method is implemented in tools such as ARES+MOOG (Sousa et al. 2008; Santos et al. 2013), FAMA (Magrini et al. 2013), GALA (Mucciarelli et al. 2013), SPECIES (Soto & Jenkins 2018), and STEPAR (Tabernero et al. 2019). Interestingly enough, other tools such as iSpec (Blanco-Cuaresma et al. 2014), FASMA (Andreasen et al. 2017; Tsantaki et al. 2020), and BACCHUS (Masseron et al. 2016) are designed to derive the stellar atmospheric parameters using both approaches. Other implementations of the synthetic method rely on Bayesian schemes to calculate the stellar parameters. These schemes represent an improvement over classical χ2 fitting methods as they can fully explore the probability distribution of the stellar atmospheric parameters associated with an observed spectrum (see, e.g., Schönrich & Bergemann 2014; Czekala et al. 2015).

In this work, we present a description of STEPARSYN, written in Python 3.X, which is designed to retrieve stellar atmospheric parameters of late-type stars under the spectral synthesis method. The code was designed to overcome the limitations of the EW method implemented in the STEPAR code (Tabernero et al. 2019). STEPARSYN represents a step forward towards the analysis of late-type stellar spectra as it relies on a Markov chain Monte Carlo (MCMC) sampler (emcee, see Foreman-Mackey et al. 2013) to explore the probability distribution of the stellar atmospheric parameters. In particular, MCMC methods allow us to see the intrinsic parameter degeneracy and provide the uncertainties directly from the sampled probability distribution. In all, the STEPARSYN code has already been applied to the study and characterisation of late-type stars. In particular, the code has been employed to study stars in open clusters (Negueruela et al. 2018, 2021; Alonso-Santiago et al. 2019, 2020), cepheids (Lohr et al. 2018), stars in the Magellanic clouds (Tabernero et al. 2018), exoplanet hosts observed under the ESPRESSO GTO programme (Borsa et al. 2021; Demangeon et al. 2021; Lillo-Box et al. 2021), the first super-AGB candidate in our Galaxy (VX Sgr, see Tabernero et al. 2021), and stars belonging to the CARMENES GTO sample (Marfil et al. 2021).

This manuscript is divided into five different sections. We describe the STEPARSYN code and its internal workflow in Sect. 2. In Sect. 3, we test the performance of the code against a sample of late-type stars. We discuss the results and compare them to those obtained in previous works in Sect. 4. Finally, the conclusions are presented in Sect. 5.

2. Description of the code

2.1. Code workflow

STEPARSYN is a Bayesian code1 designed to sample the posterior probability distribution of stellar parameters associated with an observed spectrum. Prior to the initialisation of the code the user must provide the following input data: (1) an observed spectrum; (2) a grid of synthetic spectra; (3) a list of spectral masks. First, the observed spectrum should be formatted as a plain-text file containing wavelengths, fluxes, and their corresponding uncertainties. Second, the grid should contain the wavelength regions that cover the spectral features under analysis and cover the parameter space relevant to the observations. Third, the list of spectral masks is a compilation of wavelength intervals defined by their centre and width. These masks allow the user to include only atomic features in the analysis. In addition, these spectral masks might be used to avoid parts of the wavelength regions in order to effectively remove ‘bad’ pixels that can affect the resulting stellar parameters (e.g., cosmic rays and telluric lines; see also Valenti & Fischer 2005).

After these input data are gathered the code can be initialised following the workflow displayed in Fig. 1. In the beginning, STEPARSYN performs a minimisation by means of the curvefit subroutine of the SciPy Python library (Virtanen et al. 2020) to obtain a preliminary estimation of the stellar parameters. Then, using these preliminary parameters the code calculates the residuals for each individual wavelength region in order to assess the quality of the user-provided errors. In fact, the observational flux uncertainties calculated from the photon-noise are not enough to explain the difference between models and observations (see, e.g., Hogg et al. 2010; Czekala et al. 2015). These unaccounted-for errors arise from the fact that synthetic spectra do not provide a perfect match to the observations (see, e.g., Shetrone et al. 2015; Tsantaki et al. 2018; Passegger et al. 2020). In particular, the precision of the atomic and molecular data employed to generate the model are known to be responsible for these differences. There are millions of features that introduce systematic errors that are perhaps too complex to handle in a one-by-one basis. In spite of this, STEPARSYN mitigates them by providing a new estimation on the uncertainties of the fluxes. To that aim, the code computes the variance of the residuals from the difference of the synthetic model and the observations for each wavelength region (see Czekala et al. 2015). These variances are used to compute a robust estimation of the errors for each individual wavelength region.

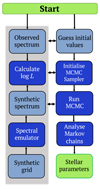thumbnail Fig. 1.

Diagram of the STEPARSYN internal workflow.

After computing the new robust flux uncertainties, the code creates a set of points centred on the result of the curvefit minimisation. These points are evaluated using a likelihood function (log L). This function takes into account the synthetic spectrum corresponding to a given point in the parameter space (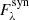), the observations (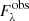), and their corresponding uncertainties (σλ). First, the synthetic spectrum 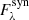is generated by means of an spectral emulator (see Sect. 2.3). Second, the synthetic spectrum is multiplied by a scaling factor given by the median value of the flux points above the third quartile. In other words, the scaling factor allows both the synthetic and observed spectra to be effectively placed at the same flux level. This process is done independently for each wavelength region included in the synthetic grid. Shortly after, the points inside the spectral masks are identified and used to compute the log L according to the following expression:

(1)

The aforementioned set of points and their corresponding log L values are used to initialise an MCMC sampler (emcee, Foreman-Mackey et al. 2013). The emcee2 package requires the user to provide the number of Markov chains (walkers) to employ and for how long they should be ran (iterations). We recommend to employ 12 walkers for a total of 1000 iterations each. Under these conditions, the code takes approximately 40 min to complete the sampling (i.e. using a seventh-generation Intel Core i7 processor). Thus, the MCMC sampler has explored the likelihood function that the code translates into the parameters and their uncertainties. At this point, the code delivers the best spectrum that reproduces the features under analysis. Finally, it marginalises the samples drawn from the posterior distribution for each atmospheric parameter and extracts the resulting parameter values and corresponding uncertainties. The former is performed by computing the median and the standard deviation of the marginalised samples.

2.2. Synthetic grid

We provide a grid of synthetic spectra with the public version of STEPARSYN. We computed this grid thanks to the radiative transfer code Turbospectrum3 (Plez 2012). In order to generate a synthetic spectrum,Turbospectrum needs the following input data: (1) wavelength region to synthesise; (2) a model atmosphere; (3) atomic and molecular data; (4) the chemical composition of the model atmosphere. To that aim, we compiled 296 Fe I and 31 Fe II lines from the following literature sources: Hekker & Meléndez (2007), Genovali et al. (2013), Tsantaki et al. (2014), and Tabernero et al. (2019). Using these iron lines, we produced a list of wavelength regions to synthesise. They were created to cover a 3Å-wide region centred around each individual line (merging them when necessary, see Table A.5), following the approach taken by Tsantaki et al. (2014). In addition, we chose the MARCS model atmospheres with a standard composition4 (Gustafsson et al. 2008) spanning from 3500 to 7000 K in Teff, 0.0 to 5.5 dex in log g, and −2.0 to 1.0 dex in [Fe/H], whereas ξ was set to the values given by the Dutra-Ferreira et al. (2016) calibration.

The atomic line data were taken from the public version of the Gaia-ESO line list (GES, see Heiter et al. 2021). The GES line list comprises Vienna Atomic Line Database (VALD3, Ryabchikova et al. 2015) data plus some highly accurate sources for the atomic parameters on top of hyperfine structure data, all of which were compiled under the framework of the GES collaboration. In addition to the atomic data, we included data for the following molecular species: CH, MgH, SiH, CaH, C2, CN, TiO, VO, and ZrO (see Table 1). We also removed some transitions from the TiO, VO, and ZrO line lists due to their overwhelming size. Consequently, we followed the automatic recipes provided with the B. Plez molecular databases5, which in turn rely on the following expression, as defined by Gray (2008):

(2)

Table 1.

Molecular data employed in this work.

where log gfi is the oscillator strength of a given transition, λi is the wavelength in Å, χl is the excitation potential of the lower level in eV, and θ = 5040/T eV−1, with T = 3500 K, and i denotes transition. This approach allowed us to reduce the size of the molecular line lists and use only those transitions that significantly contribute to the spectral synthesis.

Regarding the chemical composition of the models, we assumed the solar abundances of Asplund et al. (2009) that we scaled according to the composition of each MARCS model atmosphere. In fact, the MARCS models with standard composition take into account the galactic gradient for the so-called α-elements (i.e. O, Mg, Si, S, Ar, Ca, and Ti). In consequence, we adopted the following values of the α-enhancement ([α/Fe]) as function of metallicity ([Fe/H]): [α/Fe] = 0 if [Fe/H] ≥ 0, [α/Fe] = −0.4[Fe/H] if −1 < [Fe/H] < 0, and [α/Fe] = 0.4 if [Fe/H] ≤ −1.

Finally, under the previous assumptions, we ran Turbospectrum to compute the synthetic spectra corresponding to the wavelength regions defined in Table A.5. Then, we merged these regions into a single plain text file for each MARCS atmospheric model. These files are later stored into a binary file by means of the pickle Python library (Van Rossum 2020).

2.3. Spectral emulator

The STEPARSYN code implements a likelihood function that yields the probability of a synthetic spectrum reproducing the observations (see Eq. (2)). Unfortunately, the stellar atmospheric models are only available at discrete points that do not cover the whole parameter space in a continuous manner. Therefore, we need to be able to produce a synthetic spectrum corresponding to an arbitrary point of the parameter space. The former can be achieved thanks to a spectral emulator, which combines the principal component analysis (PCA, see Pearson 1901) decomposition with an interpolation method to reconstruct a synthetic spectrum corresponding to an arbitrary point of the parameter space (see, e.g., Urbaneja et al. 2008; Czekala et al. 2015). Thus, the PCA allows us to decompose each spectrum as a linear combination according to this formula:

(3)

Each synthetic spectrum (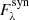) can be expressed as a combination of eigenspectra (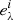) and weight coefficients (wi) that are given by the PCA. The coefficients μλ and σλ represent a linear transformation to the synthetic spectra. These weights are only known at those points belonging to the grid. Consequently, these weights must be interpolated to produce an spectrum corresponding to an arbitrary point in the parameter space. Then, these interpolated weights can be used to reconstruct a synthetic spectrum corresponding to any point of the parameter space covered by the grid by means of Eq. (3). We implemented in the spectral emulator the PCA algorithm of the scikit-learn library (Pedregosa et al. 2011) and the multi-dimensional interpolation algorithm of the SciPy (Virtanen et al. 2020). Interestingly enough, the weights obtained using the PCA are not equally important for the reconstruction of each grid spectrum. Interestingly, the grid described in Sect. 2.2 was generated using ≈2000 MARCS models, and only the top 350 weights were required to bring down the error budget below the 1% hallmark (see Fig. 2).

thumbnail Fig. 2.

Top panel: original synthetic spectrum (black line) compared to the result of the spectral emulator (shaded red line). Both spectra correspond to the following stellar parameters: Teff = 5750 K, log g 4.5 dex, and [Fe/H] = 0.0 dex. Bottom panel: differences between the reconstructed and original spectra (R–O).

Finally, the resulting reconstructed synthetic spectrum does not account for the macroturbulence (ζ), the projected rotational velocity (v sin i), and/or the instrumental resolution. These effects are taken into account by convolving, on the fly, the synthetic spectrum with a broadening kernel. Both ζ and v sin i are too degenerate in the case of FGKM-type stars and they cannot be easily disentangled from each other. One approximation is to model them by means of a single stellar rotation kernel (e.g., Gavel et al. 2019). Therefore, STEPARSYN convolves the synthetic spectrum with a Gray rotation kernel (Gray 2008) to account for both ζ and v sin i followed by a Gaussian kernel with a full width at half maximum (FWHM) corresponding to the resolving power of the observations.

3. Code performance

3.1. Test sample

We gathered a sample of 35 late-type stars in order to benchmark STEPARSYN. Our target list comprises 23 Gaia benchmark stars (Heiter et al. 2015a), ten late-type stars with measured interferometric angular diameters (see Boyajian et al. 2012a,b), and two well-known exoplanet host stars (HD 189733 and HD 209458, see Boyajian et al. 2015). All these targets have accurate Teff and log g values determined independently from spectroscopy. According to their reported parameters, they are spread across the parameter space approximately from 3700 K to 6700 K in Teff, and 0.7 dex to 4.7 dex in log g (see Table A.2). We observed them at the 1.2-m Mercator Telescope6 using the High Efficiency and Resolution Mercator Echelle Spectrograph (HERMES, see Raskin et al. 2011) located at the Observatorio del Roque de los Muchachos (La Palma, Spain) between 2010 and 2016 (see Table A.1). The HERMES spectrograph covers a wavelength range from 3770 to 9000 Å with a resolving power of R = 85 000 and they were later reduced on-site by means of the HERMES automatic reduction pipeline. We note that these observations include a solar spectrum that was taken by pointing the telescope at the asteroid Vesta (see Tabernero et al. 2017).

Finally, we shifted these spectra to the laboratory reference frame by correcting for the radial velocity (RV) of the star. We derived the RVs of our targets using the method described in Pepe et al. (2002) to compute the cross-correlation function (CCF). We sampled the CCF in the range from −200 to 200 km s−1 with a step of 0.5 km s−1, using masks that are 1 km s−1 wide and proportionally weighted to their normalised intensity with respect to the continuum. We assigned each individual weight according to the intensities given by a VALD3 extract stellar query with parameters Teff = 5750 K, log g = 4.5 dex, and [Fe/H] = 0.0 dex. We then fitted a Gaussian profile to each CCF to extract the corresponding RVs and calculated their uncertainties by means of the approach described in Zucker (2003) using the implementation of Blanco-Cuaresma et al. (2014). We list these RVs and their associated uncertainties in Table A.1.

3.2. Stellar atmospheric parameters

We derived the stellar atmospheric parameters of our targets with STEPARSYN. Thus, we employed the HERMES observations listed in Table A.1, the synthetic grid described in Sect. 2.2, and a list of spectral masks generated with a custom procedure that we detail below.

The list of spectral masks was generated to cover only the Fe I and Fe II lines in the synthetic grid. The underlying idea of deriving the atmospheric parameters using masks around iron lines is to mimic the EW method (see, e.g., Sbordone et al. 2014; Blanco-Cuaresma et al. 2014). To build the line masks, we did a Gaussian fit to our iron lines using the Levenberg-Marquardt algorithm (LMA) implemented in the Python SciPy library (Virtanen et al. 2020). In summary, our modelling provides the Gaussian parameters of the line under analysis (i.e. continuum level, centre, amplitude, depth, and σ). The fitting window is 1.5 Å, and the continuum level is assumed to be modelled by a constant value. Shortly after, we removed the features whose fitted central wavelengths deviated more than 0.05 Å from their known rest-frame wavelengths. After this filter, the line masks were constructed using an iterative algorithm. We assumed an initial span for the masks of 3σ around the centre of each line and adjusted their width to avoid including any neighbouring spectral features. The adjustment of the line masks is performed according to the quality of the Gaussian fit. To that aim, we computed the absolute value of the residuals contained with the initial interval and kept those flux points that deviated no more than 3σ from the Gaussian fit. In other words, the initial mask size is effectively reduced until it continuously covers the line of interest and it avoids the contamination of neighbouring features. However, the Gaussian approximation is no longer valid to reproduce the weak lines when v sin i > 15 km s−1. We note that only π3 Ori and θ Boo A have a v sin i above the 15 km s−1 mark. In consequence, we followed a different strategy for these two targets to build their line masks. To that aim, we gathered the lines fitted for the star θ Per A and modified them to take into account the stellar rotation. The widths of the new line masks were set to the value given by this formula: Δλ = 2λov sin i/c, where c is the speed of light in km s−1 and λo is the centre of the line given in Å. We illustrate this procedure for two representative Fe I lines belonging to the spectra of θ Per A, π3 Ori, and θ Boo A in Fig. 3.

thumbnail Fig. 3.

Line masks (shaded blue regions) around the Fe I lines at 6335.33 and 6336.82 Å for three F-type stars with different v sin i values (see text for details).

After we computed the line masks corresponding to our selected FeI,II lines, we turned to the broadening parameters of our targets. The STEPARSYN code models the total line broadening with two components. The first component (Vbroad) accounts for the broadening parameters ζ and v sin i. We chose to model both of them with a single rotation kernel following the prescription given by Gavel et al. (2019). The second component corresponds to the instrumental line spread function (LSF) that we described with a Gaussian function corresponding to the HERMES resolving power (i.e. R = 85 000). The quantity Vbroad was derived only for those stars with significant broadening parameters. In fact, when Vbroad is small enough, the total line broadening is entirely dominated by the LSF of the instrument (Reiners et al. 2018). This affects some mid-to-late K dwarf stars in our sample with reported v sin i values on or below the noise-driven limit of 2 km s−1 (Gray 2008). Moreover, they are expected to have small macroturbulent velocities (see Brewer et al. 2016) that translate into an LSF-dominated line broadening. Consequently, we fixed the Vbroad of those K-stars to the v sin i reported in the literature (see Table A.2). Then, we ran STEPARSYN and calculated the stellar atmospheric parameters for our targets. We list the stellar parameters calculated with STEPARSYN in Table A.3. We also represent the marginalised results provided by STEPARSYN for the G2 V star 18 Sco in Fig. 4 and the best fit to some representative iron lines in Fig. 5.

thumbnail Fig. 4.

Posterior marginalised distributions corresponding to the following stellar parameters: Teff, log g, [Fe/H], and Vbroad for the G2 V star 18 Sco. The 1, 2, and 3 σ levels are represented by three different colour shades.

thumbnail Fig. 5.

Four representative wavelength regions in the spectrum of 18 Sco. The shaded blue areas represent the line masks, whereas the observations are given by the black line, and the best-fitting synthetic spectrum is represented by a red line.

We then compared our results to the reference parameters (see Table A.2) and represented them in Fig. 6. Then, following Tabernero et al. (2019), we performed 10 000 Monte Carlo simulations on our data in the hope of assessing possible sources of tentatively systematic offsets. We found the following differences with the reference parameters: −12 ± 117 K in Teff, 0.04 ± 0.14 dex in log g, and 0.05 ± 0.09 dex in [Fe/H]. These differences show that SteParSyn can reproduce the reference values for our sample stars since they are compatible with zero in all instances. In parallel, we populated a Kiel diagram (see Fig. 7) with our Teff and log g values alongside the PARSEC isochrones (Bressan et al. 2012). The isochrones we represent in the Kiel diagram encompass our points and they are well-behaved even for the coolest stars in the main-sequence, contrary to what has been found in previous works (see Mortier et al. 2014; Montes et al. 2018; Tsantaki et al. 2019; Brucalassi et al. 2021). Finally, we compared our Vbroad values to those of other late-type stars. Thus, we gathered the broadening values calculated by Brewer et al. (2016) and represented them against our own as a function of Teff in Fig. 8. From this comparison, we see that our calculated Vbroad values follow the behaviour of the literature values for other late-type stars reported in (Brewer et al. 2016).

thumbnail Fig. 6.

STEPARSYN results plotted against the reference values given in Table A.2. Upper panels: one-to-one correspondence. Bottom panels: absolute differences. The dashed black lines in the upper panels correspond to a one-to-one relation, whereas in the bottom panel they correspond to zero.

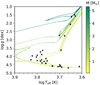thumbnail Fig. 7.

Kiel diagram (log g vs. log Teff) for all the spectra analysed alongside the PARSEC isochrones for 0.1, 0.5, 1, 5, and 10 Ga for solar metallicity (Bressan et al. 2012).

thumbnail Fig. 8.

Comparison of the Vbroad derived in this work represented by black circles and the values derived by Brewer et al. (2016) are displayed with blue circles.

3.3. Trigonometric gravities, radii, and masses

The surface gravities derived with spectroscopic data are sometimes not entirely in agreement with those calculated using evolutionary models, visual magnitudes, and parallaxes (Tsantaki et al. 2019; Brucalassi et al. 2021). The use of evolutionary models provides us with an alternative method that can be used to assess the precision of the spectroscopic log g values. For these reasons, we used the PARAM web interface7 (da Silva et al. 2006) alongside the Teff and [Fe/H] inferred with STEPARSYN, the Gaia EDR3 (Gaia Collaboration 2021) or HIPPARCOS (van Leeuwen 2007) parallax and their visual magnitude (V), and the PARSEC stellar evolutionary tracks and isochrones (Bressan et al. 2012). From this information, we calculated the so-called trigonometric surface gravity (log gtrig), mass (M*), and radius (R*) for our targets (see Table A.3). We compare the spectroscopic gravities derived with STEPARSYN against their trigonometric counterparts in Fig. 9. Again, we ran 10 000 MC simulations and computed a mean difference of −0.03 ± 0.11 dex, which is in turn compatible with zero at the 1σ level. This difference implies that our spectroscopic surface gravities are fully consistent with the PARAM trigonometric values at the 0.1 dex mark.

thumbnail Fig. 9.

STEPARSYN-based surface gravities plotted against the trigonometric values based on the parallaxes listed in Table A.3.

3.4. STEPARSYN vs. STEPAR

The analysis described in this work uses a selection of Fe I and Fe II lines to derive the stellar parameters of our sample stars. In ideal terms, the synthetic method should deliver the same stellar parameters as the EW method. To quantify the former statement, we calculated the stellar parameters for those targets that can be analysed under the EW method with the STEPAR code8. To that aim, we selected the stars of our sample with v sin i < 15 km s−1 and spectral types between F6 and K4 (see Tabernero et al. 2019). Using these criteria, we finished with a sub-sample of 28 stars. Shortly after, we used the ARES9 (version 2, see Sousa et al. 2015) code to measure the EW of the Fe lines listed listed in Table A.5 for these stars. We calculated the stellar parameters for this sub-sample with STEPAR (see Table A.4). We then compared the results of STEPARSYN and STEPAR. Thus, we retrieve the following differences between them: 40 ± 87 K for Teff, −0.04 ± 0.21 dex for log g, and 0.04 ± 0.08 dex for [Fe/H]. These differences are compatible within the error bars. Therefore, STEPAR and STEPARSYN deliver compatible results when we analyse the same observational data. Regarding the uncertainties on the parameters, STEPAR gives the following average values: ΔTeff = 50 K, Δ log g = 0.13 dex and Δ [Fe/H] = 0.04 dex; whereas, for STEPARSYN we find 29 K, 0.06 dex, and 0.03 dex. Thus, the STEPARSYN uncertainties are smaller by a factor 2 for Teff and log g, whereas both codes provide similar errors on [Fe/H].

4. Discussion

The stellar atmospheric parameters obtained with STEPARSYN for our target stars are reliable down to the 1σ level with the reference parameters (Table A.2), the trigonometric gravities of Table A.3, and the parameters provided by the EW method implemented in STEPAR (see Table A.4). Roughly speaking, these differences are at the level of 100 K for Teff, 0.1 dex for log g, and 0.1 dex for [Fe/H] (see Table 2). However, these average differences alone are not enough to explore hidden systematic uncertainties tied to the STEPARSYN stellar parameters. Thus, we calculated the correlation between the individual differences against the parameters themselves following the approach described in Tabernero et al. (2019). We performed 10 000 Monte Carlo (MC) simulations on our data to compute both Pearson and Spearman correlation coefficients (rp and rs, respectively) and their uncertainties. We provide the results of these MC simulations in Table 2. These simulations reveal that the correlation between differences and a given parameter are small. Consequently, the average differences found for the stellar atmospheric only correspond to systematic uncertainties intrinsic to the STEPARSYN code.

Table 2.

Summary of the MC simulations on Teff, log g, and [Fe/H] calculated with STEPARSYN against three samples of stellar parameters: literature values, STEPAR, and the trigonometric surface gravities derived using PARAM.

We notice that STEPARSYN [Fe/H] values for both α Cet and γ Sge are not entirely in agreement with reference parameters. However, their reference [Fe/H] values largely have error bars at the level of 0.4–0.5 dex, and they are not well-constrained. A similar argument applies to the surface gravities of some giant stars. Moreover, reproducing the surface gravities of the giant stars is by no means an easy task. Stars such as μ Leo, α Cet, and HD 107328 have surface gravities that are uncertain for a number of currently known reasons. In fact, according to Heiter et al. (2015b) their masses have large uncertainties ranging from approximately 0.5 to 1.0 M⊙ that translate into surface gravities that are not well-defined. In spite of those uncertain log g values, STEPARSYN manages to produce reliable parameters for our target stars. In addition, their Teff and log g values are in agreement with evolutionary models in the Kiel diagram (see Fig. 7). These findings are reinforced by the fact that STEPARSYN produces values of Vbroad consistent with the behaviour of those calculated by Brewer et al. (2016), as we show in Fig. 8.

Finally, we want to address the limitations of the STERPARSYN code regarding the analysis of late-type spectra under the spectral synthesis method. First, the observational data must be of high enough quality to be analysed. This means that, since low signal-to-noise ratios (S/N) translate into higher uncertainties on the stellar atmospheric parameters (Smiljanic et al. 2014). To compute the performance of STEPARSYN at different S/N, we took the spectra of 18 Sco and ϵ Eri and we degraded them to the following S/N values: 10, 20, 30, 40, 50, 80, and 100. Then, we ran STEPARSYN in order to calculate the stellar parameters of the degraded spectra. According to these calculations, the parameters have uncertainties at the level of 100 K for Teff, 0.2 dex for log g, and 0.1 dex for [Fe/H] at S/N = 20 (see Fig. 10). In addition, at S/N = 10 the errors on the stellar parameters reach the level of 200 K, 0.5 dex, and 0.2 dex. In light of these numbers, the stellar parameters become unreliable for those spectra with S/N < 20. Second, STEPARSYN cannot analyse double-lined spectra because it is not capable of disentangling two or more stellar components. A third limitation is the v sin i of the star under analysis. The fastest rotator in our sample is θ Boo A with a v sin i of ≈30 km s−1 and we were able to calculate its stellar parameters with STEPARSYN. Therefore, the limit on v sin i for the code should be above 30 km s−1. In fact, the limit on v sin i is related to the size of the spectral regions under analysis (Tsantaki et al. 2014). In general terms, the stellar rotation dilutes the spectral lines producing both narrow, broad, and likely blended spectral features. The line dilution should translate into less reliable stellar parameters, which we should be able to quantify. To that aim, we broadened the spectra of the stars 18 Sco and ϵ Eri by means of the Gray rotation kernel (Gray 2008) to different v sin i values. We chose these v sin i values to be in the 10–50 km s−1 range, taking a step of 5 km s−1. Thus, we calculated the stellar parameters of these rotationally-broadened spectra with STEPARSYN. Then, we compared this value to the parameters obtained for the original unbroadened spectra of both 18 Sco and ϵ Eri. We represent these differences as functions of v sin i in Fig. 10. In all, STEPARSYN can recover the stellar parameters up to v sin i = 30 km s−1 with differences of no more than 50 K, 0.1 dex, and 0.05 dex for Teff, log g, and [Fe/H], respectively. However, STEPARSYN does not recover the expected stellar parameters for v sin i ≥ 35 km s−1.

thumbnail Fig. 10.

Variation of the stellar atmospheric parameters as a function of S/N (top panel) and v sin i (bottom panel). The values corresponding to 18 Sco (G2 V) are represented by green circles, whereas those corresponding to ϵ Eri (K2 V) are displayed as red squares (see text for details).

5. Conclusions

In this work, we provide a description of the STEPARSYN code. The code is designed to infer the atmospheric parameters (Teff, log g, [Fe/H], and Vbroad) of FGKM-type stars under the spectral synthesis method. The STEPARSYN code is publicly available to the community in a GitHub repository. In summary, it relies on the MCMC sampler emcee in conjunction with an spectral emulator that can interpolate spectra down to a precision < 1%. We also provide a grid of synthetic spectra with the code that allow the user to characterise the spectra of FGKM-type stars with parameters in the range of 3500 to 7000 K in Teff, 0.0 to 5.5 dex in log g, and −2.0 to 1.0 dex in [Fe/H].

We tested the performance of the code against a sample of well-known 35 FGKM-type stars observed with the HERMES spectrograph. We found that STEPARSYN infers stellar parameters that are consistent with the reference values. In addition, the log g values inferred with STEPARSYN are compatible with the trigonometric surface gravities provided by PARAM down to the 0.1 dex mark. Furthermore, we found good agreement between the results provided by both STEPARSYN and STEPAR.

Finally, we want to note the limitations of the synthetic method that should be taken into consideration when using STEPARSYN. First, the spectroscopic data must have an S/N ≥ 20. Second, the code is meant to analyse only single-lined spectra as it cannot disentangle the flux of two or more stellar components. Third, the implementation of the spectral synthesis method provided in this work can only give reliable parameters for stars with v sin i on or below the 30 km s−1 mark.

1

The code is available for download at https://github.com/hmtabernero/SteParSyn under the two-clause BSD license.

Acknowledgments

We would like to thank the anonymous referee for his/her comments and suggestions that helped to improve the paper. We acknowledge financial support from the Agencia Estatal de Investigación of the Ministerio de Ciencia, Innovación y Universidades through projects PID2019-109522GB-C51,54/AEI/10.13039/501100011033. HMT and JIGH acknowledge financial support from the Centre of Excellence “Severo Ochoa” and “María de Maeztu” awards to the Instituto de Astrofísica de Canarias (SEV-2015-0548) and Centro de Astrobiología (MDM-2017-0737). JIGH also acknowledges financial support from the Spanish Ministry of Science and Innovation (MICINN) project AYA2017-86389-P, and also from the Spanish MICINN under 2013 Ramón y Cajal program RYC-2013-14875. E. M. acknowledges financial support from the Spanish Ministerio de Universidades through fellowship FPU15/01476. This work is based on observations obtained with the HERMES spectrograph, which is supported by the Research Foundation - Flanders (FWO), Belgium, the Research Council of KU Leuven, Belgium, the Fonds National de la Recherche Scientifique (F.R.S.-FNRS), Belgium, the Royal Observatory of Belgium, the Observatoire de Genève, Switzerland and the Thüringer Landessternwarte Tautenburg, Germany. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institution participating in the Gaia Multilateral Agreement. This research made use of Astropy (http://www.astropy.org), a community-developed core Python package for Astronomy (Astropy Collaboration 2013, 2018).

References

  1. Allende Prieto, C. 2016, Liv. Rev. Sol. Phys., 13, 1 [Google Scholar]
  2. Allende Prieto, C., Beers, T. C., Wilhelm, R., et al. 2006, ApJ, 636, 804 [NASA ADS] [CrossRef] [Google Scholar]
  3. Alonso-Santiago, J., Negueruela, I., Marco, A., et al. 2019, A&A, 631, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Alonso-Santiago, J., Negueruela, I., Marco, A., Tabernero, H. M., & Castro, N. 2020, A&A, 644, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Andreasen, D. T., Sousa, S. G., Tsantaki, M., et al. 2017, A&A, 600, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
  7. Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
  9. Auvergne, M., Bodin, P., Boisnard, L., et al. 2009, A&A, 506, 411 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Blanco-Cuaresma, S. 2019, MNRAS, 486, 2075 [Google Scholar]
  11. Blanco-Cuaresma, S., Soubiran, C., Heiter, U., & Jofré, P. 2014, A&A, 569, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Borsa, F., Allart, R., Casasayas-Barris, N., et al. 2021, A&A, 645, A24 [EDP Sciences] [Google Scholar]
  13. Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [Google Scholar]
  14. Boyajian, T. S., McAlister, H. A., van Belle, G., et al. 2012a, ApJ, 746, 101 [Google Scholar]
  15. Boyajian, T. S., von Braun, K., van Belle, G., et al. 2012b, ApJ, 757, 112 [Google Scholar]
  16. Boyajian, T., von Braun, K., Feiden, G. A., et al. 2015, MNRAS, 447, 846 [Google Scholar]
  17. Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [Google Scholar]
  18. Brewer, J. M., Fischer, D. A., Valenti, J. A., & Piskunov, N. 2016, ApJS, 225, 32 [Google Scholar]
  19. Brooke, J. S. A., Bernath, P. F., Schmidt, T. W., & Bacskay, G. B. 2013, J. Quant. Spectr. Rad. Transf., 124, 11 [Google Scholar]
  20. Brucalassi, A., Tsantaki, M., Magrini, L., et al. 2021, Exp. Astron, in press, [arXiv:2101.02242] [Google Scholar]
  21. Buder, S., Lind, K., Ness, M. K., et al. 2019, A&A, 624, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Buder, S., Sharma, S., Kos, J., et al. 2021, MNRAS, 506, 150 [NASA ADS] [CrossRef] [Google Scholar]
  23. Cargile, P. A., Conroy, C., Johnson, B. D., et al. 2020, ApJ, 900, 28 [NASA ADS] [CrossRef] [Google Scholar]
  24. Casasayas-Barris, N., Pallé, E., Yan, F., et al. 2020, A&A, 635, A206 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Cosentino, R., Lovis, C., Pepe, F., et al. 2012, in Ground-based and Airborne Instrumentation for Astronomy IV, eds. I. S. McLean, S. K. Ramsay, H. Takami, et al., SPIE Conf. Ser., 8446, 84461V [NASA ADS] [Google Scholar]
  26. Czekala, I., Andrews, S. M., Mandel, K. S., Hogg, D. W., & Green, G. M. 2015, ApJ, 812, 128 [NASA ADS] [CrossRef] [Google Scholar]
  27. Czesla, S., Klocová, T., Khalafinejad, S., Wolter, U., & Schmitt, J. H. M. M. 2015, A&A, 582, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Dalton, G., Trager, S., Abrams, D. C., et al. 2018, in Ground-based and Airborne Instrumentation for Astronomy VII, SPIE Conf. Ser., 10702, 107021B [Google Scholar]
  29. da Silva, L., Girardi, L., Pasquini, L., et al. 2006, A&A, 458, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  30. Davies, B., Kudritzki, R.-P., Lardo, C., et al. 2017, ApJ, 847, 112 [Google Scholar]
  31. Dawson, K. S., Schlegel, D. J., Ahn, C. P., et al. 2013, AJ, 145, 10 [Google Scholar]
  32. de Jong, R. S., Agertz, O., Berbel, A. A., et al. 2019, Messenger, 175, 3 [Google Scholar]
  33. de Medeiros, J. R., & Mayor, M. 1999, A&AS, 139, 433 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Demangeon, O. D. S., Zapatero Osorio, M. R., Alibert, Y., et al. 2021, A&A, 653, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Deng, L.-C., Newberg, H. J., Liu, C., et al. 2012, Res. Astron. Astrophys., 12, 735 [Google Scholar]
  36. De Silva, G. M., Freeman, K. C., Bland-Hawthorn, J., et al. 2015, MNRAS, 449, 2604 [NASA ADS] [CrossRef] [Google Scholar]
  37. Dutra-Ferreira, L., Pasquini, L., Smiljanic, R., Porto de Mello, G. F., & Steffen, M. 2016, A&A, 585, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
  39. Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. García Pérez, A. E., Allende Prieto, C., Holtzman, J. A., et al. 2016, AJ, 151, 144 [Google Scholar]
  41. Gavel, A., Gruyters, P., Heiter, U., et al. 2019, A&A, 629, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Genovali, K., Lemasle, B., Bono, G., et al. 2013, A&A, 554, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Ghezzi, L., Cunha, K., Smith, V. V., et al. 2010, ApJ, 720, 1290 [NASA ADS] [CrossRef] [Google Scholar]
  44. Gilmore, G., Randich, S., Asplund, M., et al. 2012, Messenger, 147, 25 [Google Scholar]
  45. Gray, D. F. 2008, The Observation and Analysis of Stellar Photospheres (Cambridge University Press) [Google Scholar]
  46. Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Hale, A. 1994, AJ, 107, 306 [NASA ADS] [CrossRef] [Google Scholar]
  48. Heiter, U., Jofré, P., Gustafsson, B., et al. 2015a, A&A, 582, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Heiter, U., Lind, K., Asplund, M., et al. 2015b, Phys. Scr., 90, 054010 [Google Scholar]
  50. Heiter, U., Lind, K., Bergemann, M., et al. 2021, A&A, 645, A106 [EDP Sciences] [Google Scholar]
  51. Hekker, S., & Meléndez, J. 2007, A&A, 475, 1003 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Hinkle, K. H., Wallace, L., Ram, R. S., et al. 2013, ApJS, 207, 26 [NASA ADS] [CrossRef] [Google Scholar]
  53. Hoeijmakers, H. J., Ehrenreich, D., Heng, K., et al. 2018, Nature, 560, 453 [CrossRef] [Google Scholar]
  54. Hogg, D. W., Bovy, J., & Lang, D. 2010, ArXiv e-prints [arXiv:1008.4686] [Google Scholar]
  55. Jenkins, J. S., Murgas, F., Rojo, P., et al. 2011, A&A, 531, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Jofré, P., Heiter, U., Soubiran, C., et al. 2014, A&A, 564, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Jofré, E., Petrucci, R., Saffe, C., et al. 2015, A&A, 574, A50 [Google Scholar]
  58. Jofré, P., Heiter, U., & Soubiran, C. 2019, ARA&A, 57, 571 [Google Scholar]
  59. Koch, D. G., Borucki, W. J., Basri, G., et al. 2010, ApJ, 713, L79 [Google Scholar]
  60. Kunder, A., Kordopatis, G., Steinmetz, M., et al. 2017, AJ, 153, 75 [Google Scholar]
  61. Kurucz, R. L. 2010, Robert L. Kurucz on-line database of molecular line lists, SiH A-X transitions (KSiH) [Google Scholar]
  62. Latham, D. W., Stefanik, R. P., Torres, G., et al. 2002, AJ, 124, 1144 [NASA ADS] [CrossRef] [Google Scholar]
  63. Lee, Y. S., Beers, T. C., Sivarani, T., et al. 2008, AJ, 136, 2022 [Google Scholar]
  64. Lillo-Box, J., Faria, J. P., Suárez Mascareño, A., et al. 2021, A&A, 654, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  65. Lohr, M. E., Negueruela, I., Tabernero, H. M., et al. 2018, MNRAS, 478, 3825 [Google Scholar]
  66. Luck, R. E. 2017, AJ, 153, 21 [Google Scholar]
  67. Magrini, L., Randich, S., Friel, E., et al. 2013, A&A, 558, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  68. Marfil, E., Tabernero, H. M., Montes, D., et al. 2020, MNRAS, 492, 5470 [NASA ADS] [CrossRef] [Google Scholar]
  69. Marfil, E., Tabernero, H. M., Montes, D., et al. 2021, A&A, 656, A162 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Marsden, S. C., Petit, P., Jeffers, S. V., et al. 2014, MNRAS, 444, 3517 [Google Scholar]
  71. Massarotti, A., Latham, D. W., Stefanik, R. P., & Fogel, J. 2008, AJ, 135, 209 [Google Scholar]
  72. Masseron, T., Plez, B., Van Eck, S., et al. 2014, A&A, 571, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  73. Masseron, T., Merle, T., & Hawkins, K. 2016, BACCHUS: Brussels Automatic Code for Characterizing High accUracy Spectra (Astrophysics Source Code Library) [Google Scholar]
  74. Mayor, M., Pepe, F., Queloz, D., et al. 2003, Messenger, 114, 20 [Google Scholar]
  75. Montes, D., González-Peinado, R., Tabernero, H. M., et al. 2018, MNRAS, 479, 1332 [Google Scholar]
  76. Mortier, A., Sousa, S. G., Adibekyan, V. Z., Brandão, I. M., & Santos, N. C. 2014, A&A, 572, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  77. Mucciarelli, A., Pancino, E., Lovisi, L., Ferraro, F. R., & Lapenna, E. 2013, ApJ, 766, 78 [NASA ADS] [CrossRef] [Google Scholar]
  78. Negueruela, I., Monguió, M., Marco, A., et al. 2018, MNRAS, 477, 2976 [NASA ADS] [CrossRef] [Google Scholar]
  79. Negueruela, I., Chené, A. N., Tabernero, H. M., et al. 2021, MNRAS, 505, 1618 [NASA ADS] [CrossRef] [Google Scholar]
  80. Nissen, P. E., & Gustafsson, B. 2018, A&ARv, 26, 6 [Google Scholar]
  81. Passegger, V. M., Bello-García, A., Ordieres-Meré, J., et al. 2020, A&A, 642, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  82. Pearson, K. 1901, LIII. On lines and planes of closest fit to systems of points in space [Google Scholar]
  83. Pedregosa, F., Varoquaux, G., Gramfort, A., et al. 2011, J. Mach. Learn. Res., 12, 2825 [Google Scholar]
  84. Pepe, F., Mayor, M., Galland, F., et al. 2002, A&A, 388, 632 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  85. Pepe, F., Cristiani, S., Rebolo, R., et al. 2021, A&A, 645, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  86. Piskunov, N., & Valenti, J. A. 2017, A&A, 597, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  87. Plez, B. 2012, Turbospectrum: Code for spectral synthesis (Astrophysics Source Code Library) [Google Scholar]
  88. Queloz, D., Allain, S., Mermilliod, J. C., Bouvier, J., & Mayor, M. 1998, A&A, 335, 183 [Google Scholar]
  89. Quirrenbach, A., CARMENES Consortium, Amado, P. J., et al. 2020, in Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, SPIE Conf. Ser., 11447, 114473C [NASA ADS] [Google Scholar]
  90. Ram, R. S., Brooke, J. S. A., Bernath, P. F., Sneden, C., & Lucatello, S. 2014, ApJS, 211, 5 [Google Scholar]
  91. Raskin, G., van Winckel, H., Hensberge, H., et al. 2011, A&A, 526, A69 [CrossRef] [EDP Sciences] [Google Scholar]
  92. Reiners, A., Zechmeister, M., Caballero, J. A., et al. 2018, A&A, 612, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  93. Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telesc. Instrum. Syst., 1, 014003 [Google Scholar]
  94. Ryabchikova, T., Piskunov, N., Kurucz, R. L., et al. 2015, Phys. Scr., 90, 054005 [Google Scholar]
  95. Santos, N. C., Sousa, S. G., Mortier, A., et al. 2013, A&A, 556, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  96. Sbordone, L., Caffau, E., Bonifacio, P., & Duffau, S. 2014, A&A, 564, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  97. Schönrich, R., & Bergemann, M. 2014, MNRAS, 443, 698 [CrossRef] [Google Scholar]
  98. Schweitzer, A., Passegger, V. M., Cifuentes, C., et al. 2019, A&A, 625, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  99. Shetrone, M., Bizyaev, D., Lawler, J. E., et al. 2015, ApJS, 221, 24 [Google Scholar]
  100. Smiljanic, R., Korn, A. J., Bergemann, M., et al. 2014, A&A, 570, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  101. Sneden, C., Lucatello, S., Ram, R. S., Brooke, J. S. A., & Bernath, P. 2014, ApJS, 214, 26 [Google Scholar]
  102. Soto, M. G., & Jenkins, J. S. 2018, A&A, 615, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  103. Soubiran, C., Le Campion, J.-F., Brouillet, N., & Chemin, L. 2016, A&A, 591, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  104. Sousa, S. G., Santos, N. C., Mayor, M., et al. 2008, A&A, 487, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  105. Sousa, S. G., Santos, N. C., Adibekyan, V., Delgado-Mena, E., & Israelian, G. 2015, A&A, 577, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  106. Sousa, S. G., Adibekyan, V., Delgado-Mena, E., et al. 2018, A&A, 620, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  107. Tabernero, H. M., Montes, D., & González Hernández, J. I. 2012, A&A, 547, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  108. Tabernero, H. M., Montes, D., González Hernández, J. I., & Ammler-von Eiff, M. 2017, A&A, 597, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  109. Tabernero, H. M., Dorda, R., Negueruela, I., & González-Fernández, C. 2018, MNRAS, 476, 3106 [NASA ADS] [CrossRef] [Google Scholar]
  110. Tabernero, H. M., Marfil, E., Montes, D., & González Hernández, J. I. 2019, A&A, 628, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  111. Tabernero, H. M., Dorda, R., Negueruela, I., & Marfil, E. 2021, A&A, 646, A98 [EDP Sciences] [Google Scholar]
  112. Takeda, Y., Sato, B., Kambe, E., et al. 2005, PASJ, 57, 13 [NASA ADS] [Google Scholar]
  113. Ting, Y.-S., Conroy, C., Rix, H.-W., & Cargile, P. 2019, ApJ, 879, 69 [Google Scholar]
  114. Torres, G., Fischer, D. A., Sozzetti, A., et al. 2012, ApJ, 757, 161 [Google Scholar]
  115. Tsantaki, M., Sousa, S. G., Santos, N. C., et al. 2014, A&A, 570, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  116. Tsantaki, M., Andreasen, D. T., Teixeira, G. D. C., et al. 2018, MNRAS, 473, 5066 [NASA ADS] [CrossRef] [Google Scholar]
  117. Tsantaki, M., Santos, N. C., & Sousa, S. G. 2019, MNRAS, 569 [Google Scholar]
  118. Tsantaki, M., Andreasen, D., & Teixeira, G. 2020, J. Open Sour. Software, 5, 2048 [NASA ADS] [CrossRef] [Google Scholar]
  119. Urbaneja, M. A., Kudritzki, R.-P., Bresolin, F., et al. 2008, ApJ, 684, 118 [NASA ADS] [CrossRef] [Google Scholar]
  120. Valenti, J. A., & Fischer, D. A. 2005, ApJS, 159, 141 [Google Scholar]
  121. Valenti, J. A., & Piskunov, N. 1996, A&AS, 118, 595 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  122. van Leeuwen, F. 2007, A&A, 474, 653 [CrossRef] [EDP Sciences] [Google Scholar]
  123. Van Rossum, G. 2020, The Python Library Reference, release 3.8.2 (Python Software Foundation) [Google Scholar]
  124. Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Methods, 17, 261 [Google Scholar]
  125. Zucker, S. 2003, MNRAS, 342, 1291 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Extra material

The sample analysed in this work is given in Table A.1, whereas Table A.2 contains the reference stellar atmospheric parameters compiled from literature sources. The stellar parameters of those stars analysed with STEPARSYN are given in Table A.3, whereas Table A.4 contains the STEPAR parameters. Finally, the wavelength regions containing the FeI,II lines studied in this work are given in Table A.5.

Table A.1.

Names, coordinates, visual magnitudes (V), spectral types (SpT), signal-to-noise ratios (S/N), radial velocities (RV), and parallaxes (π) for the stars analysed in this work. The parallaxes were collected from the Gaia EDR3 (Gaia Collaboration 2021) unless stated otherwise.

Table A.2.

Reference stellar atmospheric parameters for the stars analysed in this work.

Table A.3.

Stellar atmospheric parameters derived with STEPARSYN (Teff, log g, [Fe/H], and Vbroad), trigonometric gravities (log gtrig), mass (M*), and radius (R*) for the stars analysed in this work.

Table A.4.

Stellar atmospheric parameters (Teff, log g, [Fe/H], and ξ) for the stars analysed work using the STEPAR code. Missing values correspond to those stars that cannot be analysed under the EW method.

Table A.5.

List of Fe I and Fe II lines and spectral ranges employed in this work. The full version of this table is available at the CDS.

All Tables

Table 1.

Molecular data employed in this work.

In the text
Table 2.

Summary of the MC simulations on Teff, log g, and [Fe/H] calculated with STEPARSYN against three samples of stellar parameters: literature values, STEPAR, and the trigonometric surface gravities derived using PARAM.

In the text
Table A.1.

Names, coordinates, visual magnitudes (V), spectral types (SpT), signal-to-noise ratios (S/N), radial velocities (RV), and parallaxes (π) for the stars analysed in this work. The parallaxes were collected from the Gaia EDR3 (Gaia Collaboration 2021) unless stated otherwise.

In the text
Table A.2.

Reference stellar atmospheric parameters for the stars analysed in this work.

In the text
Table A.3.

Stellar atmospheric parameters derived with STEPARSYN (Teff, log g, [Fe/H], and Vbroad), trigonometric gravities (log gtrig), mass (M*), and radius (R*) for the stars analysed in this work.

In the text
Table A.4.

Stellar atmospheric parameters (Teff, log g, [Fe/H], and ξ) for the stars analysed work using the STEPAR code. Missing values correspond to those stars that cannot be analysed under the EW method.

In the text
Table A.5.

List of Fe I and Fe II lines and spectral ranges employed in this work. The full version of this table is available at the CDS.

In the text

All Figures

thumbnail Fig. 1.

Diagram of the STEPARSYN internal workflow.
In the text
thumbnail Fig. 2.

Top panel: original synthetic spectrum (black line) compared to the result of the spectral emulator (shaded red line). Both spectra correspond to the following stellar parameters: Teff = 5750 K, log g 4.5 dex, and [Fe/H] = 0.0 dex. Bottom panel: differences between the reconstructed and original spectra (R–O).
In the text
thumbnail Fig. 3.

Line masks (shaded blue regions) around the Fe I lines at 6335.33 and 6336.82 Å for three F-type stars with different v sin i values (see text for details).
In the text
thumbnail Fig. 4.

Posterior marginalised distributions corresponding to the following stellar parameters: Teff, log g, [Fe/H], and Vbroad for the G2 V star 18 Sco. The 1, 2, and 3 σ levels are represented by three different colour shades.
In the text
thumbnail Fig. 5.

Four representative wavelength regions in the spectrum of 18 Sco. The shaded blue areas represent the line masks, whereas the observations are given by the black line, and the best-fitting synthetic spectrum is represented by a red line.
In the text
thumbnail Fig. 6.

STEPARSYN results plotted against the reference values given in Table A.2. Upper panels: one-to-one correspondence. Bottom panels: absolute differences. The dashed black lines in the upper panels correspond to a one-to-one relation, whereas in the bottom panel they correspond to zero.
In the text
thumbnail Fig. 7.

Kiel diagram (log g vs. log Teff) for all the spectra analysed alongside the PARSEC isochrones for 0.1, 0.5, 1, 5, and 10 Ga for solar metallicity (Bressan et al. 2012).
In the text
thumbnail Fig. 8.

Comparison of the Vbroad derived in this work represented by black circles and the values derived by Brewer et al. (2016) are displayed with blue circles.
In the text
thumbnail Fig. 9.

STEPARSYN-based surface gravities plotted against the trigonometric values based on the parallaxes listed in Table A.3.
In the text
thumbnail Fig. 10.

Variation of the stellar atmospheric parameters as a function of S/N (top panel) and v sin i (bottom panel). The values corresponding to 18 Sco (G2 V) are represented by green circles, whereas those corresponding to ϵ Eri (K2 V) are displayed as red squares (see text for details).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.