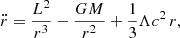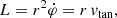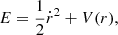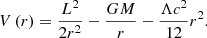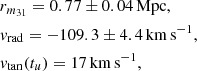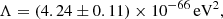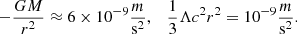EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 656 (December 2021) A&A, 656 (2021) A129 Full HTML
Free Access
Issue
A&A
Volume 656, December 2021
Article Number A129
Number of page(s) 4
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/202142096
Published online 15 December 2021

© ESO 2021

1. Introduction

Knowledge of the mass of the Local Group (LG) is crucially important. However, its observational determination is challenging as a consequence of the fact that the mass of the LG is dominated by dark matter, which cannot be directly observed. The timing argument (TA) was proposed in Peebles et al. (1989) and Lynden-Bell (1981) for the LG as one of the historical probes of the missing mass problem. The TA assumes that the Milky Way (MW) and Andromeda (M 31) have been approaching each other despite cosmic expansion. In its simplest version, the LG consists of the MW and M 31 as two isolated point masses. Briefly, after the big bang, these two galaxies must have been in the same place with zero separation. Due to the Hubble expansion, these two galaxies moved apart. After a couple billion years, they slowed down and then moved toward each other again as a consequence of gravitational pull.

Earlier estimations for the LG mass have been done with different methods: considering simulations (Carlesi et al. 2017; Gonzalez et al. 2014; Peñarrubia et al. 2014; Li & White 2008; Banik et al. 2018; Hartl & Strigari 2021), the TA as well as the viral theorem (van der Marel et al. 2012; Chernin et al. 2009), the numerical action method (Phelps et al. 2013), machine learning (McLeod et al. 2017), and likelihood-free inference (Lemos et al. 2021). The estimations predict that the mass of the LG should be around 1012 solar masses (M⊙). Zhao et al. (2013) and Benisty & Guendelman (2020) tested the LG mass in modified Newtonian dynamics gravity. The present paper investigates the effects of a possible past encounter (PE) on on the predicted mass of the LG.

The structure of this paper is as follows: Sect. 2 discusses the formalism of two-body motion with a cosmological constant (Λ). Section 3 explains the numerical method. Section 4 explains the analysis considering a possible PE. Section 5 discusses the results.

2. Two-body problem

The cosmological constant domination is considered to govern at cosmological scales as well as at the LG scale (Chernin et al. 2000, 2002, 2004, 2006, 2009; Baryshev et al. 2001; Karachentsev et al. 2003; Teerikorpi et al. 2005; Teerikorpi & Chernin 2010; Chernin 2015; Silbergleit & Chernin 2019; Benisty & Guendelman 2020). Hence, we included the cosmological constant contribution in our analysis. The center of mass coordinate system is defined by the relative distance, r, and the relative velocity, v. The masses are replaced by the total mass, M. In the polar coordinate system (r, φ), the relative distance variation reads (Emelyanov et al. 2015; Carrera & Giulini 2006)

r ¨ = L 2 r 3 − GM r 2 + 1 3 Λ c 2 r , $$ \begin{aligned} \ddot{r} = \frac{L^2}{r^3}-\frac{GM}{r^2} + \frac{1}{3}\Lambda c^2 \, r, \end{aligned} $$(1)

where L is the conserved angular momentum per mass (L = r × v), or

L = r 2 φ ˙ = r v tan , $$ \begin{aligned} L=r^2 \dot{\varphi }= r \, { v}_{\rm tan}, \end{aligned} $$(2)

where vtan is the tangential velocity. Since the potential is time independent, the associated conserved energy reads

E = 1 2 r ˙ 2 + V ( r ) , $$ \begin{aligned} E = \frac{1}{2} \dot{r}^2 + V(r), \end{aligned} $$(3)

with the effective potential

V ( r ) = L 2 2 r 2 − GM r − Λ c 2 12 r 2 . $$ \begin{aligned} V\left(r\right) = \frac{L^2}{2r^2} - \frac{GM}{r} - \frac{\Lambda c^2}{12} r^2. \end{aligned} $$(4)

Figure 1 presents the potential V(r). There are two extreme points: The closer one is a minimum, and the other is a maximum. For large distances, the repulsive force arising from the cosmological constant makes any bound structure impossible, so the cosmological constant gives us a bound on the maximum size of the bound systems.

thumbnail Fig. 1.

Effective potential vs. radius for a two-body system with or without a cosmological constant. The distance of M 31 to us is marked in the plot in light blue with a 1σ range.

3. The method

We restricted ourselves to a simple basis of the TA as an isolated, two-dimensional system. Galaxies were modeled as point masses. Moreover, as the galaxy pairs are isolated, there are no external gravitational fields. The “initial condition” of the model is r(t = 0)=0, which corresponds to the “big bang”. In order to calculate the mass of the LG, we changed the direction of time by considering the opposite direction of the measured velocity. We evaluated the measured distance of M 31 to obtain what would be the distance at the big bang for different LG masses. Figure 2 presents the distance for the big bang for different masses of the LG when the curve approaches minimum (r → 0), yielding the predicted mass The minimum recognizes the mass of the LG, as the model predicts. The location and the velocity of M 31 are:

thumbnail Fig. 2.

Evaluated distance between the MW and M 31 at t = 0 for different masses of the LG. The model predicts the correct mass when r(t = 0)=0. The first minimum (4 − 5 × 1012 M⊙) points to the predicted mass according to the TA. The second minimum points to the predicted mass with one PE (9 − 10 × 1012 M⊙). The dashed blue line corresponds to the solution without Λ, and the orange line corresponds to the solution with Λ.

r m 31 = 0.77 ± 0.04 Mpc , v rad = − 109.3 ± 4.4 km s − 1 , v tan ( t u ) = 17 km s − 1 , $$ \begin{aligned}&r_{m_{31}} = 0.77 \pm 0.04 \, {\mathrm{Mpc}}, \\&{ v}_{\rm rad} = -109.3 \pm 4.4 \, \mathrm{km\,s}^{-1}, \\&{ v}_{\rm tan}(t_u) = 17 \, \mathrm{km\,s}^{-1}, \end{aligned} $$

with a 1 σ confidence, with the region of Vtan ≤ 34.3 km s−1, which was measured in van der Marel et al. (2012). The vrad is the radial velocity toward the MW. The cosmological constant is

Λ = ( 4.24 ± 0.11 ) × 10 − 66 eV 2 , $$ \begin{aligned} \Lambda = (4.24 \pm 0.11) \times 10^{-66} \, \mathrm{eV}^2, \end{aligned} $$

as determined by the latest Planck measurements (Aghanim et al. 2020). When we estimated the initial distance at the big bang, we also used the age of the Universe as determined by the latest Planck measurements.

The acceleration terms in Eq. (1) are on the same order if we set the mass to be around M ∼ 1012 M⊙ and the distance between the galaxies to be around r ∼ 1 Mpc:

− GM r 2 ≈ 6 × 10 − 9 m s 2 , 1 3 Λ c 2 r 2 = 10 − 9 m s 2 . $$ \begin{aligned} - \frac{G M}{r^2} \approx 6 \times 10^{-9} \frac{m}{\mathrm{s^2}}, \quad \frac{1}{3}\Lambda c^2 r^2 = 10^{-9} \frac{m}{\mathrm{s^2}}. \end{aligned} $$(5)

Therefore, one has to also take the expansion effect into account despite the scale being very short.

Eingorn et al. (2013), Eingorn & Zhuk (2012), Partridge et al. (2013), Gonzalez et al. (2014), McLeod et al. (2017), and McLeod & Lahav (2020) originally showed that the cosmological constant effect on LG scales (1 Mpc) changes the predicted mass of LG, making it larger. The mass of the LG without the cosmological constant is MLG = (4.17±0.89) × 1012 M⊙, and with the cosmological constant presence we get MLG = (4.73±1.03) × 1012 M⊙. The difference is not negligible.

4. Results

The presence of the tangential velocity yields the possibility of a PE. The mass diagram versus the evaluated distance in the big bang (t = 0) is presented in Fig. 2. We see that there are several masses that fit the initial condition (r(t)→0). The left minimum is the model prediction without any PE. The right minimum is the model prediction with one PE.

Table 1 summarizes the results for the predicted mass of LG with or without a PE. Figure 3 shows the corresponding corner plots. With no cosmological constant background, the mass is 4.13 ± 0.78 M⊙. With a cosmological constant background, the mass is 4.61 ± 1.39 M⊙. For any additional encounter, the predicted mass is larger. Without Λ, the predicted mass is 9.63 ± 2.14 M⊙, and with Λ it is 9.77 ± 2.47 M⊙.

Table 1.

Summary of predicted masses of the LG for with or without Λ and with or without a PE.

thumbnail Fig. 3.

Corner plots for the predicted mass of the LG vs. the measured distance toward M 31 and the measured velocities. The upper panel shows the results without Λ, and the lower panel shows the results with Λ.

In order to track the actual motion of the galaxies, we evaluated a numerical solution for the distance between the galaxies with the extracted mass. Figure 4 shows the numerical solution of the distance versus time, with or without a PE. The solid line shows the solution from the big bang point, r(t = 0)=0, to the final stage, r(t = 13.7 Gys)=0.77 Mpc. The dashed line shows the numerical solution for the larger mass and yields a PE. Around ∼8.1 Gys after the big bang, the galaxies would have had to fly by each other if a PE did happen.

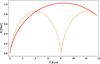thumbnail Fig. 4.

Distance between the galaxies vs. time with or without a PE. The minimal point around ∼8.1 Gys shows the galaxies’ flyby.

The model assumes that the galaxies are point masses. This assumption is correct since the size of the galaxies would be partially negligible compared to the distance between the galaxies during most of the history of the Universe if there was no PE (see Fig. 4). However, in the case of a PE, the masses predicted from the TA are twice larger and the galaxies would have had to fly by each other. In the time it took for the galaxy flyby, the strong dynamical friction (DF) from the dark matter caused the galaxies to merge (Binney & Tremaine 1987; Hammer et al. 2007). Cox & Loeb (2008) and Conselice et al. (2009) used N-body simulations to track the evolution of the LG. Their simulations also show that the DF between the galaxies would lead to the eventual merger of the LG. Therefore, from the simple TA approximation, it is possible to rule out the existence of a PE, as suggested by the other simulations.

5. Summary

In this paper we relate the mass of the LG with a possible PE using the TA. We treat the MW and M 31 galaxies as point particles that emerge briefly after the big bang at a very short distance. In order to have the same final conditions for the M 31 distance and velocity at the present time, one can extract the mass for the LG. Figure 5 shows the final comparison between the masses with or without a PE.

thumbnail Fig. 5.

Final comparison between the mass of the LG with one PE and without a PE.

M 31 and the MW are considered to be interacting point-like gravitating systems. This is partially correct because the assumption depends on the galaxy size being negligible with respect to the overall size of the LG. Taking the possibility of a PE into account yields a twice larger mass. Since the galaxies in earlier times would have had to fly by each other, the galaxies would be merged because of the larger mass with a DF presence. Therefore, from a simple analysis of the TA, the possibly of a PE is ruled out.

Acknowledgments

I thank to Eduardo I. Guendelman, Ofer Lahav, Pablo Lemos, Yehuda Hofman, Michael McLeod, Mordehai Milgrom, Indranil Banik and Hongsheng Zhao for stimulating discussions. I gratefully acknowledge the support the supports of the Blavatnik and the Rothschild fellowships. This article is supported by COST Action CA15117 “Cosmology and Astrophysics Network for Theoretical Advances and Training Action” (CANTATA) of the COST (European Cooperation in Science and Technology) and the COST actions CA15117 and CA-16104.

References

  1. Banik, I., O’Ryan, D., & Zhao, H. 2018, MNRAS, 477, 4768 [NASA ADS] [CrossRef] [Google Scholar]
  2. Baryshev, Y., Chernin, A., & Teerikorpi, P. 2001, A&A, 378, 729 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  3. Benisty, D., & Guendelman, E. I. 2020, Phys. Dark Univ., 30, 100708 [NASA ADS] [CrossRef] [Google Scholar]
  4. Binney, J., & Tremaine, S. 1987, Galactic Dynamics (Princeton) [Google Scholar]
  5. Carlesi, E., Hoffman, Y., Sorce, J. G., & Gottlöber, S. 2017, MNRAS, 465, 4886 [NASA ADS] [CrossRef] [Google Scholar]
  6. Carrera, M., & Giulini, D. 2006, ArXiv e-prints [arXiv:gr-qc/0602098] [Google Scholar]
  7. Chernin, A., Teerikorpi, P., & Baryshev, Y. 2000, ArXiv e-prints [arXiv:astro-ph/0012021] [Google Scholar]
  8. Chernin, A. D. 2015, Astron. Rep., 59, 474 [NASA ADS] [CrossRef] [Google Scholar]
  9. Chernin, A. D., Santiago, D. I., & Silbergleit, A. S. 2002, Phys. Lett. A, 294, 79 [NASA ADS] [CrossRef] [Google Scholar]
  10. Chernin, A. D., Karachentsev, I. D., Valtonen, M. J., et al. 2004, A&A, 415, 19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Chernin, A. D., Teerikorpi, P., & Baryshev, Y. V. 2006, A&A, 456, 13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Chernin, A. D., Teerikorpi, P., Valtonen, M. J., et al. 2009, ArXiv e-prints [arXiv:0902.3871] [Google Scholar]
  13. Conselice, C. J., Yang, C., & Bluck, A. F. L. 2009, MNRAS, 394, 1956 [NASA ADS] [CrossRef] [Google Scholar]
  14. Cox, T. J., & Loeb, A. 2008, MNRAS, 386, 461 [NASA ADS] [CrossRef] [Google Scholar]
  15. Eingorn, M., & Zhuk, A. 2012, JCAP, 09, 026 [Google Scholar]
  16. Eingorn, M., Kudinova, A., & Zhuk, A. 2013, JCAP, 1304, 010 [Google Scholar]
  17. Emelyanov, N. V., Kovalyov, M Yu, & Chernin, A. D. 2015, Astron. Rep., 59, 510 [NASA ADS] [CrossRef] [Google Scholar]
  18. Gonzalez, R. E., Kravtsov, A. V., & Gnedin, N. Y. 2014, ApJ, 793, 91 [CrossRef] [Google Scholar]
  19. Hammer, F., Puech, M., Chemin, L., Flores, H., & Lehnert, M. 2007, ApJ, 662, 322 [NASA ADS] [CrossRef] [Google Scholar]
  20. Hartl, O. V., & Strigari, L. E. 2021, MNRAS, submitted, [arXiv:2107.11490] [Google Scholar]
  21. Karachentsev, I. D., Chernin, A. D., & Teerikorpi, P. 2003, Astrofiz., 46, 399 [NASA ADS] [Google Scholar]
  22. Lemos, P., Jeffrey, N., Whiteway, L., et al. 2021, Phys. Rev. D, 103, 023009 [NASA ADS] [CrossRef] [Google Scholar]
  23. Li, Y.-S., & White, S. D. M. 2008, MNRAS, 384, 1459 [CrossRef] [Google Scholar]
  24. Lynden-Bell, D. 1981, Observatory, 101, 111 [NASA ADS] [Google Scholar]
  25. McLeod, M., & Lahav, O. 2020, JCAP, 09, 056 [Google Scholar]
  26. McLeod, M., Libeskind, N., Lahav, O., & Hoffman, Y. 2017, JCAP, 1712, 034 [CrossRef] [Google Scholar]
  27. Partridge, C., Lahav, O., & Hoffman, Y. 2013, MNRAS, 436, 45 [Google Scholar]
  28. Peebles, P. J. E., Melott, A. L., Holmes, M. R., & Jiang, L. R. 1989, ApJ, 345, 108 [CrossRef] [Google Scholar]
  29. Peñarrubia, J., Ma, Y.-Z., Walker, M. G., & McConnachie, A. 2014, MNRAS, 443, 2204 [Google Scholar]
  30. Phelps, S., Nusser, A., & Desjacques, V. 2013, ApJ, 775, 102 [NASA ADS] [CrossRef] [Google Scholar]
  31. Planck Collaboration VI. 2020, A&A, 641, A6; Erratum: 2021, A&A, 652, C4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Silbergleit, A., & Chernin, A. 2019, Kepler Problem in the Presence of Dark Energy, and the Cosmic Local Flow, SpringerBriefs in Physics (Springer) [Google Scholar]
  33. Teerikorpi, P., & Chernin, A. D. 2010, A&A, 516, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Teerikorpi, P., Chernin, A. D., & Baryshev, Y. V. 2005, A&A, 440, 791 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. van der Marel, R. P., Fardal, M., Besla, G., et al. 2012, ApJ, 753, 8 [NASA ADS] [CrossRef] [Google Scholar]
  36. Zhao, H., Famaey, B., Lüghausen, F., & Kroupa, P. 2013, A&A, 557, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

All Tables

Table 1.

Summary of predicted masses of the LG for with or without Λ and with or without a PE.

In the text

All Figures

thumbnail Fig. 1.

Effective potential vs. radius for a two-body system with or without a cosmological constant. The distance of M 31 to us is marked in the plot in light blue with a 1σ range.
In the text
thumbnail Fig. 2.

Evaluated distance between the MW and M 31 at t = 0 for different masses of the LG. The model predicts the correct mass when r(t = 0)=0. The first minimum (4 − 5 × 1012 M⊙) points to the predicted mass according to the TA. The second minimum points to the predicted mass with one PE (9 − 10 × 1012 M⊙). The dashed blue line corresponds to the solution without Λ, and the orange line corresponds to the solution with Λ.
In the text
thumbnail Fig. 3.

Corner plots for the predicted mass of the LG vs. the measured distance toward M 31 and the measured velocities. The upper panel shows the results without Λ, and the lower panel shows the results with Λ.
In the text
thumbnail Fig. 4.

Distance between the galaxies vs. time with or without a PE. The minimal point around ∼8.1 Gys shows the galaxies’ flyby.
In the text
thumbnail Fig. 5.

Final comparison between the mass of the LG with one PE and without a PE.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.