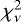| Issue |
A&A
Volume 656, December 2021
|
|
|---|---|---|
| Article Number | A126 | |
| Number of page(s) | 9 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202142013 | |
| Published online | 10 December 2021 | |
Photometry and model of near-Earth asteroid 2021 DW1 from one apparition
1
Astronomical Observatory Institute, Faculty of Physics, A. Mickiewicz University,
Słoneczna 36,
60-286
Poznań,
Poland
e-mail: tkastr@amu.edu.pl
2
Lowell Observatory,
14000 W Mars Hill Rd,
86001
Flagstaff,
AZ,
USA
3
Astronomical Observatory of Odessa I.I.Mechnikov National University,
Odessa,
Ukraine
4
Korea Astronomy & Space Science Institute,
776 Daedeok-daero,
Yuseong-gu,
Daejeon
34055,
Republic of Korea
5
National Youth Space Center,
Goheung,
Jeollanam-do
59567,
Korea
6
Deutsches Zentrum för Luft- und Raumfahrt (DLR), Institute of Planetary Research,
Berlin,
Germany
7
Departamento de Física, Ingeniería de Sistemas y Teoría de la Señal, Universidad de Alicante,
Alicante,
Spain
8
Institut de Ciencies del Cosmos (ICCUB), Universitat de Barcelona,
Barcelona,
Spain
9
Platanus Observatory (IAU code K80),
Lusówko,
Poland
10
“G.V. Schiaparelli” Astronomical Observatory,
Varese,
Italy
11
Osservatorio di San Marcello Pistoiese, GAMP Gruppo Astrofili Montagna Pistoiese,
Italy
12
Great Shefford Observatory,
Berkshire,
UK
13
British Astronomical Association,
Burlington House,
Piccadilly,
London,
UK
14
Las Cumbres Observatory,
Goleta,
CA
93117,
USA
Received:
13
August
2021
Accepted:
22
September
2021
Aims. Very small asteroids (VSAs, objects with diameters smaller than about 150 m) can be spun up by the YORP effect to rotation periods as short as tens of seconds. This effect has been observed for many of them. It is also hypothesised, that in the same process their spin axes are asymptotically drawn to the position perpendicular to the orbital plane. So far this effect has been observed only for one VSA and needs further verification. For that, spin axes of several other VSAs should be determined by observing their brightness variations at many different positions on the sky.
Methods. On 4 March 2021 at 9 UTC a 30-m in diameter near-Earth asteroid 2021 DW1 passed the Earth at a distance of 570 000 km, reaching the maximum brightness of V = 14.6 mag. We observed it photometrically from 2 March, when it was visible at V = 16.5 mag, until 7 March (V = 18.2 mag). During that time 2021 DW1 swept a 170° long arc in the northern sky, spanning solar phase angles in the range from 36° to 86°. This made it an excellent target for physical characterisation, including spin axis and shape derivation.
Results. Convex inversion of the asteroid lightcurves gives a sidereal period of rotation Psid = 0.013760 ± 0.000001 h, and two solutions for the spin axis ecliptic coordinates: (A) λ1 = 57° ± 10°, β1 = 29° ± 10° and (B) λ2 = 67° ± 10°, β2 = −40° ± 10°. The magnitude-phase curve can be fitted with a standard H, G function with H = 24.8 ± 0.5 mag and an assumed G = 0.24. The asteroid colour indices are g − i = 0.79 ± 0.01 mag, and i − z = 0.01 ± 0.02 mag which indicates an S taxonomic class, with an average geometric albedo pV = 0.23 ± 0.02. The asteroid effective diameter, derived from H and pV, is Deff = 30 ± 10 m.
Conclusions. It was found that the inclination of the spin axis of 2021 DW1 is not perpendicular to the orbital plane (obliquity ϵ = 54° ± 10° or ϵ = 123° ± 10°). More spin axes of VSAs should be determined to check, if 2021 DW1 is an exception or a typical case.
Key words: methods: observational / techniques: photometric / minor planets, asteroids: individual: 2021 DW1
© ESO 2021
1 Introduction
Very small asteroids (VSAs) are objects with diameters D < 150 m. They often rotate with periods shorter than 2 h enabling us to study their internal structure by comparing the centrifugal force with the material forces holding them together (Holsapple 2007). Because of their small sizes, VSAs are sensitive to the YORP effect (Rubincam 2000), which is a torque induced on the rotating body by the thermal radiation emitted by its surface complemented by a torque produced by scattered sunlight. YORP can either spin up or slow down the asteroid rotation as well as change the obliquity of its spin axis ϵ, which is an angle between the normal to the asteroid orbital plane and its rotation axis. While the fast rotation has been observed for many VSAs, their spin axes were not determined except for one object1, (54 509) YORP (whose name is the same as the name of the effect itself). (54 509) was the first asteroid for which the effect of YORP has been observed (Lowry et al. 2007; Taylor et al. 2007). The obliquity of the (54 509) spin axis is ϵ = 173°, which means it is nearly perpendicular to the asteroid orbital plane. Such an orientation of the spin axis was found as an end state of the YORP evolution in the simulations performed by Čapek & Vokrouhlický (2004) for objects with finite surface thermal conductivity. If their prediction is true, then for the VSAs that experienced a strong YORP effect for a long time (and the fastest rotating VSAs are such objects), we should observe spin axis obliquities close to 0° or 180°. Recently Golubov et al. (2021) have shown that for very small objects of a highly irregular shape, the transverse heat conduction (TYORP) can add new asymptotic states for the obliquity. For this reason it would be interesting to verify those predictions with observationsof VSAs. To do that, we should observe their lightcurves at many different positions on the sky to be able to determine their spin axes. For near-Earth objects (NEAs) this condition is met either by the Earth co-orbital asteroids – and (54 509) is an example of such objects – or by objects for which their close encounter with the Earth can be observed along a long arc on the sky.
The main goal of this paper is to present the observations and modelling of the near-Earth asteroid 2021 DW1, which allowed us to derive its spin axis. Apart from that, we were able to determine many other physical properties of this VSA, such as its rotation period, shape, size, and taxonomy class, adding new data to this still poorly characterised group of objects.
 |
Fig. 1 Trail made by 2021 DW1 on the sky during our observing campaign, plotted in the RA, Dec equatorial coordinates. The beginning of the arcrefers to 2 March, 4 UTC, and the end to 7 March, 7 UTC. The length of the trail is about 170°. It is important to note that two observations made on 7 March were not used in the end for lightcurve inversion due to high photometric noise. |
2 Observations and data reduction
On 16 February 2021, a near-Earth asteroid was discovered by the Pan-STARRS 1 survey at Haleakala, Hawaii. The discovery was reported in the MPEC 2021-D73 circular2 and the object was designated 2021 DW1. Its first estimate of the absolute magnitude gave a value of H = 25 mag, which translated roughly to an effective diameter of 40 m, indicating it is a VSA with a rotation period possibly shorter than 2.2 h. What differentiated that object from other, similar NEAs was its ephemeris which showed that it could be observed in favourable circumstances (V <18 mag) along a lengthy arc on the sky. Its beginning was obscured by the Milky Way, but from 2 March untill 7 March, the length of the trail was 170°, with the solar phase angle spanning the interval from 36° to 86° (Fig. 1). Such observing geometry made it possible to not only determine the rotation period and colour indices, but also to attempt derivation of the magnitude-phase angle relation, spin axis coordinates and shape.
We organised an observing campaign for 2021 DW1 by contacting a number of collaborating observatories. A call for observations was also posted on the Minor Planet Mailing List(MPML). As a result, we set up a network of ten observatories located in the Northern Hemisphere, from South Korea in the east, to Arizona in the west. The spread in longitude helped to secure observations from different parts of the asteroid trail. There were several factors which made observations difficult: the weather, a bright Moon, fast movement of an asteroid in the sky, and human mistakes. We also encountered strange problems pointing some robotic telescopes. They were probably caused by the systems using outdated ephemerides of 2021 DW1.
The asteroid aspect data and the observing log are presented in Table 1. We limit this table to only those observationsthat were used in the final analysis (their results are shown in Fig. 2). Details of all observing systems are shown in Table 2.
Most of the photometric data were reduced with the Starlink package3 (Currie et al. 2014). Raw CCD frames were corrected for bias and flat-field (and for the dark current, if necessary). Aperture photometry was then performed on the frames, on which the point spread function (PSF) of the asteroid and the comparison stars was almost circular. During the nights when fast sky motion of the object (even during short, 5 s exposures) caused significant PSF trailing, we requested observers to employ the non-sidereal telescope tracking on the asteroid. This way, the entire signal from 2021 DW1 was concentrated in a circular aperture, while the images of stars were trailed. To perform differential photometry on such CCD frames, we used ‘pill-shaped apertures’ developed by Fraser et al. (2016), and used for NEAs by Koleńczuk (2020). In this technique, an elongated aperture is created as a rectangle with two semicircular end caps. It is defined by three parameters: the trail length, the position angle, and the radius.
The data from the Great Shefford Observatory were reduced in a standard way with the help of Astrometrica and MPO Canopus commercial packages. Observations from the Platanus Observatory were done with an exposure time of 1 s. This produced a circular PSF for a fast moving asteroid, but because of a small telescope aperture (0.28-m), the S/N was low. However, during a one-hour run, more than two thousand frames were collected. After reducing the data, each set of five points was averaged into one data point, and the composite lightcurve, even if it was still rather noisy, produced a well-defined Fourier series fit (see the C005 plot on Fig. 2).
To search for the rotation period of 2021 DW1 we used a standard Fourier series analysis. This was done with the PerFit programme (Kwiatkowski et al. 2010a), which in its current version works in the following way: after correcting all times for the light-time, each differential photometry time series is divided into parts obtained with the same comparison star. Next, a Fourier series of a given order is fit to all of them with one synodic period assumed. In the process, both the Fourier series coefficients and magnitude shifts (with respect to the first time series) are determined by linear least squares. This process is repeated for each trial period from a specified interval. In most cases the fourth to sixth order Fourier series is used. The accuracy of the fit is measured with the χ2 computed from the residuals.
The period which gives the smallest χ2 is then selected as a potential synodic period of rotation. The least square fit takes the accuracy of the measured asteroid differential magnitudes into account (expressed as standard deviations). The accuracy of the derived period is estimated by a Monte Carlo method, in which all data are perturbed 30 times with the appropriate sigma values.
Using PerFit for the lightcurves of 2021 DW1, it appeared that there are two solutions for the period: P1 = 0.00688 h (this gave mono-modal composite lightcurves) and P2 = 0.01376 h (bi-modal composite lightcurves), with P2 = 2 ⋅ P1. Results for P2 = 0.01376 h (which is our preferred solution) are presented in Fig. 2. In the plots, we did not draw error bars so as not to obscure the images. The overall accuracy can be easily judged from the scatter of the data points about the Fourier fit.
Observing log.
Observatories, telescopes and detectors used in observations.
3 Sidereal period, spin axis and shape
Since the works of Kaasalainen & Torppa (2001) and Kaasalainen et al. (2001), a standard method for the determination of the asteroid sidereal rotation period, pole, and shape is through the lightcurve inversion. For that, lightcurves observed at different viewing and illuminating geometries are needed. While each case is different, a good rule of thumb for NEAs is to have data sampling an arc on the sky longer than 120° (Josef Ďurech, personal communication). While in case of 2021 DW1, we observed its trail extending up to 170°, the last twoobservations (from 7 March) were very noisy (the asteroid brightness dropped to V = 18 mag) and were not used in the analysis. This shortened the arc to 163°, from which we selected thirteen composite lighcurves well positioned along the trail (see Fig. 2). Each of them was obtained with the P2 synodic period. They were converted from magnitudes to fluxes and scaled down so that the average flux during the rotation was set to unity. We did not use any lightcurves calibrated to the standard magnitudes, as such calibrations are usually less accurate than the differential magnitudes. The data were then used for the lightcurve inversion, for which we used a C-language implementation of the code, written by Josef Ďurech. The convex shapes used in the computations were approximated by spherical harmonics of the sixth degree and order. The light scattering law was approximated by the Lommel-Seeliger-Lambert function, with c = 0.1.
Figure 3 presents a periodogram for the sidereal period, with the best result obtained for Psid = 0.013760 ± 0.000001 h. There were two solutions for the ecliptic coordinates of the spin axis A: λ1 = 57° ± 10°, β1 = 29° ± 10° and B: λ2 = 67° ± 10°, β2 = −40° ± 10°, both with the same sidereal period. The obliquities resulting from those pole orientations are the following: ϵ1 = 54° ± 10° and ϵ2 = 123° ± 10°. They are far away from the asymptotic states (ϵ = 0°, 180°) as predicted by the theory.
As it often happens, the positions are symmetric with respect to the ecliptic plane (within the specified uncertainties). Convex shapes resulting from these pole positions are presented in Fig. 4, and a fit of the modelled lightcurves to the data, for pole A, in Fig. 5. The fits obtained for solution B are very similar. For both models, the percentage of dark facets was smaller than 0.5. We note that in the final solution, we did not use LC09, which is very close in time to LC10, and does not provide any new information for the fit.
Scanning the whole celestial sphere for other solutions, we encountered cases where the fit of the model lightcurves to the observed ones was satisfactory, but the convex shapes were not physical. For example, the body was significantly elongated in the c-axis direction (which was assumed to be the axis of rotation), the shape was unrealistically flat (pan-cake like), or more than 5% of the surface was made up of dark facets. The latter would imply surface albedo variegation, which is difficult to accept for such small objects.
The same happened when we started with the P1 synodic period. Folding all data with P1, we obtained a set of mono-modal composite lightcurves, well fit by the Fourier series. However, when we used such data for lightcurve inversion, we obtained unrealistic solutions. Based on this, we reject P1 as a possible period of rotation (with the assumption of a convex shape and the lack of albedo variegation on the surface).
 |
Fig. 2 Selected composite lightcurves of 2021 DW1. |
 |
Fig. 3 Results of the search for the sidereal period of rotation for the P2 solution. The search interval has been defined by the range of change of the synodic period. On the vertical axis there is a value of |
 |
Fig. 4 Projections of convex shapes obtained for two pole solutions. The upper row is for pole A, and the lower one is for pole B. In the left column, the middle column, and on the right, wecan see a projection onto the x-z plane, onto the y-z plane, and projections on the x-y plane, respectively. The rotation axis coincides with the z-axis. |
4 Magnitude-phase curve
There are several problems that make it difficult to derive the magnitude-phase angle function (hereafter: phase function) for NEAs. Firstly, they are seldom observed close to opposition, so the non-linear part of the phase function cannot be properly determined. Secondly, during their passage close to Earth, the aspect angle (the angle formed by the object’s spin axis and the direction towards the observer) can change significantly, influencing the magnitude-phase angle relationship.Thirdly, during astrometric observations of NEAs, which are used routinely by the Minor Planet Center4 (MPC) for determination of the phase function, asteroid magnitudes from different phases of rotation are reported and the phase curve is distorted even more by the rotational brightness variations.
In the case of 2021 DW1, we observed its full lightcurves and were able to determine its rotationally averaged magnitudes. This removed the third obstacle mentioned above. Since our observations were done in different filters (and often were ‘unfiltered’), for the purpose of photometriccalibration, we used the Pan-STARRS catalogue (Tonry et al. 2012) standards of solar colours. We selected the best lightcurves reported in Table 1 and calibrated them in the SDSS r band. For each lightcurve, we used the Fourier fit to compute its mean magnitude. We also used the data from 7 March (lightcurve LC013), which were quite noisy for the convex shape modelling, but they gave a good rotationally averaged magnitude.
In the process, we had to discard some results, where the calibration was inaccurate. We also noticed that our data were strongly affected by aspect changes during the time when the asteroid was changing its ecliptic latitude from β = − 25° to β = + 20°. For this reason, we only used lightcurves observed from 4 March, 2 UTC to 7 March, 8:45 UTC. After scaling the magnitudes to unit distances from the Earth and Sun, we tried to fit them with a standard H, G phase function. Our standard programme for doing that, with an advanced non-linear minimisation, failed, so we used a simpler approach changing the H and G values in some intervals, fitting the H, G function to the data, and selecting the result with the smallest residuals. Unfortunately, the best fit was obtained for G = 1.1, which has no physical meaning because the typical values of G for asteroids fall between 0.0 and 0.5. The absolute magnitudes Hr obtained for G = 0.0 and G = 0.5, are Hr = 24.00 and Hr = 24.98, respectively. To translate them to H values in the V band, which is the standard way of reporting absolute magnitudes, one can increase them by 0.21 mag. This value can be obtained using the transformation from r to V, provided by Tonry et al. (2012).
The absolute magnitude for 2021 DW1, derived by the MPC from 284 less accurate, astrometric observations, is HMPC = 25.02. It was obtained assuming G = 0.15. To get a final value for the absolute magnitude of 2021 DW1, and as we describe in the next section, we used the fact that it is an S class asteroid, for which G = 0.24 ± 0.11 (Warner et al. 2009). With this assumption we got Hr = 24.57 which, after conversion to the V band, is HV = 24.8 (Fig. 6).
Since in our computation of H systematic effects dominate over the statistical ones, we were not able to derive a standard ‘one σ’ error for it. Instead, we estimated the accuracy of the obtained absolute magnitude by a maximum uncertainty of ΔH = 0.5 mag.
 |
Fig. 5 Superposition of the model A lightcurves (continuous line) on the data points obtained from observations. All plots were drawn in the same coordinates: the x-axis is the rotation phase (in the range from 0 to 1), and the y-axis refers to the flux scaled to unity for the average brightness. We note that our convex model has problems with recreating sharp brightness maxima in LC03, LC05, and LC06 lightcurves. They are most likely caused by concavities on the asteroid surface. |
5 Colour indices and taxonomy
On 5 March we observed the asteroid in three Sloan g, i, and z filters (see the rows in Table 1 with the codes CI01-3). For each of them, a series of 4 s exposures were obtained with the telescope tracking on the asteroid.
In the case of the observations in i and g filters, we had no problems with data reduction, while the exposures in the infrared z filter left interference fringes on the CCD frames. The reduction of fringing is possible by subtracting the so-called fringe map, which is obtained by averaging the images of the blank fields (fields with a few visible stars). We could not make blank field observations until 30 April. Unfortunately, it turned out that the fringe pattern changed too much from 5 March untill 30 April to use the obtained fringe map for the reduction.
The non-sidereal telescope tracking ensured an almost constant position of the asteroid image in relation to the fringe structure, thanks to which it was possible to avoid the influence of fringing on instrumental measurements of the asteroid. The problem was with the comparison stars, which moved quickly in relation to the fringe structure. To minimise this effect, we selected just one Pan-STARRS comparison star for which the fringing had little effect on its brightness (standard deviation of brightness measurements σ = 0.02 mag). We used this star to calibrate the z filter magnitude of the asteroid.
Next, using PerFit, we phased the g, i, and z lightcurves with the reference VR lightcurve, obtaining one composite lightcurve. For this purpose, we used part of the observations made in the VR filter on the same telescope just before the exposures in the g filter, and for control, 40 min after the exposures in the z filter. In both cases the aspect data were practically the same. The obtained values of V R − g, V R − i and V R − z magnitude shifts gave the following colour indices: g − i = 0.79 ± 0.01 mag, i − z = 0.01 ± 0.02 mag, and z − g = 0.01 ± 0.02 mag.
To determine the taxonomic type of 2021 DW1, we converted the colour indices to the reflection coefficients Ri and Rz, normalised to the reflection values in the g band, using the formula given in DeMeo & Carry (2013):
![\begin{equation*}R_{f}\,{=}\,10^{-0.4[(f-g)-(f_{\odot}-g_{\odot})]}\end{equation*}](/articles/aa/full_html/2021/12/aa42013-21/aa42013-21-eq1.png) (1)
(1)
where g and g⊙ are the g magnitudes of the asteroid and Sun, and f and f⊙ are the magnitudes in another band. In Eq. (1) we assumed the solar colours 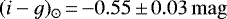 and
and 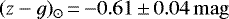 (Holmberg et al. 2006), used our colour indices, and obtained the following reflectivities: Rg ≡ 1, Ri = 1.25 ± 0.03, and Rz = 1.19 ± 0.05. Next, we compared them with spectra of different taxonomic classes, as given by DeMeo & Carry (2013). A good match was found for the S, Sq, and K spectra (Fig. 7), with the Sq class being the best.
(Holmberg et al. 2006), used our colour indices, and obtained the following reflectivities: Rg ≡ 1, Ri = 1.25 ± 0.03, and Rz = 1.19 ± 0.05. Next, we compared them with spectra of different taxonomic classes, as given by DeMeo & Carry (2013). A good match was found for the S, Sq, and K spectra (Fig. 7), with the Sq class being the best.
Since K class asteroids are typical mainly for the Eos family, and are rare in the asteroid population, the confirmation of this possibility would require a good quality spectrum of 2021 DW1. In our campaign we planned to get such a spectrum, but a fast movement of the object on the sky made it impossible even for the robotic spectrograph mounted on the 2.0-m LCO telescope. Since K class objects are very rare among asteroids, our current conclusion is that 2021 DW1 is a typical S class NEA.
 |
Fig. 6 Phase curve of 2021 DW1 and the H, G function fit. During fitting, the G parameter was kept constant at 0.24 (a value typical for S class asteroids). We note that the magnitudes used are in the SDSS r band. The obtained Hr = 24.57, after conversion to the Johnson V band, gives HV = 24.8. |
 |
Fig. 7 Plots of reflectivities Rg, Rr, Ri, and Rz of three asteroid taxonomic classes (black circles), which are most similar to the reflectivities of 2021 DW1 (red circles). All reflectivities were normalised to the g band, and the grey areas denote a dispersion of spectra in a given asteroid class. Data for the taxonomic classes were taken from DeMeo & Carry (2013). |
 |
Fig. 8 Position of 2021 DW1 on the logDeff − logP plot. The open circles were taken from the LCDB, while sloped lines indicate the minimum allowable periods (at a given diameter), computed with two different tensile strength coefficients (κ = 105 and κ = 106 N m3∕2), and a density of ρ = 2500 kgm−3. A red squareindicates the position of 2021 DW1 with the error bars being a measure of the maximum uncertainty. |
6 Physical characteristic of 2021 DW1
Having obtained the absolute magnitude HV = 24.8 ± 0.5 and an estimate of the geometric albedo pV = 0.23 ± 0.02, we are nowable to derive the asteroid effective diameter Deff 5. For that, we used a standard equation 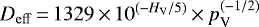 from Fowler & Chillemi (1992) and obtained Deff = 30 m. To get its uncertainty, we first converted the statistical error σpV into a maximum one: ΔpV = 3 × σpV. Then we used both ΔH = 0.5 and ΔpV = 0.06 to compute the maximum uncertainty ΔD = 10 m. With that, we finally got: Deff = 30 ± 10 m.
from Fowler & Chillemi (1992) and obtained Deff = 30 m. To get its uncertainty, we first converted the statistical error σpV into a maximum one: ΔpV = 3 × σpV. Then we used both ΔH = 0.5 and ΔpV = 0.06 to compute the maximum uncertainty ΔD = 10 m. With that, we finally got: Deff = 30 ± 10 m.
One of the methods for studying physical properties of asteroids is to plot their rotation periods versus effective diameters. In Fig. 8 we present the results taken from the last issue of the Light Curve Data Base (LCDB)6 (Warner et al. 2009). The plot includes not only VSAs, but also larger objects – both NEAs and main-belt asteroids – up to 10 kilometres in diameter. What is clearly visible in this figure is that most asteroids with Deff > 1 km (in the lower right corner of the plot) have periods P > 2.2 h, while most of VSAs display much faster rotation. This is possible because VSAs are held together by tensile strength rather than gravity. However, there is a lower limit to their periods, set by centrifugal forces. Holsapple (2007) derived an approximate formula, which, on the logDeff – logP plot, makes it possible to draw a line of minimum allowable periods (which we refer to as critical periods, Pc) for the asteroid in the strength regime. We used a slightly modified equation for Pc, given by Kwiatkowski et al. (2010b), to compute such lines on Fig. 8 for two tensile strength coefficients (κ = 105 and κ = 106 N m3∕2). A justification of our choice of κ can be found in Kwiatkowski et al. (2010b). We also assumed a typical angle of friction ϕ = 40° (Richardson et al. 2005), a density ρ = 2500 kgm−3, and the triaxial ellipsoid approximation of the 2021 DW1 shape given by c∕a = 0.48, b∕a = 0.88. The last two parameters were derived by measuring the extension of the asteroid shape along the x, y, and z axes, and computing the average from Model A and B. We note that the position of the Pc line is most sensitive to κ and ρ.
In Fig. 8 we also mark a position of 2021 DW1 with its uncertainty. Since we ruled out the P1 solution for the rotation period, the entire uncertainty now lies along the diameter axis. As can be seen, 2021 DW1 is far from the lines denoting the rotational fission. In the future, depending on the YORP-TYORP cycles, it will move vertically up (or down), or may be trapped in some equilibrium point, where its period and spin axis will not change.
7 Conclusions
We have derived the spin axis coordinates for 2021 DW1. In the ecliptic reference frame, the two solutions are: (A) λ1 = 57° ± 10°, β1 = 29° ± 10° and (B) λ2 = 67° ± 10°, β2 = −40° ± 10°, with obliquities ϵ1 = 54° ± 10° and ϵ2 = 123° ± 10°, respectively.It shows that the spin axis of 2021 DW1 is far from the asymptotic states of ϵ = 0°, 180° predicted by simulations and theory (Čapek & Vokrouhlický 2004; Golubov et al. 2021) for asteroids with high thermal conductivity. Interestingly, both ϵ1 and ϵ2 have the same values as the obliquities, at which the period change component of YORP vanishes, as shown by Eq. (13) in Golubov et al. (2021). The same effect has been observed in numerical simulations by Čapek & Vokrouhlický (2004) (their Figs. 6–8). However, this is only a temporary situation because the obliquity change component of YORP at those two positions is still significant. After some time, as the obliquity continues to change, the rotation period can be altered again.
We also obtained other physical parameters of 2021 DW1: a sidereal period Psid = 0.01376 ± 0.00001 h as well as the parameters of its magnitude-phase function H = 24.8 ± 0.5 mag and G = 0.24. The asteroid colour indices are g − i = 0.79 ± 0.01 mag and i − z = 0.01 ± 0.02 mag, which indicates an S taxonomic class, with an average geometric albedo pV = 0.23 ± 0.02. The asteroid effective diameter, derived from H and pV, is Deff = 30 ± 10 m.
Unfortunately, no new observations of this object will be possible in the near future. According to the JPL Horizons service, the only close approach of 2021 DW1 to Earth in the next 100 yr will take place on 20 February 2047. At this time, however, the asteroid will reach the maximum brightness of V = 21 mag and, with such rapid rotation, would require the biggest telescopes for observations.
Acknowledgements
T.K., A.K., and D.O. were supported by a grant No.2017/25/B/ST9/00740 from the National Science Centre, Poland. T. Kim was supported by the Korea Astronomy and Space Science Institute under the R&D program (Project No. 2020-1-600-05) supervised by the Ministry of Science and ICT (MSIT), and the National Research Foundation of Korea (NRF) Grant No. 2020R1A2C3011091, funded by MSIT. The work by T.S.-R. was carried out through a grant APOSTD/2019/046 by Generalitat Valenciana (Spain). He was also supported by the MINECO (Spanish Ministry of Economy) through a grant RTI2018-095076-B-C21 (MINECO/FEDER, UE). During observations the NASA JPL Horizons service was used extensively. We would like to thank the reviewer, David Vokrouhlický, for his useful comments which improved the article. This research hasmade use of the OWL-Net system operated by the Korea Astronomy and Space Science Institute (KASI).
References
- Čapek, D., & Vokrouhlický, D. 2004, Icarus, 172, 526 [Google Scholar]
- Currie, M. J., Berry, D. S., Jenness, T., et al. 2014, ASP Conf. Ser., 485, 391 [Google Scholar]
- DeMeo, F. E., & Carry, B. 2013, Icarus, 226, 723 [NASA ADS] [CrossRef] [Google Scholar]
- Ďurech, J., Sidorin, V., & Kaasalainen, M. 2010, A&A, 513, A46 [Google Scholar]
- Fowler, J. W., & Chillemi, J. 1992, in The IRAS Minor Planet Survey, ed. E. Tedesco, G. Veeder, J. Fowler, & J. Chillemi (Hanscom Air Force Base, MA: Phillips Laboratory), 17 [Google Scholar]
- Fraser, W., Alexandersen, M., Schwamb, M. E., et al. 2016, AJ, 151, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Golubov, O., Unukovych, V., & Scheeres, D. J. 2021, AJ, 162, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Holmberg, J., Flynn, C., & Portinari, L. 2006, MNRAS, 367, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Holsapple, K. A. 2007, Icarus, 187, 500 [NASA ADS] [CrossRef] [Google Scholar]
- Kaasalainen, M., & Torppa, J. 2001, Icarus, 153, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Kaasalainen, M., Torppa, J., & Muinonen, K. 2001, Icarus, 153, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Koleńczuk, P. 2020, in XXXIX Polish Astronomical Society Meeting, ed. K. Małek, M. Polińska, A. Majczyna, et al., 10, 101 [Google Scholar]
- Kwiatkowski, T., Buckley, D. A. H., O’Donoghue, D., et al. 2010a, A&A, 509, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kwiatkowski, T., Polinska, M., Loaring, N., et al. 2010b, A&A, 511, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lowry, S. C., Fitzsimmons, A., Pravec, P., et al. 2007, Science, 316, 272 [NASA ADS] [CrossRef] [Google Scholar]
- Richardson, D. C., Elankumaran, P., & Sanderson, R. E. 2005, Icarus, 173, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Rubincam, D. P. 2000, Icarus, 148, 2 [Google Scholar]
- Taylor, P. A., Margot, J.-L., Vokrouhlický, D., et al. 2007, Science, 316, 274 [NASA ADS] [CrossRef] [Google Scholar]
- Tonry, J. L., Stubbs, C. W., Lykke, K. R., et al. 2012, ApJ, 750, 99 [Google Scholar]
- Warner, B. D., Harris, A. W., & Pravec, P. 2009, Icarus, 202, 134 [NASA ADS] [CrossRef] [Google Scholar]
To be exact, in the DAMIT database (Ďurech et al. 2010) there are two other VSAs (2008 TC3 and 2012 TC4), for which spin axes have been determined, but both of them are non-principal axis rotators and show the effect of tumbling.
All Tables
All Figures
 |
Fig. 1 Trail made by 2021 DW1 on the sky during our observing campaign, plotted in the RA, Dec equatorial coordinates. The beginning of the arcrefers to 2 March, 4 UTC, and the end to 7 March, 7 UTC. The length of the trail is about 170°. It is important to note that two observations made on 7 March were not used in the end for lightcurve inversion due to high photometric noise. |
| In the text | |
 |
Fig. 2 Selected composite lightcurves of 2021 DW1. |
| In the text | |
 |
Fig. 3 Results of the search for the sidereal period of rotation for the P2 solution. The search interval has been defined by the range of change of the synodic period. On the vertical axis there is a value of |
| In the text | |
 |
Fig. 4 Projections of convex shapes obtained for two pole solutions. The upper row is for pole A, and the lower one is for pole B. In the left column, the middle column, and on the right, wecan see a projection onto the x-z plane, onto the y-z plane, and projections on the x-y plane, respectively. The rotation axis coincides with the z-axis. |
| In the text | |
 |
Fig. 5 Superposition of the model A lightcurves (continuous line) on the data points obtained from observations. All plots were drawn in the same coordinates: the x-axis is the rotation phase (in the range from 0 to 1), and the y-axis refers to the flux scaled to unity for the average brightness. We note that our convex model has problems with recreating sharp brightness maxima in LC03, LC05, and LC06 lightcurves. They are most likely caused by concavities on the asteroid surface. |
| In the text | |
 |
Fig. 6 Phase curve of 2021 DW1 and the H, G function fit. During fitting, the G parameter was kept constant at 0.24 (a value typical for S class asteroids). We note that the magnitudes used are in the SDSS r band. The obtained Hr = 24.57, after conversion to the Johnson V band, gives HV = 24.8. |
| In the text | |
 |
Fig. 7 Plots of reflectivities Rg, Rr, Ri, and Rz of three asteroid taxonomic classes (black circles), which are most similar to the reflectivities of 2021 DW1 (red circles). All reflectivities were normalised to the g band, and the grey areas denote a dispersion of spectra in a given asteroid class. Data for the taxonomic classes were taken from DeMeo & Carry (2013). |
| In the text | |
 |
Fig. 8 Position of 2021 DW1 on the logDeff − logP plot. The open circles were taken from the LCDB, while sloped lines indicate the minimum allowable periods (at a given diameter), computed with two different tensile strength coefficients (κ = 105 and κ = 106 N m3∕2), and a density of ρ = 2500 kgm−3. A red squareindicates the position of 2021 DW1 with the error bars being a measure of the maximum uncertainty. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.