| Issue |
A&A
Volume 656, December 2021
|
|
|---|---|---|
| Article Number | A163 | |
| Number of page(s) | 10 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/202141673 | |
| Published online | 17 December 2021 | |
Dielectronic recombination strengths and plasma rate coefficients of multiply charged ions
1
Helmholtz-Institut Jena,
Fröbelstieg 3,
07743
Jena,
Germany
2
GSI Helmholtzzentrum für Schwerionenforschung,
64291
Darmstadt,
Germany
e-mail: s.fritzsche@gsi.de
3
Theoretisch-Physikalisches Institut, Friedrich-Schiller-Universität Jena,
07743
Jena,
Germany
Received:
30
June
2021
Accepted:
10
September
2021
Context. Dielectronic recombination (DR) has been known as the dominant electron-ion recombination process in different astrophysical and laboratory plasmas, and that it determines the level population and ionization balance over a range of temperatures. Apart from a fundamental interest into the details of this process, DR plasma rate coefficients are frequently applied to estimate plasma densities and temperatures, but have been found to be notoriously difficult to calculate as they require good knowledge of the ionic resonances, which are embedded into the continuum of the next higher charges states.
Aims. In this paper we explain and demonstrate how DR resonance strengths and plasma rate coefficients can be readily computed within the framework of the Jena Atomic Calculator (JAC). In contrast to other available codes, the JAC toolbox supports a much simpler handling and control of different approximations, shell structures and temperature regions, for which doubly excited resonances need to be taken into account.
Methods. A multi-configuration Dirac–Hartree–Fock expansion of all atomic states is generated and applied in order to compute the transition rates (radiative and nonradiative) that contribute to the DR process. For the plasma rate coefficients, moreover, a cascade model has been developed that automatically determines and incorporates all doubly excited configurations of interest for the given plasma temperatures.
Results. To demonstrate the quite flexible use of JAC, we discuss and compare the DR of initially fluorine-like Ni19+ ions with previous measurements and computations. Since it is based on Dirac’s equation, the JAC toolbox is suitable for most ions across the periodic table.
Key words: atomic data / atomic processes / relativistic processes
© S. Fritzsche 2021
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Since the early work by Burgess (1964) and others, the important role of dielectronic recombination (DR) in understanding the dynamics of plasma has been widely known, from low-temperature laboratory plasma and fusion and solar plasma to observations of various astrophysical objects and environments. This electron-ion recombination process determines not only the level population and ionization balance within a plasma, but also its radiative energy loss at different frequencies. In many experiments the DR is often characterized in terms of the position and strength of its individual resonances; however, the DR rate coefficient has been utilized to estimate the plasma density and temperature, and hence the temporal evolution of different plasma environments.
While a few very accurate measurements of DR spectra are known for selected ions (e.g., Schippers et al. 2001; Kieslich et al. 2003; Schuch et al. 2005; Bernhardt et al. 2016), more often than not detailed ab initio calculations are required in order to describe the resonances and plasma rate coefficients for a wide range of ions across the periodic table. Especially, and perhaps apart from few-electron ions with rather simple shell structures, the low-lying DR resonances and strengths are still a challenge for current atomic theory. Here we explain and demonstrate how these resonances and plasma rate coefficients can be readily computed within the framework of the Jena Atomic Calculator (Fritzsche 2019). This toolbox1 supports not only relativistic atomic structure calculations, but also a good number of atomic processes, as well as most atoms and ions across the periodic table. With the present extension of this toolbox we help compute DR resonance strengths and rate coefficients for as-yet-unexplored ions with quite arbitrary shell structures. Moreover, this extension facilitates the combined treatment of DR studies with other processes, such as the radiative recombination or electron-impact processes, and may hence support larger astrophysical surveys and simulations (Evrard et al. 2002; Ferland et al. 2013; Huang et al. 2018; Mendoza et al. 2021).
This work is organized as follows. In Sect. 2, we recall the dielectronic recombination process, along with some basic notations and formulas for the DR resonance strength and rate coefficient. In Sect. 3, emphasis is placed upon the implementation of this process within the framework of JAC. Apart from a brief overview of the JAC toolbox (Fritzsche 2019), here we outline two strategies for simulating the DR spectra and rate coefficients for ions with complex shell structure. These strategies make use of a correlated representation of all low-lying DR resonances in Sect. 3.2 and an approximate treatment of the relevant resonances in terms of cascade computations in Sect. 3.3. The latter strategy, in particular, enables the user to deal with a much larger range of plasma temperatures and associated inner-shell excitation. Section 4 then demonstrates the simple use of these tools for calculating the DR resonance strength and plasma rate coefficients for fluorine-like Ni19+ ions. A comparison is made with previous measurements (Wang et al. 2019) and computations (Gu 2008; Mao et al. 2017), and generally shows good agreement. The simple and flexible use of the JAC toolbox will therefore support the astrophysical community to expand their studies toward other ions and simulations.
2 Dielectronic recombination of multiply charged ions
2.1 Resonance strength and cross sections
The DR of an atomic ion in charge state q+ is described by the two-step process Aq+ + e− → A(q−1)+* → A(q−1)+(*) + ℏ ω, in which an electron is first captured resonantly from the continuum in order to form a doubly excited ion of the next lower charge state, and which subsequently stabilizes under photon emission. For an N-electron target ion in the initial level 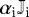 the resonant electron capture then leads to the [(N + 1)-electron] resonance level
the resonant electron capture then leads to the [(N + 1)-electron] resonance level 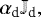 embedded within the continuum of the initial ion, and often with two or more excited electrons. In the second step of the DR process the excited ion in level
embedded within the continuum of the initial ion, and often with two or more excited electrons. In the second step of the DR process the excited ion in level 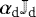 then either decays radiatively by photon emission to some final level
then either decays radiatively by photon emission to some final level 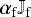 below of the ionization threshold of the ion, or it returns by auto-ionization back to its initial charge stage well before the radiative stabilization occurs. In this notation of the initial, resonance, and final levels,
below of the ionization threshold of the ion, or it returns by auto-ionization back to its initial charge stage well before the radiative stabilization occurs. In this notation of the initial, resonance, and final levels,  here refers to the total angular momentum and parity of the levels and α to all further quantum numbers that are needed for a unique specification of the atomic fine-structure of the ions.
here refers to the total angular momentum and parity of the levels and α to all further quantum numbers that are needed for a unique specification of the atomic fine-structure of the ions.
For a single narrow and non-overlapping DR resonance, the cross section σ(DR) (E ≃ Ed; i →d) is nonzero just near the resonance energy E ≃ Ed of the intermediate resonance level d, and can then be expressed as convolution of the resonance strength S(Ed; i →d) and a normalized (either Lorentzian or Gaussian) line-shape function L (E; d), with ∫ dE L (E; d) = 1. Moreover, if the radiative stabilization results in a well-defined level 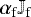 , the DR process is characterized by the partial resonance strength (Dubau & Volonte 1980; Griffin 1989)
, the DR process is characterized by the partial resonance strength (Dubau & Volonte 1980; Griffin 1989)
 (1)
(1)
which can be solely expressed in terms of the Auger and radiative rates of the resonance level d as well as its half-widths Γd. In expression (1), furthermore,kd is the wave number of the incident electron to form d, Aa (d→i) the Auger rate, which describes the electron capture from the initial level 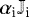 into the doubly excited resonance level
into the doubly excited resonance level 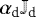 due to the principle of kinetic balance, andAr(d →f) the rate for the radiative stabilization into the state
due to the principle of kinetic balance, andAr(d →f) the rate for the radiative stabilization into the state 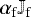 . In the DR spectra, the resonance strength S(i →d →f) refers to the area under the energy-dependent differential DR cross sections and is typically given in units of [cm2 eV].
. In the DR spectra, the resonance strength S(i →d →f) refers to the area under the energy-dependent differential DR cross sections and is typically given in units of [cm2 eV].
Often, as at storage rings, the radiative stabilization of the ions due to the formation of the final level 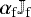 is not observed explicitly and, hence, the individual radiative rates Ar(d →f) in the partial resonance strength (Eq. (1)) need to be replaced by the total radiative rate Ar (d →f) → ∑fAr(d →f) of the doubly excited resonance
is not observed explicitly and, hence, the individual radiative rates Ar(d →f) in the partial resonance strength (Eq. (1)) need to be replaced by the total radiative rate Ar (d →f) → ∑fAr(d →f) of the doubly excited resonance 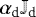 . This gives rise to the total resonance strength
. This gives rise to the total resonance strength
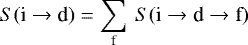
which is appropriate, especially if the energy-dependent DR cross section has a Lorentzian profile
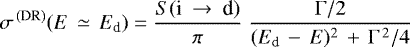
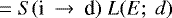
or some similar distribution around the resonance energy E ≃ Ed as well as a natural width less than or comparable to the energy spread of the incident electron beam. In general, this condition is well fulfilled for most Δ n ≥ 1 resonances (i.e., with an excitation of one of the bound electrons from shell ni → nf, and for which the total widths are small in most cases), but the same condition has also been utilized for Δ n = 0 lines if the shape of the individual resonances is not considered in detail.
The partial S(i →d →f) and total resonance strengths S(i →d) are central to the simulation of all dielectronic recombination spectra and processes. They help trace these simulations back to the computation of Auger decay rates Aa(d →i′) of the intermediate resonance 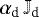 to levels
to levels 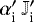 of the initial charge state as well as the Einstein Ar(d →f′) coefficients to levels above and below the ionization threshold. All these rates can be readily calculated within the JAC toolbox. Owing to the energy dependence
of the initial charge state as well as the Einstein Ar(d →f′) coefficients to levels above and below the ionization threshold. All these rates can be readily calculated within the JAC toolbox. Owing to the energy dependence 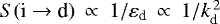 on the energy of the free incident electrons, however, the resonance strength increases quite rapidly toward the threshold of such a dielectronic recombination, and makes this process particularly sensitive to low kinetic energies of the incoming electrons.
on the energy of the free incident electrons, however, the resonance strength increases quite rapidly toward the threshold of such a dielectronic recombination, and makes this process particularly sensitive to low kinetic energies of the incoming electrons.
Close to the threshold, however, the isolated-resonance approach is formally no longer valid and should then be replaced by some unified treatment of the DR and radiative recombination (RR) since the transition amplitude of both processes diverge for εi → 0 (Alber et al. 1984; Nahar et al. 1994). For heavy ions in particular, the interference of DR and RR may result in an asymmetric Fano profile (Knapp et al. 1995; Pindzola et al. 1995; Schippers et al. 2004; Tu et al. 2016). Such a unified treatment usually requires a more advanced mathematical machinery, but does not seriously affect the DR spectra at finite electron energies or in plasma. At electron-beam ion traps, in addition, the radiative stabilization often appears to be angular and polarization dependent, and then requires modifying the formula above for the resonance strength. Both of these refined treatments are beyond the scope of the present work, but could be incorporated into the JAC toolbox if the need should arise.
2.2 Temperature-dependent plasma rate coefficients
In a plasma, the electron-ion recombination is temperature-dependent owing to the Maxwellian distribution of the free electrons that are captured by the ions. For a single ion per unit volume in the initial level 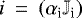 , the DR plasma rate coefficient
, the DR plasma rate coefficient
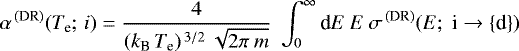
![\begin{equation*}\times\; \exp \left(-\, \frac{E}{k_{\textrm{B}}\, T_{\textrm{e}}} \right)\qquad\qquad\left[{\frac{\textrm{cm}^3}{s}} \right] \,\end{equation*}](/articles/aa/full_html/2021/12/aa41673-21/aa41673-21-eq21.png)
describes the explicit rate to recombine at plasma temperature Te due to its dielectronic recombination with a Maxwell-distributed electron. Since for delta-like DR resonances, the total DR cross section is σ(DR) (E;i →{d}) = ∑d S(i →d) δ (E − εd) = ∑d S(i →d) δ (E − Ed + Ei), the plasma rate coefficient
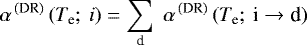
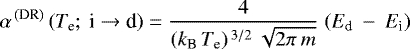
![\begin{equation*}\times\: S (\textrm{i} \to {\textrm{d}})\:\exp \left(-\, \frac{E_{\textrm{d}} - E_{\textrm{i}}}{k_{\textrm{B}}\,T_{\textrm{e}}} \right) \quad \left[{\frac{\textrm{cm}^3}{s}} \right] \,\end{equation*}](/articles/aa/full_html/2021/12/aa41673-21/aa41673-21-eq24.png)
can be expressed as a sum over partial DR rate coefficients α(DR)(Te; i →d), as associated with the electron capture into the resonance level 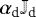 . Here εd = Ed − Ei is the kinetic energy of the initially free electron that help form the resonance. Although the summation over d formally runs over all valences and inner-shell excited resonances of the [(N + 1)-electron] recombined ion, it can be readily truncated due to the temperature-dependent factor
. Here εd = Ed − Ei is the kinetic energy of the initially free electron that help form the resonance. Although the summation over d formally runs over all valences and inner-shell excited resonances of the [(N + 1)-electron] recombined ion, it can be readily truncated due to the temperature-dependent factor 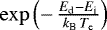 for high-enough electron energies εd (Chen 1986).
for high-enough electron energies εd (Chen 1986).
It is this form of the DR plasma rate coefficient that has been utilized in most computations in order to estimate the rate for the dielectronic recombination of ions in plasma. Although the DR plasma rate coefficient here refers to the low-density limit, this approximation remains valid for most astrophysical plasma as well. Moreover, the Auger rates Aa (d →i) are often much larger than the Einstein coefficients Ar(d →f), which then simplifies the computations of the rates to Ar(d →f) Aa(d →i)∕Γd ≈ Ar(d →f).
Most RR and DR plasma rate coefficients of multiply charged ions are based on (more or less detailed) computations. Although good progress has been made during the past decades, the accurate prediction of DR resonance positions still remains a challenge for atomic theory because of their sensitivity to correlations between the ionic core and because of the excited and captured electrons. Often, the accuracy of calculated DR resonances are better for the Δ n = 0 core excitation as they are less affected by correlations (Fritzsche 2002; Schmidt et al. 2007). In practice, however, even rather small or medium-sized uncertainties in the low-energy DR resonances can lead to quite large discrepancies in the theoretically predicted plasma rate coefficients (Schippers et al. 2004). This emphasizes and calls for the need for alternative implementations of these rate coefficients and for accurate experimental DR rate coefficients in order to extract useful data for astrophysically relevant ions.
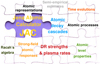 |
Fig. 1 Overview of the JAC toolbox (Fritzsche 2019; see footnote 1) for calculating the level structure, processes, and cascades of atoms and ions, based on Dirac’s equation. This toolbox facilitates a good number of different relativistic computations as briefly shown in this jigsaw puzzle. In this work, JAC has been expanded to model dielectronic capture processes and DR plasma rate coefficients. |
3 Tools and implementation
3.1 Brief overview of JAC
As seen in the last section, accurate calculations of the level structure and decay rates are crucial for predicting the DR resonance spectra and plasma rate coefficients for multiply charged ions. For medium and heavy elements, moreover, a relativistic description of the electronic structure is required to reproduce the experimentally observed resonances and level splitting. Here we make use of and expand the JAC toolbox to perform all the necessary computations and to establish a relativistic code for such DR studies.
The general design of JAC has been described elsewhere (Fritzsche 2019; Fritzsche 2020), and the code can readily be downloaded from the web. This toolbox facilitates atomic structure calculations of different kinds and complexities, and it can be applied without much prior knowledge of the implementation. A primary goal with JAC was to develop a general and easy-to-use toolbox for the atomic physics community that integrates different atomic processes within a single computational framework, and hence ensures good self-consistency of the generated data. For many standard computations, JAC provides a simple interface that is equally accessible for working spectroscopists, theoreticians, and code developers; see Fig. 1 for a short overview of the various features of JAC. This toolbox is based on Julia, a new programming language for scientific computing2, which includes a number of modern attributes, such as dynamic types, optional type annotations, type-specializing, just-in-time compilation of code, dynamic code loading, and garbage collection (Bezanson et al. 2018).
Apart from relativistic calculations of the electronic structure and properties of free atoms and ions, the recent focus of JAC has been on simulations of a large number of atomic processes and cascades in order to analyze atomic behavior within different environments. Here, a central term within the JAC toolbox refers to a function called Atomic.Computation that enables the user to perform atomic calculations with minor input (see also Fig. 3). These Atomic.Computations are based on explicitly specified electron configurations and can provide level energies, the representation of atomic state functions, or selected level properties. They also help evaluate the transition amplitudes and rates for several excitation and auto-ionization processes. In this work, we explain and discuss how this toolbox has been expanded to also support computations of DR spectra and plasma rate coefficients. This especially includes the computation and simulation of dielectronic capture cascades, a crucial stepping stone for computing DR rate coefficients over a wide range of temperatures.
The JAC toolbox is entirely built upon the concept of many-electron transition amplitudes, and makes use of them internally in order to implement the energy shifts, rates, and cross sections for a large number of processes. These transition amplitudes generally combine two atomic bound states of the same or two different charge states, and often also include free electrons from the continuum. They also readily help to express the Auger and radiative rates from the last subsection, and hence to implement the DR resonance strength and plasma rate coefficients. The consequent use of these many-electron amplitudes in the setup of the code distinguishes JAC from most other atomic structure codes that are often based on prior decomposition of these amplitudes into various coefficients and radial integrals, well before any implementation or coding is done. The explicit use of these amplitudes has been found useful also for implementing approximate atomic Green functions (Fritzsche & Surzhykov 2021) as well as a number of atomic cascades (Fritzsche et al. 2021), such as the step-wise decay following inner-shell excitation or the creation of holes by photoexcitation or photoionization; they will enable us also to treat interference phenomena in the future. In this work, we here expand this concept to the formation and stabilization of doubly excited levels and, hence, to the computation of DR plasma rate coefficients for quite general open-shell structures.
3.2 Computation of DR strength and spectra
As outlined above, the partial resonance strength S(i →d →f) in (1) is the key for calculating all DR spectra and rate coefficients. In the isolated-resonance approximation and by applying the principle of detailed balance (Pindzola et al. 1992), this resonance strength is determined by the Auger rate Aa (d →i) to the ground level 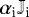 , the Einstein coefficient Ar(d →f) to the final level
, the Einstein coefficient Ar(d →f) to the final level 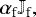 and the widths of the resonance,
and the widths of the resonance, 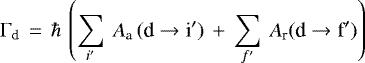 . In atomic structure theory, these rates are readily traced back to the many-electron amplitudes of the electron–photon and electron–electron interaction, respectively. Since these amplitudes are the building blocks of JAC, they can be easily accessed for further data processing. However, a reasonably accurate representation of all atomic levels with E ≲ Ed is required in order to represent a single partial strength, not to mention the summation over all resonances for the calculation of the rate coefficients. The representation of the resonance levels, along with all the associated approximations, make the main differences between the various implementations available and usually require special care.
. In atomic structure theory, these rates are readily traced back to the many-electron amplitudes of the electron–photon and electron–electron interaction, respectively. Since these amplitudes are the building blocks of JAC, they can be easily accessed for further data processing. However, a reasonably accurate representation of all atomic levels with E ≲ Ed is required in order to represent a single partial strength, not to mention the summation over all resonances for the calculation of the rate coefficients. The representation of the resonance levels, along with all the associated approximations, make the main differences between the various implementations available and usually require special care.
Two strategies are followed in this work in order to implement and simulate the partial resonance strength within the JAC toolbox, and to ensure self-consistency of all generated data. These strategies refer to (i) the explicit and well-correlated representation of all atomic levels and (ii) the implementation of a cascade scheme, which includes fewer correlations in the representation of the atomic levels, but supports a much greater flexibility in dealing with high-n and inner-shell excitation of the ions. Both strategies in principle give rise to the DR resonance strength and plasma rate coefficients, though at rather different costs and with different applications in mind. As typical for the JAC toolbox, each of these strategies is built upon a few explicitly designed data structures that help keep the computations feasible.
To describe and deal with the electronic structure of atoms and ions with complex shell structures, JAC is built upon a large number of well-designed data structures. These data structures define the central objects for the transfer of data within the program and its communication with the user. For the correlated computation of the DR resonance strengths, for example, the module Dielectronic provides a number of data structures that are specific to the computation of DR spectra and properties. Two such central data structures are a Dielectronic.Pathway to deal with the information about any individual dielectronic-capture and stabilization path i → d →f as well as aDielectronic.Resonance to comprise the data about the resonance level 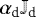 for the capture i → d, which starts from level
for the capture i → d, which starts from level 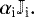 Figure 2 shows the internal definition of these two data structures, though not all the details are explained here. However, as is easily seen from the two last fields of a Pathway, the computation of the Auger and radiative transition amplitudes are just obtained from the corresponding modules AutoIonization and PhotoEmission, respectively.
Figure 2 shows the internal definition of these two data structures, though not all the details are explained here. However, as is easily seen from the two last fields of a Pathway, the computation of the Auger and radiative transition amplitudes are just obtained from the corresponding modules AutoIonization and PhotoEmission, respectively.
For DR resonances reasonably close to the threshold, for instance, the resonance strengths and rate coefficients can be calculated by means of the Atomic.Computation mentioned above if the proper settings are provided by the user. This is analogous to the calculation of most other processes within the JAC toolbox. The lower panel of Fig. 1 displays the internal definition of the Dielectronic.Settings, which facilitates the detailed control of the computations. Apart from the multipoles and gauges, which are to be considered for the radiative stabilization, these settings enable the user to select individual pathways, to shift the electron and photon energies by a constant amount, and to provide a minimum photon energy, below whichall rates are neglected from the computations. The transition operator for the auto-ionization is the Coulomb operator by default, though relativistic corrections due to the Breit interaction can, in principle, be taken into account, and has attracted previous attention for multiple and highly charged ions (Fritzsche et al. 1991; Zimmermann et al. 1997; Zakowicz et al. 2004; Nakamura et al. 2008, Bernhardt et al. 2011).
Most useful calculations of DR spectra critically depend on the simple control and handling of all the radiative and nonradiative decay branches of the resonantly excited ion. In particular, the number of relevant radiative transitions often grows rapidly since the intermediate resonances 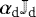 lay within the continuum of the next higher charge state, e.g., above an infinite number of levels from the bound part of the spectrum. Moreover, the need for an efficient computation of the Einstein coefficients Ar (d →f) for all excited ionic levels arises in all those DR studies in which single-electron excitation occurs in high-n shells. This situation especially applies if either resonances with high-n electrons are considered or if a large number of excited levels of the (N +1)-electron ion occur just below the threshold. In many of these cases, however, it is sufficient to just deal with the Δ n ≠ 0 radiative transitions of the electron that is bound stronger to the ionic core. Apart from the large overlap of the radial orbital functions for deeply bound electrons, this ‘propensity rule’ can also be explained by the scaling
lay within the continuum of the next higher charge state, e.g., above an infinite number of levels from the bound part of the spectrum. Moreover, the need for an efficient computation of the Einstein coefficients Ar (d →f) for all excited ionic levels arises in all those DR studies in which single-electron excitation occurs in high-n shells. This situation especially applies if either resonances with high-n electrons are considered or if a large number of excited levels of the (N +1)-electron ion occur just below the threshold. In many of these cases, however, it is sufficient to just deal with the Δ n ≠ 0 radiative transitions of the electron that is bound stronger to the ionic core. Apart from the large overlap of the radial orbital functions for deeply bound electrons, this ‘propensity rule’ can also be explained by the scaling 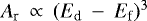 of the Einstein coefficients with the third power of the transition energies, and which is largest for electrons in low-n shells. For the same reason, it is usually enough to include only a subset of low-lying final levels
of the Einstein coefficients with the third power of the transition energies, and which is largest for electrons in low-n shells. For the same reason, it is usually enough to include only a subset of low-lying final levels 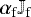 in order to estimate a reasonable DR strength or branching fraction. All these arguments can be taken into account for both the fully correlated and the cascade computations within JAC, though at different levels of control.
in order to estimate a reasonable DR strength or branching fraction. All these arguments can be taken into account for both the fully correlated and the cascade computations within JAC, though at different levels of control.
Once a dielectronic recombination computation has been specified in terms of an Atomic.Computation above, it can be readily carried out by typing3
perform(comp::Atomic.Computation)
as for all other properties and processes within the JAC toolbox. An example of such a computation is discussed in Sect. 4.1. In JAC, both the partial S(i →d →f) and total resonance strengths S(i →d) are then calculated and tabulated by default for all selected pathways from the initial-, intermediate-, and final-state configurations of the DR process, while further properties are only printed if proper control flags were set earlier.
 |
Fig. 2 Internal definition of the data structures Dielectronic.Pathway (upper panel) to select and specify a pathway i → d →f for the capture and subsequent stabilization as well as Dielectronic.Resonance (middle panel) to deal with individual resonances. Moreover, the data structure Dielectronic.Settings (lower panel) enables the user to control the physical model, size, and a few semi-empirical adaptations of the DR computations. |
3.3 Dielectronic recombination cascades. Simulation of plasma rate coefficients
Correlated calculations of DR resonance strengths and rate coefficients are, more often than not, restricted to just the low-lying part of the spectrum near the threshold as they prompt the user to specify explicitly all the configurations that contribute to the representation of the level structure. This quickly becomes cumbersome for resonances with electrons in high-n shells or if plasma rate coefficients need to be calculated, in which case a dielectronic capture cascade is a useful alternative. Such a cascade starts from the capture of an electron into various nℓ shells, and then models the subsequent electron and photon emission as a step-wise decay of the ion toward its ground configuration. The calculation of other cascade schemes has already been part of the JAC toolbox and has been explained in detail elsewhere (Fritzsche et al. 2021). Here, we therefore restrict ourselves to a few central features of such dielectronic cascade computations and just discuss how the DR plasma rate coefficients can be readily extracted from these computations.
To model the initial excitation and capture of electrons, together with the subsequent electron and photon emission of all doubly excited levels, JAC clearly distinguishes between so-called cascade computations and cascade simulations. While a cascade computation generates all the necessary (i.e., radiative and nonradiative) transition data (e.g., amplitudes, rates), the subsequent simulation serves to combine these data and to extract the desired information. Usually, the prior cascade computations cause the major effort as they require a proper representation of all the atomic levels involved. To this end, moreover, a hierarchy of cascade approaches has been defined within the JAC toolbox in order to keep the computations overall feasible. These approaches mainly differ by the quantum-mechanical representation of the level structures, and thus enables the user to control the extent to which inter-electronic correlations are taken into account. The representation of the atomic levels is based on different classes of electron excitation with regard to a set of reference configurations as well as a multi-configuration Dirac–Hartree–Fock expansion of the associated fine-structure levels. In these cascade computations, however, no attempt is internally made in order to decide that all relevant data are indeed computed nor that all computed data are relevant for the subsequent simulations. The control of these cascade computations therefore requires some insight of the user into the DR process that cannot be fully formalized in advance. In Sect. 4.2, we show how such cascade computations can be performed for initially fluorine-like Ni19+ ions, along with the succeeding cascade simulations.
While the cascade computations are performed independently of the data to be derived about the recombination of the atoms or ions, the subsequent cascade simulations are done for one or a few well-defined properties, and often in close contact with the observations and/or experiment. For plasma rate coefficients, for instance, the temperaturedependence mainly arises from different combinations of the partial resonance strengths and can be easily estimated, if a sufficiently large number of doubly excited levels are included before in the cascade computations. These cascade simulations are much faster than the prior computations, and often quite similar simulations are performed repeatedly for different temperatures, initial levels, and others, though based on the same transition data.
3.4 Requirements for the calculation of plasma rate coefficients
Reasonably accurate predictions of DR plasma rate coefficients remain a challenge for atomic theory. Serious difficulties often arise from (i) the proper representation of all levels involved; (ii) the crucial, though not obvious, role of different resonances for certain plasma temperature; and (iii) the quite large number of resonances that may contribute to the plasma rate coefficient. For ions of medium andheavy elements, moreover, (iv) the relevance of the auto-ionizing and radiative transitions can no longer be derived from just term- or configuration-averaged transition rates, but typically requires more detailed treatment of all fine-structure transitions. These difficulties have made accurate calculations almost an art, even for ions with otherwise simple shell structures. With the present expansion of the JAC toolbox, we aim to overcome these difficulties and to account for the DR in plasma, from simple estimates to more sophisticated computations of the DR plasma rate coefficients.
In the DR resonance strength in Eq. (1), the nonradiative capture is described by first-order perturbation theory. Therefore, the standard plasma rate coefficients, as discussed in this work, are first of all suitable for low-density plasma. This simple parameterization of the ion-electron recombination will need to be modified if additional external (micro-)fields occur, or if the ions are also collisionally excited in a plasma (Krylstedt et al. 1990; Kaur et al. 2018).
In dynamic plasma, moreover, the ions may also recombine from meta-stable states, and this requires incorporating long-lived levels into the modeling. In such a dynamic plasma, both the electron temperature Te and density ne may indeed change within the lifetime of the meta-stable levels of the plasma ions. Furthermore, ions in these meta-stable levels will not always decay down to their ground level, but can be collisionally excited and/or ionized before. Obviously, all these finite-density effects will make a detailed treatment of the plasma dynamics not only much more sophisticated, but will require a flexible toolbox, such as JAC for its modeling.
To support such studies and forthcoming observations in astrophysics and plasma diagnostics, current requirements include the following (see Badnell et al. 2003):
- (i)
the computation of rate coefficients for different stable and meta-stable initial levels;
- (ii)
partial rate coefficients for certain groups of final levels, if the recombined ions not all return to their ionic ground-state level;
- (iii)
information on the Auger rates to all levels i′, into which the re-combined ion can re-autoionize after the electron capture.
In practice, however, and more importantly for these requirements, is a fast and reliable access to the DR resonance strengths and plasma rate coefficients for several, if not many, ions across the periodic table.
4 Dielectronic recombination of fluorine-like Ni19+ ions
The dielectronic recombination and plasma rate coefficients of fluorine-like Ni19+ ions due to Δ n = 0 core excitation have attracted recurrent interest in the literature. For instance, the radiative emission from these ions has been identified bydifferent space-based observatories, such as the Solar and Heliospheric Observatory (SOHO, NASA; Del Zanna & Mason 2018) or the XMM-Newton (ESA; Steenbrugge et al. 2003) space missions. A detailed understanding of the associated DR spectra is therefore crucial also for deducing the charge-state distributions within different plasma environments (Beiersdorfer 2003).
For initially fluorine-like Ni19+ ions, the low-lying Δ n = 0 DR can be summarized as (Wang et al. 2019)
![\begin{equation*}\mathrm{Ni}^{19+}\: [\textrm{2s}^2\, 5\textrm{p}^5\;\: ^2\textrm{P}_{3/2}] \:+\: e^- \end{equation*}](/articles/aa/full_html/2021/12/aa41673-21/aa41673-21-eq35.png)
![\begin{equation*}\quad \Longrightarrow\quad \left\{\begin{array}{l} \mathrm{Ni}^{18+}\: [\textrm{2s}^2\, \textrm{2\textrm{p}}^5\;\: ^2\textrm{P}_{1/2}\;(17.8486~\mathrm{eV})]\; (17\ell + 18\ell + ...) \\\mathrm{Ni}^{18+}\: [\textrm{2s}\, \textrm{2p}^6\;\: ^2\textrm{S}_{1/2}\;(149.054~\mathrm{eV})]\; (6\ell + 7\ell + ...)\end{array} \right. \end{equation*}](/articles/aa/full_html/2021/12/aa41673-21/aa41673-21-eq36.png)
![\begin{equation*}\quad \Longrightarrow \;\;\ldots\;\;\;\Longrightarrow\; \;\; \mathrm{Ni}^{18+} [\textrm{2s}^2\, \textrm{2p}^6\;\: ^1\textrm{S}_{0}] \:+\: \gamma\primes \,.\end{equation*}](/articles/aa/full_html/2021/12/aa41673-21/aa41673-21-eq37.png)
For these ions, and by applying a merged-beam technique at the cooler storage ring (CSRm) in Lanzhou, Wang et al. (2019) measured with high precision the DR spectrum and resonance strengths for free-electron energies in the range 0–160 eV (i.e., for all the Δ n = 0 excitation of the fluorine-like core). From the individual resonance strengths the DR plasma rate coefficients were then derived for temperatures between 103 –108 K and compared with simulations and data from the literature. These temperatures comprise the formation of Ni19+ ions in bothphotoionized and collisionally ionized plasma. In practice, therefore, the DR of fluorine-like Ni19+ ions provides a good testbed for the implementation and computations in this work.
 |
Fig. 3 Input to the JAC toolbox for the Atomic.Computation of the partial and total DR resonance strengths following the formation of the 2s2p6 (6s + 6p + 6d + ... + 7d) levels and their stabilization via the dominant 2s 2p6 nℓ →2s2 2p5 nℓ radiative transitions of the ionic core, leaving the 6ℓ or 7ℓ electrons as a spectator. |
4.1 DR resonance energies and strength
The position and strength of the low-lying resonances are known to be very sensitive to electron-electron correlations, and hence require a quite detailed representation of all atomic levels involved. For this low-lying part of the DR spectrum we therefore perform a correlated Atomic.Computation, as described in Sect. 3.2 above. We focus here on the 2s 2p6 2S1∕2 (6ℓ + 7ℓ) resonances, but consider two computational models A and B of different size. In model A, we just consider the capture into the 2s 2p6 (6ℓ + 7ℓ), ℓ ≤ d resonances and the major 2s2p6 nℓ →2s22p5 nℓ (n = 6, 7) stabilizationof the ionic core.
Figure 3 displays the input for this computation within the JAC toolbox. Apart from the specification of the units, a name (string) as well as the radial grid, this input first of all explains how the various lists of configurations are generated. This refers to both the list of shells and the nonrelativistic configurations to be considered as a whole. As readily seen from Fig. 3, we include excitation from 2s to 2p (fromShells, toShells) and the capture into 6s + 6p + 6d + ... + 7d (ℓ ≤ d) to form the low-lying resonances. With these specifications, we first generate all configurations that can be formed by electron capture, starting from the 1s22s22p5 ground configuration. The list aconfs in Fig. 3 therefore comprises the configurations 1s22s2p6 (6s + 6p + 6d + 7s + 7p + 7d), while the configurations 1s22s22p5 (6s + 6p + 6d + 7s + 7p + 7d) occur in bconfs, and it becomes obvious how this number rapidly increases if we include shells with n > 7 or ℓ > d. For the radiative stabilization, these configuration are then merged with those for a 2s 2p6 →2s2 2p5 core stabilization (cf. intoShells).
These calls can all be made line-wise to immediately see and check the consistency of the given specifications. Here, we do not display all the output explicitly. However, the lists of initial-, intermediate-, and final-state levels decide the number of correlations within the computations, and also that all major decay channels are indeed taken into account. These lists of configurations are then provided to the Atomic.Computation, along with the nuclear model (Z = 28) and the proper settings to calculate DR strength and rates. In Fig. 3, we restrict the stabilization to just electric-dipole (E1) transitions and request a shift of all electron energies by − 2.7 eV in order to reproduce the measured low-lying resonances. In addition, we only consider the DR resonance strengths for the 1s22s22p5 2P3∕2 ground level by selecting all pathways (i, n, f) that starts from level i = 1, and where n = f = 0 refer to all available levels of the intermediate and final-state multiplets. Further settings can be specified, but need not be discussed here (lower panel of Fig. 2). Once the computations are perform ed, the partial and total resonance strengths are printed by default for all selected pathways. On request (calcRateAlpha=true), moreover, the plasma rate coefficients can be calculated for all intermediate resonances, but are usually of limited value because of the missing intermediate levels at sufficiently high electron energies for such correlated computations.
The computations in Fig. 3 refer to model A in Table 1, which displays the DR resonance energies Ed and total strengths S(i →d) for the low-lying 2s 2p6 2S1∕2 (6ℓ + 7ℓ) resonances. Quite similar computations have also been performed in model B, but by including the orbital angular momenta ℓ ≤ i as well as the radiative stabilizationinto the 2s2 2p5 (6ℓ + 7ℓ) + 2s 2p6 (3ℓ′ + 4ℓ′), ℓ ≤ i, ℓ′ ≤ f configurations in addition to those from model A. Apart from further high-lying excitation, model B therefore represents a quite well-correlated computation. These computations include the configuration mixing among all levels that can be formed with the capture and decay shells (i.e., the intoShells and toShells in the example in Fig. 3). In practice, however, the number of configurations (and levels) increases very rapidly and makes further restrictions necessary, especially if two or more open shells already occur in the ionic core. The incorporation of further correlations may then require the distinction of different symmetry blocks JP in the treatment of the intermediate- and final-state multiplets, as well as a properly adopted combination of the underlying amplitudes and rates, a feature that has not yet been implemented in JAC.
DR resonance energies Ed and strength Sd for the low-lying 2s2p6 2S1∕2 (6ℓ + 7ℓ) resonances.
4.2 Plasma rate coefficients for fluorine-like Ni19+ ions
Dielectronic recombination plasma rate coefficients are required in order to interpret observations in astrophysics and plasma diagnostics. Usually, a temperature-dependent Maxwellian distribution is assumed for the free electrons in the plasma, and this requires including all resonances up to 5–10 times the mean free-electron energy in the plasma to not accidentally omit relevant contributions from high-lying resonances. For most plasma temperatures, this demand rapidly requests large-scale calculations,and often the incorporation of both valence and inner-shell (core) excitations into the list of doubly excited levels.
For these high-lying resonances, a correlated treatment of the DR resonance strengths and plasma rate coefficients appear neither feasible nor desirable for most applications. Apart from the sheer size of the computations, the understanding and interpretation of individual contributions gets quickly lost as the representation of the intermediate resonances is distributed among too many configurations. A cascade-type computation is suggested for calculating plasma rate coefficients, in which the nonradiative and radiative transition rates are first compiled among all relevant configurations, and these rates are combined afterward in order to derive (or simulate) the rate coefficients in a subsequent step. In such a cascade model the relevant configurations are treated independently or are combined to moderate groups of configurations by using physical insight into the strong-mixing configurations. Various quite simple rules can be established internally to generate the valence and inner-shell (core) configurations. For example, the energetically allowed shells of the captured electron can be easily estimated for any number of core excitation, if constructed with regard to the reference configuration. Such a cascade model is analogous to the treatment of other cascade schemes in the JAC toolbox, and directly leads us to a dielectronic cascade scheme. As outlined above, this approach also suggests clearly distinguishing between the cascade computations to generate all the necessary transition data and the subsequent simulations for extracting the desired rate coefficients.
For fluorine-like Ni19+ ions, our example above, Fig. 4 displays the input for the necessary Cascade.Computation (upper panel) and the Cascade.Simulation (lower panel). As before, we first need to specify the allowed shells for the excitation of the ionic core (fromShells, toShells), for the capture of the initially free electrons (intoShells), and for their radiative stabilization (decayShells). From these shell lists all the possible configurations are generated automatically and their mean energies compared with regard to a maximum excitation energy of the resonances that is to be considered. In Fig. 4, we include all the resonances up to 10.0 hartree as well as single excitations of core electrons with regard to the initial reference configuration. A more detailed explanation of all input parameters can be obtained from: ? Cascade.DielectronicCaptureScheme.
The cascade computations can be further controlled by choosing a proper cascade approach, which is currently based on single configurations (Cascade.AverageSCA). In this approach, each single configuration forms an individual multiplet block for which orbitals are generated independently by using a Dirac–Fock–Slater potential. The configuration mixing is included for each block, based on the Dirac-Coulomb Hamiltonian, H(DC), and all requested multipoles are considered for the stabilization. The detailed design and interplay in JAC of the currently available cascade schemes and approaches have been explained recently (Fritzsche et al. 2021), and further approaches will likely be considered in the future. While the present cascade computations just take ~ 1 h at a standard desktop, the complexity of such calculations increases very rapidly, if high electron temperatures (which may cause double-valence and inner-shell excitation) or ions with a complex shell structure need to be considered. Further work is likely required in order to accelerate, and perhaps parallelize, these computations, while the given description and implementation of the cascade computations can be applied rather generally.
For the subsequent cascade simulations in the lower panel of Fig. 4, we specify DrRateCoefficients(..) as the property of interest here along with the initial level number of the ground level, an energy shift of all resonances with regard to the ground configuration, and the temperatures of the plasma. These simulations are fast when compared with the corresponding computations, and simply return the plasma rate coefficients for the given temperatures (and transition data). Of course, analogous simulations could be performed for other temperatures of the plasma or for deriving the photon intensity distribution that arises from the radiative stabilization. However, care has to be taken that all relevant transition data (levels, energies, rates) are indeed available from the prior computations.
Figure 5 displays the plasma rate coefficients for the fluorine-like Ni19+ ions. Obviously, our quite simple cascade simulations agree reasonably well with previous studies in the temperature region T = 104 − 5 × 106 K, while some larger discrepancies occur for T ≤ 104 K and at high temperatures. At low temperatures, the plasma rate coefficient is strongly affected by the correct position of the low-lying resonances, and these are less accurate in cascade computations, despite an overall shift of all resonance energies. At high plasma temperatures, T ≳ 5 × 106 K, a large number of high-lying resonances become important, and then likely require including double-valence and core-shell excitation from 2s, as in the work by Zatsarinny et al. (2006). Despite the present limitations, however, the simplicity and straightforward use of such dielectronic cascade computations and simulations may indeed facilitate studies toward the DR of other ions or temperature regions.
Apart from the total DR plasma rate coefficients in Fig. 5, quite different dependencies have been analyzed in the literature in order to explore the relevant contributions to these rate coefficients. Such dependencies include, for example, the contribution to α(DR) (Te; i; n) for an ion, initially in level 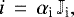 but for just one series of the doubly excited configurations, such as 2s2p6 nℓ or 2s22p5 nℓ, and as a function of the valence shell n. Here it is possible to either fix the temperature Te and display curves for different partial waves κ = κ (ℓ) or to sum over κ and display curves for different temperatures. Moreover, curves for different temperatures can be displayed quite readily for a group of selected intermediate levels or configurations in order to distinguish the contribution due to the capture into different high-n shells. Finally, comparison of the total DR plasma rate coefficients can be made for different classes of inner-shell excitation. Although none of these features has yet been implemented into the JAC toolbox, this can be done quite readily if the need arises from the user’s side.
but for just one series of the doubly excited configurations, such as 2s2p6 nℓ or 2s22p5 nℓ, and as a function of the valence shell n. Here it is possible to either fix the temperature Te and display curves for different partial waves κ = κ (ℓ) or to sum over κ and display curves for different temperatures. Moreover, curves for different temperatures can be displayed quite readily for a group of selected intermediate levels or configurations in order to distinguish the contribution due to the capture into different high-n shells. Finally, comparison of the total DR plasma rate coefficients can be made for different classes of inner-shell excitation. Although none of these features has yet been implemented into the JAC toolbox, this can be done quite readily if the need arises from the user’s side.
 |
Fig. 4 Input to the JAC toolbox for the cascade computation (upper panel) and simulation (lower panel) of DR plasma rate coefficients for fluorine-like N19+ ions. Here, rate coefficients are calculated for plasma temperatures Te ≲ 108 K, and by including 2s →2s, 2p valence-shellexcitation with electron capture into high-nℓ shells (n = 6..20, ℓ ≤ h) and by including the radiative stabilization into 2ℓ, 3ℓ, and 4ℓ (ℓ ≤ f) shells. |
 |
Fig. 5 Plasma rate coefficients for initially fluorine-like Ni19+ ions. The present computations (blue line) are compared with experimental data (red line; Wang et al. 2019) and with previous computations from the same work (red line), and from Gu (2003; violet line) and Zatsarinny et al. (2006, brown line). See text for further discussion. |
5 Conclusions
Based on the JAC toolbox, in this paper we explained and discussed how the DR of multiply charged ions can be computed quite readily. Emphasis was placed on the partial or total strength of resonances near the threshold and on estimating the plasma rate coefficients over a wide range of temperatures. In particular, two strategies were implemented in JAC in order to support (i) an explicit and well-correlated representation of the low-lying resonances and (ii) a dielectronic cascade approach. This latter approach takes into account fewer electron-electron correlations, but allows a greater flexibility in selecting and dealing with high-n and/or inner-shell excitation of ions.
In addition to the DR, the JAC toolbox was developed from the start for atoms and ions with arbitrary shell structures. As an example, we discussed and computed the DR of initially fluorine-like Ni19+ ions, along with previous measurements and computations. Based on Dirac’s equation, the JAC toolbox is suitable for most atoms and ions from the periodic table in order to compute energy shifts, rates, and cross sections for a good number of atomic processes and experimental scenarios (Fritzsche 2012, 2019). This makes JAC an excellent tool for analyzing and estimating different atomic processes as they occur in the design and realization of measurements. Moreover, this toolbox also helps analyze atomic line energies and decay rates under different plasma environments (Deprince et al. 2019, 2020). Finally, the present extension of JAC will facilitate a combined, and perhaps unified, treatment of DR studies with other processes, such as the radiative recombination or electron-impact processes, and hence may support larger surveys and improved astrophysical simulations in the future.
Acknowledgements
I would like to thank Stefan Schippers for the helpful discussions.
References
- Alber, G., Cooper, J., & Rau A. R. P. 1984, Phys. Rev., A30, 2845 (R) [NASA ADS] [CrossRef] [Google Scholar]
- Badnell, N. R., O’Mullane, M. G., Summers, H. P., et al. 2003, A&A, 406, 1151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beerwerth, R., Buhr, T., Perry-Sassmannshausen A., et al. 2019, ApJ, 887, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Beiersdorfer, P. 2003, ARA&A, 41, 343 [NASA ADS] [CrossRef] [Google Scholar]
- Bernhardt, D., Brandau, C., Harman, Z., et al. 2011, Phys. Rev., A83, 020701(R) [NASA ADS] [CrossRef] [Google Scholar]
- Bernhardt, D., Becker, A., Brandau, C., et al. 2016, J. Phys., B49, 074004 [NASA ADS] [Google Scholar]
- Bezanson, J., Chen, J., Chung, B., et al. 2018, Proc. ACM Progr. Lang., 2, 120 [Google Scholar]
- Burgess, A. 1964, ApJ, 139, 776 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, M. H. 1986, Phys. Rev., A34, 1073 [NASA ADS] [Google Scholar]
- Del Zanna, G., & Mason, H.E. 2018, Living Rev. Sol. Phys., 15, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Deprince, J., Bautista, M. A., Fritzsche, S., et al. 2019, A&A, 624, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deprince, J., Bautista, M. A., Fritzsche, S., et al. 2020, A&A, 635, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dubau, & J., Volonte, S. 1980, Rep. Prog. Phys., 43, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Evrard, A. E., MacFarland, T. J., Couchman, H. M. P., et al. 2002, ApJ, 573, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Ferland, G. J., Kisielius, R., Keenan, F. P., et al. 2013, ApJ, 767, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Fritzsche, S. 2002, Phys. Scr., T100, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Fritzsche, S. 2012, Comp. Phys. Commun., 183, 1525 [NASA ADS] [CrossRef] [Google Scholar]
- Fritzsche, S. 2019 Comp. Phys. Commun., 240, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Fritzsche, S. 2020, JAC: User Guide, Compendium & Theoretical Background, unpublished, https://github.com/OpenJAC/JAC.jl (accessed: 10.01.2021). [Google Scholar]
- Fritzsche, S., & Surzhykov, A. 2021, Molecules, 26, 2660 [Google Scholar]
- Fritzsche, S., Zschornack, G., Musiol, G., & Soff, G. 1991, Phys. Rev., A44, 388 [NASA ADS] [CrossRef] [Google Scholar]
- Fritzsche, S., Fricke, B., & Sepp, W.-D. 1992, Phys. Rev. A, 45, 1465 [NASA ADS] [CrossRef] [Google Scholar]
- Fritzsche, S., Palmeri, P., & Schippers, S. 2021, Symmetry, 13, 520 [NASA ADS] [CrossRef] [Google Scholar]
- Grant, I. P. Relativistic Quantum Theory of Atoms and Molecules: Theory and Computation (Springer), 2007 [CrossRef] [Google Scholar]
- Griffin, D. C. 1989, Phys. Scr., T28, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Gu, M. F. 2003, ApJ, 590, 1131 [NASA ADS] [CrossRef] [Google Scholar]
- Gu, M. F. 2008, Can. J. Phys., 86, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, Z. K, Wen, W. Q., Xu, X., et al. 2008, ApJ, 235, 2 [NASA ADS] [Google Scholar]
- Kaur, J., Gorczyca, T. W., & Badnell, N. R. 2018, A&A, 610, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kieslich, S., Böhm, S., Brandau, C., et al. 2003, Nucl. Instr. Meth., 205, 99 [Google Scholar]
- Knapp, D. A., Beiersdorfer, P., Chen, M. H., et al. 1995, Phys. Rev. Lett., 74, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Krylstedt, P., Pindzola, M. S., & Badnell, N. R. 1990, Phys. Rev., A41, 2506 [NASA ADS] [CrossRef] [Google Scholar]
- Mao, J., Kaastra, J., & Badnell, N. R. 2017, A&A, 599, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mendoza, C., Bautista, M. A., Deprince, J., et al. 2021, Atoms, 9, 12 [CrossRef] [Google Scholar]
- Nahar, S. N., & Pradhan, A. K. 1994, Phys. Rev., A49, 1816 [NASA ADS] [CrossRef] [Google Scholar]
- Nakamura, N., Kavanagh, A. P., Watanabe, H., et al. 2008, Phys. Rev. Lett., 100, 073203 [NASA ADS] [CrossRef] [Google Scholar]
- Pindzola, M. S., Badnell, N. R., & Griffin, D. C. 1992, Phys. Rev., A46, 5725 [NASA ADS] [CrossRef] [Google Scholar]
- Pindzola, M. S., Robicheaux, F. J., Badnell, N. R., et al. 1995, Phys. Rev., A52, 420 [NASA ADS] [CrossRef] [Google Scholar]
- Schippers, S., Müller, A., & Gwinner, G. 2001, ApJ, 555, 1027 [NASA ADS] [CrossRef] [Google Scholar]
- Schippers, S., Schnell, M., Brandau, C., et al. 2004, A&A, 421, 1185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schippers, S., Beerwerth, R., Abrok, L., et al. 2016 Phys. Rev., A94, 041401(R) [NASA ADS] [CrossRef] [Google Scholar]
- Schippers, S., Martins, M., Beerwerth, R., et al. 2017, ApJ, 849, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, E. W., Bernhardt, D., Müller, A., et al. 2007, Phys. Rev., A76, 032717 [NASA ADS] [CrossRef] [Google Scholar]
- Schuch, R., Lindroth, E., Madzunkov, S., et al. 2005, Phys. Re. Lett., 95, 183003 [CrossRef] [Google Scholar]
- Steenbrugge, K. C., Kaastra, J. S., de Vries, C. P, & Edelson, R. 2003, A&A, 402, 477 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tu, B., Xiao, J., Shen, Y., et al. 2016, Phys. Plasma, 23, 053301 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, S.-X., Huang, Z.-K., Wen, W.-Q., et al. 2019, A&A, 627, A171 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zakowicz, S., Scheid, W., & Grün, N. 2004, J. Phys., B37, 131 [NASA ADS] [Google Scholar]
- Zatsarinny, O., Gorcyca, T., Fu, J., et al. 2006, A&A, 447, 379 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zimmermann, M., Grün, N., & Scheid, W. 1997, J. Phys., B30, 5259 [NASA ADS] [Google Scholar]
See https://github.com/OpenJAC/JAC.jl (accessed: 10.09.2021).
See https://docs.julialang.org/ (accessed: 10.01.2021).
All Tables
DR resonance energies Ed and strength Sd for the low-lying 2s2p6 2S1∕2 (6ℓ + 7ℓ) resonances.
All Figures
 |
Fig. 1 Overview of the JAC toolbox (Fritzsche 2019; see footnote 1) for calculating the level structure, processes, and cascades of atoms and ions, based on Dirac’s equation. This toolbox facilitates a good number of different relativistic computations as briefly shown in this jigsaw puzzle. In this work, JAC has been expanded to model dielectronic capture processes and DR plasma rate coefficients. |
| In the text | |
 |
Fig. 2 Internal definition of the data structures Dielectronic.Pathway (upper panel) to select and specify a pathway i → d →f for the capture and subsequent stabilization as well as Dielectronic.Resonance (middle panel) to deal with individual resonances. Moreover, the data structure Dielectronic.Settings (lower panel) enables the user to control the physical model, size, and a few semi-empirical adaptations of the DR computations. |
| In the text | |
 |
Fig. 3 Input to the JAC toolbox for the Atomic.Computation of the partial and total DR resonance strengths following the formation of the 2s2p6 (6s + 6p + 6d + ... + 7d) levels and their stabilization via the dominant 2s 2p6 nℓ →2s2 2p5 nℓ radiative transitions of the ionic core, leaving the 6ℓ or 7ℓ electrons as a spectator. |
| In the text | |
 |
Fig. 4 Input to the JAC toolbox for the cascade computation (upper panel) and simulation (lower panel) of DR plasma rate coefficients for fluorine-like N19+ ions. Here, rate coefficients are calculated for plasma temperatures Te ≲ 108 K, and by including 2s →2s, 2p valence-shellexcitation with electron capture into high-nℓ shells (n = 6..20, ℓ ≤ h) and by including the radiative stabilization into 2ℓ, 3ℓ, and 4ℓ (ℓ ≤ f) shells. |
| In the text | |
 |
Fig. 5 Plasma rate coefficients for initially fluorine-like Ni19+ ions. The present computations (blue line) are compared with experimental data (red line; Wang et al. 2019) and with previous computations from the same work (red line), and from Gu (2003; violet line) and Zatsarinny et al. (2006, brown line). See text for further discussion. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


