EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 656 (December 2021) A&A, 656 (2021) A27 Full HTML
Issue
A&A
Volume 656, December 2021
Solar Orbiter First Results (Cruise Phase)
Article Number A27
Number of page(s) 8
Section The Sun and the Heliosphere
DOI https://doi.org/10.1051/0004-6361/202140949
Published online 14 December 2021

© ESO 2021

1. Introduction

In the context of the Earth’s magnetosphere, flux ropes (i.e., helical magnetic field structures with a central core field) have long been established as a common feature of current sheets both at the magnetopause (Russell & Elphic 1978; Rijnbeek et al. 1984) and in the magnetotail (Hones 1977; Baker et al. 1996), and have been observed at a variety of scales (Fermo et al. 2011). The primary mechanism for the formation of flux ropes in current sheets is magnetic reconnection; multiple X-line reconnection will naturally form flux ropes (or O-lines and islands in the case that the reconnection is anti-parallel), and secondary instabilities near an X-line can also form small-scale flux ropes (Slavin et al. 2003; Eastwood et al. 2005, 2016). The production of flux ropes is related to time-dependent reconnection more generally, and therefore provides insight into the general nature of reconnection-related instabilities which may also lead to other fluctuations and turbulence (Drake et al. 2006; Daughton et al. 2011; Innocenti et al. 2015). Observations of flux ropes at other planets are used as a standard tracer of the reconnection process, often in the absence of comprehensive plasma measurements (e.g., Brain et al. 2010; Jackman et al. 2014; Vogt et al. 2014; DiBraccio et al. 2015). Furthermore, flux ropes have also been cited as sites for particle acceleration (Drake et al. 2006), provoking the development of a variety of particle acceleration models both in magnetospheric and heliospheric contexts (Zank et al. 2014; Khabarova et al. 2015; Wang et al. 2016; Khabarova et al. 2016; Roux et al. 2019; Zhao et al. 2019).

Flux ropes are also observed in the solar wind, and whilst it is generally understood that large-scale flux ropes associated with coronal mass ejections and magnetic clouds are formed at the Sun directly, small-scale flux ropes also exist which may be generated locally by reconnection at solar wind current sheets (Moldwin et al. 1995, 2000; Zhao et al. 2020). Unambiguous observations of solar wind reconnection were subsequently reported in the mid-2000s (Gosling et al. 2005), and more recently evidence has been presented showing a direct link to flux rope formation (Teh et al. 2009; Feng & Wu 2009; Eriksson et al. 2014, 2015; Enžl et al. 2017). In particular, Eriksson et al. (2014) directly showed the existence of a relatively small-scale elongated island (4 Earth radius (Re) × 43 Re) at a reconnecting solar wind current sheet produced by multiple X-line reconnection. In separate studies, the existence of islands and multiple X-line reconnection was deduced from tripolar perturbations to the reconnection guide field (Eriksson et al. 2015), and analysis of a solar wind reconnection exhaust exhibiting complex structure (Enžl et al. 2017).

Observations of solar wind reconnection are made as spacecraft pass through the exhausts that are convected anti-sunward in the solar wind flow. In contrast to the Earth’s magnetosphere, reconnection exhausts can become very large, growing to 100 s or even 1000 s of Re in size (Phan et al. 2006; Gosling et al. 2007; Lavraud et al. 2009; Gosling 2012; Tilquin et al. 2020). Observations of solar wind reconnection exhausts are therefore typically made far from the X-line (Phan et al. 2009, 2020; Enžl et al. 2014; Mistry et al. 2017). Consequently, questions still remain about the mechanisms by which solar wind reconnection can form flux ropes, the frequency with which they occur, and their size distribution down to small scales. In particular, the extent to which they may survive over long distances from their X-line, or instead merge with one another, potentially resulting in more laminar exhausts with less magnetic structure, is not well understood.

Solar Orbiter (Müller et al. 2020), which launched on 10 February 2020 04:03 UT, provides a new opportunity to examine the properties of solar wind current sheets and flux ropes. We present new observations from the Solar Orbiter magnetometer (MAG; Horbury et al. 2020) of an ion-scale magnetic flux rope confined within a bifurcated current sheet in the solar wind. At the time of observation, Solar Orbiter was still relatively close to Earth, and large-scale context is provided by Wind at the Sun-Earth L1 Lagrange point. The Solar Orbiter observations are presented and analysed in Sect. 2, the Wind data and the large-scale context is examined in Sect. 3, the implications of the data are discussed in Sect. 4, and conclusions are presented in Sect. 5.

2. Solar Orbiter observations

2.1. Event overview

The observations presented in this paper were obtained on 4 March 2020 when MAG was operating in burst mode (128 vectors/s). This was during the early commissioning phase and relevant data from other instruments (particularly the calibrated d.c. electric field and measurements of the solar wind plasma) were not available. On this date Solar Orbiter was located at 0.98 au from the Sun, at a Heliographic Inertial (HGI) latitude of −6.6° and HGI longitude of 83°. Earth was located at 0.99 au, −7.2° latitude, 86.8° longitude. Relative to Solar Orbiter, the Earth was therefore primarily separated in the +T direction in the radial tangential normal (RTN) coordinate system.

Figure 1 shows a solar wind current sheet encountered by Solar Orbiter at 04:58 UT. The duration of the current sheet crossing, based on the drop in |B| between 04:56:45.35 UT and 04:57:29.80 UT and marked by vertical solid black lines is 44.45 s. Figure 1a shows that the field strength is relatively symmetric on either side of the current sheet, with a much weaker field during the current sheet. For context, the solar wind magnetic field during this day was relatively quiescent, with |B| varying between approximately 3 nT and 7 nT (as discussed in more detail in Sect. 3). Figure 1b shows the magnetic field components in the RTN coordinate system. BT is positive before the current sheet and negative afterwards, whereas BR is initially negative and then positive. BT and BR are relatively constant in the middle (aside from the interval marked by vertical orange lines) and so we conclude that the current sheet is bifurcated with the current density confined to the edges of the current sheet.

thumbnail Fig. 1.

Solar Orbiter observations of a bifurcated current sheet in the solar wind. (a) Magnetic field strength, (b) Magnetic field in RTN coordinates, (c–e) Magnetic field at the current sheet in MVA coordinates.

Minimum variance analysis (MVA) was applied to the interval 04:56:35 UT–04:57:40 UT (marked by vertical black dashed lines), and used to rotate the data into a current sheet coordinate system (Sonnerup & Cahill 1967). Relative to RTN, the maximum, intermediate, and minimum variance directions were found to be XSolO = [ − 0.6175, 0.7214, 0.3135], YSolO = [ − 0.2598, −0.5633, 0.7843], ZSolO = [0.7424, 0.4029, 0.5353] (λX = 3.190, λY = 0.189, λZ = 0.154). Figure 1c shows the maximum variance direction component BX which contains the main field reversal across the current sheet. Figure 1d shows the intermediate variance direction component BY which is identified as the out-of-plane direction, and Fig. 1e shows the minimum variance direction component BZ which is identified as the direction normal to the current sheet. Although the eigenvalues in YSolO and ZSolO are not well separated, the analysis nevertheless recovers an appropriate coordinate system.

We note that the MVA intermediate and minimum eigenvalues are not well separated, and so to check the current sheet orientation, we also use hybrid-MVA where the normal direction is derived from the cross-product of the magnetic fields either side of the current sheet (see Gosling & Phan 2013 for full details). The hybrid-MVA X direction was found to be within 2° of the MVA X-direction, with a rotation of approximately 20° in the Y − Z plane. Very similar features were observed, and we find that the essential features of the current sheet are robust and not dependent on the exact choice of coordinate system; here we use MVA as it does not force BZ = 0 either side of the current sheet, unlike in hybrid-MVA. This means that the data is less constrained and also allows for the possibility of potential X-line geometry to be studied.

To establish the current sheet magnetic field geometry, we compute the average field before and after the current sheet crossing. In the current sheet coordinate system, the average magnetic field before the current sheet crossing from the start of the MVA interval to the start of the field rotation is B1 = [2.93, −1.03, 0.62] nT and |B1| = 3.17 nT. After the current sheet crossing, the average magnetic field from the end of the field rotation to the end of the MVA interval is B2 = [ − 3.06, −0.95, 0.75] nT and |B2| = 3.30 nT. The out-of-plane field, or guide field, is found to be BG = −0.99 nT and the normalised guide field is |BG/⟨BX⟩| = 0.33. The magnetic shear across the current sheet is found to be 136°. Finally, the normal magnetic field is 0.69 nT, and the ion gyrofrequency is 0.049 Hz.

A spike in magnetic field strength lasting 10 s is observed between the two solid orange lines during the current sheet crossing. Referring to Fig. 1b, this increase in field strength corresponds to a localised negative peak in BN, as opposed to BR or BT. The magnitude of this peak in BN exceeds the values outside the current sheet. We may therefore immediately rule out the possibility that this corresponds to a partial crossing of the edge of the current sheet. Referring to the current sheet coordinate system in Figs. 1c–e, there is a strong, more-negative deviation in BY, a positive/negative variation in BZ normal to the current sheet, with little signature in BX. This is the classic signature of a flux rope in a current sheet, where the enhanced magnetic field along the axis of the flux rope is predominantly in the out-of-plane direction and surrounded by loop-like magnetic fields, the signatures of which are largely manifested in the current sheet normal direction with opposite polarity either side of the enhanced core field. We therefore identify this feature as an isolated discrete flux rope confined within the bifurcated current sheet.

2.2. Flux rope properties

To better understand the properties of the structure identified as a flux rope, MVA was applied to the interval 04:57:13 UT–04:57:23 UT as shown in Fig. 2. This results in XFR = [0.0236, 0.3587, 0.9331], YFR = [−0.2019, −0.9125, 0.3559], ZFR = [0.9791, −0.1968, 0.05086] (λX, FR = 0.619, λY, FR = 0.372, λZ, FR = 0.029). BX, FR exhibits a unipolar variation, whereas BY, FR is bipolar and BZ, FR remains close to 0. We therefore identify the XFR direction as corresponding to the flux rope axis. We note that often in force-free flux ropes the intermediate direction contains the component with unipolar variation, however it is not uncommon for these two directions to be switched (e.g., Brain et al. 2010), particularly if the flux rope is not force-free.

thumbnail Fig. 2.

MVA applied to the flux rope at Solar Orbiter. (a) Magnetic field strength, (b) magnetic field in the RTN coordinate system, (c) magnetic field in the current sheet XYZ coordinate system, (d–f) magnetic field in the flux rope coordinate system.

The wavelet spectrogram of the normalised reduced magnetic helicity σm was computed to further examine the properties of the flux rope, which can be estimated by

σ m ( ν , t ) = 2 Im [ W T ∗ ( ν , t ) · W N ( ν , t ) ] | W R ( ν , t ) | 2 + | W T ( ν , t ) | 2 + | W N ( ν , t ) | 2 , $$ \begin{aligned} \sigma _{\rm m}(\nu ,t) = \frac{2 \text{ Im}[W_{\rm T}^*(\nu ,t) \cdot W_{\rm N}(\nu ,t)]}{|W_{\rm R}(\nu ,t)|^2 + |W_{\rm T}(\nu ,t)|^2 + |W_{\rm N}(\nu ,t)|^2}, \end{aligned} $$(1)

where ν is the frequency associated with the Wavelet function (Matthaeus et al. 1982). The spectra WR(ν, t), WT(ν, t), and WN(ν, t) are the wavelet transforms of time series of BR, BT, and BN, respectively, and the asterisk represents the complex conjugate. The details of the magnetic helicity-based technique of identifying magnetic flux ropes are presented in Zhao et al. (2020). From the spectrogram of σm, one can determine the flux rope handedness (chirality). A positive σm corresponds to right-handed chirality and a negative value to left-handed chirality.

As shown in Fig. 3, the flux rope is clearly identified in the spectrogram as a left-handed magnetic structure with a highly negative magnetic helicity. The scale or duration of this structure in the spectrogram is approximately 12 s, consistent with the visual identification in the time series. Comparison of the observations with a standard force-free model fit shows that the central peak in field strength is stronger in the observations, which may provide tentative evidence for compression of the flux rope. Finally, the orientation of the flux rope axis in the overall current sheet coordinate system [XSolO, YSolO, ZSolO] is found to be [0.5367, 0.5237, 0.6616] and the angle between the flux rope axis and the current sheet out-of-plane direction is 58.4°. This angle would be 0 for a flux rope that is perfectly aligned and the possible implications of this are discussed in more detail below.

thumbnail Fig. 3.

Normalised magnetic helicity analysis of the Solar Orbiter data. (a) Magnetic field observations. (b) Spectrogram of the reduced normalised magnetic helicity σm. The contour line in panel b is drawn at levels of |σm| = 0.7. The vertical dashed vertical lines represents the current sheet interval, and the vertical dashed-dotted lines the flux rope interval.

2.3. Current sheet fluctuations and turbulence

Figure 1 shows that there are enhanced fluctuations in the magnetic field inside the current sheet and the nature of these fluctuations is shown in more detail in Fig. 4. Measurements of power spectral density (PSD) for three 32 s intervals are shown: before the current sheet (04:56:08 UT–04:56:40 UT, in blue); during the current sheet (04:56:50 UT–04:56:22 UT, in black); and after the current sheet (04:57:40 UT–04:58:13 UT, in light red). In each case, two PSD traces are shown, one computed from the sum of the fast Fourier transform (FFT) of each component, and one computed from the sum of the wavelet spectrum of each component. In each case the PSD calculated using wavelets produces a smoother profile at mid-to-higher frequencies.

thumbnail Fig. 4.

Power spectral density measurements of the magnetic field at Solar Orbiter before (blue), during (black), and after (light red) the current sheet crossing shown in Fig. 1. Red dashed lines show −5/3 and −8/3 spectra and the black dashed line marks the ion inertial length.

Figure 4 shows that the PSD is enhanced in the current sheet compared to either side, up to frequencies of ∼10 Hz where flattening of the spectrum is associated with the noise floor of the instrument being reached; the roll-off above 10 Hz is due to the anti-aliasing filter of the instrument (Horbury et al. 2020). Outside the current sheet, the noise floor of the instrument is reached at ∼1 Hz. An enhancement in power at 0.2 Hz in the light red curve is associated with coherent long period oscillations which are visible after the current sheet crossing in Fig. 1.

The vertical black dashed line marks the ion inertial length, based on a density of 4.1 cm−3 (see Sect. 3 for more details). Red dashed lines show −5/3 and −8/3 spectra which intersect at the ion inertial length and which are scaled to the FFT-calculated PSD curve measured inside the current sheet. At lower frequencies, above the ion scale, there is good agreement with the −5/3 curve, but at higher frequencies past the ion scale the PSD curve breaks to follow a −8/3 spectrum.

3. Large scale structure and comparison with Wind

3.1. Wind observations

As mentioned in Sect. 2.1, Solar Orbiter was ∼0.08 au from Earth, at approximately the same heliocentric distance, and trailing the Earth in its orbit. To provide context for the Solar Orbiter observations, we therefore examined the Wind dataset to find corresponding large-scale features in the magnetic field. This allows what may be the same current sheet at Wind to be identified as we now describe. Figure 5 shows the Solar Orbiter data (red) together with the Wind data (black) shifted forward in time by 4 h 35 min. This time shift was applied on the basis of the large-scale reversal in BT from positive to negative values, together with associated changes in |B| and BN. Before this long-duration reversal in BT, there are current sheets in the magnetic field with corresponding drop-outs in |B|. We therefore focus on these features in the Wind data, as we expect the current sheet to have a similar magnetic shear at both spacecraft, even if the orientation of the current sheet is distorted by inhomogeneities in the solar wind flow. Closer examination of the Wind data allows a sharp reversal in BR from negative to positive values with a minimum in |B| to be identified, in overall solar wind magnetic field structure which is similar to that seen at Orbiter.

thumbnail Fig. 5.

Solar Orbiter data (red) compared to time-shifted Wind data (black). (a,b) Magnetic field strength, (c,d) radial magnetic field component, (e,f) tangential magnetic field component, (g,h) normal magnetic field component.

The current sheet was observed at Wind between 09:29:42 UT and 09:32:36 UT and Fig. 6 shows the crossing in more detail. Magnetic field data from the magnetic field instrument (MFI; Lepping et al. 1995) is shown at 11 vector/s cadence, and ion plasma moments measured by the 3DP instrument (Lin et al. 1995) are calculated on board at 3 s resolution. MVA was again used to find the current sheet coordinate system, and was applied to the interval 09:28:42 UT–09:33:36 UT. This resulted in XWind = [ − 0.8553, −0.0083, −0.5181], YWind = [ − 0.2017, −0.9157, 0.3475], ZWind = [ − 0.4774, 0.4017, 0.7815] (λX, Wind = 3.191, λY, Wind = 0.230, λZ, Wind = 0.134). Comparing the Solar Orbiter and Wind observations, we find that BX and BY have similar magnitudes either side of the current sheet; the magnetic shear across the current sheet at Wind is 123°, comparable to the shear observed at Solar Orbiter. The absence of plasma data at Solar Orbiter limits inter-comparison to the magnetic field measurements but within the available data, it is likely that this is the same current sheet in the same patch of solar wind plasma.

thumbnail Fig. 6.

Wind current sheet observations. (a) Ion density, (b) magnetic field strength, (c) magnetic field in RTN coordinates, (d) radial component of the ion velocity, (e–g) magnetic field at the current sheet in MVA coordinates, (h–j) ion velocity at the current sheet in MVA coordinates.

A reconnection exhaust is clearly visible in the vX, Wind component of the ion velocity. The speed of this jet (∼15 km s−1) is comparable to the Alfvén speed (VA = 26.5 km s−1) based on the local ion density (ni = 4.12 cm−3) and external reconnecting field (BX, Wind = 2.46 nT). This sub-Alfvénic flow is typical of reconnection exhausts in a variety of settings (Paschmann et al. 1986; Haggerty et al. 2018; Phan et al. 2020).

The Wind plasma data thus provides characteristic values for the solar wind speed (∼400 km s−1) and ion density (4.1 cm−3), and we use these values in analysing the Solar Orbiter observations as mentioned earlier in Sect. 2. In particular, we find a characteristic ion inertial length di = c/ωpi = 107 km. For completeness, based on an ion temperature of 5.62 eV, the ion gyroradius is found to be 147 km (with an ion gyrofrequency of 0.043 Hz) and the ion plasma beta is 1.15.

3.2. Large scale structure of the current sheet

The current sheet shown in Fig. 6 was observed at 09:30 UT, and at this time Wind was located at [ − 1.412 × 108, 4.007 × 107, 4.357 × 104] km in the inertial ECLIPJ2000 coordinate system. Using an observed solar wind speed of 400 km s−1, we can back-trace the point at which Wind crossed the current sheet and find its location at 04:57 UT, allowing for an estimate of the large-scale current sheet orientation to be made, as shown in Fig. 7.

thumbnail Fig. 7.

Relative location of Solar Orbiter and Wind shown in the ECLIPJ2000 coordinate system. (a) XECLIPJ2000 − YECLIPJ2000 projection, (b) YECLIPJ2000 − ZECLIPJ2000 projection, (c) XECLIPJ2000 − YECLIPJ2000 projection.

Figure 7a shows the position of Solar Orbiter (solid black circle), Wind (outline black circle), and the Earth (black cross) in the ECLIPJ2000 X − Y plane. The back-traced trajectory is shown as an orange dotted line. The dashed orange line connects the back-traced Wind crossing point to the location of Solar Orbiter. At 04:57 UT, Solar Orbiter was located at [ − 1.371 × 108, 5.044 × 107, 1.521 × 106] km. The separation of the crossing points was therefore found to be 1.246 × 107 km or 1955 Re.

At each spacecraft the blue, green, and red lines show the locally-defined X, Y, and Z directions. Figure 7 shows that the Y directions at both spacecraft point in the +YECLIPJ2000 direction with a 32° angular separation, and are somewhat aligned with the dashed orange line connecting the two crossing points. However there are significant differences in the orientations of the X direction at each spacecraft which reflects the fact that although the data in Figs. 1b and 6c show qualitative similarity, quantitative differences lead to a significant change in the orientation of the magnetic field at Wind and Solar Orbiter.

Previous observations with widely separated spacecraft have typically found simple quasi-1-dimensional solar wind reconnection exhausts with extended X-lines (e.g., Phan et al. 2009; Gosling et al. 2007; Lavraud et al. 2009). The observations presented here suggest that this behaviour breaks down on large scales, and possible interpretations of this are discussed in more detail below.

4. Discussion

The thickness of the current sheet at Solar Orbiter can be estimated based on a fiducial solar wind speed of 400 km s−1 antisunward (derived from Wind observations as discussed in Sect. 3). Given the current sheet orientation, the normal speed of Solar Orbiter through the current sheet in the solar wind rest frame is 297 km s−1 in the +N direction. The current sheet duration is 44.45 s which corresponds to a distance of 13 200 km or 123 di.

As mentioned in Sect. 2, there is a significant angular separation between the flux rope axis and the current sheet out-of-plane direction. In fact the geometry is such that Solar Orbiter’s speed along the flux rope axis XFR is ∼9 km s−1. Furthermore, since BZ, FR ∼ 0, this suggests that Solar Orbiter passed close to the flux rope axis. Therefore, based on a duration of 10 s, the flux rope radius is estimated to be 2000 km, corresponding to 18.7 di. We therefore class this flux rope as ion-scale, consistent with previous observations on the magnetopause where for example flux ropes with 7 di radius have been observed by MMS (Eastwood et al. 2016). This leads to a picture where the flux rope occupies approximately 30% of the width of the current sheet. Even acknowledging uncertainties in flux rope and current sheet coordinate systems, this potentially points to significant writhe of the flux rope inside the current sheet, in a manner consistent with the simulations of e.g. Daughton et al. (2011).

At its minimum at the centre of the flux rope, BX, FR = −2.47 nT at 04:57:18.196 UT. At this time, |B| = 2.61 nT. Over the 10 s flux rope interval, the average core field ⟨BX, FR⟩ = −0.398 nT. Given a flux rope radius of 2000 km, the estimated flux content ϕ = |⟨BX, FR⟩|πr2 ∼ 5 kWb. Ion scale flux ropes on the magnetopause appear to have somewhat larger flux content (e.g. 22 kWb) despite being similar size (Eastwood et al. 2016), but this is consistent with the overall lower magnetic field strengths in the solar wind, compared to the magnetosheath and magnetosphere.

The Solar Orbiter measurements also reveal the presence of enhanced fluctuations inside the current sheet. This is consistent with magnetotail observations (Eastwood et al. 2009; Ergun et al. 2018), and recent simulations (Adhikari et al. 2020) where reconnection causes an enhancement of the turbulence following a −5/3 power law breaking to −8/3 above the ion scale. These observations therefore show that enhanced fluctuations appear to exist far downstream and not just close to the X-line.

Given the evidence for reconnection at Wind, and the fact that reconnection is the most likely mechanism for flux rope production, we now further explore the interpretation of the Solar Orbiter data in this context. The overall geometry is illustrated in Fig. 8. Orbiter was moving in the +X direction in the current sheet frame, and was moving faster than the expected Alvénic outflow. The positive/negative variation in BZ is therefore consistent with Solar Orbiter ‘overtaking’ a flux rope as it passes through the current sheet, in the context of the overall current sheet magnetic topology. This trajectory leads to the reconstruction of a left-handed flux rope, which is confirmed by the wavelet spectrogram analysis of magnetic helicity discussed in Sect. 2. Finally, in solar wind reconnection it has been found that out-of-plane Hall fields can be observed at one edge of the current sheet hundreds of di from the X-line (Mistry et al. 2016). In the geometry shown in Fig. 8, the spike in +BY at the entry of current sheet in Fig. 1d matches this expected out-of-plane Hall field, providing further evidence consistent with a scenario where the flux rope is produced by magnetic reconnection.

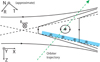thumbnail Fig. 8.

Schematic of the Solar Orbiter current sheet and flux rope encounter.

The Solar Orbiter data are therefore consistent with a reconnection exhaust oriented in the +BX direction. Consequently, using a half-thickness of 61 di and assuming a generic reconnection exhaust opening angle of 0.1, we find that the distance to the X-line is ∼600 di. A key difference between these observations and prior observations on the Earth’s magnetopause and magnetotail is therefore the distance from the X-line. Since the flux rope does not span the exhaust, this may rule out the possibility that it formed as a result of tearing across the current sheet in a multiple-X-line formation scenario. However, if sourced from secondary processes occurring closer to the X-line, and travelling out in the exhaust at a local Alfvén speed of 25 km s−1, this implies a lifetime of at least 2568 s, or 126 ion gyroperiods (given an ion gyrofrequency of 0.049 Hz) implying that flux ropes can exist as quasi-stable structures for a prolonged period of time.

Turning to the Wind observations, based on the normal speed of Wind through the current sheet and the duration of the crossing, the exhaust thickness at Wind is found to be 35 744 km, or 333 di. This gives a half thickness of 166 di, and an estimated distance to the X-line of 1660 di, which is about three times that of Solar Orbiter, but much less than the separation of the two spacecraft.

We now discuss what may be inferred from comparing the Wind and Solar Orbiter data. Whilst only the magnetic field data can be compared, the large-scale context and qualitative similarities between the current sheet encounters suggest that a single large-scale current sheet was encountered. If it is the same current sheet, then the differences in the local current sheet orientation can be interpreted in different ways. One cause may be large-scale warping of the current sheet. Curved solar wind phase fronts are not unusual, with dual spacecraft analysis suggesting several hundred Re for a typical radius of curvature (e.g., Lepping et al. 2003). Alternatively, small-scale ripples, distortion, and bending may occur over the current sheet, caused either internally by current-driven instabilities (Mistry et al. 2015) or externally by differences in the ambient solar wind. The magnetic field measurements at Solar Orbiter and Wind further suggest large-scale distortion of the reconnecting magnetic field either side of the current sheet. The correlation lengths for magnetic field components in the solar wind are ∼45 Re (e.g., Richardson & Paularena 2001), and so differences in the orientation of the magnetic field are not unexpected. It is likely that all these effects combine to explain the observations, but more multi-point reconnection studies at a variety of spacecraft separations are required to understand their relative importance.

The apparent proximity of both Wind and Solar Orbiter to X-lines despite their large separation raises separate questions about the nature and extent of reconnection in this event. Figure 7 shows that the outflows are not aligned, and so an interpretation in terms of a single highly-extended X-line implies that it is highly distorted, and not a straight line as reported with spacecraft at smaller separations. However, this raises the question as to whether reconnection can grow to produce such a long X-line. Following the procedure of Shepherd & Cassak (2012), we assume that the X-line grows with speed VG ∼ 12 km s−1 (the Alfvén speed based on the guide field strength). Assuming that reconnection is initiated at the Sun, and further assuming that the current sheet is carried out at the observed solar wind speed of 400 km s−1, we find that the maximum X-line length is ∼700 Re. To create an X-line of sufficient length, an average growth speed of ∼34 km s−1 would be required. Although this calculation provides only an order-of-magnitude estimate (and does not account for e.g. the fact that the Alfvén speed will be higher closer to the Sun), together with the different local orientations it may suggest that the observations correspond to patchy reconnection, initiated independently at different locations on the same current sheet. If this is the case, this fortuitous encounter provides new evidence that solar wind reconnection can be patchy on very large scales.

5. Conclusions

The Solar Orbiter observations constitute a remarkably clean observation of an ion-scale flux rope embedded inside a bifurcated current sheet in the solar wind. In contrast to previous observations, the flux rope does not span the entire exhaust. It is also not precisely oriented along the out-of-plane direction, indicating a writhe of the structure in the current sheet. This provides new insight into the relationship between solar wind current sheets and flux ropes, and new evidence that such flux ropes can exist on a hierarchy of scales down to the ion scale.

The general level of fluctuations and turbulence inside the current sheet is also enhanced, following a −5/3 power law which breaks to −8/3 above the ion scale. By comparing the large-scale structure of the solar wind magnetic field at Solar Orbiter and Wind, the same current sheet is identified at Wind and found to be reconnecting. The separation of the current sheet crossing points is nearly 2000 Re, and so this extends the range of distances over which active reconnection has been observed at a solar wind current sheet. Whilst it is difficult to reach definitive conclusions, the data may suggest that patchy solar wind reconnection can occur, notwithstanding the need for improved understanding and modeing of how solar wind X-lines develop in time as they are carried out into the heliosphere. Further work examining other widely separated reconnection events would shed more light on this question, as would a more careful comparison with simulations, although we note that simulations of uniform reconnection may not be sufficient to capture the structure of the solar wind inflow.

Magnetic reconnection is the most likely mechanism causing the formation of flux ropes in current sheets and as noted in Sect. 1, flux ropes are widely used widely as evidence of reconnection even in absence of comprehensive plasma data (e.g. in planetary magnetospheric studies). In this context, the geometry at Solar Orbiter implies a distance to the X-line of ∼600 di, which in turn suggests that flux ropes sourced from secondary instabilities near the X-line can survive for long periods as they are carried out in the reconnection exhaust. This has important implications for models of particle acceleration by extending the range of sizes and time-scales on which flux ropes may exist in solar wind current sheets, and opens the possibility of future studies further characterising flux rope properties using the novel combination of inner heliospheric missions that are now operational.

Acknowledgments

Solar Orbiter is a space mission of international collaboration between ESA and NASA, operated by ESA. Solar Orbiter magnetometer operations are funded by the UK Space Agency (grant ST/T001062/1). JPE and TSH are supported by UKRI/STFC grant ST/S000364/1. TDP is supported by NASA contract NNN06AA01C. JES is supported by a Royal Society University Research Fellowship URF/R1/201286. LZ and GPZ acknowledge the partial support of the NSF EPSCoR RII-Track-1 Cooperative Agreement OIA-1655280 and a NASA award 80NSSC20K1783. Solar Orbiter data is available from the ESA Solar Orbiter archive http://soar.esac.esa.int/soar/ and Wind data from NASA’s Coordinated Data Analysis Web https://cdaweb.gsfc.nasa.gov/istp_public/.

References

  1. Adhikari, S., Shay, M. A., Parashar, T. N., et al. 2020, Phys. Plasmas, 27, 042305 [NASA ADS] [CrossRef] [Google Scholar]
  2. Baker, D. N., Pulkkinen, T. I., Angelopoulos, V., Baumjohann, W., & McPherron, R. L. 1996, J. Geophys. Res., 101, 12975 [NASA ADS] [CrossRef] [Google Scholar]
  3. Brain, D. A., Baker, A. H., Briggs, J., et al. 2010, Geophys. Res. Lett., 37, L14108 [Google Scholar]
  4. Daughton, W., Roytershteyn, V., Karimabadi, H., et al. 2011, Nat. Phys., 7, 539 [Google Scholar]
  5. DiBraccio, G. A., Slavin, J. A., Imber, S. M., et al. 2015, Planet. Space Sci., 115, 77 [NASA ADS] [CrossRef] [Google Scholar]
  6. Drake, J. F., Swisdak, M., Che, H., & Shay, M. A. 2006, Nature, 443, 553 [Google Scholar]
  7. Drake, J. F., Swisdak, M., Schoeffler, K. M., Rogers, B. N., & Kobayashi, S. 2006, Geophys. Res. Lett., 33, L13105 [Google Scholar]
  8. Eastwood, J. P., Sibeck, D. G., Slavin, J. A., et al. 2005, Geophys. Res. Lett., 32, L11105 [NASA ADS] [CrossRef] [Google Scholar]
  9. Eastwood, J. P., Phan, T. D., Bale, S. D., & Tjulin, A. 2009, Phys. Rev. Lett., 102, 035001 [NASA ADS] [CrossRef] [Google Scholar]
  10. Eastwood, J. P., Phan, T. D., Cassak, P. A., et al. 2016, Geophys. Res. Lett., 43, 4716 [CrossRef] [Google Scholar]
  11. Enžl, J., Přech, L., Šafránková, J., & Němeček, Z. 2014, ApJ, 796, 21 [CrossRef] [Google Scholar]
  12. Enžl, J., Šafránková, J., Němeček, Z., & Přech, L. 2017, ApJ, 851, 86 [CrossRef] [Google Scholar]
  13. Ergun, R. E., Goodrich, K. A., Wilder, F. D., et al. 2018, Geophys. Res. Lett., 45, 3338 [CrossRef] [Google Scholar]
  14. Eriksson, S., Newman, D. L., Lapenta, G., & Angelopoulos, V. 2014, Plasma Phys. Contr. Fusion, 56, 064008 [CrossRef] [Google Scholar]
  15. Eriksson, S., Lapenta, G., Newman, D. L., et al. 2015, ApJ, 805, 43 [NASA ADS] [CrossRef] [Google Scholar]
  16. Feng, H. Q., & Wu, D. J. 2009, ApJ, 705, 1385 [NASA ADS] [CrossRef] [Google Scholar]
  17. Fermo, R. L., Drake, J. F., Swisdak, M., & Hwang, K.-J. 2011, J. Geophys. Res., 116, A09226 [NASA ADS] [Google Scholar]
  18. Gosling, J. T. 2012, Space Sci. Rev., 172, 187 [Google Scholar]
  19. Gosling, J. T., & Phan, T. D. 2013, ApJ, 763, L39 [Google Scholar]
  20. Gosling, J. T., Skoug, R. M., McComas, D. J., & Smith, C. W. 2005, J. Geophys. Res., 110, A01107 [NASA ADS] [Google Scholar]
  21. Gosling, J. T., Eriksson, S., Blush, L. M., et al. 2007, Geophys. Res. Lett., 34, L20108 [NASA ADS] [CrossRef] [Google Scholar]
  22. Haggerty, C. C., Shay, M. A., Chasapis, A., et al. 2018, Phys. Plasmas, 25, 102120 [Google Scholar]
  23. Hones, E. W. 1977, J. Geophys. Res., 82, 5633 [NASA ADS] [CrossRef] [Google Scholar]
  24. Horbury, T. S., O’Brien, H., Carrasco Blazquez, I., et al. 2020, A&A, 642, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Innocenti, M. E., Goldman, M., Newman, D., Markidis, S., & Lapenta, G. 2015, ApJ, 810, L19 [NASA ADS] [CrossRef] [Google Scholar]
  26. Jackman, C. M., Slavin, J. A., Kivelson, M. G., et al. 2014, J. Geophys. Res.: Space Phys., 119, 5465 [NASA ADS] [CrossRef] [Google Scholar]
  27. Khabarova, O., Zank, G. P., Li, G., et al. 2015, ApJ, 808, 181 [Google Scholar]
  28. Khabarova, O. V., Zank, G. P., Li, G., et al. 2016, ApJ, 827, 122 [Google Scholar]
  29. Lavraud, B., Gosling, J. T., Rouillard, A. P., et al. 2009, Sol. Phys., 256, 379 [Google Scholar]
  30. Lepping, R. P., Acũna, M. H., Burlaga, L. F., et al. 1995, Space Sci. Rev., 71, 207 [Google Scholar]
  31. Lepping, R. P., Wu, C. C., & McClernan, K. 2003, J. Geophys. Res., 108, 1279 [NASA ADS] [CrossRef] [Google Scholar]
  32. Lin, R. P., Anderson, K. A., Ashford, S., et al. 1995, Space Sci. Rev., 71, 125 [CrossRef] [Google Scholar]
  33. Matthaeus, W. H., Goldstein, M. L., & Smith, C. 1982, Phys. Rev. Lett., 48, 1256 [Google Scholar]
  34. Mistry, R., Eastwood, J. P., & Hietala, H. 2015, J. Geophys. Res.: Space Phys., 120, 30 [NASA ADS] [CrossRef] [Google Scholar]
  35. Mistry, R., Eastwood, J. P., Haggerty, C. C., et al. 2016, Phys. Rev. Lett., 117, 185102 [NASA ADS] [CrossRef] [Google Scholar]
  36. Mistry, R., Eastwood, J. P., Phan, T. D., & Hietala, H. 2017, J. Geophys. Res.: Space Phys., 122, 5895 [NASA ADS] [CrossRef] [Google Scholar]
  37. Moldwin, M. B., Phillips, J. L., Gosling, J. T., et al. 1995, J. Geophys. Res., 100, 19903 [Google Scholar]
  38. Moldwin, M. B., Ford, S., Lepping, R., Slavin, J., & Szabo, A. 2000, Geophys. Res. Lett., 27, 57 [NASA ADS] [CrossRef] [Google Scholar]
  39. Müller, D., St. Cyr, O. C., Zouganelis, I., et al. 2020, A&A, 642, A1 [Google Scholar]
  40. Paschmann, G., Papamastorakis, I., Baumjohann, W., et al. 1986, J. Geophys. Res., 91, 11099 [NASA ADS] [CrossRef] [Google Scholar]
  41. Phan, T. D., Gosling, J. T., Davis, M. S., et al. 2006, Nature, 439, 175 [Google Scholar]
  42. Phan, T. D., Gosling, J. T., & Davis, M. S. 2009, Geophys. Res. Lett., 36, L09108 [Google Scholar]
  43. Phan, T. D., Bale, S. D., Eastwood, J. P., et al. 2020, ApJS, 246, 34 [Google Scholar]
  44. Richardson, J. D., & Paularena, K. I. 2001, J. Geophys. Res., 106, 239 [NASA ADS] [CrossRef] [Google Scholar]
  45. Rijnbeek, R. P., Cowley, S. W. H., Southwood, D. J., & Russell, C. T. 1984, J. Geophys. Res., 89, 786 [NASA ADS] [CrossRef] [Google Scholar]
  46. Roux, J. A. L., Webb, G. M., Khabarova, O. V., Zhao, L.-L., & Adhikari, L. 2019, ApJ, 887, 77 [Google Scholar]
  47. Russell, C. T., & Elphic, R. C. 1978, Space Sci. Rev., 22, 681 [NASA ADS] [CrossRef] [Google Scholar]
  48. Shepherd, L. S., & Cassak, P. A. 2012, J. Geophys. Res., 117, A10101 [NASA ADS] [Google Scholar]
  49. Slavin, J. A., Lepping, R. P., Gjerloev, J., et al. 2003, J. Geophys. Res., 108, SMP 10 [Google Scholar]
  50. Sonnerup, B. U. O., & Cahill, L. J., Jr. 1967, J. Geophys. Res., 72, 171 [NASA ADS] [CrossRef] [Google Scholar]
  51. Teh, W. L., Sonnerup, B. U. Ö., Hu, Q., & Farrugia, C. J. 2009, Ann. Geophys., 27, 807 [NASA ADS] [CrossRef] [Google Scholar]
  52. Tilquin, H., Eastwood, J. P., & Phan, T. D. 2020, ApJ, 895, 68 [NASA ADS] [CrossRef] [Google Scholar]
  53. Vogt, M. F., Jackman, C. M., Slavin, J. A., et al. 2014, J. Geophys. Res.: Space Phys., 119, 821 [NASA ADS] [CrossRef] [Google Scholar]
  54. Wang, H., Lu, Q., Huang, C., & Wang, S. 2016, ApJ, 821, 84 [CrossRef] [Google Scholar]
  55. Zank, G. P., le Roux, J. A., Webb, G. M., Dosch, A., & Khabarova, O. 2014, ApJ, 797, 28 [Google Scholar]
  56. Zhao, L. L., Zank, G. P., Chen, Y., et al. 2019, ApJ, 872, 4 [Google Scholar]
  57. Zhao, L. L., Zank, G. P., Adhikari, L., et al. 2020, ApJS, 246, 26 [Google Scholar]

All Figures

thumbnail Fig. 1.

Solar Orbiter observations of a bifurcated current sheet in the solar wind. (a) Magnetic field strength, (b) Magnetic field in RTN coordinates, (c–e) Magnetic field at the current sheet in MVA coordinates.
In the text
thumbnail Fig. 2.

MVA applied to the flux rope at Solar Orbiter. (a) Magnetic field strength, (b) magnetic field in the RTN coordinate system, (c) magnetic field in the current sheet XYZ coordinate system, (d–f) magnetic field in the flux rope coordinate system.
In the text
thumbnail Fig. 3.

Normalised magnetic helicity analysis of the Solar Orbiter data. (a) Magnetic field observations. (b) Spectrogram of the reduced normalised magnetic helicity σm. The contour line in panel b is drawn at levels of |σm| = 0.7. The vertical dashed vertical lines represents the current sheet interval, and the vertical dashed-dotted lines the flux rope interval.
In the text
thumbnail Fig. 4.

Power spectral density measurements of the magnetic field at Solar Orbiter before (blue), during (black), and after (light red) the current sheet crossing shown in Fig. 1. Red dashed lines show −5/3 and −8/3 spectra and the black dashed line marks the ion inertial length.
In the text
thumbnail Fig. 5.

Solar Orbiter data (red) compared to time-shifted Wind data (black). (a,b) Magnetic field strength, (c,d) radial magnetic field component, (e,f) tangential magnetic field component, (g,h) normal magnetic field component.
In the text
thumbnail Fig. 6.

Wind current sheet observations. (a) Ion density, (b) magnetic field strength, (c) magnetic field in RTN coordinates, (d) radial component of the ion velocity, (e–g) magnetic field at the current sheet in MVA coordinates, (h–j) ion velocity at the current sheet in MVA coordinates.
In the text
thumbnail Fig. 7.

Relative location of Solar Orbiter and Wind shown in the ECLIPJ2000 coordinate system. (a) XECLIPJ2000 − YECLIPJ2000 projection, (b) YECLIPJ2000 − ZECLIPJ2000 projection, (c) XECLIPJ2000 − YECLIPJ2000 projection.
In the text
thumbnail Fig. 8.

Schematic of the Solar Orbiter current sheet and flux rope encounter.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.