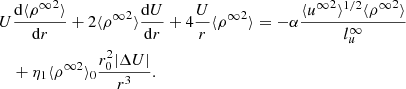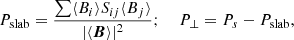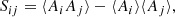| Issue |
A&A
Volume 656, December 2021
Solar Orbiter First Results (Cruise Phase)
|
|
|---|---|---|
| Article Number | A6 | |
| Number of page(s) | 14 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202140672 | |
| Published online | 14 December 2021 | |
Evolution of anisotropic turbulence in the fast and slow solar wind: Theory and Solar Orbiter measurements
1
Center for Space Plasma and Aeronomic Research (CSPAR), University of Alabama in Huntsville, Huntsville, AL 35899, USA
e-mail: la0004@uah.edu
2
Department of Space Science, University of Alabama in Huntsville, Huntsville, AL 35899, USA
3
National Institute for Astrophysics–Astrophysical Observatory of Torino Via Osservatorio 20, 10025 Pino Torinese, Italy
4
Department of Physics, The Blackett Laboratory, Imperial College London, London, UK
5
Mullard Space Science Laboratory, University College London, Holmbury St. Mary, UK
6
Institut de Recherche en Astrophysique et Planétologie (IRAP), Toulouse Université de Toulouse, CNRS 5 UMR5277, Toulouse, France
Received:
26
February
2021
Accepted:
19
April
2021
Aims. Solar Orbiter (SolO) was launched on February 9, 2020, allowing us to study the nature of turbulence in the inner heliopshere. We investigate the evolution of anisotropic turbulence in the fast and slow solar wind in the inner heliosphere using the nearly incompressible magnetohydrodynamic (NI MHD) turbulence model and SolO measurements.
Methods. We calculated the two dimensional (2D) and the slab variances of the energy in forward and backward propagating modes, the fluctuating magnetic energy, the fluctuating kinetic energy, the normalized residual energy, and the normalized cross-helicity as a function of the angle between the mean solar wind speed and the mean magnetic field (θUB), and as a function of the heliocentric distance using SolO measurements. We compared the observed results and the theoretical results of the NI MHD turbulence model as a function of the heliocentric distance.
Results. The results show that the ratio of 2D energy and slab energy of forward and backward propagating modes, magnetic field fluctuations, and kinetic energy fluctuations increases as the angle between the mean solar wind flow and the mean magnetic field increases from θUB = 0° to approximately θUB = 90° and then decreases as θUB → 180°. We find that solar wind turbulence is a superposition of the dominant 2D component and a minority slab component as a function of the heliocentric distance. We find excellent agreement between the theoretical results and observed results as a function of the heliocentric distance.
Key words: solar wind / turbulence
© ESO 2021
1. Introduction
Anisotropy is a local property of turbulence in solar wind plasma in which the properties of velocity and magnetic field fluctuations are different in directions perpendicular and parallel to the mean magnetic field B0. The anisotropy of solar wind turbulence exhibits different properties in fast and slow solar wind (Dasso et al. 2005; Adhikari et al. 2018). Anisotropy takes different forms, such as in that (i) the power spectral indices can differ for parallel k|| and perpendicular k⊥ wavenumbers with respect to the mean magnetic field (Horbury et al. 2008; Podesta 2009; Wicks et al. 2010; Narita et al. 2010; Bruno & Telloni 2015), (ii) the power differs in parallel and perpendicular fluctuations (Montgomery 1982; Matthaeus et al. 1990; Bieber et al. 1996; Milano et al. 2004; Ruiz et al. 2011; Pine et al. 2020), and (iii) the correlation functions differ in directions parallel and perpendicular to the mean magnetic field (Dasso et al. 2005, 2008; Matthaeus et al. 2005; Weygand et al. 2009; Osman & Horbury 2007; Wang et al. 2019). Anisotropy has been studied theoretically and numerically (Montgomery & Turner 1981; Shebalin et al. 1983; Grappin 1986; Zank & Matthaeus 1992a,b, 1993; Grappin et al. 1993; Goldreich & Sridhar 1995; Ghosh et al. 1998; Dong et al. 2014; Verdini & Grappin 2015, 2016; Zank et al. 2017, 2020; Adhikari et al. 2017a).
Pine et al. (2020), using two approaches, calculated the anisotropy of magnetic field fluctuations in the inertial range from 1 to 45 au using Voyager and Advanced Composition Explorer (ACE) observations. In the first method, Pine et al. (2020) computed the ratio of the power in fluctuations perpendicular to the mean magnetic field to the power in fluctuations parallel to the mean field. They find that the anisotropy depends on the plasma beta βp (≡2nkBT/(B2/2μ0), where n is the solar wind density, kB is Boltzmann’s constant, T is the solar wind temperature, B is the magnetic field, and μ0 is the magnetic permeability) and the ratio of the fluctuation level of the magnetic field to the mean magnetic field. In the second method, Pine et al. (2020) computed the anisotropy from the distribution of energy between parallel and perpendicular wavevectors. The results show that the anisotropy does not depend on the direction of the mean magnetic field relative to the radial direction (see also Tessein et al. 2009) and that the expansion of the solar wind contributes to the measured anisotropy.
Klein et al. (1993) examined the anisotropy, minimum variance, and related distinguishing plasma parameters of small-scale fluctuations in the inner heliosphere using Helios 2 measurements. They found that the variance direction of the fluctuations is generally aligned with the average magnetic field in the high speed and relatively low plasma beta βp solar wind, but the fluctuation direction is more isotropic in low speed and high plasma beta regions. Klein et al. (1991) studied the anisotropy of magnetic field fluctuations and solar wind fluctuations from 1 to 10 au using the Voyager 2 magnetometer and plasma data set. They found that the ratio of the fluctuating magnetic power in the perpendicular direction to that in the parallel direction is 5:1 at 1 au, which decreases to 3:1 farther out. In the velocity fluctuations, the direction of minimum variance is radial and is less directed along the mean field with increasing heliocentric distance. They found that velocity fluctuations are more isotropic than magnetic fluctuations between 1 and 10 au.
Wang et al. (2014) found that intermittency may affect the spectral index of parallel fluctuations. The spectral index for parallel fluctuations is found to be −2 in the presence of intermittency. When intermittency is absent, the spectral power index is similar for k⊥ and k||. In a later study by Wang et al. (2015), they found that the spectral index of parallel fluctuations is −2 for moderate amplitude fluctuations and close to −5/3 for small amplitude parallel fluctuations.
Recently, Zank et al. (2020) proposed a detailed spectral theory based on the NI MHD quasi-2D or 2D plus slab turbulence superposition model. The NI MHD model shows that the perpendicular energy spectrum follows a kolmogorov-type of power law 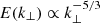 (Zank et al. 2017). The 2D plus slab model predicts
(Zank et al. 2017). The 2D plus slab model predicts 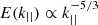 for arbitrary values of the normalized cross-helicity σc. Furthermore, the 2D plus slab model can also explain the power law
for arbitrary values of the normalized cross-helicity σc. Furthermore, the 2D plus slab model can also explain the power law 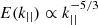 that is observed by WIND and Parker Solar Probe (PSP) in highly field-aligned flows (σc ∼ ±1) (Telloni et al. 2019; Zhao et al. 2020). This result is quite distinct from the prediction of critical balance theory (Goldreich & Sridhar 1995), which requires σc ∼ 0. Some observational work find a spectral index of −5/3 for θBR = 90°, and −2 for θBR ∼ 0°, where θBR is the angle between the local mean magnetic field and radial direction (Horbury et al. 2008; Podesta 2009). We note that in Horbury et al. (2008), the wavelet technique is used to determine the local mean magnetic field, while in Telloni et al. (2019) and Zhao et al. (2020), the mean magnetic field and mean solar wind speed are determined by the average value of selected intervals. Telloni et al. (2019) identified 17 highly field-aligned fast solar wind flow intervals of length > 1 h by searching 12 years of Wind measurements, finding that these intervals admitted a Kolmogorov-type of power law
that is observed by WIND and Parker Solar Probe (PSP) in highly field-aligned flows (σc ∼ ±1) (Telloni et al. 2019; Zhao et al. 2020). This result is quite distinct from the prediction of critical balance theory (Goldreich & Sridhar 1995), which requires σc ∼ 0. Some observational work find a spectral index of −5/3 for θBR = 90°, and −2 for θBR ∼ 0°, where θBR is the angle between the local mean magnetic field and radial direction (Horbury et al. 2008; Podesta 2009). We note that in Horbury et al. (2008), the wavelet technique is used to determine the local mean magnetic field, while in Telloni et al. (2019) and Zhao et al. (2020), the mean magnetic field and mean solar wind speed are determined by the average value of selected intervals. Telloni et al. (2019) identified 17 highly field-aligned fast solar wind flow intervals of length > 1 h by searching 12 years of Wind measurements, finding that these intervals admitted a Kolmogorov-type of power law 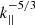 during strong turbulence. Zhao et al. (2020) found two highly field-aligned intervals of ∼20 min in the slow solar wind in the first and second encounters of PSP, and, similar to Telloni et al. (2019), find that the turbulence is unidirectional (σc ∼ −1) and exhibits a Kolmogorov-like spectrum in the parallel wavenumber, that is with a
during strong turbulence. Zhao et al. (2020) found two highly field-aligned intervals of ∼20 min in the slow solar wind in the first and second encounters of PSP, and, similar to Telloni et al. (2019), find that the turbulence is unidirectional (σc ∼ −1) and exhibits a Kolmogorov-like spectrum in the parallel wavenumber, that is with a 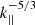 power law.
power law.
In this manuscript, we study the evolution of the variance anisotropy (Belcher & Davis 1971; Pine et al. 2020) of the energy in forward and backward propagating modes, the fluctuating magnetic energy, and the fluctuating kinetic energy in the fast and slow solar wind in the inner heliosphere using Solar Orbiter measurements and interpret the results in terms of the nearly incompressible magnetohydrodynamic (NI MHD) turbulence transport model equations (Zank et al. 2017). The theory of NI MHD in the plasma beta regime βp ∼ 1 or ≪1 predicts that MHD-scale turbulence is a superposition of the dominant quasi-2D (relative to the mean magnetic field) turbulence and a minority NI/slab turbulence (Zank & Matthaeus 1992b, 1993; Hunana & Zank 2010; Zank et al. 2017). Adhikari et al. (2017a) proposed a theoretical model to explain the evolution of power anisotropy in magnetic field fluctuations in the inertial range throughout the heliopshere using the NI MHD model, and found that the ratio between the quasi-2D fluctuating magnetic energy and the NI/slab fluctuating magnetic energy is close to 1 in the outer heliosphere at 75 au.
The outline of the manuscript is as follows. Section 2 introduces the solar wind plus NI MHD turbulence transport model. Section 3 presents the data analysis. Section 4 discusses 2D and slab turbulence as a function of the angle between the mean solar wind speed and the mean magnetic field. Section 5 presents a comparison between theory and observations. Section 6 discusses the radial evolution of background profile. Finally, Sect. 7 provides discussion and conclusions.
2. Solar wind plus NI MHD turbulence transport model
As the solar wind expands from the surface of the Sun to the outer heliosphere, the continuity equation describes the evolution of solar wind mass density ρ, the momentum equation describes the evolution of solar wind speed U, and the pressure equation describes the evolution of solar wind thermal pressure. The one dimensional (1D) steady-state continuity equation and momentum equation in a spherically symmetric coordinate system are given by,
where Pp is the thermal proton pressure and Pe is the thermal electron pressure. On the right hand side (rhs) of Eq. (2), the first term is the proton pressure gradient, and the second term the electron pressure gradient. The thermal pressure gradients exert forces on the solar wind that drives the solar wind from a subsonic speed to a supersonic speed despite the attractive gravitational force G M⊙ρ/r2 (where G is the gravitational constant, and M⊙ is the solar mass) (Parker 1958; Verdini et al. 2010; Chhiber et al. 2019; Adhikari et al. 2020a). The gravitational force is neglected in Eq. (2) because it is negligible in comparison to the proton and electron thermal force. Similarly, the magnetic force (J × B)r = −1/(μ0r)Bϕd/dr(rBϕ) is also neglected because this is less important compared to the thermal force. In the outer heliosphere, terms related to charge exchange between the solar wind protons and interstellar neutrals, and photoionization appear on the rhs of Eq. (2) (see Zank et al. 2018b), which leads to the deceleration of the solar wind (Richardson & Wang 2003; Zank et al. 2018b; Elliott et al. 2019). Using a conservative formulation of the solar wind equations and turbulence (magnetic) transport equations, Adhikari et al. (2020b) showed that a term related to a stream-shear turbulence appears on the rhs of the momentum equation. Here we do not include this, and we assume that the electron density ne and the proton density np are approximately the same.
It is established that the dissipation of turbulence energy heats the solar wind protons and electrons simultaneously. However, it is not only the turbulence energy but also Coulomb collisions between solar wind protons and electrons, and the electron heat flux that influence the heating profile of the solar wind protons and electrons (Cranmer et al. 2009; Breech et al. 2009; Engelbrecht & Strauss 2018; Chhiber et al. 2019; Adhikari et al. 2021). By including electrons, the 1D steady-state transport equations for the proton and electron pressure are given by
where St is a turbulent heating term, fp denotes a fraction of turbulence energy that heats the solar wind protons, (1 − fp) is the fraction of turbulence energy that heats the solar wind electrons, γ(= 5/3) is the polytropic index, and νpe and νep are the rates of proton-electron Coulomb collisions (Barakat & Schunk 1982; Zank 2014). Here, neνep ≈ npνpe because the Coulomb collisional frequencies are balanced (assumed equal for protons and electrons). The rate of proton-electron Coulomb collisions is given by (Cranmer et al. 2009),
Equations (3) and (4) assume isotropic models for the electron pressure (or temperature) and the proton pressure (or temperature), and include the electron heat flux qe. The proton heat flux is neglected (Braginskii 1965) because it is small. Here, the contribution to the electron pressure (or temperature) is primarily due to the Maxwellian core, while the parallel and perpendicular contributions to the pressure (or temperature) are less important (Tang et al. 2020). The electron heat flux is determined by the electron strahl in the direction parallel to the magnetic field (Cranmer et al. 2009) and is zero for the Maxwellian core electrons. By fitting the electron heat flux measured by Helios 2 from 0.3 to 1 au (Pilipp et al. 1990; Cranmer et al. 2009) obtained an empirical formula for the electron heat flux,
where x ≡ ln(r/1 au) and q0 = 0.01 erg cm−2 s−1. The term ∇ ⋅ qe can be expressed as (Cranmer et al. 2009)
where ϕ is the Parker spiral angle,
and Ω = 2.7 × 10−6 rad s−1 is the solar rotation frequency. We choose a colatitude θ = 90°, because we compare the model results with Solar Orbiter measurements.
The turbulent heating term St in (3) and (4) can be derived using a Kolmogorov phenomenology, and is given by (Verdini et al. 2010; Zank et al. 2018b; Adhikari et al. 2021)
where mp is the proton mass, ns is the solar wind proton density, α is a von-Kármán Taylor constant, and 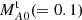 is the turbulent Alfvén Mach number. The terms inside the […] correspond to the dissipation of quasi-2D turbulence and NI/slab turbulence, in which the last term is related to the Alfvén effect in the NI/slab turbulence, and is derived using NI/slab time-scale introduced by Zank et al. (2020). This term vanishes for the unidirectional Alfvén waves (
is the turbulent Alfvén Mach number. The terms inside the […] correspond to the dissipation of quasi-2D turbulence and NI/slab turbulence, in which the last term is related to the Alfvén effect in the NI/slab turbulence, and is derived using NI/slab time-scale introduced by Zank et al. (2020). This term vanishes for the unidirectional Alfvén waves (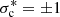 ; Adhikari et al. 2019). The parameter
; Adhikari et al. 2019). The parameter 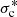 is the NI/slab normalized cross-helicity and the remaining terms are defined in detail below.
is the NI/slab normalized cross-helicity and the remaining terms are defined in detail below.
NI MHD in the βp ∼ 1 or ≪1 regimes predicts that solar wind turbulence is a superposition of majority quasi-2D and minority NI/slab turbulence (Zank & Matthaeus 1992b, 1993; Zank et al. 2017). The total Elsässer variables can be written as the sum of quasi-2D and NI/slab Elsässer variables, that is z± = z∞± + z*±, provided that it follows the symmetries of the underlying turbulence (Zank et al. 2017). The majority quasi-2D and a minority NI/slab Elsässer variables are defined as (Zank et al. 2017)
respectively. Similarly, the quasi-2D and NI/slab variances of the Elsässer variables, and the residual energy ED are given by (Zank et al. 2012, 2017),
The correlation function corresponding to forward and backward propagating modes, and the residual energy is given by
where y = |y| is the spatial lag between fluctuations, 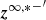 the lagged Elsässer variables, and λ± and λD are the correlation lengths corresponding to forward and backward propagating modes, and the residual energy.
the lagged Elsässer variables, and λ± and λD are the correlation lengths corresponding to forward and backward propagating modes, and the residual energy.
A radial magnetic field B is assumed and is given by,
where B0 is the magnetic field at the reference point r0 and 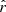 denotes the direction of the magnetic field.
denotes the direction of the magnetic field.
The 1D steady-state majority quasi-2D turbulence transport model equations under the assumption of spherical expansion are given by (Zank et al. 2017)
where 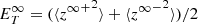 is the quasi-2D total turbulent energy. The first term on the rhs in Eq. (9) is the nonlinear dissipation term that describes the dissipation of quasi-2D energy in forward and backward propagating modes. In the transport equation for the residual energy, Eq. (10), the first term on the rhs is the dissipation term and the second term is the turbulent dynamo term (Grappin et al. 1982, 1983; Zank et al. 2012; Adhikari et al. 2021). The second and third terms in Eqs. (9) and (10) are shear driving sources for the quasi-2D energy in forward and backward propagating modes, and the residual energy. The parameter
is the quasi-2D total turbulent energy. The first term on the rhs in Eq. (9) is the nonlinear dissipation term that describes the dissipation of quasi-2D energy in forward and backward propagating modes. In the transport equation for the residual energy, Eq. (10), the first term on the rhs is the dissipation term and the second term is the turbulent dynamo term (Grappin et al. 1982, 1983; Zank et al. 2012; Adhikari et al. 2021). The second and third terms in Eqs. (9) and (10) are shear driving sources for the quasi-2D energy in forward and backward propagating modes, and the residual energy. The parameter 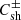 and
and 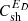 describe the strength of the shear source of turbulence. The parameter |ΔU| is the difference between the fast and slow solar wind speed, and VA0 is the Alfvén velocity at a reference point r0. The fast solar wind emerges from open field polar coronal holes and we assume that the turbulent shear source has no effect on the fast solar wind, similar to Zank et al. (2018a), Adhikari et al. (2020a, 2021). The slow solar wind that emerges from the equatorial region of the Sun is considered to be affected by the turbulent shear source (see Adhikari et al. 2020c). Kelvin-Helmholtz instabilities may develop in the inner and outer corona (DeForest et al. 2016; Yuan et al. 2019), which may provide a source of turbulence shear source close to the Sun (Ruffolo et al. 2020) and may affect the slow and fast solar wind from above the sonic point. We will address this issue in a future paper.
describe the strength of the shear source of turbulence. The parameter |ΔU| is the difference between the fast and slow solar wind speed, and VA0 is the Alfvén velocity at a reference point r0. The fast solar wind emerges from open field polar coronal holes and we assume that the turbulent shear source has no effect on the fast solar wind, similar to Zank et al. (2018a), Adhikari et al. (2020a, 2021). The slow solar wind that emerges from the equatorial region of the Sun is considered to be affected by the turbulent shear source (see Adhikari et al. 2020c). Kelvin-Helmholtz instabilities may develop in the inner and outer corona (DeForest et al. 2016; Yuan et al. 2019), which may provide a source of turbulence shear source close to the Sun (Ruffolo et al. 2020) and may affect the slow and fast solar wind from above the sonic point. We will address this issue in a future paper.
The 1D steady-state transport equations of NI/slab turbulence are given by (Zank et al. 2017)
where VA is the Alfvén velocity, 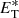 is the NI/slab total turbulent energy, and
is the NI/slab total turbulent energy, and 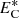 is the NI/slab cross helicity. The parameter b describes the geometry of NI/slab turbulence and is associated with the closure hypothesis for off-diagonal 2-point correlations. In Eq. (13), the first and second rhs terms are the nonlinear dissipation terms for the energy in forward and backward propagating modes. In Eq. (14), the first term is a turbulent dissipation term, the second and fourth terms represent the turbulent small-scale dynamo effect, and the third term represents the Alfvén effect. We note that the Alfvén effect is not included in the quasi-2D equations because the Alfvén velocity does not appear in quasi-2D turbulence. The third and fifth terms in Eqs. (13) and (14) are the shear source of turbulence for the NI/slab energy in forward and backward propagating modes, and the residual energy with strengths
is the NI/slab cross helicity. The parameter b describes the geometry of NI/slab turbulence and is associated with the closure hypothesis for off-diagonal 2-point correlations. In Eq. (13), the first and second rhs terms are the nonlinear dissipation terms for the energy in forward and backward propagating modes. In Eq. (14), the first term is a turbulent dissipation term, the second and fourth terms represent the turbulent small-scale dynamo effect, and the third term represents the Alfvén effect. We note that the Alfvén effect is not included in the quasi-2D equations because the Alfvén velocity does not appear in quasi-2D turbulence. The third and fifth terms in Eqs. (13) and (14) are the shear source of turbulence for the NI/slab energy in forward and backward propagating modes, and the residual energy with strengths 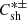 and
and 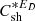 , respectively.
, respectively.
The transport equation for the variance of the density fluctuations can be written as (Zank et al. 2017, 2018b; Adhikari et al. 2017b)
Here, we introduce a shear source of turbulence for the density variance with a strength η1. The quasi-2D fluctuating kinetic energy can be expressed as 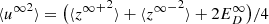 ,
, ![$ l_u^\infty = \big[{ (E_{\rm T}^\infty+E_{C}^\infty) \lambda^+_\infty + (E_{\rm T}^\infty - E_{C}^\infty) \lambda^-_\infty + E_{D}^\infty \lambda_D^\infty}\big]/{2(E_{\rm T}^\infty + E_D^\infty)} $](/articles/aa/full_html/2021/12/aa40672-21/aa40672-21-eq41.gif) is the correlation length of the quasi-2D fluctuating kinetic energy, and
is the correlation length of the quasi-2D fluctuating kinetic energy, and 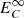 is the quasi-2D cross-helicity. ⟨ρ∞2⟩0 is the density variance at a reference position r0.
is the quasi-2D cross-helicity. ⟨ρ∞2⟩0 is the density variance at a reference position r0.
3. Data analysis
We use SolO magnetometer (Horbury et al. 2020) and Solar Wind Analyser – Proton and Alpha Sensor (SWA-PAS) plasma data (Owen et al. 2020) from July 7, 2020 to August 31, 2020 because PAS data was turned off prior to July 7, 2020. In this period, SolO is moving in an outbound direction. For the fast solar wind, we use the data sets at times (YY:MN:DD): 2020-07-15, 2020-08-27, 2020-08-28, 2020-08-29. For the slow solar wind, we use the data sets at times (YY:MN:DD): 2020-07-17, 2020-07-18, 2020-07-22, 2020-07-30, 2020-08-02, 2020-08-03, 2020-08-04, 2020-08-05, 2020-08-07, 2020-08-08, 2020-08-09, 2020-08-11, 2020-08-13. During this period, SolO covers a heliocentric distance of 140 − 193 R⊙ and stays within a latitude of 5°, which means that SolO basically observes the same kind of plasma, whether in the slow solar wind flow or in the fast solar wind flow. In the data, the slow solar wind speed ranges from 300–420 km s−1 and the fast solar wind speed is greater than 420 km s−1.
Using methods similar to those described in our series of papers (Zank et al. 1996; Adhikari et al. 2014, 2015, 2017b; Shiota et al. 2017; Zhao et al. 2018), the various turbulence quantities, such as the energy in forward and backward propagating modes, the normalized residual energy, the normalized cross-helicity, the fluctuating kinetic and magnetic energy, the relevant correlation lengths, and the variance of the density fluctuations are obtained from the R, T, and N components of the solar wind speed and the magnetic field, and the solar wind density. Furthermore, the perpendicular (or 2D) and slab variances of the Elsässer variables, the fluctuating magnetic energy, and the fluctuating kinetic energy with respect to the direction of the mean magnetic field are calculated from (Belcher & Davis 1971),
where P⊥ and Pslab denote the variances of the turbulence quantities in the direction perpendicular and parallel to the mean magnetic field ⟨B⟩. The ⟨…⟩ denotes averaging over a specified time interval, and i and j denote the R, T, and N components of the solar wind speed, magnetic field, and Elsässer variables. Ps denotes the trace of S, where
is a 3 × 3 matrix, formed by the R, T, and N components of a vector A.
4. 2D and slab turbulence versus θUB in the fast and slow solar wind
According to the NI MHD theory, solar wind turbulence is assumed to be a superposition of quasi-2D or perpendicular or 2D turbulence (hereafter we call it 2D turbulence) and NI/slab or slab turbulence (hereafter called slab turbulence) (Zank & Matthaeus 1992b, 1993), in which the 2D turbulence dominates the slab turbulence throughout the heliosphere (Zank & Matthaeus 1992b, 1993; Bieber et al. 1996; Zank et al. 2017, 2018a,b; Adhikari et al. 2017a, 2021; Pine et al. 2020). Recently, Pine et al. (2020) calculated the power corresponding to perpendicular and parallel components of the fluctuating magnetic energy using ACE and Voyager magnetometer data sets, and found that the power in the perpendicular component is higher than that in the parallel component.
Here we calculate (i) the turbulence energy by the method of mean field decomposition, in which we first subtract the mean quantity from the solar wind variable and then we calculate the variance of that quantity, and (ii) the 2D and slab turbulence energy by Eq. (18). We show the observed total energy1, 2D energy, and slab energy corresponding to forward (Figs. 1-A1/B1) and backward propagating modes (Figs. 1-A2/B2), magnetic field fluctuations (Figs. 1-A3/B3), and kinetic energy fluctuations (Figs. 1-A4/B4) as a function of the angle between the mean solar wind speed and the mean magnetic field (θUB). In the top panel of (a) and (b), the green scatter plots with error bars denote the total energy, the red scatter plots with error bars denote the perpendicular energy, the blue scatter plots with error bars denote the slab energy, and the black scatter plots with error bars indicate the perpendicular plus slab energy corresponding to the energy in forward propagating modes, the energy in backward propagating modes, the fluctuating magnetic energy, and the fluctuating kinetic energy. Here, the black and green scatter plots overlap each other and cannot be distinguished. The error bar denotes a standard error σ/n, where σ is the standard deviation and n is the number of data points over the angle dθ = 3° and dθ = 2.8° for the slow and fast wind, respectively. For the slow and fast solar wind, the turbulence quantities are calculated in an interval of 3 h and 1 h, and then we take an average over the angle dθ = 3° and dθ = 2.8°, respectively.
 |
Fig. 1. Top and third panels: total (green), perpendicular (red), slab (blue) and summation of perpendicular and slab, that is perpendicular plus slab (black) turbulence energy corresponding to the energy in forward propagating modes (A1/B1), the energy in backward propagating modes (A2/B2), the fluctuating magnetic energy (A3/B3), and the fluctuating kinetic energy (A4/B4) for the slow and fast solar wind as a function of the angle between the mean solar wind speed and the mean magnetic field (θUB). Second and fourth panels: ratio between the 2D and slab variances of energy in forward propagating modes (a1/b1) and backward propagating modes (a2/b2), the fluctuating magnetic energy (a3/b3), and the fluctuating kinetic energy (a4/b4) as a function of θUB. (a) Slow solar wind. (b) Fast solar wind. |
The top panel of (a) and (b) in Fig. 1 shows that the perpendicular plus slab (black scatter plots) energy in forward propagating modes is similar to the total energy in forward propagating modes (green scatter plots). Again, we note that the green and black scatter plots overlap each other. Similarly, the perpendicular plus slab energy in backward propagating modes, fluctuating magnetic energy, and fluctuating kinetic energy are equal to the total energy in backward propagating modes, fluctuating magnetic energy, and fluctuating kinetic energy. This is an important result, that indicates that solar wind turbulence is a superposition of 2D and slab turbulence. Similarly, it shows that the perpendicular energy in forward and backward propagating modes, the fluctuating magnetic energy, and the fluctuating kinetic energy are larger than the corresponding slab energies, indicating that 2D turbulence is the dominant component. We discuss this further below, however, these results are consistent with the NI MHD theory (Zank & Matthaeus 1992b, 1993; Zank et al. 2017, 2018a,b; Adhikari et al. 2017a, 2021) and observations (Bieber et al. 1996), that show that solar wind turbulence is a superposition of the dominant 2D turbulence and a minority slab turbulence components. This result is consistent with Pine et al. (2020), who studied the magnetic field fluctuations anisotropy of the power spectral components using Voyager and ACE magnetometer data sets, and showed that the ratio of the perpendicular power to the parallel power increases from θBR = 0° to about θBR = 90°, where θBR is the angle between the mean magnetic field and the radial direction. Here we show the variances of the turbulence quantities (the energy in forward and backward propagating modes, the fluctuating magnetic energy, and the fluctuating kinetic energy) in the direction parallel and perpendicular to the mean magnetic field. In the NI MHD theory, the majority 2D component and a minority slab component are the turbulence energy in the direction perpendicular and parallel to the large-scale magnetic field, respectively. Pine et al. (2020) also pointed out that the ratio of the power of the perpendicular fluctuations to the power of the parallel fluctuations can be influenced by the plasma beta βp.
In the slow solar wind, the total energy and the 2D energy in backward propagating modes (Fig. 1-A2) increase as a function of θUB until 90° and then decrease as θUB → 180°. The total energy, 2D energy, and slab energy in forward propagating modes are approximately constant between θUB = 0° and θUB = 180°. In the fast solar wind, the total energy and the 2D energy in backward propagating modes also show a higher value at about θUB = 88°, indicating the generation of the energy in backward propagating modes. It shows that the slab energy in backward propagating modes has a minimum value between 93° −107°, however, such a minimum value of the energy in backward propagating modes is not observed in the slow solar wind. The fast solar wind results can be improved with further statistical analysis because SolO did not observe many fast solar wind intervals in our selected time interval.
The bottom panels of each case in Fig. 1 show the ratio between the perpendicular variances and the slab variances of the energy in forward propagating modes (Figs. 1-a1/b1), the energy in backward propagating modes (Figs. 1-a2/b2), the fluctuating magnetic energy (Figs.1-a3/b3), and the fluctuating kinetic energy (Figs. 1-a4/b4) as a function of θUB for the slow solar wind and the fast solar wind. In the slow solar wind, the ratio between the 2D energy and slab energy in (i) forward propagating modes is about 5 when θUB = 0°, which increases to about 12 at θUB = 98° and then decreases as θUB → 180°; (ii) backward propagating modes is about 1 when θUB = 0°, which increases to about 14 at θUB = 86° and then decreases as θUB → 180°; (iii) magnetic field fluctuations is about 7 at θUB = 0°, which increases to about 18 at θUB = 80° and then decreases as θUB → 180°, and (iv) kinetic energy fluctuations is about 2 at θUB = 0°, which increases to about 12 at θUB = 92° and then decreases as θUB → 180°.
In the fast solar wind, the ratio between the 2D energy and slab energy in forward propagating modes (Fig. 1-b1), energy in backward propagating modes (Fig. 1-b2), magnetic field fluctuations (Fig. 1-b3), and kinetic energy fluctuations (Fig. 1-b4) increases from about θUB = 60° to θUB = 95°−101° and then decreases as θUB → 180°. The results are similar to those in the slow solar wind, but they are not symmetrical about θUB = 90° as in the slow solar wind.
5. Radial evolution of 2D and slab turbulence
We compare the theoretical results of the coupled solar wind equations and the NI MHD 2D plus slab turbulence transport equations with observations of fast and slow solar wind made by Solar Orbiter in the outbound direction. For the first time, we compare the theoretical and observed 2D energy and slab energy in forward propagating modes, energy in backward propagating modes, magnetic field fluctuations, and kinetic energy fluctuations as a function of the heliocentric distance in the inner heliosphere. Similarly, we also compare the theoretical and observed normalized cross-helicity and normalized residual energy for 2D turbulence and slab turbulence. The theoretical results for the slow solar wind and fast solar wind are obtained by solving the coupled solar wind equations (that is Eqs. (1)–(4)) and the quasi-2D and NI/slab turbulence transport model equations (that is Eqs. (9)–(16)) using a Runge-Kutta fourth order method, and the boundary conditions shown in Table 1. Table 2 shows the parameter values used for the slow solar wind and fast solar wind turbulence transport model equations.
Boundary values for solar wind parameters and turbulence quantities for the slow solar wind (SW) and fast solar wind (FW).
Values of the parameters used for the slow solar wind (SW) and fast solar wind (FW) turbulence model.
Using the same format as Fig. 1, in the top panels of (a) and (b) in Fig. 2, we compare the theoretical and observed total energy, 2D energy and slab energy corresponding to forward propagating modes (Figs. 2-A1/B1), backward propagating modes (Figs. 2-A2/B2), magnetic energy fluctuations (Figs. 2-A3/B3), and kinetic energy fluctuations (Figs. 2-A4/B4) for the slow and fast solar wind as a function of the heliocentric distance. In Fig. 2, the dashed blue curve and the blue scatter plots denote the theoretical and observed slab energy, the solid red curve and the red scatter plots the theoretical and observed 2D energy, and the solid black curve and the black scatter plots the theoretical total energy2 and the observed total energy. Similarly, in the second and third panels of Fig. 2, we compare the ratio of the theoretical 2D and slab turbulence energy for the forward propagating modes (Figs. 2-a1/b1), the backward propagating modes (Figs. 2-a2/b2), the variance of the magnetic field fluctuations (Figs. 2-a3/b3), and the kinetic energy fluctuations (Figs. 2-a4/b4) with the corresponding observed ratios as a function of the heliocentric distance (the solid black curves denote the theoretical results, and the black scatter plots with error bars show the observed results).
 |
Fig. 2. Comparison between the theoretical and observed total turbulence energy, perpendicular turbulence energy and slab turbulence energy, and the ratio between the perpendicular and slab turbulence energy as a function of the heliocentric distance for the slow and fast solar wind. Figures A1/B1, A2/B2, A3/B3, and A4/B4 show the energy in forward propagating modes, the energy in backward propagating modes, the fluctuating magnetic energy, and the fluctuating kinetic energy. Figures a1/b1, a2/b2, a3/b3, and a4/b4 show the corresponding ratios between the perpendicular and slab turbulence energy. The solid and dashed curves show the theoretical results, and the scatter plots with error bars show the observed results. See the text for details. (a) Slow solar wind. (b) Fast solar wind. |
Figure 2-A1 shows good agreement between the theoretical and observed total energy, 2D energy, and slab energy in forward propagating modes. The theoretical total energy, 2D energy, and slab energy in forward propagating modes decrease as r−1.21, r−1.28, and r−0.67 with increasing heliocentric distance. This shows that the 2D energy in forward propagating modes decreases more rapidly than the slab energy in forward propagating modes. Similar to Fig. 1, the observed total energy (green scatter plots) and 2D plus slab energy (black scatter plots) in forward propagating modes are almost similar, indicating that the turbulence is a superposition of 2D turbulence and slab turbulence, and the radial evolution is determined primarily by the 2D majority component. Furthermore, the 2D (theoretical and observed) energy in forward propagating modes is close to the total (theoretical and observed) energy in forward propagating modes and larger than the slab energy in forward propagating modes. Figure 2-a1 shows that the 2D energy in forward propagating modes is about 8 times larger than the slab energy in forward propagating modes over the heliocentric distance 140–170 R⊙. Hence, the energy in 2D forward propagating modes is a dominant component in the inner heliosphere, which is consistent with previous theoretical and observational work (Zank & Matthaeus 1992b; Bieber et al. 1996)- that predicted that 2D turbulence dominates solar wind turbulence.
For the fast solar wind, Fig. 2-B1 shows the theoretical and observed total energy, 2D energy, and slab energy in forward propagating modes with increasing heliocentric distance. The total energy, 2D energy, and slab energy in forward propagating modes of fast solar wind are relatively larger than those of the slow solar wind (see Fig. 2-A1), and decrease as r−1.15, r−1.22, and r−0.51, respectively. In Fig. 2-b1, the ratio between the theoretical 2D energy and slab energy in forward propagating modes (solid black curve), and the ratio of the observed 2D energy and slab energy in forward propagating modes (scatter plots) is reasonably consistent. The ratio between the theoretical 2D energy and slab energy is ∼12 at 140 R⊙, and ∼10 at 193 R⊙, indicating that the energy in forward propagating modes of fast solar wind in the direction perpendicular to the mean magnetic field remains the dominant component.
In contrast to the energy in forward propagating modes for the slow and fast solar wind, the energy in backward propagating modes of slow and fast solar wind increases with increasing distance (Figs. 2-A2/B2). In Fig. 2-A2, the theoretical and observed total energy, 2D energy, and slab energy in backward propagating modes of slow solar wind follow heliocentric power laws with r1.47, r0.69, and r1.34, respectively. As suggested by Coleman (1968), the turbulent shear source generated by the difference between fast solar wind and slow solar wind produces backward propagating modes in the inner heliosphere (Adhikari et al. 2015). Similarly, the gradients in the solar wind speed, solar wind density, and magnetic field can also generate backward propagating modes. These effects are reflected in Fig. 2-A2, where the energy density of backward propagating modes increases with increasing distance. Figure 2-a2 compares the observed and theoretical ratio between the 2D and slab energy in backward propagating modes as a function of heliocentric distance. Both theoretical and observed ratios corresponding to the energy in backward propagating modes increase from about 4 to about 6 over the distance the range 140–170 R⊙, again indicating the dominance of the 2D turbulence energy of backward propagating modes.
Similarly, in the fast solar wind, the theoretical total energy, 2D energy, and slab energy in backward propagating modes follow power laws r0.35, r0.14, and r0.32, respectively (Fig. 2-B2). The energy in backward propagating modes in the fast solar wind increases more slowly than that in slow solar wind. We note that in this case, only the gradients in the solar wind speed, solar wind density, and magnetic field are responsible for the increase of energy in backward propagating modes (Adhikari et al. 2021). Figure 2-b2 compares the ratio of the observed and theoretical 2D energy and slab energy in backward propagating modes. In contrast to the result in the slow solar wind, the theoretical result increases initially and then flattens as a function of the heliocentric distance, which may be due to the absence of a turbulent shear source.
Figure 2-A3 shows the radial evolution of total energy, 2D energy, and slab energy for the variance of the magnetic field fluctuations in the slow solar wind as a function of the heliocentric distance. In the figure, the theoretical and observed 2D, slab, and total fluctuating magnetic energy decrease approximately as r−2.54, r−2.04, and r−2.49 with increasing heliocentric distance. In the slow solar wind, the result shows that the 2D (theoretical and observed) fluctuating magnetic energy is about 10 times larger than the slab (theoretical and observed) fluctuating magnetic energy over the heliocentric distance 140–170 R⊙ (Fig. 2-a3). Figure 3-B3 shows that the total, 2D, and slab fluctuating magnetic energy in the fast solar wind are relatively higher than those in the slow solar wind (Fig. 2-A3). The comparison between the theoretical and observed results in the fast solar wind shows good agreement. The theoretical 2D, slab, and total turbulent magnetic energy decrease as r−2.87, r−1.94, and r−2.79, respectively, indicating that the fluctuating magnetic energy of fast solar wind decreases more rapidly than that in the slow solar wind. Similarly, the ratio between the theoretical and observed 2D and slab fluctuating magnetic energy (Fig. 2-b3) shows that the theoretical and observed results decrease with increasing heliocentric distance. The 2D fluctuating magnetic energy remains the dominant component of the fast solar wind turbulence.
 |
Fig. 3. Comparison between the theoretical and observed normalized cross-helicity (A1/B1), normalized residual energy (A2/B2), and the variance of the density fluctuations (A3/B3) as a function of heliocentric distance for the slow and fast solar wind. The solid curves indicate the theoretical results. The scatter plots with error bars identify the observed results. (a) Slow solar wind. (b) Fast solar wind. |
Figure 2-A4 shows that the theoretical and observed total fluctuating kinetic energy, 2D fluctuating kinetic energy, and slab fluctuating kinetic energy of slow solar wind decrease as a function of the heliocentric distance. In the figure, the theoretical 2D fluctuating kinetic energy follows a power law of r−1.24, the theoretical slab fluctuating kinetic energy decays as r−0.02, and the theoretical total fluctuating kinetic energy drops as r−0.99. The theoretical and observed results show excellent agreement over the heliocentric distance 140–170 R⊙. Figure 2-a4 shows that the (theoretical and observed) 2D fluctuating kinetic energy is higher than the (theoretical and observed) slab fluctuating kinetic energy by about 4–5 over the range 140–170 R⊙. This illustrates that the 2D turbulent kinetic energy is the dominant component in the slow solar wind as well. Similarly, in the fast solar wind, Fig. 2-B4 shows that the theoretical and observed fluctuating kinetic energy is in reasonable agreement with increasing heliocentric distance. The 2D fluctuating kinetic energy, slab fluctuating kinetic energy, and total fluctuating kinetic energy exhibit power laws of r−1.59, r0.08, and r−1.29, respectively. Furthermore, the theoretical and observed ratio between the 2D and slab fluctuating kinetic energy in the fast solar wind decreases as a function of the heliocentric distance. Both theoretical and observed ratios are greater than 1 over the heliocentric distance 140–193 R⊙ (Fig. 2-b4).
Figures 3-A1 and B1 show the theoretical and observed normalized cross-helicity as a function of the heliocentric distance in the slow and fast solar wind, respectively. In the figure, the solid red, blue, and green curves represent the theoretical 2D normalized cross-helicity, slab normalized cross-helicity, and total normalized cross-helicity. Similarly, the red, blue, and green scatter plots with error bars denote the corresponding observed normalized cross-helicity. In Fig. 3-A1, the theoretical and observed 2D normalized cross-helicity, the slab normalized cross-helicity, and the total normalized cross-helicity of slow solar wind decrease with increasing heliocentric distance. The normalized cross-helicity of the fast solar wind (Fig. 3-B1) also decreases as distance increases. It shows that the normalized cross-helicity of fast solar wind is larger than that of slow solar wind.
The comparisons between the theoretical and observed 2D normalized residual energy (solid red curve and red scatter plot), the slab normalized residual energy (solid blue curve and blue scatter diagram), and the total normalized residual energy (green curve and green scatter plot) of slow and fast solar wind as a function of the heliocentric distance are shown in Figs. 3-A2 and-B2, respectively. In the slow and fast solar wind, the theoretical 2D, slab, and total normalized residual energy are in good agreement with the corresponding observed normalized residual energy. However, the observed normalized residual energy in the fast solar wind scatters at about 193 R⊙. The theoretical and observed results for the slow and fast solar wind show that the quasi-2D turbulence is dominated more by turbulent magnetic energy and the slab normalized residual energy is less dominated by turbulent magnetic energy. In the slow solar wind, the slab normalized residual energy is close to 0, while that in the fast wind the slab fluctuating magnetic energy is larger than the slab fluctuating kinetic energy.
Figures 3-A3 and B3 compare the theoretical and observed variance of the density fluctuations in the slow and fast solar wind as a function of the heliocentric distance, respectively. The theoretical variance of the density fluctuations in the slow solar wind decreases as r−4.65 (Fig. 3-A3), while the observed variance of the density fluctuations does not decrease with increasing heliocentric distance. This may be related to Fig. 5-A4, showing that the observed solar wind density of the slow solar wind is approximately constant. The theoretical and observed variances of the density fluctuations in the fast solar wind decrease with increasing heliocentric distance, and the theoretical density variance follows a power law of r−5.44, quite different from the slow solar wind.
The theoretical and observed correlation lengths corresponding to the energy in forward propagating modes (Figs. 4-A1/B1), the energy in backward propagating modes (Figs. 4-A2/B2), the residual energy (Figs. 4-A3/B3), the fluctuating kinetic energy (Figs. 4-A4/B4), and the fluctuating magnetic energy (Figs. 4-A5/B5) are shown for the slow and fast solar wind as a function of the heliocentric distance in Fig. 4. The theoretical and observed correlation lengths corresponding to forward propagating modes in the slow solar wind (Fig. 4-A1) and in the fast solar wind (Fig. 4-B1) increase with increasing heliocentric distance. In the slow solar wind, the theoretical correlation length of 2D energy in forward propagating modes is similar to the observed correlation length. In the fast solar wind, the theoretical correlation length of the slab energy in forward propagating modes is similar to the observed correlation length.
 |
Fig. 4. Comparison between the theoretical and observed correlation lengths corresponding to energy in forward propagating modes (A1/B1), energy in backward propagating modes (A2/B2), residual energy (A3/B3), fluctuating kinetic energy (A4/B4), and fluctuating magnetic energy (A5/B4) as a function of the heliocentric distance. The solid curve show the correlation length corresponding to 2D turbulence. The dashed curve shows the correlation length of slab turbulence. The scatter plot with an error bar shows the observed correlation length. (a) Slow solar wind. (b) Fast solar wind. |
In the slow solar wind, the theoretical and observed correlation lengths corresponding to backward propagating modes decrease as a function of the heliocentric distance (Fig. 4-A2). In the fast solar wind, both correlation lengths increase with increasing heliocentric distance (Fig. 4-B2). The decrease of correlation length in the slow solar wind may be related to the turbulent shear source produced by fast and slow solar wind in the inner heliosphere, which is not included in the fast solar wind turbulence model.
The theoretical and observed 2D correlation length corresponding to the residual energy of the slow solar wind increases with increasing heliocentric distance, and shows good agreement as a function of the heliocentric distance (Fig. 4-A3). The theoretical slab correlation length for the residual energy decreases initially and then increases. In the fast solar wind, the theoretical slab correlation length for the residual energy shows good agreement with that observed correlation length and the theoretical 2D correlation length for the residual energy increases with increasing heliocentric distance. The theoretical and observed correlation lengths corresponding to the fluctuating kinetic energy (Figs. 4-A4/B4) and the fluctuating magnetic energy (Figs. 4-A5/B5) for the slow and fast solar wind do not show good agreement as a function of the heliocentric distance. In the slow solar wind, the observed correlation length corresponding to the fluctuating kinetic energy and the fluctuating magnetic energy is approximately constant, while in the fast solar wind, the observed correlation length of velocity fluctuations and magnetic field fluctuations increases as distance increases.
6. Radial evolution of solar wind background profile
As discussed in Sect. 2, the solar wind equations are coupled with the NI MHD turbulence transport model equations. Therefore, the background profiles and turbulence influence each other. Here, we assume that the background magnetic field is inversely proportional to the square of distance. Figure 5 compares the theoretical and observed solar wind temperature (Figs. 5-A1/B1), solar wind entropy (Figs. 5-A2/B2), solar wind speed (Figs. 5-A3/B3), and solar wind proton density (Figs. 5-A4/B4) of the slow and fast solar wind as a function of heliocentric distance. In the figure, the solid and dashed curves represent the theoretical results and the scatter plots with error bars identify the observed results. In Fig. 5-A1, the theoretical proton temperature of the slow solar wind decreases gradually as r−0.98, similar to the observed solar wind proton temperature and is consistent with the temperature of the slow solar wind measured by Parker Solar Probe during its first encounter (Adhikari et al. 2020c). The theoretical electron temperature of the slow solar wind flattens slightly as a function of heliocentric distance. Coulomb collisions between solar wind protons and electrons do not influence the solar wind proton and electron temperature. However, the electron heat flux and the turbulence heating influence the solar wind electron temperature, and the turbulence heating alone affects the solar wind proton temperature. In this study, we assume that sixty percent of the available turbulent energy heats the solar wind protons, and forty percent the solar wind electrons (Breech et al. 2009; Engelbrecht & Strauss 2018; Adhikari et al. 2021). In the fast solar wind, the theoretical proton temperature decreases as r−1.26, which is more rapidly than the radial profile of the slow solar wind temperature. Interestingly, this theoretical radial profile of temperature of fast solar wind is approximately similar to the observed radial temperature profile of the fast solar wind measured by PSP in its first encounter (Adhikari et al. 2020a). The observed proton temperature for the fast solar wind in Fig. 5-B1 shows a large scatter. The dashed curve shows that the theoretical solar wind electron temperature of fast solar wind decreases as r−0.48 with increasing heliocentric distance.
 |
Fig. 5. Comparison between the theoretical and observed solar wind proton temperature Tp (first column), solar wind proton entropy Sp (second column), solar wind speed U (third column), and solar wind proton density ρ (fourth column) as a function of the heliocentric distance for the slow and fast solar wind. The solid curve shows the theoretical result. The black scatter plot with an error bar shows the observed value. The dashed curve shows the theoretical solar wind electron temperature (Te) and the theoretical solar wind electron entropy (Se). (a) Slow solar wind. (b) Fast solar wind. |
Figure 5-A2/B2 displays the comparison between the theoretical and observed solar wind proton entropy 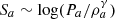 (a ≡ (p, e), where p indicates protons and e electrons) for the slow and fast solar wind as a function of the heliocentric distance. In both cases, the theoretical and observed proton entropy agree very well with increasing heliocentric distance. In the slow solar wind (Fig. 5-A2), the theoretical proton and electron entropy increase as r0.01 and r0.04, which results in the proton and electron entropy increasing by about 0.17% and 0.8% from 142 R⊙ to 169 R⊙. Similarly, in the fast solar wind (Fig. 5-B2), the solar wind proton and electron entropy behave as power laws of r0.002 and r0.02, respectively, indicating that the proton entropy remains approximately constant, while the electron entropy increases by about 0.6% within 27 R⊙. As suggested by Adhikari et al. (2020b), the dissipation of turbulence leads to an increase in the solar wind entropy. The electron heat flux may also influence the solar wind entropy (e.g., Adhikari et al. 2021).
(a ≡ (p, e), where p indicates protons and e electrons) for the slow and fast solar wind as a function of the heliocentric distance. In both cases, the theoretical and observed proton entropy agree very well with increasing heliocentric distance. In the slow solar wind (Fig. 5-A2), the theoretical proton and electron entropy increase as r0.01 and r0.04, which results in the proton and electron entropy increasing by about 0.17% and 0.8% from 142 R⊙ to 169 R⊙. Similarly, in the fast solar wind (Fig. 5-B2), the solar wind proton and electron entropy behave as power laws of r0.002 and r0.02, respectively, indicating that the proton entropy remains approximately constant, while the electron entropy increases by about 0.6% within 27 R⊙. As suggested by Adhikari et al. (2020b), the dissipation of turbulence leads to an increase in the solar wind entropy. The electron heat flux may also influence the solar wind entropy (e.g., Adhikari et al. 2021).
The fast and slow solar wind exhibit different turbulence properties. The fast solar wind originates from polar coronal holes and the slow solar wind originates from the equatorial region of the Sun. Figure 5-A3/B3 shows that SolO observes the slow solar wind with an average speed of about 345 km s−1 between 140 R⊙ and 170 R⊙, and the fast solar wind with an average speed of 475 km s−1 over the heliocentric distance 140 − 170 R⊙. The theoretical speed of the slow solar wind agrees very well with the observed speed of slow solar wind, with the theoretical slow solar wind speed increasing slowly as r0.01 as a function of the heliocentric distance. Similarly, the theoretical speed of fast solar wind agrees reasonably with the observed speed, and exhibits a power law of r0.02. The slight increase in the fast and slow solar wind speed is due to the electron pressure and proton pressure gradients. In the outer heliosphere in the upwind direction, theory (Zank et al. 2018b) and observations (Richardson & Wang 2003; Elliott et al. 2019) show that the solar wind speed decelerates due to the presence of pickup ions. Such a decrease in the solar wind speed is not observed in the downwind direction until 75 au because of the reduced production of pickup ions (Nakanotani et al. 2020). Furthermore, Adhikari et al. (2020b) demonstrated that stream-shear interactions can also lead to a decrease in the solar wind speed, although it is not significant.
Figure 5-A4/B4 compares the theoretical and observed solar wind proton densities as a function of the heliocentric distance. The theoretical proton density of the slow solar wind and fast solar wind are in good agreement with the corresponding observed proton density. In the slow solar wind, the theoretical proton density exhibits a power law of r−2.01, while in the fast solar wind, the proton density follows a radial profile of r−2.02. The proton density of the fast solar wind drops more rapidly than that of the slow solar wind, which is consistent with the higher speed of the fast solar wind than the slow solar wind.
7. Discussion and conclusions
Turbulence in the solar wind is considered as a superposition of the majority 2D turbulence and a minority slab turbulence. We studied anisotropic turbulence in the slow and fast solar wind as a function of the angle between the mean solar wind speed and the mean magnetic field (θUB) and as a function of the heliocentric distance. We used Solar Orbiter measurements from July 7, 2020 – August 31, 2020, in which the Solar Orbiter measures the slow solar wind with an average speed of 340 km s−1, and the fast solar wind with an average speed of 475 km s−1. In two solar wind streams, we calculated the perpendicular energy and slab energy in forward and backward propagating modes, normalized residual energy, normalized cross-helicity, fluctuating magnetic energy, and fluctuating kinetic energy in the direction perpendicular and parallel to the mean magnetic field as a function of the heliocentric distance and θUB. We compared the observed results with the solar wind plus NI MHD turbulence transport model equations (Zank et al. 2017; Adhikari et al. 2021), and found excellent agreement between the theoretical and observed results in the slow and fast solar wind as a function of the heliocentric distance.
We summarize our basic results as follows.
-
The total turbulence energy in forward and backward propagating modes, fluctuating magnetic energy, and fluctuating kinetic energy in the slow and fast solar wind is approximately similar to the corresponding 2D plus slab turbulence energy. The 2D energy in forward and backward propagating modes, fluctuating magnetic energy, and fluctuating kinetic energy is similar to the corresponding total energy and higher than the corresponding slab turbulence energy. This result is consistent with the NI MHD theory (Zank & Matthaeus 1992b, 1993; Zank et al. 2017), which predicts that solar wind turbulence is a superposition of the majority 2D component and a minority slab component.
-
The anisotropy in the Elsässer energies, the magnetic field fluctuations, and the kinetic energy fluctuations, that is the ratio between the 2D component and the slab component (
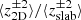 ,
, 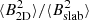 , and
, and 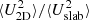 ) in the slow and fast solar wind increases from θUB = 0° to close to θUB = 90° and then decreases as θUB → 180°.
) in the slow and fast solar wind increases from θUB = 0° to close to θUB = 90° and then decreases as θUB → 180°. -
In the slow solar wind, the theoretical total energy, 2D energy, and slab energy in forward propagating modes decreases as r−1.21, r−1.28, and r−0.67 with increasing heliocentric distance, respectively. In the fast solar wind, the theoretical total energy, 2D energy, and slab energy in forward propagating modes decreases as r−1.15, r−1.22, and r−0.51 with increasing heliocentric distance. The ratio between the 2D energy and slab energy in forward propagating modes
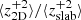 decreases as a function of the heliocentric distance, and
decreases as a function of the heliocentric distance, and 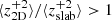 over the heliocentric distance 140–193 R⊙.
over the heliocentric distance 140–193 R⊙. -
In the slow and fast solar wind, the energy in backward propagating modes increases with increasing heliocentric distance, which is due to a turbulent shear source (Coleman 1968; Adhikari et al. 2015) and gradients in the solar wind speed, solar wind density, and magnetic field. The total energy, 2D energy, and slab energy in backward propagating modes follows radial profiles of r1.47, r0.69, and r1.34 in the slow solar wind, and r0.35, r0.14, and r0.32 in the fast solar wind, respectively. The ratio between the 2D energy and slab energy in backward propagating modes
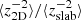 increases in the slow solar wind and slightly flattens in the fast solar wind as a function of the heliocentric distance. The ratio
increases in the slow solar wind and slightly flattens in the fast solar wind as a function of the heliocentric distance. The ratio 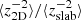 is greater than 1 between 140–193 R⊙, indicating that the energy in backward propagating modes in the direction perpendicular to the mean magnetic field is the dominant component.
is greater than 1 between 140–193 R⊙, indicating that the energy in backward propagating modes in the direction perpendicular to the mean magnetic field is the dominant component. -
The total fluctuating magnetic energy, the 2D fluctuating magnetic energy, and the slab fluctuating magnetic energy decreases as r−2.49, r−2.54, and r−2.04 in the slow wind, and r−2.79, r−2.87, and r−1.94 in the fast wind, respectively. In the slow wind, the ratio between the 2D fluctuating magnetic energy and the slab fluctuating magnetic energy
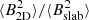 decreases more slowly than that in the fast solar wind. In both cases, the
decreases more slowly than that in the fast solar wind. In both cases, the 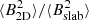 is greater than 1 in the heliocentric distance 140–193 R⊙.
is greater than 1 in the heliocentric distance 140–193 R⊙. -
In the slow solar wind, the total fluctuating kinetic energy drops as r−0.99, the 2D fluctuating kinetic energy decreases as r−1.24, and the slab fluctuating kinetic energy falls as r−0.02. In the fast solar wind, the total, 2D, and slab fluctuating kinetic energy follows the power of r−1.59, r0.08, and r−1.29, respectively. The theoretical
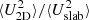 decreases as a function of the heliocentric distance in the slow and fast solar wind and shows that
decreases as a function of the heliocentric distance in the slow and fast solar wind and shows that 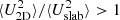 in the inner heliosphere.
in the inner heliosphere. -
In the slow and fast solar wind, the total normalized cross-helicity, the 2D normalized cross-helicity, and the slab normalized cross-helicity decreases with increasing heliocentric distance. The normalized cross-helicity in the fast solar wind is larger than that in the slow solar wind over the heliocentric distance 140–193 R⊙.
-
In the slow and fast solar wind, the total normalized residual energy, the 2D normalized residual energy, and the slab normalized residual energy decrease with increasing heliocentric distance. In both cases, the 2D normalized residual energy is dominated more by the turbulent magnetic energy. In the slow solar wind, the slab normalized residual energy is close to 0, while in the fast solar wind, the slab normalized residual energy is dominated by turbulent magnetic energy, but it is not as large when compared to the 2D normalized residual energy.
-
The theoretical variance of the density fluctuations in the slow solar wind follows a power law of r−4.65 and that in the fast solar wind follows a power law of r−5.44, indicating that the density variance in the slow solar wind decreases more slowly than that in the fast solar wind.
-
In the slow solar wind, the theoretical correlation length of quasi-2D energy in forward and backward propagating modes, and the residual energy is similar to the corresponding observed correlation lengths. In the fast solar wind, the theoretical correlation length of slab energy in forward and backward propagating modes and residual energy is similar to the corresponding observed correlation lengths.
-
The proton temperature of slow solar wind follows a power law of r−0.98 and that of fast solar wind exhibits the power law of r−1.26, which indicates that the proton temperature of fast solar wind decreases more rapidly than that of slow solar wind. The presence of a turbulent shear source in the slow solar wind leads to a slow decrease in proton temperature in the slow solar wind.
-
The solar wind density in the fast solar wind decreases slightly more rapidly than that in the slow solar wind, which is consistent with the higher speed of fast solar wind than slow wind.
We studied the evolution of anisotropic turbulence in the fast and slow solar wind in the inner heliopshere through the 2D and slab variances of Elsässer energies, magnetic field fluctuations, and kinetic energy fluctuations in the direction perpendicular and parallel to the mean magnetic field (e.g., Robinson & Rusbridge 1971; Zweben et al. 1979; Belcher & Davis 1971) and NI MHD turbulence model (Zank et al. 2017). Since PSP and Helios 2 also measure fast and slow solar wind streams, it will be of great significance to compare these results with the 2D and slab turbulence quantities derived from the PSP and Helios 2 data sets in the inner heliosphere. This will be a subject of the follow-up study. In addition, we will study the evolution of anisotropic turbulence in the outer heliosphere in the upwind direction (Pine et al. 2020) using Voyager 2 measurements and in the downwind direction using Pioneer 10 measurements with the NI MHD turbulence model.
Acknowledgments
We acknowledge the partial support of a Parker Solar Probe contract SV4-84017, an NSF EPSCoR RII-Track-1 cooperative agreement OIA-1655280, and a NASA award 80NSSC20K1783.
References
- Adhikari, L., Zank, G. P., Hu, Q., & Dosch, A. 2014, ApJ, 793, 52 [Google Scholar]
- Adhikari, L., Zank, G. P., Bruno, R., et al. 2015, ApJ, 805, 63 [Google Scholar]
- Adhikari, L., Zank, G. P., Telloni, D., et al. 2017a, ApJ, 851, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Adhikari, L., Zank, G. P., Hunana, P., et al. 2017b, ApJ, 841, 85 [Google Scholar]
- Adhikari, L., Zank, G. P., Zhao, L. L., et al. 2018, J. Phys. Conf. Ser., 1100 [Google Scholar]
- Adhikari, L., Zank, G. P., & Zhao, L. L. 2019, ApJ, 876, 26 [Google Scholar]
- Adhikari, L., Zank, G. P., & Zhao, L. L. 2020a, ApJ, 901, 14 [Google Scholar]
- Adhikari, L., Zank, G. P., Zhao, L. L., & Webb, G. M. 2020b, ApJ, 891, 34 [Google Scholar]
- Adhikari, L., Zank, G. P., Zhao, L. L., et al. 2020c, ApJ, 246, 38 [NASA ADS] [Google Scholar]
- Adhikari, L., Zank, G. P., Zhao, L. L., Nakanotani, M., & Tasnim, S. 2021, A&A, 650, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barakat, A. R., & Schunk, R. W. 1982, Plasma Phys., 24, 389 [Google Scholar]
- Belcher, J. W., & Davis, L., Jr 1971, J. Geophys. Res., 76, 3534 [NASA ADS] [CrossRef] [Google Scholar]
- Bieber, J. W., Wanner, W., & Matthaeus, W. H. 1996, J. Geophys. Res., 101, 2511 [NASA ADS] [CrossRef] [Google Scholar]
- Braginskii, S. I. 1965, Rev. Plasma Phys., 1, 205 [Google Scholar]
- Breech, B., Matthaeus, W. H., Cranmer, S. R., Kasper, J. C., & Oughton, S. 2009, J. Geophys. Res. (Space Phys.), 114, A09103 [Google Scholar]
- Bruno, R., & Telloni, D. 2015, ApJ, 811, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Chhiber, R., Usmanov, A. V., Matthaeus, W. H., Parashar, T. N., & Goldstein, M. L. 2019, ApJS, 242, 12 [Google Scholar]
- Coleman, P. J., Jr 1968, ApJ, 153, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Cranmer, S. R., Matthaeus, W. H., Breech, B. A., & Kasper, J. C. 2009, ApJ, 702, 1604 [Google Scholar]
- Dasso, S., Milano, L. J., Matthaeus, W. H., & Smith, C. W. 2005, ApJ, 635, L181 [Google Scholar]
- Dasso, S., Matthaeus, W. H., Weygand, J. M., et al. 2008, Int. Cosmic Ray Conf., 1, 625 [NASA ADS] [Google Scholar]
- DeForest, C. E., Matthaeus, W. H., Viall, N. M., & Cranmer, S. R. 2016, ApJ, 828, 66 [Google Scholar]
- Dong, Y., Verdini, A., & Grappin, R. 2014, ApJ, 793, 118 [Google Scholar]
- Elliott, H. A., McComas, D. J., Zirnstein, E. J., et al. 2019, ApJ, 885, 156 [Google Scholar]
- Engelbrecht, N. E., & Strauss, R. D. T. 2018, ApJ, 856, 159 [Google Scholar]
- Ghosh, S., Matthaeus, W. H., Roberts, D. A., & Goldstein, M. L. 1998, J. Geophys. Res., 103, 23705 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Sridhar, S. 1995, ApJ, 438, 763 [Google Scholar]
- Grappin, R. 1986, Phys. Fluids, 29, 2433 [CrossRef] [Google Scholar]
- Grappin, R., Frisch, U., Pouquet, A., & Leorat, J. 1982, A&A, 105, 6 [Google Scholar]
- Grappin, R., Leorat, J., & Pouquet, A. 1983, A&A, 126, 51 [Google Scholar]
- Grappin, R., Velli, M., & Mangeney, A. 1993, Phys. Rev. Lett., 70, 2190 [NASA ADS] [CrossRef] [Google Scholar]
- Horbury, T. S., Forman, M., & Oughton, S. 2008, Phys. Rev. Lett., 101, 175005 [Google Scholar]
- Horbury, T. S., O’Brien, H., Carrasco Blazquez, I., et al. 2020, A&A, 642, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hunana, P., & Zank, G. P. 2010, ApJ, 718, 148 [Google Scholar]
- Klein, L. W., Roberts, D. A., & Goldstein, M. L. 1991, J. Geophys. Res., 96, 3779 [NASA ADS] [CrossRef] [Google Scholar]
- Klein, L., Bruno, R., Bavassano, B., & Rosenbauer, H. 1993, J. Geophys. Res., 98, 17461 [NASA ADS] [CrossRef] [Google Scholar]
- Matthaeus, W. H., Goldstein, M. L., & Roberts, D. A. 1990, J. Geophys. Res., 95, 20673 [Google Scholar]
- Matthaeus, W. H., Dasso, S., Weygand, J. M., et al. 2005, Phys. Rev. Lett., 95, 231101 [NASA ADS] [CrossRef] [Google Scholar]
- Milano, L. J., Dasso, S., Matthaeus, W. H., & Smith, C. W. 2004, Phys. Rev. Lett., 93, 155005 [NASA ADS] [CrossRef] [Google Scholar]
- Montgomery, D. 1982, Phys. Scr., 1982, 83 [CrossRef] [Google Scholar]
- Montgomery, D., & Turner, L. 1981, Phys. Fluids, 24, 825 [Google Scholar]
- Nakanotani, M., Zank, G. P., Adhikari, L., et al. 2020, ApJ, 901, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Narita, Y., Glassmeier, K.-H., Sahraoui, F., & Goldstein, M. L. 2010, Phys. Rev. Lett., 104, 171101 [NASA ADS] [CrossRef] [Google Scholar]
- Osman, K. T., & Horbury, T. S. 2007, ApJ, 654, L103 [NASA ADS] [CrossRef] [Google Scholar]
- Owen, C. J., Bruno, R., Livi, S., et al. 2020, A&A, 642, A16 [EDP Sciences] [Google Scholar]
- Parker, E. N. 1958, ApJ, 128, 664 [Google Scholar]
- Pilipp, W. G., Muehlhaeuser, K. H., Miggenrieder, H., Rosenbauer, H., & Schwenn, R. 1990, J. Geophys. Res., 95, 6305 [Google Scholar]
- Pine, Z. B., Smith, C. W., Hollick, S. J., et al. 2020, ApJ, 900, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Podesta, J. J. 2009, ApJ, 698, 986 [NASA ADS] [CrossRef] [Google Scholar]
- Richardson, J. D., & Wang, C. 2003, in Solar Wind Ten, eds. M. Velli, R. Bruno, F. Malara, & B. Bucci, AIP Conf. Ser., 679, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Robinson, D. C., & Rusbridge, M. G. 1971, Phys. Fluids, 14, 2499 [CrossRef] [Google Scholar]
- Ruffolo, D., Matthaeus, W. H., Chhiber, R., et al. 2020, ApJ, 902, 94 [Google Scholar]
- Ruiz, M. E., Dasso, S., Matthaeus, W. H., Marsch, E., & Weygand, J. M. 2011, J. Geophys. Res. (Space Phys.), 116, A10102 [Google Scholar]
- Shebalin, J. V., Matthaeus, W. H., & Montgomery, D. 1983, J. Plasma Phys., 29, 525 [Google Scholar]
- Shiota, D., Zank, G. P., Adhikari, L., et al. 2017, ApJ, 837, 75 [Google Scholar]
- Tang, B., Zank, G. P., & Kolobov, V. I. 2020, ApJ, 892, 95 [Google Scholar]
- Telloni, D., Carbone, F., Bruno, R., et al. 2019, ApJ, 887, 160 [Google Scholar]
- Tessein, J. A., Smith, C. W., MacBride, B. T., et al. 2009, ApJ, 692, 684 [NASA ADS] [CrossRef] [Google Scholar]
- Verdini, A., & Grappin, R. 2015, ApJ, 808, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Verdini, A., & Grappin, R. 2016, ApJ, 831, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Verdini, A., Velli, M., Matthaeus, W. H., Oughton, S., & Dmitruk, P. 2010, ApJ, 708, L116 [Google Scholar]
- Wang, X., Tu, C., & He, J. 2014, ApJ, 783, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, X., Tu, C., He, J., et al. 2015, ApJ, 810, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, X., Tu, C., & He, J. 2019, ApJ, 871, 93 [Google Scholar]
- Weygand, J. M., Matthaeus, W. H., Dasso, S., et al. 2009, J. Geophys. Res. (Space Phys.), 114, A07213 [Google Scholar]
- Wicks, R. T., Horbury, T. S., Chen, C. H. K., & Schekochihin, A. A. 2010, MNRAS, 407, L31 [Google Scholar]
- Yuan, D., Shen, Y., Liu, Y., et al. 2019, ApJ, 884, L51 [CrossRef] [Google Scholar]
- Zank, G. P. 2014, in Transport Processes in Space Physics and Astrophysics (Berlin: Springer Verlag), Lecture Notes Phys., 877 [CrossRef] [Google Scholar]
- Zank, G. P., & Matthaeus, W. H. 1992a, J. Plasma Phys., 48, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Zank, G. P., & Matthaeus, W. H. 1992b, J. Geophys. Res., 97, 17189 [Google Scholar]
- Zank, G. P., & Matthaeus, W. H. 1993, Phys. Fluids, 5, 257 [Google Scholar]
- Zank, G. P., Matthaeus, W. H., & Smith, C. W. 1996, J. Geophys. Res., 101, 17093 [Google Scholar]
- Zank, G. P., Dosch, A., Hunana, P., et al. 2012, ApJ, 745, 35 [Google Scholar]
- Zank, G. P., Adhikari, L., Hunana, P., et al. 2017, ApJ, 835, 147 [Google Scholar]
- Zank, G. P., Adhikari, L., Hunana, P., et al. 2018a, ApJ, 854, 32 [Google Scholar]
- Zank, G. P., Adhikari, L., Zhao, L. L., et al. 2018b, ApJ, 869, 23 [Google Scholar]
- Zank, G. P., Nakanotani, M., Zhao, L. L., Adhikari, L., & Telloni, D. 2020, ApJ, 900, 115 [Google Scholar]
- Zhao, L.-L., Adhikari, L., Zank, G. P., Hu, Q., & Feng, X. S. 2018, ApJ, 856, 94 [Google Scholar]
- Zhao, L. L., Zank, G. P., Adhikari, L., et al. 2020, ApJ, 898, 113 [Google Scholar]
- Zweben, S. J., Menyuk, C. R., & Taylor, R. J. 1979, Phys. Rev. Lett., 42, 1270 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Boundary values for solar wind parameters and turbulence quantities for the slow solar wind (SW) and fast solar wind (FW).
Values of the parameters used for the slow solar wind (SW) and fast solar wind (FW) turbulence model.
All Figures
 |
Fig. 1. Top and third panels: total (green), perpendicular (red), slab (blue) and summation of perpendicular and slab, that is perpendicular plus slab (black) turbulence energy corresponding to the energy in forward propagating modes (A1/B1), the energy in backward propagating modes (A2/B2), the fluctuating magnetic energy (A3/B3), and the fluctuating kinetic energy (A4/B4) for the slow and fast solar wind as a function of the angle between the mean solar wind speed and the mean magnetic field (θUB). Second and fourth panels: ratio between the 2D and slab variances of energy in forward propagating modes (a1/b1) and backward propagating modes (a2/b2), the fluctuating magnetic energy (a3/b3), and the fluctuating kinetic energy (a4/b4) as a function of θUB. (a) Slow solar wind. (b) Fast solar wind. |
| In the text | |
 |
Fig. 2. Comparison between the theoretical and observed total turbulence energy, perpendicular turbulence energy and slab turbulence energy, and the ratio between the perpendicular and slab turbulence energy as a function of the heliocentric distance for the slow and fast solar wind. Figures A1/B1, A2/B2, A3/B3, and A4/B4 show the energy in forward propagating modes, the energy in backward propagating modes, the fluctuating magnetic energy, and the fluctuating kinetic energy. Figures a1/b1, a2/b2, a3/b3, and a4/b4 show the corresponding ratios between the perpendicular and slab turbulence energy. The solid and dashed curves show the theoretical results, and the scatter plots with error bars show the observed results. See the text for details. (a) Slow solar wind. (b) Fast solar wind. |
| In the text | |
 |
Fig. 3. Comparison between the theoretical and observed normalized cross-helicity (A1/B1), normalized residual energy (A2/B2), and the variance of the density fluctuations (A3/B3) as a function of heliocentric distance for the slow and fast solar wind. The solid curves indicate the theoretical results. The scatter plots with error bars identify the observed results. (a) Slow solar wind. (b) Fast solar wind. |
| In the text | |
 |
Fig. 4. Comparison between the theoretical and observed correlation lengths corresponding to energy in forward propagating modes (A1/B1), energy in backward propagating modes (A2/B2), residual energy (A3/B3), fluctuating kinetic energy (A4/B4), and fluctuating magnetic energy (A5/B4) as a function of the heliocentric distance. The solid curve show the correlation length corresponding to 2D turbulence. The dashed curve shows the correlation length of slab turbulence. The scatter plot with an error bar shows the observed correlation length. (a) Slow solar wind. (b) Fast solar wind. |
| In the text | |
 |
Fig. 5. Comparison between the theoretical and observed solar wind proton temperature Tp (first column), solar wind proton entropy Sp (second column), solar wind speed U (third column), and solar wind proton density ρ (fourth column) as a function of the heliocentric distance for the slow and fast solar wind. The solid curve shows the theoretical result. The black scatter plot with an error bar shows the observed value. The dashed curve shows the theoretical solar wind electron temperature (Te) and the theoretical solar wind electron entropy (Se). (a) Slow solar wind. (b) Fast solar wind. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



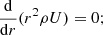
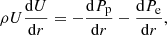
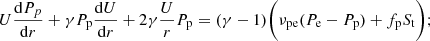
![$$ \begin{aligned} \begin{split} {U}&\frac{\mathrm{d} P_{\rm e}}{\mathrm{d}r} + \gamma P_{\rm e} \frac{\mathrm{d}U}{\mathrm{d}r} + 2 \gamma \frac{U}{r} P_{\rm e} \\&= (\gamma -1) \bigg [\nu _{\rm ep}(P_{\rm p} - P_{\rm e}) - \nabla \cdot \boldsymbol{q}_{\rm e} + (1-f_{\rm p}) S_{\rm t} \bigg ], \end{split} \end{aligned} $$](/articles/aa/full_html/2021/12/aa40672-21/aa40672-21-eq9.gif)
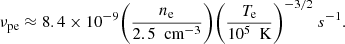
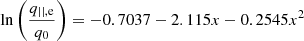
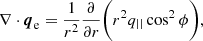
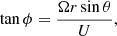
![$$ \begin{aligned} \begin{split} S_{\rm t}&= \alpha m_{\rm p} n_{\rm s} \bigg [ \frac{\langle {{z^\infty }^+}^2 \rangle ^2 \langle {{z^\infty }^-}^2 \rangle ^{1/2}}{L_\infty ^+} + \frac{\langle {{z^\infty }^-}^2 \rangle ^2 \langle {{z^\infty }^+}^2 \rangle ^{1/2}}{L_\infty ^-} \\&\quad + E_D^\infty \bigg (\frac{\langle {{z^\infty }^+}^2 \rangle ^{1/2}}{\lambda ^-_\infty } + \frac{\langle {{z^\infty }^-}^2 \rangle ^{1/2}}{\lambda ^+_\infty } \bigg ) + 2 \frac{\langle {{z^*}^+}^2 \rangle \langle {{z^\infty }^+}^2 \rangle \langle {{z^\infty }^-}^2 \rangle ^{1/2}}{L_\infty ^+} \\&\quad + 2\frac{\langle {{z^*}^-}^2 \rangle \langle {{z^\infty }^-}^2 \rangle \langle {{z^\infty }^+}^2 \rangle ^{1/2}}{L_\infty ^-} + \frac{\langle {{z^*}^+}^2 \rangle ^2 \langle {{z^*}^-}^2 \rangle ^{1/2}}{L_*^+}\\&\quad + \frac{\langle {{z^*}^-}^2 \rangle ^2 \langle {{z^*}^+}^2 \rangle ^{1/2}}{L_*^-} + E_D^* \bigg ( \frac{\langle {{z^\infty }^-}^2 \rangle }{\lambda _\infty ^+} + \frac{\langle {{z^\infty }^+}^2 \rangle }{\lambda ^-} \bigg ) \\&\quad - \frac{\langle {{z^*}^+}^2 \rangle \langle {{z^\infty }^-}^2 \rangle ^{1/2}}{\lambda _\infty ^+} - \frac{\langle {{z^*}^-}^2 \rangle \langle {{z^\infty }^+}^2 \rangle ^{1/2}}{\lambda _\infty ^-} \\&\quad + E_D^* \frac{V_A}{\lambda ^+_* + \lambda ^-_*} (1-\sigma _{\rm c}^*)^{1/2} {M^t_{A0}}^2 \bigg ], \end{split} \end{aligned} $$](/articles/aa/full_html/2021/12/aa40672-21/aa40672-21-eq14.gif)
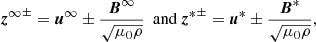
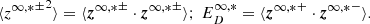
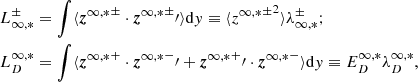
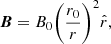
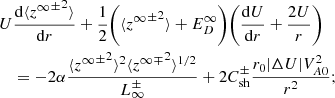
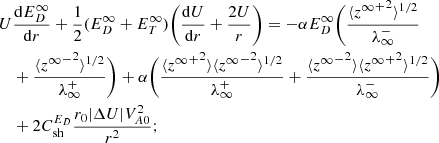
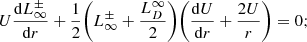
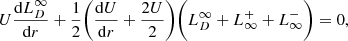
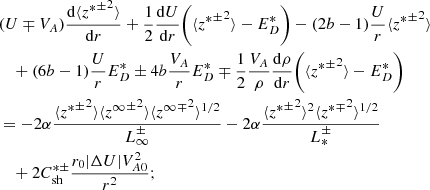
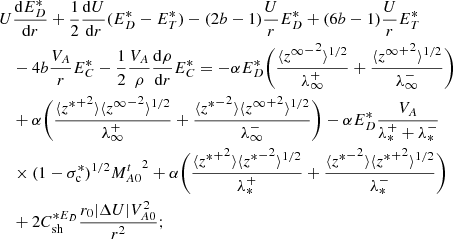
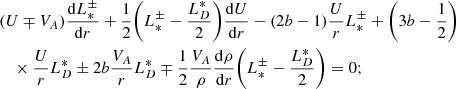
![$$ \begin{aligned} \begin{split}&U \frac{\mathrm{d}L_D^*}{\mathrm{d}r} + \frac{1}{2}(L_D^* - L_*^+ - L_*^-) \frac{\mathrm{d}U}{\mathrm{d}r} - \frac{2U}{r} \bigg [\bigg (b-\frac{1}{2}\bigg )L_D^* - \bigg (3b-\frac{1}{2}\bigg ) \\&\quad \times (L_*^- + L_*^+) \bigg ] - 4b\frac{V_A}{r}(L_*^+ - L_*^-) - \frac{1}{2} \frac{V_A}{\rho } \frac{\mathrm{d}\rho }{\mathrm{d}r} (L_*^+ - L_*^-) = 0, \end{split} \end{aligned} $$](/articles/aa/full_html/2021/12/aa40672-21/aa40672-21-eq34.gif)