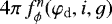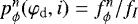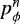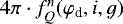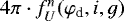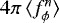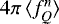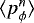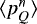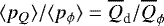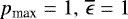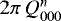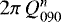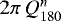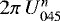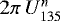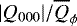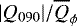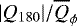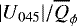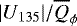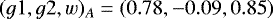| Issue |
A&A
Volume 655, November 2021
|
|
|---|---|---|
| Article Number | A83 | |
| Number of page(s) | 21 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202140405 | |
| Published online | 23 November 2021 | |
Quadrant polarization parameters for the scattered light of circumstellar disks
Analysis of debris disk models and observations of HR 4796A
ETH Zurich, Institute for Particle Physics and Astrophysics,
Wolfgang-Pauli-Strasse 27,
8093
Zurich,
Switzerland
e-mail: schmid@astro.phys.ethz.ch
Received:
23
January
2021
Accepted:
19
August
2021
Context. Modern imaging polarimetry provides spatially resolved observations for many circumstellar disks and quantitative results for the measured polarization which can be used for comparisons with model calculations and for systematic studies of disk samples.
Aims. This paper introduces the quadrant polarization parameters Q000, Q090, Q180, Q270 for Stokes Q and U045, U135, U225, U315 for Stokes U for circumstellar disks and describes their use for the polarimetric characterization of the dust in debris disks.
Methods. We define the quadrant polarization parameters Qxxx and Uxxx and illustrate their properties with measurements of the debris disk around HR 4796A from Milli et al. (2019, A&A, 626, A54).. We calculate quadrant parameters for simple models of rotationally symmetric and optically thin debris disks and the results provide diagnostic diagrams for the determination of the scattering asymmetry of the dust. This method is tested with data for HR 4796A and compared with detailed scattering phase curve extractions in the literature.
Results. The parameters Qxxx and Uxxx are ideal for a well-defined and simple characterization of the azimuthal dependence of the polarized light from circumstellar disk because they are based on the “natural” Stokes Q and U quadrant pattern produced by circumstellar scattering. For optically thin and rotationally symmetric debris disks the quadrant parameters normalized to the integrated azimuthal polarization Qxxx∕Qϕ and Uxxx∕Qϕ or quadrant ratios like Q000∕Q180 depend only on the disk inclination i and the polarized scattering phase function fϕ(θ) of the dust, and they do not depend on the radial distribution of the scattering emissivity. Because the disk inclination i is usually well known for resolved observations, we can derive the shape of fϕ(θ) for the phase angle range θ sampled by the polarization quadrants. This finding also applies to models with vertical extensions as observed for debris disks. Diagnostic diagrams are calculated for all normalized quadrant parameters and several quadrant ratios for the determination of the asymmetry parameter g of the polarized Henyey-Greenstein scattering phase function fϕ(θ, g). We apply these diagrams to the measurement of HR 4796A, and find that a phase function with only one parameter does not reproduce the data well. We find a better solution with a three-parameter phase function fϕ(θ, g1, g2, w), but it is also noted that the well-observed complex disk of HR 4796A cannot be described in full detail with the simple quadrant polarization parameters.
Conclusions. The described quadrant polarization parameters are very useful for quantifying the azimuthal dependence of the scattering polarization of spatially resolved circumstellar disks illuminated by the central star. They provide a simple test of the deviations of the disk geometry from axisymmetry and can be used to constrain the scattering phase function for optically thin disks without detailed model fitting of disk images. The parameters are easy to derive from observations and model calculations and are therefore well suited to systematic studies of the dust scattering in circumstellar disks.
Key words: stars: pre-main sequence / protoplanetary disks / techniques: polarimetric / stars: individual: HR 4796A / circumstellar matter
© H. M. Schmid 2021
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Circumstellar disks reflect the light from the central star, and the produced scattered intensity and polarization contain a lot of information about the disk geometry and the scattering dust particles. The scattered light of disks is usually only a contribution of a few percent or less to the direct light from the central star and therefore requires observations with sufficiently high resolution and contrast to resolve the disk from the star. This was achieved in recent years for many circumstellar disks with adaptive optics (AO) systems at large telescopes using polarimetry, a powerful high-contrast technique, to disentangle the scattered and therefore polarized light of the disk from the direct and typically unpolarized light of the central star (e.g., Apai et al. 2004; Oppenheimer et al. 2008; Quanz et al. 2011; Hashimoto et al. 2011; Muto et al. 2012).
With AO systems, the observational point spread function (PSF) depends to a large extent on the atmospheric turbulence and is highly variable (e.g., Cantalloube et al. 2019). For this reason, the disks are often only detected in polarized light and it is not possible to disentangle the disk intensity signal from the strong, variable PSF of the central star (see e.g., Esposito et al. 2020). Therefore, analyses of the scattered light from the disk are often based on the differential polarization alone and only in favorable cases can one combine this with measurements of the disk intensity. For the data analysis, the observed polarization must first be corrected for instrumental polarization effects, and this is relatively difficult for complex AO systems (e.g., Schmid 2021, and references therein). For this reason, the first generation of AO systems with polarimetric mode provided useful qualitative polarimetric results but hardly any quantitative results.
This situation has changed with the new extreme AO systems GPI (Macintosh et al. 2014) and SPHERE (Beuzit et al. 2019), which, in addition to better image quality, also provide polarimetrically calibrated data for the circumstellar disk (Perrin et al. 2015; Schmid et al. 2018; de Boer et al. 2020; van Holstein et al. 2020). Thus, quantitative polarization measurements are now possible for many circumstellar disks. However, the technique is not yet well established, and detailed studies haveonly been made for a few bright, extended disks; for example for HR 4796A (Perrin et al. 2015; Milli et al. 2019; Arriaga et al. 2020), HIP 79977 (Engler et al. 2017), HD 34700A (Monnier et al. 2019), HD 169142 (Tschudi & Schmid 2021), and HD 142527 (Hunziker et al. 2021). There also exist a few polarimetric studies based on HST polarimetry, such as those for the disks of AU Mic (Graham et al. 2007) or AB Aur (Perrin et al. 2009). The large majority of polarimetric disk observations in the literature focus their analysis on the high-resolution disk geometry (e.g., Benisty et al. 2015; Garufi et al. 2016; Avenhaus et al. 2018), and therefore the measurements are not calibrated and polarimetric cancelation effects introduced by the limited spatial resolution are not taken into account. Even for the detailed polarimetric studies mentioned above, the derived photo-polarimetric parameters are relatively heterogeneous. Convolution effects are only sometimes taken into account, and measurements are given as observed maps, azimuthal or radial profiles, or as dust parameters of a well-fitting disk model. This makes a comparison of results between different studies difficult and inaccurate, in particular because measuring uncertainties and model ambiguities are rarely discussed in detail.
Therefore, this paper introduces Stokes Q and U quadrant polarization parameters, which are simple to derive but still well defined, and facilitate systematic, quantitative studies of larger samples of circumstellar disks in order to make polarimetric measurements more valuable for our understanding of the physical properties of the scattering dust. Quantitative polarimetry of disks might be very useful to clarify whether dust properties are different or similar for systems with different morphology, age, level of illumination, or dust composition. The quadrant polarization parameters should also be useful for model simulations describing the appearance of a given disk for different inclinations so that intrinsic properties can be disentangled from the effects of a particular disk inclination. The same parameters can also be used to quantify the impact of the convolution of the intrinsic disk signal or of simulated images with instrumental PSF profiles to correct the observable polarization of small and large disks for the effects of smearing and polarimetric degradation (Schmid et al. 2006).
Using Stokes Q and U quadrant parameters for the description of the polarization of disks is a new approach and to the best of our knowledge this is the first publication using this type of analysis. These quadrant polarization parameters are introduced in Sect. 2 using the published data of Milli et al. (2019) for the bright debris disk HR 4796A as an example. The interpretation of the measured values is illustrated with corresponding model calculations for optically thin debris disks, which are described in Sect. 3. The models are similar to the classical simulation for the scattered intensity of debris disks of Artymowicz et al. (1989) and Kalas & Jewitt (1996), but they also consider the scattering polarization as in the models of Graham et al. (2007) and Engler et al. (2017). It is shown in Sect. 4 that the relative quadrant polarization values for optically thin, axisymmetric (and flat) debris disks are independent of the radial dust distribution and they depend only on the disk inclination i and the shape of the polarized scattering phase function fϕ(θ). Therefore, in Sect. 5 we construct simple diagnostic diagrams for quadrant polarization parameters which constrain the fϕ (θ) function for a given i, or directly yield the scattering asymmetry parameter g if we adopt a Henyey-Greenstein scattering function for the dust. The diagnostic diagrams are applied to the quadrant polarization measurements of HR 4796A and the obtained results are compared with the detailed, model-free phase-curve extraction of Milli et al. (2019). Finally, in Sect. 6 we discuss the potential and limitations of the quadrant polarization parameters for the analysis of disk observations and model simulations in a broader context.
2 Quadrant polarization parameters for disks
2.1 Polarization parameters in sky coordinates
Polarimetric imaging of stellar systems with circumstellar disks provides typically sky images for the intensity Iobs (α, δ) and the Stokes linear polarization parameters Qobs(α, δ) and Uobs(α, δ). For dust scattering, the circular polarization is expected to be much smaller than the linear polarization and is usually not measured; it is therefore neglected in this work. Q and U are differential quantities for the linear polarization components
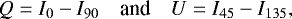 (1)
(1)
which can also be expressed as polarization flux 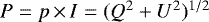 and polarization position angle θP = 0.5 atan2(U, Q)1. The polarized flux p × I is by definition a positive quantity, which, for noisy Q or U imaging data, suffers from a significant bias effect (Simmons & Stewart 1985).
and polarization position angle θP = 0.5 atan2(U, Q)1. The polarized flux p × I is by definition a positive quantity, which, for noisy Q or U imaging data, suffers from a significant bias effect (Simmons & Stewart 1985).
The azimuthal Stokes parameter Qϕ can be used as an alternative for P for circumstellar disks. Qϕ measures polarization in the azimuthal direction with respect to the central star (α0, δ0) and Uϕ in a direction rotated by 45° with respect to azimuthal. Circumstellar dust, which scatters light from the central star, mostly produces polarization with azimuthal orientations θP ≈ ϕαδ + 90°, while Uϕ is almost zero. Therefore, Qϕ can be considered as a good approximation for the polarized flux of the scattered radiation from circumstellar disks 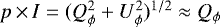 , and this approximation also avoids the noise bias problem (Schmid et al. 2006). For the model calculations of optically thin disks presented in this work, there is strictly p × I = Qϕ, while small signals Uϕ < 0.05 Qϕ can be produced by multiple scattering in optically thick disks (Canovas et al. 2015) or disks with aligned aspherical scattering particles. The Uϕ signal is often much larger, that is, Uϕ ≳ 0.1 Qϕ, in observations because of the PSF convolution problem for poorly resolved disks and polarimetric calibration errors. Both effects should be taken into account and corrected for the polarimetric measurements of disks. The azimuthal Stokes parameters are defined by
, and this approximation also avoids the noise bias problem (Schmid et al. 2006). For the model calculations of optically thin disks presented in this work, there is strictly p × I = Qϕ, while small signals Uϕ < 0.05 Qϕ can be produced by multiple scattering in optically thick disks (Canovas et al. 2015) or disks with aligned aspherical scattering particles. The Uϕ signal is often much larger, that is, Uϕ ≳ 0.1 Qϕ, in observations because of the PSF convolution problem for poorly resolved disks and polarimetric calibration errors. Both effects should be taken into account and corrected for the polarimetric measurements of disks. The azimuthal Stokes parameters are defined by
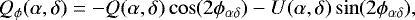 (2)
(2)
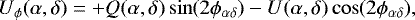 (3)
(3)
according to the description of Schmid et al. (2006) for the radial Stokes parameters Qr, Ur, and using Qϕ = −Qr and Uϕ = −Ur.
2.2 Disk integrated polarization parameters
Quantitative measurements of the scattered radiation from circumstellar disks were obtained in the past with aperture polarimetry, which provided the disk-integrated Stokes parameters 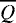 ,
, 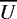 or the polarized flux
or the polarized flux 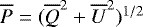 usually expressed as fractional polarization relative to the system-integrated intensity
usually expressed as fractional polarization relative to the system-integrated intensity 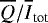 ,
, 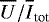 , or
, or 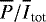 and the averaged polarization position angle
and the averaged polarization position angle 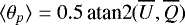 (e.g., Bastien 1982; Yudin & Evans 1998). This polarization signal can be attributed to the scattered light from the disk if the star produces no polarization and if the interstellar polarization can be neglected, or if these contributions can be corrected. Usually, the disk intensity
(e.g., Bastien 1982; Yudin & Evans 1998). This polarization signal can be attributed to the scattered light from the disk if the star produces no polarization and if the interstellar polarization can be neglected, or if these contributions can be corrected. Usually, the disk intensity 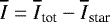 cannot be distinguished from the stellar intensity with aperture polarimetry, apart from a few exceptional cases, such as that of β Pic.
cannot be distinguished from the stellar intensity with aperture polarimetry, apart from a few exceptional cases, such as that of β Pic.
Aperture polarimetry provides only the net scattering polarization, but misses potentially strong positive and negative polarization components + Q, −Q and + U, −U which cancel each other in unresolved observations. Therefore, 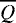 and
and 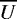 , or
, or 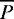 and ⟨θp⟩ provide onlyone value and one direction for circumstellar disks, which agglomerate all possible types of deviations from axisymmetry of the scattering polarization of a circumstellar disk.
and ⟨θp⟩ provide onlyone value and one direction for circumstellar disks, which agglomerate all possible types of deviations from axisymmetry of the scattering polarization of a circumstellar disk.
Disk-resolved polarimetric imaging avoids or strongly reduces the destructive cancellation effect and provides therefore much more information about the scattering polarization of disks. The most basic polarization parameter for the characterization of a resolved disk is the disk integrated azimuthal polarization 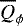 which can be considered as equivalent to the polarized flux for resolved observations
which can be considered as equivalent to the polarized flux for resolved observations 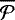 2. The integrated polarized flux
2. The integrated polarized flux  depends on the spatial resolution of the data; this aspect is not considered in this work because for well-resolved disks, like that of HR 4796A, the effect of limited spatial resolution is small and can be corrected with modeling of the instrumental smearing.
depends on the spatial resolution of the data; this aspect is not considered in this work because for well-resolved disks, like that of HR 4796A, the effect of limited spatial resolution is small and can be corrected with modeling of the instrumental smearing.
If the disk intensity 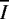 is measurable, one can also determine the disk-averaged fractional polarization
is measurable, one can also determine the disk-averaged fractional polarization  . Unfortunately, it is still often very difficult to measure the disk intensity I(α, δ) with AO-observations because the signal cannot be separated from the intensity of the variable point spread function Istar (α, δ) of the much brighter central star. In these cases, the fractional polarization can only be expressed relative to the total system intensity
. Unfortunately, it is still often very difficult to measure the disk intensity I(α, δ) with AO-observations because the signal cannot be separated from the intensity of the variable point spread function Istar (α, δ) of the much brighter central star. In these cases, the fractional polarization can only be expressed relative to the total system intensity  . Integrated or averaged quantities are well defined but not well suited to characterizing the polarimetric features and the azimuthal dependence of the polarization for circumstellar disks. Therefore, we introduce new polarization parameters to quantify the individual positive and negative polarimetric components + Q, − Q and + U, − U of spatially resolved disk observations and models.
. Integrated or averaged quantities are well defined but not well suited to characterizing the polarimetric features and the azimuthal dependence of the polarization for circumstellar disks. Therefore, we introduce new polarization parameters to quantify the individual positive and negative polarimetric components + Q, − Q and + U, − U of spatially resolved disk observations and models.
 |
Fig. 1 Illustration of the definition of the quadrant polarization parameters (panels e and f) for the observations of the debris disk around HR 4796A from Milli et al. (2019). Left: Azimuthal polarization Qϕ and Stokes Q and U in relative α, δ-sky coordinates. Right: Qϕ, Qd, and Ud in x, y-disk coordinates. |
2.3 Quadrant polarization parameters in disk coordinates
For polarimetric imaging of circumstellar disks, the geometric orientation of the disk and the Stokes Q and U parameters are often described in sky coordinates. This is inconvenient for the characterization of the intrinsicscattering geometry of the disk and therefore we define new polarization parameters Qd and Ud in the disk coordinate system (x, y), where the central star is at x0 = 0, y0 = 0 and the x and y are aligned with the major and minor axis of the projected disk, respectively. The positive x-axis is pointing left to ease the comparison with observations in relative sky coordinates α − α0 and δ − δ0 and to get the same convention for the Qd and Ud orientations in x, y and sky images. Thus, the relative α − α0, δ − δ0 sky coordinates of the observed images I, Qϕ, Q, and U must be rotated according to
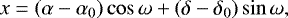 (5)
(5)
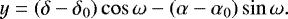 (6)
(6)
as shown in Fig. 1 for the imaging polarimetry of HR 4796A using ω = 242° (− 118°). We use the convention that ω aligns the more distant semi-minor axis of the projected disk with the positive (upward) y-axis.
Also, the Stokes parameters for the linear polarization must be rotated from the Q, U sky system to the Qd, Ud disk system using the geometrically rotated (x, y)-frames
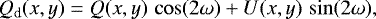 (7)
(7)
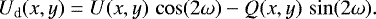 (8)
(8)
We define for the Qd(x, y) and Ud(x, y) polarization images the quadrant parameters Q000, Q090, Q180, and Q270 for Stokes Qd and U045, U135, U225, and U315 for Stokes Ud, which are obtained by integrating the Stokes Qd or Ud disk polarization signal in the corresponding quadrants as shown in Figs. 1e and f. This selection of polarization parameters is of course motivated by the natural Q and U quadrant patterns for circumstellar scattering where the signal in a given quadrant typically has the same sign everywhere and is almost zero at the borders of the defined integration region. This is strictly the case for all the model calculations for optically thin debris disks presented in this work and the same type of quadrant pattern is also predominant for the scattering polarization of proto-planetary disks. Multiple scattering and grain alignment effects can introduce deviations from a “clean” quadrant polarization pattern which may be measurable in high-quality observations (Canovas et al. 2015). However, the smearing and polarization cancellation effects introduced by the limited spatial resolution are typically much more important in affecting the quadrant pattern. For poor spatial resolution or very small disks, the quadrant pattern disappears (Schmid et al. 2006) or is strongly disturbed for asymmetric systems (Heikamp & Keller 2019).
Eight quadrant polarization values seems to be a useful number for the characterization of the azimuthal distribution of the polarization signal of disks. The parameters provide some redundancy to check and verify systematic effects, or to allow alternative disk characterizations if one parameter is not easily measurable or is affected by a special disk feature. Let us consider the redundancy in the context of the geometrical symmetry of disks and the dust scattering asymmetry.
For an inclined, but intrinsically axisymmetric disk, the Stokes Qd quadrants have the symmetry
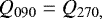 (9)
(9)
and the Stokes Ud quadrants have the anti-symmetries
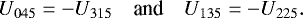 (10)
(10)
Special cases generate additional equalities; for example the models with isotropic scattering (see Fig. 5) have a front–back symmetry and therefore there is also Q000 = Q180 and U045 = −U135 = U225 = −U315. For an axisymmetric disk seen pole-on, all quadrant parameters have the same absolute value. If a disk deviates from an intrinsically symmetric geometry, for example a brighter + x side, then this would result in |Q090| > |Q270| for Stokes Qd and |U045| > |U315| or |U135| > |U225| for Stokes Ud.
Dust, which is predominantly forward scattering, produces more signal for front side polarization quadrants compared to the backside quadrants and this is equivalent to |Q180| > |Q000| or |U135| > |U045| and |U225| > |U315|. Properties that can be deduced from parameter ratios derived from the same data set are important because this reduces the impact of at least some systematic uncertainties in the measurements.
The quadrant parameters are also linked to the integrated polarization parameters 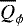 ,
, 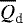 , and
, and 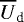 . For the sum of all four Stokes Qd and Stokes Ud quadrants, there is
. For the sum of all four Stokes Qd and Stokes Ud quadrants, there is
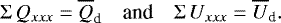 (11)
(11)
For pole-on systems, there is 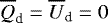 , because of the symmetric cancellation of positive and negative quadrants and intrinsically axis-symmetric systems have
, because of the symmetric cancellation of positive and negative quadrants and intrinsically axis-symmetric systems have 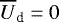 for all disk inclinations because of the left–right antisymmetry. Axisymmetric but inclined systems have
for all disk inclinations because of the left–right antisymmetry. Axisymmetric but inclined systems have 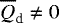 in general. For disks with larger inclination i, a smaller fraction of the disk is “located” in the quadrants Q000 and Q180 and a larger fraction is located in Q090 and Q270 near the major axis because of the disk projection. Edge-on disks are almost only located in the quadrants Q090 and Q270 and quadrant sums approach Q000 + Q180 → 0 and
in general. For disks with larger inclination i, a smaller fraction of the disk is “located” in the quadrants Q000 and Q180 and a larger fraction is located in Q090 and Q270 near the major axis because of the disk projection. Edge-on disks are almost only located in the quadrants Q090 and Q270 and quadrant sums approach Q000 + Q180 → 0 and 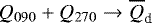 for i → 90°.
for i → 90°.
For the sums of the four absolute quadrant parameters for Stokes Qd, there is of course
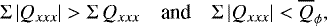 (12)
(12)
and the equivalent exists for sums of the Stokes Ud quadrants. For a pole-on view, the system is axisymmetric with respect to the line of sight and there is
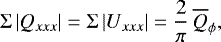 (13)
(13)
where each quadrant has the same absolute value of 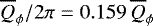 . These sums will converge for edge-on disks i = 90° to
. These sums will converge for edge-on disks i = 90° to 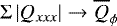 for Stokes Qd and to Σ |Uxxx|→ 0 for Stokes Ud.
for Stokes Qd and to Σ |Uxxx|→ 0 for Stokes Ud.
 |
Fig. 2 Apertures used for the measurements of the integrated azimuthal polarization |
2.4 Quadrant polarization parameters for HR 4796A
We use the high-quality differential polarimetric imaging (DPI) of the bright debris disk HR 4796A from Milli et al. (2019) shown in Fig. 1 as an example for the measurement of the quadrant polarization parameters. The data were taken with the SPHERE/ZIMPOL instrument (Beuzit et al. 2019; Schmid et al. 2018) in the very broad band (VBB) filter with the central wavelength λc = 735 nm and full width of Δλ = 290 nm.
These data provide “only” the differential Stokes Q(x, y) and U(x, y) signals or the corresponding azimuthal quantities Qϕ(x, y) and Uϕ(x, y), but no intensity signal because it is difficult with AO-observations to separate the disk intensity from the variable intensity PSF of the much brighter central star. The scattered light of the disk around HR 4796A was previously detected in polarization and intensity with AO systems in the near-IR (e.g., Milli et al. 2017; Chen et al. 2020; Arriaga et al. 2020), and in intensity in the visual with HST (e.g., Schneider et al. 2009).
Quadrant polarization parameters Qxxx and Uxxx for HR 4796A derived from the data shown in Figs. 1e and f are given in Table 1 as relative values using the integrated polarized flux 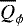 as reference.The quadrant values were obtained by integrating the counts in the annular apertures sections as illustrated in Fig. 2, which avoid the high noise regions from the PSF peak in the center. The uncertainties indicated in Table 1 account for the image noise, but do not account for systematic effects related to the selected aperture geometry or polarimetric calibration uncertainties. The noise errors are particularly large for the quadrants Q000 and Q180 because of the small separation of these disk sections from the bright star and additional negative noise spikes which are particularly strong for the Q000 quadrant. Because of this noise, the formal integration gives
as reference.The quadrant values were obtained by integrating the counts in the annular apertures sections as illustrated in Fig. 2, which avoid the high noise regions from the PSF peak in the center. The uncertainties indicated in Table 1 account for the image noise, but do not account for systematic effects related to the selected aperture geometry or polarimetric calibration uncertainties. The noise errors are particularly large for the quadrants Q000 and Q180 because of the small separation of these disk sections from the bright star and additional negative noise spikes which are particularly strong for the Q000 quadrant. Because of this noise, the formal integration gives 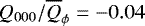 . From the decreasing trend of the signal in for example Qϕ towards theback side of the disk and the measured disk signals of about 0.03 for
. From the decreasing trend of the signal in for example Qϕ towards theback side of the disk and the measured disk signals of about 0.03 for 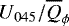 or
or 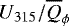 , an absolute signal of less than
, an absolute signal of less than 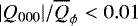 is expected fora smooth dust distribution in the ring and any reasonable assumptions for the dust scattering. Therefore, we do not consider the noisy Q000-measurement in the quadrant sums ΣQxxx. The noise in the Q180-quadrant is also significantly enhanced when compared to other quadrants despite the relatively strong signal and the small integration area. A detailed analysis of the noise pattern might improve the measuring accuracy, but this is beyond the scope of this paper.
is expected fora smooth dust distribution in the ring and any reasonable assumptions for the dust scattering. Therefore, we do not consider the noisy Q000-measurement in the quadrant sums ΣQxxx. The noise in the Q180-quadrant is also significantly enhanced when compared to other quadrants despite the relatively strong signal and the small integration area. A detailed analysis of the noise pattern might improve the measuring accuracy, but this is beyond the scope of this paper.
Because of the noise, the apertures for Qϕ and the quadrants U045 and U135 were restricted to avoid the noisy and essentially signal-free region around ϕxy ≈ 0°. One should note that uncertainties for the quadrant measurements, for example for Q180, also affect the Qϕ value and a dominant noise feature therefore has an enhanced impact on relative parameters such as 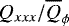 , which include the disk integrated azimuthal polarization
, which include the disk integrated azimuthal polarization 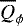 . These are typical problems for high-contrast observations of inclined disks and it can be very useful to select only high-signal-to-noise quadrant values for the characterization of the azimuthal dependence of the disk polarization.
. These are typical problems for high-contrast observations of inclined disks and it can be very useful to select only high-signal-to-noise quadrant values for the characterization of the azimuthal dependence of the disk polarization.
Asymmetries between the left and right or the positive and negative sides of the x-axis can be deduced from the absolute quadrant parameters |Q090| and |Q270|, |U045| and |U315|, and |U135| and |U225|. Table 1 gives relative left–right brightness differences 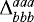 calculated according to
calculated according to
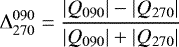 (14)
(14)
for Stokes Qd parameters and equivalent for 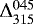 and
and 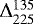 for Stokes Ud.
for Stokes Ud.
The asymmetry values 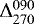 and
and 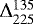 both yield more flux on the left side of the (x, y)-plane, which is the SW-side for the HR 4796A disk. This does not agree with previous determinations, including even the analysis of the same data by Milli et al. (2019) who measured more flux on the NE side. A more detailed investigation reveals that the peak surface brightness is indeed higher for the disk on the NE side and that the left–right asymmetry depends on the width of the annular apertures used for the flux extraction. If we integrate only a narrow annular region with a full width of Δx = 0.1″ at the location of the major axis then we also get more flux for the NE side or negative
both yield more flux on the left side of the (x, y)-plane, which is the SW-side for the HR 4796A disk. This does not agree with previous determinations, including even the analysis of the same data by Milli et al. (2019) who measured more flux on the NE side. A more detailed investigation reveals that the peak surface brightness is indeed higher for the disk on the NE side and that the left–right asymmetry depends on the width of the annular apertures used for the flux extraction. If we integrate only a narrow annular region with a full width of Δx = 0.1″ at the location of the major axis then we also get more flux for the NE side or negative 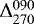 -values of − 3 ± 2% but still less than the “negative” (SW-NE) asymmetry measured by Milli et al. (2019) for Qϕ or Schneider et al. (2018) for the intensity. We therefore conclude that there are subtle asymmetries at the level of Δ ≈ 10% present for the disk HR 4796A, which are positive for a wide flux extraction and negative for a narrow flux extraction. Measurement uncertainties in the left–right differences are at the few percent level for bright quadrant pairs.
-values of − 3 ± 2% but still less than the “negative” (SW-NE) asymmetry measured by Milli et al. (2019) for Qϕ or Schneider et al. (2018) for the intensity. We therefore conclude that there are subtle asymmetries at the level of Δ ≈ 10% present for the disk HR 4796A, which are positive for a wide flux extraction and negative for a narrow flux extraction. Measurement uncertainties in the left–right differences are at the few percent level for bright quadrant pairs.
The back-side to front-side brightness contrast can be expressed with quadrant ratios such as
 (15)
(15)
and their equivalents for other quadrant ratios. These ratios are small ≲ 0.5 for HR 4796A which is indicative of dust with a strong forward scattering phase function. For isotropic scattering in an axisymmetric disk, the ratios would be 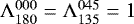 for all inclinations. Because the polarization flux in the backside quadrants is small, one can also assess the disk forward scattering with a comparison of the brighter Q090 and Q270 quadrants with the Stokes Qd front quadrant Q180 or the Stokes Ud front quadrants U135 and U225 as given in Table 1.
for all inclinations. Because the polarization flux in the backside quadrants is small, one can also assess the disk forward scattering with a comparison of the brighter Q090 and Q270 quadrants with the Stokes Qd front quadrant Q180 or the Stokes Ud front quadrants U135 and U225 as given in Table 1.
As demonstrated in Table 1, the polarization quadrants provide a useful set of parameters for the quantitativecharacterization of the geometric distribution of the polarization signal in circumstellar disks. Comparisons with model calculations are required to assess the diagnostic power of the derived values for the determination of the scattering properties of the dust or for the interpretation of the strength of disk asymmetries.
Measured relative quadrant polarization parameters for HR 4796A, deviations Δ (in %) from left–right symmetry and ratios Λ for back–front flux ratios.
3 Disk model calculations
The simple disk models presented in this work follow the basic calculations for the scattered intensity from debris disks (Artymowicz et al. 1989; Kalas & Jewitt 1996) and the scattering polarization (e.g., Bastien & Menard 1988; Whitney & Hartmann 1992; Graham et al. 2007; Engler et al. 2017) but focus on the azimuthal dependence of the scattering polarization and the determination of the quadrant polarization values. The model disks are described by a dust-density distribution in cylindrical coordinates ρ(r, φd, h) where r is the radius vector 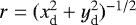 and φd the azimuthal angle in the disk plane3, where xd coincides with x for the major axis of the projected, inclined disk. We consider in this work very simple, optically thin τ ≪ 1, axisymmetric models ρ(r, h), where the dust scattering cross-section per unit mass σsca is independent of the location. The total dust scattering emissivity (integrated over all directions) ϵ(r, h) of a volume element is given by the stellar flux Fλ(r, h) = Lλ∕(4π(r2 + h2)), the disk density ρ(r, h), and σsca:
and φd the azimuthal angle in the disk plane3, where xd coincides with x for the major axis of the projected, inclined disk. We consider in this work very simple, optically thin τ ≪ 1, axisymmetric models ρ(r, h), where the dust scattering cross-section per unit mass σsca is independent of the location. The total dust scattering emissivity (integrated over all directions) ϵ(r, h) of a volume element is given by the stellar flux Fλ(r, h) = Lλ∕(4π(r2 + h2)), the disk density ρ(r, h), and σsca:
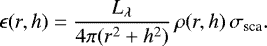 (16)
(16)
The incident flux decreases as Fλ ∝ 1∕R2 with R2 = r2 + h2, because in our optically thin scattering model we neglect the extinction of stellar light by the dust and the addition of diffuse light produced by the scatterings in the disk.
The resulting images for the scattered light intensity I(x, y) and the azimuthal polarization Qϕ(x, y) are obtained with a line of sight or z-axis integration of the scattering emissivity ϵ and the scattering phase functions fI(θxyz, g) for the intensity
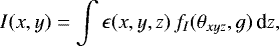 (17)
(17)
and fϕ(θxyz, g, pmax) for the polarized intensity
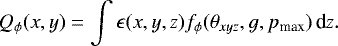 (18)
(18)
The transformations from the disk coordinate system (r, φd, h) with xd = rsinφd and yd = rcosφd to the sky coordinate system (x, y, z) is given by x = xd, y = yd cosi + hsini and z = yd sini − hcosi where i is the disk inclination. This also defines the scattering angle θxyz and the radial separation to the central star Rxyz for each point (x, y, z).
3.1 Scattering phase functions
The scattering phase function fI(θ, g) for the intensity is described by the Henyey-Greenstein function or HG-function (Henyey & Greenstein 1941), where θ is the angle of deflection
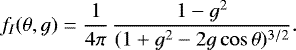 (19)
(19)
The asymmetry parameter g is defined between − 1 and + 1 and backward scattering dominates for negative g, forward scattering dominates for positive g, while the scattering is isotropic for g = 0.
The scattering phase function fϕ(θ, g, pmax) for the polarized flux adopts the same angle dependence for the fractional polarization as Rayleigh scattering, but with the scale factor pmax ≤ 1 for the maximum polarization at θ = 90°. This description is often used (e.g., Graham et al. 2007; Buenzli & Schmid 2009; Engler et al. 2017) as a simple approximation for a Rayleigh scattering-like angle dependence but reduced polarization induced by dust particles (e.g., Kolokolova & Kimura 2010; Min et al. 2016; Tazaki et al. 2019).
The angle dependence of the fractional polarization of the scattered light is
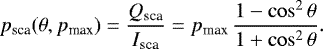 (20)
(20)
The scattered intensity Isca can be split into the perpendicular I⊥ and parallel I∥ polarization components with respect to the scattering plane, so that Isca = I⊥ + I∥, Qsca = I⊥− I∥ and I⊥ = (Isca + Qsca)∕2, I∥ = (Isca − Qsca)∕2. Together with psca, this yields
![\begin{equation*}I_{\perp}(p_{\textrm{max}},\theta) =I_{\textrm{sca}}\cdot \Bigl[0.5 +p_{\textrm{max}}\Bigl(\frac{1}{1+\cos^2\theta}-0.5\Bigr)\Bigr],\end{equation*}](/articles/aa/full_html/2021/11/aa40405-21/aa40405-21-eq64.png) (21)
(21)
![\begin{equation*}I_{\parallel}(p_{\textrm{max}},\theta) = I_{\textrm{sca}}\cdot \Bigl[0.5 +p_{\textrm{max}}\Bigl(\frac{\cos^2\theta}{1+\cos^2\theta}-0.5\Bigr)\Bigr],\end{equation*}](/articles/aa/full_html/2021/11/aa40405-21/aa40405-21-eq65.png) (22)
(22)
or, expressed as scattering phase functions, f⊥ = fI k⊥ (θ, pmax) and f∥ = fI k∥ (θ, pmax), where k⊥ and k∥ are the expressions in the square brackets and psca = k⊥− k∥.
The scattering plane in a projected image of a circumstellar disk has always a radial orientation with respect to the central star. Therefore the induced scattering polarization Qsca, which is perpendicular to the scattering plane, translates into an azimuthal polarization Qϕ for the projected disk map. The scattering phase functions are related by
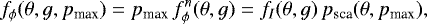 (23)
(23)
where fϕ can be separated into a normalized part 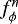 for pmax = 1 and the scale factor pmax.
for pmax = 1 and the scale factor pmax.
Figure 3 illustrates the scattering phase functions for g = 0.2 for the total intensity fI and the corresponding polarization components f⊥ and f∥ for pmax = 0.5 and 0.2. The differential phase function fϕ = f⊥− f∥ has the same θ-dependence 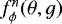 for both cases, and only the amplitude scales with pmax. In this formalism, the total intensity phase function fI(g, θ) does not depend on the adopted polarization parameter pmax. Expected values for approximating dust scattering with HG scattering functions are pmax ≈ 0.05−0.8, but we often set this scale factor in this work to pmax = 1 because this allows us to plot the intensity and polarization on the same scale. A value pmax = 1 applies for Rayleigh scattering but the HG-function with g = 0 (isotropic scattering) differs from the Rayleigh scattering function for the intensity4. Hereafter, fϕ (θ, g, pmax) and
for both cases, and only the amplitude scales with pmax. In this formalism, the total intensity phase function fI(g, θ) does not depend on the adopted polarization parameter pmax. Expected values for approximating dust scattering with HG scattering functions are pmax ≈ 0.05−0.8, but we often set this scale factor in this work to pmax = 1 because this allows us to plot the intensity and polarization on the same scale. A value pmax = 1 applies for Rayleigh scattering but the HG-function with g = 0 (isotropic scattering) differs from the Rayleigh scattering function for the intensity4. Hereafter, fϕ (θ, g, pmax) and 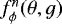 are also referred to as the HGpol-function and normalized HGpol-function, respectively.
are also referred to as the HGpol-function and normalized HGpol-function, respectively.
The polarimetric scattering phase function for the azimuthal Stokes parameters fϕ can be converted into phase functions fQ and fU for the Stokes Qd and Ud parameters
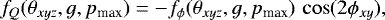 (24)
(24)
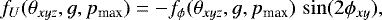 (25)
(25)
where ϕxy = atan2(y, x) is the azimuthal angle in the sky coordinates aligned with the disk as illustrated in Fig. 1. These simple relations are valid in our optical thin (single scattering) models because Uϕ (x, y) = 0 and the Stokes Qd(x, y) and Ud (x, y) model images can then be calculated as in Qϕ in Eq. (18) but using the phase functions for fQ and fU.
 |
Fig. 3 Scattering phase functions for the HG asymmetry parameter g = 0.2 for the total intensity 4π fI(θ) (black), for the polarized intensities 4π f⊥(θ) (dashed) and 4π f∥(θ) (dotted), for the two values pmax = 0.5 (red) and 0.2 (blue), and the corresponding scattering phase functions for the polarized flux 4π fϕ (θ) (full, colored lines). |
3.2 Flat disk models and azimuthal phase functions
The calculations for the scattered flux I(x, y) and polarization Qϕ(x, y) with Eqs. (17) and (18) are strongly simplified for a flat disk because the integrations for a given x-y coordinate along the z-coordinate can be replaced by single values for the separation rxy from the star, for the scattering emissivity ϵ(rxy), and for the scattering angle θxy. The volume density ρ must be replaced by a vertical surface density Σ(r) or a line-of-sight surface density Σ(r)∕cosi. Of course, the scattering in the disk plane must still be treated as in an optically thin disk,
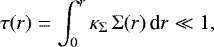 (26)
(26)
where κΣ = aΣ + σΣ is the disk extinction coefficient composed of the contributions from absorption aΣ and scattering σΣ.
3.2.1 Projected flat disk image
The scattered intensity and polarization for a flat disk are given by
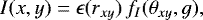 (27)
(27)
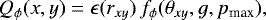 (28)
(28)
and similar for the Stokes Qd(x, y) and Ud(x, y) using the phase function from Eqs. (24) and (25). The scattering emissivity
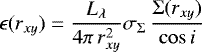 (29)
(29)
is proportional to the line-of-sight surface density Σ(rxy)∕cos i, which considers the disk inclination, and where 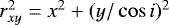 and θxy = acos(−zxy∕rxy) = acos(−ytani∕rxy), because y = yd cosi and zxy = yd sini.
and θxy = acos(−zxy∕rxy) = acos(−ytani∕rxy), because y = yd cosi and zxy = yd sini.
In these equations for I(x, y), Qϕ (x, y), Qd (x, y), and Ud (x, y), the radial dependence of the scattering emissivity ϵ(rxy) is separatedfrom the azimuthal dependence described by the scattering phase functions fI (θxy), fϕ (θxy), fQ (θxy), and fU (θxy). This is very favorable forthe introduced quadrant parameters, which describe the polarization of the scattered light of disks with an azimuthal splitting of the signalQd(x, y) → Q000, Q090, Q180, Q270 and Ud(x, y) → U045, U135, U225, U315 by integrating the polarization in the corresponding quadrants outlined by the black lines in the Qd and Ud panels of Figs. 4 and 5.
Disk images for I(x, y), Qd (x, y), Ud (x, y), and Qϕ (x, y) for flat diskmodels are shown in Fig. 4 for the asymmetry parameter g = 0.3, the scale factor pmax = 1, and three different inclinations i = 0°, 45°, and 75°. For the radial surface scattering emissivity, a radial dependence ϵ(r) ∝ 1∕r is adopted extending from an inner radius r1 to the outer radius r2 = 2 r1. Along the x-axis, the scattering angle is always θxy = 90° and the surface brightness increases for higher inclinations as in the inclined surface emissivity ∝ 1∕cosi.
The scattering asymmetry parameter g is relatively small and therefore the front–back brightness differences are not strong in Fig. 4. The forward scattering effect is much clearer in Fig. 5, where two disks are plotted with the same i and ϵ(r), but for isotropic scattering g = 0 and strong forward scattering g = 0.6.
For the disks shown in Figs. 4 and 5, the absolute signal drops in the radial direction for all azimuthal angles ϕxy = atan2(x, y) by exactly a factor of two from the inner edge 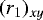 to the outer edge
to the outer edge 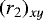 according to the adopted radial dependence of the scattering emissivity ϵ(r)∝ 1∕r. This is equivalent to the statement that the (relative) azimuthal dependence along the ellipse rxy describing aring in the inclined disk is the same for all separations in a given disk image I(rxy, φd), Qϕ (rxy, φd), Qd (rxy, φd), or Ud (rxy, φd). This is also valid if the azimuthal angle φd for the disk plane is replaced by the on-sky azimuthal angle ϕ.
according to the adopted radial dependence of the scattering emissivity ϵ(r)∝ 1∕r. This is equivalent to the statement that the (relative) azimuthal dependence along the ellipse rxy describing aring in the inclined disk is the same for all separations in a given disk image I(rxy, φd), Qϕ (rxy, φd), Qd (rxy, φd), or Ud (rxy, φd). This is also valid if the azimuthal angle φd for the disk plane is replaced by the on-sky azimuthal angle ϕ.
Therefore, it is possible to determine the azimuthal dependence of the scattered light in a very simple way using azimuthal phase functions defined in the disk plane, without considering the radial distribution of the scattering emissivity.
 |
Fig. 4 I-, Qd -, Ud - and Qϕ -images for a flat disk with g = 0.3, pmax = 1, and for inclinations i = 0°, i = 45°, and 75°. The same gray scale from + a (white) to −a (black) is used for all panels. The black lines in the Qd and Ud panels indicate the polarization quadrants. |
 |
Fig. 5 I-, Qd -, Ud - and Qϕ -images for flat disks with i = 45°, pmax = 1, and for scattering asymmetry parameter g = 0.0 and 0.6. The same gray scale from + a (white) to −a (black) is used for all panels. |
 |
Fig. 6 Upper panel: azimuthal dependence of the disk scattering phase function for the intensity 4π fI (φd, i, g) and the normalized (pmax = 1) polarized intensity |
3.2.2 Scattering phase functions for the disk azimuth angle
The azimuthal dependence of the scattered light can be calculated easily for flat, rotationally symmetric, and optically thin disks as a function of the azimuthal angle φd in the disk plane. For this, we have to express the scattering angle θ as a function of φd and the diskinclination i according to
 (30)
(30)
where φd = 0 for the far-side semi-minor axis of the projected disk.
The dependence of the scattered intensity and polarization flux with disk azimuthal angle φd follows directly from the scattering phase functions fI and fϕ and the change of the scattering angle θ as a function of φd and i
 (31)
(31)
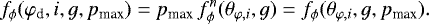 (32)
(32)
Figure 6 shows the azimuthal scattering functions 4π fI(φd, i, g) for the intensity and 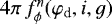 for the polarized flux for g = 0.3 and for different inclinations. The factor 4π normalizes the isotropic scattering case 4π fI(φd, i, g = 0) = 1 and scales all other cases g≠0 accordingly.
for the polarized flux for g = 0.3 and for different inclinations. The factor 4π normalizes the isotropic scattering case 4π fI(φd, i, g = 0) = 1 and scales all other cases g≠0 accordingly.
The enhanced forward scattering for fI(φd) around φd = 180° is clearly visible for inclined disks. The polarization function 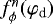 has for backward scattering around φd = 0° and forward scattering around φd = 180° strongly reduced values in highly inclined disks when compared to the intensity as can be seen for the green and red curves in Fig. 6. At φd = 90° and 270°, the functions fI and
has for backward scattering around φd = 0° and forward scattering around φd = 180° strongly reduced values in highly inclined disks when compared to the intensity as can be seen for the green and red curves in Fig. 6. At φd = 90° and 270°, the functions fI and 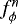 have (for given g) the same value for all inclinations because the scattering angles are always θφ,i = 90° (cos φd = 0 in Eq. (30)).
have (for given g) the same value for all inclinations because the scattering angles are always θφ,i = 90° (cos φd = 0 in Eq. (30)).
The azimuthal dependence of the fractional polarization is given by
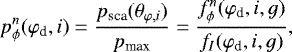 (33)
(33)
and this function does not depend on the asymmetry parameter g. This dependence is equivalent to Rayleigh scattering and is shown in Fig. 6 for completeness.
For the phase function fQ and fU one needs to consider that the Stokes Qd and Ud parameters are defined in the disk coordinate system projected onto the sky while fϕ is given for the azimuthal angle φd for the xd, yd-coordinates of the disk midplane. For the splitting of fϕ(φd, i, g, pmax) into fQ and fU, the azimuthal angle ϕxy defined in the x-y sky plane must be used. The relation between φd and ϕxy is
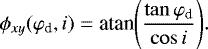 (34)
(34)
The phase functions for Qd and Ud are then equivalent to the conversion given in Eqs. (24) and (25):
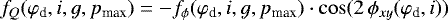 (35)
(35)
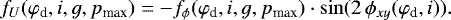 (36)
(36)
These azimuthal function of the “on-sky” Stokes parameters fQ and fU is shown in Fig. 7. The functions are characterized by their double wave, which for i = 0° are exact double-wave cosine fQ(φd) ∝−cos2φd and double-wavesine fU(φd) ∝−sin2φd functions. Deviations from the sine and cosine function become larger with increasing i, particularly for large asymmetry parameters g. The positive and negative sections of the fQ(φd) and fU(φd) functions correspond to the positive and negative polarimetric quadrants. The fQ and fU functions can also be expressed as normalized functions 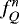 and
and 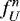 for pmax = 1 and as fractional polarization
for pmax = 1 and as fractional polarization 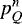 and
and 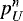 equivalent to
equivalent to 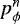 given above.
given above.
For the adopted HGpol dust scattering phase function, these phase functions fφ provide a universal description of the azimuthal flux and polarized flux dependence as a function of inclination i for all flat, optically thin, rotationally symmetric disks.
 |
Fig. 7 Azimuthal dependence for the Stokes scattering phase functions |
3.2.3 Disk-averaged scattering functions
The total intensity 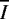 for our disk model can be conveniently calculated in r, φd-coordinates because the integration can be separated between the r-dependent scattering emissivity ϵ and the φd-dependent scattering phase function fI according to
for our disk model can be conveniently calculated in r, φd-coordinates because the integration can be separated between the r-dependent scattering emissivity ϵ and the φd-dependent scattering phase function fI according to
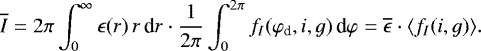 (37)
(37)
The first term represents the total scattering emissivity 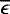 of the disk, and the second term is the disk averaged scattering phase function for the intensity ⟨fI (i, g)⟩.
of the disk, and the second term is the disk averaged scattering phase function for the intensity ⟨fI (i, g)⟩.
For the integrated polarization parameters, the same type of relation can be used
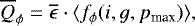 (38)
(38)
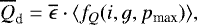 (39)
(39)
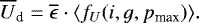 (40)
(40)
The scale factor pmax can be separated from the normalized versions of the disk-averaged scattering functions as
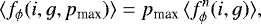 (41)
(41)
and similar for fQ and fU. The disk-averaged fractional polarization follows from
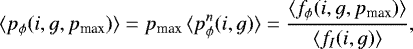 (42)
(42)
and similar for pQ or pU, where the latter is always zero for rotationally symmetric disks. Unlike for the azimuthal dependence of the fractional polarization pn (φd, g), the disk-averaged parameters  depend on the g-parameter because in this average g shifts the flux weight between disk regions producing higher or lower levels of scattering polarization.
depend on the g-parameter because in this average g shifts the flux weight between disk regions producing higher or lower levels of scattering polarization.
3.3 Normalized quadrant polarization parameters
The Stokes Qxxx and Uxxx quadrant polarization parameters correspond to the individual positive and negative sections of the fQ (φd) and fU (φd) disk phase function shown in Fig. 7. The relation between quadrant parameters and phase function follow the same scheme as for the disk-integrated quantities 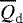 and
and 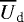 described by Eq. (37) but the integration is limited to the azimuthal angle range φ1 to φ2 of a given quadrant instead of 0 to 2π. For Stokes Qd, there is
described by Eq. (37) but the integration is limited to the azimuthal angle range φ1 to φ2 of a given quadrant instead of 0 to 2π. For Stokes Qd, there is
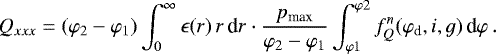 (43)
(43)
The first term is the disk scattering emissivity ϵ integrated for the quadrant and the second term is the averaged 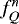 scattering phase function for this quadrant. Because ϵ is independent of the azimuthal angle, the first term can be expressed as a fraction of the disk integrated emissivity
scattering phase function for this quadrant. Because ϵ is independent of the azimuthal angle, the first term can be expressed as a fraction of the disk integrated emissivity 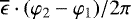 and the equation takes the form
and the equation takes the form
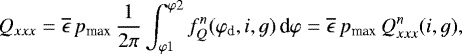 (44)
(44)
where we introduce the normalized quadrant polarization 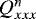 . The same scaling factors
. The same scaling factors 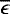 and pmax are involved as for the equations for the integrated polarization parameters
and pmax are involved as for the equations for the integrated polarization parameters 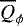 ,
, 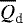 , and
, and 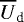 , and therefore
, and therefore 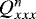 and ⟨fQ (i, g)⟩ are related with the same factors
and ⟨fQ (i, g)⟩ are related with the same factors 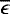 and pmax to observed quantities Qxxx and
and pmax to observed quantities Qxxx and 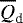 . The same formalism applies to the Stokes Ud quadrants.
. The same formalism applies to the Stokes Ud quadrants.
According to Eq. (44), the normalized polarization quadrants 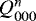 ,
, 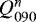 ,
, 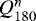 ,
, 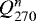 and
and 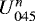 ,
, 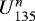 ,
, 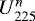 ,
, 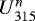 depend only on i and g as in the disk-averaged functions
depend only on i and g as in the disk-averaged functions 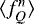 or
or 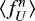 . The azimuthal integration range φ1 to φ2 is of course different for each quadrant, as summarized in Table 2. For the Qd -quadrants, the geometric projection effect introduces an inclination dependence for the integration boundaries φ1 and φ2. For increased i, the fraction of the sampled disk surfaces sxxx = (φ1(i) − φ2(i))∕2π in the left and right quadrants
. The azimuthal integration range φ1 to φ2 is of course different for each quadrant, as summarized in Table 2. For the Qd -quadrants, the geometric projection effect introduces an inclination dependence for the integration boundaries φ1 and φ2. For increased i, the fraction of the sampled disk surfaces sxxx = (φ1(i) − φ2(i))∕2π in the left and right quadrants 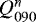 and
and 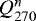 is enhanced s090 = s270 = 0.5 −atan(cosi)∕π and the disk surface fraction located in the front and back quadrants
is enhanced s090 = s270 = 0.5 −atan(cosi)∕π and the disk surface fraction located in the front and back quadrants 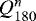 and
and 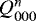 is reduced s000 = s180 = atan(cosi)∕π, respectively (we note that atan(cos0°) = π∕4 and atan(cos90°) = 0). There is no i-dependence for the splitting of the Stokes Ud quadrants, because the “left-side” back and front quadrants and the “right-side” back and front quadrants sample the same disk surface fraction s045 = s135 = s225 = s315 = 0.25 for all inclinations.
is reduced s000 = s180 = atan(cosi)∕π, respectively (we note that atan(cos0°) = π∕4 and atan(cos90°) = 0). There is no i-dependence for the splitting of the Stokes Ud quadrants, because the “left-side” back and front quadrants and the “right-side” back and front quadrants sample the same disk surface fraction s045 = s135 = s225 = s315 = 0.25 for all inclinations.
4 Calculation of disk polarization parameters
The previous section shows that the disk-integrated radiation parameters such as 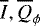 and the quadrant polarization parameters Qxxx and Uxxx can be expressed as disk-averaged phase functions ⟨f(i, g)⟩ and normalized polarization parameters
and the quadrant polarization parameters Qxxx and Uxxx can be expressed as disk-averaged phase functions ⟨f(i, g)⟩ and normalized polarization parameters 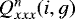 and
and 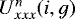 describing the azimuthal dependence of the scattering, and scale factors for the total disk-scattering emissivity
describing the azimuthal dependence of the scattering, and scale factors for the total disk-scattering emissivity 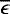 and the maximum scattering polarization pmax.
and the maximum scattering polarization pmax.
This simplicity allows a concise but comprehensive graphical presentation covering the full parameter space of the disk model parameters for the intensity and polarization, including the newly introduced quadrant polarization parameters. The Appendix gives a few IDL code lines for calculation of the numerical values. In addition, we explore the deviation of the results from vertically extended disk models and from the flat disk models.
Integration ranges for Stokes Qd and Ud polarization quadrants for on-sky azimuthal angles ϕx,y = atan2(y, x) and disk azimuthal angles φd = atan2(yd, xd).
 |
Fig. 8 Disk-averaged scattering phase functions for the intensity 4π ⟨fI⟩, the normalized (pmax=1) azimuthal polarization |
4.1 Calculations of the disk-averaged intensity and polarization scattering functions
The disk-averaged scattering phase functions ⟨f(i, g)⟩ are equivalent to the basic integrated quantities 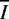 ,
, 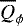 , and
, and 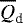 if normalized scale factors
if normalized scale factors 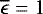 and pmax = 1 are used (Eqs. (37) to (39)). The functions ⟨fI(i, g)⟩,
and pmax = 1 are used (Eqs. (37) to (39)). The functions ⟨fI(i, g)⟩, 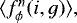 and
and 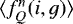 are plotted in Fig. 8 as a function of inclination for the four asymmetry parameters g = 0, 0.3, 0.6, and 0.9. The plot includes the results from calculation of vertically extended, three-dimensional disk rings (crosses) for comparison, which are discussed in Sect. 4.3. The results for ⟨f(i, g)⟩ are multiplied by the factor 4π because this sets the special reference case for isotropically scattering dust g = 0 for all inclinations to
are plotted in Fig. 8 as a function of inclination for the four asymmetry parameters g = 0, 0.3, 0.6, and 0.9. The plot includes the results from calculation of vertically extended, three-dimensional disk rings (crosses) for comparison, which are discussed in Sect. 4.3. The results for ⟨f(i, g)⟩ are multiplied by the factor 4π because this sets the special reference case for isotropically scattering dust g = 0 for all inclinations to 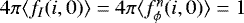 and simplifies the discussion.
and simplifies the discussion.
For pole-on disks i = 0°, there is 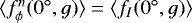 for all g parameters because the scattering angle is θ = 90° everywhere. For enhanced scattering asymmetry parameters g > 0 (but also for g < 0), the disk intensity is below the isotropic case 4π⟨fI⟩ < 1 for lesser and moderately inclined disks i ≲ 60°, because theenhanced forward scattering (or backward scattering) produces enhanced scattered flux in directions near to the disk plane and reduced flux for polar viewing angles.
for all g parameters because the scattering angle is θ = 90° everywhere. For enhanced scattering asymmetry parameters g > 0 (but also for g < 0), the disk intensity is below the isotropic case 4π⟨fI⟩ < 1 for lesser and moderately inclined disks i ≲ 60°, because theenhanced forward scattering (or backward scattering) produces enhanced scattered flux in directions near to the disk plane and reduced flux for polar viewing angles.
The forward scattering enhances the scattered intensity to 4π⟨fI⟩ > 1 for i≳60° and this effect becomes particularly strong for g → 1 and i → 90°. This behavior is well known and produces a strong detection bias for high-inclination debris disks (e.g., Artymowicz et al. 1989; Kalas & Jewitt 1996; Esposito et al. 2020).
For the polarized flux 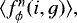 an enhanced inclination does not produce an enhancement of the ⟨fϕ ⟩ signal because the strong increase in scattered flux from the forward scattering direction (or backward direction for g < 1) is predominantly unpolarized. For moderate asymmetry parameter |g| ≲ 0.6, this causes an overall decrease of ⟨fϕ ⟩ with inclination (Fig. 8) while for extreme values |g|≳ 0.9 the huge flux increase compensates for the lower fractional polarization for forward and backward scattering.
an enhanced inclination does not produce an enhancement of the ⟨fϕ ⟩ signal because the strong increase in scattered flux from the forward scattering direction (or backward direction for g < 1) is predominantly unpolarized. For moderate asymmetry parameter |g| ≲ 0.6, this causes an overall decrease of ⟨fϕ ⟩ with inclination (Fig. 8) while for extreme values |g|≳ 0.9 the huge flux increase compensates for the lower fractional polarization for forward and backward scattering.
The phase function for the Stokes Qd parameter 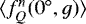 is zero for the pole-on view because of the symmetric cancellation of + Qd and − Qd signals. The function increases steadily with i (Fig. 8) and for i = 90° or edge-on disks there is
is zero for the pole-on view because of the symmetric cancellation of + Qd and − Qd signals. The function increases steadily with i (Fig. 8) and for i = 90° or edge-on disks there is 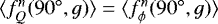 , because all dust is aligned with the major axis and produces polarization in the + Qd direction.
, because all dust is aligned with the major axis and produces polarization in the + Qd direction.
Fractional polarization
The fractional polarizations 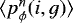 and
and 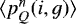 in Fig. 9 can be deduced from the ratio of the phase functions shown in Fig. 8. Observationally, a fractional polarization determination requires a measurement of the integrated disk polarization and the integrated disk intensity.
in Fig. 9 can be deduced from the ratio of the phase functions shown in Fig. 8. Observationally, a fractional polarization determination requires a measurement of the integrated disk polarization and the integrated disk intensity.
As shown in Fig. 9, the fractional azimuthal polarization 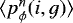 only depends to a very small extent on g for small inclinations i ≤ 35° with deviations <± 0.02 and the i-dependence is well described by
only depends to a very small extent on g for small inclinations i ≤ 35° with deviations <± 0.02 and the i-dependence is well described by
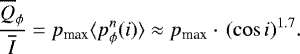 (45)
(45)
A measurement of the fractional azimuthal polarization for low-inclination disks is therefore equivalent to a determination of the pmax-parameter.
The lower panel of Fig. 9 includes also the purely polarimetric ratio 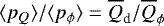 , which includes no scaling factor pmax and systematic uncertainties from the polarimetric measurements might be particularly small. Therefore, the ratio
, which includes no scaling factor pmax and systematic uncertainties from the polarimetric measurements might be particularly small. Therefore, the ratio 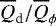 can be used to determine the scattering asymmetry parameter g, if polarimetric cancellation effects for
can be used to determine the scattering asymmetry parameter g, if polarimetric cancellation effects for 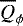 are taken into account for poorly resolved disks. For the extended disk HR 4796A, cancellation can be neglected, and we can use
are taken into account for poorly resolved disks. For the extended disk HR 4796A, cancellation can be neglected, and we can use 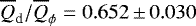 (
(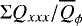 from Table 1) and the inclination i = 75°, which yields a value of about g = 0.7 from Fig. 9. This method is useful for systems with i ≈ 30°−80° because the separations between the g-parameter curves are quite large. The curves in Fig. 9 for flat disk models are not applicable for edge-on disks i≳80° with a vertical extension (see Sect. 4.3).
from Table 1) and the inclination i = 75°, which yields a value of about g = 0.7 from Fig. 9. This method is useful for systems with i ≈ 30°−80° because the separations between the g-parameter curves are quite large. The curves in Fig. 9 for flat disk models are not applicable for edge-on disks i≳80° with a vertical extension (see Sect. 4.3).
 |
Fig. 9 Upper panel: disk averages of the fractional azimuthal polarization |
4.2 Calculations of the normalized quadrant polarization parameters
The normalized quadrant polarization parameters 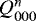 ,
, 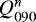 ,
, 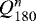 , and
, and 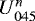
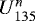 are plotted in Fig. 10 as a function of i for different g parameters. The “right-side” quadrants
are plotted in Fig. 10 as a function of i for different g parameters. The “right-side” quadrants 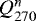 ,
, 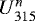 ,
, 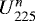 have the same absolute values as the corresponding “left-side” quadrants because of the disk symmetry. All values are multiplied by the factor 2π so that the reference case g = 0 and i = 0° is set to
have the same absolute values as the corresponding “left-side” quadrants because of the disk symmetry. All values are multiplied by the factor 2π so that the reference case g = 0 and i = 0° is set to 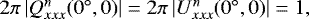 similar to the normalization for the disk-averaged scattering function
similar to the normalization for the disk-averaged scattering function 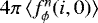 .
.
For pole-on disks, all the normalized quadrant polarization values have the same absolute value 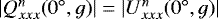 for a given g. This value is lower for larger g-parameter because lesslight is scattered perpendicularly to the disk plane in the polar direction, as in the
for a given g. This value is lower for larger g-parameter because lesslight is scattered perpendicularly to the disk plane in the polar direction, as in the 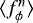 function. For i > 0° the quadrant values show different types of dependencies on i and g.
function. For i > 0° the quadrant values show different types of dependencies on i and g.
As described in Sect. 3.3, for the Stokes Qd quadrants the disk inclination introduces a geometric projection effect which increases the sampled disk area for the “left” and “right” quadrants for larger i, and therefore the 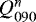 and
and 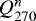 -values reach a maximum of (
-values reach a maximum of (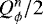 ) for i = 90°. The areas for the front and back quadrants go to zero for i → 90° and therefore so do the values
) for i = 90°. The areas for the front and back quadrants go to zero for i → 90° and therefore so do the values 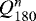 and
and 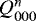 , but with a difference which depends strongly on g. The effect of the scattering asymmetry is already clearly visible for relatively small values, g ≈ 0.3, and inclinations, i ≈ 10°, and becomes even stronger for larger g and i as can be seen from the enhanced |Q180| values relative to |Q000|. A similar front–back quadrant effect also occurs for the Ud-components with enhanced absolute values for the front-side quadrant |U135| and reduced values for the backside quadrant |U045|.
, but with a difference which depends strongly on g. The effect of the scattering asymmetry is already clearly visible for relatively small values, g ≈ 0.3, and inclinations, i ≈ 10°, and becomes even stronger for larger g and i as can be seen from the enhanced |Q180| values relative to |Q000|. A similar front–back quadrant effect also occurs for the Ud-components with enhanced absolute values for the front-side quadrant |U135| and reduced values for the backside quadrant |U045|.
4.3 Comparison with three-dimensional disk ring models
The polarization parameters derived in the previous sections are calculated for geometrically flat disks because this simplifies the calculations enormously. Of course, real disks have a vertical extension but observations of highly inclined debris disks typically show a small ratio h∕r≲0.1 (see e.g., Thébault 2009). Therefore, the flat disk models could serve as an approximation for 3D disks, and we explore the differences. For this, we calculated models for a rotationally symmetric, optically thin disk ring with a central radius rring and a Gaussian density distribution for the ring cross-section,
![\begin{equation*}\rho(r,h) = \rho_0\, \textrm{exp}(-[(r-r_{\textrm{ring}}){}^2+h^2]/2\,\delta^2),\end{equation*}](/articles/aa/full_html/2021/11/aa40405-21/aa40405-21-eq172.png) (46)
(46)
with full width at half maximum (FWHM) of ΔFWHM = 2.355 δ. Figure 11 compares images of such 3D disk rings with ΔFWHM = 0.2 rring, g = 0.6, and different i with flat disk models. The vertical extension of the 3D model is most obvious for the edge-on (i =90°) case for which the flat disk model gives only a profile along the x-axis.
For i < 90°, the differences between flat disks and vertically extended disks are already small for i = 75° and hardly recognizable for lower inclination. In particular, the values for the disk-averaged scattering functions ⟨f⟩ and the normalized quadrant polarization parameters 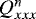 and
and 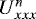 are equal or very similar as can be seen in Figs. 8 and 10 where the results from the 3D disks are plotted as small crosses together with those from the flat disk models. The agreement is typically better than ± 0.01. An example of a systematic difference between 3D disks and flat disks is a slightly lower value (about 0.01) for the azimuthal polarization ⟨fϕ ⟩ in Fig. 8 for pole-on (i = 0°) 3D disks. For disks with a vertical extension, not all scatterings are occurring exactly in the disk midplane, but also slightly above and below where the scattering angle is smaller or larger than 90° and therefore (1 − cos2θ)∕(1 + cos2θ) in Eq. (20) is smaller than one. Another example is the reduced ⟨fI ⟩ for edge-on (i = 90°) 3D disks, because less material lies exactly in front of the star where forward scattering would produce a strong maximum for large g-parameter. This is most visible for g = 0.6 (the effect is even stronger for g = 0.9 but this point is outside the plotted range). Similar but typically also very small effects are visible for the normalized quadrant polarization parameters in Fig. 10. The presence or absence of the vertical extension produces a strong difference for the Stokes Ud which is also clearly apparent in Fig. 11 for i = 90°.
are equal or very similar as can be seen in Figs. 8 and 10 where the results from the 3D disks are plotted as small crosses together with those from the flat disk models. The agreement is typically better than ± 0.01. An example of a systematic difference between 3D disks and flat disks is a slightly lower value (about 0.01) for the azimuthal polarization ⟨fϕ ⟩ in Fig. 8 for pole-on (i = 0°) 3D disks. For disks with a vertical extension, not all scatterings are occurring exactly in the disk midplane, but also slightly above and below where the scattering angle is smaller or larger than 90° and therefore (1 − cos2θ)∕(1 + cos2θ) in Eq. (20) is smaller than one. Another example is the reduced ⟨fI ⟩ for edge-on (i = 90°) 3D disks, because less material lies exactly in front of the star where forward scattering would produce a strong maximum for large g-parameter. This is most visible for g = 0.6 (the effect is even stronger for g = 0.9 but this point is outside the plotted range). Similar but typically also very small effects are visible for the normalized quadrant polarization parameters in Fig. 10. The presence or absence of the vertical extension produces a strong difference for the Stokes Ud which is also clearly apparent in Fig. 11 for i = 90°.
These comparisons show that the quadrant polarization parameters derived from flat, optically thin, rotationally symmetric disk models are for most cases essentially indistinguishable from those derived from 3D disk models with a vertical extension typical for debris disks. Only for edge-on or close to edge-on disks, i≳80°, can the vertical extension introduce significant differences, which needs to be taken into account.
 |
Fig. 10 Normalized ( |
 |
Fig. 11 Comparison of the 3D-ring model with the flat disk model. Left: I, Qd, Ud and Qϕ for a 3D disk ring with a full width at half maximum density distribution of ΔFWHM∕rring = 0.2. Scattering parameters are g = 0.6 and pmax = 1 for inclinations i = 0°, 45°, 75° and 90°. The same gray scale from + a (white) to −a (black) is used for all panels. The black lines in the Qd and Ud panels indicate the polarization quadrants. Right: same but for the flat disk model. |
5 Diagnostic diagrams for the scattering asymmetry g
The normalized quadrant polarization parameters and quadrant ratios for disk models using the HGpol-function depend only on the scattering asymmetry parameter g and the diskinclination i as shown in Fig. 10. From imaging polarimetry of debris disks one can often accurately measure the disk inclination, and therefore the quadrant polarization parameters are ideal for the determination of g. The method described in this work for the single parameter HGpol-function can be generalized to other, more sophisticated parameterizations for the polarized scattering phase function of the dust.
This diagnostic method is based on the strong assumption that the intrinsic disk geometry is rotationally symmetric, which is often a relatively good assumption for debris disks, but there are also several cases known with significant deviations from axisymmetry (e.g., Debes et al. 2009; Maness et al. 2009; Hughes et al. 2018). This can affect the determination of the g-parameter and one should always assess possible asymmetries in the disk symmetry using for example the left–right symmetry parameters 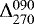 or
or 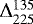 (Sect. 2.4).
(Sect. 2.4).
 |
Fig. 12 Relative quadrant polarization values |
5.1 Relative quadrant parameters
The azimuthal dependence of the scattering polarization can be described by the relative quadrant parameters 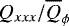 and
and 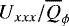 . These parameters are directly linked to the normalized scattering phase functions
. These parameters are directly linked to the normalized scattering phase functions 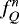 ,
, 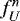 , and
, and 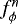 for the polarization according to
for the polarization according to
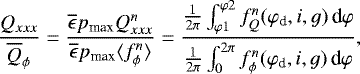 (47)
(47)
and equivalent to 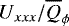 .
.
The relative quadrant polarization parameters 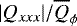 and
and 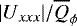 are plotted in Fig. 12 as a function of g for disk inclinations i = (0°), 15°, 30°, 45°, 60°, and 75°. For pole-on disks, all relative quadrant values are equal to
are plotted in Fig. 12 as a function of g for disk inclinations i = (0°), 15°, 30°, 45°, 60°, and 75°. For pole-on disks, all relative quadrant values are equal to 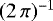 independent of the g-parameter, because of the normalization with
independent of the g-parameter, because of the normalization with 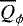 .
.
With increasing g and i, the quadrant parameters show the expected steady increase for the front-side quadrants 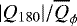 and
and 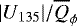 (red lines) and the steady decrease for the backside quadrants
(red lines) and the steady decrease for the backside quadrants 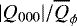 and
and 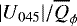 (blue lines). The separation between red and blue lines produces particularly large ratios for high inclination because the range of scattering angles extends from strong forward scattering to strong backward scattering.
(blue lines). The separation between red and blue lines produces particularly large ratios for high inclination because the range of scattering angles extends from strong forward scattering to strong backward scattering.
For high inclination disks, the substantial contribution of forward and backward scattering strongly reduces the fractional scattering polarization in the front-side and back-side quadrants and the relative quadrant values are therefore 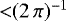 for small g. For the Q000 and Q180 quadrants, the reduction is further accentuated by the disk projection which reduces the sampled disk area for inclined disks. Strong forward scattering g → 1 compensates these two effects to a certain degree for the front-side quadrants (red curves), while it further diminishes the flux in the (blue) back side quadrants.
for small g. For the Q000 and Q180 quadrants, the reduction is further accentuated by the disk projection which reduces the sampled disk area for inclined disks. Strong forward scattering g → 1 compensates these two effects to a certain degree for the front-side quadrants (red curves), while it further diminishes the flux in the (blue) back side quadrants.
The two positive Qd quadrant parameters 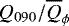 and
and 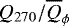 depend mainly on the disk inclination. For higher inclination, a greater area of the disk is included in these two quadrants and therefore their relative contribution to the total polarized flux Q090∕Qϕ increases from
depend mainly on the disk inclination. For higher inclination, a greater area of the disk is included in these two quadrants and therefore their relative contribution to the total polarized flux Q090∕Qϕ increases from 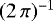 for i = 0° to 0.5 for i = 90°. For edge-on systems, there is
for i = 0° to 0.5 for i = 90°. For edge-on systems, there is 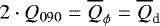 or all polarized flux of a disk is located only in the left and right quadrants Q090 and Q270.
or all polarized flux of a disk is located only in the left and right quadrants Q090 and Q270.
Figure 12 includes the relative quadrant parameters measured for HR 4796A from Table 1. This disk has an inclination of about 76° (e.g., Chen et al. 2020; Milli et al. 2019)and the i = 75°-lines match this value well. For Stokes Qd the front side value 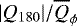 is very sensitive for the determination of the g-parameter because the corresponding curve in Fig. 12 is steep. This results in a value of g = 0.72 ± 0.03 with a relative uncertainty of only about ±4%, despite the relatively large measuring error of about ±13% for
is very sensitive for the determination of the g-parameter because the corresponding curve in Fig. 12 is steep. This results in a value of g = 0.72 ± 0.03 with a relative uncertainty of only about ±4%, despite the relatively large measuring error of about ±13% for 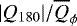 . The polarization signal is strong near the major axis and the corresponding quadrant values
. The polarization signal is strong near the major axis and the corresponding quadrant values 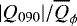 and
and 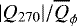 can be measured with high precision of roughly ±3%. However, because the
can be measured with high precision of roughly ±3%. However, because the 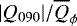 curve is rather flat in Fig. 12, the resulting uncertainty on the derived g-values is also about ±3%. The obtained g-values for
curve is rather flat in Fig. 12, the resulting uncertainty on the derived g-values is also about ±3%. The obtained g-values for 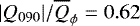 and
and 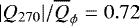 differ significantly because of the described deviation of the HR 4796A disk geometry from axisymmetry.
differ significantly because of the described deviation of the HR 4796A disk geometry from axisymmetry.
For the backside quadrant, only an upper limit of about 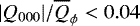 could be measured. This limit is not useful for constraining the g-value because expected values for an inclination of 75° are very low, namely
could be measured. This limit is not useful for constraining the g-value because expected values for an inclination of 75° are very low, namely 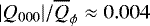 for g = 0.0 and ≈0.001 for g = 0.6, and the corresponding curve is below the plot range covered in Fig. 12.
for g = 0.0 and ≈0.001 for g = 0.6, and the corresponding curve is below the plot range covered in Fig. 12.
The relative quadrant values of HR 4796A for Stokes Ud yield low asymmetry parameters g ≈ 0.4 for the back-side quadrants 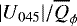 and
and 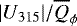 , and larger values of g ≈ 0.5 and g ≈ 0.7 for the front side, with again a significant left–right asymmetry.
, and larger values of g ≈ 0.5 and g ≈ 0.7 for the front side, with again a significant left–right asymmetry.
 |
Fig. 13 Quadrant polarization ratios for flat disk models for |Q000|∕|Q180|, |U045 |∕|U135|, |Q090 |∕|Q180|, and |Q090|∕|Q135| with measured values from HR 4796A (similar to Fig. 12). |
5.2 Quadrant ratios
The scattering asymmetry g can also be derived from quadrant ratios describing the brightness contrast between the front and back sides of the disk as shown in Fig. 13, which includes the measurements from HR 4796A.
High-quality determinations of g are achievedif the front- and the back-side quadrant polarizations can be accurately measured. For low-inclination systems, this should be possible for ratios like |Q000|∕|Q180| or |U045|∕|U135| where both the front side and back side are bright. For high-inclination systems, as in HR 4796A, the back side can be faint and the ratios |Q000|∕|Q180| or |U045|∕|U135| are small (≲ 0.1) and therefore difficult to measure accurately. As an alternative, one can use ratios based on the bright quadrants like |Q090|∕|Q180| or |Q090|∕|U135| or equivalent ratios using the right-side quadrants Q270 and U225. Many aspects of the diagnostic diagrams plotted in Fig. 13 are similar to the description of the relative quadrant parameters in the previous section.
5.3 Polarized scattering phase function for HR 4796A
5.3.1 Comparison of different g determinations
The measured quadrant polarization parameters for HR 4796A can be used to strongly constrain the asymmetry parameter g of the adopted HGpol scattering phase function fϕ(θ), but only for the θ-range sampled by the used quadrant parameters (see also Hughes et al. 2018). The flux-weighted distribution of scattering angles θ sampled by a quadrant strongly depends on inclination i, but also on g as illustrated in Fig. 14. Indeed, all quadrants of a nearly pole-on disks probe fϕ (θ) only near the scattering angle of 90°, while some quadrants probe a large θ-range for strongly inclined disks.
We define the median angle θmed for the anglethat represents the 50th percentile of a cumulative polarized intensity distribution covered by one quadrant. The back and front quadrants Q000 and Q180 sample a narrow range, the median angle θmed is close to the most extreme backward and forward scattering angle θmed ≈ 90° ± i for a disk with inclination i, and θmed are essentially identical for different g. The ranges of scattering angles θ covered by the quadrants Q090, U045, and U135 are very broad for larger i and the θmed depend significantly on g as shown in Fig. 14. For example, θmed(Q000) is 90° for isotropic scattering, and becomes smaller for i → 90° and g → 1 as indicated by the colored θmed points (diamonds) and the dotted lines.
The quadrants U045 and U135 sample the back- and front-side parts of the disk and their θmed-angles lie between those of the Qd-quadrants. The front-side quadrant also shows a strong tendency towards smaller θmed(U135) values for larger g and i, as in the Q090-quadrant, while the g-dependence of θmed(U045) is much smaller.
Figure 15 shows the g-parameters obtained for HR 4796A as a function of the θ-angle probed by the used quadrant parameters. The angle θ corresponds for relative quadrant parameters to θmed for i = 75° and g = 0.6 as given in Fig. 14 and the horizontal uncertainty bar spans two-thirds of the plotted θ-distribution (from the 16.6 to the 83.3 percentiles). For the quadrant ratios, the adopted θ-values are the mean of the θmed of the two quadrants and the horizontal bars illustrate their separation. In principle, one should consider for the θmed-values the systematic trend of g(θmed) from higher g-values (≈ 0.7) for forward-scattering quadrants to lower values (≈0.4) for the backward scattering quadrants. We neglect this effect which would introduce θmed shifts of about − 5° for U135 and U225, shifts of about + 5° for Q090 and Q270, and smaller shifts for the other quadrants.
Figure 15 shows for HR 4796A a systematic dependence of the derived g-parameters with scattering angle θ. The results from the relative quadrant parameters and the quadrant ratios are roughly consistent. The colors indicate measurements for the left (blue) and right (red) sides of the disk and g-values differ significantly between the two sides for θmed = 35° and 70° because of the left–right disk brightness asymmetry. On the fainter side, this effect reduces the derived g-value for 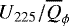 , while g is enhanced for
, while g is enhanced for 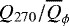 because the intrinsic faintness of Q270 mimics a disk with relatively little 90°-scattering because of the normalization with
because the intrinsic faintness of Q270 mimics a disk with relatively little 90°-scattering because of the normalization with 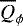 . The intrinsic left–right brightness asymmetry of HR 4796A has less impact on the g determination based on quadrants ratios from the same side. This redundancy helps to disentangle the effects of the scattering asymmetry g from geometric or left–right disk brightness asymmetries.
. The intrinsic left–right brightness asymmetry of HR 4796A has less impact on the g determination based on quadrants ratios from the same side. This redundancy helps to disentangle the effects of the scattering asymmetry g from geometric or left–right disk brightness asymmetries.
 |
Fig. 14 Angular distribution of the polarized intensity in the polarization quadrants for i = 15°, 30°, 45°, 60° and 75° and differentasymmetry parameter g (colors). For quadrants Q000 and Q180 only the caseg = 0 is shown, because differences for other g-parameters are very small. The distributions are normalized for each quadrant individually. For the quadrants Q000, U045, and U135, the median angles θmed (diamonds) for large g-values increase with inclination as illustrated with the dotted lines. |
 |
Fig. 15 Scattering asymmetry parameters for HR 4796A derived from relative quadrant parameters (open symbols) and quadrant ratios (filled symbols) as a function of the θmed or the mean of θmed, respectively.Colors indicate measurements from the left or SW (blue) and the right or NE (red) disk sides. |
 |
Fig. 16 (a) Comparison of the best single parameter HGpol fit model for fixed i = 75° and measured relative quadrant polarization parameters for HR 4796A. (b) Deviations from the best-fitting HGpol (i = 75°, g = 0.65) for the measured values, for the best fits for slightly different disk inclinations HGpol (i = 73°, g = 0.60) and HGpol(i = 77°, g = 0.71) and for the HGpol fit from Milli et al. (2019) (green dashed line). (c) HGpol phase functions and the directly extracted phase function fϕ(θ) (dotted black line) with corresponding uncertainty range (grey shaded area) from Milli et al. (2019). (d) HG intensity phase functions. The measured quadrant values and the different fit curves are identified in panel b. |
5.3.2 A “mean” asymmetry parameter g for HR 4796A
The clear trend of the derived g-parameter with scattering angle θ for HR 4796A in Fig. 15 reveals that the used HGpol-function is an oversimplified description of the polarized scattering phase function for this object. For fainter or less well resolved disks, and for those with low inclination, it may not be possible to recognize such systematic deviations from a HGpol function, and for all these cases the derived g-value from the HGpol-function could serve as a good starting point for the analysis of quadrant polarization parameters.
Therefore, for HR 4796A we also derive a “mean” value for the HG asymmetry parameter g despite the discussed trend. To this end, for the seven measured relative quadrant values |U045|∕Qϕ, |Q090|∕Qϕ, |U135|∕Qϕ, |U180|∕Qϕ, |U225|∕Qϕ, |U270|∕Qϕ, and |U315|∕Qϕ from Table 1, we determine the best-fitting g-asymmetry parameter for the adopted disk inclination i = 75°. This yields HGpol(i = 75°, g = 0.65) with a weighted sum of squared deviations of χ2 = 15.4, and the corresponding calculated and measured values are plotted in Fig. 16a. The differences between the models are more visible in Fig. 16b, where the deviations of data points and calculations from the best-fit model are shown. The large χ2 -value indicates that the adopted HGpol-fit does not describe the data well because of the significant left–right asymmetry between |Q090| and |Q270|, or |U135| and |U225| at the level of about 4σ (σ: standard deviations), which cannot be described with an axisymmetric disk model. Additionally, the best fit underestimates the quadrant values at small (θmed = 16°) and large (124°) scattering angles. Panel b also includes the best-fit results for slightly different disk inclinations HGpol(i = 73°, g = 0.60) and HGpol(i = 77°, g = 0.71), which differ very little and produce deviations between fit and data that are similar to the i = 75° solution. The corresponding Henyey-Greenstein scattering phase functions HGpol (or fϕ (θ)) are given in panel c, while panel d shows the HG intensity function (fI(θ)) for the best quadrant solution for i = 75° and the solution from Milli et al. (2019).
Fortunately, we can compare the result from the quadrant parameter fitting with the analysis of the same HR 4796A data by Milli et al. (2019). They extracted from the polarimetric imaging data a detailed phase curve shown in Fig. 16c covering the scattering angle range θ = 13° to 145°. They also fitted the extracted phase curve with a single parameter HGpol-function and obtained an asymmetry parameter of g = 0.43 which is much smaller than our value of g = 0.65 (Fig. 16c). An important reason for this discrepancy is the sampling of the scattering angles of the data used for the fitting. In this work, the fitting is based on seven quadrant polarization values – for a disk with i = 75° and g > 0.4 – which are strongly biased towards small θ-values because of the forward “distorted” distribution of the polarized flux. In addition, the back-side quadrants U045 and U315 are weak and the corresponding measurements have a low signal-to-noise ratio of S∕N < 5 and therefore a small weight. Thus, the fit to the quadrant values predominantly samples the range θ ≈ 16°–67° of the scattering phase function. The analysis of Milli et al. (2019) samples a much broader range and particularly also more backward scattering angles. Therefore, the result of these latter authors of g = 0.43 closely matches the g-values derived in this work by the quadrant ratios |U045|∕|U135| and |U315|∕|U225| (Fig. 13). On the other hand, the HGpol-fit of Milli et al. (2019) underestimates their extracted phase function in the forward-scattering range θ ≈ 16° to 35°. This comparison illustrates the bias effect that can be introduced by different kinds of phase curve sampling, if the adopted model curves fϕ(θ) do not match well the real scattering phase function of the dust.
5.3.3 A fit with a double HGpol-function
A better agreement between measured and calculated quadrant values can be obtained using a double HG-function for the dust scattering
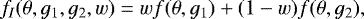 (48)
(48)
because three parameters provide more freedom for the polarized phase curve 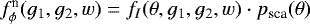 in the quadrant fitting. Calculating quadrant polarization values for i = 75° and a grid of phase function parameter g1 and w ∈ [0.00, 0.01, ..., 1.00], and g2 ∈ [−1.00, −0.99, ..., g1] gives a best-fit solution of (g1, g2, w) = (0.78, −0.09, 0.85) with χ2 = 10.2 which is plotted in Fig. 17.
in the quadrant fitting. Calculating quadrant polarization values for i = 75° and a grid of phase function parameter g1 and w ∈ [0.00, 0.01, ..., 1.00], and g2 ∈ [−1.00, −0.99, ..., g1] gives a best-fit solution of (g1, g2, w) = (0.78, −0.09, 0.85) with χ2 = 10.2 which is plotted in Fig. 17.
Compared to the case of the best single parameter HGpol function (Fig. 16), this fit does not underestimate the relative quadrant values at θmed = 16° and 124° and passes in the middle of the discrepant quadrant values at 35° and 67° for the left and right disk sides (see Figs. 17a and b). The corresponding polarized scattering phase function fϕ (θ) in Fig. 17c has a much wider peak extending from θ ≈ 20° to ≈ 90°, closely matching the directly extracted phase curve from Milli et al. (2019).
It is interesting to compare our results with the double HGpol function obtained by Milli et al. (2019) from the fit to the detailed phase-curve extraction which is included in Fig. 17 as a green dashed line. Unfortunately, there is an error in the indicated fit parameters in Fig. 5 of Milli et al. (2019) but the plotted fit curve is correct. The fit parameters should be 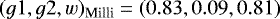 (J. Milli, personal communication) which also provide a very good fit to the quadrant values derived in this work as shown in Figs. 17a and b.
(J. Milli, personal communication) which also provide a very good fit to the quadrant values derived in this work as shown in Figs. 17a and b.
The good agreement between the double HGpol-fits of Milli et al. (2019) and the solution found for the quadrant polarization values shows that the selection of a more appropriate scattering phase function strongly reduces the large difference in the deduced g-determination described in Sect. 5.3.2 using only the single HGpol function. It should also be noted that the polarized phase function fit fϕ (θ) of Milli et al. (2019) does not consider the left–right asymmetry of the disk in HR 4796A and therefore the phase curve uncertainty attained by these latter authors is larger than their measurement uncertainties. It seems likely that the azimuthal polarization signal extracted by Milli et al. (2019) would probably allow the determination of a better constrained empirical fϕ (θ)-function for HR 4796A if the significant azimuthal dependence on the dust density is included in the fitting. Using a more detailed disk model for the fitting of the derived quadrant polarization parameters seems to be less useful because of the small number of measured values, a matter that is discussed further in Sect. 6.3.
This example shows that selecting a good model fit function is important for the analysis of the quadrant polarization parameters and this should be investigated in more detail. The double HGpol is probably not an ideal choice, because in the intensity scattering function significant weight is given to the forward and backward scattering angles, which produce less polarization and therefore contribute less to the signal in the corresponding polarization quadrants Q000 or Q180. This could explain the substantial differences for θ < 16° or for θ > 124° between the two derived best-fitting functions in Fig. 17d where the quadrant parameters provide no or only weak constraints on the shape of the scattering phase function.
In a future study, alternative polarized scattering phase functions fϕ (θ) should be investigated for the fitting of polarimetric data, which give more weight to intermediate scattering angles θ ≈ 90° ± i. Such a curve should also consider deviations of the fractional scattering polarization from a symmetric curve (Rayleigh-like) with respect to θ = 90° as already derived from observations of HR 4796A by Perrin et al. (2015) and Arriaga et al. (2020). Considering this could be particularly important when constrainingfϕ(θ) for the dustin debris disks with smaller inclinations and a more limited observable range of θ-angles.
 |
Fig. 17 Same as Fig. 16 but for the best-fitting double HGpol scattering phase function |
6 Discussion
6.1 New polarization parameters for circumstellar disks
In recent years, the scattering light of many proto-planetary and debris disks has been spatially resolved with high-resolution polarimetric imaging using modern AO systems at large telescopes (Schmid 2021). Unfortunately, the presented results for the measurements of the polarized light from circumstellar disks are highly heterogeneous and are rarely flux calibrated, and it is therefore very difficult to compare the results from different studies for a systematic investigation of disks.
The main motivation of the present paper is the promotion of a photo-polarimetric parameter system which should help to homogenize the polarimetric measurements for circumstellar disks and allow more straightforward comparisons between measurements of different disks and model results. The introduced quadrant polarization parameters Q000, Q090, Q180, Q270 and U045, U135, U225, U315 are defined for the Stokes Qd and Ud parameters aligned with the apparent major and minor axis of the projected disk; they are based on the “natural” quadrant pattern produced by circumstellar scattering and measure within these quadrants the integrated Stokes Qd and Stokes Ud flux, respectively.
These eight quadrants are very well suited for the description of the azimuthal dependence of the polarization signal of disks, except for edge-on or nearly edge-on systems. Furthermore, they can be used to quantify geometric deviations of the disk from axisymmetry from differences between left and right quadrants or characterize the disk inclination effects and the dust scattering asymmetry from ratios between back-side and front-side quadrants.
This disk characterization only requires differential polarization measurements, like relative quadrant parameters 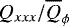 and
and 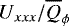 , or quadrant ratios like Q000∕Q180. No absolute flux calibration with respect to the intensity of the star Istar or the disk
, or quadrant ratios like Q000∕Q180. No absolute flux calibration with respect to the intensity of the star Istar or the disk 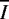 are required and therefore one can also use polarimetric imaging of disks obtained in coronagraphic mode or with the central star saturated. In addition, the eight quadrant parameters are partially redundant and offer multiple options for the characterization of a disk, meaning that problems with a particular quadrant, for example because of the peculiarities of a disk or observational effects, can be mitigated.
are required and therefore one can also use polarimetric imaging of disks obtained in coronagraphic mode or with the central star saturated. In addition, the eight quadrant parameters are partially redundant and offer multiple options for the characterization of a disk, meaning that problems with a particular quadrant, for example because of the peculiarities of a disk or observational effects, can be mitigated.
The quadrant polarization measurements should be particularly well adapted for well-resolved, extended, low-surface-brightness debris disks, which are relatively common (Esposito et al. 2020). The integration of the Q and U polarization for entire quadrants helps to improve the signal, and restricting the measurements of the azimuthal dependence to a few values is appropriate for a faint source where it is hard to get sufficient signal for a detailed characterization. Of course, the calibration of the polarization zero point must be determined very accurately for faint sources and this can be achieved for many debris disks because the central star is often a very good zero polarization reference source.
Model calculations exploring the parameter space for the dust scattering in circumstellar disks are of particular importance for advancing our understanding of the properties of the scattering dust in disks. The quadrant polarization parameters are very well suited to characterizing the azimuthal dependence of the polarization signal for different models. Because these model results can be expressed as relative values or ratios, they can be readily compared with each other for the evaluation of dependencies on the scattering asymmetry for optically thin disks or the angle dependencies of the surface reflectivity in optically thick disks, even if parameters such as stellar illumination, disk size, or radial dust density distribution in optically thin disks are different.
The modeled values can also be compared with observations, but important issues are the PSF smearing and polarimetriccancelation effects between positive and negative quadrants. This can significantly reduce the measurable polarization for poorly resolved disks (Schmid et al. 2006; Tschudi & Schmid 2021) and change the appearance of the Q and U quadrant patterns of inclined or asymmetric disks (Heikamp & Keller 2019). For example, for the Stokes Qd quadrants, the PSF convolution reduces the total signal of the positive quadrants Q090 and Q270 by the same amount as it enhances the signal (less negative signal) in the negative quadrants Q000 and Q180; the same is true for the Stokes Ud quadrants. If the PSF is well known for a given observation then the smearing and cancelation effects can be taken into account accurately in order to minimize the introduced effects (Tschudi & Schmid 2021).
The measurements of the quadrant polarization parameters for circumstellar disks provide a simple and model-independent method for the description of the azimuthal distribution of the scattering polarization and the obtained results can be easily tested by comparing the measured and calculated model values. Similarly, the quality of the measured quadrant data can be verified with alternative measurements of the same target. Of course, a detailed analysis of the polarimetric imaging data with 2D synthetic model images would provide a more detailed comparison, but this is a very laborious procedure which requires detailed knowledge of the observational effects for each data set and a good understanding of the modeling aspects for each individual disk (see e.g., Milli et al. 2019; Olofsson et al. 2020; Chen et al. 2020, for the case of HR 4796A). Therefore, it appears attractive to base a quick analysis of many disks on the simple quadrant polarization parameters. Once measured and corrected for the PSF smearing, they remain unchanged until higher quality measurements become available and the interpretation of the measurements obtained can be continuously improved if additional information about the corresponding disk model can be taken into account.
6.2 Investigation of debris disks
The usefulness of the quadrant polarization parameters is tested in this work with simple models of debris disks and with observations of the prototype debris-disk system HR 4796A. Debris disks are optically thin and therefore the azimuthal dependence of the polarization signal depends directly on the polarized scattering phase function fϕ (θ) of the dust. Because the quadrant polarization parameters measure the azimuthal dependence, they are ideal for determining fϕ (θ). This is shown with model calculation of flat axisymmetric debris disks using the simple HGpol function forthe parameterization of the polarized scattering phase function fϕ (θ, g). For optically thin, rotationally symmetric disks, the azimuthal dependence of the polarization signal can be directly described by a disk scattering phase function fϕ (φd, i, g), which only depends on the disk inclination i and the scattering asymmetry parameter g of the HG function. This function also defines the relative quadrant polarization values 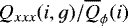 as an eight-parameter condensation of the azimuthal polarization dependence, from which one can also derive quadrant ratios like Q000(i, g)∕Q180(i, g) as alternative results. These parameters yield a measure for the dust-scattering asymmetry for a given i and corresponding diagnostic diagrams have been calculated for relative quadrant values and quadrant ratios. If the selected HGpol function is an appropriate parametrization for the dust scattering of an observed debris disk then all the measured quadrant parameters should yield the same g parameter. The same method can be applied for investigations of other scattering phase functions.
as an eight-parameter condensation of the azimuthal polarization dependence, from which one can also derive quadrant ratios like Q000(i, g)∕Q180(i, g) as alternative results. These parameters yield a measure for the dust-scattering asymmetry for a given i and corresponding diagnostic diagrams have been calculated for relative quadrant values and quadrant ratios. If the selected HGpol function is an appropriate parametrization for the dust scattering of an observed debris disk then all the measured quadrant parameters should yield the same g parameter. The same method can be applied for investigations of other scattering phase functions.
We tested the polarized phase-curve determination based on the quadrant polarization parameters for data of the “prototype” debris disk around HR 4796A from Milli et al. (2019). First, we noticed a significant disk asymmetry between the “left” and “right” sides with respect to the minor axis of the disk ring as projected on the sky. We did not consider this disk asymmetry and simply derived a “mean” scattering phase curve accepting that this introduces some uncertainties in the phase curve analysis. The diagnostic diagrams for the HGpol scattering phase function were used and the obtained g parameter determination shows a clear trend from high values g ≈ 0.7 for quadrants sampling small scattering angles θ ≈ 30° to lower values g ≈ 0.4 for larger scattering angles θ ≈ 120°. This is a clear indication that the adopted HGpol-scattering function is not adequately describing the dust in HR 4796A. The over-simplified fit model introduces strong bias effects responsible for significant differences between the g-value determination based on a detailed phase-curve extraction and the one based on the quadrant parameters.
As alternative, we used a three-parameter double HGpol function as description for the dust scattering fϕ(θ). The best fit solution to the quadrant values that we find is in good agreement with the detailed phase curve extraction of Milli et al. (2019) based on the same data. This is surprising because the covered θ-range for the phase curve from about 16° to 164° is large for the high-inclination (i ≈ 75°) system HR 4796A and a characterization of fϕ(θ) based on a few quadrant values yields only a relatively coarse θ resolution. The main reason the detailed fϕ(θ)-extraction of Milli et al. (2019) is not clearly superior when compared to the quadrant method is the significant deviations of the dust density distribution from axisymmetry, which were also not taken into account by Milli et al. (2019) for their phase-curve fitting. The detailed extraction contains much more information on the nonsymmetric disk brightness distribution which is discussed in detail in Milli et al. (2019). Also, small-scale structures are seen in the extracted azimuthal polarization curve of HR 4796A for which the quadrant parameters are “blind”.
However, the HR 4796A example shows that the analysis on the quadrant polarization parameters performs rather well for high-quality data of a bright target if we are “only” interested in the global azimuthal polarization dependence of debris disks caused by the polarized scattering phase function fϕ (θ) of the dust.
6.3 Limitations
The quadrant polarization parameters are designed for a simple description and analysis of the azimuthal dependence of the scattering polarization of circumstellar disks. The method is well defined but it has limitations, which must be taken into account in the interpretation of the results.
Importantly, one should be aware that real disks are often quite complex and a description using only eight parameters or less only yields rough information about the left–right disk asymmetry and the differences in the front–back brightness distribution. There are various effects that can cause significant departures from axisymmetry in the disk geometry: an intrinsic ellipticity introduced by noncircular orbits of dust particles, different types of hydrodynamic instabilities introducing spiral structures, azimuthal density features, lobsided disks, shadows cast by unresolved dust structures near the central star, dynamical interactions with proto-planets or other gravitating bodies in the system, and probably other effects.
Such asymmetries can be identified easily as left–right differences but they can also produce brightness effects between thedisk front- and backside which are then blended with front–back brightness effects caused by the dust-scattering asymmetry in optically thin disks or the angle-dependent surface reflectivity in optically thick disks.
For a disk with complex morphology based on a small number of measured polarization quadrant parameters, it can be difficult to recognize whether the asymmetries are caused by the disk geometry, the scattering phase function, optical depth effects, or an observational problem. Therefore, it is certainly always useful to examine the disk polarization images for the presence of strong azimuthal structures which can be taken into account for disentangling the effects of the disk geometry from those of the dust scattering phase function for an interpretation of the data.
Using only eight quadrant polarization parameters for the characterization of the detailed structure of a well-observed disk can of course only provide limited information as demonstrated for HR 4796A. In such a case, a detailed extraction of the polarized flux or a two-dimensional model fitting to the data as in Milli et al. (2019) or Arriaga et al. (2020) will provide more accurate results and a less ambiguous interpretation. For example, a detailed model analysis for HR 4796A could consider two or three parameters for the intensity scattering phase function fI (θ), one or two parameters for the shape of the fractional scattering polarization psca(θ) (and not only the fixed Rayleigh scattering like curve given in Eq. (20)), a description of the ring geometry, and three or more parameters for the azimuthal dust density distribution.
Therefore, the quadrant polarization parameters are less suitable for a detailed investigation of well-observed disks, and are more suitable for the exploration and the approximate description of the global properties of the scattering dust in many disks. However, it is still useful to derive these parameters for well-observed disk prototypes for a comparison with disks for which a detailed analysis is hardly possible, or for multi-wavelength studies of a given disk where a few well-defined parameters are sufficient to recognize and quantify wavelength dependencies for the polarized dust scattering phase function.
6.4 Conclusions
The quadrant polarization parameters introduced in this work seem to be very useful for a simple description of the azimuthal dependence of the polarization signal of circumstellar disks. These parameters can be determined from observations of many different types of circumstellar disks, for example debris disks around young or old stars, with or without strong illumination or dust blow-out signatures, or for proto-planetary disks with small or large central cavities and different kinds of hydrodynamical features.
The measured quadrant parameters can be compared with disk models that take the PSF smearing and cancelation effects into account and can explore the expected polarization signatures introduced by different descriptions for the scattering dust. Accumulating such data for a larger sample will allow a search for systematic trends in dust scattering properties for different disk types and for different wavelengths and inform us about the homogeneity or heterogeneity of dust-scattering properties in circumstellar disks. This can be achieved with relatively small uncertainties when compared to circumstellar shells or clouds, because the scattering angles θ, which have an important impact on the produced polarization signal, are typically very well known for resolved circumstellar disks. Investigations of the dust in circumstellar disks are also very attractive because many studies indicate that the dust evolves strongly in these systems and this could produce systematic trends for different disk types, which could be measurable with the new generation of AO polarimeters.
Acknowledgements
I am very grateful to Julien Milli for the reduced Qϕ and Uϕ images of HR 4796A used in this study, for the polarized scattering phase curves derived in Milli et al. (2019), and for many useful comments on an earlier version of this manuscript. I am indebted to an anonymous referee who made a very detailed and thoughtful review of the submitted manuscript which helped to improve the final paper significantly. I also thank Jie Ma for a careful reading of the manuscript and for checking the mathematical formulas. This work has been carried out within the framework of the National Center for Competence in Research PlanetS supported by the Swiss National Science Foundation.
Appendix A Radiation parameters for debris disks.
The following IDL procedure calculates disk-averaged scattering functions and normalized quadrant polarizationparameters for flat, rotationally symmetric, and optical thin disks with HG and HGpol scattering phase functions. Input parameters are the disk inclination in degrees ideg ∈ [0°, 90°] and the scattering asymmetry parameter g ∈] − 1, +1[. Output parameters are fiavg for the disk averaged intensity scattering phase function ⟨fI(i, g)⟩ (Eq. 37) and fphiavg for the corresponding normalized function for the azimuthal polarization 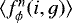 (Eq. 38). In addition, the procedure provides the five normalized quadrant polarization parameter qpp[0], qpp[1], qpp[2], qpp[3], and qpp[4] corresponding to
(Eq. 38). In addition, the procedure provides the five normalized quadrant polarization parameter qpp[0], qpp[1], qpp[2], qpp[3], and qpp[4] corresponding to 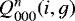 ,
, 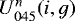 ,
, 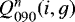 ,
, 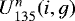 and
and 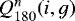 , respectively (Sect. 3.3). The Stokes Qd phase function follows from the quadrant sum
, respectively (Sect. 3.3). The Stokes Qd phase function follows from the quadrant sum 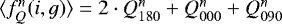 .
.
IDL procedure for the calculation of disk-averaged scattering functions and normalized quadrant polarization parameters.
References
- Apai, D., Pascucci, I., Brandner, W., et al. 2004, A&A, 415, 671 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arriaga, P., Fitzgerald, M. P., Duchêne, G., et al. 2020, AJ, 160, 79 [Google Scholar]
- Artymowicz, P., Burrows, C., & Paresce, F. 1989, ApJ, 337, 494 [NASA ADS] [CrossRef] [Google Scholar]
- Avenhaus, H., Quanz, S. P., Garufi, A., et al. 2018, ApJ, 863, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Bastien, P. 1982, A&AS, 48, 153 [NASA ADS] [Google Scholar]
- Bastien, P., & Menard, F. 1988, ApJ, 326, 334 [NASA ADS] [CrossRef] [Google Scholar]
- Benisty, M., Juhasz, A., Boccaletti, A., et al. 2015, A&A, 578, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beuzit, J. L., Vigan, A., Mouillet, D., et al. 2019, A&A, 631, A155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buenzli, E., & Schmid, H. M. 2009, A&A, 504, 259 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Canovas, H., Ménard, F., de Boer, J., et al. 2015, A&A, 582, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cantalloube, F., Dohlen, K., Milli, J., Brandner, W., & Vigan, A. 2019, The Messenger, 176, 25 [NASA ADS] [Google Scholar]
- Chen, C., Mazoyer, J., Poteet, C. A., et al. 2020, ApJ, 898, 55 [CrossRef] [Google Scholar]
- Debes, J. H., Weinberger, A. J., & Kuchner, M. J. 2009, ApJ, 702, 318 [NASA ADS] [CrossRef] [Google Scholar]
- de Boer, J., Langlois, M., van Holstein, R. G., et al. 2020, A&A, 633, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Engler, N., Schmid, H. M., Thalmann, C., et al. 2017, A&A, 607, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Esposito, T. M., Kalas, P., Fitzgerald, M. P., et al. 2020, AJ, 160, 24 [Google Scholar]
- Garufi, A., Quanz, S. P., Schmid, H. M., et al. 2016, A&A, 588, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Graham, J. R., Kalas, P. G., & Matthews, B. C. 2007, ApJ, 654, 595 [Google Scholar]
- Hashimoto, J., Tamura, M., Muto, T., et al. 2011, ApJ, 729, L17 [Google Scholar]
- Heikamp, S., & Keller, C. U. 2019, A&A, 627, A156 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Henyey, L. G., & Greenstein, J. L. 1941, ApJ, 93, 70 [Google Scholar]
- Hughes, A. M., Duchêne, G., & Matthews, B. C. 2018, ARA&A, 56, 541 [Google Scholar]
- Hunziker, S., Schmid, H. M., Ma, J., et al. 2021, A&A, 648, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kalas, P., & Jewitt, D. 1996, AJ, 111, 1347 [NASA ADS] [CrossRef] [Google Scholar]
- Kolokolova, L., & Kimura, H. 2010, A&A, 513, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Macintosh, B., Graham, J. R., Ingraham, P., et al. 2014, Proc. Natl. Acad. Sci., 111, 12661 [NASA ADS] [CrossRef] [Google Scholar]
- Maness, H. L., Kalas, P., Peek, K. M. G., et al. 2009, ApJ, 707, 1098 [NASA ADS] [CrossRef] [Google Scholar]
- Milli, J., Vigan, A., Mouillet, D., et al. 2017, A&A, 599, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Milli, J., Engler, N., Schmid, H. M., et al. 2019, A&A, 626, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Min, M., Rab, C., Woitke, P., Dominik, C., & Ménard, F. 2016, A&A, 585, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Monnier, J. D., Harries, T. J., Bae, J., et al. 2019, ApJ, 872, 122 [Google Scholar]
- Muto, T., Grady, C. A., Hashimoto, J., et al. 2012, ApJ, 748, L22 [Google Scholar]
- Olofsson, J., Milli, J., Bayo, A., Henning, T., & Engler, N. 2020, A&A, 640, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oppenheimer, B. R., Brenner, D., Hinkley, S., et al. 2008, ApJ, 679, 1574 [NASA ADS] [CrossRef] [Google Scholar]
- Perrin, M. D., Schneider, G., Duchene, G., et al. 2009, ApJ, 707, L132 [Google Scholar]
- Perrin, M. D., Duchene, G., Millar-Blanchaer, M., et al. 2015, ApJ, 799, 182 [Google Scholar]
- Quanz, S. P., Schmid, H. M., Geissler, K., et al. 2011, ApJ, 738, 23 [Google Scholar]
- Schmid, H. M. 2021, IAU Symp., 360, submitted [Google Scholar]
- Schmid, H. M., Joos, F., & Tschan, D. 2006, A&A, 452, 657 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schmid, H. M., Bazzon, A., Roelfsema, R., et al. 2018, A&A, 619, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, G., Weinberger, A. J., Becklin, E. E., Debes, J. H., & Smith, B. A. 2009, AJ, 137, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, G., Debes, J. H., Grady, C. A., et al. 2018, AJ, 155, 77 [Google Scholar]
- Simmons, J. F. L., & Stewart, B. G. 1985, A&A, 142, 100 [NASA ADS] [Google Scholar]
- Tazaki, R., Tanaka, H., Muto, T., Kataoka, A., & Okuzumi, S. 2019, MNRAS, 485, 4951 [NASA ADS] [CrossRef] [Google Scholar]
- Thébault, P. 2009, A&A, 505, 1269 [Google Scholar]
- Tschudi, C., & Schmid, H. M. 2021, A&A, 655, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Holstein, R. G., Girard, J. H., de Boer, J., et al. 2020, A&A, 633, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Whitney, B. A., & Hartmann, L. 1992, ApJ, 395, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Yudin, R. V., & Evans, A. 1998, A&AS, 131, 401 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Measured relative quadrant polarization parameters for HR 4796A, deviations Δ (in %) from left–right symmetry and ratios Λ for back–front flux ratios.
Integration ranges for Stokes Qd and Ud polarization quadrants for on-sky azimuthal angles ϕx,y = atan2(y, x) and disk azimuthal angles φd = atan2(yd, xd).
IDL procedure for the calculation of disk-averaged scattering functions and normalized quadrant polarization parameters.
All Figures
 |
Fig. 1 Illustration of the definition of the quadrant polarization parameters (panels e and f) for the observations of the debris disk around HR 4796A from Milli et al. (2019). Left: Azimuthal polarization Qϕ and Stokes Q and U in relative α, δ-sky coordinates. Right: Qϕ, Qd, and Ud in x, y-disk coordinates. |
| In the text | |
 |
Fig. 2 Apertures used for the measurements of the integrated azimuthal polarization |
| In the text | |
 |
Fig. 3 Scattering phase functions for the HG asymmetry parameter g = 0.2 for the total intensity 4π fI(θ) (black), for the polarized intensities 4π f⊥(θ) (dashed) and 4π f∥(θ) (dotted), for the two values pmax = 0.5 (red) and 0.2 (blue), and the corresponding scattering phase functions for the polarized flux 4π fϕ (θ) (full, colored lines). |
| In the text | |
 |
Fig. 4 I-, Qd -, Ud - and Qϕ -images for a flat disk with g = 0.3, pmax = 1, and for inclinations i = 0°, i = 45°, and 75°. The same gray scale from + a (white) to −a (black) is used for all panels. The black lines in the Qd and Ud panels indicate the polarization quadrants. |
| In the text | |
 |
Fig. 5 I-, Qd -, Ud - and Qϕ -images for flat disks with i = 45°, pmax = 1, and for scattering asymmetry parameter g = 0.0 and 0.6. The same gray scale from + a (white) to −a (black) is used for all panels. |
| In the text | |
 |
Fig. 6 Upper panel: azimuthal dependence of the disk scattering phase function for the intensity 4π fI (φd, i, g) and the normalized (pmax = 1) polarized intensity |
| In the text | |
 |
Fig. 7 Azimuthal dependence for the Stokes scattering phase functions |
| In the text | |
 |
Fig. 8 Disk-averaged scattering phase functions for the intensity 4π ⟨fI⟩, the normalized (pmax=1) azimuthal polarization |
| In the text | |
 |
Fig. 9 Upper panel: disk averages of the fractional azimuthal polarization |
| In the text | |
 |
Fig. 10 Normalized ( |
| In the text | |
 |
Fig. 11 Comparison of the 3D-ring model with the flat disk model. Left: I, Qd, Ud and Qϕ for a 3D disk ring with a full width at half maximum density distribution of ΔFWHM∕rring = 0.2. Scattering parameters are g = 0.6 and pmax = 1 for inclinations i = 0°, 45°, 75° and 90°. The same gray scale from + a (white) to −a (black) is used for all panels. The black lines in the Qd and Ud panels indicate the polarization quadrants. Right: same but for the flat disk model. |
| In the text | |
 |
Fig. 12 Relative quadrant polarization values |
| In the text | |
 |
Fig. 13 Quadrant polarization ratios for flat disk models for |Q000|∕|Q180|, |U045 |∕|U135|, |Q090 |∕|Q180|, and |Q090|∕|Q135| with measured values from HR 4796A (similar to Fig. 12). |
| In the text | |
 |
Fig. 14 Angular distribution of the polarized intensity in the polarization quadrants for i = 15°, 30°, 45°, 60° and 75° and differentasymmetry parameter g (colors). For quadrants Q000 and Q180 only the caseg = 0 is shown, because differences for other g-parameters are very small. The distributions are normalized for each quadrant individually. For the quadrants Q000, U045, and U135, the median angles θmed (diamonds) for large g-values increase with inclination as illustrated with the dotted lines. |
| In the text | |
 |
Fig. 15 Scattering asymmetry parameters for HR 4796A derived from relative quadrant parameters (open symbols) and quadrant ratios (filled symbols) as a function of the θmed or the mean of θmed, respectively.Colors indicate measurements from the left or SW (blue) and the right or NE (red) disk sides. |
| In the text | |
 |
Fig. 16 (a) Comparison of the best single parameter HGpol fit model for fixed i = 75° and measured relative quadrant polarization parameters for HR 4796A. (b) Deviations from the best-fitting HGpol (i = 75°, g = 0.65) for the measured values, for the best fits for slightly different disk inclinations HGpol (i = 73°, g = 0.60) and HGpol(i = 77°, g = 0.71) and for the HGpol fit from Milli et al. (2019) (green dashed line). (c) HGpol phase functions and the directly extracted phase function fϕ(θ) (dotted black line) with corresponding uncertainty range (grey shaded area) from Milli et al. (2019). (d) HG intensity phase functions. The measured quadrant values and the different fit curves are identified in panel b. |
| In the text | |
 |
Fig. 17 Same as Fig. 16 but for the best-fitting double HGpol scattering phase function |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.